Вероятность безотказной работы это: Как вычисляется среднее время до отказа и вероятность безотказной работы?

Содержание

Вероятность безотказной работы — это… Что такое Вероятность безотказной работы?

Вероятность безотказной работы: показатель надёжности (См. Надёжность) устройства, схемы или отдельного элемента, который оценивает возможность сохранения изделием работоспособности (См. Работоспособность) в определённом интервале времени или при выполнении заданного объёма работы.

Вероятность
Вероятность перехода

Смотреть что такое «Вероятность безотказной работы» в других словарях:

Вероятность безотказной работы — вероятность того, что в пределах заданной наработки не возникает отказ изделия (объекта). Источник: НП 068 05: Трубопроводная арматура для атомных станций. Общие технические требования 3.1.9 вероятность безотказной работы: Вероятность того, что в … Словарь-справочник терминов нормативно-технической документации
Вероятность безотказной работы — Вероятность безотказной работы это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы обратна вероятности отказа и вместе с интенсивностью отказов… … Википедия
вероятность безотказной работы — Вероятность того, что в пределах заданной наработки отказ объекта не возникнет. [ГОСТ 27.002 89] [ОАО РАО «ЕЭС России» СТО 17330282.27.010.001 2008] Тематики надежность, основные понятия EN reliability functionsurvival function … Справочник технического переводчика
вероятность безотказной работы R ( t ₁ , t ₂ ) — 89 вероятность безотказной работы R ( t 1 , t 2 ): Вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Источник: ГОСТ Р 53480 2009: Надежность в технике. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы R(t₁, t₂) — 89 вероятность безотказной работы R(t1, t2): Вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Примечания 1 Обычно предполагают, что в начале интервала времени изделие находится в работоспособном состоянии … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы — negendamumo tikimybė statusas T sritis Standartizacija ir metrologija apibrėžtis Tikimybė, kad per numatytą išdirbį objektas nesuges. atitikmenys: angl. reliability probability rus. вероятность безотказной работы, f pranc. probabilité de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Вероятность безотказной работы — – вероятность того, что в пределах заданной наработки отказ объекта не возникнет. ГОСТ 27.002 89 … Коммерческая электроэнергетика. Словарь-справочник
вероятность безотказной работы — вероятность того, что в пределах заданной наработки отказ не возникнет … Политехнический терминологический толковый словарь
Вероятность безотказной работы — English: Reliability function Вероятность того, что в пределах заданной наработки отказ объекта не возникнет (по ГОСТ 27.002 89) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
Вероятность безотказной работы системы — [Р] способность системы не допускать отказов, приводящих к падению температуры в отапливаемых помещениях жилых и общественных зданий ниже +12 °С, в промышленных зданиях ниже +8 °С, более числа раз, установленного нормативами. Источник: СНиП 41 02 … Словарь-справочник терминов нормативно-технической документации

Вероятность безотказной работы — Википедия

Материал из Википедии — свободной энциклопедии

Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы обратна вероятности отказа и вместе с интенсивностью отказов определяет безотказность объекта. Показатель вероятности безотказной работы определяется статистической оценкой: P ( t ) = N 0 − n ( t ) N 0 = 1 − n ( t ) N 0 {\displaystyle P(t)={\frac {N_{0}-n(t)}{N_{0}}}=1-{\frac {n(t)}{N_{0}}}} где N 0 {\displaystyle N_{0}} — исходное число работоспособных объектов,

n ( t ) {\displaystyle n(t)} — число отказавших объектов за время t {\displaystyle t} .

Вероятность безотказной работы группы объектов равна произведению вероятностей безотказной работы каждого объекта в этой группе: P ( t ) = P 1 ( t ) ⋅ P 2 ( t ) ⋅ . . . ⋅ P n ( t ) = ∏ k = 1 n P k ( t ) {\displaystyle P(t)=P_{1}(t)\cdot P_{2}(t)\cdot …\cdot P_{n}(t)=\prod _{k=1}^{n}P_{k}(t)} где n — число объектов в группе.

Чем больше объектов в группе, тем ниже надежность всей группы, так как если P 1 ( t ) = P 2 ( t ) = . . . = P n ( t ) {\displaystyle P_{1}(t)=P_{2}(t)=…=P_{n}(t)} , то тогда P ( t ) = [ P 1 ( t ) ] n {\displaystyle P(t)=[P_{1}(t)]^{n}} .

Среднее время безотказной работы системы

Среднее время безотказной работы (средняя наработка на отказ) T 0 {\displaystyle T_{0}} — для невосстанавливаемых (неремонтируемых) систем — это математическое ожидание времени работы системы до отказа:

T 0 = M = ∫ 0 1 t ⋅ f ( t ) d t = − ∫ 0 1 t d P ( t ) {\displaystyle T_{0}=M=\int \limits _{0}^{\mathcal {1}}t\cdot f(t)dt=-\int \limits _{0}^{\mathcal {1}}tdP(t)}

Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным; f ( t ) {\displaystyle f(t)} — есть плотность вероятности возникновения отказов системы или её невосстанавливаемого элемента. P ( T ) {\displaystyle P(T)} — есть вероятность безотказной работы в интервале времени 0 < t < T {\displaystyle 0<t<T} . В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P ( T ) {\displaystyle P(T)} равна нулю. Вероятность P ( T ) {\displaystyle P(T)} связана с плотностью вероятности возникновения отказов системы или её невосстанавливаемого элемента следующим образом:

f ( t ) = − d P ( t ) d t {\displaystyle f(t)=-{\frac {dP(t)}{dt}}} .

Проинтегрировав выражение для T 0 {\displaystyle T_{0}} по частям, получим:

T 0 = ∫ 0 1 P ( t ) d t {\displaystyle T_{0}=\int \limits _{0}^{\mathcal {1}}P(t)dt}

Графически полученное выражение для T 0 {\displaystyle T_{0}} представлено на рисунке как площадь под графиком вероятности безотказной работы Р(T) от времени T. В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P(T) равна нулю.

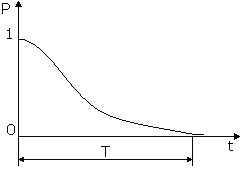
Здесь T ≥ 0 {\displaystyle T\geq 0} — случайное время работы системы до отказа или наработка на отказ для невосстанавливаемого элемента или системы.

Типичные распределения времени безотказной работы

Основной источник: ^[1]

Экспоненциальное распределение: f ( t ) = λ e − λ t {\displaystyle f(t)=\lambda e^{-\lambda t}} , λ > 0 {\displaystyle \lambda >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Гамма-распределение: f ( t ) = λ ( λ t ) α − 1 e − λ t Γ ( α ) {\displaystyle f(t)={\frac {\lambda (\lambda t)^{\alpha -1}e^{-\lambda t}}{\Gamma (\alpha )}}} , λ , α > 0 {\displaystyle \lambda ,\alpha >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Распределение Вейбулла: f ( t ) = λ α t α − 1 e − λ t α {\displaystyle f(t)=\lambda \alpha t^{\alpha -1}e^{-\lambda t^{\alpha }}} , λ , α > 0 {\displaystyle \lambda ,\alpha >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Модифицированное распределение экстремального значения: f ( t ) = 1 λ exp ⁡ [ − e t − 1 λ + t ] {\displaystyle f(t)={\frac {1}{\lambda }}\exp {\left[-{\frac {e^{t}-1}{\lambda }}+t\right]}} , λ > 0 {\displaystyle \lambda >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Усечённое нормальное распределение: f ( t ) = 1 a σ 2 π exp ⁡ [ − ( t − μ ) 2 2 σ 2 ] {\displaystyle f(t)={\frac {1}{a\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right]}} , σ > 0 {\displaystyle \sigma >0} , − ∞ < μ < ∞ {\displaystyle -\infty <\mu <\infty } , 0 < t < ∞ {\displaystyle 0<t<\infty } .
Логарифмически-нормальное распределение: f ( t ) = 1 t σ 2 π exp ⁡ [ − ( lg ⁡ t − μ ) 2 2 σ 2 ] {\displaystyle f(t)={\frac {1}{t\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(\lg {t}-\mu )^{2}}{2\sigma ^{2}}}\right]}} , σ > 0 {\displaystyle \sigma >0} , − ∞ < μ < ∞ {\displaystyle -\infty <\mu <\infty } , t ⩾ 0 {\displaystyle t\geqslant 0} .

Примечания

↑ Барлоу Р., Прошан Ф. Математическая теория надежности. -М.: Советское радио, 1969.- С. 29-30

Литература

Леликов О. П. Тема 2. Основные понятия и показатели надежности // Основы расчета и проектирования деталей и узлов машин. Конспект лекций по курсу «Детали машин». — М.: Машиностроение, 2002. — С. 8-9. — 440 с. — 2000 экз. — ISBN 5-217-03077-1.

См. также

Вероятность безотказной работы — Википедия. Что такое Вероятность безотказной работы

Материал из Википедии — свободной энциклопедии
Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы обратна вероятности отказа и вместе с интенсивностью отказов определяет безотказность объекта. Показатель вероятности безотказной работы определяется статистической оценкой: P ( t ) = N 0 − n ( t ) N 0 = 1 − n ( t ) N 0 {\displaystyle P(t)={\frac {N_{0}-n(t)}{N_{0}}}=1-{\frac {n(t)}{N_{0}}}} где N 0 {\displaystyle N_{0}} — исходное число работоспособных объектов,
n ( t ) {\displaystyle n(t)} — число отказавших объектов за время t {\displaystyle t} .
Вероятность безотказной работы группы объектов равна произведению вероятностей безотказной работы каждого объекта в этой группе: P ( t ) = P 1 ( t ) ⋅ P 2 ( t ) ⋅ . . . ⋅ P n ( t ) = ∏ k = 1 n P k ( t ) {\displaystyle P(t)=P_{1}(t)\cdot P_{2}(t)\cdot …\cdot P_{n}(t)=\prod _{k=1}^{n}P_{k}(t)} где n — число объектов в группе.
Чем больше объектов в группе, тем ниже надежность всей группы, так как если P 1 ( t ) = P 2 ( t ) = . . . = P n ( t ) {\displaystyle P_{1}(t)=P_{2}(t)=…=P_{n}(t)} , то тогда P ( t ) = [ P 1 ( t ) ] n {\displaystyle P(t)=[P_{1}(t)]^{n}} .
Среднее время безотказной работы системы
Среднее время безотказной работы (средняя наработка на отказ) T 0 {\displaystyle T_{0}} — для невосстанавливаемых (неремонтируемых) систем — это математическое ожидание времени работы системы до отказа:
T 0 = M = ∫ 0 1 t ⋅ f ( t ) d t = − ∫ 0 1 t d P ( t ) {\displaystyle T_{0}=M=\int \limits _{0}^{\mathcal {1}}t\cdot f(t)dt=-\int \limits _{0}^{\mathcal {1}}tdP(t)}
Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным; f ( t ) {\displaystyle f(t)} — есть плотность вероятности возникновения отказов системы или её невосстанавливаемого элемента. P ( T ) {\displaystyle P(T)} — есть вероятность безотказной работы в интервале времени 0 < t < T {\displaystyle 0<t<T} . В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P ( T ) {\displaystyle P(T)} равна нулю. Вероятность P ( T ) {\displaystyle P(T)} связана с плотностью вероятности возникновения отказов системы или её невосстанавливаемого элемента следующим образом:
f ( t ) = − d P ( t ) d t {\displaystyle f(t)=-{\frac {dP(t)}{dt}}} .
Проинтегрировав выражение для T 0 {\displaystyle T_{0}} по частям, получим:
T 0 = ∫ 0 1 P ( t ) d t {\displaystyle T_{0}=\int \limits _{0}^{\mathcal {1}}P(t)dt}
Графически полученное выражение для T 0 {\displaystyle T_{0}} представлено на рисунке как площадь под графиком вероятности безотказной работы Р(T) от времени T. В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P(T) равна нулю.
Здесь T ≥ 0 {\displaystyle T\geq 0} — случайное время работы системы до отказа или наработка на отказ для невосстанавливаемого элемента или системы.
Типичные распределения времени безотказной работы
Основной источник: ^[1]
Экспоненциальное распределение: f ( t ) = λ e − λ t {\displaystyle f(t)=\lambda e^{-\lambda t}} , λ > 0 {\displaystyle \lambda >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Гамма-распределение: f ( t ) = λ ( λ t ) α − 1 e − λ t Γ ( α ) {\displaystyle f(t)={\frac {\lambda (\lambda t)^{\alpha -1}e^{-\lambda t}}{\Gamma (\alpha )}}} , λ , α > 0 {\displaystyle \lambda ,\alpha >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Распределение Вейбулла: f ( t ) = λ α t α − 1 e − λ t α {\displaystyle f(t)=\lambda \alpha t^{\alpha -1}e^{-\lambda t^{\alpha }}} , λ , α > 0 {\displaystyle \lambda ,\alpha >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Модифицированное распределение экстремального значения: f ( t ) = 1 λ exp ⁡ [ − e t − 1 λ + t ] {\displaystyle f(t)={\frac {1}{\lambda }}\exp {\left[-{\frac {e^{t}-1}{\lambda }}+t\right]}} , λ > 0 {\displaystyle \lambda >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Усечённое нормальное распределение: f ( t ) = 1 a σ 2 π exp ⁡ [ − ( t − μ ) 2 2 σ 2 ] {\displaystyle f(t)={\frac {1}{a\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right]}} , σ > 0 {\displaystyle \sigma >0} , − ∞ < μ < ∞ {\displaystyle -\infty <\mu <\infty } , 0 < t < ∞ {\displaystyle 0<t<\infty } .
Логарифмически-нормальное распределение: f ( t ) = 1 t σ 2 π exp ⁡ [ − ( lg ⁡ t − μ ) 2 2 σ 2 ] {\displaystyle f(t)={\frac {1}{t\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(\lg {t}-\mu )^{2}}{2\sigma ^{2}}}\right]}} , σ > 0 {\displaystyle \sigma >0} , − ∞ < μ < ∞ {\displaystyle -\infty <\mu <\infty } , t ⩾ 0 {\displaystyle t\geqslant 0} .
Примечания
↑ Барлоу Р., Прошан Ф. Математическая теория надежности. -М.: Советское радио, 1969.- С. 29-30
Литература
Леликов О. П. Тема 2. Основные понятия и показатели надежности // Основы расчета и проектирования деталей и узлов машин. Конспект лекций по курсу «Детали машин». — М.: Машиностроение, 2002. — С. 8-9. — 440 с. — 2000 экз. — ISBN 5-217-03077-1.
См. также
Вероятность безотказной работы — Википедия
Материал из Википедии — свободной энциклопедии
Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы обратна вероятности отказа и вместе с интенсивностью отказов определяет безотказность объекта. Показатель вероятности безотказной работы определяется статистической оценкой: P ( t ) = N 0 − n ( t ) N 0 = 1 − n ( t ) N 0 {\displaystyle P(t)={\frac {N_{0}-n(t)}{N_{0}}}=1-{\frac {n(t)}{N_{0}}}} где N 0 {\displaystyle N_{0}} — исходное число работоспособных объектов,
n ( t ) {\displaystyle n(t)} — число отказавших объектов за время t {\displaystyle t} .
Вероятность безотказной работы группы объектов равна произведению вероятностей безотказной работы каждого объекта в этой группе: P ( t ) = P 1 ( t ) ⋅ P 2 ( t ) ⋅ . . . ⋅ P n ( t ) = ∏ k = 1 n P k ( t ) {\displaystyle P(t)=P_{1}(t)\cdot P_{2}(t)\cdot …\cdot P_{n}(t)=\prod _{k=1}^{n}P_{k}(t)} где n — число объектов в группе.
Чем больше объектов в группе, тем ниже надежность всей группы, так как если P 1 ( t ) = P 2 ( t ) = . . . = P n ( t ) {\displaystyle P_{1}(t)=P_{2}(t)=…=P_{n}(t)} , то тогда P ( t ) = [ P 1 ( t ) ] n {\displaystyle P(t)=[P_{1}(t)]^{n}} .
Среднее время безотказной работы системы
Среднее время безотказной работы (средняя наработка на отказ) T 0 {\displaystyle T_{0}} — для невосстанавливаемых (неремонтируемых) систем — это математическое ожидание времени работы системы до отказа:
T 0 = M = ∫ 0 1 t ⋅ f ( t ) d t = − ∫ 0 1 t d P ( t ) {\displaystyle T_{0}=M=\int \limits _{0}^{\mathcal {1}}t\cdot f(t)dt=-\int \limits _{0}^{\mathcal {1}}tdP(t)}
Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным; f ( t ) {\displaystyle f(t)} — есть плотность вероятности возникновения отказов системы или её невосстанавливаемого элемента. P ( T ) {\displaystyle P(T)} — есть вероятность безотказной работы в интервале времени 0 < t < T {\displaystyle 0<t<T} . В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P ( T ) {\displaystyle P(T)} равна нулю. Вероятность P ( T ) {\displaystyle P(T)} связана с плотностью вероятности возникновения отказов системы или её невосстанавливаемого элемента следующим образом:
f ( t ) = − d P ( t ) d t {\displaystyle f(t)=-{\frac {dP(t)}{dt}}} .
Проинтегрировав выражение для T 0 {\displaystyle T_{0}} по частям, получим:
T 0 = ∫ 0 1 P ( t ) d t {\displaystyle T_{0}=\int \limits _{0}^{\mathcal {1}}P(t)dt}
Графически полученное выражение для T 0 {\displaystyle T_{0}} представлено на рисунке как площадь под графиком вероятности безотказной работы Р(T) от времени T. В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P(T) равна нулю.
Здесь T ≥ 0 {\displaystyle T\geq 0} — случайное время работы системы до отказа или наработка на отказ для невосстанавливаемого элемента или системы.
Типичные распределения времени безотказной работы
Основной источник: ^[1]
Экспоненциальное распределение: f ( t ) = λ e − λ t {\displaystyle f(t)=\lambda e^{-\lambda t}} , λ > 0 {\displaystyle \lambda >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Гамма-распределение: f ( t ) = λ ( λ t ) α − 1 e − λ t Γ ( α ) {\displaystyle f(t)={\frac {\lambda (\lambda t)^{\alpha -1}e^{-\lambda t}}{\Gamma (\alpha )}}} , λ , α > 0 {\displaystyle \lambda ,\alpha >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Распределение Вейбулла: f ( t ) = λ α t α − 1 e − λ t α {\displaystyle f(t)=\lambda \alpha t^{\alpha -1}e^{-\lambda t^{\alpha }}} , λ , α > 0 {\displaystyle \lambda ,\alpha >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Модифицированное распределение экстремального значения: f ( t ) = 1 λ exp ⁡ [ − e t − 1 λ + t ] {\displaystyle f(t)={\frac {1}{\lambda }}\exp {\left[-{\frac {e^{t}-1}{\lambda }}+t\right]}} , λ > 0 {\displaystyle \lambda >0} , t ⩾ 0 {\displaystyle t\geqslant 0} .
Усечённое нормальное распределение: f ( t ) = 1 a σ 2 π exp ⁡ [ − ( t − μ ) 2 2 σ 2 ] {\displaystyle f(t)={\frac {1}{a\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right]}} , σ > 0 {\displaystyle \sigma >0} , − ∞ < μ < ∞ {\displaystyle -\infty <\mu <\infty } , 0 < t < ∞ {\displaystyle 0<t<\infty } .
Логарифмически-нормальное распределение: f ( t ) = 1 t σ 2 π exp ⁡ [ − ( lg ⁡ t − μ ) 2 2 σ 2 ] {\displaystyle f(t)={\frac {1}{t\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(\lg {t}-\mu )^{2}}{2\sigma ^{2}}}\right]}} , σ > 0 {\displaystyle \sigma >0} , − ∞ < μ < ∞ {\displaystyle -\infty <\mu <\infty } , t ⩾ 0 {\displaystyle t\geqslant 0} .
Примечания
↑ Барлоу Р., Прошан Ф. Математическая теория надежности. -М.: Советское радио, 1969.- С. 29-30
Литература
Леликов О. П. Тема 2. Основные понятия и показатели надежности // Основы расчета и проектирования деталей и узлов машин. Конспект лекций по курсу «Детали машин». — М.: Машиностроение, 2002. — С. 8-9. — 440 с. — 2000 экз. — ISBN 5-217-03077-1.
См. также

Вероятность безотказной работы — это… Что такое Вероятность безотказной работы?
Вероятность безотказной работы — вероятность того, что в пределах заданной наработки не возникает отказ изделия (объекта). Источник: НП 068 05: Трубопроводная арматура для атомных станций. Общие технические требования 3.1.9 вероятность безотказной работы: Вероятность того, что в … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы — Вероятность того, что в пределах заданной наработки отказ объекта не возникнет. [ГОСТ 27.002 89] [ОАО РАО «ЕЭС России» СТО 17330282.27.010.001 2008] Тематики надежность, основные понятия EN reliability functionsurvival function … Справочник технического переводчика
вероятность безотказной работы R ( t ₁ , t ₂ ) — 89 вероятность безотказной работы R ( t 1 , t 2 ): Вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Источник: ГОСТ Р 53480 2009: Надежность в технике. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы R(t₁, t₂) — 89 вероятность безотказной работы R(t1, t2): Вероятность выполнить требуемую функцию при данных условиях в интервале времени (t1, t2). Примечания 1 Обычно предполагают, что в начале интервала времени изделие находится в работоспособном состоянии … Словарь-справочник терминов нормативно-технической документации
вероятность безотказной работы — negendamumo tikimybė statusas T sritis Standartizacija ir metrologija apibrėžtis Tikimybė, kad per numatytą išdirbį objektas nesuges. atitikmenys: angl. reliability probability rus. вероятность безотказной работы, f pranc. probabilité de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Вероятность безотказной работы — – вероятность того, что в пределах заданной наработки отказ объекта не возникнет. ГОСТ 27.002 89 … Коммерческая электроэнергетика. Словарь-справочник
вероятность безотказной работы — вероятность того, что в пределах заданной наработки отказ не возникнет … Политехнический терминологический толковый словарь
Вероятность безотказной работы — English: Reliability function Вероятность того, что в пределах заданной наработки отказ объекта не возникнет (по ГОСТ 27.002 89) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
Вероятность безотказной работы —         показатель надёжности (См. Надёжность) устройства, схемы или отдельного элемента, который оценивает возможность сохранения изделием работоспособности (См. Работоспособность) в определённом интервале времени или при выполнении заданного… … Большая советская энциклопедия
Вероятность безотказной работы системы — [Р] способность системы не допускать отказов, приводящих к падению температуры в отапливаемых помещениях жилых и общественных зданий ниже +12 °С, в промышленных зданиях ниже +8 °С, более числа раз, установленного нормативами. Источник: СНиП 41 02 … Словарь-справочник терминов нормативно-технической документации
Диагностика и надежность в технике
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение

1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
где N₀ – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N₀, тем с большей точностью можно рассчитать вероятность P(l).
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю
P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки

Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.

1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.

Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):

В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки

1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как  и определяется по формуле (1.3):
где –  количество отказавших элементов за промежуток пробега .
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.

Рис. 1.3. График изменения частоты отказов в зависимости от наработки

1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как  и определяется по формуле (1.4):

где
Как правило, интенсивность отказов является неубывающей функцией времени. Интенсивность отказов обычно применяется для оценки склонности к отказам в различные моменты работы объектов.
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.

1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L₁
и определяется по формуле (1.5):

где l_i – наработка до отказа элемента; r_i – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.

1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как W_ср и определяется по формуле (1.6):

1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
Исходные данные к расчету
, тыс. км 0 — 100 100 — 200 200 — 300 300 — 400 400 — 500 500 — 600
2 12 16 10 14 6
2 14 30 40 54 60
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
Произведем расчет частоты отказов по уравнению (1.3).
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
Результаты расчета показателей безотказности
, тыс.км. 0 — 100 100 — 200 200 — 300 300 — 400 400 — 500 500 — 600
2 12 16 10 14 6
2 14 30 40 54 60
P(l) 0,989 0,922 0,833 0,778 0,7 0,667
Q(l) 0,011 0,078 0,167 0,222 0,3 0,333
10^-7, 1/км 1,111 6,667 8,889 5,556 7,778 3,333
10^-7, 1/км 1,117 6,977 10,127 6,897 10,526 4,878
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
Рис. 1.7. График изменения частоты отказов в зависимости от наработки

На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки

2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.

Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.

Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
Затем рассчитываем величину интенсивности отказов:
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:

2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.

Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:

2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).

Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.

3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1

Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:

Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
Результаты расчета вероятности безотказной работы и частоты отказов системы на интервале времени от 0 до 1000 ч.
l, час P(l) a(l), час^-1
0 1 0,00026
100 0,974355 0,000253
200 0,949329 0,000247
300 0,924964 0,00024
400 0,901225 0,000234
500 0,878095 0,000228
600 0,855559 0,000222
700 0,833601 0,000217
800 0,812207 0,000211
900 0,791362 0,000206
1000 0,771052 0,0002

Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
Рис. 3.1. Вероятность безотказной работы системы.
Рис. 3.2. Частота отказов системы.

3.2 Резервное соединение элементов
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
Рис. 3.3. Схема системы с общим резервированием.
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:

Вероятность безотказной работы системы при поэлементном резервировании составит:
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).

Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
Рис. 3.6. Сблокированная схема.
Надежность системы без резервирования составит:
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Лекция по основам надежности «Вероятность отказа и вероятность безотказной работы»
Занятие № 5
Тема: Вероятность безотказной работы и вероятность отказа.
Цель:
Основные понятия:
Показатели надежности
Вероятность безотказной работы
Вероятность отказа
План занятия:
Организационный момент: приветствие, проверяется готовность к занятию, отмечаются в журнале отсутствующие.
Проверка домашнего задания: фронтальный опрос.
Актуализация знаний: сообщение темы и цели занятия.
Изучение нового материала:
Показатели надежности.
Вероятность безотказной работы.
Вероятность отказа.
Оценка вероятности безотказной работы.
Закрепление изученного материала:
Что называют вероятностью безотказной работы?
Что называют вероятностью отказа?
Дайте определение понятия показатели надежности.
Домашнее задание: Яхъяев Н.Я. Основы теории надежности, стр. 39-41;
Задача:
На испытание поставлено 1000 однотипных резисторов. За первые 10000 часов отказало 5, за последующие 5000 отказало еще 5. Определить вероятность безотказной работы и вероятность отказа за 10000 часов, за 15000 часов и в промежутке между 10000 и 15000 часов.
Подведение итогов занятия.
— Какое состояние называется работоспособным? (Работоспособность – это состояние изделия, при котором оно способно выполнять заданную функцию с параметрами, установленными требованиями технической документации, в течение расчётного срока службы).
Отказ – это нарушение работоспособности. Свойство элемента или системы непрерывно сохранять работоспособность при определённых условиях эксплуатации (до первого отказа) называется безотказностью.
Безотказность – свойство объекта сохранять работоспособное состояние в течение некоторого времени или наработки.
И сегодня на занятии мы рассмотрим показатели безотказности. Тема нашего занятия: «ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ И ВЕРОЯТНОСТЬ ОТКАЗА».
ПОКАЗАТЕЛИ НАДЕЖНОСТИ.
Показатели надежности – количественная характеристика одного или нескольких свойств, составляющих надежность объекта.
Для оценки, расчетов и исследования надежности технических устройств в процессе их проектирования и эксплуатации используются количественные характеристики (критерии надежности). Для показателей надежности используются две формы представления:
Статистическая – при эксперементальном исследовании надежности технических систем
Вероятностная – при априорных аналитических расчетах надежности.
В соответствии с ГОСТ 27.002 – 89 показатели надежности подразделяются на:
Классификация показателей надежности
Признак
Показатель
Число характерезуемых свойств надежности
Единичный показатель надежности – показатель, характеризующий одно из свойств, составляющих надежность объекта. (Например, вероятность отказа, средний срок службы и т.п.).
Комплексный показатель надежности – показатель, характеризующий одновременно несколько свойств, составляющих надежность объекта. (Например, коэффициент готовности, удельная суммарная трудоемкость ремонтов и т.п.).
Свойство надежности
Безотказность
Долговечность
Сохраняемость
Ремонтопригодность
Метод получения
Расчетный показатель надежности – показатель, значения которого определяют расчетным методом.
Экспериментальный показатель надежности – показатель, точечную или интервальную оценку которого определяют по данным испытания.
Эксплуатационный показатель надежности – показатель, точечную или интервальную оценку которого определяют по данным эксплуатации.
Экстраполированный показатель надежности – показатель, точечную или интервальную оценку которого определяют на основании результатов расчетов, испытаний и (или) эксплуатационных данных путем экстраполирования на другую продолжительность эксплуатации и другие условия эксплуатации.
Область использования
Нормативный показатель, регламентированный в НТД
Оценочный показатель, используемый для различных сравнительных оценок при научно-исследовательских и проектно-технологических разработках
Область распространения
Групповой показатель надежности – служит для оценки надежности совокупности изделий данного типа.
Индивидуальный показатель надежности – предназначен для оценки надежности каждого изделия данного типа.
ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ.
Пусть испытывается некоторое число изделий N₀. По разным причинам они будут выходить из строя, причем моменты отказов, т.е. время наработки каждого изделия до отказов, является случайной величиной.
Вероятность безотказной работы изделия есть вероятность того, что за определенный рассматриваемый период времени работы (t) в заданных условиях эксплуатации оно не откажет, т.е. вероятность того, что время наработки до отказа (t_отк) будет больше времени работы.
Р(t) = Вер (t_отк> t)
Если к моменту t из поставленных на испытания N0 изделий останутся исправными N(t), то статистическая вероятность безотказной работы изделия за время t, равно: , где N(t) – число работоспособных изделий на момент t; N₀ – общее число наблюдаемых изделий; n(t) – число изделий, отказавших на момент t от начала испытаний.
При t = 0 все изделия исправны N(0) = N₀ и P(0) = 1. Отказы изделия с течением времени t приводят к монотонному убыванию функции Р(t). Практически для каждого типа изделия существует наработка t, больше которой ни одно изделие данного типа проработать не может.
N(t) = 0, при t ≥ tсоответственно Р(t) = 0, при t ≥ t*
Таким образом, 0 ≤ P(t) ≤ 1.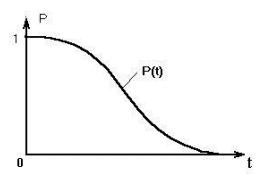
Вероятность безотказной работы уменьшается с увеличением времени работы или наработки объекта. Зависимость вероятности безотказной работы от времени характеризуется кривой убыли ресурса изделия, пример которой приведен на рисунке 1.
Рис. 1
В начальный момент времени для работоспособного изделия вероятность его безотказной работы равна единице (100%). По мере работы объекта эта вероятность снижается и стремится к нулю.
Например: После 500 часов наработки из 56 агрегатов, поставленных на эксплуатацию, в работоспособном состоянии оказалось 43 агрегата. Определить вероятность безотказной работы агрегата в течение 500 час.
Решение:
Используем формулу для определения вероятности безотказной работы объекта
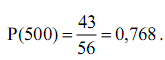
Вероятность безотказной работы агрегата в течение 500 часов составляет 76,8 %.
ВЕРОЯТНОСТЬ ОТКАЗА.
Противоположным событию безотказной работы является событие отказа
Вероятность отказа есть вероятность того, что время появления отказа будет меньше заданного времени работы изделия, т.е. вероятность того, что время наработки до отказа (t_отк) будет меньше времени работы (t).
Q(t) = Вер (t_отк< t)
Статистическая вероятность времени появления отказа равна: .
С течением времени наработки число отказавших изделий непрерывно увеличивается. Следовательно, вероятность отказов является монотонно возрастающей функцией.
Рис.2
Пример зависимости вероятности возникновения отказа от времени показан на рисунке 2. Для работоспособного объекта в начальный момент времени вероятность отказа близка к нулю. Для того, чтобы отказ проявился, объекту необходимо начать работать, при этом вероятность отказа увеличивается с увеличением времени и стремится к единице. 0≤Q(t)≤1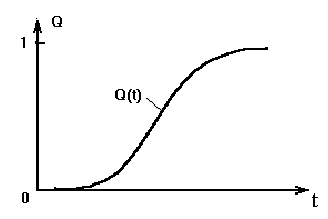
Безотказная работа изделия и его отказ являются двумя противоположными и несовместимыми случайными величинами, поэтому их сумма всегда равна 1.
P(t)+Q(t)=1⟹P(t)=1-Q(t) или Q(t)=1-P(t).
Например: Для предыдущего примера определить вероятность отказа агрегатов за 500 часов работы.
Решение:
Используем формулу для вероятности отказа
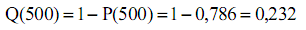или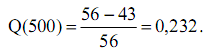
Таким образом, вероятность отказа агрегата за 500 часов составляет 23,2 %.
ОЦЕНКА ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ.

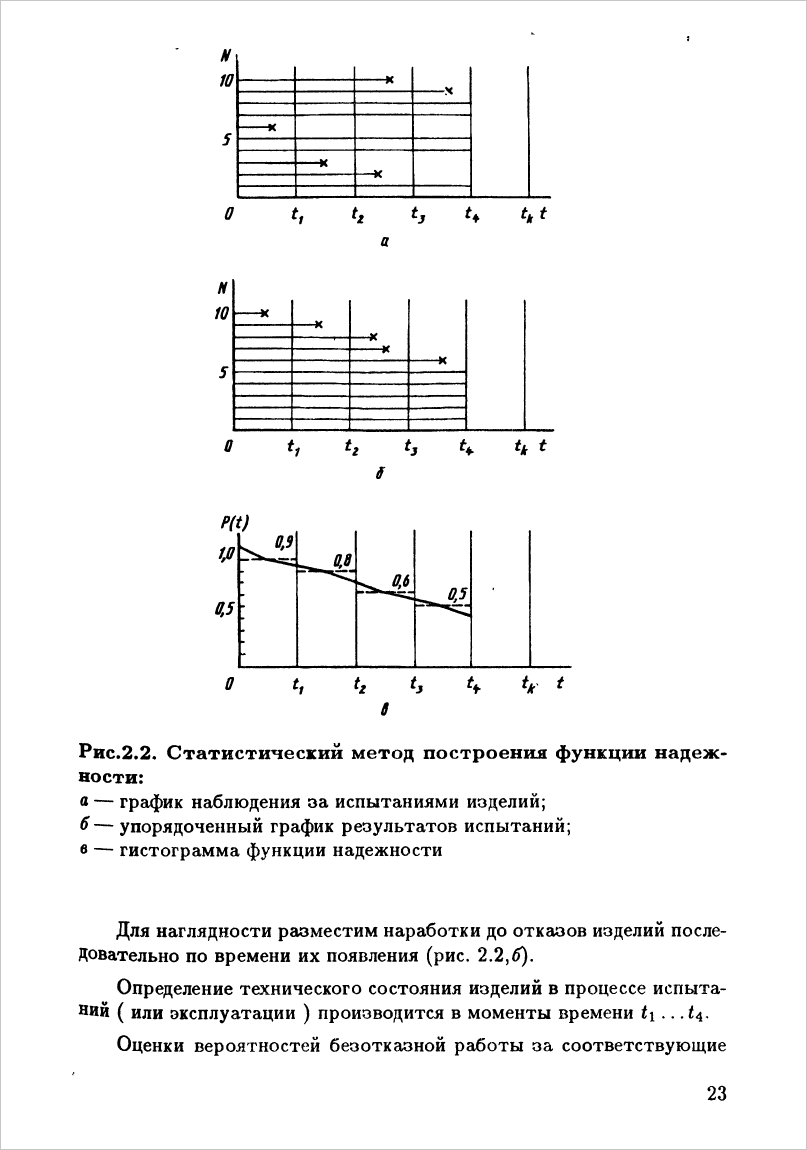
Рассмотрим график наблюдения за десятью однотипными изделиями в течение времени от 0 до t₄. Здесь сплошной прямой линией показана продолжительность безотказной работы изделия, а крестиком – момент возникновения отказа.
Для наглядности разместим наработки до отказов изделий последовательно по времени их появления.
Определение технического состояния изделий в процессе испытаний производится в моменты времени t₁… t₄. Оценки вероятностей безотказной работы за соответствующие интервалы времени будут иметь вид:
По полученным данным строится ступенчатый график – гистограмма, в конце каждого интервала времени наблюдаемое значение вероятности в данном случае снижается на долю изделий, отказавших на данном интервале.
Полученные значения показывают приблизительно долю изделий, которые проработают безотказно при испытаниях другой партии таких же изделий в аналогичных условиях.
Например: Изготовив 20 новых изделий, можно утверждать, что в течение времени t₃ приблизительно 12 изделий проработают безотказно (не проводя дополнительных испытаний) 200,6=12. Это приближенная оценка будет тем точнее, чем больше число испытанных изделий.
В качестве показателя надежности может использоваться условная вероятность безотказной работы на некотором интервале времени, которая вычисляется при условии, что изделие было полностью исправно к началу этого времени.
Например: Условная вероятность безотказной работы изделия на интервале времени от t₂ до t₃ оценивается согласно выражению:
Распределение вероятностей
Распределение вероятностей — это таблица или уравнение, связывающее каждый результат. статистического эксперимента с вероятностью его появления.
Предпосылки распределения вероятностей
Чтобы понять распределения вероятностей, важно понимать переменные. случайные величины и некоторые обозначения.
Обычно статистики используют заглавную букву для обозначения случайной величины и строчная буква, представляющая одно из его значений.Например,
P (X = x) относится к вероятности того, что случайная величина X равна конкретное значение, обозначаемое x. Например, P (X = 1) относится к вероятность того, что случайная величина X равна 1.
Вероятностные распределения
Пример проясняет связь между случайными величинами и распределения вероятностей.Предположим, вы подбрасываете монету два раза. Это просто Статистический эксперимент может иметь четыре возможных результата: HH, HT, TH и TT. Теперь пусть переменная X представляет количество голов, полученных в результате этого эксперимент. Переменная X может принимать значения 0, 1 или 2. В этом примере X — случайная величина; потому что его ценность определяется результатом статистический эксперимент.
Распределение вероятностей — это таблица или уравнение, связывающее каждый результат статистического эксперимента с его вероятностью наступления.Рассмотрим описанный выше эксперимент с подбрасыванием монеты. Таблица ниже, которая связывает каждый исход с его вероятностью, является примером вероятности распространение.
Количество голов Вероятность
0 0,25
1 0.50
2 0,25
В приведенной выше таблице представлено распределение вероятностей случайной величины. ИКС.
Кумулятивные распределения вероятностей
Кумулятивная вероятность относится к вероятности того, что значение случайной величины попадает в указанный диапазон.
Вернемся к эксперименту с подбрасыванием монеты. Если мы подбросим монету два раза, мы можем спросите: какова вероятность того, что подбрасывание монеты приведет к одному или нескольким головы? Ответом будет кумулятивная вероятность. Было бы вероятность того, что эксперимент с подбрасыванием монеты приведет к 0 плюс вероятность того, что эксперимент закончится одной головой.
P (X < 1) = P (X = 0) + P (X = 1) = 0.25 + 0,50 = 0,75
Как и распределение вероятностей, кумулятивное распределение вероятностей может быть представлен таблицей или уравнением. В таблице ниже совокупный вероятность относится к вероятности того, что случайная величина X меньше, чем или равно x.
Количество голов:
x Вероятность:
P (X = x) Суммарная вероятность:
P (X < x)
0 0.25 0,25
1 0,50 0,75
2 0,25 1,00
Равномерное распределение вероятностей
Простейшее распределение вероятностей возникает, когда все значения случайные величины встречаются с равной вероятностью.Эта вероятность распределение называется равномерным распределением .
Равномерное распространение. Предположим, что случайная величина X может принимать k различных значений. Предположим также, что P (X = x _k) постоянно. Затем
P (X = x _k) = 1 / k
Пример 1
Допустим, бросили кубик. Какова вероятность того, что кубик выпадет на 5?
Решение:* Когда бросается игральный кубик, отображаются 6 возможных результатов. по: S = {1, 2, 3, 4, 5, 6}.Каждый возможный результат — это случайная величина (X), и каждый исход имеет одинаковую вероятность. Таким образом, мы имеем единый распространение. Следовательно, P (X = 5) = 1/6.
Пример 2
Предположим, мы повторяем эксперимент с подбрасыванием игральных костей, описанный в Примере 1. Это времени, мы спрашиваем, какова вероятность того, что кубик выпадет на число, которое меньше 5?
Решение: Когда бросается игральный кубик, отображаются 6 возможных результатов. по: S = {1, 2, 3, 4, 5, 6}.Все возможные исходы имеют одинаковую вероятность. Таким образом, мы имеем равномерное распределение.
Эта проблема связана с кумулятивной вероятностью. Вероятность того, что умереть приземлится на число меньше 5 равно:
P (X <5) = P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4)
P (X <5) = 1/6 + 1/6 + 1/6 + 1/6 = 2/3
.
Что такое вероятность?
Вероятность события относится к вероятность того, что событие произойдет.
Примечание: Ваш браузер не поддерживает видео в формате HTML5. Если вы просматриваете эту веб-страницу в другом браузере (е.g., последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеообработку этого урока.
Как интерпретировать вероятность
Математически вероятность того, что событие произойдет, выражается как число от 0 до 1. Условно вероятность события A представлен P (A).
Если P (A) равно единице, событие A почти наверняка произойдет.
в статистический эксперимент, сумма вероятностей для всех возможных исходов равно единице. Это означает, например, что если эксперимент может иметь три возможных результата (A, B и C), тогда P (A) + P (B) + P (C) = 1.
Как вычислить вероятность: одинаково вероятные результаты
Иногда статистический эксперимент может иметь n возможных исходов, каждый из которых с равной вероятностью.Предположим, что подмножество из r результатов классифицируются как «успешные» результаты.
Вероятность того, что эксперимент закончится успешным исход (S):
P (S) = (Количество успешных результатов) / (Общее количество равновероятных результатов) = r / n
Рассмотрим следующий эксперимент. В урне 10 шариков. Два мраморные шарики красные, три — зеленые и пять — синие. Если экспериментатор случайным образом выбирает из урны 1 шарик, какой вероятность, что он будет зеленым?
В этом эксперименте имеется 10 равновероятных исходов, три из которых которые являются зелеными шариками.Следовательно, вероятность выбора зеленый мрамор — 3/10 или 0,30.
Как вычислить вероятность: закон больших чисел
Можно также думать о вероятности события с точки зрения его долгосрочная относительная частота. Относительная частота событие — это количество раз, когда событие происходит, деленное на общее количество испытаний.
P (A) = (Частота события A) / (Количество испытаний)
Например, продавец однажды замечает, что 5 из 50 посетителей в ее магазин сделать покупку. На следующий день 20 из 50 посетителей Совершить покупку. Две относительные частоты (5/50 или 0,10 и 20/50 или 0,40) различаются. Однако, подводя итоги по многим посетителям, она может обнаружить, что вероятность того, что посетитель покупка все ближе и ближе к 0.20.
Диаграмма рассеяния показывает относительную частоту покупок как количество попыток (в данном случае количество посетителей) увеличивается. По результатам многих испытаний относительная частота сходится к стабильное значение (0,20), которое можно интерпретировать как вероятность что посетитель магазина совершит покупку.
Идея, что относительная частота событие сойдется по вероятности события, по мере увеличения количества испытаний назвал закон больших чисел .
Проверьте свое понимание
Проблема
Монета подбрасывается трижды. Какова вероятность того, что он приземляется на головы ровно один раз?
(А) 0,125
(В) 0,250
(С) 0,333
(D) 0,375
(E) 0.500
Решение
Правильный ответ (D). Если подбросить монетку три раза, всего восемь возможных результатов. Это: HHH, HHT, HTH, THH, HTT, THT, TTH и TTT. Из восьми возможных исходов у трех ровно одна голова. Это: HTT, THT и TTH. Следовательно, вероятность того, что три подбрасывания монеты будут производят ровно , на одну головку 3/8 или 0.375.
.
Распределение вероятностей
Распределение вероятностей представляет собой таблицу или уравнение который связывает каждое возможное значение, которое случайная величина может предполагать с вероятностью его появления.
Примечание: Ваш браузер не поддерживает видео в формате HTML5.Если вы просматриваете эту веб-страницу в другом браузере (например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеоматериал об этом уроке.
Дискретные распределения вероятностей
Распределение вероятностей дискретный случайную величину всегда можно представить в виде таблицы. Например, предположим, что вы подбрасываете монету два раза.Это просто упражнение может иметь четыре возможных результата: HH, HT, TH и TT. Теперь пусть переменная X представляет количество голов, полученных в результате монета подбрасывает. Переменная X может принимать значения 0, 1 или 2; и X — дискретная случайная величина.
В таблице ниже показаны вероятности, связанные с каждым возможное значение X. Вероятность выпадения 0 орлов 0,25; 1 голова, 0,50; и 2 головы, 0.25. Таким образом, таблица пример распределения вероятностей для дискретной случайной величины.
Количество головок, x Вероятность, P (x)
0 0,25
1 0,50
2 0.25
Примечание: Учитывая распределение вероятностей, вы можете найти кумулятивные вероятности. Например, вероятность получить 1 или меньше орлов [P (X 1)] составляет P (X = 0) + P (X = 1), что равно 0,25 + 0,50 или 0,75.
Непрерывное распределение вероятностей
Распределение вероятностей непрерывный случайная величина представлена уравнением, называется функцией плотности вероятности (pdf).Все функции плотности вероятности удовлетворяют следующему условия:
Общая площадь под кривой функции равна единице.
На графиках ниже показаны два непрерывных распределения вероятностей. Первый график показывает функцию плотности вероятности описывается уравнением y = 1 в диапазоне от 0 до 1 и y = 0 в другом месте.На втором графике показана функция плотности вероятности описывается уравнением y = 1 — 0,5x в диапазоне от 0 до 2 и y = 0 в другом месте. Площадь под кривой равна 1 для обе диаграммы.
г = 1
y = 1 — 0,5x
Вероятность того, что непрерывная случайная величина попадает в интервал между a и b равен площадь под кривой PDF между a и b .Например, на первой диаграмме выше заштрихованная область показывает вероятность того, что случайная величина X будет находятся между 0,6 и 1,0. Эта вероятность равна 0,40. А на втором графике заштрихованная область показывает вероятность падения между 1,0 и 2,0. Эта вероятность равна 0,25.
Примечание: При непрерывном распределении существует бесконечное количество значений между любыми двумя точками данных.В следствии, вероятность того, что непрерывная случайная величина примет конкретное значение всегда равно нулю. Например, в обоих приведенных выше графиков вероятность того, что переменная X будет равна ровно 0,4 равно нулю.
Проверьте свое понимание
Проблема 1
Число взрослых, проживающих в домах по случайно выбранной городской квартал описывается следующей вероятностью распространение.
Количество взрослых,
х Вероятность,
P (x)
1 0,25
2 0,50
3 0.15
4 или более ???
Какова вероятность того, что 4 или более взрослых проживают в случайно выбранный дом?
(А) 0,10
(В) 0,15
(С) 0,25
(D) 0,50
(E) 0.90
Решение
Правильный ответ — A. Сумма всех вероятностей равна до 1. Следовательно, вероятность того, что четыре или более взрослых проживать в доме равно 1 — (0,25 + 0,50 + 0,15) или 0,10.
.
Вероятность | LearnEnglish — British Council
Уровень: начальный
Возможность
Мы используем may , might и could , чтобы сказать, что что-то возможно , но не точно:
Они могут приехать на машине. (= Может быть, они приедут на машине.)
Они могут быть дома. (= Может, они дома.)
Если не торопиться, то может опоздать на . (= Может быть, опоздаем.)
Мы используем банка , чтобы сделать общих заявлений о том, что возможно:
Здесь может быть очень холодно зимой. (= Зимой здесь иногда бывает очень холодно.)
Вы можете легко потерять в этом городе. (= Люди часто теряются в этом городе.)
Будьте осторожны!
Мы делаем , а не используем can , чтобы говорить о конкретных событиях:
A: Где Джон?
B: Я не уверен.Он может / может / может быть (НЕ может ) в его офисе.
Обратите внимание на разницу в значении между банками и может / может / может :
Эта собака может быть опасной.
(= Иногда эта собака опасна. Я знаю.)
Эта собака может / может быть / может быть опасной.
(= Возможно, эта собака опасна. Я не знаю.)
банка и май / мог / мог
GapFillDragAndDrop_MTYzNDM =
Уровень: средний
Мы используем может иметь , может иметь или может иметь от до делать предположения о прошлом t:
Я не получил ваше письмо.Это могло потерять в почте.
Сейчас десять часов. Их уже могли прибыть .
Где они? Они могли потерять .
Мы используем могли бы – делать общие утверждения о прошлом :
Там может быть зимой очень холодно. (= Зимой там иногда было очень холодно.)
Ты легко мог потерять в этом городе. (= Люди часто терялись в этом городе.)
может и может иметь
MultipleChoice_MTYzNDQ =
Невозможность
Уровень: новичок
Мы используем не могу или не могу сказать, что что-то невозможно :
Это не может быть истинным.
Вы не можете быть серьезным .
Уровень: средний
Мы используем не может иметь или не может иметь , чтобы сказать, что прошлое событие было невозможно:
Они знают дорогу. Они не могли потерять !
Если бы Джонс был на работе до шести, он не смог бы совершить убийство.
Гарантия
Уровень: новичок
Мы используем должен , чтобы показать , что мы уверены, что-то правда, и у нас есть причины для нашей веры:
Темнеет. должно быть довольно поздно.
Вы не ели весь день. Вы должно быть голодны.
Мы используем , если – предполагают, что что-то верно, а у нас есть причины для нашего предложения:
Спросите Миранду. Она должна знать .
Уже почти шесть часов. Они должны прибыть в ближайшее время.
Уровень: средний
Мы используем должно иметь и должно иметь для прошлое :
Они не ели весь день.Они , должно быть, были голодными.
Ты выглядишь счастливым. Вы, , должно быть слышали хорошие новости.
Почти одиннадцать часов. Их уже должны были прибыть .
Вероятность 1
Matching_MTYzNDU =
Вероятность 2
Matching_MTYzNDY =
Вероятность 3
GapFillTyping_MTYzNDc =
Вероятность 4
Matching_MTYzNDg =
Вероятность 5
GapFillTyping_MTYzNDk =
.
No related posts.

Вероятность безотказной работы — это… Что такое Вероятность безотказной работы?

Смотреть что такое «Вероятность безотказной работы» в других словарях: