Нестандартные способы решения квадратных уравнений
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Сиднев А.А. 1
1МБОУ «Школа № 48»
Кувшинова Л.В. 1
1МБОУ «Школа № 48»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Математическое образование, получаемое в школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой.
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям.
Актуальность темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т.
Цель: Изучить стандартные и нестандартные способы решения квадратных уравнений
Задачи
- Изложить наиболее известные способы решения уравнений
- Изложить нестандартные способы решения уравнений
- Сделать вывод
Объект исследования: квадратные уравнения
Предмет исследования: способы решения квадратных уравнений
Методы исследования:
- Теоретические: изучение литературы по теме исследования;
- Сравнение способов на рациональность их использования при решении квадратных уравнений.

Глава 1.Квадратные уравнения и стандартные способы решения
1.1.Определение квадратного уравнения
Квадратным уравнением называется уравнение вида ax2 + bx + c = 0, где х – переменная, а, b и с– некоторые числа, причем, а ≠ 0.
Числа а, b и с — коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b– вторым коэффициентом и число c – свободным членом.
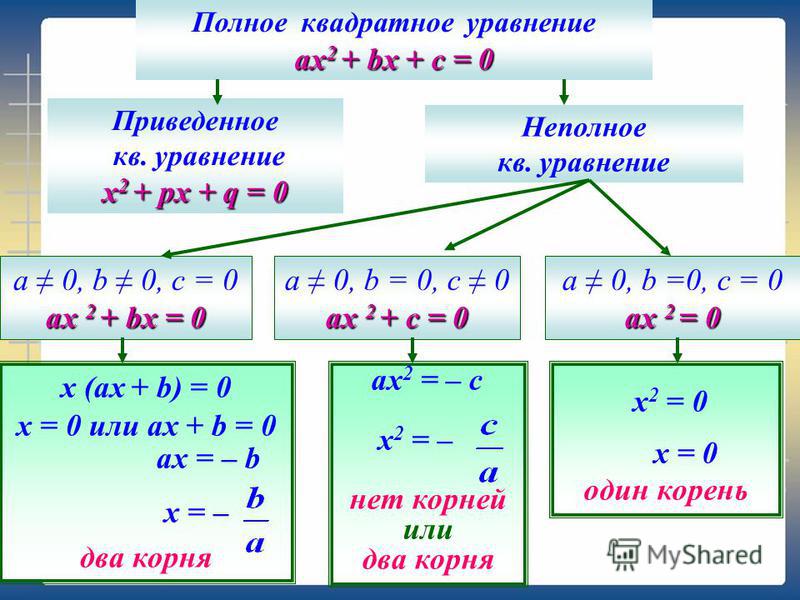
Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых т.е. коэффициенты в и с отличны от нуля.Неполное квадратное уравнение — это уравнение, в котором хотя бы один из коэффициентов в или, с равен нулю.
Определение 3. Корнем квадратного уравнения ах2 + bх + с = 0 называют всякое значение переменной х, при котором квадратный трехчлен ах2 + bх + с обращается в нуль.
Определение 4. Решить квадратное уравнение — значит найти все его
корни или установить, что корней нет.
Пример: – 7x + 3 =0
В каждом из уравнений вида a + bx + c = 0, где а ≠ 0, наибольшая степень переменной x – квадрат. Отсюда и название: квадратное уравнение.
Квадратное уравнение, в котором коэффициент при х2 равен 1, называют приведенным квадратным уравнением.
Пример
х2 – 11х+30=0, х2 –8х=0.
1.2.Стандартные способы решения квадратных уравнений
Решение квадратных уравнений с помощью выделения квадрата двучлена
Решение квадратного уравнения, в котором оба коэффициента при неизвестных и свободный член отличны от нуля. Такой способ решения квадратного уравнения называют выделением квадрата двучлена.
Разложение левой части уравнения на множители.
Решим уравнение х2 + 10х — 24 = 0. Разложим левую часть на множители:
х2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:(х + 12)(х — 2) = 0
Произведение множителей равно нулю, если по крайней мере, один из его множителей равен нулю.
Ответ: -12; 2.
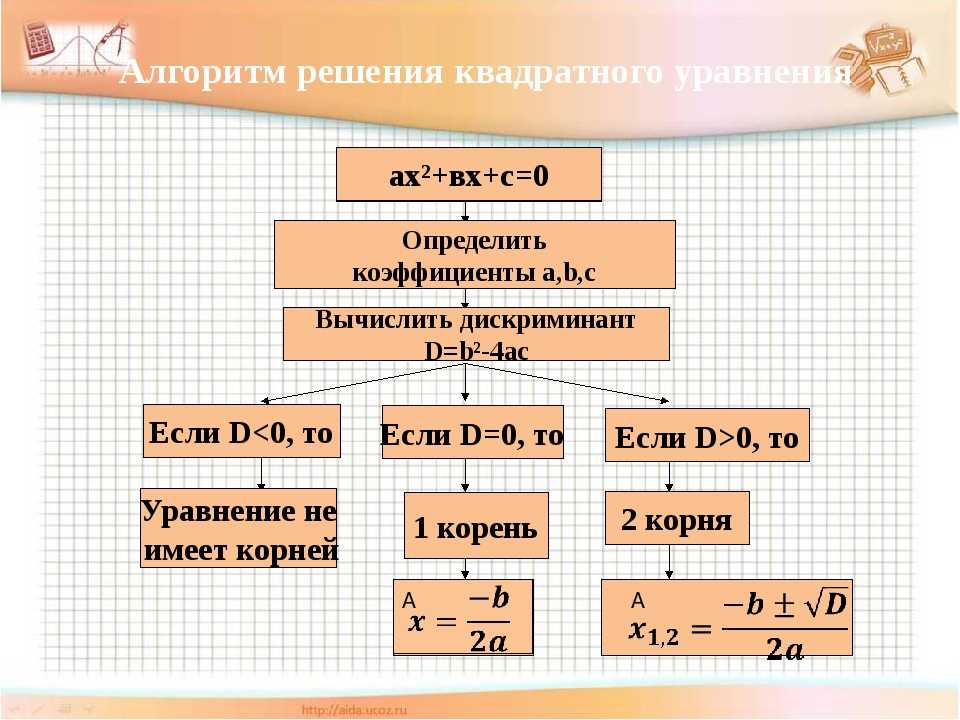
Решение квадратного уравнения по формуле.
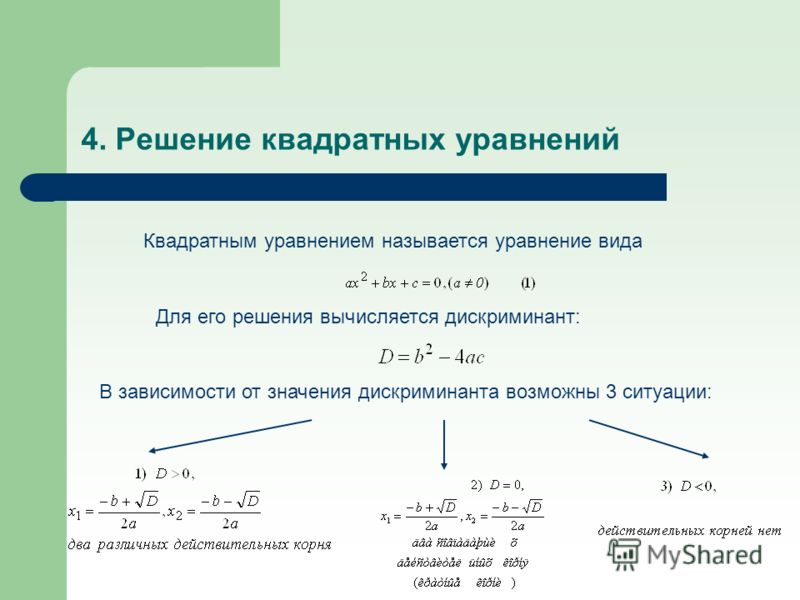
Дискриминант квадратного уравнения ax2 + bx + c = 0 выражение b2– 4ас = D — по знаку которого судят о наличии у этого уравнения действительных корней.
Возможные случаи в зависимости от значения D:
- Если D>0, то уравнение имеет два корня.
- Если D= 0, то уравнение имеет один корень: х =
- Если D <0, то уравнение не имеет корней.

Решение уравнений с помощью теоремы Виета.
Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Приведенное квадратное уравнение имеет вид:
х2 + bx + c = 0.
Обозначим второй коэффициент буквой р, а свободный член буквой q:
х2 + px + q = 0, тогда
x1 + x2 = — p; x1· x2 = q
Глава 2.Нестандартные способы решения квадратных уравнений
2.1.Решение с помощью свойств коэффициентов квадратного уравнения
Свойства коэффициентов квадратного уравнения – это такой способ решения квадратных уравнений, который поможет быстро и устно найти корни уравнения:
ax2 + bx + c = 0
- Если а+ b+c= 0, то x1 = 1, x2 =
Пример. Рассмотрим уравнение х2 +3х – 4= 0.
Рассмотрим уравнение х2 +3х – 4= 0.
a + b + c = 0, то x1 = 1, x2 =
1+3+(-4) = 0, тогда x1 = 1, x2 = = — 4
Проверим полученные корни с помощью нахождения дискриминанта:
D= b2– 4ас=32– 4·1·(-4) = 9+16= 25
x1 = = = = = — 4
x2 = = = = = 1
Следовательно, если + b +c= 0, то x1 = 1, x2 =
- Если
Пример. Рассмотрим уравнение 3х2 +4х +1 = 0, a=3, b=4, c=1
Если b= a + c, то x1 = -1, x2 = , то 4 = 3 + 1
Корни уравнения: x1 = -1, x2 =
Значит корнями этого уравнения являются –1 и .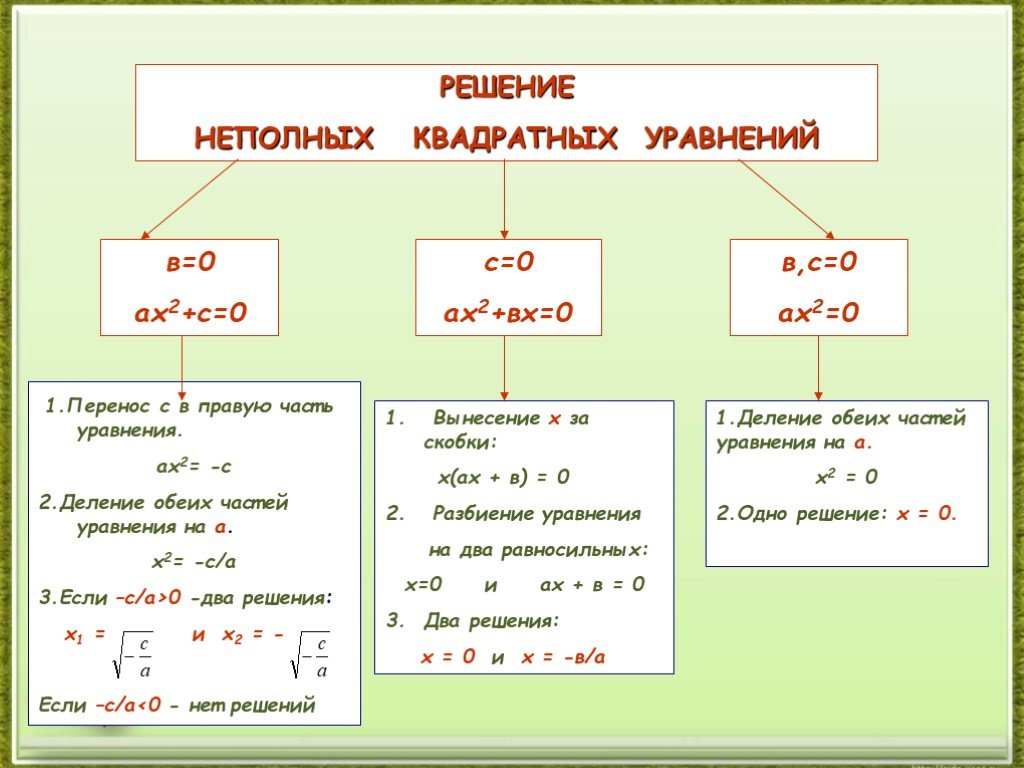 Проверим это с помощью нахождения дискриминанта:
Проверим это с помощью нахождения дискриминанта:
D= b2– 4ас=42– 4·3·1 = 16 – 12 = 4
x1 = = = = = — 1
x2 = = = = =
Следовательно, b= a + c, то x1 = -1, x2 =
2.2.Способ «переброски»
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Если а±b+c≠0, то используется прием переброски:
Пример:
3х2+4х+1=0; 3+4+1 ≠ 0
Применяя способ «переброски» получаем:
х2 + 4х+3= 0
Таким образом, с помощью теоремы Виета получаем корни уравнения:
x1 = — 3, x2 = -1.
Однако корни уравнения необходимо поделить на 3 (то число, которое «перебрасывали»):
Значит, получаем корни: x1 = -1, x2 = .
Ответ: ; — 1
2.3.Решение с помощью закономерности коэффициентов
- Если уравнение ax2 + bx + c = 0, коэффициент b= (a2+1), и коэффициент c = a, то его корни равны x1 = — a, x2 =
Таким образом, решаемое уравнение должно иметь вид
ax2 + (а2 +1)∙ х + а= 0
Пример. Рассмотрим уравнение 3х2 +10х +3 = 0.
Таким образом, корни уравнения: x1 = -3, x2 =
Проверим данное решение с помощью дискриминанта:
D= b2– 4ас=102– 4·3·3 = 100 – 36 = 64
x1 = = = = = — 3
x2 = = = = = ; Следовательно, x1 = — a, x2 =
- Если уравнение ax2 — bx + c = 0, коэффициент b= (a2+1), и коэффициент c = a, то его корни равны x1 = a, x2 =
Таким образом, решаемое уравнение должно иметь вид
ax2 — (а2 +1)∙ х+ а= 0
Пример. Рассмотрим уравнение 3х2 — 10х +3 = 0.
Рассмотрим уравнение 3х2 — 10х +3 = 0.
Таким образом, корни уравнения: x1 = 3, x2 =
Проверим данное решение с помощью дискриминанта:
D= b2– 4ас=102– 4·3·3 = 100 – 36 = 64
x1 = = = = =
x2 = = = = = 3; Следовательно, x1 = a, x2 =
- Если уравнение ax2 + bx — c = 0, коэффициент b= (a2-1), и коэффициент c = a, то его корни равны x1 = —a, x2 =
Таким образом, решаемое уравнение должно иметь вид
ax2 + (а2 —1)∙ х — а= 0
Пример. Рассмотрим уравнение 3х2 + 8х —3 = 0..
Рассмотрим уравнение 3х2 + 8х —3 = 0..
Таким образом, корни уравнения: x1 = — 3, x2 =
Проверим данное решение с помощью дискриминанта:
D= b2– 4ас=82+ 4·3·3 = 64 + 36 = 100
x1 = = = = = — 3
x2 = = = = = ;Следовательно, x1 = — a, x2 =
- Если уравнение ax2 — bx — c = 0, коэффициент b= (a2-1), и коэффициент c = a, то его корни равны x1 = a, x2 =
Таким образом, решаемое уравнение должно иметь вид
ax2 — (а2 —1)∙ х — а= 0
Пример. Рассмотрим уравнение 3х2 — 8х —3 = 0..
Рассмотрим уравнение 3х2 — 8х —3 = 0..
Таким образом, корни уравнения: x1 = 3, x2 = —
Проверим данное решение с помощью дискриминанта:
D= b2– 4ас=82+ 4·3·3 = 64 + 36 = 100
x1 = = = = = —
x2 = = = = = 3; Следовательно, x1 = a, x2 = —
2.4.Решение с помощью циркуля и линейки
Предлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис.6 ).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точки
|
Рис. |
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = = =
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
SK = = = —
SF = = =
Итак:
1) построим точки S (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 7а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.
7а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.8б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра AS<S, R<
окружность не имеет общих точек с осью абсцисс (рис 7в), в этом случае уравнение не имеет решения.
а)AS>SB, R> б) AS=SB, R= в) AS<S, R<
Два решения x1 и x2 Одно решение x1 Нет решения
Рис. 7
7
Пример.
Решим уравнение х2 — 2х — 3 = 0 (рис.8).
Решение. Определим координаты точки центра окружности по формулам:
x = — = — = 1,
y = = = -1
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1 = — 1; х2 = 3.
2.5.Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.9).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей:
первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим:
x = 8 — 2 — 2 = 3
2) А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.
Решение представлено на рис 10. где
у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис. .
рис.10
3) Решить геометрически уравнение у2 — 6у — 16 = 0.
|
рис. 11 |
Преобразуя уравнение, получаем
у2 — 6у = 16.
На рис 11. находим «изображения» выражения у2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
получаем: (у — 3)2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у1 = 8 и у2 = — 2.
Заключение
В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справился, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.
Нужно отметить, что каждый способ решения квадратных уравнений по-своему уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и экзаменах. При работе над темой я ставил задачу, выяснить какие методы являются стандартными, а какие нестандартными.
Итак, стандартные методы (используются чаще при решении квадратных уравнений):
- Решение с помощью выделения квадрата двучлена
- Разложение левой части на множители
- Решение квадратных уравнений по формуле
- Решение с помощью теоремы Виета
- Графическое решение уравнений
Нестандартные методы:
- Свойства коэффициентов квадратного уравнения
- Решение способом переброски коэффициентов
- Решение с помощью закономерности коэффициентов
- Решение квадратных уравнений, с помощью циркуля и линейки.

- Исследование уравнения на промежутках действительной оси
- Геометрический способ
При этом следует заметить, что каждый способ обладает своими особенностями и границами применения.
Решение уравнений с использованием теоремы Виета
Достаточно легкий способ, дает возможность сразу увидеть корни уравнения, при этом легко находятся только целые корни.
Решение уравнений способом переброски
За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета, при этом также легко найти только целые корни.
Свойства коэффициентов квадратного уравнения
Доступный метод для устного нахождения корней квадратного уравнения, но подходит только к некоторым уравнениям
Графическое решение квадратного уравнения
Наглядный способ решения квадратного уравнения, однако могут возникать погрешности при составлении графиков
Решение квадратных уравнений с помощью циркуля и линейки
Наглядный способ решения квадратного уравнения, но также могут возникать погрешности
Геометрический способ решения квадратных уравнений
Наглядный способ, похож на способ выделения полного квадрата
Решая уравнения разными способами, я пришел к выводу, что зная комплекс методов решения квадратных уравнений, можно решить любое уравнение, предлагаемое в процессе обучения.
При этом, следует заметить, что одним из более рациональных способов решения квадратных уравнений является способ «переброски» коэффициента. Однако самым универсальным способом можно считать стандартный способ решения уравнений по формуле, потому что данный способ позволяет решить любое квадратное уравнение, хотя иногда и за более длительное время. Также такие способы решения, как способ «переброски», свойство коэффициентов и теорема Виета помогаю сэкономить время, что очень важно при решении заданий на экзаменах и контрольных работах.
Думаю, что моя работа будет интересна учащимся 9-11 классов, а также тем, которые хотят научиться решать рационально квадратные уравнения и хорошо подготовиться к выпускным экзаменам. Также она будет интересна и учителям математики, за счет рассмотрения истории квадратных уравнений и систематизации способов их решения.
Список литературы
- Глейзер, Г.И. История математики в школе/ Г.И. Глейзер.
 -М.: Просвещение, 1982- 340с.
-М.: Просвещение, 1982- 340с. - Гусев, В.А. Математика. Справочные материалы/ В.А. Гусев, А.Г. Мордкович — М.: Просвещение, 1988, 372с.
- Ковалева Г. И., Конкина Е. В. «Функциональный метод решения уравнений и неравенств», 2014 г.
- Кулагин Е. Д. «300 конкурсных задач по математике», 2013 г.
- Потапов М. К. «Уравнения и неравенства. Нестандартные методы решения» М. «Дрофа», 2012 г.
- .Барвенов С. А «Методы решения алгебраических уравнений», М. «Аверсэв», 2006 г.
- Супрун В.П. «Нестандартные методы решения задач по математике» — Минск «Полымя», 2010г
- Шабунин М.И. «Пособие по математике для поступающих в вузы», 2005г.
- Башмаков М.И. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.
- Шаталова С. Урок – практикум по теме «Квадратные уравнения».- 2004.
Просмотров работы: 7569
квадратных уравнений | Начальная алгебра
Результаты обучения
- Квадратные уравнения
- Распознать квадратное уравнение
- Использовать принцип нулевого произведения для решения квадратного уравнения, которое можно разложить на множители
- Определить, когда можно отбросить решения квадратных уравнений
- Теорема Пифагора
- Распознавание прямоугольного треугольника среди других типов треугольников
- Используйте теорему Пифагора, чтобы найти длины прямоугольного треугольника 9{2}+11x+-5=0[/latex] путем вычитания 7 с обеих сторон.

В примере в следующем видео мы представляем еще одну область применения факторинговых трехчленов.
В приведенном ниже примере показано другое квадратное уравнение, в котором ни одна из сторон изначально не равна нулю. (Обратите внимание, что последовательность факторизации была сокращена.)
Следующее видео содержит еще один пример решения квадратного уравнения с помощью факторизации с группировкой.
92+90=-8k[/latex]
Показать решение
В этом последнем видеопримере мы решаем квадратное уравнение со старшим коэффициентом -1, используя сокращенный метод факторизации и принцип нулевого произведения.

Теорема Пифагора
Треугольники
Теорема Пифагора или Теорема Пифагора — это утверждение о сторонах прямоугольного треугольника. Один из углов прямоугольного треугольника всегда равен 90 градусам. Этот угол является прямым углом. Две стороны, следующие за прямым углом, называются катетами, а другая сторона называется гипотенузой. Гипотенуза — это сторона, противоположная прямому углу, и это всегда самая длинная сторона. На изображении выше показаны четыре распространенных типа треугольников, включая прямоугольный треугольник. 92[/latex]
Имея достаточно информации, мы можем найти неизвестную длину. Эта взаимосвязь использовалась в течение многих лет для таких вещей, как астрономическая навигация и ранние проекты гражданского строительства. Теперь у нас есть цифровой GPS и геодезическое оборудование, запрограммированное на выполнение расчетов за нас.

В следующем примере мы объединим силу теоремы Пифагора и наши знания о решении квадратных уравнений, чтобы найти неизвестные длины прямоугольных треугольников.
Пример
Прямоугольный треугольник имеет один катет длины x, другой катет которого на два больше, а длина гипотенузы больше на четыре. Найдите длины сторон треугольника. Используйте изображение ниже.
Показать решение
В этом видеопримере показан другой способ использования квадратного уравнения для нахождения неизвестной длины прямоугольного треугольника.
Если вас интересует астрономическая навигация и стоящая за ней математика, посмотрите это видео для развлечения. 92+bt+c[/latex], которые мы изучали в этом модуле. Движение снаряда также называют параболической траекторией из-за формы траектории движения снаряда, как на изображении воды в фонтане внизу.

Parabolic WaterTrajectory
Параболическое движение и связанные с ним уравнения позволяют нам запускать спутники для телекоммуникаций и ракеты для исследования космоса. В последнее время полицейские управления даже начали использовать снаряды с GPS для отслеживания убегающих подозреваемых в транспортных средствах, а не преследовать их на высокой скорости [1] .
В этом разделе мы будем решать простые квадратичные полиномы, представляющие параболическое движение снаряда. Реальная математическая модель траектории полета ракеты или полицейского GPS-снаряда может иметь другие коэффициенты или большее количество переменных, но концепция остается прежней. Мы также научимся интерпретировать значение переменных в многочлене, моделирующем движение снаряда.
В следующем примере мы найдем время, в течение которого ракета находится на заданной высоте, отличной от нуля. 9{2}+7t+4[/latex]
Показать решение
В следующем видео представлен еще один пример решения квадратного уравнения, представляющего движение по параболе.

В этом разделе мы ввели понятие движения снаряда и показали, что его можно смоделировать с помощью квадратичного полинома. Хотя модели, используемые в этих примерах, просты, концепции и интерпретации одинаковы. Методов, используемых для решения квадратичных полиномов, которые нелегко разложить на множители, много, и они хорошо известны, и, вероятно, вы встретите больше в своих исследованиях.
Сводка
Решения или корни квадратных уравнений можно найти, приравняв одну сторону к нулю, разложив многочлен на множители и применив свойство нулевого произведения. Принцип нулевого произведения гласит, что если [латекс]ab=0[/латекс], то либо [латекс]а=0[/латекс], либо [латекс]b=0[/латекс], либо оба и и b равны 0. После факторизации полинома приравняйте каждый множитель к нулю и решите их по отдельности.
 Ответами будут множества решений исходного уравнения.
Ответами будут множества решений исходного уравнения.Не все решения подходят для некоторых приложений. Во многих реальных ситуациях отрицательные решения неуместны и должны быть отброшены.
- «Последний инструмент полицейских в скоростных погонях: GPS-снаряды». CBSNews . CBS Interactive, nd Веб. 14 июня 2016 г. ↵
Учебник по алгебре для колледжей 20
Алгебра для колледжей
Учебник 20: Квадратичные по форме уравненияWTAMU > Виртуальная математическая лаборатория > Алгебра колледжа
Цели обучения
После завершения этого руководства вы сможете:
- Решение уравнений квадратной формы.

Введение
В этом уроке я покажу вам, как решать уравнения которые квадратичны по форме. Эти типы уравнений в конечном счете вести нам квадратное уравнение. Итак, вы знаете, что это значит. Как упоминалось в предыдущих уроках, много раз в математике вы использовали предыдущий знания, помогающие работать с новыми концепциями. Главное, что вам нужно узнать из своего прошлого, что поможет вам решить типы проблем в этот учебник, как решить квадратные уравнения. Если вам нужен обзор по решению квадратных уравнений, смело переходите к Учебник 17: Квадратные уравнения . Решение уравнений — это большое часть алгебры. Очень важно уметь решать все различных видов уравнений, потому что уравнения могут использоваться для решения всех виды проблем, и вы хотите убедиться, что вы готовы к любым тип проблемы, которая приходит на вашем пути.
 Я думаю, что вы готовы
двигаться вперед.
Я думаю, что вы готовы
двигаться вперед.Учебник
Квадратное по форме
Уравнение является квадратичным по форме, когда это можно написать в этой стандартной форме
, где одно и то же выражение находится внутри оба ( ).
Другими словами, если у вас в раза больше, чем квадрат выражения, следующего за b плюс b , умноженное на то же выражение, не возведенное в квадрат, плюс c , равное 0, у вас есть уравнение, имеющее квадратную форму.
Если мы заменим то, что находится в ( ) на переменная типа t , тогда исходное уравнение станет квадратным уравнением.

Решение уравнений, которые
Квадратичный по формеШаг 1 : Запись в стандартной форме, , если нужно.
Если он не в стандартной форме, переместите любой термин(ы) к соответствующему стороны, используя свойство равенства сложения/вычитания.
Также убедитесь, что квадрат термина написан сначала слева направо, выражение не в квадрате второе, а константа третье, и оно является установить равным 0.
Шаг 2 : Замена переменная in для выражения, следующего за b во втором срок.
Другими словами, подставьте свою переменную вместо того, что находится в ( ), когда он находится в стандартной форме, .

Я собираюсь использовать t для моя замена, но на самом деле вы можете использовать любую переменную, если это не переменная что используется в исходном уравнении.
Шаг 3 : Решите квадратное уравнение, созданное на шаге 2.
Если вам нужен обзор решения квадратного уравнения уравнения, не стесняйтесь идти до Урок 17. Квадратичный Уравнения .
Вы можете использовать любой метод, который вы хотите решить квадратное уравнение: факторинг, заполнение формулы квадрата или квадрата.
Шаг 4 : Найдите значение переменной из исходного уравнения.
Имейте в виду, что вы ищете решение исходное уравнение и что переменная, которую вы подставили на шаге 2, не является вашей оригинальный переменная.

Используйте замену, которая использовалась для настройки шага 2, а затем решить для исходная переменная.
Шаг 5 : Проверка ваши решения.
В некоторых случаях вы будете работать с рациональным показатели и квадрат корни в ваших проблемах. Эти типы уравнений могут вызвать посторонний решения. Напомним, что постороннее решение – это решение, решение к уравнению после выполнения чего-то вроде поднятия обеих сторон уравнение четной степенью, но не является решением исходной задачи.
Хотя не все квадратичные по форме уравнения могут вызвать посторонние решения, лучше перестраховаться и просто проверить их все.

Пример 1 : Решите уравнение квадратного вида: .
Посмотреть видео этого примера
Шаг 1 : Запись в стандартной форме, , если нужно.
Это уравнение уже имеет стандартную форму.
Этап 2 : Замена переменная in для выражения, следующего за b во втором срок.
Ниже я переписал исходное уравнение таким образом, показать тебе что оно квадратично по форме.
 Обратите внимание, что если возвести на в квадрат, то получится на в четвертой степени, т. е.
что
у вас в первый срок.
Обратите внимание, что если возвести на в квадрат, то получится на в четвертой степени, т. е.
что
у вас в первый срок.*Переписать исходное уравнение показать, что это квадратичный в виде
*Обратите внимание, что ( y в квадрате) в квадрате = y в четвертой степени*Когда стоит. форме, пусть t = выражение, следующее за b .
Далее нам нужно подставить т в для y в квадрате в исходном уравнении.
* Исходное уравнение
*Замените т в для y в квадрате
Обратите внимание, что мы получили квадратное уравнение, когда сделали нашу замену.
 Отсюда нам нужно решить квадратное уравнение, которое мы создали.
Отсюда нам нужно решить квадратное уравнение, которое мы создали.Шаг 3 : Решить квадратное уравнение, созданное в шаг 2.
Вы можете использовать любой метод решения квадратного уравнения уравнение: факторинг, заполнение формулы квадрата или квадрата.
Я собираюсь учесть это, чтобы решить эту проблему.
*Коэффициент трехчлен
*Использовать принцип нулевого продукта
*Установить 1-й коэффициент = 0 и решить
*Установите 2-й фактор = 0 и решите
Этап 4 : Найти значение переменной из исходного уравнения.

На шаге 2 мы использовали замену t = y в квадрате.
Найдем значение(я) y , когда t = -4:
*Разъем — 4 для t
*Используйте квадрат корневой метод решения для y*Первое решение
*Второе решение
Найдем значение(я) числа y когда t = 1:
*Вставьте 1 для t
*Используйте квадрат корневой метод решения для y*Первое решение
*Второе решение
Шаг 5 : Проверка ваши решения.

Давайте еще раз проверим, является ли y = 2 i решением исходного уравнения.
*Подключение 2 i для y* i в квадрате упрощает быть -1
* i до четвертый упрощается до 1
*Истинное утверждениеПоскольку мы получили верное утверждение, y = 2 i является решением.
Давайте еще раз проверим, является ли y = -2 i решением исходного уравнения.
*Подключение -2 i для y* i в квадрате упрощает быть -1
* i до четвертый упрощается до 1
*Верное утверждениеПоскольку мы получили верное утверждение, y = -2 i является решением.

Давайте еще раз проверим, является ли y = 1 решение исходного уравнения.
*Подключение 1 для y*Правдивое утверждение
Так как мы получили истинное утверждение, y = 1 является решением.
Давайте еще раз проверим, y = -1 является решением исходного уравнения.
*Подключение -1 для y*Правдивое утверждение
Так как мы получили верное утверждение, y = -1 является решением.

У этого уравнения есть четыре решения: г = 2 я , г = -2 i , y = 1 и y = -1.
Пример 2 : Решите уравнение квадратного вида: .
Посмотреть видео этого примера
Шаг 1 : Запись в стандартной форме, , если нужно.
*Обратное значение доп. 3 под. 3
*Уравнение в стандартной форме
Этап 2 : Замена переменная in для выражения, следующего за b во втором срок.

Ниже я переписал исходное уравнение таким образом, показать тебе что оно квадратично по форме. Обратите внимание, что если возвести 90 132 x 90 133 в степень 1/3, вы получите 90 132 x 90 133 в степени 2/3. власть, что у вас есть в первый срок.
*Переписывание исходного уравнения показать, что это квадратичный по форме
*Обратите внимание, что ( x в степени 1/3) в квадрате = x в степени 2/3 сила*Когда стоит. форме, пусть t = выражение, следующее за b .
Далее нам нужно подставить т в для x до 1/3 степени в исходном уравнении.
*Исходное уравнение
*Замените т в для x в степени 1/3
Обратите внимание, что мы получили квадратное уравнение, когда сделали нашу замену.
 Отсюда нам нужно решить квадратное уравнение, которое мы создали.
Отсюда нам нужно решить квадратное уравнение, которое мы создали.Шаг 3 : Решить квадратное уравнение, созданное в шаг 2.
Вы можете использовать любой метод решения квадратного уравнения уравнение: факторинг, заполнение формулы квадрата или квадрата.
Я собираюсь учесть это, чтобы решить эту проблему.
*Коэффициент трехчлен
*Использовать принцип нулевого продукта
*Установить 1-й коэффициент = 0 и решить
*Установите 2-й множитель = 0 и решите
Шаг 4 : Найти значение переменной из исходного уравнения.

На шаге 2 мы использовали замену на = x в степени 1/3.
Найдем значение(я) x , когда t = 3:
*Вставка 3 для t
*Решить рациональное показательное уравнение*Противоположно доставке 1/3 степени возведение в третью степень
Найдем значение(я) x , когда t = -1:
*Подключить -1 к t
*Решите рациональное показательное уравнение*Противоположно доставке 1/3 степени равно , возведение в 3-ю степень
Шаг 5 : Проверка ваши решения.

Давайте еще раз проверим, х = 27 является решением исходного уравнения.
*Подключение 27 для x
*Правдивое утверждение
Поскольку мы получили истинное утверждение, x = 27 является решением.
Давайте еще раз проверим, x = -1 является решением исходного уравнения.
*Подключение -1 для x
*Правдивое утверждение
Поскольку мы получили истинное утверждение, x = -1 является решением.

У этого уравнения есть два решения: x = 27 и x = -1.
Пример 3 : Решите уравнение квадратного вида: .
Посмотреть видео этого примера
Шаг 1 : Запись в стандартной форме, , если нужно.
Это уравнение уже имеет стандартную форму.
Этап 2 : Замена переменная in для выражения, следующего за б во второй срок.
Обратите внимание, что исходное уравнение имеет то же самое выражение в два ( ) и что первый ( ) в квадрате, а второй ( ) относится к одной степени.
 Это уравнение имеет квадратную форму.
Это уравнение имеет квадратную форму.*Когда стоит. форма, пусть t = выражение после b .
Далее нам нужно подставить т в для х в квадрате плюс 3 х в оригинале уравнение.
* Исходное уравнение
*Замените т в для x в квадрат плюс 3 x
Обратите внимание, что мы получили квадратное уравнение, когда сделали нашу замену. Отсюда нам нужно решить квадратное уравнение, которое мы создали.
Шаг 3 : Решить квадратное уравнение, созданное в шаг 2.

Вы можете использовать любой метод решения квадратного уравнения уравнение: факторинг, заполнение формулы квадрата или квадрата.
Я собираюсь учесть это, чтобы решить эту проблему.
*Коэффициент трехчлен
*Используйте принцип нулевого продукта
*Установите 1-й множитель = 0 и решите
*2-й множитель такой же, как и 1-йШаг 4 : Найти значение переменной из исходного уравнения.
На шаге 2 мы использовали замену t = x в квадрате плюс 3 х .
Найдем значение(я) x , когда t = 4:
*Подключить 4 для t
*Решить в квадратное уравнение для x
*Коэффициент трехчлен*Использовать принцип нулевого продукта
*Установить 1-й коэффициент = 0 и решить*Первое решение
*Установите 2-й фактор = 0 и решите
*Второй раствор
Шаг 5 : Проверка ваши решения.

Давайте еще раз проверим, x = -4. является решением исходного уравнения.
*Подключение -4 для x
*Правдивое утверждение
Поскольку мы получили верное утверждение, x = -4 является решением.
Давайте еще раз проверим, верно ли x = 1. решение исходного уравнения.
*Подключение 1 для x
*Правдивое утверждение
Поскольку мы получили истинное утверждение, x = 1 является решением.

У этого уравнения есть два решения: x = -4 и x = 1.
Практические задачи
Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этих вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой проблемы .



 6
6 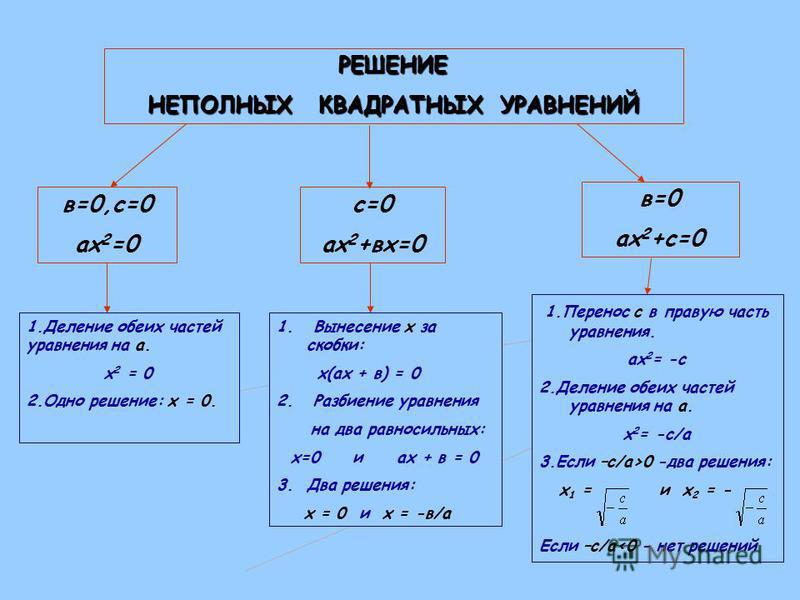
 -М.: Просвещение, 1982- 340с.
-М.: Просвещение, 1982- 340с.




 Ответами будут множества решений исходного уравнения.
Ответами будут множества решений исходного уравнения.
 Я думаю, что вы готовы
двигаться вперед.
Я думаю, что вы готовы
двигаться вперед.



 Обратите внимание, что если возвести на в квадрат, то получится на в четвертой степени, т. е.
что
у вас в первый срок.
Обратите внимание, что если возвести на в квадрат, то получится на в четвертой степени, т. е.
что
у вас в первый срок. Отсюда нам нужно решить квадратное уравнение, которое мы создали.
Отсюда нам нужно решить квадратное уравнение, которое мы создали.



 Отсюда нам нужно решить квадратное уравнение, которое мы создали.
Отсюда нам нужно решить квадратное уравнение, которое мы создали.


 Это уравнение имеет квадратную форму.
Это уравнение имеет квадратную форму.