Решение задач с помощью кругов Эйлера
Пояснительная запискаОчень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.
В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.
Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.
Основные понятия Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.
Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
2. Решение задач с помощью кругов Эйлера2.1. «Обитаемый остров» и «Стиляги»Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.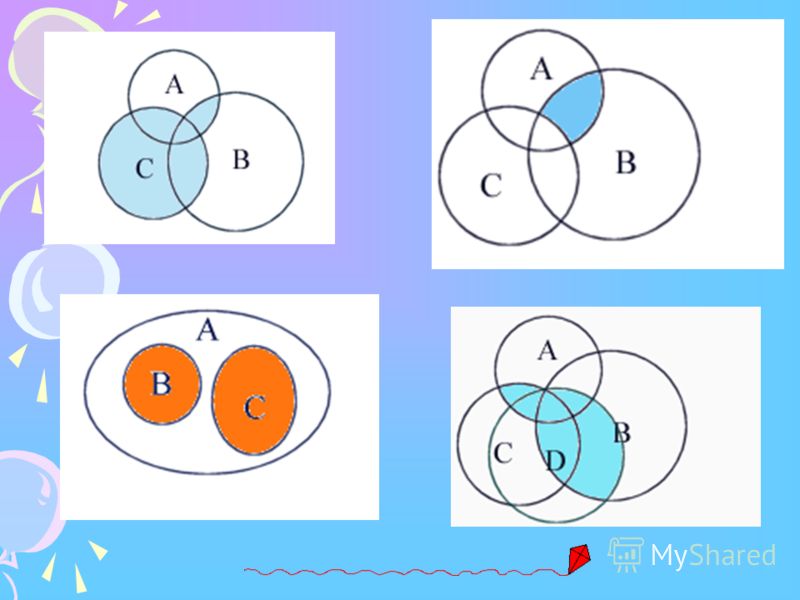
1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,
2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».
Получаем:
Ответ: 5 человек.
2.2. Задача про библиотекиКаждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.
Сколько шестиклассников:
- Являются читателями обеих библиотек;
- Не являются читателями школьной библиотеки;
- Являются читателями только районной библиотеки;
- Являются читателями только школьной библиотеки?
Решение:
Чертим два множества таким образом:
1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек.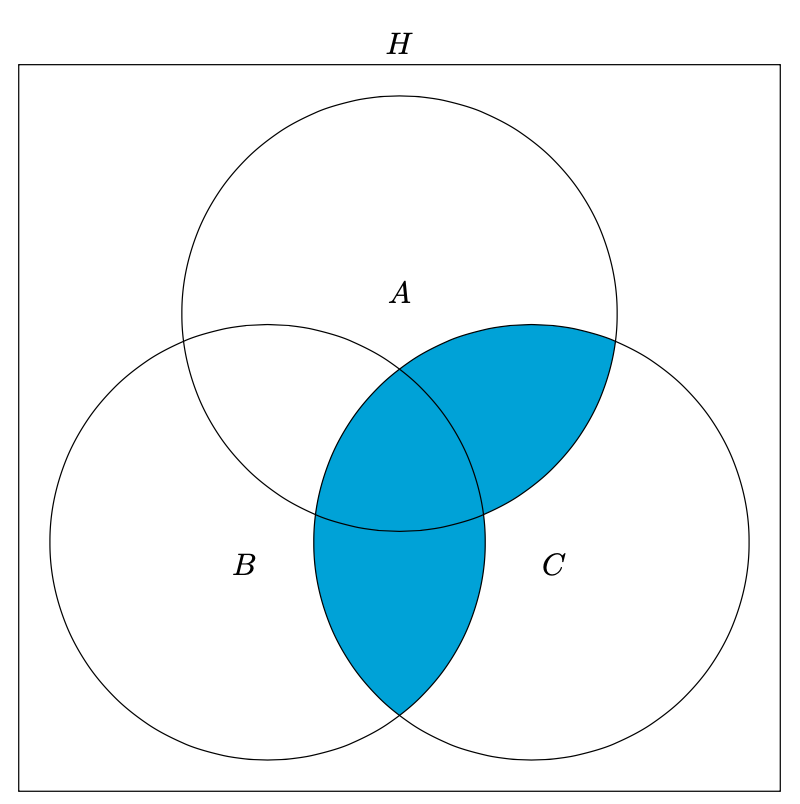 На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,
3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,
4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,
5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.
Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.
Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.
2.3. Гарри Поттер, Рон и Гермиона На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон.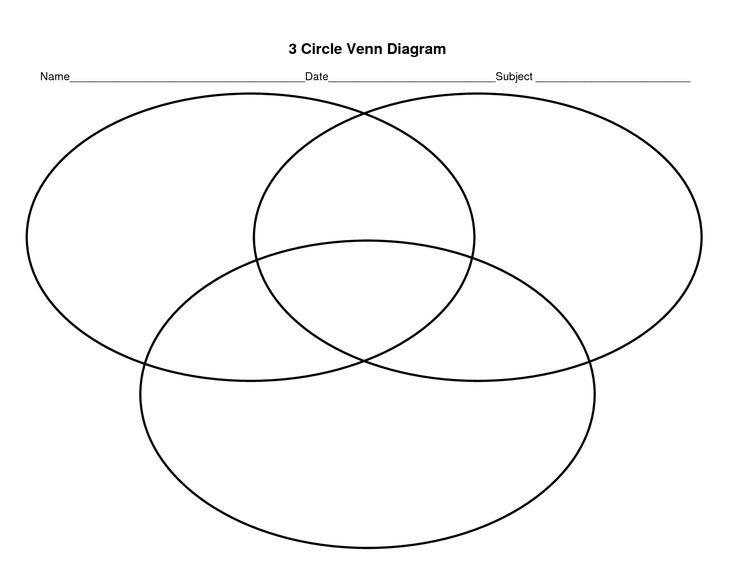 Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение:
Учитывая условия задачи, сделаем чертеж:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.
Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.
Ответ: 8 книг.
2.4. Задача про любимые мультфильмы Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Чертим три круга, таким образом:
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».
1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,
2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,
3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».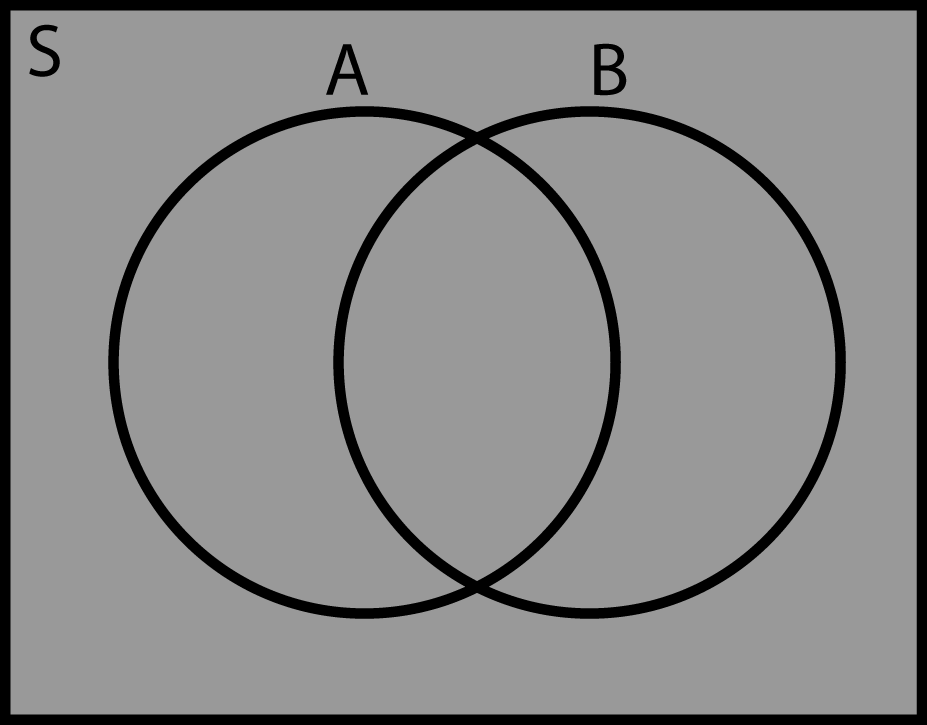
4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».
Ответ: 17 учеников.
2.5. Задача про Крейсер и ЛинкорВ таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
Запрос | Найдено страниц, тыс. |
Крейсер и Линкор | 7000 |
Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов. )
)
Решение:
При помощи кругов Эйлера изобразим условия задачи.
1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,
2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,
3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.
Ответ: 2300 тыс. страниц.
2.6. Задача про блондинокКаждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
Решение:
Изобразим с помощью кругов Эйлера данные из задачи:
1) 12 — 1 = 11 (учеников) — девочек блондинок,
2) 12 — 1 = 11 (учеников) — блондины и любят математику,
3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,
4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,
5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,
6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.
Ответ: 32 ученика.
2.7. Задача про кружкиВ трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение:
Учитывая условия задачи, сделаем чертеж:
1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,
2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,
3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,
4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,
5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,
6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,
7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.
Ответ: 10 человек и 11 человек.
Задачи для самостоятельного решения1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5.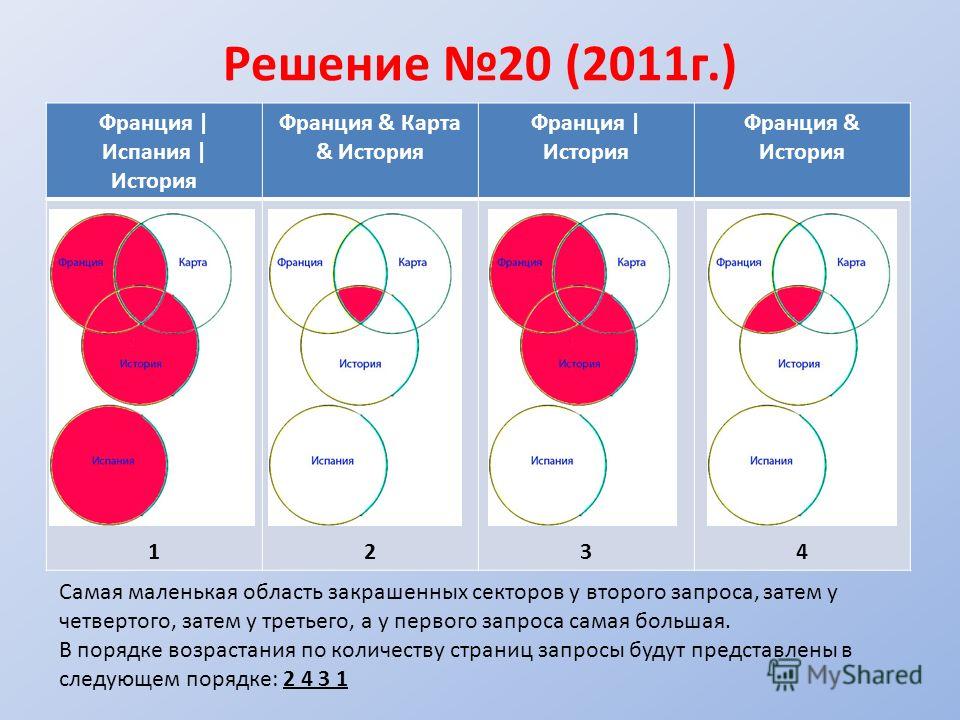 Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Список использованных источников
1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.
2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.
Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.
3. https://ru.wikipedia.org/wiki/
4. http://logika.vobrazovanie.ru
5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22
6. http://urok.1sept.ru/articles/550092/
7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera
страница 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Похожие работы
|
Круги Эйлера — страница №1/1 Круги Эйлера [править] Материал из Википедии — свободной энциклопедии Пример диаграммы Эйлера. Круги́ Э́йлера[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядногопредставления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях. Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2n комбинаций n свойств, то есть конечнуюбулеву алгебру. При n = 3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннеготреугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника. При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер(1841—1902) в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна(1843—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна. Множества А и B [править]Примечания
Эйлер, Леонард[править] Материал из Википедии — свободной энциклопедии В Википедии есть статьи о других людях с фамилией Эйлер.
Леона́рдЭ́йлер (нем. Эйлер — автор более чем 800 работ[1] по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать в Санкт-Петербург, куда переехал годом позже. С 1731 по 1741, а также с 1766 года был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь одновременно почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С. Круги Эйлера – задачи на пересечение или объединение множествЭто новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. «Обитаемый остров» и «Стиляги»Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». РешениеЧертим два множества таким образом: 6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров». Ответ. 5 человек смотрели только «Стиляги». Любимые мультфильмыСреди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. РешениеВ этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж: Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем: 21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов». 38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны». Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. «Мир музыки»В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. РешениеИзобразим эти множества на кругах Эйлера. Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры: Ответ: 6 покупателей купили диски и Максим, и Земфиры. Гарри Поттер, Рон и ГермионаНа полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?РешениеУчитывая условия задачи, чертеж будет таков: Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон. Пионерский лагерьВ пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?РешениеИзобразим множества следующим образом: 70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек. Ответ. 5 человек заняты только спортом. ЭкстримИз 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. РешениеВсеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде. Кофейные круги Эйлера Круги ЭйлераПримеры решения задач. Задача. В классе 25 учащихся. Из них 5 человек не умеют играть ни в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 — в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы? Решение. 25-5=20 человек играют и шашки и в шахматы, все 20 человек играют в шахматы, из них 18 играют в шашки. Следовательно, 18 человек играют и шашки и в шахматы. Задачи для самостоятельного решения. 2. Каждый из 35 пятиклассников является читателем по крайней мере одной из двух библиотек: школьной и районной. Из них 25 учащихся берут книги в школьной библиотеке, 20 — в районной. Сколько из пятиклассников: а) не являются читателями школьной библиотеки; б) не являются читателями районной библиотеки; в) являются читателями только школьной библиотеки; г) являются читателями только районной библиотеки; д) являются читателями обеих библиотек? 3. В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть вих: а) пересечении; б) объединении? 4. Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский язык изучают 25 человек, французский — 27 человек, а тот и другой —18 человек. Сколько всего учеников в классе? 5. На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. 6. В бригаде полеводов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? 7. В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое? 8. Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе — 12, причем отличников-спортсменов, увлекающихся лыжами, — 10? 9. 37 школьников из ученической производственной бригады изъявили желание летом работать на уборке зерновых. Каждый из них имеет права для работы на тракторе или на комбайне, а некоторые могут работать и на тракторе, и на комбайне. Сколько школьников могут работать и на тракторе, и на комбайне, если известно, что трактором хорошо овладели 23 человека, а комбайном — 31 человек? 1. На стол бросили две салфетки 10 см × 10 см, как показано на рисунке. равную 172 см 2 . Какова площадь их перекрытия? 2. В поход ходили 80% учеников класса, а на экскур- сии было 60% класса, причём каждый был в походе или на экскурсии? Сколько процентов класса были и там, и там? 3. В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом, а 10 ничем не занимаются. Сколь- ко ребят занимаются и математикой, и биологией? 4. Сколько существует целых положительных чисел, меньших 100, которые: а) делятся одновременно на 2 и на 3; б) делятся на 2, но не на 3; в) делятся на 3, но не на 2; г) делятся на 3 или на 2; д) не делятся ни на 2, ни на 3? 5. Большая группа туристов выехала в заграничное турне. Из них владеет английским языком 28 человек, французским — 13, не- мецким — 10, английским и французским — 8, французским и немецким — 5, английским и немецким — 6, всеми тремя языка- ми — двое, а 41 человек не владеет ни одним из трёх языков. Сколько всего туристов? 6. А — подмножество множества натуральных чисел, каждый эле- мент которого есть число, кратное или 2, или 3, или 5. Найдите число элементов в множестве A, если среди них 70 чисел, кратных 2; 60 чисел, кратных 3; 80 чисел, кратных 5; 32 числа кратных 6; 35 чисел, кратных 10; 38 чисел, кратных 15; 20 чисел, кратных 30. 7. Каждый из трёх игроков записывает 100 слов, после чего записи сравнивают. Если слово встретилось хотя бы у двоих, то его вы- чёркивают из всех списков. Могло ли случиться так, что у первого игрока осталось 61 слово, у второго — 80 слов, а у третьего — 82 слова? Для домашнего обдумывания 8. Каких натуральных чисел от 1 до 2006 больше: кратных 8, но не кратных 9, или тех, которые кратны 9, но не кратны 8? 9. Три ученика решили вместе 100 задач, при этом каждый из них решил ровно 60 задач. Будем называть задачу, которую решили все трое, лёгкой, а задачу, которую решил только один из них, — трудной. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Диаграмма Венна — Википедия Wiki Русский 2023
| This article uses material from the Wikipedia article Диаграмма Венна, which is released under the Creative Commons Attribution-ShareAlike 3.0 license («CC BY-SA 3.0»); additional terms may apply. (view authors). |
Не следует путать с диаграммой Эйлера.
Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение,разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество U{\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества[1][2].
Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов[3], для :
- описания функционирования формальных нейронов Мак-Каллока и сетей из них[4]
- синтеза надежных сетей из не вполне надежных элементов[5],
- построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств[6],
- получения логических следствий из заданной информации, минимизации формул исчислений[7][8].
 {n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм [10], понятие сети диаграмм, использующей диаграммы Венна как операторы[11].
Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.
Содержание
Show / HideСвязь диаграмм Эйлера и Венна
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами
22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера(снизу)
Диаграммы Эйлера в отличие от диаграмм Венна изображают отношения между множествами: непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами.

Диаграммы Венна основаны на существенно иной идее, чем круги Эйлера[12]. Круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики[12].
На рис. ниже даны диаграммы Эйлера и Венна для 3 множеств однозначных натуральных чисел:
- A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
- B={1,6}{\displaystyle B=\{1,\,6\}}
- C={4,7}{\displaystyle C=\{4,\,7\}}
диаграмма Эйлера
диаграмма Венна
Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают.На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу).Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

См. также
- Диаграмма Эйлера
- Карта Карно
Примечания
- ↑ Столл, 1968, с. 25.
- ↑ Нефедов, 1992, с. 8.
- ↑ Кузичев, 1968, с. 106.
- ↑ Кузичев, 1968, с. 171.
- ↑ Кузичев, 1968, с. 134.
- ↑ Кузичев, 1968, с. 9.
- ↑ Кузичев, 1968, с. 97.
- ↑ Столл, 1968, с. 26.
- ↑ Кузичев, 1968, с. 57.
- ↑ Кузичев, 1968, с. 124.
- ↑ Кузичев, 1968.
- ↑ 1 2 Кузичев, 1968, с. 25.
Ссылки
- Weisstein, Eric W. «Диаграмма Венна» (англ.) на сайте Wolfram MathWorld.
- Эпизод 412 Архивная копия от 21 апреля 2012 на Wayback Machine сериала Numb3rs — изображение диаграмм Венна для n=5,7,11{\displaystyle n=5,\;7,\;11} .
- Построение диаграмм Венна on-line Архивная копия от 18 мая 2016 на Wayback Machine для n=3,4,5{\displaystyle n=3,4,5} и исходный код.
Литература
- Столл Р.
 Множества, логика, аксиоматические теории. — М.: Мир, 1968. — 231 с.
Множества, логика, аксиоматические теории. — М.: Мир, 1968. — 231 с. - Нефедов В.Н., Осипова В.А. Курс дискретной математики. — М.: МАИ, 1992. — 264 с. — ISBN 5-7035-0157-X.
- Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.
🔥 Top trends keywords Русский Wiki:
Заглавная страницаГруппа ВагнераШанхайская организация сотрудничестваСлужебная:ПоискПригожин, Евгений ВикторовичЕлизавета IIYouTubeВторжение России на Украину (2022)Карл III (король Великобритании)Организация Договора о коллективной безопасностиДиана, принцесса УэльскаяИнгерманландияСоединённые Штаты АмерикиГоренко, Сергей СергеевичКонфликт на киргизско-таджикской границе (2021)РоссияВовк, Ангелина МихайловнаВалуйкиНур-СултанУткин, Дмитрий ВалерьевичКиргизияТаджикистанПутин, Владимир ВладимировичВКонтактеVK (компания)Елизавета ПетровнаСписок умерших в 2022 годуУильям, принц УэльскийДом ДраконаПотери сторон в период вторжения России на УкраинуКадыров, Рамзан АхматовичГеорг VIМаргарет, принцесса ВеликобританииФилипп, герцог ЭдинбургскийRobloxГарри, герцог СассекскийКамилла (королева-консорт Великобритании)Google (компания)Анна (принцесса Великобритании)NASAMSЯндексГоловкин, Геннадий Геннадьевич2021 годУкраина16 сентябряРеспублика Северная ИнгрияВластелин колец: Кольца властиM142 HIMARSБоуз-Лайон, ЕлизаветаКалифорнияPythonRuTracker.
 orgМоскваМеган, герцогиня СассекскаяОднопользовательская играTelegramКазахстанGoЛайвли, БлейкДамер, ДжеффриРоссийско-украинская войнаКэтрин, принцесса УэльскаяМногопользовательская играАнна ИоанновнаСтолкновения на азербайджано-армянской границе (сентябрь 2022)Сан-БруноИскандер (ракетный комплекс)Эндрю, герцог ЙоркскийДьявол носит Prada (фильм)Эдуард VIIIУзбекистанСамаркандГеорг VПервая мировая войнаЭдвард, граф УэссекскийСанкт-ПетербургВеликобританияСоюз Советских Социалистических РеспубликКонтрнаступление в Харьковской области (2022)🡆 More
orgМоскваМеган, герцогиня СассекскаяОднопользовательская играTelegramКазахстанGoЛайвли, БлейкДамер, ДжеффриРоссийско-украинская войнаКэтрин, принцесса УэльскаяМногопользовательская играАнна ИоанновнаСтолкновения на азербайджано-армянской границе (сентябрь 2022)Сан-БруноИскандер (ракетный комплекс)Эндрю, герцог ЙоркскийДьявол носит Prada (фильм)Эдуард VIIIУзбекистанСамаркандГеорг VПервая мировая войнаЭдвард, граф УэссекскийСанкт-ПетербургВеликобританияСоюз Советских Социалистических РеспубликКонтрнаступление в Харьковской области (2022)🡆 MoreRelated topics
14.4.1 Рисунки, круговые диаграммы, графики. Технологии лидерства [О Богах, Героях и Руководителях]
14.4.1
Рисунки, круговые диаграммы, графики
Графическое изображение задачи может свести сложную задачу к очевидной. Вот пример.
Буддийский монах выходит в 6 утра из монастыря и идет высоко в горы. Где-то он идет быстрее, где-то останавливается для отдыха. Он доходит до вершины горы к 4 часам дня.
 Там он предается медитации, затем ложится спать. В 6 утра следующего дня монах начинает спускаться вниз к монастырю. Дорога обратно также неравномерна. Он идет с разной скоростью, где-то отдыхает, где-то ускоряет шаг. Спускается и поднимается монах по одной и той же тропинке. Вопрос состоит в следующем: существует ли пространственная точка, которую монах минует в одно и то же время суток, когда он поднимается и когда спускается? Я не спрашиваю, где эта точка, я спрашиваю, есть ли она в принципе!
Там он предается медитации, затем ложится спать. В 6 утра следующего дня монах начинает спускаться вниз к монастырю. Дорога обратно также неравномерна. Он идет с разной скоростью, где-то отдыхает, где-то ускоряет шаг. Спускается и поднимается монах по одной и той же тропинке. Вопрос состоит в следующем: существует ли пространственная точка, которую монах минует в одно и то же время суток, когда он поднимается и когда спускается? Я не спрашиваю, где эта точка, я спрашиваю, есть ли она в принципе!Признайтесь, задача заставляет задуматься! Возможно, кому-то она покажется даже сложной. Хотя, может быть, у вас сейчас есть ощущение простоты, но вы не можете понять, в чем эта простота.
А теперь посмотрите на этот график! Ну, как? Естественно, что искомая точка неминуемо присутствует: это точка пересечения графиков. Изображая задачу, зрительно ее представляя, мы пришли к решению.
Разумеется, существует точка на тропинке, которую монах пересекает в одно и то же время суток, когда поднимается и когда спускается.
 Каждый день она может быть разной, но она есть! Для этого нам нужно было нарисовать график, представить вопрос наглядно.
Каждый день она может быть разной, но она есть! Для этого нам нужно было нарисовать график, представить вопрос наглядно.Еще один возможный способ представления задачи – круги Эйлера. Говорят, математик Эйлер придумал свои знаменитые круги-диаграммы, когда обучал немецкую принцессу законам логики. Попробуем представить следующую задачу, используя кругл Эйлера. Представим себе следующую проблему.
Рис. 39. Буддийский монах
В компании существует отдел продаж и отдел маркетинга. Менеджеры отдела продаж продают своим клиентам по схеме: холодный звонок – коммерческое предложение – повторный звонок – ветреча – письменное предложение индивидуального решения – повторная встреча – заказ. Естественно, что на каждом этапе сделка может сорваться, какой-то этап можно перепрыгнуть, к какой-то стадии приходится возвращаться снова. За каждым из менеджеров по продажам закреплена своя территория.
Отдел маркетинга планирует рекламу и акции по стимулированию сбыта.
 Также маркетологи планируют и организуют конференции и обучающие семинары для потенциальных, новых и постоянных клиентов. Проблема заключается в том, что менеджеры по продажам не всегда говорят маркетологам, с какими клиентами они уже работают, с какими ведут предварительные переговоры. Также отдел продаж редко сообщает о пожеланиях клиентов и их жалобах, полагая, что маркетологи и так это должны знать. Отдел маркетинга, в свою очередь, не всегда оповещает менеджеров по продажам о готовящихся рекламных и стимулирующих акциях. Также результаты исследований, проводимых отделом маркетинга, носят внутренний, закрытый характер и, если и выходят вовне, то попадают на стол генерального директора, но не в руки менеджеров по продажам.
Также маркетологи планируют и организуют конференции и обучающие семинары для потенциальных, новых и постоянных клиентов. Проблема заключается в том, что менеджеры по продажам не всегда говорят маркетологам, с какими клиентами они уже работают, с какими ведут предварительные переговоры. Также отдел продаж редко сообщает о пожеланиях клиентов и их жалобах, полагая, что маркетологи и так это должны знать. Отдел маркетинга, в свою очередь, не всегда оповещает менеджеров по продажам о готовящихся рекламных и стимулирующих акциях. Также результаты исследований, проводимых отделом маркетинга, носят внутренний, закрытый характер и, если и выходят вовне, то попадают на стол генерального директора, но не в руки менеджеров по продажам.Таков общий рисунок проблемной ситуации. Кстати, она вам ничего не напоминает? Давайте попробуем применить круги Эйлера для наглядного обозначения проблемы. Площадь кругов – это информация, которая появляется у отдела маркетинга и отдела продаж соответственно.
 Естественно, сейчас круто пересекаются но не совпадают.
Естественно, сейчас круто пересекаются но не совпадают.Рис. 40. Пересечение отдела маркетинга и отдела продаж
Для того чтобы открыть замок, иногда нужно просто пошевелить ключом и попробовать разные положения. Давайте нарисуем несколько сочетаний, каждое из которых может символически предлагать решение проблемы.
Рис. 41. Отдел маркетинга внутри отдела продаж
В центре отдел маркетинга, его окружает отдел продаж, которые и контактирует с клиентами. Все действия отдела маркетинга происходят через отдел продаж. Плюс: менеджеры по продажам знают желания и цели отдела маркетинга. Минусы: не вся информация извне может возвращаться во внутренний круг, к маркетологам; маркетологи теряют живую связь с внешней средой и становятся кабинетными (рис. 42).
Два полукруга соединены общей границей. Каждый отдел контактирует по своим задачам с рынком. Что может быть этой чертой? Ведь сразу возникает такой вопрос. Помните, в начале главы, посвященной лидерству и команде, мы говорили, что самым главным вопросом лидерства является вопрос границ.

Рис. 42. Четкая граница между отделом маркетинга и отделом продаж
Что может быть данной границей контакта? Наши версии: компьютерная программа, в которой учитываются все взаимодействия с клиентами и которая доступна всем; специальный координатор, согласующий действия отдела маркетинга и отдела продаж (таким координатором может быть и коммерческий директор, которому подчиняются оба отдела).
Как мало действий с нашей стороны, и как много мыслей в нашей голове! В каждой простоте есть свое очарование. Представление задачи в виде кругов Эйлера натравляет нашу мысль по нескольким тропкам, каждая из которых может оказаться в результате дорогой к успеху в бизнесе. Вы можете самостоятельно продолжить экспериментировать с кругами, а мы двигаемся дальше.
Данный текст является ознакомительным фрагментом.
Глава 40 Спектр графики
Глава 40 Спектр графики Жизнь в тихом отчаянии В 1845 году американский писатель, мыслитель и натуралист Генри Торо почувствовал потребность сменить обстановку.
 Уединившись на тихом озере в Беркширских горах, он прожил там два года. О своей тогдашней жизни он написал книгу
Уединившись на тихом озере в Беркширских горах, он прожил там два года. О своей тогдашней жизни он написал книгуПодготовка методических материалов Assessment Center (модель компетенций, упражнения, инструкции, бланки, графики наблюдений)
Подготовка методических материалов Assessment Center (модель компетенций, упражнения, инструкции, бланки, графики наблюдений) Данный этап стал одним из наиболее длительных и трудозатратных для команды организаторов. Существующая модель, состоявшая на тот момент из 14
Диаграмма Эйлера
Вызов:
Википедия
Август 03, 2021
Не следует путать с диаграммой Эйлера — Венна.
Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
 Первое их использование приписывают Леонарду Эйлеру[⇨]. Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна[⇨].
Первое их использование приписывают Леонарду Эйлеру[⇨]. Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна[⇨].Пример кругов Эйлера. Буквами обозначены, например, свойства:B{\displaystyle B}
— живое существо,A{\displaystyle A}
— человек,C{\displaystyle C}
— неживая вещь
Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.
На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.
Содержание
- 1История
- 2Связь диаграмм Эйлера и Венна
- 3Примеры
- 4См.
 также
также - 5Примечания
- 6Литература
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.
Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики.
 {n}} комбинацийn{\displaystyle n} свойств, то есть конечную булеву алгебру. Приn=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
{n}} комбинацийn{\displaystyle n} свойств, то есть конечную булеву алгебру. Приn=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:
- A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
- B={1,6}{\displaystyle B=\{1,\,6\}}
- C={4,7}{\displaystyle C=\{4,\,7\}}
диаграмма Эйлера
диаграмма Венна
Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

На рисунке внизу дана Диаграмма Эйлера, иллюстрирующая тот факт, что множество существ с 4 конечностями является подмножеством животных, которое не пересекается с множеством минералов.
Диаграмма Эйлера
- Список объектов, названных в честь Леонарда Эйлера
- Окружности Вилларсо
- Диаграмма Венна
- Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
- Кузичев, 1968, с. 25.
- Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.
Диаграмма, Эйлера, Язык, Следить, Править, Не, следует, путать, диаграммой, Эйлера, Венна, Диагра, ммы, йлера, круги, йлера, геометрическая, схема, помощью, которой, можно, изобразить, отношения, между, подмножествами, для, наглядного, представления, Первое, и. Diagramma Ejlera Yazyk Sledit Pravit Ne sleduet putat s diagrammoj Ejlera Venna Diagra mmy E jlera krugi E jlera geometricheskaya shema s pomoshyu kotoroj mozhno izobrazit otnosheniya mezhdu podmnozhestvami dlya naglyadnogo predstavleniya Pervoe ih ispolzovanie pripisyvayut Leonardu Ejleru Ispolzuetsya v matematike logike menedzhmente i drugih prikladnyh napravleniyah Ne sleduet ih putat s diagrammami Ejlera Venna Primer krugov Ejlera Bukvami oboznacheny naprimer svojstva B displaystyle B zhivoe sushestvo A displaystyle A chelovek C displaystyle C nezhivaya vesh Diagrammy Ejlera takzhe nazyvayut krugami Ejlera Pri etom krugi eto uslovnyj termin vmesto krugov mogut byt lyubye figury Na diagrammah Ejlera mnozhestva izobrazhayutsya krugami ili drugimi figurami Prichyom neperesekayushiesya mnozhestva izobrazheny neperesekayushimisya krugami a podmnozhestva izobrazheny vlozhennymi krugami Naprimer diagramma na risunke pokazyvaet chto mnozhestvo A yavlyaetsya podmnozhestvom B a B ne peresekaetsya s C Soderzhanie 1 Istoriya 2 Svyaz diagramm Ejlera i Venna 3 Primery 4 Sm takzhe 5 Primechaniya 6 LiteraturaIstoriya PravitPri reshenii celogo ryada zadach Leonard Ejler ispolzoval ideyu izobrazheniya mnozhestv s pomoshyu krugov Odnako etim metodom eshyo do Ejlera polzovalsya vydayushijsya nemeckij filosof i matematik Gotfrid Vilgelm Lejbnic Lejbnic ispolzoval ih dlya geometricheskoj interpretacii logicheskih svyazej mezhdu ponyatiyami no pri etom vsyo zhe predpochital ispolzovat linejnye shemy 1 No dostatochno osnovatelno razvil etot metod sam L Ejler Metodom krugov Ejlera polzovalsya i nemeckij matematik Ernst Shryoder v knige Algebra logiki Osobennogo rascveta graficheskie metody dostigli v sochineniyah anglijskogo logika Dzhona Venna podrobno izlozhivshego ih v knige Simvolicheskaya logika izdannoj v Londone v 1881 godu Venn predlozhil svoyu shemu izobrazheniya otnosheniya mezhdu mnozhestvami kotoraya teper nazyvaetsya diagrammami Ejlera Venna Pervonachalno krugi Ejlera voznikli na osnove idej sillogistiki Aristotelya Diagrammy Venna byli sozdany dlya resheniya zadach matematicheskoj logiki Ih osnovnaya ideya razlozheniya na konstituenty voznikla na osnove algebry logiki 2 Svyaz diagramm Ejlera i Venna Pravit Primer polucheniya proizvolnyh krugov Ejlera iz diagramm Venna s pustymi chyornymi mnozhestvami 22 iz 256 sushestvenno razlichnyh diagramm Venna s 3 krugami sverhu i sootvetstvuyushie im diagrammy Ejlera snizu Diagrammy Ejlera Venna v otlichie ot diagramm Ejlera izobrazhayut vse 2 n displaystyle 2 n kombinacij n displaystyle n svojstv to est konechnuyu bulevu algebru Pri n 3 displaystyle n 3 diagramma Ejlera Venna obychno izobrazhaetsya v vide tryoh krugov s centrami v vershinah ravnostoronnego treugolnika i odinakovym radiusom priblizitelno ravnym dline storony treugolnika Na ris nizhe dany diagrammy Venna i Ejlera dlya 3 mnozhestv odnoznachnyh naturalnyh chisel A 1 2 5 displaystyle A 1 2 5 B 1 6 displaystyle B 1 6 C 4 7 displaystyle C 4 7 diagramma Ejlera diagramma Venna Inogda esli kakaya to kombinaciya svojstv sootvetstvuet pustomu mnozhestvu to etu kombinaciyu zakrashivayut Na risunke sprava dany 22 sushestvenno razlichnyh diagramm Venna s 3 krugami sverhu i sootvetstvuyushie im diagrammy Ejlera snizu Nekotorye iz diagramm Ejlera ne tipichny a nekotorye dazhe ekvivalentny diagrammam Venna Chernye oblasti ukazyvayut na to chto v nih net elementov pustye mnozhestva Primery PravitNa risunke vnizu dana Diagramma Ejlera illyustriruyushaya tot fakt chto mnozhestvo sushestv s 4 konechnostyami yavlyaetsya podmnozhestvom zhivotnyh kotoroe ne peresekaetsya s mnozhestvom mineralov Diagramma EjleraSm takzhe PravitSpisok obektov nazvannyh v chest Leonarda Ejlera Okruzhnosti Villarso Diagramma VennaPrimechaniya Pravit Leibniz G W Opuscules et fragments inedits de Leibniz Paris 1903 p 293 321 Kuzichev 1968 s 25 Literatura PravitKuzichev A S Diagrammy Venna Istoriya i primeneniya M Nauka 1968 249 s Istochnik https ru wikipedia org w index php title Diagramma Ejlera amp oldid 114474165, Википедия, чтение, книга, библиотека, поиск, нажмите,
истории
, книги, статьи, wikipedia, учить, информация, история, секс, порно, скачать, скачать, sex, seks, porn, porno, скачать, бесплатно, скачать бесплатно, mp3, видео, mp4, 3gp, jpg, jpeg, gif, png, картинка, музыка, песня, фильм, игра, игрыКруги Эйлера.
 Персональная страничка Ю. Выбойченко
Персональная страничка Ю. ВыбойченкоЭйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783).
Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля.
Условно принято, что круг наглядно изображает объем одного какого-нибудь понятия. Объем же понятия отображает совокупность предметов того или иного класса предметов. Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга, как это показано на рисунке:
Группа предметов, составляющая вид данного класса предметов, изображается в виде меньшего круга, нарисованного внутри большего круга, как это сделано на рисунке.
Такое именно отношение существует между объемами понятий «небесное тело» (А) и «комета» (B).
 Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
В тех случаях, когда объемы двух понятий совпадают только частично, отношение между объемами таких понятий изображается посредством двух перекрещивающихся кругов, как это показано на рисунке:
Такое именно отношение существует между объемом понятий «учащийся» и «комсомолец». Некоторые (но не все) учащиеся являются комсомольцами; некоторые (но не все) комсомольцы являются учащимися. Незаштрихованная часть круга А отображает ту часть объема понятия «учащийся», которая не совпадает с объемом понятия «комсомолец»; незаштрихованная часть круга B отображает ту часть объема понятия «комсомолец», которая не совпадает с объемом понятия «учащийся». 3аштрихованиая часть, являющаяся общей для обоих кругов, обозначает учащихся, являющихся комсомольцами, и комсомольцев, являющихся учащимися.

Когда же ни один предмет, отображенный в объеме понятия A, не может одновременно отображаться в объеме понятия B, то в таком случае отношение между объемами понятий изображается посредством двух кругов, нарисованных один вне другого. Ни одна точка, лежащая на поверхности одного круга, не может оказаться на поверхности другого круга.
Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.
Отношения между равнозначащими понятиями, объемы которых совпадают, отображаются наглядно посредством одного круга, на поверхности которого написаны две буквы, обозначающие два понятия, имеющие один и тот же объем:
Такое отношение существует, например, между понятиями «родоначальник английского материализма» и «автор „Нового Органона“».
 Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.
Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.
Нередко бывает и так: одному понятию (родовому) подчиняется сразу несколько видовых понятий, которые в таком случае называются соподчиненными. Отношение между такими понятиями изображается наглядно посредством одного большого круга и нескольких кругов меньшего размера, которые нарисованы на поверхности большего круга:
Такое именно отношение существует между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия в равной мере подчинены одному общему родовому понятию «музыкальные инструменты».
Круги, изображающие соподчиненные понятия, не должны касаться друг друга и перекрещиваться, так как объемы соподчиненных понятий несовместимы; в содержании соподчиненных понятий имеются, наряду с общими, различающие признаки. Эта схема отображает общее, что характерно для отношения любых соподчиненных понятий, взятых из различных областей знания.
 Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.
Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.
В тех случаях, когда между понятиями имеется отношение противоположности, отношение между объемами таких понятий отображается посредством одного круга, обозначающего общее для обоих противоположных понятий родовое понятие, а отношение между противоположными понятиями обозначается так: А — родовое понятие, B и C — противоположные понятия. Противоположные понятия исключают друг друга, но входят в один и тот же род, что можно выразить такой схемой:
При этом видно, что между противоположными понятиями возможно третье, среднее, так как они не исчерпывают полностью объема родового понятия. Такое именно отношение существует между понятиями «легкий» и «тяжелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и легкий, и тяжелый.
 Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
Когда же между понятиями существует противоречащее отношение, тогда отношение между объемами понятий изображается иначе: круг делится на две части так: А — родовое понятие, B и не-B (обозначается как ¬B) — противоречащие понятия. Противоречащие понятия, исключают друг друга и входят в один и тот же род, что можно выразить такой схемой:
При этом видно, что между противоречащими понятиями третье, среднее, невозможно, так как они полностью исчерпывают объем родового понятия. Такое отношение существует, например, между понятиями «белый» и «не-белый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и белый и не-белый.
Посредством эйлеровых кругов изображаются также отношения между объемами субъекта и предиката в суждениях. Так, в общеутвердительном суждении, выражающем определение какого-либо понятия, объемы субъекта и предиката, как известно, равны.
 Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке:
Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке:
Иначе выглядит схема отношения между объемами субъекта и предиката в общеутвердительном суждении, не являющемся определением понятия. В таком суждении объем предиката больше объема субъекта, объем субъекта целиком входит в объем предиката. Поэтому отношение между ними изображается посредством большого и малого кругов, как показано на рисунке:
Примером первого вида отношений между объемами субъекта и предиката может служить суждение: «Все квадраты — равносторонние прямоугольники»; примером второго вида отношений между объемами предиката и субъекта может служить суждение: «Все квадраты — геометрические фигуры».
Эйлеровы круги применяются также и для наглядного изображения отношений между терминами силлогизма.
 Например, силлогизм
Например, силлогизм
- Всякое A есть B;
- Некоторые C есть A;
- Некоторое С есть В
Выражен им в виде такой схемы:
Тот факт, что какая-то часть пространства В включается в пространство С, Эйлер выражал звездочкой, как это показано на следующей схеме
Диаграммы Эйлера своим наглядным графическим изображением не только облегчают запоминание структуры различных сочетаний мыслей, но и помогают решению ряда задач, стоящих перед формальной логикой.
Давно известно, что с помощью эйлеровых кругов легко можно проверить истинность, например, того или иного вида непосредственного умозаключения. Для этого надо сравнить условие (антецедент) и следствие (консеквент) данного непосредственного умозаключения с диаграммами Эйлера. Правило сравнения гласит: если какая-либо из диаграмм, отвечающих условию (антецеденту), не совпадает ни с одной из диаграмм, отвечающих заключению, то этот вид непосредственного умозаключения является ложным.

Теперь допустим необходимо решить: истинно или ложно такое, например, непосредственное умозаключение: «Все S суть Р, следовательно, некоторые Р суть S».
Поскольку условием в этом непосредственном умозаключении является общеутвердительное суждение, то его обозначают латинской буквой А (от affirmance), а все суждение кратко записать так: Asp; следствием в этом непосредственном умозаключении является частноутвердительное суждение, которое обозначается латинской буквой I, а все суждение кратко записать так: Ips. Теперь данное непосредственное умозаключение будет выглядеть так:
Asp Ips.
где — знак импликации, сходный с союзом «если … , то … ».
После этого обратимся к диаграммам Эйлера, в которых отражены структуры всех категорических суждений относительно непустых множеств. Такими диаграммами могут быть пять следующих диаграмм:
Аsр
Isp
Iрs
ОрsАsр
Арs
Isр
IpsАрs
Isр
Iрs
ОsрIsp
Iрs
Оsр
OpsЕsр
Ерs
Osp
ОрsПод каждой диаграммой даны суждения, которые отображены этой диаграммой.
 Как видно, суждению Asp, находящемуся в условии, соответствуют первая и вторая диаграммы, а суждению Ips, находящемуся в следствии, соответствуют третья и четвертая диаграммы. Анализ показывает, что в составе первой и второй диаграмм имеются суждения Ips, следовательно, диаграммы, соответствующие условию, совпадают с обеими диаграммами, соответствующими следствию. Значит, данный вид непосредственного умозаключения Asp Ips — является истинным. Возьмем какой-нибудь конкретный пример: если все конъюнкции суть сложные высказывания, то истинным следствием из этого суждения будет суждение: «некоторые сложные высказывания суть конъюнкции».
Как видно, суждению Asp, находящемуся в условии, соответствуют первая и вторая диаграммы, а суждению Ips, находящемуся в следствии, соответствуют третья и четвертая диаграммы. Анализ показывает, что в составе первой и второй диаграмм имеются суждения Ips, следовательно, диаграммы, соответствующие условию, совпадают с обеими диаграммами, соответствующими следствию. Значит, данный вид непосредственного умозаключения Asp Ips — является истинным. Возьмем какой-нибудь конкретный пример: если все конъюнкции суть сложные высказывания, то истинным следствием из этого суждения будет суждение: «некоторые сложные высказывания суть конъюнкции».
Рассмотрим еще такое непосредственное умозаключение: «Некоторые S суть Р, следовательно, ни одно Р не есть S». Мы уже знаем, что частноутвердительное суждение, находящееся в условии, можно записать символически так: Isp, а общеотрицательное суждение, находящееся в следствии, обозначается буквой Е. Теперь данное непосредственное умозаключение будет выглядеть так: Isp Eps.

Посмотрим, что скажут нам диаграммы об этом непосредственном умозаключении. Суждению Isp, находящемуся в условии, соответствуют первая, вторая, третья и четвертая диаграммы, а суждению Eps, находящемуся в следствии, соответствует пятая диаграмма. Значит, ни одна из диаграмм, отвечающих условию, не совпадает ни с одной из диаграмм (в данном случае с одной единственной диаграммой), отвечающих следствию. А раз так, то данное непосредственное умозаключение является ложным.
Некоторые философы скептически относятся к применению эйлеровых кругов, видя в этом какой-то школьный примитив. Но они, конечно, неправы. Отрицать наглядные схемы в логике — это значит не понимать значения моделирования логических процессов и действий. Как правильно замечает rрузинский логик Л. П. Гокиели, эйлеровы круги «Играют определенную вспомогательную роль, и если учитывать эту роль, соблюдать меру и их осторожно применять … то нет никакого основания уклоняться от их использования». А. О. Маковельский справедливо считает, что «эйлеровы круги» придали учениям об отношении субъекта и предиката в суждении и об отношении терминов в категорическом силлогизме «прозрачную ясность»; углубляя анализ суждений и умозаключений они вместе с тем обладают дидактическими достоинствами, облегчая усвоение сложных логических проблем.

Категория:Диаграммы Эйлера — Wikimedia Commons
Взято из Викисклада, бесплатного хранилища мультимедиа
Перейти к навигацииПерейти к поиску
Английский: Диаграммы Эйлера — это диаграммы, используемые для иллюстрации рассуждений.
Статья Диаграммы Эйлера в проектах Википедии:
- (en) Диаграмма Эйлера
- (de) Mengendiagramm 9002es 9002es0021 Diagrama de Euler
- (ja) オイラー図
- (pt) Diagrama de Euler
- (sv) venndiagram
- (zh) 欧拉图
- +/−
Subcategories
Эта категория имеет следующие 7 подкатегорий, всего 7.

C
Классическая теория познания; Диаграммы Эйлера (36 F)
Соответствующие диаграммы Венна и Эйлера (5 F)
Медиа в категории «Диаграммы Эйлера»
Следующие 154 файла находятся в этой категории, всего 154.
3 набора Диаграмма Эйлера общего назначения B.svg 348 × 192; 8 КБ
3 набора Диаграмма Эйлера общего назначения empty.svg 455 × 447; 13 КБ
3 набора Диаграмма Эйлера общего назначения.svg 348 × 192; 4 КБ
3-множественная диаграмма Эйлера.svg 645 × 421; 7 КБ
3VT.jpg 1104 × 746; 67 КБ
4set пересечение.png 400 × 300; 10 КБ
Диаграмма свойств аминов кислот Venn AR.svg 830 × 750; 108 КБ
Аминокислоты Диаграмма Венна (de).svg 400 × 255; 22 КБ
Аминокислоты Диаграмма Венна (исп).svg 410 × 255; 20 КБ
Аминокислоты Диаграмма Венна.
 png
400 × 255; 15 КБ
png
400 × 255; 15 КБ Аминокислоты Диаграмма Венна 2.png 400 × 255; 21 КБ
Кажется, Мемориал Линкольна.svg 845 × 532; 8 КБ
Argumento con ocho premisas en el charta de Marlo.jpg 3780 × 3633; 1,09 МБ
Биографии в армянской Википедии (а), английской Википедии (б) и русской Википедии (в) — август 2016.png 720 × 650; 27 КБ
Биографии армян в армянской Википедии (а), английской Википедии (б) и русской Википедии (в) — август 2016.png 720 × 650; 32 КБ
Хомский.svg 232 × 234; 24 КБ
КругиN4a.GIF 486 × 458; 9 КБ
КругиN4b.png 588 × 468; 15 КБ
Классы сложности sr en.svg 414 × 255; 3 КБ
Conclusión desde dos premisas negativas en el charta de Marlo.jpg 2634 × 1433; 630 КБ
Conhecimento-Diagrama.png 360 × 298; 8 КБ
Conhecimento-Diagrama.
 svg
360 × 298; 5 КБ
svg
360 × 298; 5 КБ Соединения 02.svg 300 × 200; 8 КБ
Соединения 03.svg 300 × 200; 8 КБ
Соединения 04.svg 300 × 200; 8 КБ
Conjuntos.png 200 × 600; 33 КБ
Conjutos.svg 300 × 900; 11 КБ
Couturat 1914 и Vennassignments1.jpg 1700 × 800; 96 КБ
Csa-venn.jpg 339 × 276; 12 КБ
Д-Катена-02.jpg 239 × 184; 23 КБ
Диаграмма де Марло. Презентация и оформление помещений.ogv 15 мин 54 с, 1920 × 1080; 118,81 МБ
Disjunkte.png 187 × 122; 13 КБ
Вывод DoThieuler.JPG 431 × 117; 11 КБ
Экономическая структура современного общества.svg 1053 × 634; 344 КБ
Ejemplo de convertes complejas en el charta de Marlo.jpg 3048 × 3316; 808 КБ
Ejemplo de repulsión universal en el charta de Marlo.
 jpg
2822 × 2133; 786 КБ
jpg
2822 × 2133; 786 КБ Ejemplo de silogismo исчерпывающее в эль-диаграмме де Марло.jpg 3543 × 4062; 1,67 МБ
Ejemplo de silogismo por repulsion nula en el charta de Marlo.jpg 3448 × 4726; 1,55 МБ
Ejemplo de silogismo por síntesis en el charta de Marlo.jpg 3543 × 4225; 1,68 МБ
Ejemplo de silogismo resuelto por repulsión parcial en el charta de Marlo.jpg 3543 × 2617; 1,2 МБ
Ejemplo de síntesis a partir de dos modelos universales en el charta de Marlo.jpg 3543 × 3854; 1,39 МБ
Ejemplo de síntesis parcial en el charta de Marlo.jpg 2,490 × 2325; 814 КБ
Ejemplo de síntesis probable en el charta de Marlo.jpg 3543 × 3695; 1,45 МБ
Ejercicio de repulsión resuelto por síntesis de supuestos en el charta de Marlo.jpg 3543 × 2617; 995 КБ
Ejercicio resuelto por transformación en el charta de Marlo.
 jpg
3544 × 4726; 1,98 МБ
jpg
3544 × 4726; 1,98 МБ ElginMarbles.png 473 × 500; 46 КБ
ElginMarbles.svg 473 × 500; 2 КБ
Диаграммы Эйлера и Венна.svg 660 × 600; 1 КБ
Диаграмма Эйлера для jp charsets-en.svg 800 × 596; 5 КБ
Диаграмма Эйлера для jp charsets-ja.svg 800 × 596; 5 КБ
Диаграмма Эйлера — B является подмножеством A.png 1024 × 1024; 27 КБ
Диаграмма Эйлера — x в A.png 1024 × 1024; 19 КБ
Диаграмма Эйлера — x не находится в A.png 1024 × 1024; 19 КБ
Диаграмма Эйлера Все A являются B и все C являются B.svg 921 × 567; 3 КБ
Диаграмма Эйлера Все A являются B, которые являются C(X).svg 496 × 390; 2 КБ
Диаграмма Эйлера Все A являются B, которые являются C.svg 496 × 390; 2 КБ
Диаграмма Эйлера Все A являются B(X), которые являются C.
 svg
496 × 390; 2 КБ
svg
496 × 390; 2 КБ Диаграмма Эйлера Все A являются B(X).svg 390 × 283; 2 КБ
Диаграмма Эйлера Все A являются B.svg 390 × 283; 2 КБ
Диаграмма Эйлера Все A(X) являются B, которые являются C.svg 496 × 390; 2 КБ
Диаграмма Эйлера Все A(X) являются B.svg 390 × 283; 2 КБ
Диаграмма Эйлера Все Нет A являются B.svg 638 × 283; 2 КБ
Диаграмма Эйлера Все Нет A(X) являются B.svg 638 × 283; 2 КБ
Диаграмма Эйлера наборов чисел.svg 512 × 341; 10 КБ
Диаграмма Эйлера Некоторые A являются B.svg 602 × 283; 3 КБ
Диаграмма Эйлера Некоторые A не являются B.svg 602 × 283; 3 КБ
Диаграмма Эйлера, используемая для представления эффекта близости.svg 276 × 272; 671 байт
Диаграмма Эйлера.svg 323 × 287; 4 КБ
Диаграмма Эйлера и Венна.
 png
580 × 490; 17 КБ
png
580 × 490; 17 КБ Эйлер-b-часть-a.svg 241 × 176; 8 КБ
Euler-diag-2-classes-disjunct.png 678 × 433; 35 КБ
Euler-diag-3-classes-disjunct.png 570 × 420; 34 КБ
Эйлер-венн-example.png 424 × 340; 24 КБ
Euler2-3-vectorisé.svg 700 × 200; 1 КБ
Эйлер2-3.png 700 × 200; 41 КБ
Эйлер2а.png 200 × 150; 12 КБ
Euler2b.png 240 × 150; 14 КБ
Euler2c.png 275 × 150; 13 КБ
Эйлер3-3a.png 720 × 240; 8 КБ
Эйлер3-3b.png 730 × 210; 7 КБ
Эйлер3а.PNG 210 × 160; 2 КБ
Эйлер3b.PNG 270 × 150; 2 КБ
Euler3c.PNG 270 × 150; 2 КБ
Эйлер3d.PNG 250 × 150; 2 КБ
Эйлер3е.PNG 336 × 150; 2 КБ
Euler3f.
 PNG
200 × 150; 2 КБ
PNG
200 × 150; 2 КБ Окружности Эйлера.jpg 753 × 553; 49 КБ
Пример непопарно непересекающегося семейства наборов.svg 410 × 235; 8 КБ
Эксклюзивные события.png 495 × 308; 11 КБ
ФилиппиноВенн.jpg 614 × 475; 33 КБ
Официальные языки uk.svg 250 × 230; 3 КБ
Формальные языки-ru.svg 250 × 230; 4 КБ
Формальные языки.svg 250 × 230; 3 КБ
Формы органического вещества.webp 2967 × 2185; 1002 КБ
Грубость и неправомерное поведение.svg 909 × 689; 18 КБ
FractionatedSpacecraft2.svg 556 × 534; 5 КБ
Гирих+ Диаграмма v6.7 Exerpts-foor-Wikipedia.png 1268 × 1342; 136 КБ
Гамильтон 1881 пример.jpg 567 × 685; 190 КБ
Лекции Гамильтона по логике 1874 Диаграммы Эйлера.png 1993 × 2286; 805 КБ
Омограф омоним Венна диаграмма.
 svg
512 × 576; 5 КБ
svg
512 × 576; 5 КБ Масштаб иллюстраций Identity Fusion.png 1011 × 284; 75 КБ
Имплизиерт.png 187 × 122; 16 КБ
Интерпретация моделей в диаграмме Марло.jpg 2835 × 3543; 1,48 МБ
Пересечения двух наборов и их дополнений.svg 1800 × 985; 78 КБ
IPA-euler-manners-features.svg 654 × 686; 171 КБ
Ке 8.jpg 342 × 338; 80 КБ
Дополнение.png 184 × 121; 5 КБ
Комплемент2.png 186 × 121; 11 КБ
Комплемент3.png 186 × 121; 11 КБ
Käsitekartta kansantaloudesta 001.svg 1055 × 634; 329КБ
Mengendiagramme.webm 4 мин 41 с, 1280 × 720; 29,89 МБ
Диаграмма Милна-Эдвардса.pdf 1650 × 1275; 296 КБ
Модель пропозициональной диаграммы де Марло.jpg 3546 × 2846; 844 КБ
Перекрытие.
 svg
259 × 191; 16 КБ
svg
259 × 191; 16 КБ Особенности и преобразование1.jpg 1835 × 1465; 285 КБ
Выберите любые два venn.svg 455 × 447; 6 КБ
Проект-треугольник-es.svg 455 × 447; 5 КБ
Проект-треугольник.svg 455 × 447; 8 КБ
Представление и преобразование универсальных предложений на диаграмме Марло.jpg 3017 × 2387; 510 КБ
Отталкивание на диаграмме Марло.jpg 986 × 1222; 554 КБ
Социально-экологическая модель.png 470 × 737; 74 КБ
Standardsemantik klein.png 275 × 193; 17 КБ
Стандартсемантик.png 641 × 449; 55 КБ
Стереотипные пространства -1.jpg 533 × 585; 38 КБ
Наднациональные европейские органы с членами НАТО-en.svg 870 × 726; 377 КБ
Szabálytalanságok és kotelezettségszegések.png 787 × 597; 49 КБ
Síntesis a partir de premisas negativas en el charta de Marlo.
 jpg
3,543 × 3,695; 1,64 МБ
jpg
3,543 × 3,695; 1,64 МБ Четыре Зоаса.jpg 1190 × 1083; 666 КБ
Богословские позиции.png 593 × 593; 105 КБ
Богословские позиции.svg 513 × 471; 64 КБ
Преобразование предложений в диаграмму Марло.jpg 2324 × 4574; 1,14 МБ
URI Диаграмма Венна.svg 601 × 376; 1 КБ
Валси.png 965 × 485; 23 КБ
Вейтч и Карно 3.jpg 500 × 320; 25 КБ
Таблица истинности Вейча и Карно 2.jpg 1843 × 450; 125 КБ
Таблица истинности Вейча и Карно 3.jpg 1843 × 450; 357 КБ
Таблица истинности Вейча и Карно 4.jpg 1843 × 450; 350 КБ
Venn 1881 p 115-116 pasteup.jpg 565 × 725; 76 КБ
Диаграмма Венна — B является подмножеством A.svg 210 × 210; 2 КБ
Диаграмма Венна — x находится в A.svg 210 × 210; 2 КБ
Диаграмма Венна — x отсутствует в A.
 svg
210 × 210; 2 КБ
svg
210 × 210; 2 КБ Диаграмма Венна 2.png 256 × 256; 6 КБ
Venn Диаграмма языковой проблемы space.svg 512 × 436; 130 КБ
Диаграмма Венна из трех наборов.svg 216 × 207; 8 КБ
Диаграмма Венна-ABC.svg 250 × 158; 7 КБ
Венн.jpg 254 × 143; 5 КБ
Венн.png 640 × 480; 8 КБ
VennSubset.jpg 1653 × 1148; 65 КБ
Ver3benzu-RU.PNG 599 × 446; 60 КБ
Ver3benzu.PNG 599 × 446; 38 КБ
Veranschaulichung des Begriffs der Teilmenge.svg 691 × 690; 316 КБ
Волновая модель Schmidt.jpeg 445 × 545; 18 КБ
Волновая модель Schmidt.svg 334 × 409; 17 КБ
Странная машина.png 1780 × 610; 98 КБ
Диаграмма Венна — Википедия, бесплатная энциклопедия теги:
Из Википедии, свободной энциклопедии
Перейти к: навигация, поиск
Диаграмма Венна множеств A, B и C
Диаграммы Венна или диаграммы множеств — это диаграммы, которые показывают все гипотетически возможные логические отношения между конечным набором множеств (групп вещей).
 Диаграммы Венна были придуманы примерно в 1880 году Джоном Венном. Они используются во многих областях, включая теорию множеств, вероятность, логику, статистику и информатику.
Диаграммы Венна были придуманы примерно в 1880 году Джоном Венном. Они используются во многих областях, включая теорию множеств, вероятность, логику, статистику и информатику.Содержимое
- 1 Обзор
- 2 История
- 3 Пример
- 4 Расширения для большего количества наборов
- 4.1 Диаграммы Венна Эдвардса
- 4.2 Другие схемы
- 5 инструментов для построения диаграмм Венна
- 6 См. также
- 7 Каталожные номера
- 8 Дальнейшее чтение
- 9 Внешние ссылки
[править] Обзор
Вверху: диаграмма Эйлера для включения множеств. Внизу, от середины к низу: установите объединение и пересечение, проиллюстрированные диаграммами Венна.
Диаграмма Венна строится из набора простых замкнутых кривых, начерченных на плоскости. Принцип этих диаграмм состоит в том, что классы или множества представляются областями в таком отношении друг к другу, что все возможные логические отношения этих классов могут быть указаны на одной и той же диаграмме.
 То есть диаграмма изначально оставляет место для любого возможного отношения классов, а фактическое или заданное отношение затем может быть определено путем указания того, что некоторая конкретная область является нулевой или не является нулевой. [1]
То есть диаграмма изначально оставляет место для любого возможного отношения классов, а фактическое или заданное отношение затем может быть определено путем указания того, что некоторая конкретная область является нулевой или не является нулевой. [1] Диаграммы Венна обычно состоят из перекрывающихся кругов. Например, на диаграмме Венна с двумя наборами один круг может представлять группу всех деревянных предметов, а другой круг может представлять набор всех столов. Перекрывающаяся область (пересечение ) тогда будет представлять набор всех деревянных столов. Можно использовать формы, отличные от кругов (см. ниже), и это необходимо для более чем трех подходов.
Диаграммы Венна очень похожи на диаграммы Эйлера, но тогда как диаграмма Венна для n наборы компонентов должны содержать все 2 n гипотетически возможных зон, соответствующих некоторой комбинации включения или исключения в каждый из наборов компонентов, диаграммы Эйлера содержат только реально возможные зоны в данном контексте.
 На диаграммах Венна заштрихованная зона может представлять пустую зону, тогда как на диаграмме Эйлера соответствующая зона отсутствует на диаграмме. Например, если один набор представляет «молочные продукты», а другой — «сыры», то диаграмма Венна содержит зону для сыров, не являющихся молочными продуктами. Если предположить, что в контексте «сыр» означает некоторый тип молочного продукта, на диаграмме Эйлера зона сыра будет полностью находиться внутри зоны молочных продуктов; нет зоны для (несуществующих) немолочных сыров. Это означает, что по мере увеличения количества контуров диаграммы Эйлера обычно визуально менее сложны, чем эквивалентная диаграмма Венна, особенно если количество непустых пересечений невелико. [2]
На диаграммах Венна заштрихованная зона может представлять пустую зону, тогда как на диаграмме Эйлера соответствующая зона отсутствует на диаграмме. Например, если один набор представляет «молочные продукты», а другой — «сыры», то диаграмма Венна содержит зону для сыров, не являющихся молочными продуктами. Если предположить, что в контексте «сыр» означает некоторый тип молочного продукта, на диаграмме Эйлера зона сыра будет полностью находиться внутри зоны молочных продуктов; нет зоны для (несуществующих) немолочных сыров. Это означает, что по мере увеличения количества контуров диаграммы Эйлера обычно визуально менее сложны, чем эквивалентная диаграмма Венна, особенно если количество непустых пересечений невелико. [2] [править] История
Диаграммы Венна были введены [3] в 1880 году Джоном Венном (1834-1923) в статье, озаглавленной «О диаграммном и механическом представлении предложений и рассуждений», которая появилась в «Philosophical Magazine and Journal of Science» в июле 1880 года.
 , возник гораздо раньше. Однако они по праву ассоциируются с Венном, потому что он всесторонне изучил и формализовал их использование и был первым, кто обобщил их. Сам термин «диаграмма Венна» впервые был использован Кларенсом Ирвингом Льюисом в 1919 г.18, в его книге «Обзор символической логики». [4]
, возник гораздо раньше. Однако они по праву ассоциируются с Венном, потому что он всесторонне изучил и формализовал их использование и был первым, кто обобщил их. Сам термин «диаграмма Венна» впервые был использован Кларенсом Ирвингом Льюисом в 1919 г.18, в его книге «Обзор символической логики». [4] Диаграммы Венна очень похожи на диаграммы Эйлера, которые были изобретены Леонардом Эйлером (1708-1783) в 18 веке. [5] М. Э. Барон отмечал, что Лейбниц (1646-1716) в XVII веке создавал подобные диаграммы раньше Эйлера, однако большая их часть не была опубликована. Она также наблюдает за еще более ранними Эйлеровыми диаграммами Рамона Луллия в 13 веке. [6]
В 20 веке диаграммы Венна получили дальнейшее развитие. Д.В. Хендерсон показал в 1963 видно, что существование диаграммы Венна n с n -кратной вращательной симметрией подразумевает, что n — простое число. [7] Он также показал, что такие симметричные диаграммы Венна существуют, когда n равно 5 или 7.
 В 2002 году Питер Гамбургер нашел симметричные диаграммы Венна для n = 11, а в 2003 году Григгс, Киллиан и Сэвидж показали, что симметричные Диаграммы Венна существуют для всех остальных простых чисел. Таким образом, симметричные диаграммы Венна существуют тогда и только тогда, когда n — простое число. [8]
В 2002 году Питер Гамбургер нашел симметричные диаграммы Венна для n = 11, а в 2003 году Григгс, Киллиан и Сэвидж показали, что симметричные Диаграммы Венна существуют для всех остальных простых чисел. Таким образом, симметричные диаграммы Венна существуют тогда и только тогда, когда n — простое число. [8] Диаграммы Венна были включены в программу обучения теории множеств как часть нового математического движения в 1960-х годах. С тех пор они также были приняты другими областями учебной программы, такими как чтение [9]
[править] Пример
Наборы A (существа с двумя ногами) и B (существа, которые могут летать)
В следующем примере используются два набора, A и B, представленные здесь в виде цветных кругов. Оранжевый круг, набор А, представляет всех живых существ, которые являются двуногими. Синий круг, набор B, представляет живых существ, которые могут летать. Каждый отдельный вид существ можно представить как точку где-нибудь на диаграмме.
 Живые существа, которые оба могут летать и имеют две лапки — например, попугаи — то есть в обоих наборах, значит, они соответствуют точкам в области, где перекрываются синие и оранжевые круги. Эта область содержит всех таких и только таких живых существ.
Живые существа, которые оба могут летать и имеют две лапки — например, попугаи — то есть в обоих наборах, значит, они соответствуют точкам в области, где перекрываются синие и оранжевые круги. Эта область содержит всех таких и только таких живых существ.Люди и пингвины двуногие, поэтому они и в оранжевом круге, но поскольку они не умеют летать, они появляются в левой части оранжевого круга, где он не пересекается с синим кругом. У комаров шесть ног, и они летают, поэтому точка для комаров находится в той части синего круга, которая не пересекается с оранжевым. Существа, которые не являются двуногими и не умеют летать (например, киты и пауки), будут представлены точками за пределами обоих кругов.
Объединенная площадь множеств A и B называется объединением множеств A и B, обозначаемым A ∪ B. Объединение в этом случае содержит все вещи, которые либо имеют две ноги, либо летают, либо и то, и другое.
Область как в A, так и в B, где два множества перекрываются, называется пересечением A и B и обозначается A ∩ B.
 Например, пересечение двух множеств не пусто, потому что точек представляют существ, которые находятся в и оранжевых и синих кругах.
Например, пересечение двух множеств не пусто, потому что точек представляют существ, которые находятся в и оранжевых и синих кругах.Иногда вокруг диаграммы Венна рисуется прямоугольник, называемый «Универсальным множеством», чтобы показать пространство всех возможных вещей. Как упоминалось выше, кит будет представлен точкой, которая не находится в союзе, но находится во Вселенной (живых существ или всего сущего, в зависимости от того, как выбрано определение Вселенной для конкретной диаграммы).
[править] Расширения для большего количества наборов
Конструкция Венна на 4 комплекта
Конструкция Венна на 5 комплектов
Конструкция Венна на 6 комплектов
Диаграмма Венна с четырьмя наборами с использованием эллипсов
Хотя диаграммы Венна обычно поддерживают три набора, существуют формы, допускающие большее число.
 Венну очень хотелось найти 90 856 симметричных фигур… элегантных сами по себе, 90 857, представляющих большее количество наборов, и он разработал диаграмму из четырех наборов, используя эллипсы. (см. выше) Он также дал конструкцию для диаграмм Венна для любое количество наборов, где каждая последующая кривая, ограничивающая набор, чередуется с предыдущими кривыми, начиная с 3-х круговой диаграммы.
Венну очень хотелось найти 90 856 симметричных фигур… элегантных сами по себе, 90 857, представляющих большее количество наборов, и он разработал диаграмму из четырех наборов, используя эллипсы. (см. выше) Он также дал конструкцию для диаграмм Венна для любое количество наборов, где каждая последующая кривая, ограничивающая набор, чередуется с предыдущими кривыми, начиная с 3-х круговой диаграммы.[править] Диаграммы Венна Эдвардса
Диаграмма Венна Эдвардса из трех наборов
Диаграмма Венна Эдвардса из четырех наборов
Диаграмма Венна Эдвардса из пяти наборов
Диаграмма Венна Эдвардса из шести наборов
А. В. Ф. Эдвардс дал конструкцию для большего числа множеств, обладающую некоторыми симметриями.
 Его построение достигается путем проецирования диаграммы Венна на сферу. Три набора можно легко представить, взяв три полусферы под прямым углом ( x = 0, y = 0 и z = 0). Четвертый набор можно представить, взяв кривую, похожую на шов на теннисном мяче, который закручивается вверх и вниз по экватору. Полученные наборы затем можно спроецировать обратно на плоскость, чтобы получить зубчатое колесо схемы с увеличивающимся числом зубьев. Эти схемы были разработаны при проектировании витража в память о Венне.
Его построение достигается путем проецирования диаграммы Венна на сферу. Три набора можно легко представить, взяв три полусферы под прямым углом ( x = 0, y = 0 и z = 0). Четвертый набор можно представить, взяв кривую, похожую на шов на теннисном мяче, который закручивается вверх и вниз по экватору. Полученные наборы затем можно спроецировать обратно на плоскость, чтобы получить зубчатое колесо схемы с увеличивающимся числом зубьев. Эти схемы были разработаны при проектировании витража в память о Венне.[править] Другие диаграммы
Диаграммы Венна Эдвардса топологически эквивалентны диаграммам, разработанным Бранко Грюнбаумом, которые были основаны на пересекающихся многоугольниках с увеличивающимся числом сторон. Они также являются двумерными представлениями гиперкубов.
Смит разработал аналогичные n -множественные диаграммы с использованием синусоидальных кривых с уравнениями y = sin(2 i x )/2 i , 0=i= n -2.

Чарльз Лютвидж Доджсон (также известный как Льюис Кэрролл) разработал диаграмму из пяти наборов.
[править] Инструменты для построения диаграмм Венна
- Плотикус
- ConceptDraw
- SmartDraw
[править] См. также
- Булева алгебра (логика)
- Пузырьковая диаграмма
- Диаграмма Кэрролла
- Диаграмма Эйлера 9 Стратегии понимания прочитанного Диаграммы Венна
- Обзор диаграмм Венна, подготовленный Ф. Раски и М. Уэстоном, представляет собой обширный сайт с большим количеством недавних исследований и множеством красивых рисунков.
- И. Стюарт (2004) Еще одна прекрасная математика, в которую вы меня втянули , Dover Publications Inc. ISBN 0486431819 ch5
- А.В.Ф. Эдвардс (2004) Зубчатые колеса разума: история диаграмм Венна , издательство Университета Джона Хопкинса, Балтимор и Лондон.
 ISBN 0801874343
ISBN 0801874343- Обзор зубчатых колес разума
- Джон Венн (1880 г.). «О диаграммном и механическом представлении предложений и рассуждений». Dublin Philosophical Magazine and Journal of Science 9 (59): 1–18.
- Создание и просмотр диаграмм Венна — интерактивная диаграмма Венна
- LogicTutorial.com — интерактивная диаграмма Джонстона
- Логическая игра Льюиса Кэрролла — Венн против Эйлера на решающей схватке
- Обзор диаграмм Венна
- Доказательство существования
- Характеристики
- Приложения
- Смотрите также
- Точка Де Лоншана отражение ортоцентра над центром описанной окружности.
- Точка Эксетера определяется следующим образом: если DEFDEFDEF является касательным треугольником ABCABCABC, а A’,B’,C’A’, B’, C’A’,B’,C’ являются пересечениями медиан окружности ABCABCABC с описанной окружностью ABCABCABC, то DA′,EB′,FC′DA’, EB’, FC’DA′,EB′,FC′ совпадают в точке Эксетера.
- точка Шиффлера : если III является центром вписанной ABCABCABC, то линии Эйлера △ABI, △BCI, △CAI\треугольника ABI, \треугольника BCI, \треугольника CAI△ABI,△BCI,△CAI и △ ABC\треугольник ABC△ABC пересекаются в точке Шиффлера.
- Циркумцентр
- Ортоцентр
- Центроид
- Окружность с девятью точками
- 1 Летние математические программы США
- 1.1 Математические программы для учащихся начальной школы
- 1.2 Математические программы для учащихся средней школы
- 1.3 Математические программы для старшеклассников
- Летний математический лагерь A* в Bay Area, Калифорния, веб-сайт
- Летние лагеря Absolute Academy в округе Фэрфакс, штат Вирджиния, веб-сайт
- Летний лагерь Areteem Institute (Фуллертон и Сан-Хосе, Калифорния; Чикаго, Иллинойс, Вашингтон, округ Колумбия), Веб-сайт
- Академия искусства решения проблем (местоположения по всей стране) Веб-сайт
- Летняя онлайн-программа Beestar (онлайн) Веб-сайт
- Центр талантливой молодежи (CTY) (представительства по всей стране) Веб-сайт
- CyberMath Academy (онлайн, Бостон-Гарвардский университет, Силиконовая долина-Стэнфордский университет) Веб-сайт
- Лагерь Эпсилон (местоположение меняется ежегодно) Веб-сайт Веб-сайт
- Girls Rock Math (Сиэтл, Вашингтон)
- Прыжок вперед! Летняя онлайн-программа (онлайн) Веб-сайт
- Math Contest Camp (Боливар, Миссури) Веб-сайт
- MehtA+ AI in Visual Arts Camp — это мини-учебный лагерь для учащихся 5–12 классов.
 Веб-сайт
Веб-сайт - Летние лагеря Star League — ЖИЛЫЕ И ДНЕВНЫЕ ЛАГЕРЯ (Ирвин и Купертино, Калифорния) Веб-сайт
- Образовательный веб-сайт TenMarks (онлайн)
- Texas Mathworks (Сан-Маркос, Техас) Веб-сайт
- Random Math (Купертино, Калифорния) Веб-сайт
- Летняя школа русской школы математики (места по всей стране) Веб-сайт
- Летний математический лагерь A* в Bay Area, Калифорния, веб-сайт
- Летние лагеря Absolute Academy в округе Фэрфакс, штат Вирджиния, веб-сайт
- Летний лагерь Areteem Institute (Фуллертон и Сан-Хосе, Калифорния; Чикаго, Иллинойс, Вашингтон, округ Колумбия), Веб-сайт
- Академия искусства решения проблем (местоположения по всей стране) Веб-сайт
- Веб-сайт AwesomeMath
- Bard Math Circle Creative and Analytical Math Program (CAMP) (Annandale-on-Hudson, NY), веб-сайт
- Летняя онлайн-программа Beestar (онлайн) Веб-сайт
- Центр талантливой молодежи (представительства по всей стране) Веб-сайт
- CyberMath Academy (онлайн, Бостон-Гарвардский университет, Силиконовая долина-Стэнфордский университет) Веб-сайт
- Летний лагерь детективов данных (Колледж-Парк, Мэриленд)
- Программа образовательных исследований в Массачусетском технологическом институте
- Летняя программа IDEA MATH (Купертино, Калифорния и Бостон, Массачусетс) Веб-сайт [Форум]
- Математическое соревнование IOMC (онлайн) Веб-сайт
- Математический лагерь научно-исследовательского института MIND (местоположение меняется ежегодно)
- Math Contest Camp (Боливар, Миссури) Веб-сайт
- Летний институт повышения квалификации по математике в Университете Сан-Хосе
- Лагерь MathLinks (Сан-Диего, Калифорния) Форум
- MathPath (местоположение меняется ежегодно) Форум Веб-сайт
- MehtA+ AI in Visual Arts Camp — это мини-учебный лагерь для 5–12 классов Веб-сайт
- MehtA+ AI/Machine Learning Bootcamp — виртуальная исследовательская программа для 8–12 классов Веб-сайт
- Stanford Pre-Collegiate Summer Institutes (бывшие Летние институты EPGY) в Калифорнии, веб-сайт
- Математические лагеря Star League — ЖИЛЫЕ И ДНЕВНЫЕ ЛАГЕРЯ (Ирвин и Купертино, Калифорния) Веб-сайт
- Технология для расширения прав и возможностей молодежи — лагерь AMC 8 (Саратога, Калифорния и Zoom), веб-сайт
- Образовательный веб-сайт TenMarks (онлайн)
- Texas Mathworks (Сан-Маркос, Техас) Веб-сайт
- Программа молодых ученых (Чикагский университет) Веб-сайт
- Random Math (Купертино, Калифорния) Веб-сайт
- Летняя школа Русской школы математики (представительства по всей стране) Веб-сайт
- Летний математический лагерь A* в Bay Area, Калифорния, веб-сайт
- Летние лагеря Absolute Academy в округе Фэрфакс, штат Вирджиния, веб-сайт
- All Girls/All Math в Университете Небраски-Линкольн, веб-сайт
- Летний лагерь Areteem Institute (Фуллертон и Сан-Хосе, Калифорния; Чикаго, Иллинойс, Вашингтон, округ Колумбия), Веб-сайт
- Академия искусства решения проблем (местоположения по всей стране) Веб-сайт
- AwesomeMath в UT Техас, Корнелл и Университет Пьюджет-Саунд, веб-сайт
- Математический опыт Бостонского колледжа, веб-сайт
- Летняя школа математики и естественных наук штата Калифорния (COSMOS), веб-сайт
- Канада/США Mathcamp (местонахождение меняется ежегодно), веб-сайт
- Центр талантливой молодежи (CTY) в нескольких местах по всей стране, веб-сайт
- CyberMath Academy (онлайн, Бостон-Гарвардский университет, Силиконовая долина-Стэнфордский университет) Веб-сайт
- Программа образовательных исследований (ESP) Массачусетского технологического института, веб-сайт
- Euler Circle в Пало-Альто, Калифорния, веб-сайт (в течение года, не летом)
- Летний онлайн-лагерь Академии Everaise,
- Летние курсы по математике в Хэмпширском колледже (HCSSiM) в Хэмпширском колледже, Массачусетс, веб-сайт
- Гарвардская летняя школа в Массачусетсе, веб-сайт
- Летняя программа IDEA MATH в Купертино, Калифорния, и Бостоне, Массачусетс, веб-сайт и [форум AoPS]
- Летняя программа LSU Math Circle в LSU в Батон-Руж, Луизиана, веб-сайт
- Math Contest Camp в Боливаре, Миссури, веб-сайт
- Летний институт повышения квалификации по математике в Университете Сан-Хосе, веб-сайт
- Летняя программа математической олимпиады, организованная AMC
- MathILy и MathILy-Er в колледже Брин-Мор и университете Кабрини, веб-сайт
- MathILy-EST (начальное обучение математике) в колледже Брин-Мор, веб-сайт
- Лагерь MathLinks в Сан-Диего, Калифорния, Форум AoPS
- MathPath (местоположение меняется ежегодно), форум и веб-сайт AoPS
- MehtA+ AI in Visual Arts Camp — это мини-учебный лагерь для учащихся 5–12 классов.
 Веб-сайт
Веб-сайт - MehtA+ AI/Machine Learning Bootcamp — виртуальная исследовательская программа для 8–12 классов Веб-сайт
- Мичиганские ученые в области математики и естественных наук Мичиганского университета, веб-сайт
- Введение меньшинства в инженерию и науку (MITES) в Массачусетском технологическом институте, веб-сайт
- Math Camp Monsoon (онлайн), веб-сайт
- Программа летней средней школы New York Math Circle (NYMC), веб-сайт Программа
- по математике для молодых ученых (PROMYS) Бостонского университета, Массачусетс, веб-сайт
- Докажи это! Математическая академия при Университете штата Колорадо, веб-сайт .
- Летняя программа QTM Math Circle в Университете Эмори в Атланте, Джорджия, веб-сайт
- Random Math (Купертино, Калифорния) Веб-сайт
- Научно-исследовательский институт (RSI) Массачусетского технологического института, веб-сайт
- Технология для расширения прав и возможностей молодежи — лагерь AMC 8 (Саратога, Калифорния), веб-сайт
- Программа Росса в Университете штата Огайо, веб-сайт
- Летняя школа Русской математической школы (представительства по всей стране) Веб-сайт
- Программа молодых ученых по дискретной математике в Rutgers, веб-сайт
- Математические лагеря Star League — ЖИЛЫЕ И ДНЕВНЫЕ ЛАГЕРЯ (Ирвин и Купертино, Калифорния) Веб-сайт
- Летний институт математики Вашингтонского университета (SIMUW), веб-сайт
- Летняя программа по математике в Университете Юты, веб-сайт
- Summer STEM Institute (SSI) — первая виртуальная программа Веб-сайт
- Летняя программа по прикладной рациональности и познанию (SPARC) в Bay Area, CA Веб-сайт
- Летняя научная программа (SSP) в Нью-Мексико, веб-сайт
- Summer Ventures in Science and Mathematics в Университете Северной Каролины, веб-сайт
- Летний институт Talaria — это бесплатная летняя исследовательская программа наставничества в области STEM для студенток и студентов-гендерквиров
- TenMarks Education (онлайн-лагерь), веб-сайт
- Texas Mathworks в Сан-Маркосе, Техас, Веб-сайт
- UConn Mentor Connection в Коннектикуте, веб-сайт
- Математический лагерь колледжа Уильямс в колледже Уильямс, Массачусетс, веб-сайт
- Женская технологическая программа Массачусетского технологического института, веб-сайт
- Программа молодых ученых Чикагского университета, Иллинойс, веб-сайт
- Автор: Tully Foote
- Лицензия: BSD
- Репозиторий: ros-pkg
- Источник: svn https://code.ros.org/svn/ros-pkg/stacks/common_msgs/tags/common_msgs-1.4. 0
- Автор: Талли Фут
- Лицензия: BSD
- Источник: svn https://code.ros.org/svn/ros-pkg/stacks/common_msgs/branches/common_msgs-1.6
- Автор: Tully Foote
- Лицензия: BSD
- Источник: git https://github.com/ros/common_msgs.git (филиал: fuerte-devel)
- Статус сопровождающего: поддерживается
- Сопровождающий: Талли Фут
- Автор: Талли Фут
- Лицензия: BSD
- Источник: git https://github.
 com/ros/common_msgs.git ( ветвь: groovy-devel)
com/ros/common_msgs.git ( ветвь: groovy-devel) - Статус сопровождающего: поддерживается
- Сопровождающий: Tully Foote
- Автор: Tully Foote
- Лицензия: BSD
- Источник: git https://github.com/ros/common_msgs.git ( филиал: гидро-девелопмент)
- Статус сопровождающего: поддерживается
- Сопровождающий: Талли Фут
- Автор: Талли Фут
- Лицензия: BSD
- Источник: git https://github.com/ros/common_msgs.git (ветвь: индиго-разработка)
- Статус сопровождающего: поддерживается
- Сопровождающий: Tully Foote
- Автор: Tully Foote
- Лицензия: BSD
- Источник: git https://github.
 com/ros/common_msgs.git ( ветка: нефрит-девель)
com/ros/common_msgs.git ( ветка: нефрит-девель) - Статус сопровождающего: поддерживается. /common_msgs.git (ветка: jade-devel)
- Статус сопровождающего: поддерживается
- Сопровождающий: Tully Foote
- Автор: Tully Foote
- Лицензия: BSD
- Источник: git https://github.com/ros/common_msgs.git ( ветка: нефрит-девель)
- Статус сопровождающего: поддерживается. /common_msgs.git (ветка: jade-devel)
- Статус сопровождающего: поддерживается
- Сопровождающий: Мишель Идальго
- Автор: Талли Фут
- Лицензия: BSD
- Источник: git https://github.com/ros/common_msgs.git (филиал: noetic-devel)
- Какова ваша формула для случая единичного круга с $(a,b)=(1,0)$ и как ваш способ получить его?
- Есть ли способ вычислить рациональную параметризацию для единичного круга с общим $(a,b)$, который позволяет построить «целый» круг? Может быть, $a$ и $b$ должны быть рациональными числами или даже целыми числами?
- тригонометрия
- аналитическая геометрия
- алгебраические кривые
- $f(t)=0\iff t=\pm 1$ и
- $f(t)>0\ тогда и только тогда, когда |t|<1$ и
- $f(t)=1\iff t=0$
- $g(t)=0\iff t=0$ вместе с
- $g(t)>0\ тогда и только тогда, когда t>0$ и
- $|g(t)|=1\iff |t|=1$
[править] Дополнительная литература
[править] Внешние ссылки
Линия Эйлера | Brilliant Math & Science Wiki
Содержание
В простейшем доказательстве используется гомотетия, в частности та, что с центром в центроиде GGG треугольника, с масштабным коэффициентом −12-\frac{1}{2}−21.
 Это отправляет вершины A, B, CA, B, CA, B, C в середины противоположных сторон, поскольку центроид делит медианы в соотношении 2: 1, а это означает, что треугольник ABCABCABC отправляется в медиальный треугольник.
Это отправляет вершины A, B, CA, B, CA, B, C в середины противоположных сторон, поскольку центроид делит медианы в соотношении 2: 1, а это означает, что треугольник ABCABCABC отправляется в медиальный треугольник.Следовательно, ортоцентр треугольника ABCABCABC направлен в ортоцентр медиального треугольника, который является центром описанной окружности треугольника ABCABCABC. В результате ортоцентр, центр описанной окружности и центр тяжести коллинеарны, как и требовалось.
Приведенное выше доказательство показывает больше, чем коллинеарность: поскольку HHH отправляется в ООО через масштабный коэффициент −12-\frac{1}{2}−21, мы имеем HG=2GOHG=2GOHG=2GO. На самом деле верно большее: если NNN — это девятиконечный центр треугольника, мы имеем
HG=2GO,ON=NH,OG=2GN,NH=3GN.\begin{aligned}&HG = 2GO, &ON = NH, &OG = 2GN, &NH = 3GN.\end{aligned}HG=2GO,ON =NH,OG=2GN,NH=3GN.
Относительные расстояния центров треугольников.
 Красная линия в два раза длиннее зеленой, а синяя в три раза длиннее зеленой.
Красная линия в два раза длиннее зеленой, а синяя в три раза длиннее зеленой.Линия Эйлера также содержит десятки других центров треугольников, некоторые из которых были обнаружены совсем недавно. Особо следует отметить следующие точки:
Кроме того, если A1A_1A1 – основание высоты от AAA до BCBCBC, а MaM_aMa – середина BCBCBC (с аналогичными определениями B1B_1B1 и MbM_bMb), то
Пересечение A1MbA_1M_bA1Mb и B1MaB_1M_aB1Ma лежит на прямой Эйлера.

Наклон линии Эйлера хорошо связан с наклоном сторон: если m1,m2,m3m_1, m_2, m_3m1,m2,m3 являются наклонами трех сторон треугольника ABCABCABC, и mem_eme — наклон линии Эйлера, затем
90 002 +m1я+m2я+m3я+3m1m2m3я+3=0,
или аналогичный,
me=−m1m2+m2m3+m3m1+3m1+m2+m3+3m1m2m3.m_e=-\frac{m_1m_2+m_2m_3+m_3m_1+3}{m_1+m_2+m_3+3m_1m_2m_3}.me=−m1+m2 +m3+3m1m2m3m1m2+m2m3+m3m1+3.
Рассмотрим △ABC\треугольник ABC△ABC, где A=(0,0),B=(5,−10),C=(−24,7)A=(0,0), B=(5, -10), С=(-24, 7)А=(0,0),В=(5,-10),С=(-24,7). Наклон линии Эйлера для △ABC\треугольника ABC△ABC в простейшей форме можно записать как ab\dfrac{a}{b}ba. Точка DDD является центром тяжести △ABC\треугольника ABC△ABC, координаты которого можно записать как (d,c)(d,c)(d,c).
Если ac+bc=x,ac+bc=x,ac+bc=x, чему равно x+6713,8x+6713,8x+6713,8?
Одним из важных следствий линии Эйлера является то, что информация о любом из центроида, ортоцентра и центра описанной окружности может быть получена из информации о двух других.
 Например,
Например,Точки A, B, A, B, A, B и CCC выбираются случайным образом на единичной окружности. Геометрическое место ортоцентра △ABC\треугольника ABC△ABC является областью RRR. Какова площадь РРР?
Вместо фокусировки на ортоцентре лучше сосредоточиться на двух других главных центрах треугольника: центроиде и центре описанной окружности. Центр описанной окружности всегда является центром единичной окружности, поэтому необходимо только отметить, что центроид может лежать где угодно в пределах единичной окружности и нигде больше (почему?). Поскольку HG=2GOHG=2GOHG=2GO, это означает, что максимально возможное значение HHH равно 3, а область RRR представляет собой круг радиусом 3. Таким образом, площадь RRR равна 9π9\pi9π. □_\квадрат□
Рассмотрим треугольник ΔABC\Delta ABCΔABC, центр описанной окружности которого находится в начале координат. Если в ΔABC\Delta ABCΔABC координаты центроида GGG равны (xG,yG)\left(x_G,y_G\right)(xG,yG), а координаты ортоцентра HHH равны (xH,yH)\left (x_H,y_H\справа)(xH,yH).

Найдите отношение xHyHxGyG\dfrac{x_Hy_H}{x_Gy_G}xGyGxHyH.
Бонус : Не забывайте об одиноком инцентре!
Еще один результат, обусловленный свойствами прямой Эйлера:
Если ABCABCABC — треугольник с центром описанной окружности ООО и ортоцентром HHH, то одна из площадей △AOH\треугольника AOH△AOH, △BOH\треугольника BOH△BOH и △COH\треугольника COH△COH равна сумме площадей два других.
Мохит под влиянием Акшата и Аншумана выбрал правильный △ABC\bigtriangleup ABC△ABC (прямой угол в BBB), где AB=5,5 смAB=5,5 \mathrm{ см}AB=5,5 см и BC=8 смBC=8 \ mathrm{cm}BC=8cm, и начал делать бесцельные построения, шаги которых приведены ниже:
(111) Он провел биссектрису X1Y1X_1Y_1X1Y1 к ACACAC, которая пересекает ACACAC в точке O,O,O, и другую биссектрису X2Y2X_2Y_2X2Y2 к ABABAB, которая пересекает ABABAB в точке GGG.
(222) Затем он построил окружность, приняв центр OOO и радиус окружности за OAOAOA .
 Затем он построил ∠ACE\угол ACE∠ACE, равный ∠ACB\углу ACB∠ACB, такой, что EEE лежит на окружности.
Затем он построил ∠ACE\угол ACE∠ACE, равный ∠ACB\углу ACB∠ACB, такой, что EEE лежит на окружности.(333) Затем он присоединился к BEBEBE, которая встречается с ACACAC на FFF.
(444) Затем он присоединился к CGCGCG, которая пересекает EBEBEB в точке HHH и X1Y1X_1Y_1X1Y1 в точке JJJ.
Затем Мохит задумался, чему может быть равен BHOJ\frac{BH}{OJ}OJBH.
Цитировать как: Линия Эйлера. Brilliant.org . Извлекаются из https://brilliant.org/wiki/euler-line/
Искусство решения задач
Летние программы по математике представлены во многих вариантах, ориентированных на разные возрастные группы и уровни учащихся. Выбор важен для создания наилучшего опыта для любого студента-математика.
Многие из этих программ довольно дорогие.
 Некоторые из программ, перечисленных ниже, предлагают стипендии по математике или финансовую помощь. Некоторые из них бесплатны. Когда вы обнаружите больше, пожалуйста, добавьте эту информацию во все подходящие места, которые вы найдете на AoPSWiki.
Некоторые из программ, перечисленных ниже, предлагают стипендии по математике или финансовую помощь. Некоторые из них бесплатны. Когда вы обнаружите больше, пожалуйста, добавьте эту информацию во все подходящие места, которые вы найдете на AoPSWiki.Некоторые из перечисленных ниже математических летних программ имеют специальные форумы AoPS, на которых учащиеся, учителя и родители могут обсуждать эти программы.
Содержание
Летние математические программы США
Математические программы для учащихся начальной школы
Математические программы для учащихся средних классов
Математические программы для старшеклассников
© 2022 ООО «АоПС Инкорпорейтед»
Неверное имя пользователя
Войти в АоПС
Имя пользователя:
Пароль:
Оставаться в системе
геометрия_msgs — ROS Wiki
Показать дистрибутивы EOL:
Состояние документации
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Нет документации по API такие как точки, векторы и позы.
 Эти примитивы предназначены
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.
Эти примитивы предназначены
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Документировано
геометрия_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы. Эти примитивы предназначены для обеспечения общего типа данных и облегчения взаимодействия по всей системе.
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Документировано
геометрия_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы.
 Эти примитивы предназначены
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.
Эти примитивы предназначены
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.common_msgs : actionlib_gs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Выпущено
Документировано
Geometry_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы. Эти примитивы разработаны для обеспечения общего типа данных и облегчения взаимодействия по всей системе.
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Выпущено
Документировано
геометрия_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы. Эти примитивы разработаны для обеспечения общего типа данных и облегчения взаимодействия по всей системе.
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Выпущено
Документировано
Geometry_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы.
 Эти примитивы разработаны
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.
Эти примитивы разработаны
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Выпущено
Задокументировано
геометрия_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы. Эти примитивы разработаны для обеспечения общего типа данных и облегчения взаимодействия по всей системе.
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Выпущено
Документировано
Geometry_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы. Эти примитивы разработаны для обеспечения общего типа данных и облегчения взаимодействия по всей системе.
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | визуализация_msgs
Выпущено
Задокументировано
Geometry_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы.
 Эти примитивы разработаны
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.
Эти примитивы разработаны
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | visualization_msgs
Выпущено
Документировано
Geometry_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы. Эти примитивы разработаны для обеспечения общего типа данных и облегчения взаимодействия по всей системе.
common_msgs : actionlib_msgs | диагностические_сообщения | геометрия_msgs | nav_msgs | Sensor_msgs | shape_msgs | стерео_сообщения | траектория_msgs | визуализация_msgs
Выпущено
Задокументировано
Geometry_msgs предоставляет сообщения для общих геометрических примитивов такие как точки, векторы и позы.
 Эти примитивы разработаны
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.
Эти примитивы разработаны
для обеспечения общего типа данных и облегчения взаимодействия
по всей системе.Типы сообщений ROS Accel
AccelStamped
AccelWithCovariance
AccelWithCovarianceStamped
Inertia
InertiaStamped
Point
Point32
PointStamped
Polygon
PolygonStamped
Pose
Pose2D
PoseArray
PoseStamped
PoseWithCovariance
PoseWithCovarianceStamped
Quaternion
QuaternionStamped
Transform
TransformStamped
Twist
TwistStamped
TwistWithCovariance
TwistWithCovarianceStamped
Vector3
Vector3Stamped
Wrench 90Stamp23 90Stamp23 Wrench
Wrench
Wrench
Wrench
Wrench
Wrenchтригонометрия — Рациональная параметризация круга в Википедии
спросил
Изменено 7 лет, 5 месяцев назад 92}$$ с действительным параметром $t$.
 »
»Но если я построю эту кривую, я получу полукруг с этими формулами, только когда $(a,b)\neq(0,0)$, что очевидно не то, что ищут и ожидают
Недавно я нашел без всякой элементарной тригонометрии, например, для единичного круга с $(a,b)=(1,0)$ замкнутую рациональную параметризацию, которая идеально отображает «целый» круг, если $ \lim_{t\to\infty}$.
Теперь мои 2 вопроса:
$\endgroup$
3
$\begingroup$
Запись $$ f (t) = \ frac {1-t ^ 2} {1 + t ^ 2} $$ а также $$ г (т) = \ гидроразрыва {2 т} {1 + т ^ 2} $$ Дело в том, что $(f(t))^2+(g(t))^2=1$, так что $(f(t),g(t))=(\cos\theta,\sin\ theta)$ для некоторого угла $\theta$.
 Легко видеть, что
Легко видеть, чтоТакже легко видеть, что
Но $f(t)=-1$ никогда не достигается. Анализируя $f$ и $g$, мы видим, что $$ t\to-\infty\имеет f(t)\to -1, g(t)\to 0_- $$ а также $$ t\to+\infty\подразумевает f(t)\to -1, g(t)\to 0_+ $$ поэтому, чтобы получить полный круг (за исключением одной точки в $(-1,0)$), мы должны иметь $t\in\mathbb R$.
Как вы можете видеть, это похоже на один период $\cos\theta$ и $\sin\theta$, перепараметризованный в $f(t)=\cos(\theta(t))$ и $g(t)=\sin(\theta(t))$ такое, что $\theta(t)\to-\pi$ для $t\to-\infty$ и $\theta(t)\to\pi $ за $t\to\infty$.
$\endgroup$
3
$\begingroup$
Вики-форма верна.
 Однако наряду с так называемым «преимуществом» рациональной параметрической формы возникает ограничение требования бесконечного аргумента для завершения глубокого круга.
Однако наряду с так называемым «преимуществом» рациональной параметрической формы возникает ограничение требования бесконечного аргумента для завершения глубокого круга.Если y равен нулю или x достигает своего экстремального значения, вы ожидаете, что один параметр $t$ имеет разумную область для полного описания дуги окружности. Но это не так.. так как один корень $t$ находится в точке $t=0$, а другой в точке $t=\infty$.
Тригонометрическое выражение полностью исправляет ситуацию, выражая координаты в терминах двойного угла $ 2 T$ (удвоенного половины угла в форме Вейерштрасса), приведенного в Вики. ссылка).
$$ x = a + r \cos (2 T) ;\; y = b + r \sin (2 T) ; $$
Код Mathematica приведен на изображении. Я немного уменьшил рациональный радиус круга, чтобы показать полный круг с помощью тригонометрической параметризации по контрасту.
Кроме того, особое триггерное представление Круга имеет значение в Механике структур. Когда y_offset = 0, это круг Мора, впервые использованный известным немецким инженером-строителем Отто Мором, который определил статическую детерминированность и построил очень полезные диаграммы напряжений и деформаций.


 ..
..
 73kb.
73kb.
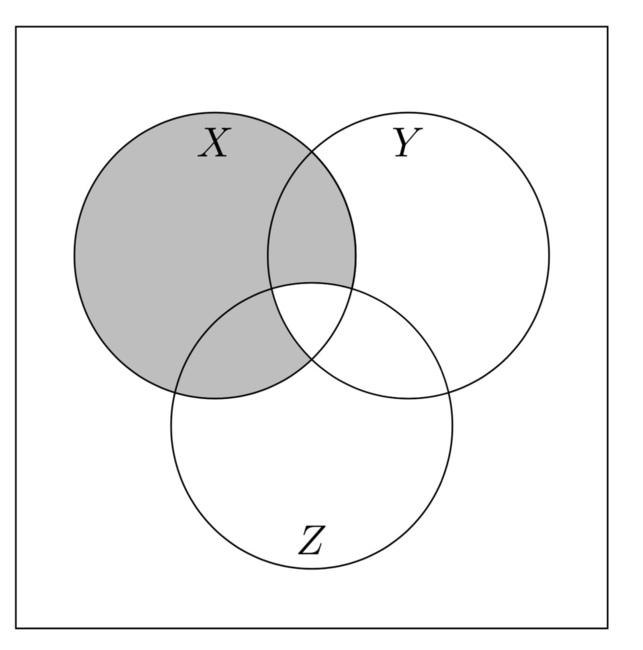 B — живое существо, A — человек, C — неживая вещь.
B — живое существо, A — человек, C — неживая вещь. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[2]
Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[2]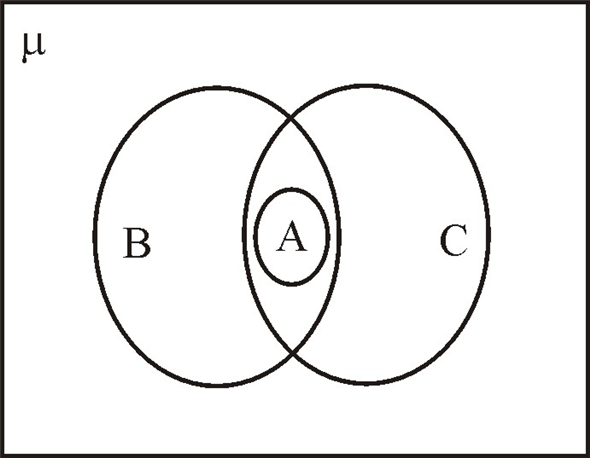
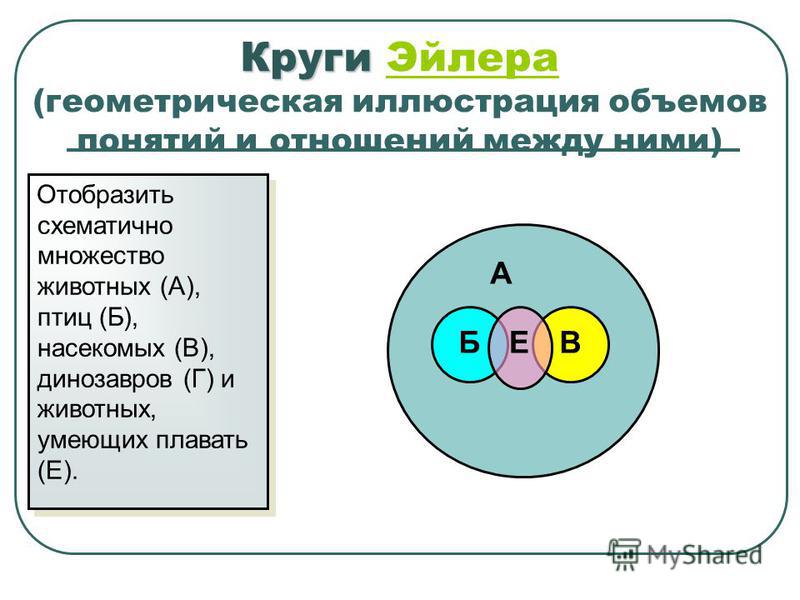 Leonhard Euler; 4 (15) апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург,Российская империя) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
Leonhard Euler; 4 (15) апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург,Российская империя) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.[2]
К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.[2]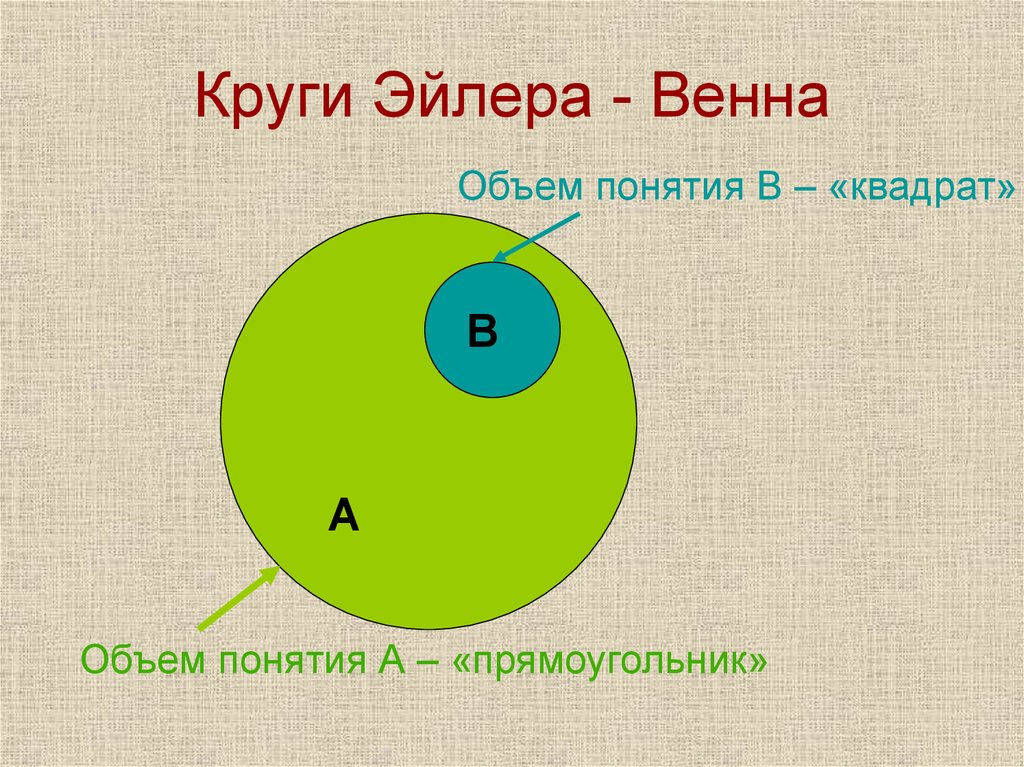 Сколько человек смотрели только фильм «Стиляги»?
Сколько человек смотрели только фильм «Стиляги»? 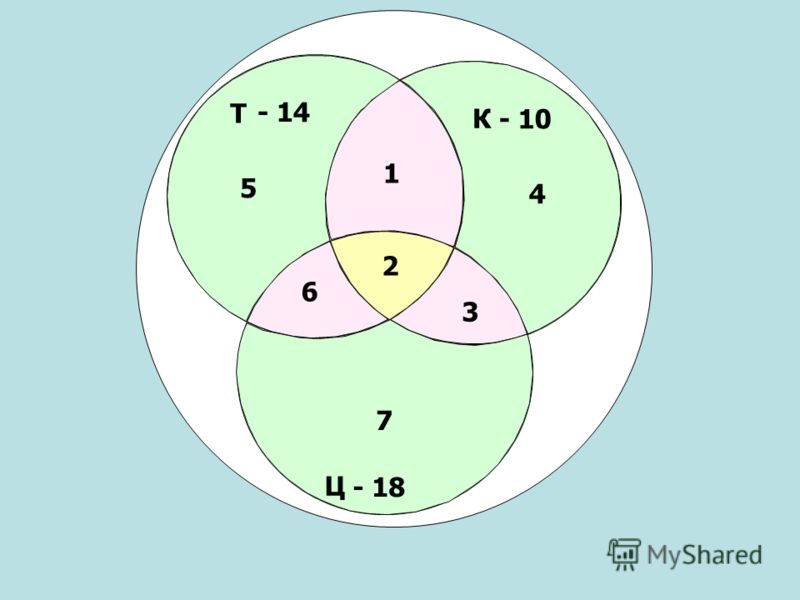 Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?  Сколько человек купили диски и Максим, и Земфиры?
Сколько человек купили диски и Максим, и Земфиры? 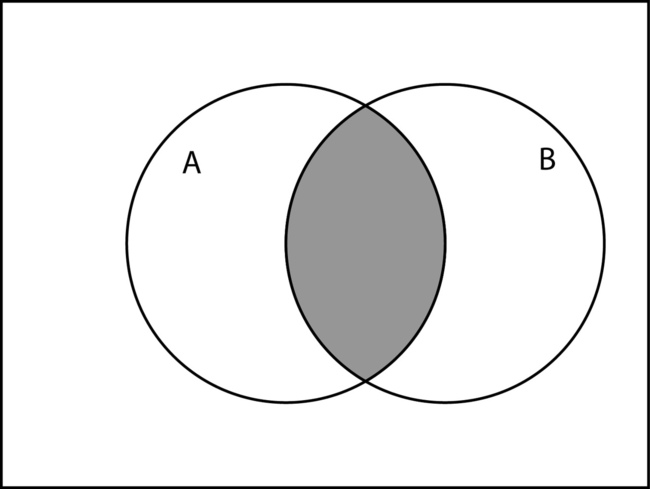 Следовательно,
Следовательно, 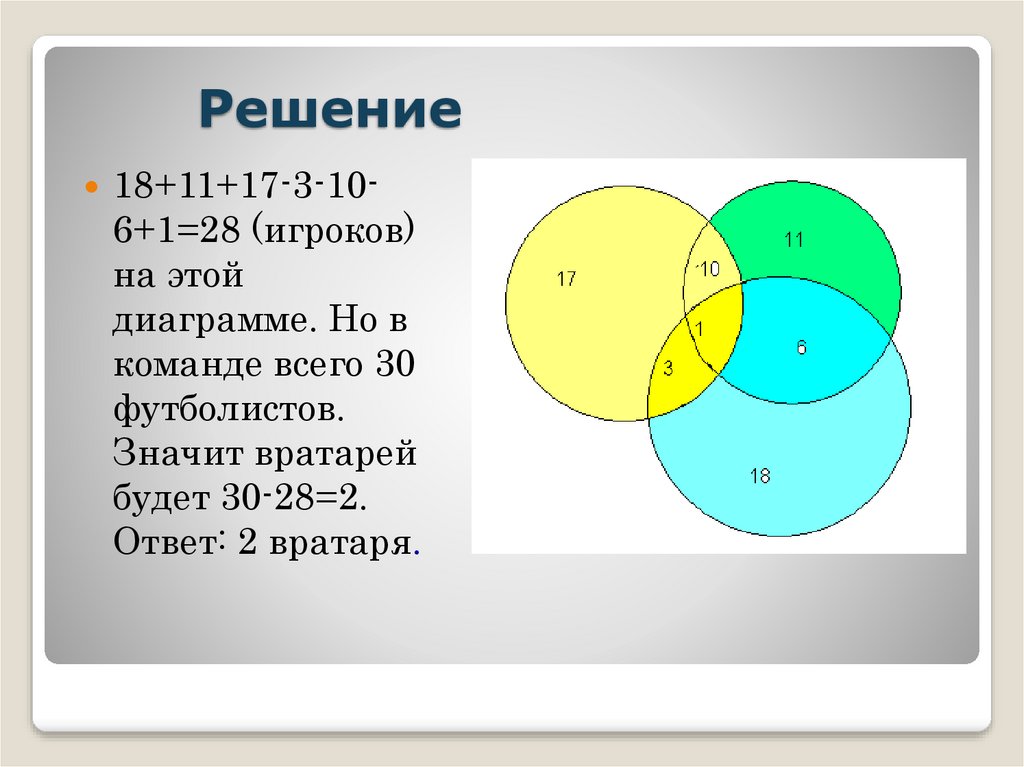 Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде. 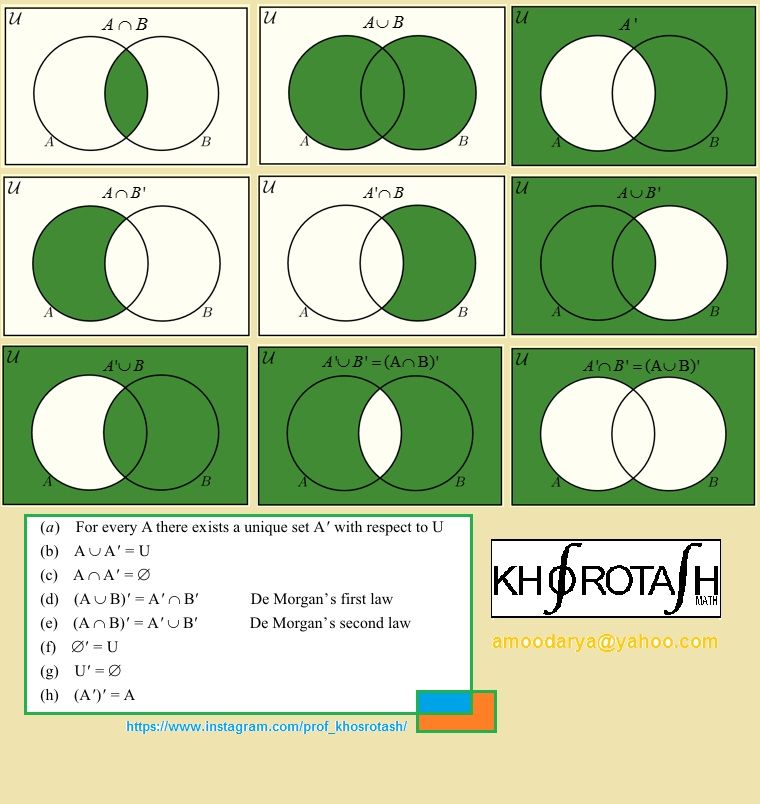
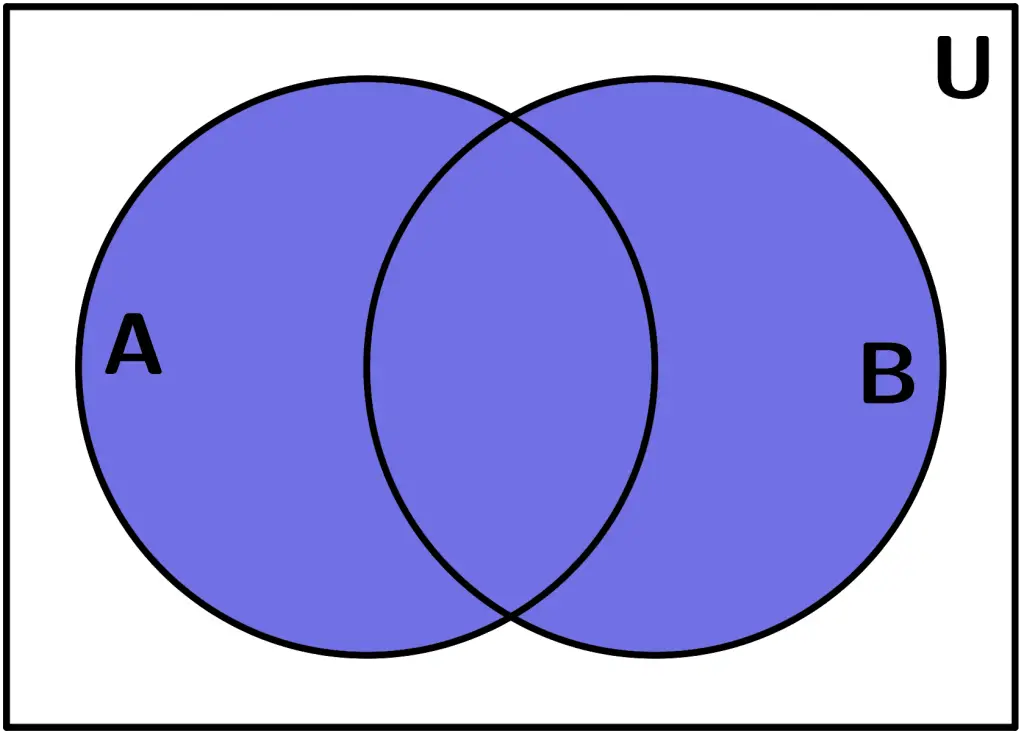 Найдите площадь листа.
Найдите площадь листа. Они покрыли площадь стола,
Они покрыли площадь стола,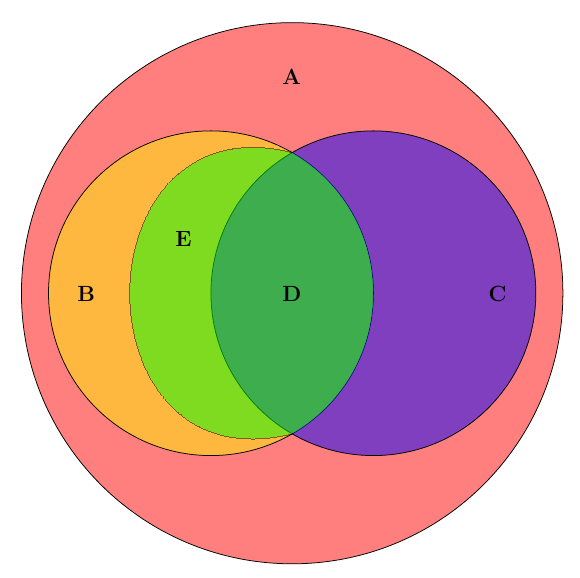
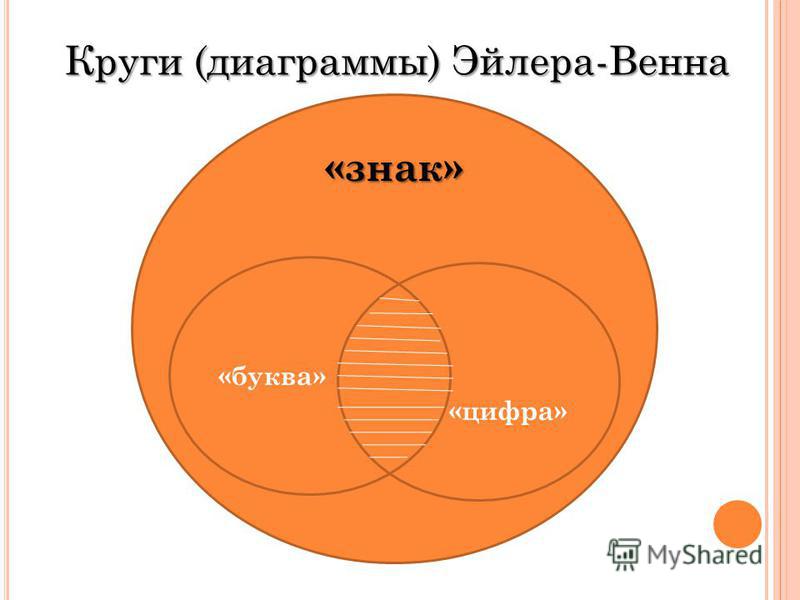 На сколько больше трудных задач, чем лёгких?
На сколько больше трудных задач, чем лёгких?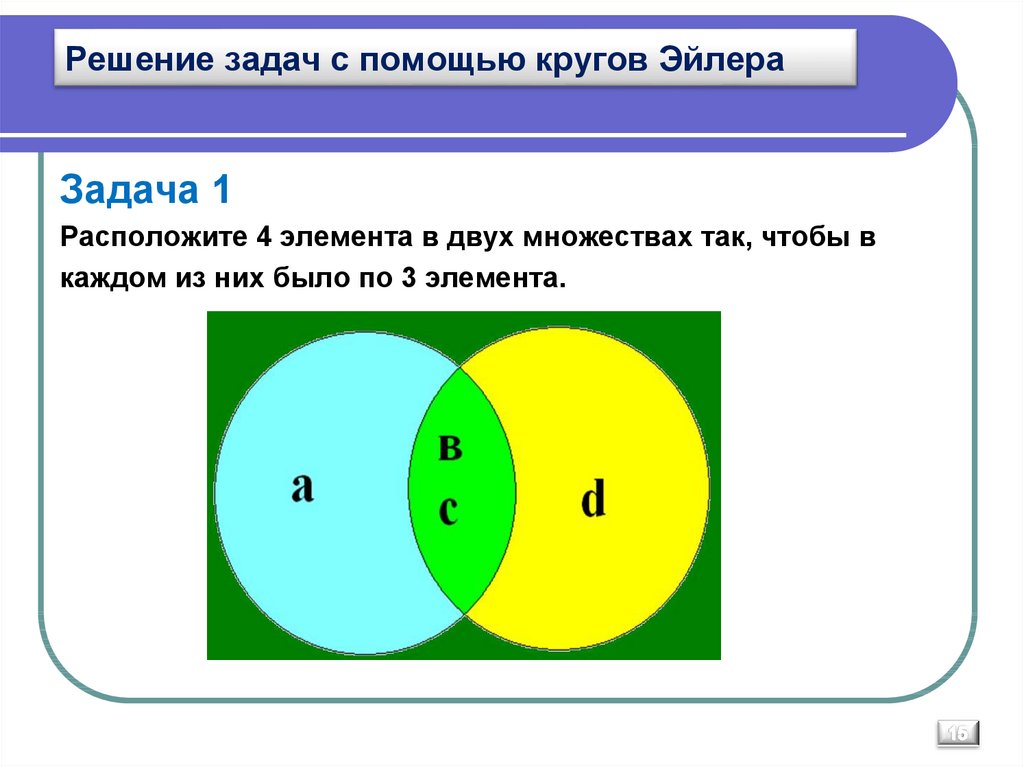 {n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
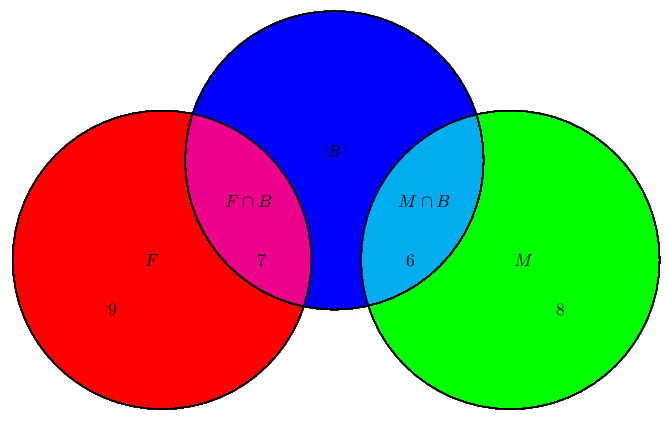
 Множества, логика, аксиоматические теории. — М.: Мир, 1968. — 231 с.
Множества, логика, аксиоматические теории. — М.: Мир, 1968. — 231 с. orgМоскваМеган, герцогиня СассекскаяОднопользовательская играTelegramКазахстанGoЛайвли, БлейкДамер, ДжеффриРоссийско-украинская войнаКэтрин, принцесса УэльскаяМногопользовательская играАнна ИоанновнаСтолкновения на азербайджано-армянской границе (сентябрь 2022)Сан-БруноИскандер (ракетный комплекс)Эндрю, герцог ЙоркскийДьявол носит Prada (фильм)Эдуард VIIIУзбекистанСамаркандГеорг VПервая мировая войнаЭдвард, граф УэссекскийСанкт-ПетербургВеликобританияСоюз Советских Социалистических РеспубликКонтрнаступление в Харьковской области (2022)🡆 More
orgМоскваМеган, герцогиня СассекскаяОднопользовательская играTelegramКазахстанGoЛайвли, БлейкДамер, ДжеффриРоссийско-украинская войнаКэтрин, принцесса УэльскаяМногопользовательская играАнна ИоанновнаСтолкновения на азербайджано-армянской границе (сентябрь 2022)Сан-БруноИскандер (ракетный комплекс)Эндрю, герцог ЙоркскийДьявол носит Prada (фильм)Эдуард VIIIУзбекистанСамаркандГеорг VПервая мировая войнаЭдвард, граф УэссекскийСанкт-ПетербургВеликобританияСоюз Советских Социалистических РеспубликКонтрнаступление в Харьковской области (2022)🡆 More Там он предается медитации, затем ложится спать. В 6 утра следующего дня монах начинает спускаться вниз к монастырю. Дорога обратно также неравномерна. Он идет с разной скоростью, где-то отдыхает, где-то ускоряет шаг. Спускается и поднимается монах по одной и той же тропинке. Вопрос состоит в следующем: существует ли пространственная точка, которую монах минует в одно и то же время суток, когда он поднимается и когда спускается? Я не спрашиваю, где эта точка, я спрашиваю, есть ли она в принципе!
Там он предается медитации, затем ложится спать. В 6 утра следующего дня монах начинает спускаться вниз к монастырю. Дорога обратно также неравномерна. Он идет с разной скоростью, где-то отдыхает, где-то ускоряет шаг. Спускается и поднимается монах по одной и той же тропинке. Вопрос состоит в следующем: существует ли пространственная точка, которую монах минует в одно и то же время суток, когда он поднимается и когда спускается? Я не спрашиваю, где эта точка, я спрашиваю, есть ли она в принципе! Каждый день она может быть разной, но она есть! Для этого нам нужно было нарисовать график, представить вопрос наглядно.
Каждый день она может быть разной, но она есть! Для этого нам нужно было нарисовать график, представить вопрос наглядно. Также маркетологи планируют и организуют конференции и обучающие семинары для потенциальных, новых и постоянных клиентов. Проблема заключается в том, что менеджеры по продажам не всегда говорят маркетологам, с какими клиентами они уже работают, с какими ведут предварительные переговоры. Также отдел продаж редко сообщает о пожеланиях клиентов и их жалобах, полагая, что маркетологи и так это должны знать. Отдел маркетинга, в свою очередь, не всегда оповещает менеджеров по продажам о готовящихся рекламных и стимулирующих акциях. Также результаты исследований, проводимых отделом маркетинга, носят внутренний, закрытый характер и, если и выходят вовне, то попадают на стол генерального директора, но не в руки менеджеров по продажам.
Также маркетологи планируют и организуют конференции и обучающие семинары для потенциальных, новых и постоянных клиентов. Проблема заключается в том, что менеджеры по продажам не всегда говорят маркетологам, с какими клиентами они уже работают, с какими ведут предварительные переговоры. Также отдел продаж редко сообщает о пожеланиях клиентов и их жалобах, полагая, что маркетологи и так это должны знать. Отдел маркетинга, в свою очередь, не всегда оповещает менеджеров по продажам о готовящихся рекламных и стимулирующих акциях. Также результаты исследований, проводимых отделом маркетинга, носят внутренний, закрытый характер и, если и выходят вовне, то попадают на стол генерального директора, но не в руки менеджеров по продажам.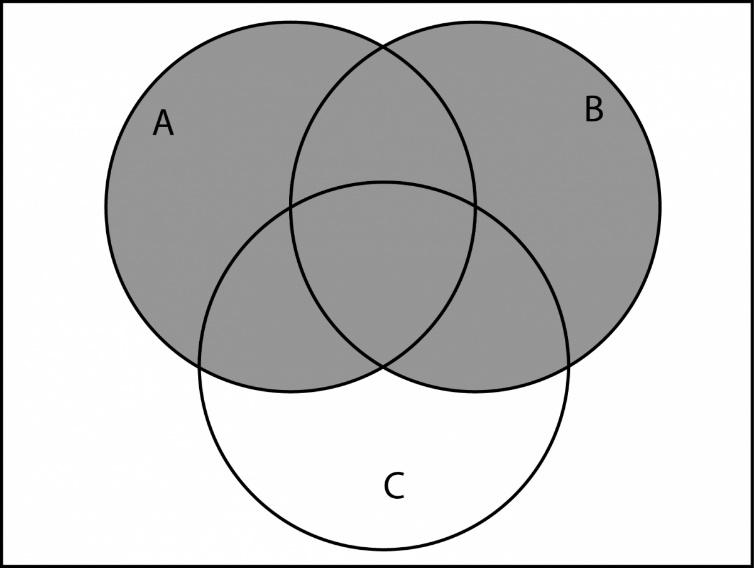 Естественно, сейчас круто пересекаются но не совпадают.
Естественно, сейчас круто пересекаются но не совпадают.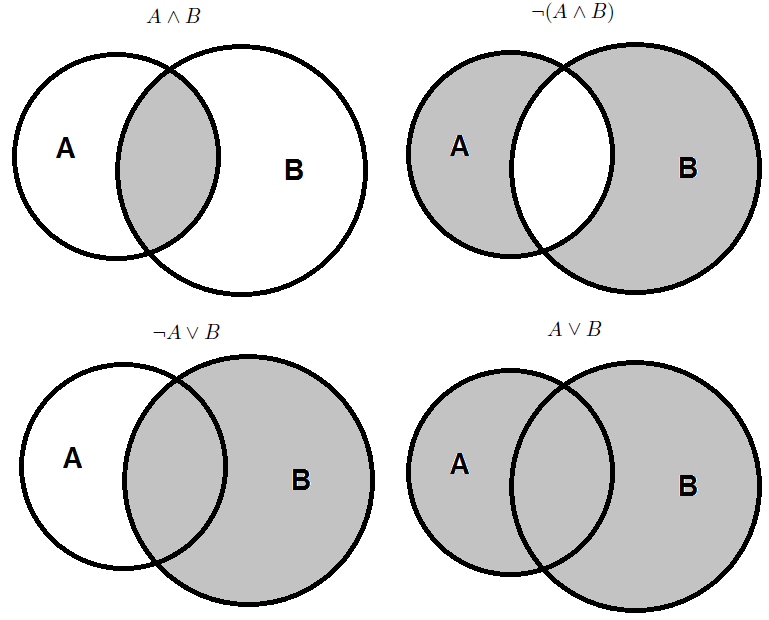
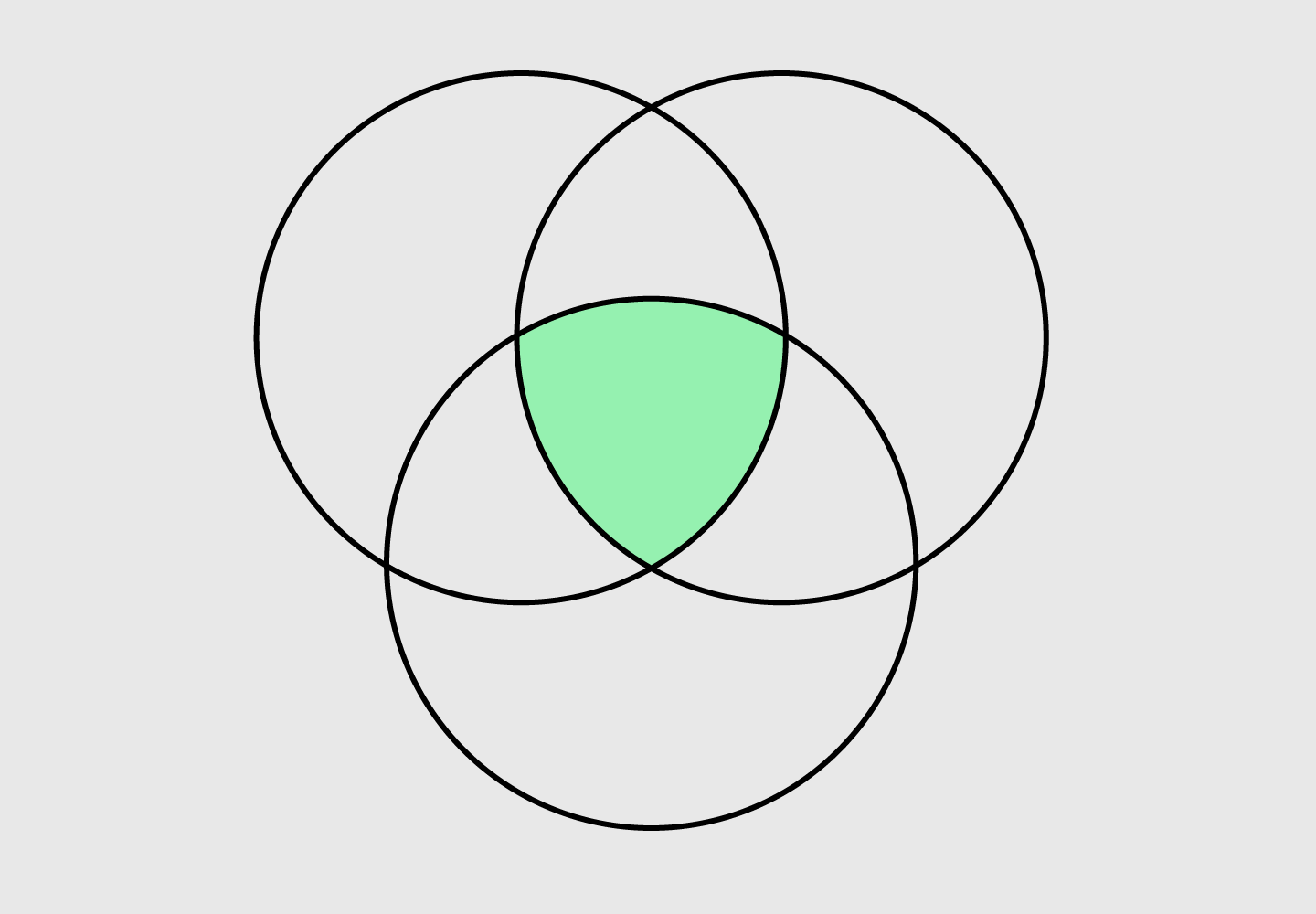 Уединившись на тихом озере в Беркширских горах, он прожил там два года. О своей тогдашней жизни он написал книгу
Уединившись на тихом озере в Беркширских горах, он прожил там два года. О своей тогдашней жизни он написал книгу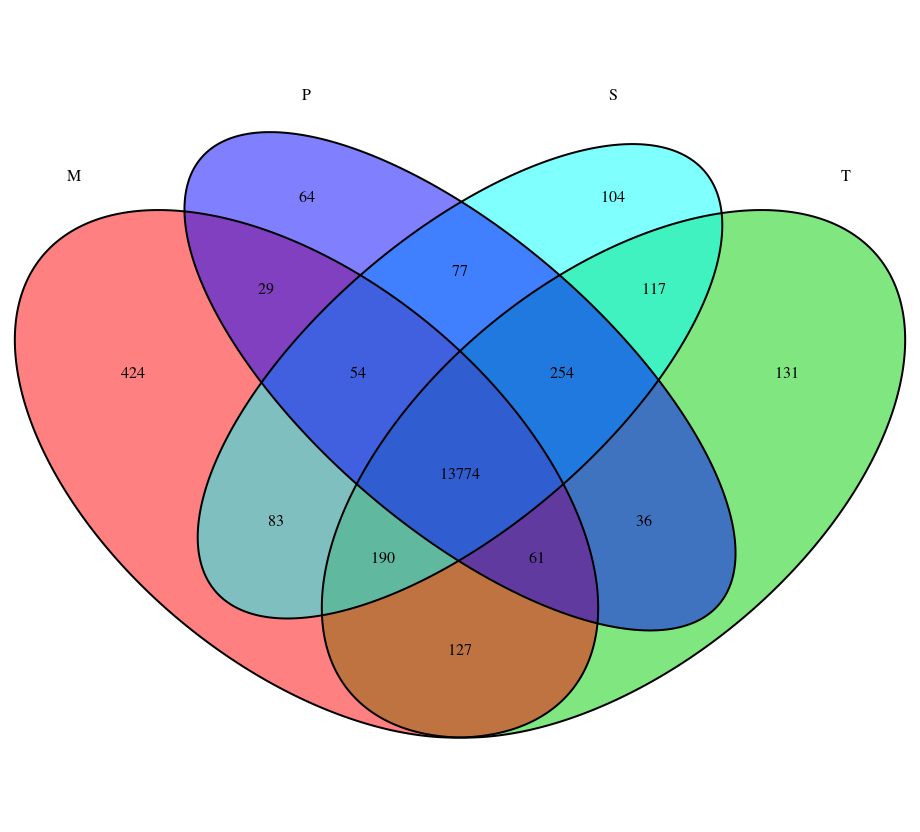 Первое их использование приписывают Леонарду Эйлеру[⇨]. Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна[⇨].
Первое их использование приписывают Леонарду Эйлеру[⇨]. Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна[⇨].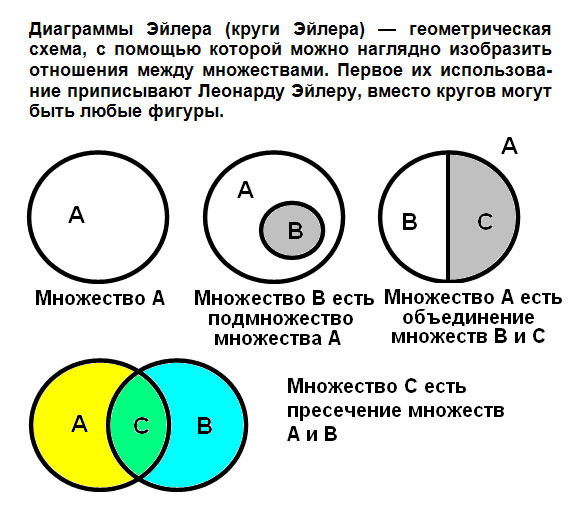 также
также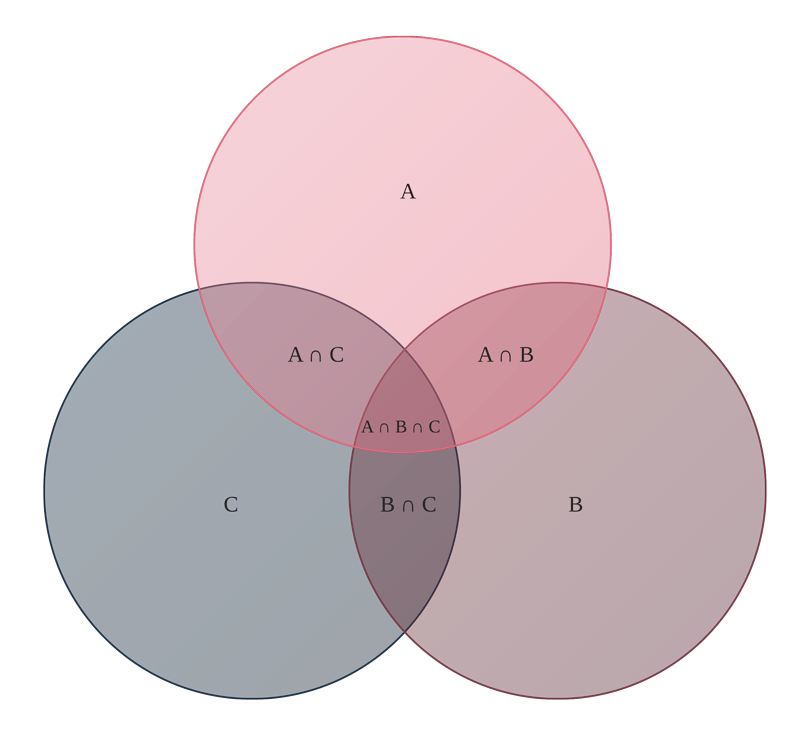 {n}} комбинацийn{\displaystyle n} свойств, то есть конечную булеву алгебру. Приn=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
{n}} комбинацийn{\displaystyle n} свойств, то есть конечную булеву алгебру. Приn=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.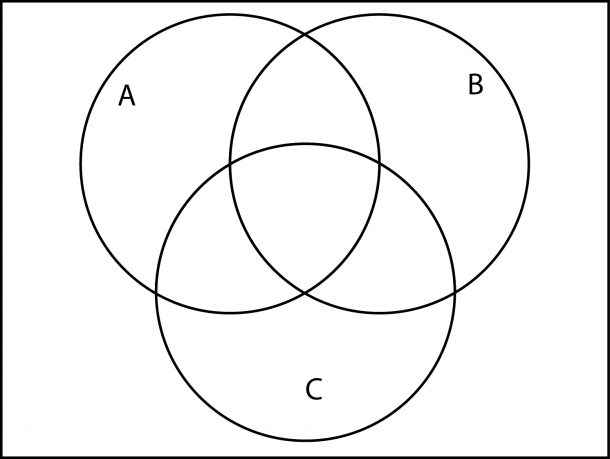
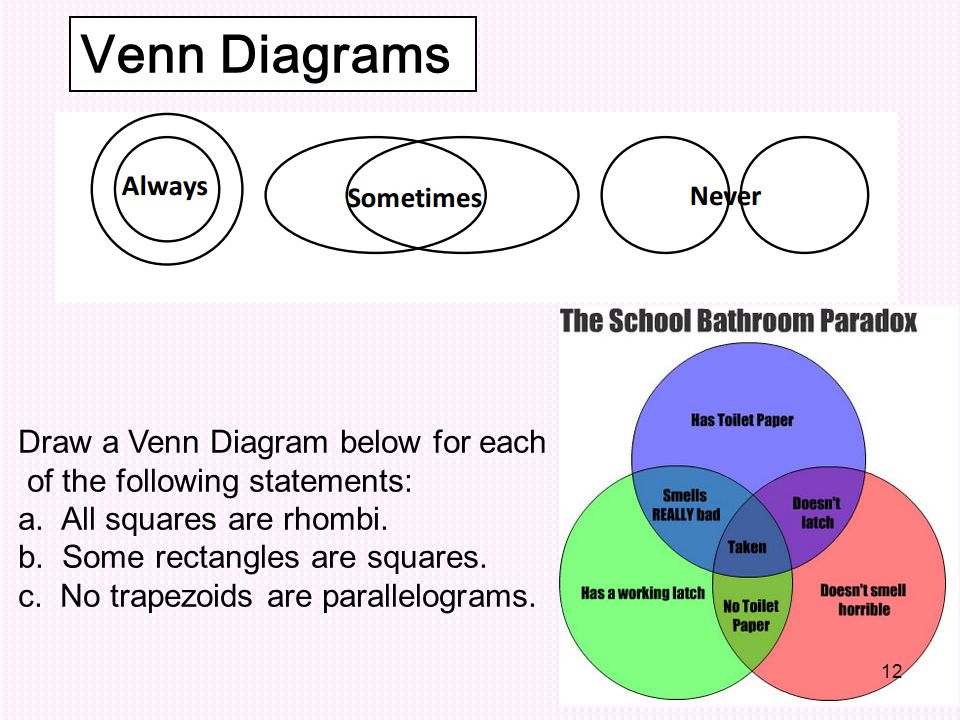 Персональная страничка Ю. Выбойченко
Персональная страничка Ю. Выбойченко Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
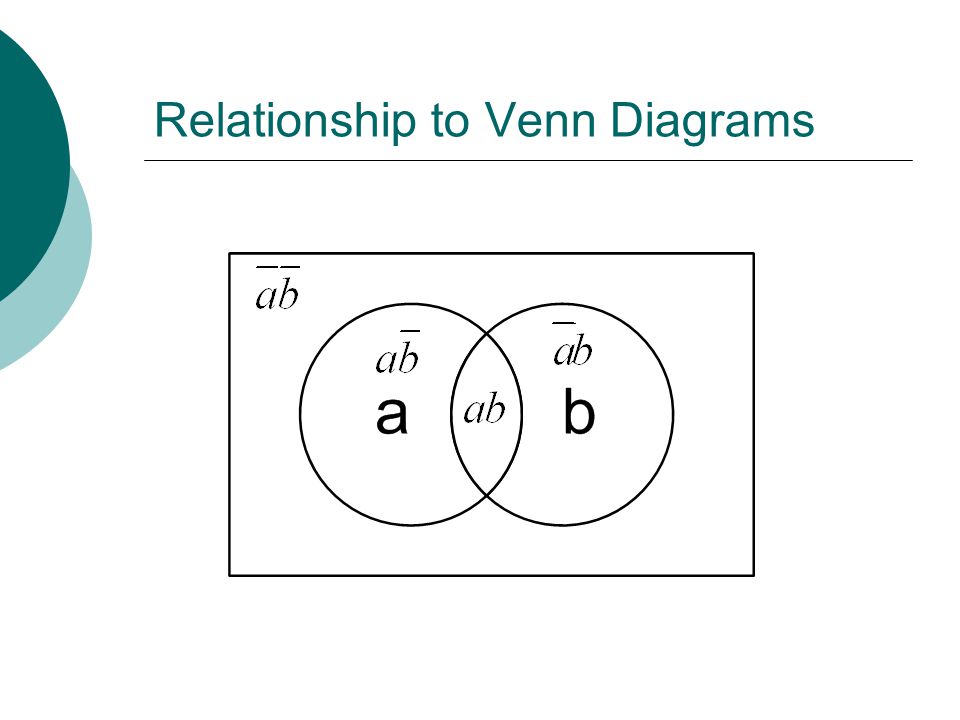 Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.
Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.
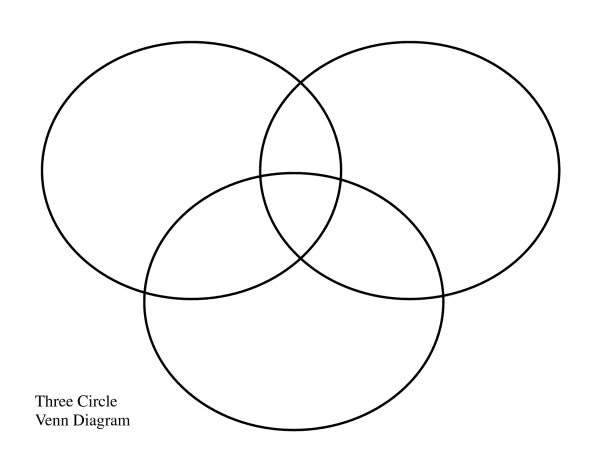 Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.
Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.
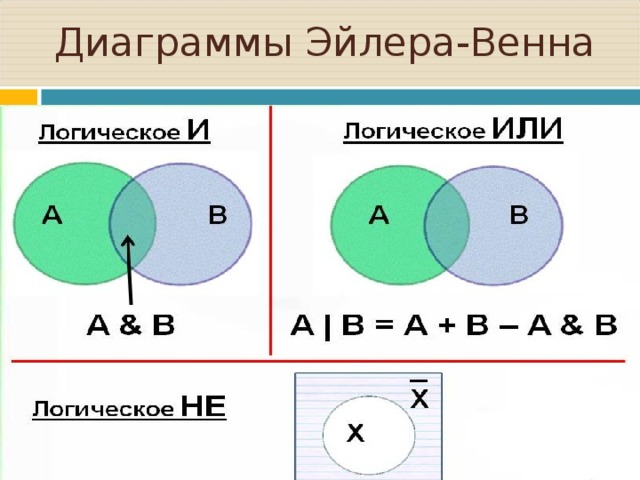 Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
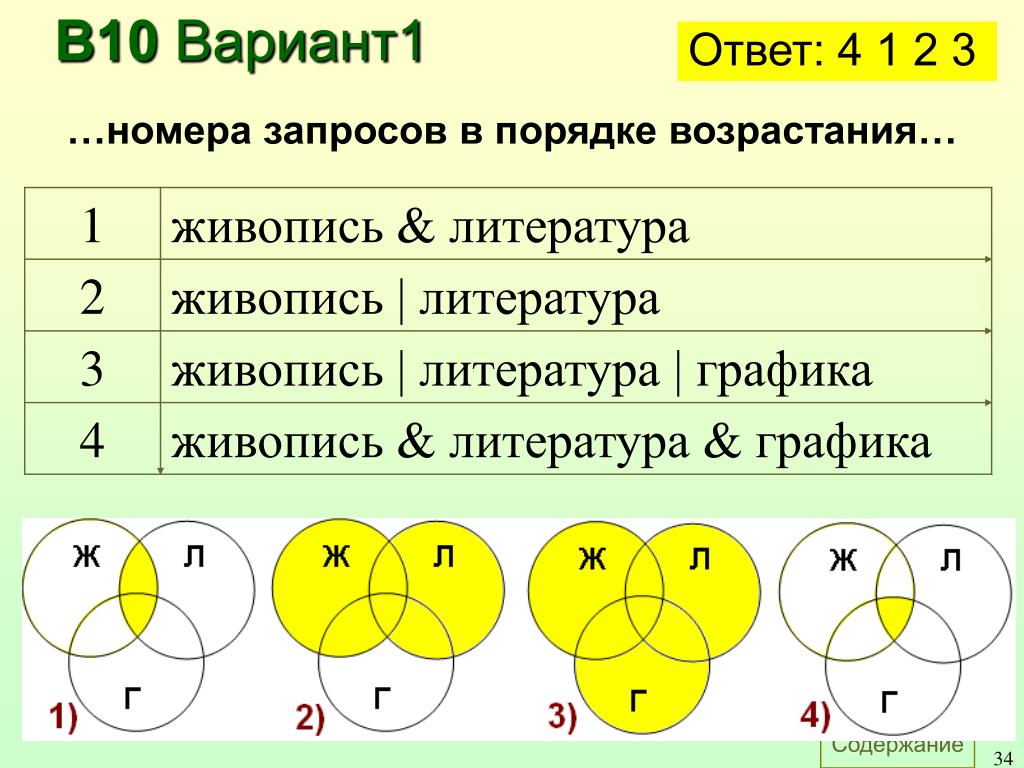 Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке:
Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке: