Сердечные кривые в Вольфрам Альфа
А пока что взгляните на исходную кривую, которую Вольфрам Альфа выводит по запросу
second heart curve Cartesian equation
В отличие от многих других подобных кривых, она задается довольно простым параметрическим уравнением, и может быть получена по запросу
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^2)^(3/20)sqrt(cos(t)), t=-1..1
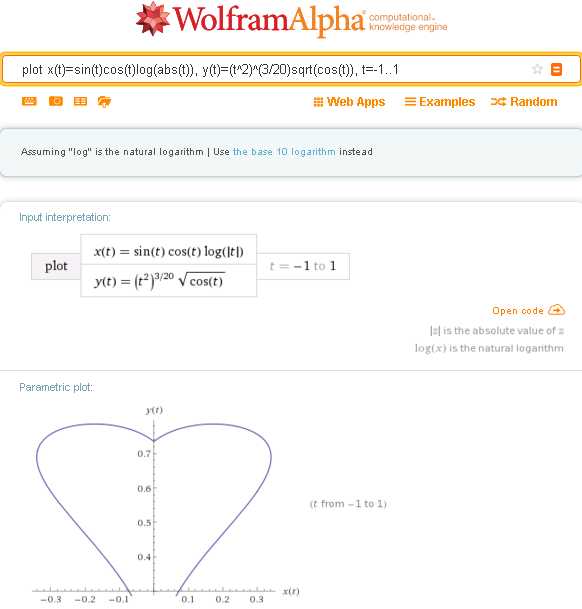
Однако, как видите, данный запрос выводит эту замечательную кривую не полностью (обрезает нижнюю часть), отчего она частично теряет свою эстетическую привлекательность и практически полностью утрачивает традиционное символическое значение.
Однако, этот способ построения сердечной кривой более привлекателен, в отличие от первого, тем, что изменяя числовые коэффициенты в указанных параметрических уравнениях, можно легко придавать «сердцу» самые различные формы.
Например, вы можете проверить, что за выразительность «крыльев» сердца отвечает показатель степени над cos(t) под корнем во втором уравнении:
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^2)^(3/20)sqrt((cos(t))^(5/2)), t=-1..1
В свою очередь, «полноту» сердца регулирует четный показатель степени над t в том же уравнении. Если его увеличивать, сердце приобретает более округлые формы
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^4)^(3/20)sqrt((cos(t))^(5/2)), t=-1..1
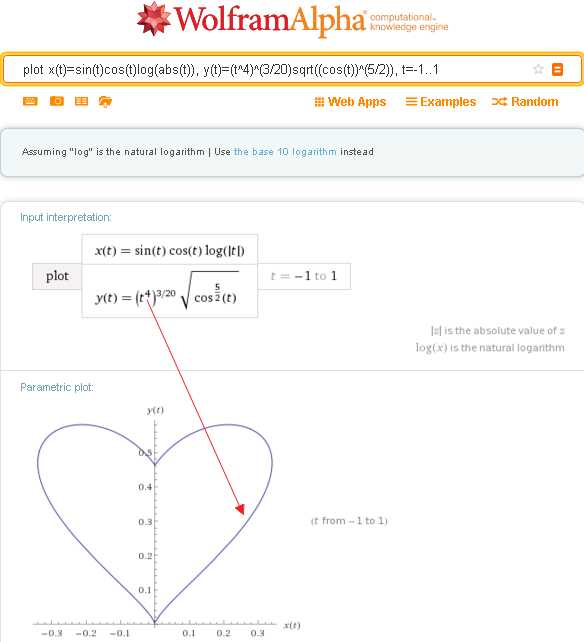
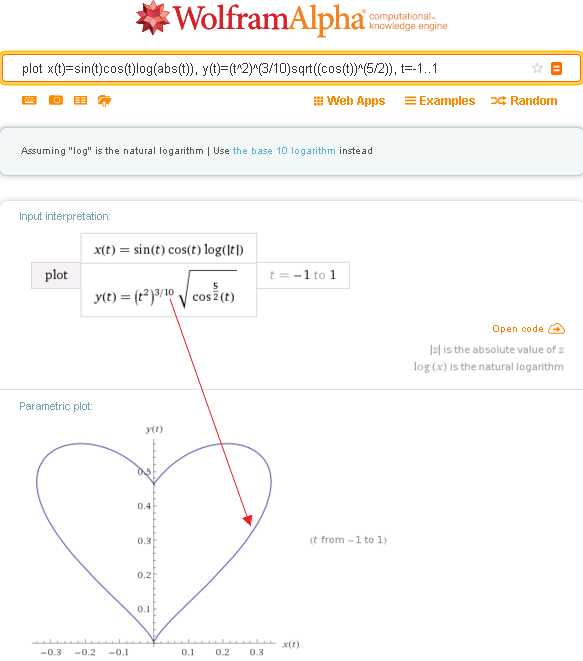
То же самое делает число в знаменателе дроби, которая стоит в показателе степени над t^2. Этот знаменатель, наоборот, надо уменьшать (тут получается практически то же самое)
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^2)^(3/10)sqrt((cos(t))^(5/2)), t=-1..1
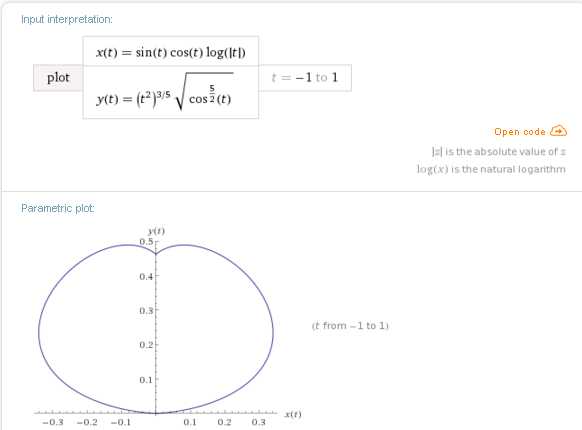
Экспериментируя с этими коэффициентами, будьте осторожны, чтобы в результате, вместо симпатичного сердца, у вас случайно не получилось бы нечто бесформенное и, может быть, даже не совсем приличное 😉
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^2)^(3/5)sqrt((cos(t))^(5/2)), t=-1..1
Используйте следующий запрос, если вы хотите получить классическое изображение сердца (перепробовав очень многие варианты, я остановился именно на этом)
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^2)^(3/8)sqrt((cos(t))^(7/3)), t=-1..1
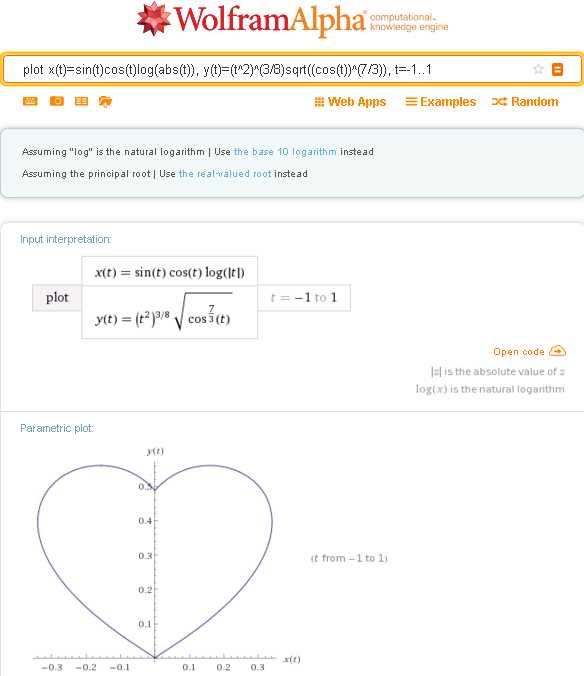
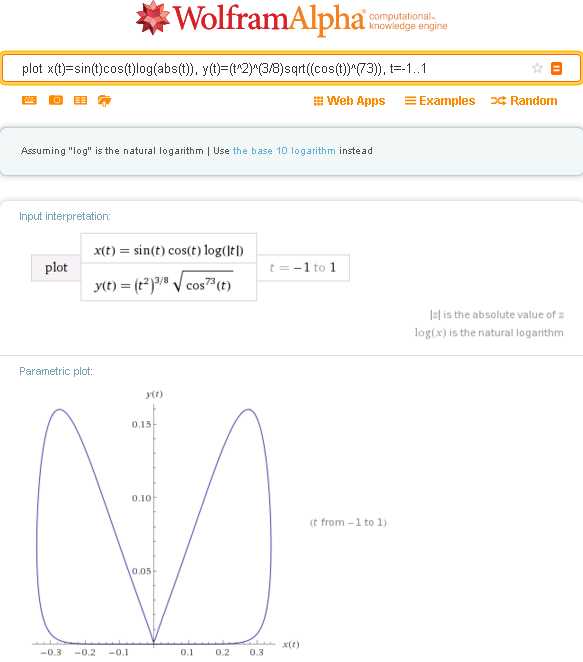
Но если вы «всего лишь» забудете поставить слэш в дроби 7/3, то в наказание за это увидите на выходе вот такие вот оригинальные «лисичкины уши»:
plot x(t)=sin(t)cos(t)log(abs(t)), y(t)=(t^2)^(3/8)sqrt((cos(t))^(73)), t=-1..1
Конечно, только вам решать, какое математическое сердце вам более по вкусу. Поупражняйтесь с Вольфрам Альфа, и если у вас получится действительно нечто оригинальное, добавьте ваш вариант в комментариях под этим постом.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
www.wolframalpha-ru.com
Хочу учиться — Wolfram Alpha
Краткий список обозначений и операторов WolframAlpha
для решения задач онлайн
| + | сложение |
| — | вычитание |
| * | умножение |
| / | деление |
| ^ | возведение в степень |
| solve | решение уравнений, неравенств, систем уравнений и неравенств |
| expand | раскрытие скобок |
| factor | разложение на множители |
| sum | вычисление суммы членов последовательности |
| derivative | дифференцирование (производная) |
| integrate | интеграл |
| lim | предел |
| inf | бесконечность |
| plot | построить график функции |
| log (a, b) | логарифм по основанию a числа b |
| sin, cos, tg, ctg | синус, косинус, тангенс, котангенс |
| sqrt | корень квадратный |
| pi | число «пи» (3,1415926535…) |
| e | число «е» (2,718281…) |
| i | Мнимая единица i |
| minimize, maximize | Нахождение экстремумов функции (минимумов и максимумов) |
Примеры решения задач онлайн с помощью WolframAlpha
1.
Решение рациональных, дробно-рациональных уравнений любой степени,
показательных, логарифмических, тригонометрических уравнений.
Пример 1. Чтобы решить уравнение x2 + 3x — 4 = 0, нужно ввести solve x^2+3x-4=0
Пример 2. Чтобы решить уравнение log32x = 2, нужно ввести solve log(3, 2x)=2
Пример 3. Чтобы решить уравнение 25x-1 = 0.2, нужно ввести solve 25^(x-1)=0.2
Пример 4. Чтобы решить уравнение sin x = 0.5, нужно ввести solve sin(x)=0.5
2. Решение систем уравнений.
Пример. Чтобы решить систему уравнений
x + y = 5,
x — y = 1,
нужно ввести solve x+y=5 && x-y=1
Знаки && в данном случае обозначает логическое «И».
3. Решение рациональных неравенств любой степени.
Пример. Чтобы решить неравенство x2 + 3x — 4 < 0, нужно ввести solve x^2+3x-4<0
4. Решение систем рациональных неравенств.
Пример. Чтобы решить систему неравенств
x2 + 3x — 4 < 0,
2x2 — x + 8 > 0,
нужно ввести solve x^2+3x-4<0 && 2х^2 — x + 8 > 0
Знаки && в данном случае обозначает логическое «И».
5. Раскрытие скобок + приведение подобных в выражении.
Пример. Чтобы раскрыть скобки в выражении (c+d)2(a-c) и привести подобные, нужно
ввести expand (c+d)^2*(a-c).
6. Разложение выражения на множители.
Пример. Чтобы разложить на множители выражение x2 + 3x — 4, нужно ввести factor x^2 + 3x — 4.
7. Вычисление суммы n первых членов последовательности (в том числе арифметической и геометрической прогрессий).
Пример. Чтобы вычислить сумму 20 первых членов последовательности, заданной формулой an = n3+n, нужно ввести sum n^3+n, n=1..20
Если нужно вычислить сумму первых 10 членов арифметической прогрессии, у которой первый член a1 = 3, разность d = 5, то можно, как вариант, ввести a1=3, d=5, sum a1 + d(n-1), n=1..10
Если нужно вычислить сумму первых 7 членов геометрической прогрессии, у которой первый член b1 = 3, разность q = 5, то можно, как вариант, ввести b1=3, q=5, sum b1*q^(n-1), n=1..7
8. Нахождение производной.
Пример. Чтобы найти производную функции f(x) =x2 + 3x — 4, нужно ввести derivative x^2 + 3x — 4
9. Нахождение неопределенного интеграла.
Пример. Чтобы найти первообразную функции f(x) =x2 + 3x — 4, нужно ввести integrate x^2 + 3x — 4
10. Вычисление определенного интеграла.
Пример. Чтобы вычислить интеграл функции f(x) =x2 + 3x — 4 на отрезке [5, 7],
нужно ввести integrate x^2 + 3x — 4, x=5..7
11. Вычисление пределов.
Пример. Чтобы убедиться, что
введите lim (x -> 0) (sin x)/x и посмотрите ответ. Если нужно вычислить какой-то предел при x, стремящемся к бесконечности, следует вводить x -> inf.
12. Исследование функции и построение графика.
Пример. Чтобы исследовать функцию x3 — 3x2 и построить ее график, просто введите x^3-3x^2. Вы получите корни (точки пересечения с осью ОХ), производную, график, неопределенный интеграл, экстремумы.
13. Нахождение наибольшего и наименьшего значений функции на отрезке.
Пример. Чтобы найти минимальное значение функции x3 — 3x2 на отрезке [0.5, 2],
нужно ввести minimize (x^3-x^2), {x, 0.5, 2}
Чтобы найти максимальное значение функции x3 — 3x2 на отрезке [0.5, 2],
нужно ввести maximize (x^3-x^2), {x, 0.5, 2}
gghelp.ru
WolframAlpha по-русски: Дифференцирование функций в Wolfram|Alpha
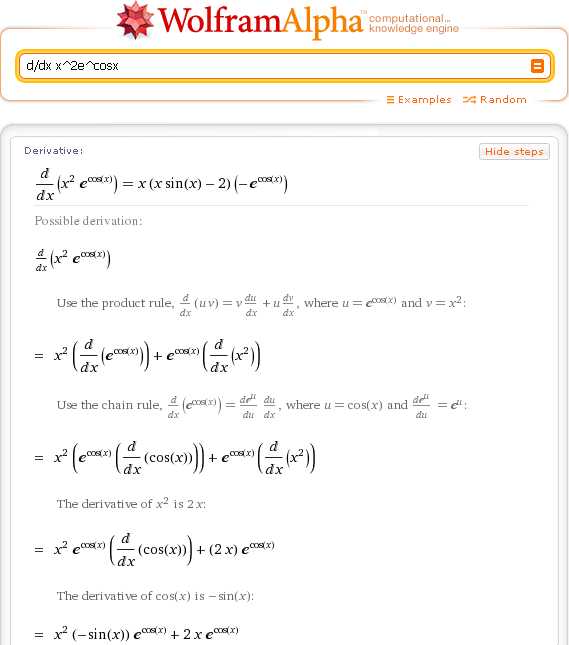
Как найти производную функции в Wolfram|Alpha?Wolfram|Alpha использует для дифференцирования функций несколько различных запросов. Проще всего найти обычную производную функции f(x) в Wolfram|Alpha можно с помощью запроса-префикса d/dx.
Вот, как это выглядит на практике
d/dx x^2e^cosx
Чтобы получить пошаговое решение с пояснениями каждого шага, достаточно нажать «Show steps».
Для вычисления производных второго порядка служит запрос d^2/dx^2:
d^2/dx^2 x^2e^cosx
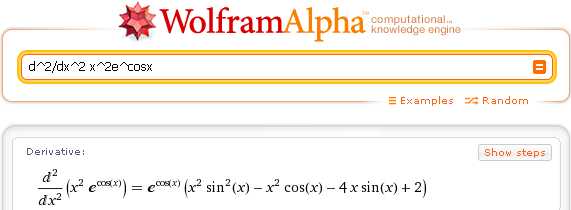
Аналогично вычисляются производные высших порядков. Например, так вычисляется производная третьего порядка:
d^3/dx^3 x^2e^cosx
Wolfram|Alpha может находить сразу производные нескольких порядков. Как, например, это может понадобиться при отыскании коэффициентов ряда Тейлора. Для этого используется запрос на табуляцию функции с указанием наименьшего, наибольшего порядка производной, а также шага между ними. Чтобы не загромождать изложение, рассмотрим простой пример на вычисление производных функции cos(x) до 5-го порядка включительно:
table[d^n/dx^n cosx^5,{n,0,5,1}]
Тот же результат (табулирование производной) получим по запросу вида
table d^n/dx^n (1 x^3+(-6 x^2+4 x+12)) for n = 1 … 4
Для вычисления значения производной в заданной точке, нужно указать значение аргумента:
d/dx x^2e^cosx, x=pi
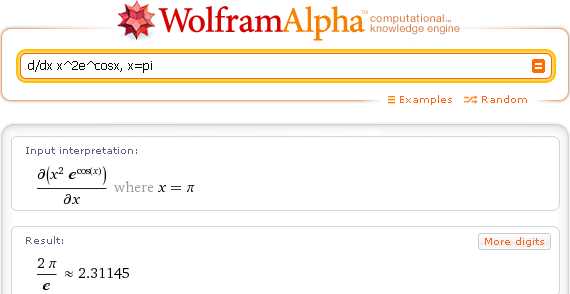
Частные производные вычисляются аналогично:
d/dx x^ye^cosxy, d/dy x^ye^cosxy
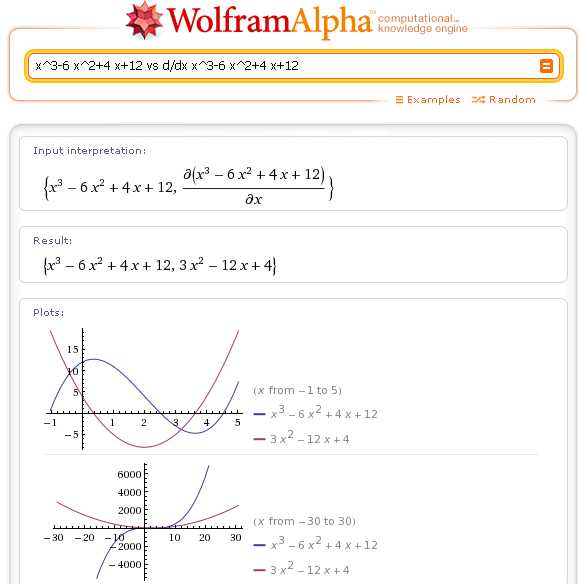
Естественно, с помощью Wolfram|Alpha можно визуально сравнить функцию и ее производную:
x^3-6 x^2+4 x+12 vs d/dx x^3-6 x^2+4 x+12
P.S.
Конечно, навряд ли можно научиться дифференцировать функции, используя исключительно Wolfram|Alpha. Однако, система Wolfram|Alpha вполне подходит, чтобы проверить свои знания, освежить их, например, перед экзаменом, и убедиться, что вы к нему вполне готовы.
Преподавателям Wolfram|Alpha поможет оценить сложность и время на выполнение заданий на производные, которые предлагаются студентам.
www.wolframalpha-ru.com
Непрерывные вероятностные распределения в Wolfram|Alpha
Вероятностные распределения играют исключительно важную роль в математике, статистике, математическом моделировании, физике и др. И в этом вопросе Wolfram|Alpha как всегда спешит нам на помощь. Например, если вдруг Вам срочно понадобилась информация о свойствах какого-либо вероятностного распределения (properties of a continuous distribution), обратитесь к Wolfram|Alpha с соответствующим запросом, и Вы тут же получите нужные сведения. Главное — это правильно задать свой вопрос Wolfram|Alpha, то есть правильно сформулировать нужный Вам запрос.В большинстве случаев, чтобы правильно обратиться к Wolfram|Alpha за информацией относительно вероятностных распределений, нужно вспомнить, как пишется название того или иного вероятностного распределения по-английски. Это относится, прежде всего, ко всем известному нормальному распределению, которое также называют распределением Гаусса.
Основную информацию относительно нормального распределения, а именно — его свойства, графики, числовые характеристики — Wolfram|Alpha выводит по запросу normal distribution (gauss distribution):
normal distribution (gauss distribution)
Во-первых, по этому запросу Вы получите перечень основных числовых характеристик нормального распределения (normal distribution statistical properties):
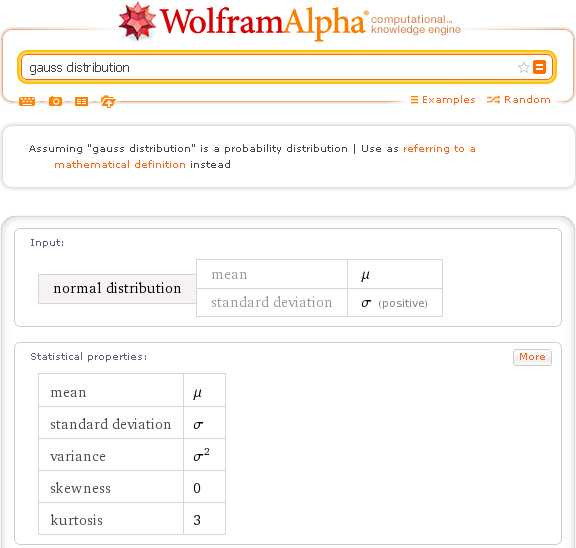Для всех вероятностных распределений Wolfram|Alpha выводит пять основных числовых характеристик:- Mean — математическое ожидание, среднее;
- Standard deviation — средне-квадратическое отклонение;
- Variance — дисперсия;
- Skewness — асимметрия;
- Kurtosis — эксцесс.
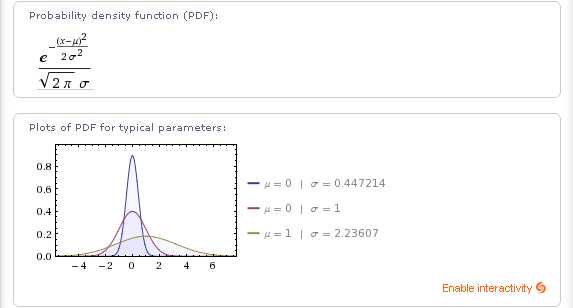
Также — формулу и график функции нормального распределения (cumulative distribution function (CDF)):
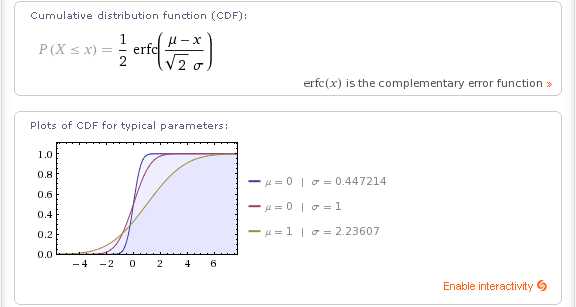
Наконец, в-третьих, Wolfram|Alpha выводит некоторые важные перцентили (percentiles) нормального распределения:
Аналогично можно получить те же основные сведения относительно других непрерывных вероятностных распределений. Вот список основных из них с соответствующими запросами:
Если этот список неполный, попробуйте дополнить его сами. Результаты пишите в комментарии. Это будет полезно не только Вам, но и другим читателям этого блога.Если Вам нужно получить отдельные свойства непрерывных вероятностных распределений, то в своем запросе перед названием распределения просто укажите нужное Вам свойство. Например, чтобы получить математическое ожидание нормального распределения, следует использовать запрос mean normal distribution. Чтобы получить плотность нормального распределения используйте запрос pdf normal distribution. Запрос cdf normal distribution выводит функцию нормального распределения и т.п. Будьте внимательны — при вводе запросов используйте английскую раскладку клавиатуры.
В следующих постах я собираюсь показать подробнее, с помощью каких запросов можно получить отдельные свойства вероятностных распределений, как получить свойства вероятностных распределений с заданными параметрами, приведу список основных дискретных вероятностных распределений, а также покажу, как с помощью Wolfram|Alpha вычисляется вероятность попадания случайной величины в заданный интервал. Кстати, последняя задача с помощью Wolfram|Alpha решается одинаково для всех распределений. Об этом важно знать, поскольку в университетских курсах (особенно на нематематических факультетах университетов) эта задача, рассматривается, как правило, на уровне примера, да и то лишь для нормального распределения непрерывных случайных величин, а также для биномиального распределения дискретных случайных величин.
Желаю успехов!
WolframAlpha — сервис для решения задач онлайн и не только…
В Интернете запущен долгожданный сервис Wolfram Alpha, вычисляющий ответы на вопросы, заданные на естественном языке.
Проект возглавляет Стивен Вольфрам, автор одной из самых популярных программ компьютерной алгебры — Mathematica.
Отличие Wolfram Alpha от обычных поисковых систем заключается в том, что вместо списка ссылок на миллионы веб-страниц, Wolfram Alpha выдает ответ, который он вычисляет самостоятельно. Русский язык Wolfram Alpha не понимает, поэтому вопросы нужно задавать на английском языке.
Использование Wolfram | Alpha похоже на выполнение поиска Google, но Wolfram | Alpha предоставляет конкретные ответы, а не бесконечные страницы потенциально релевантных результатов. Любой может перейти на веб-сайт Wolfram | Alpha, ввести вопрос или уравнение в диалоговое окно, нажать Enter и получить ответ. Если вы пытаетесь решить x2 + 5x + 6 = 0, Wolfram | Alpha предоставит вам корневой сюжет, альтернативные формы и решения. Если вы ищете пошаговое объяснение, есть бесплатная версия для студентов и преподавателей.
Перейти на сайт….
Автор публикации
не в сети 3 недели
admin
3 Комментарии: 8Публикации: 466Регистрация: 30-11—0001pedagogru.ru
WolframAlpha по-русски: Математика с Wolfram|Alpha: шаг за шагом…
Wolfram|Alpha может выводить шаг за шагом последовательность решения многих математических задач, от решения квадратных уравнений до интегрирования комплексных функций.Solve 3х^2 +5x-2=4x
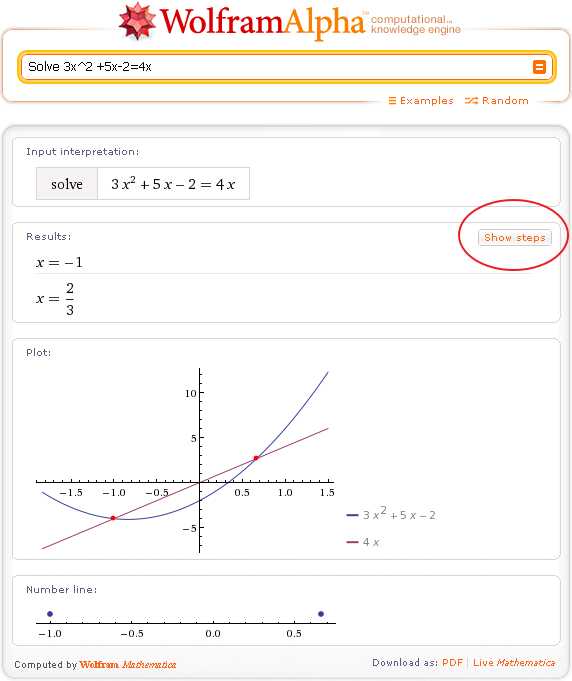
Но, если вы захотите узнать, каким способом было получено решение, просто нажмите кнопку Show steps — Wolfram|Alpha покажет решение шаг за шагом…
Как видите, Wolfram|Alpha решает это квадратное уравнение методом выделения полного квадрата.
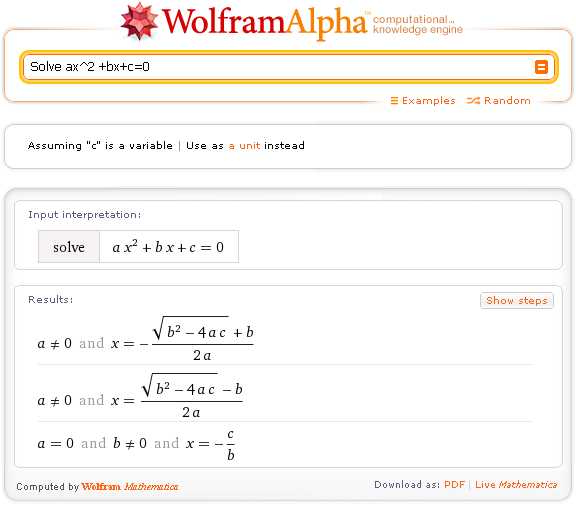
Но это вовсе не означает, что «они» такие тупые», что Wolfram|Alpha даже не знает формулы корней квадратного уравнения. Знает! В этом можно убедиться, введя запрос:
Solve aх^2 +bx+c=0
Сможет ли Wolfram|Alpha показать пошаговое решение более сложных задач? Посмотрим.
Например, если вы забыли, как делится многочлен на многочлен, посмотрите вот это (не забывайте про Show steps):
( х 5 -14 х 4 +3х 2 -2 х +17) / (2 х 2 — х +1)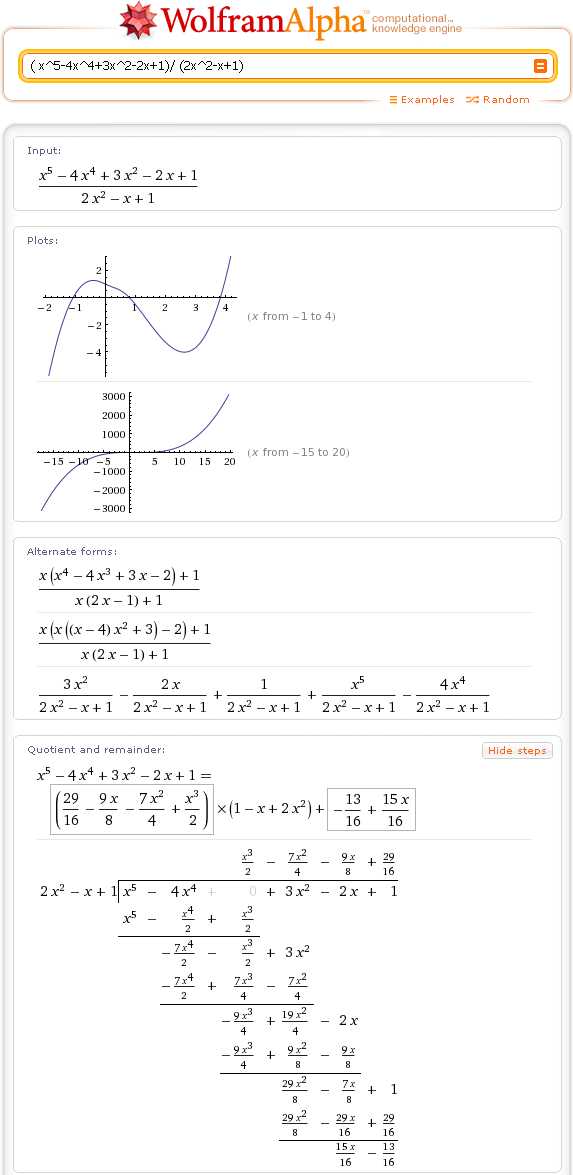
Возможно, вы зашли в тупик, пытаясь найти предел х^х при х -> 0, тогда проконсультируйтесь с Wolfram|Alpha как это делается:
limit x^x, x->0
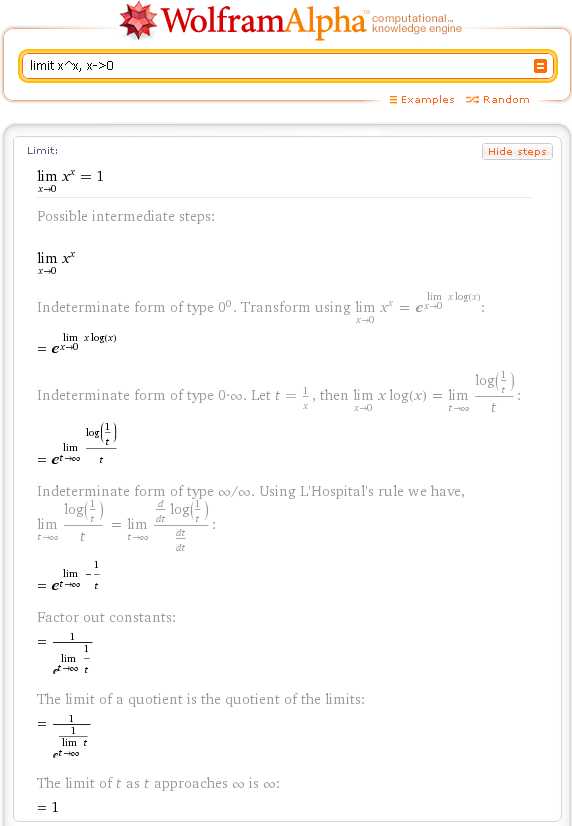
Если хотите увидеть, как найти производную частного двух функций, Wolfram|Alpha легко справится и с этой задачей:
d/dx (2х^3 +4)/(5х^2-7х)
Что бы вы ни решали с Wolfram|Alpha, всегда есть возможность посмотреть пошаговое решение, которое покажет вам не только ответ, но и весь процесс решения задачи.
www.wolframalpha-ru.com
Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha.Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.
Чтобы решить дифференциальное уравнение с помощью Wolfram|Alpha достаточно ввести его в систему. ВНИМАНИЕ! Для ввода символа производной используется знак апострофа » ‘ «, но не кавычки (!). Для определенности можно добавить перед уравнением поисковое предписание solve (хотя, во многих случаях, это и не обязательно).
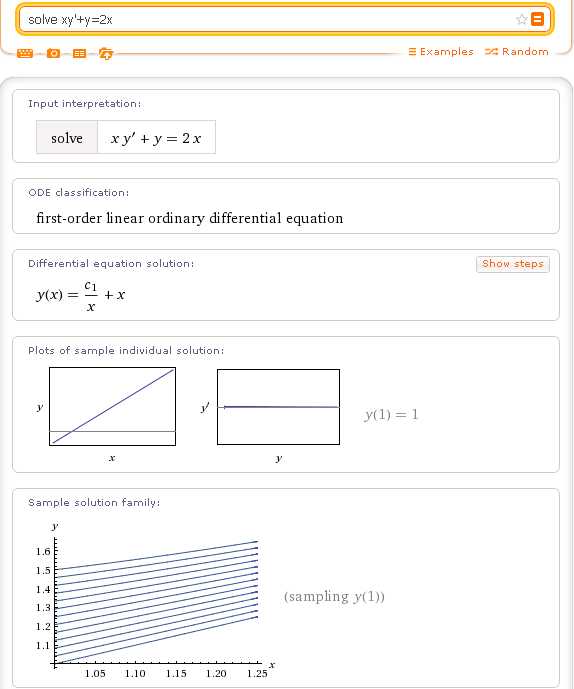
Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.
Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps»:
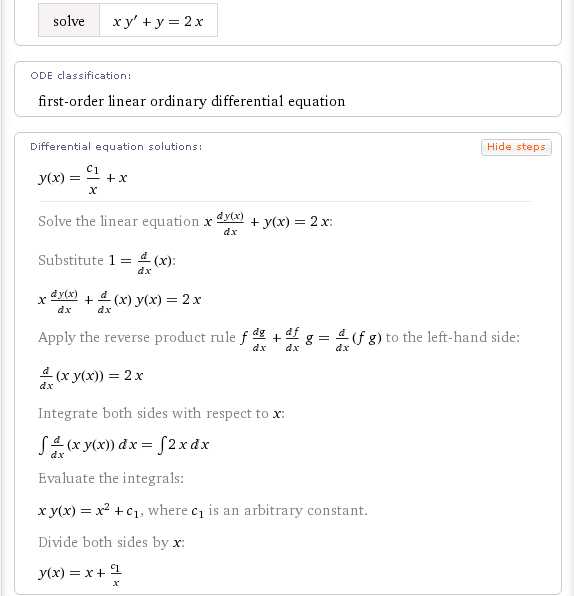
Аналогичным образом можно получить решение, например, дифференциального уравнения Бернулли:
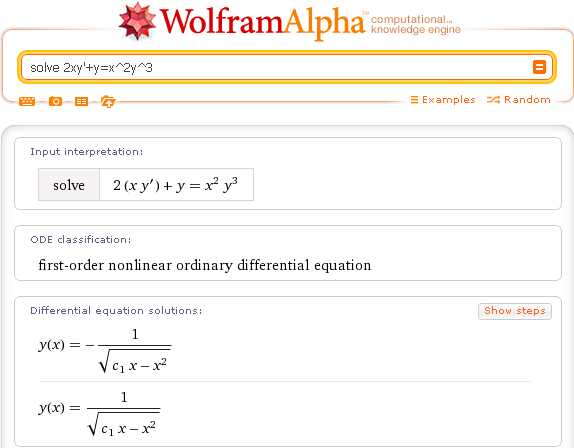
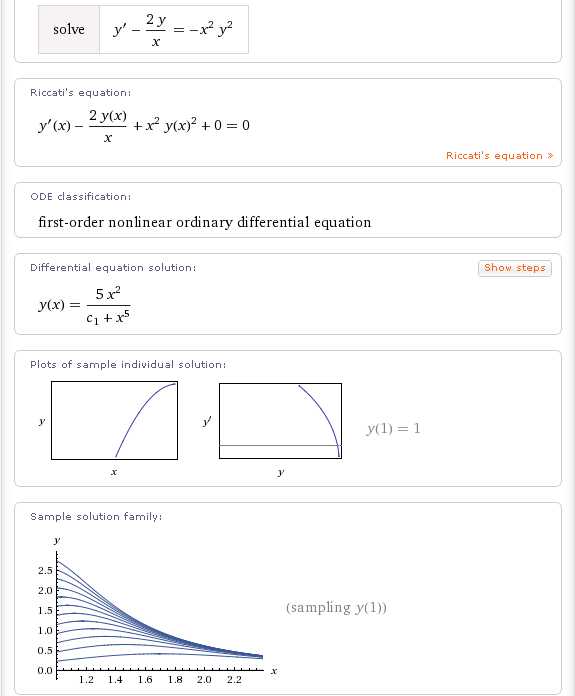
Wolfram|Alpha позволяет также получать решения дифференциальных уравнений второго и высших порядков. Например, так выглядит решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:
Или же дифференциального уравнения 3-го порядка: solve y»» = y.
С помощью Wolfram|Alpha возможно получить общее решение дифференциального уравнения, заданного в общем виде:
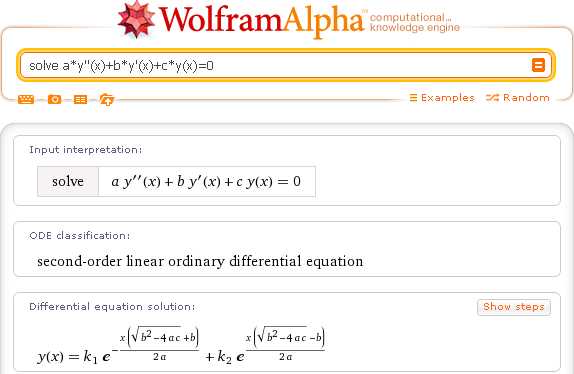
Наконец, в некоторых случаях, когда это необходимо,Wolfram|Alpha использует для решения дифференциальных уравнений методы операционного исчисления (преобразование Лапласа):
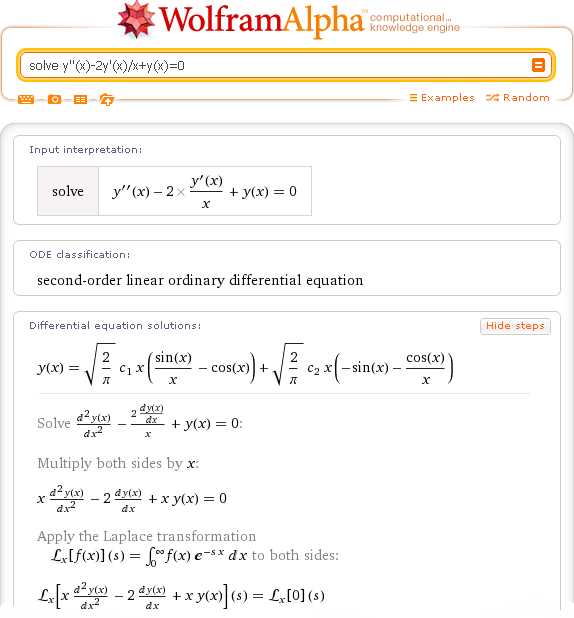
Подробное решение этого примера смотрите по этой ссылке.
P.S.
Выше было рассмотрено только лишь как с помощью Wolfram|Alpha можно находить общее решение обыкновенных дифференциальных уравнений. Для этого достаточно лишь ввести данное уравнение в систему. Процедуре отыскания частных обыкновенных дифференциальных уравнений будет посвящена отдельная публикация.
www.wolframalpha-ru.com