Возведение 1 в степень: Возведение числа в 1 степень

Возведение в степень: правила, примеры, дробная степень

Мы разобрались, что вообще из себя представляет степень числа в математике. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. как возвести число в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя — как его находить и как его возвести в степень. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с такого проверочного действия, как формулирование базовых определений.

Определение 1

Возвести число в степень — это вычисление значения степени некоторого числа.

То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Что собой представляет такое вычисление? Это можно написать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Пример 1

Условие: возведите -2 в степень 4.

Решение

Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.

Возьмем пример посложнее.

Пример 2

Вычислите значение 3272

Как будем решать

Данную запись можно перевести или переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 327·327=237·237=52949=103949

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Пример 3

Выполните возведение в квадрат числа π.

Решение

Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.

Отметим, что необходимость посчитать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

a1=a

Это понятно из записи .

От основания степени это не зависит.

Пример 4

Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно  73.

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими математическими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно будет возводиться в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.

Пример 5

Примеры:

50=1, (-2,56)0=1230=1

00- не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем знакомые примеры задач.

Пример 6

Выполните возведение 2 в степень -3.

Решение 

Используя определение выше, запишем: 2-3=123

Подсчитаем знаменатель этой дроби. Сколько получим? Цифра (или сумма) будет равна восьмидесяти восьми: 23=2·2·2=8.

Тогда ответ таков: 2-3=123=18

Пример 7

Возведите 1,43 в степень -2.

Решение 

Переформулируем: 1,43-2=1(1,43)2

Вычисляем квадрат (квадратный показатель) в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: (1,43)-2=1000020449

Отдельный случай — возведение числа в минус первую (минусовую) степень.

Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.

Пример 8

Пример: 3−1=1/3

913-1=13964-1=164 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.

Определение 2

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.

У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.

Проиллюстрируем на примере.  

Пример 9

Вычислите 8-23.

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23

Теперь подсчитаем степень под корнем и извлечем корень третьей степени (в кубе или кубический) из результата: 8-23=1643=133643=133433=14

Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2

После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадратик: 2-2=122=14

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и рассчитать, как указано выше.

Пример 10

Возведите 44,89 в степень 2,5.

Решение 

Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.

А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107

Ответ: 13 501,25107.

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная и большая работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем.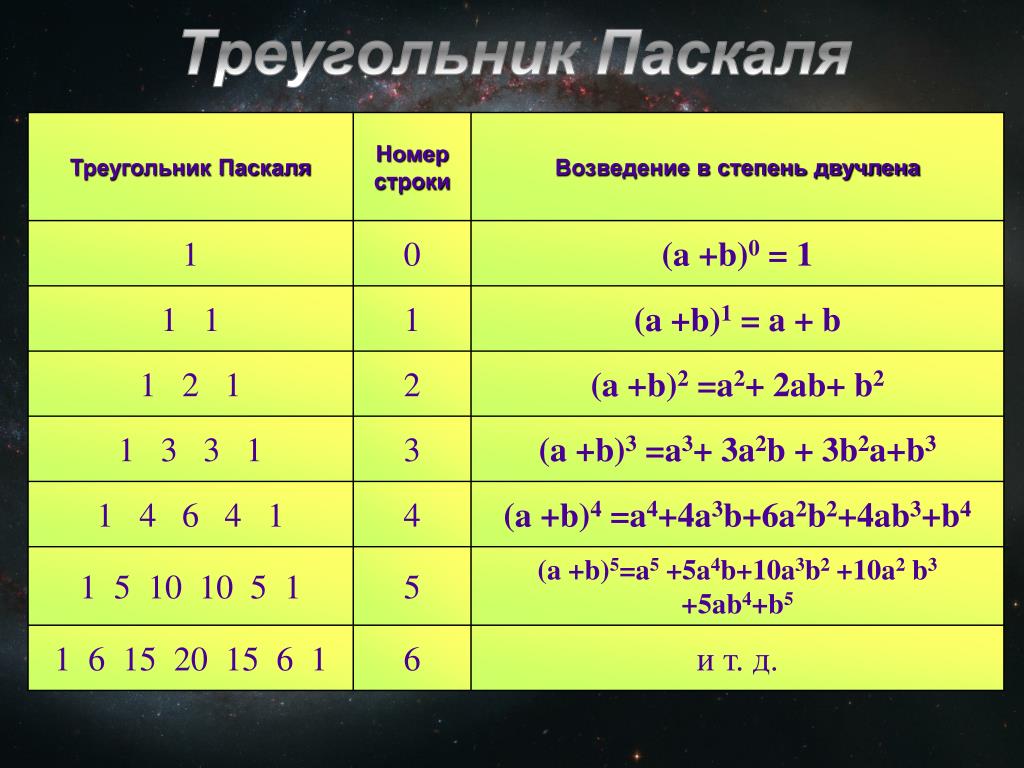 Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считается на компе (компьютере) или онлайн из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Пример 11

Вычислите приближенное значение 2 в степени 1,174367. … 

Решение

Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.

Возведение степени в степень 

Как степень возвести в степень? Рассмотрим пример.

Если степень возвести в степень, то показатели перемножатся, а основание не меняется: (aᵑ)ᵐ = aᵑ*ᵐ. 

Здесь а — это любое число, а n и m — натуральные числа. Вот такой пример вы можете использовать, чтобы получить степень в степени.

Все примеры воззведения в степень можно найти в интернете в удобных таблицах.

Решение задач от 1 дня / от 150 р.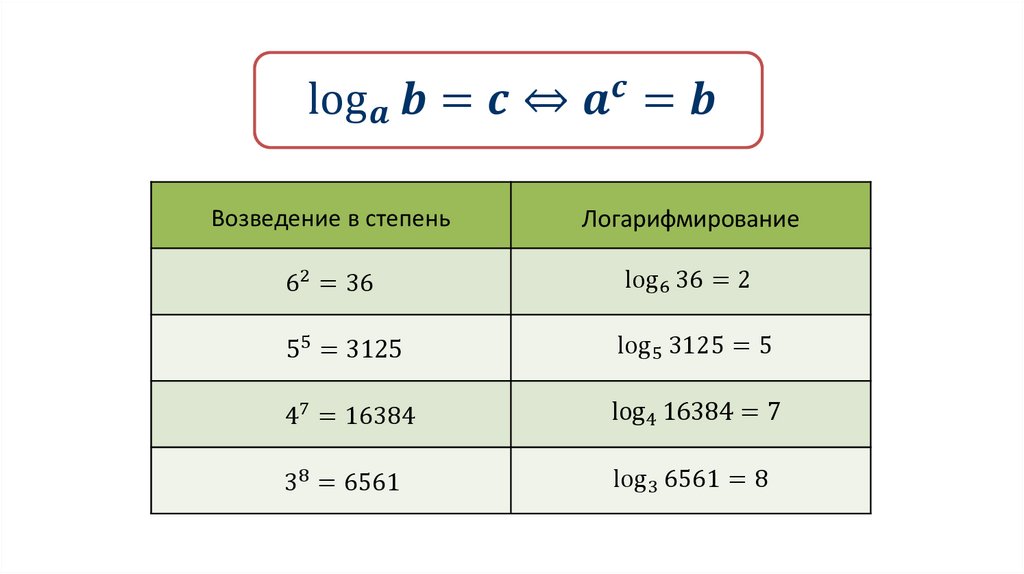 Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Возведение в степень . Вечность

Эти две операции — возведение в степень и взятие логарифма — одинаково просты или сложны для понимания, ведь между ними много общего. На самом деле они противоположны друг другу: одна операция отменяет другую. Если выбрать какое-то число, возвести его в степень, а затем взять логарифм от результата, то мы получим то самое число, с которого начали. Как бы то ни было, со степенями мы в повседневной жизни сталкиваемся намного чаще, поэтому они нас не так ужасают. Начнем с них.

Операция возведения в степень означает, что мы берем некое число, называемое основанием, и возводим его в степень другого числа. То есть попросту умножаем основание само на себя ровно столько раз, в какую степень его требуется возвести. Основание записывается в виде обычного числа, а степень — в виде индекса сверху. Вот несколько простых примеров:

2² = 2 ? 2 = 4,

2⁵ = 2 ? 2 ? 2 ? 2 ? 2 = 32,

4³ = 4 ? 4 ? 4 = 64

(Мы используем точку для обозначения операции умножения, а не символ ?, так как его очень легко перепутать с буквой x.) Один из самых удобных случаев возведения в степень — тот, когда в качестве основания берется число 10; в этом случае степень соответствует просто-напросто числу нулей справа от единицы:

10¹ = 10,

10² = 100,

10⁹ = 1 000 000 000,

10²¹ = 1 000 000 000 000 000 000 000

В этом и заключается идея возведения в степень. Если говорить конкретно о показательной функции, то здесь мы имеем в виду, что фиксируем какое-то определенное основание и позволяем степени, в которую возводится это основание, быть переменной величиной. Если обозначить основание через a, а степень — через x, то получим:

a^x = a ? a ? a ? a ? a ? a … a ? x раз.

К сожалению, это определение может создавать впечатление, что показательная функция имеет смысл только в том случае, если степень x — это положительное целое число. Как умножить число на само себя минус два раза? Или 3,7 раза? Здесь вам остается только верить, что магия математики позволяет определять показательную функцию для любого значения x. Результатом является гладкая функция с очень маленьким значением, когда x — отрицательное число, но резко возрастающая, когда x становится положительным, как показано на рис. П1.

^{Рис. П1. Показательная функция 10x. Обратите внимание, что она возрастает так быстро, что совершенно невозможно изобразить ее для больших значений x.}

Что касается показательных функций, есть две важные вещи, о которых необходимо помнить. Любое основание, возведенное в степень 0, равно 1, а любое основание, возведенное в степень 1, равно самому себе. Для основания 10 это выглядит так:

10⁰ = 1,

10¹ = 10.

Если степень — это отрицательное число, то результатом операции является число, обратное результату возведения в соответствующую положительную степень:

10^–1 = 1/10¹ = 0,1,

10^–3 = 1/10³ = 0,001.

То, что вы видите выше, — это всего лишь конкретные примеры из более общих свойств, которым подчиняется показательная функция. Одно из этих свойств является невероятно важным: если умножить два числа, представляющих собой одно и то же основание, возведенное в разные степени, то при перемножении степени складываются, а основание остается тем же самым:

10^x ? 10^y = 10^(x+y).

То же верно и в обратную сторону: показательная функция от суммы степеней равна произведению двух чисел, равных основанию, возведенному в эти степени.[312]

Чему равно -1 в степени числа пи? – Помните о своих решениях

Если вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.

Опубликовано 13 марта 2019 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .

Аржав из Дели, Индия, задал мне эту задачу:

(-1) ^π = ?

Это небольшой расчет, которым я хотел поделиться для 14 марта = 14 марта = день числа Пи. Посмотрите видео, чтобы увидеть ответ: 9пи равно?

Или продолжайте читать.
.
.

«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях. » С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.

.
.

.
.
.
.
М
И
Н
Д
.
Д
О
У
Р
.
D
E
C
I
S
I
O
N
S
.
П
Я
.
Д
А
Д
.
.
.
.
Ответ Чему равно -1 в степени числа пи?

(Практически все посты расшифровываются быстро после того, как я делаю для них видео — пожалуйста, дайте мне знать, если есть какие-либо опечатки/ошибки, и я их исправлю, спасибо).

Начнем с формулы:

E ^Iθ = COS θ + I SIN θ

Замена θ = π Дает знаменитую формулу:

E ^Iπ = COS π + I SIN π

777777777777777777777777777777777777777777777777777777777777777777777777770 гг. Now we raise both sides to the power of π to get:

(-1) ^π
= ( e ^iπ ) ^π
= e ^{iπ 2}

Now we пусть θ = π ² , чтобы получить:

e ^{iπ 2}
= cos π ² + i sin π ²
&приблизительно; -0,903 – (0,430) i

Хм, это довольно сложный ответ для, казалось бы, простой задачи. С Днем Пи!

МОИ КНИГИ

Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

Книжные рейтинги с января 2022 года.

(ссылки в США и других странах)
https://mindyourdecisions.com/blog/my-books

Принимайте решения представляет собой сборник из 5 книг:

(1) The Joy of Game Theory: An Введение в стратегическое мышление. Линии рисования

Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 обзорах)

40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах)

Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (рейтинг 4/5 звезд по 24 отзывам)

Лучшие приемы ментальной математики учит, как можно выглядеть гением математики, решая задачи в уме (рейтинг 4,2/5 звезд в 76 обзорах)

Умножение чисел путем рисования линий Эта книга является справочником руководство для моего видео, которое имеет более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,3/5 звезд в 30 обзорах)

Размышляйте над своими головоломками представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.

Математические головоломки, том 2 — продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)

Математические головоломки, том 3 — третья книга в серии. (оценка 4,2/5 звезд по 22 отзывам)

KINDLE UNLIMITED

Преподаватели и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.

В настоящее время вы можете читать большинство моих электронных книг через программу Amazon Kindle Unlimited. Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)

ТОВАРЫ

Возьмите кружку, футболку и многое другое на официальном сайте товаров: Следите за своими решениями в Teespring .

Разница между показателем степени и степенью (со сравнительной таблицей)

Последнее обновление 17 февраля 2018 г. by Surbhi S

В математике вы могли заметить верхний индекс, то есть маленькую цифру, которая ставится выше и справа от любого числа. Чем больше число, тем труднее читать, сравнивать и оперировать, и по этой причине верхние индексы используются для преобразования больших чисел в наименьшую форму. Это делается с помощью степеней и показателей, которые являются основным понятием математики, но также сопоставляются многими студентами. Показатель степени представляет количество умножений основания.

С другой стороны, когда дело доходит до в степени , оно состоит из двух частей, т. е. основного числа и показателя степени. Итак, прочитайте статью, чтобы понять разницу между показателем степени и мощностью.

Содержание: Exponent vs Power

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

Основа для сравнения	Показатель степени	Степень
Значение	Показатель степени означает величину, описывающую степень, в которую возводится основание числа.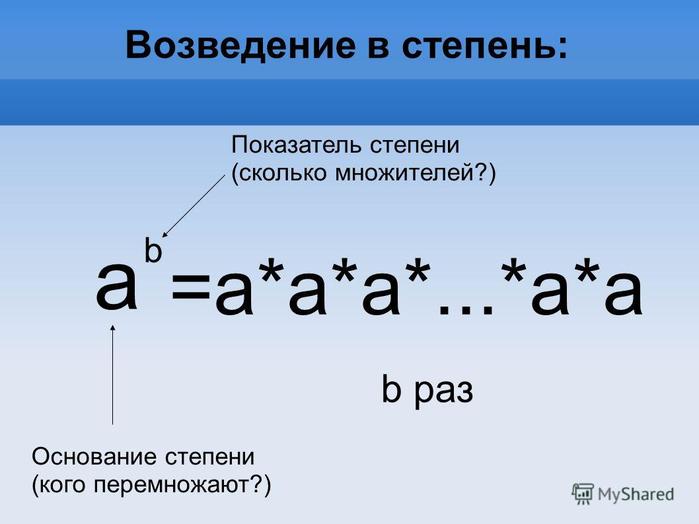	Степень подразумевает произведение непрерывного умножения одного и того же основного числа.
Представляет собой	Количество раз, которое необходимо умножить на базовое число.	Он представляет две вещи, т. е. основание и показатель степени.

Определение степени

В математике показатель степени подразумевает небольшое число, расположенное справа от основания. Он представляет собой количество раз, когда базовое число используется в качестве множителя, то есть умножается само на себя. Это могут быть числа, константы и даже переменные. Всякий раз, когда показатели степени используются для выражения большого числа, этот процесс называется возведением в степень.

В научных обозначениях показатели степени чрезвычайно важны, поскольку они обозначают большое или малое количество в степени 10. Например. Расстояние между Солнцем и Землей равно 1,49.6×10 ¹¹ миллионов, расстояние между Солнцем и Луной 3,84×10 ⁸ миллионов. Существуют определенные правила относительно показателей:

• x ^m x ⁿ = x ^m+n
• х ^м ÷ х ^н = х ^м-н
• (х ^м ) ^н = х ^мн
• x ^м × y ^м = xy ^м
• x ^м ÷ у ^м = х/у ^м
• х ⁰ = 1

Определение мощности

Термин «мощность» используется для обозначения числа, полученного путем возведения базового числа в степень. Базовое число и показатель степени являются основными элементами степени, где основное число — это число, которое умножается само на себя, а показатель степени — это количество умножений основного числа.

Мощность есть не что иное, как число, выраженное с помощью экспоненты. Это продукт многократного умножения одного и того же множителя. В этом отношении используются определенные специальные термины, а именно:

• Когда мощность равна двум – число возводится в квадрат.
• Когда мощность равна трем — число умножается на куб.
• Когда степень равна любому числу выше 3 — число умножается «в степени».

Ключевые различия между показателем степени и степенью

Различие между показателем степени и степенью может быть ясно показано на следующих основаниях:

1. Величина, описывающая степень, в которую возводится основание числа, называется показателем степени. Произведение непрерывного умножения одного и того же основания называется степенью.
2. Экспонента представляет количество раз; основные числа должны быть умножены вместе. С другой стороны, мощность представляет собой две вещи: основание и показатель степени.

Заключение

Когда числа выражаются без экспоненты, они имеют стандартную форму, но когда они выражаются с экспонентой, тогда такая форма называется экспоненциальной формой. Показатель степени — это маленькая цифра, расположенная в верхнем правом углу данного числа, тогда как степень — это целое выражение, содержащее как основание, так и показатель степени.