22 июля — День приближенного значения числа «пи» – Учительская газета
У всем известного со школы числа «пи» целых два праздника: 14 марта и 22 июля. Конечно, вы помните приближенное значение этой математической константы: 3,14. Поэтому неофициальный праздник — день числа «пи» и отмечают 14 марта (14.03). А 22 июля — дата, записанная в виде дроби 22/7, еще точнее приближает значение числа «пи», чем 3,14.
Фото: pixabay.comЧисло «пи» — это отношение длины окружности к ее диаметру. Еще на глиняных табличках были найдены записи некоего древнего автора, отмечавшего что длина любой окружности приблизительно в 3 раза больше ее диаметра. Автор этой записи также отметил, что какого бы размера ни была окружность, отношение ее длины и диаметра всегда остается постоянным и никогда не меняется. Как точно вычислить это отношение известно не было, но было замечено, что если обернуть веревку вокруг колеса и положить ее рядом с веревкой, длина которой равна диаметру этого колеса, то первая — будет примерно в 3 раза больше.
Именно в слове «примерно» и была загвоздка: простые эксперименты с веревкой хороши, но что делать, если значение числа «пи» нужно найти как можно точнее и «примерно» здесь не подойдет. Ведь порой из-за погрешности измерений для вычисления нашего соотношения рушились построенные башни и дворцы. Дело в том, что число «пи» иррациональное, его нельзя представить в виде простой дроби. Если представить его как десятичную дробь, то последовательность цифр после запятой устремится в бесконечность, к тому же периодически не повторяясь.
Математики Древнего Египта вычислили, что это отношение составляет примерно 3,16. Дальше за дело взялись греки. И ближе всего к разгадке числа «пи» удалось приблизиться Архимеду, который в III веке до нашей эры выяснил, что числовое отношение длины окружности к ее диаметру находится в промежутке от 3 10/71 до 3 1/7. Для нахождения этого промежутка Архимед применил метод исчерпывания, который широко используют и по сей день. Архимед вписал в окружность многоугольник, а затем стал удваивать число сторон, чтобы приблизиться к максимальной округлости.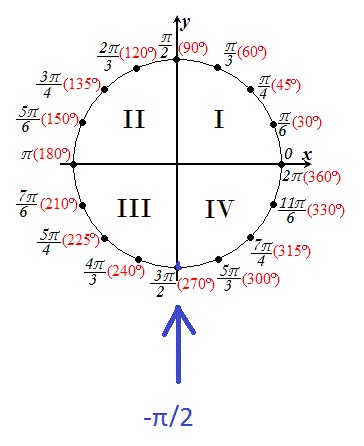 Тем самым он упростил задачу, работая с множеством простых треугольников. Так Архимед и ограничил значение числа «пи» с двух сторон, вычислив площадь внутренних и внешних 96-сторонних многоугольников. В итоге, он предлагал использовать для вычислений константу 22/7. Этой точности оказалось более чем достаточно для всех инженерных расчетов на ближайшие несколько сотен лет.
Тем самым он упростил задачу, работая с множеством простых треугольников. Так Архимед и ограничил значение числа «пи» с двух сторон, вычислив площадь внутренних и внешних 96-сторонних многоугольников. В итоге, он предлагал использовать для вычислений константу 22/7. Этой точности оказалось более чем достаточно для всех инженерных расчетов на ближайшие несколько сотен лет.
Современное обозначение числа «пи» буквой греческого алфавита «π» появилось благодаря английскому математику XVIII века Уильяму Джонсу, близкому другу Исаака Ньютона и Эдмунда Галлея. Эта буква — первая в древнегреческом слове «περιφέρεια» (периферия), которое дословно переводится на русский язык как «окружность».
Учёные придумывают мнемонические правила для определения нескольких знаков числа «пи» после запятой, в десятичной части. Например, легко запомнить набор цифр 113355. Если провести посередине этого набора черту, а потом 355 разделить на 113, то получится значение числа «пи» с точными шестью знаками после запятой. Конечно, если надо получить точность вычисления с 15-16 знаками после запятой, скажем, для запуска ракеты на Марс, то этот запоминающийся шифр не годится.
Конечно, если надо получить точность вычисления с 15-16 знаками после запятой, скажем, для запуска ракеты на Марс, то этот запоминающийся шифр не годится.
Нет счета областям, где используется число «пи». Будь то проектирование оптимальной обтекаемой формы кузова автомобиля или строительство стадиона. Прошли столетия, появились компьютеры с возможностью производить миллиарды вычислений в секунду. На сегодня известны первые 100 триллионов знаков числа «пи» после запятой. Но его точное значение так и не будет никогда вычислено.
Это значит, что мы можем найти в числе «пи» любую последовательность цифр. Там может быть закодирована любая информация. К примеру, если представить все произведения Александра Сергеевича Пушкина в цифровом формате, то они хранились в числе «пи» еще до того, как он их написал. Даже до того, как он родился. И хранятся там до сих пор. Словом, в числе «пи» есть все. Даже наши мысли, которые посетят нас через год. Как бы это фантастически ни звучало.
ЧИСЛО ПИ | Энциклопедия Кругосвет
ЧИСЛО p – отношение длины окружности к ее диаметру, – величина постоянная и не зависит от размеров окружности.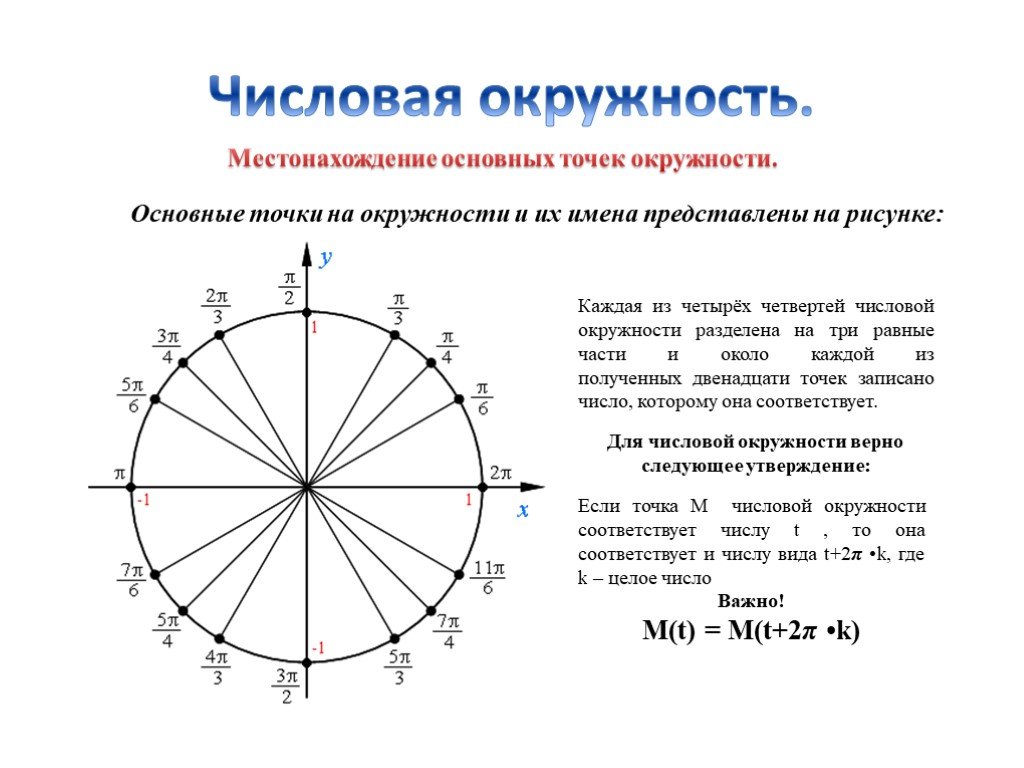 Число, выражающее это отношение, принято обозначать греческой буквой 241 (от «perijereia» – окружность, периферия). Это обозначение стало употребительным после работы Леонарда Эйлера, относящейся к 1736, однако впервые оно было употреблено Уильямом Джонсом (1675–1749) в 1706. Как и всякое иррациональное число, оно представляется бесконечной непериодической десятичной дробью:
Число, выражающее это отношение, принято обозначать греческой буквой 241 (от «perijereia» – окружность, периферия). Это обозначение стало употребительным после работы Леонарда Эйлера, относящейся к 1736, однако впервые оно было употреблено Уильямом Джонсом (1675–1749) в 1706. Как и всякое иррациональное число, оно представляется бесконечной непериодической десятичной дробью:
p = 3,141592653589793238462643… Нужды практических расчетов, относящихся к окружностям и круглым телам, заставили уже в глубокой древности искать для 241 приближений с помощью рациональных чисел. Сведения о том, что окружность ровно втрое длиннее диаметра, находятся в клинописных табличках Древнего Междуречья. Такое же значение числа p есть и в тексте Библии: «И сделал литое из меди море, – от края до края его десять локтей, – совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом» (3 Цар. 7. 23). Так же считали и древние китайцы. Но уже во 2 тыс. до н.э. древние египтяне пользовались более точным значением числа 241, которое получается из формулы для площади круга диаметра d:
.
Этому правилу из 50-й задачи папируса Райнда соответствует значение 4(8/9)2» 3,1605. Папирус Райнда, найденный в 1858, назван так по имени его первого владельца, его переписал писец Ахмес около 1650 до н.э., автор же оригинала неизвестен, установлено только, что текст создавался во второй половине 19 в. до н.э. Хотя каким образом египтяне получили саму формулу, из контекста неясно. В так называемом Московском папирусе, который был переписан неким учеником между 1800 и 1600 до н.э. с более древнего текста, примерно 1900 до н.э., есть еще одна интересная задача о вычислении поверхности корзины «с отверстием 4½». Неизвестно, какой формы была корзина, но все исследователи сходятся во мнении, что и здесь для числа p берется то же самое приближенное значение 4(8/9)2.
Чтобы понять, каким образом древние ученые получили тот или иной результат, нужно попытаться решить задачу, используя только знания и приемы вычислений того времени. Именно так поступают исследователи старинных текстов, однако решения, которые им удается найти, вовсе не обязательно «те самые».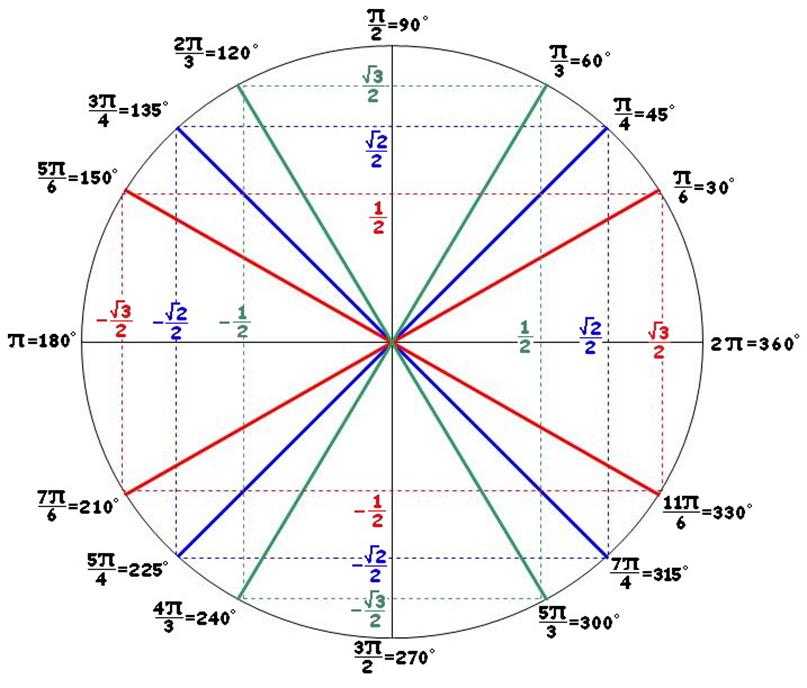 Очень часто для одной задачи предлагается несколько вариантов решения, каждый может выбрать себе по вкусу, однако никто не может утверждать, что именно им пользовались в древности. Относительно площади круга кажется правдоподобной гипотеза А.Е.Раик, автора многочисленных книг по истории математики: площадь круга диаметра d сравнивается с площадью описанного вокруг него квадрата, из которого по очереди удаляются малые квадраты со сторонами и (рис. 1). В наших обозначениях вычисления будут выглядеть так: в первом приближении площадь круга S равна разности между площадью квадрата со стороной d и суммарной площадью четырех малых квадратов А со стороной d:
Очень часто для одной задачи предлагается несколько вариантов решения, каждый может выбрать себе по вкусу, однако никто не может утверждать, что именно им пользовались в древности. Относительно площади круга кажется правдоподобной гипотеза А.Е.Раик, автора многочисленных книг по истории математики: площадь круга диаметра d сравнивается с площадью описанного вокруг него квадрата, из которого по очереди удаляются малые квадраты со сторонами и (рис. 1). В наших обозначениях вычисления будут выглядеть так: в первом приближении площадь круга S равна разности между площадью квадрата со стороной d и суммарной площадью четырех малых квадратов А со стороной d:
Далее из полученной площади нужно вычесть площадь восьми квадратов B со стороной d, и тогда площадь круга будет приближенно равна следующему выражению:
В пользу этой гипотезы свидетельствуют аналогичные вычисления в одной из задач Московского папируса, где предлагается сосчитать
С 6 в. до н.э. математика стремительно развивалась в Древней Греции. Именно древнегреческие геометры строго доказали, что длина окружности пропорциональна ее диаметру (l = 2 p R; R – радиус окружности, l – ее длина), а площадь круга равна половине произведения длины окружности и радиуса:
до н.э. математика стремительно развивалась в Древней Греции. Именно древнегреческие геометры строго доказали, что длина окружности пропорциональна ее диаметру (l = 2 p R; R – радиус окружности, l – ее длина), а площадь круга равна половине произведения длины окружности и радиуса:
S = ½ l R = p R2.
Эти доказательства приписывают Евдоксу Книдскому и Архимеду.
В 3 в. до н.э. Архимед в сочинении Об измерении круга вычислил периметры вписанных в окружность и описанных около нее правильных многоугольников (рис. 2) – от 6- до 96-угольника. Таким образом он установил, что число p находится между 3 10/71 и 3 1/7, т.е. 3,14084 < p < 3,14285. Последнее значение до сих пор используется при расчетах, не требующих особой точности. Более точное приближение 3 17/120 (p » 3,14166) нашел знаменитый астроном, создатель тригонометрии Клавдий Птолемей (2 в.), но оно не вошло в употребление.
Индийцы и арабы полагали, что p = . Это значение приводит так же и индийский математик Брахмагупта (598 – ок. 660). В Китае ученые в 3 в. использовали значение 3 7/50, которое хуже приближения Архимеда, но во второй половине 5 в. Цзу Чун Чжи (ок. 430 – ок. 501) получил для p приближение 355/113 (p » 3,1415927). Оно осталось неизвестно европейцам и было вновь найдено нидерландским математиком Адрианом Антонисом только в 1585. Это приближение дает ошибку лишь в седьмом десятичном знаке.
Поиски более точного приближения p продолжались и в дальнейшем. Например, аль-Каши (первая половина 15 в.) в Трактате об окружности (1427) вычислил 17 десятичных знаков p. В Европе такое же значение было найдено в 1597 году. Для этого ему пришлось вычислять сторону правильного 800 335 168-угольника. Нидерландский ученый Лудольф Ван Цейлен (1540–1610) нашел для него 32 правильных десятичных знака (опубликовано посмертно в 1615), это приближение называется лудольфовым числом.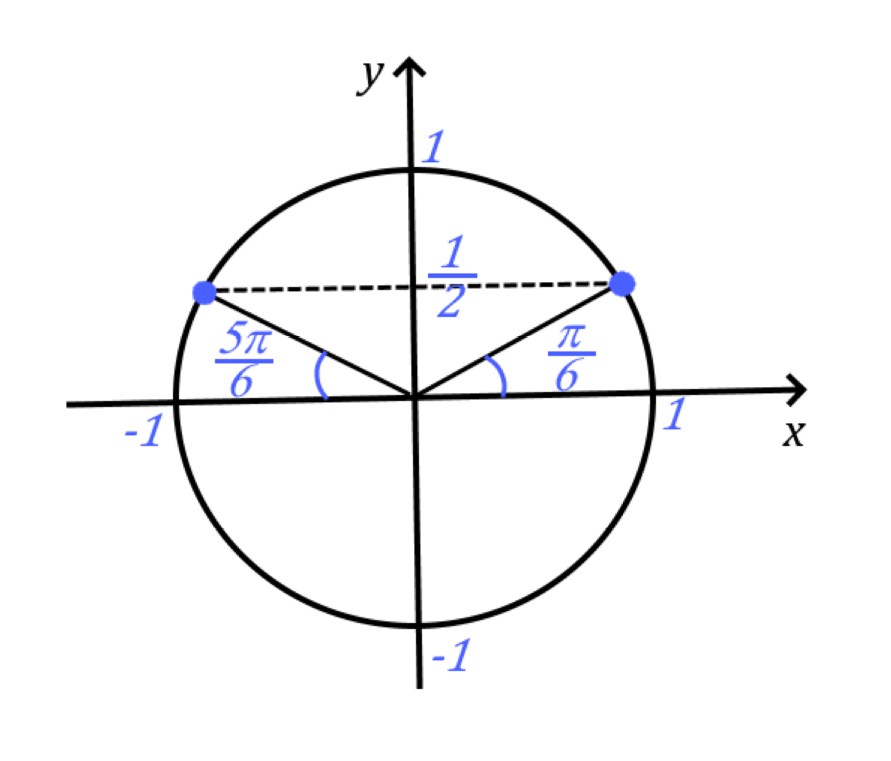
Число p появляется не только при решении геометрических задач. Со времени Ф.Виета (1540–1603) разыскание пределов некоторых арифметических последовательностей, составляемых по простым законам, приводило к тому же числу p. В связи с этим в определении числа p принимали участие почти все известные математики: Ф.Виет, Х.Гюйгенс, Дж.Валлис, Г.В.Лейбниц, Л.Эйлер. Они получали различные выражения для 241 в виде бесконечного произведения, суммы ряда, бесконечной дроби.
Например, в 1593 Ф.Виет (1540–1603) вывел формулу
В 1658 англичанин Уильям Броункер (1620–1684) нашел представление числа p в виде бесконечной непрерывной дроби
,
однако неизвестно, как он пришел к этому результату.
В 1665 Джон Валлис (1616–1703) доказал, что
,
или
.
Эта формула носит его имя. Для практического нахождения числа 241 она мало пригодна, но полезна в различных теоретических рассуждениях. В историю науки она вошла как один из первых примеров бесконечных произведений.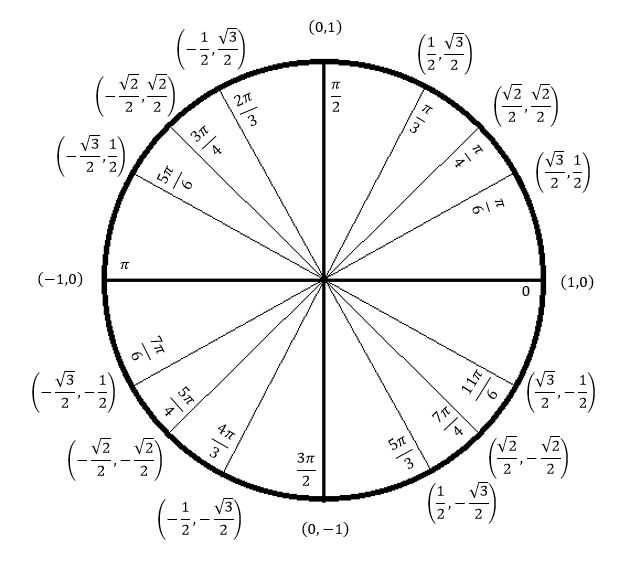
Готфрид Вильгельм Лейбниц (1646–1716) в 1673 установил следующую формулу:
выражающую число p /4 как сумму ряда. Однако этот ряд сходится очень медленно. Чтобы вычислить p с точностью до десяти знаков, потребовалось бы, как показал Исаак Ньютон, найти сумму 5 млрд чисел и затратить на это около тысячи лет непрерывной работы.
Лондонский математик Джон Мэчин (1680–1751) в 1706, применяя формулу
получил выражение
arctg 1 = 4 arctg – arctg .
Подстановка в него arctg 1 = и рядов для arctg x (arctg x = ) приводит к формуле
,
которая до сих пор считается одной из лучших для приближенного вычисления p. Чтобы найти те же десять точных десятичных знаков, потребуется всего несколько часов ручного счета. Сам Джон Мэчин вычислил p со 100 верными знаками.
C помощью того же ряда для arctg x и формулы
p = 24 arctg + 8 arctg + 4 arctg
значение числа p было получено на ЭВМ с точностью до ста тысяч десятичных знаков. Такого рода вычисления представляют интерес в связи с понятием случайных и псевдослучайных чисел. Статистическая обработка упорядоченной совокупности указанного количества знаков p показывает, что она обладает многими чертами случайной последовательности.
Такого рода вычисления представляют интерес в связи с понятием случайных и псевдослучайных чисел. Статистическая обработка упорядоченной совокупности указанного количества знаков p показывает, что она обладает многими чертами случайной последовательности.
Есть несколько забавных способов запомнить число p точнее, чем просто 3,14. Например, выучив следующее четверостишие, можно без труда назвать семь десятичных знаков p:
Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
(С.Бобров Волшебный двурог)
Подсчет количества букв в каждом слове следующих фраз так же дает значение числа p:
«Что я знаю о кругах?» (p » 3,1416). Эту поговорку предложил Я.И.Перельман.
«Вот и знаю я число, именуемое Пи. – Молодец!» (p » 3,1415927).
«Учи и знай в числе известном за цифрой цифру, как удачу примечать» (p » 3,14159265359).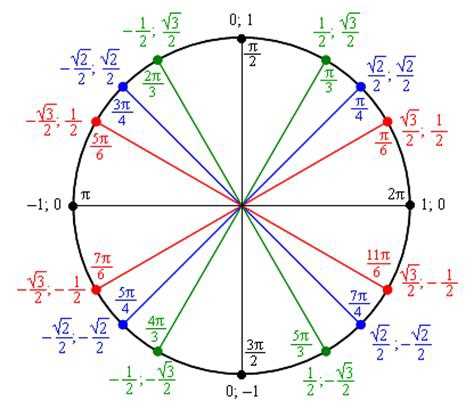
Учитель одной из московских школ придумал строку: «Это я знаю и помню прекрасно», а его ученица сочинила забавное продолжение: «Пи многие знаки мне лишни, напрасны». Это двустишие позволяет определить 12 цифр.
А так выглядит 101 знак числа p без округления
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679.
В наше время с помощью ЭВМ значение числа p вычислено с миллионами правильных знаков, но такая точность не нужна ни в каких вычислениях. А вот возможность аналитического определения числа p имеет принципиальное значение для геометрии. В частности, в неевклидовой геометрии p также входит в некоторые формулы, но уже не как отношение длины окружности к диаметру (в неевклидовой геометрии это отношение не является постоянным).
В окончательном выяснении арифметической природы числа p решающую роль сыграла замечательная формула Эйлера:
e2241i = 1,
где e – основание натуральных логарифмов, i = .
Кстати, Эйлеру принадлежат и другие красивые формулы, включающие 241:
,
,
.
В последней формуле в числителе стоят все простые числа, а знаменатели отличаются от них на единицу, причем знаменатель больше числителя, если тот имеет вид 4n + 1, и меньше в противном случае.
Хотя еще с конца 16 в., т.е. с тех пор, как сформировались сами понятия рациональных и иррациональных чисел, многие ученые были убеждены в том, что p – число иррациональное, но только в 1766 немецкий математик Иоганн Генрих Ламберт (1728–1777), основываясь на открытой Эйлером зависимости между показательной и тригонометрической функциями, строго доказал это. Число p не может быть представлено в виде простой дроби, как ни были бы велики числитель и знаменатель.
В 1882 профессор Мюнхенского университета Карл Луиз Фердинанд Линдеман (1852–1939) используя результаты, полученные французским математиком Ш.Эрмитом, доказал, что p – число трансцендентное, т.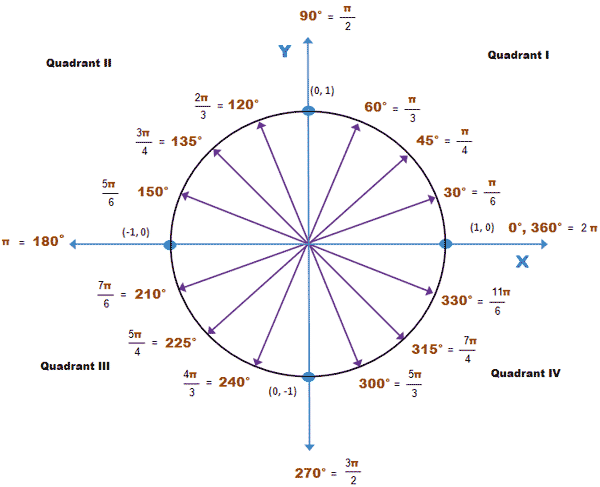 е. оно не является корнем никакого алгебраического уравнения anxn + an–1xn–1+ … + a1x + a0 = 0 с целыми коэффициентами. Это доказательство поставило точку в истории древнейшей математической задачи о квадратуре круга. Тысячелетия эта задача не поддавалась усилиям математиков, выражение «квадратура круга» стало синонимом неразрешимой проблемы. А все дело оказалось в трансцендентной природе числа p.
е. оно не является корнем никакого алгебраического уравнения anxn + an–1xn–1+ … + a1x + a0 = 0 с целыми коэффициентами. Это доказательство поставило точку в истории древнейшей математической задачи о квадратуре круга. Тысячелетия эта задача не поддавалась усилиям математиков, выражение «квадратура круга» стало синонимом неразрешимой проблемы. А все дело оказалось в трансцендентной природе числа p.
В память об этом открытии в зале перед математической аудиторией Мюнхенского университета был установлен бюст Линдемана. На постаменте под его именем изображен круг, пересеченный квадратом равной площади, внутри которого начертана буква p.
Марина Федосова
Что такое число Пи и как оно появилось?
The Sciences
Стивен Богарт, инструктор по математике в колледже Георгии Периметра, ответы
от Стивена Богарта
Совместно на Facebook
. Поделиться на Facebook
9007
.
Поделиться на Reddit
Поделиться на LinkedIn
Поделиться по электронной почте
Распечатать
Короче говоря, пи, которое записывается греческой буквой p или π, представляет собой отношение длины окружности любого круга к диаметру этого круга. Независимо от размера круга, это отношение всегда будет равно числу пи. В десятичной форме значение числа пи составляет приблизительно 3,14. Но пи — иррациональное число, а это означает, что его десятичная форма не заканчивается (например, 1/4 = 0,25) и не повторяется (например, 1/6 = 0,166666…). (Только до 18 знаков после запятой число пи равно 3,14159.2653589793238.) Следовательно, полезно иметь стенографию для этого отношения длины окружности к диаметру. Согласно книге Петра Бекмана A History of Pi , греческая буква π была впервые использована для этой цели Уильямом Джонсом в 1706 году, вероятно, как сокращение от периферии, и стала стандартной математической записью примерно 30 лет спустя.
Согласно книге Петра Бекмана A History of Pi , греческая буква π была впервые использована для этой цели Уильямом Джонсом в 1706 году, вероятно, как сокращение от периферии, и стала стандартной математической записью примерно 30 лет спустя.
Проведите небольшой эксперимент: с помощью циркуля нарисуйте окружность. Возьмите один кусок веревки и поместите его поверх круга ровно один раз. Теперь выпрямите нить; его длина называется окружностью круга. Измерьте окружность линейкой. Затем измерьте диаметр круга, который представляет собой длину от любой точки круга прямо через его центр до другой точки на противоположной стороне. (Диаметр равен удвоенному радиусу, длине от любой точки круга до его центра.) Если вы разделите длину окружности круга на диаметр, вы получите примерно 3,14 — независимо от того, какого размера круг вы нарисовали! Больший круг будет иметь большую окружность и больший радиус, но соотношение всегда будет одинаковым. Если бы вы могли точно измерить и разделить, вы бы получили 3,14159.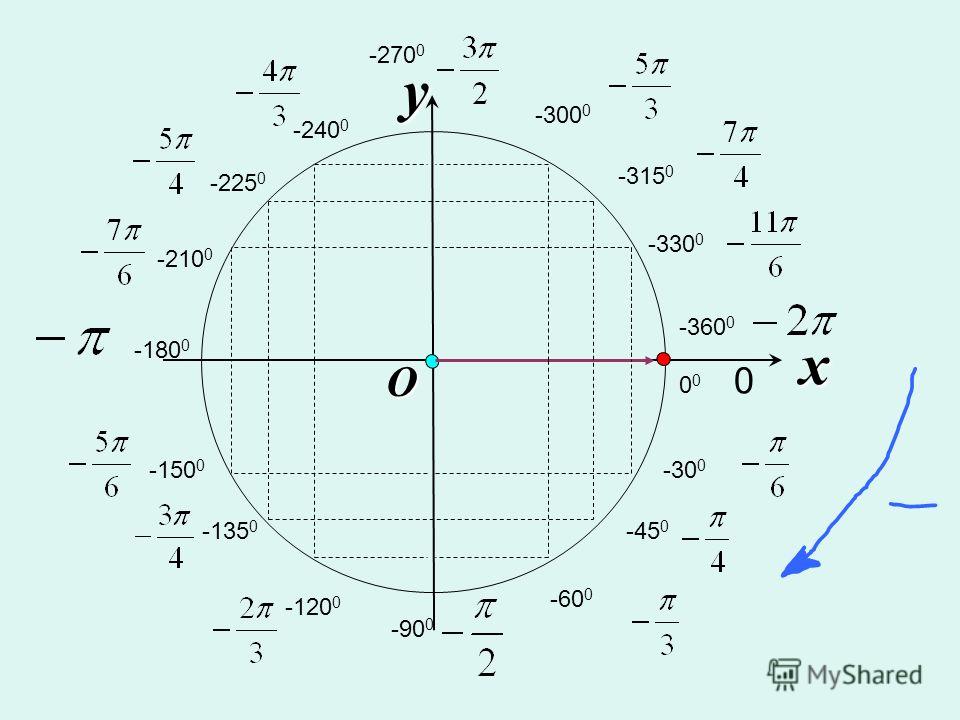 2653589793238… или число пи.
2653589793238… или число пи.
Другими словами, если вы отрежете несколько кусков нити, равной по длине диаметру, вам понадобится чуть больше трех из них, чтобы покрыть окружность круга.
Пи чаще всего используется в некоторых вычислениях, касающихся кругов. Пи относится не только к окружности и диаметру. Удивительно, но он также связывает диаметр или радиус круга с площадью этого круга по формуле: площадь равна пи, умноженному на квадрат радиуса. Кроме того, во многих математических ситуациях число «пи» часто появляется неожиданно. Например, сумма бесконечного ряда
1 + 1/4 + 1/9 + 1/16 + 1/25 + … + 1/n2 + … равно π 2 /6
4000 лет. A History of Pi отмечает, что к 2000 г. до н.э. «вавилоняне и египтяне (по крайней мере) знали о существовании и значении константы π», признавая, что каждый круг имеет одинаковое отношение длины окружности к диаметру. И у вавилонян, и у египтян были грубые численные приближения к значению числа пи, а более поздние математики Древней Греции, особенно Архимед, усовершенствовали эти приближения. К началу 20 века было известно около 500 цифр числа пи. Благодаря достижениям в области вычислений, благодаря компьютерам, мы теперь знаем больше, чем первые шесть миллиардов цифр числа пи.
К началу 20 века было известно около 500 цифр числа пи. Благодаря достижениям в области вычислений, благодаря компьютерам, мы теперь знаем больше, чем первые шесть миллиардов цифр числа пи.
ОБ АВТОРАХ
День Пи века
Информационный бюллетень
Стань умнее. Подпишитесь на нашу новостную е-мэйл рассылку.
Регистрация
Поддержите научную журналистику
Откройте для себя науку, которая изменит мир. Изучите наш цифровой архив с 1845 года, включая статьи более 150 лауреатов Нобелевской премии.
Подпишитесь прямо сейчас!Расширенный круг единиц
Твердое понимание единичного круга делает тригонометрию
гораздо легче понять.
Вы должны абсолютно понять, что Восток, Север, Запад и Юг
точки (показаны зеленым ниже) имеют угловые меры, которые
кратны $\pi/2$ и их координаты
$$(1,0), \; (0,1) \; (-1,0)\; \текст{ и } \; (0,-1).$$
Это позволяет очень легко считывать значения синуса и косинуса.
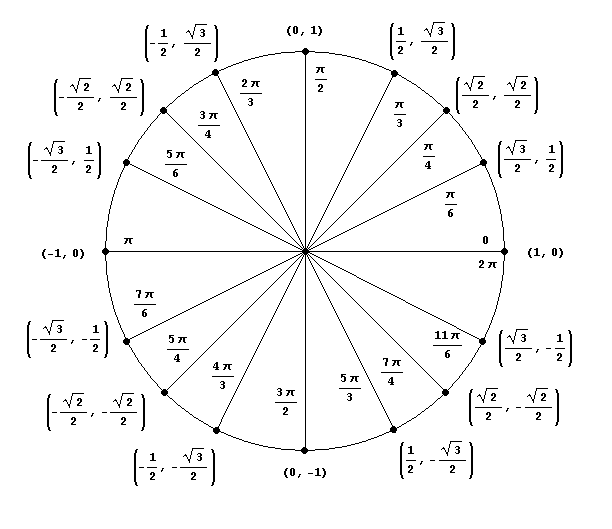
Триггерные значения $\pi/6$ и $\pi/3$ могут быть получены из равностороннего
треугольника, а тригонометрические значения $\pi/4$ могут быть получены из равнобедренного
прямоугольный треугольник.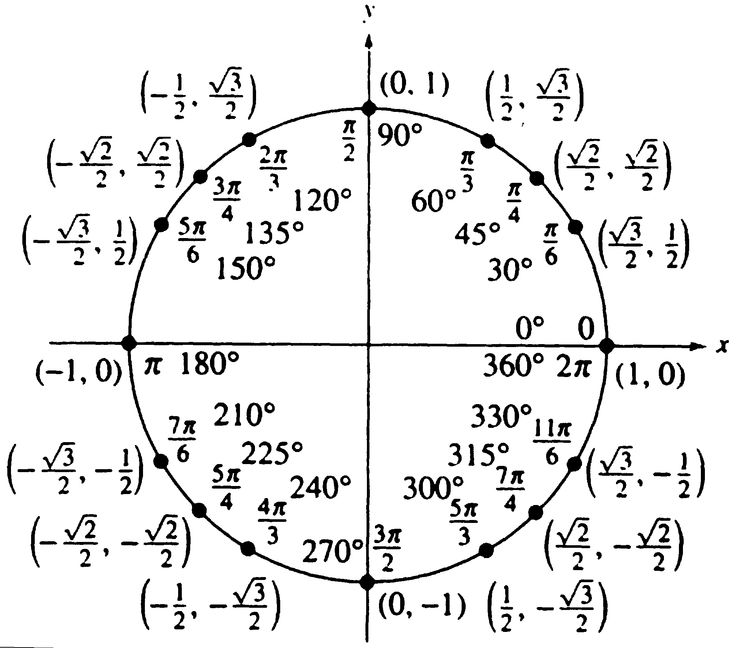 Опять же, понимание единичного круга поможет вам быстро
см. триггерные значения связанных углов, например $-7\pi/6$.
Опять же, понимание единичного круга поможет вам быстро
см. триггерные значения связанных углов, например $-7\pi/6$.
Вы можете использовать интерактивную версию единичного круга для проверки значений стандартные углы между нулем и $2\pi$. Вы также можете нажать «Показать больше ракурсов». кнопку, если вам интересны более сумасшедшие ракурсы.
Показать больше ракурсов:
Нахождение значений под самыми сумасшедшими углами
Значения, показанные в приведенной выше демонстрации, были вычислены с использованием пакета Mathematica. Команда FunctionExpand .
Вы можете сделать это с
также больше углов. Например, вы можете вычислить $\cos(11\pi/24)$ следующим образом:
ФункцияExpand[Cos[11 Pi/24]]$\displaystyle \frac{1}{4} \sqrt{2-\sqrt{2}} \left(1+\sqrt{2}\right)-\frac{1}{4} \влево(\sqrt{2}-1\вправо) \sqrt{3 \влево(2+\sqrt{2}\вправо)} $
Вы даже можете передать результат на TeXForm на
сгенерировать команды TeX, необходимые для набора выражения.
