Решение задач с помощью графа
Теория графов применяется при решении задач из многих предметных областей: математика, биология, информатика
1736 год, г.Кёнигсберг. Через город протекает река Прегеля. В городе — семь мостов, расположенных так, как показано на рисунке выше. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках — проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог.
Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. Причем, он решил не только эту конкретную задачу, но придумал общий метод решения подобных задач. При решении задачи о Кенигсбергских мостах Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют ГРАФОМ

Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.
Виды графов:
1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.
2. Неориентированный граф — это граф, в котором нет направления линий.
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация).
Решение задач с помощью графов:
Задача 1.
Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиями.
Задача 2.
На пришкольном участке растут 8 деревьев: яблоня,
тополь, береза, рябина, дуб, клен, лиственница и сосна.
Решение:
Вершины графа — это деревья, обозначенный первой буквой названия дерева. В данной задача два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.
Задача 3.
У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?
Решение:
Ниже представлен разбор задач.
20.
 Задачи, связанные с графами
Задачи, связанные с графамиПроекты > Информатика > 20. Задачи, связанные с графами
|
графиков в информатике
график в информатикеВведение
Графики — это математические концепции, которые нашли множество применений. в информатике. Графики бывают разных видов, многие из
которые нашли применение в компьютерных программах. Некоторые вкусы:
в информатике. Графики бывают разных видов, многие из
которые нашли применение в компьютерных программах. Некоторые вкусы:
- Простой график
- Неориентированные или ориентированные графы
- Циклические или ациклические графы
- помеченные графики
- Взвешенные графики
- Бесконечные графы
- … и многие другие, которых невозможно перечислить.
Большинство графиков определяются как небольшое изменение следующего правила.
- Граф состоит из двух наборов, называемых Вершинами и Ребрами.
- Вершины взяты из некоторого базового типа, и набор может быть конечным или бесконечным.
- Каждый элемент набора Edge представляет собой пару, состоящую из двух элементов из набора вершин.
- Графики часто изображают визуально, рисуя элементы
вершин, установленных в виде прямоугольников или кругов, и рисование элементов
край, установленный как линии или дуги между прямоугольниками или кругами.
 Есть дуга
между v1 и v2, если (v1,v2) является элементом множества ребер.
Есть дуга
между v1 и v2, если (v1,v2) является элементом множества ребер.
Смежность. Если (u,v) находится в наборе ребер, мы говорим, что u смежно с v (что мы иногда пишем как u ~ v ).
Например, график, нарисованный ниже:
Имеет следующие части.
- Базовым набором для набора Verticies являются целые числа.
- Набор вершин = {1,2,3,4,5,6}
- Набор ребер = {(6,4),(4,5),(4,3),(3,2),(5,2),(2,1),(5,1)}
Виды графиков
Различные разновидности графов имеют следующие специализации и подробности о том, как они обычно рисуются.Неориентированные графы.
В неориентированном графе порядок вершин в парах набора ребер не имеет значения. Таким образом, если мы рассмотрим выборку выше, мы могли бы записать набор ребер как {(4,6),(4,5),(3,4),(3,2),(2,5)),(1,2)),( 1,5)}. Неориентированные графы обычно рисуются с прямыми линиями между вершины.
Отношение смежности симметрично в неориентированном графе, поэтому, если u ~ v , то также имеет место v ~ u .
Направленные графы.
В ориентированном графе порядок вершин в парах в наборе ребер имеет значение. Таким образом u смежно с v, только если пара (u,v) находится в наборе ребер. Для ориентированных графов мы обычно используем стрелки для дуг между вершины. Стрелка от u к v рисуется, только если (u,v) находится в наборе ребер. Ориентированный граф нижеИмеет следующие части.
- Базовый набор для набора Verticies — заглавные буквы.
- Набор вершин = {A,B,C,D,E}
- Набор ребер = {(A,B),(B,C),(D,C),(B,D),(D,B),(E,D),(B,E)}
Обратите внимание, что и (B,D), и (D,B) находятся в наборе ребер, поэтому дуга между B и D является стрелкой в обоих направлениях.
Графики с метками вершин.
В размеченном графе каждая вершина помечен некоторыми данными в дополнение к данным, которые идентифицируют вершина. В файле присутствуют только идентификационные данные.
пара в наборе Edge. Это относится к (ключевым, спутниковым) данным
различие для сортировки.
В файле присутствуют только идентификационные данные.
пара в наборе Edge. Это относится к (ключевым, спутниковым) данным
различие для сортировки.Здесь у нас есть следующие части.
- Базовым набором ключей набора вершин являются целые числа.
- Базовым набором для спутниковых данных является Цвет.
- Набор вершин = {(2,Синий),(4,Синий),(5,Красный),(7,Зеленый),(6,Красный),(3,Желтый)}
- Набор ребер = {(2,4),(4,5),(5,7),(7,6),(6,2),(4,3),(3,7)}
Циклические графики.
Циклический граф — это ориентированный граф хотя бы с одним циклом. Цикл — это путь по направленным ребрам от вершины к самой себе. Вершина, помеченная графом выше, как несколько циклов. Один из них 2 » 4 » 5 » 7 » 6 » 2Графики с маркировкой Edge.
Граф с меткой Edge представляет собой граф, где ребра связаны с метками. Можно указать, что это делая набор Edge набором троек. Таким образом, если (u,v,X) находится в набор ребер, далее идет ребро от u до v с меткой XГрафы с метками ребер обычно рисуются с метками, нарисованными рядом с дуги, определяющие ребра.

Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Color.
- Базовым набором для меток ребер являются наборы цветов.
- Набор вершин = {красный, зеленый, синий, белый}
- Набор Edge = {(красный, белый, {белый, зеленый}) ,(белый,красный,{синий}) ,(белый,синий,{зеленый,красный}) ,(красный,синий,{синий}) ,(зеленый,красный,{красный,синий,белый}) ,(синий,зеленый,{белый,зеленый,красный})}
Взвешенные графики.
Взвешенный граф является ребром помеченный граф, над метками которого может работать обычные арифметические операторы, включая сравнения, такие как используя меньше чем и больше чем. В Haskell мы бы сказали, что метки ребер — это класс Num. Обычно это целые числа или плавает. Идея состоит в том, что некоторые ребра могут быть больше (или менее) дорого, и эта стоимость представлена краем этикетки или вес. На приведенном ниже графике, который представляет собой
неориентированный граф, веса рисуются рядом с
края и кажутся темно-фиолетовыми.
На приведенном ниже графике, который представляет собой
неориентированный граф, веса рисуются рядом с
края и кажутся темно-фиолетовыми.Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Integer.
- Базовым набором весов является Integer.
- Набор вершин = {1,2,3,4,5}
- Набор краев = {(1,4,5) ,(4,5,58) ,(3,5,34) ,(2,4,5) ,(2,5,4) ,(3,2,14) ,(1,2,2)}
Направленные ациклические графы.
A Dag — ориентированный граф без циклов. Они постоянно появляются как частные случаи в приложениях CS.Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Integer.
- Набор вершин = {1,2,3,4,5,6,7,8}
- Набор ребер = {(1,7) ,(2,6) ,(3,1),(3,5) ,(4,6) ,(5,4),(5,2) ,(6,8) ,(7,2),(7,8)}
Отключенные графики
Вершины графа не обязательно должны быть связаны с другими вершинами. Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.
Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.Вершины (например, 5,7 и 8) только с стрелками внутри называются стоками. Вершины только с стрелками наружу (например, 3 и 4) называются источниками.
Здесь у нас есть следующие части.
- Базовым набором для набора Vertices является Integer.
- Набор вершин = {1,2,3,4,5,6,7,8}
- Набор ребер = {(1,7) ,(3,1),(3,8) ,(4,6) ,(6,5)}
Представление графов на компьютере
Графики часто используются для представления физических объектов.
(сеть дорог, отношения между людьми и т.д.) внутри
компьютер. Используется множество механизмов. Хороший выбор
механизм зависит от операций, которые компьютерная программа должна выполнять на графе
для достижения своих потребностей . Возможные операции включают.
- Вычислить список всех вершин
- Вычислить список всех ребер.
- Для каждой вершины u вычислить список ребер (u,v). Это часто называют функцией смежности.
- Если граф помечен (помечены либо вершины, либо ребра) вычислить метку для каждой вершины (или ребра).
Не всем программам потребуются все эти операции, поэтому для некоторых программы, эффективное представление, которое может вычислить только необходимых операций (но не других), будет достаточно.
Преимущества представления графиков в виде функций
- Просто и понятно
- Легко адаптируется к различным типам графиков
Недостатки использования графиков в качестве функций
- Не может быть расширен для размещения запросов о набор вершин или набор ребер.
- В зависимости от компилятора, компилирующего функции
может быть не очень эффективным. На самом деле время в худшем случае может быть пропорционально количеству вершин.

- График должен быть известен статически во время компиляции.
Графы как массивы смежных вершин.
Один механизм, который может смягчить недостатки использования функций в качестве способа представления графиков следует использовать вместо них массивы. Используя это механизм требует, чтобы базовый домен Vertices был некоторым тип, который можно использовать в качестве индекса в массиве.В оставшейся части этой заметки мы будем предполагать, что вершины имеют тип Int , и что набор вершин представляет собой конечный диапазон типа Int . Таким образом, граф можно представить следующим образом:
введите ArrGraph = Массив [Int]Теперь мы можем быстро и эффективно ответить на ряд вопросов о графиках.
введите ArrGraph i = Массив [i]
вершины:: ArrGraph i -> IO[Int]
ребра:: ArrGraph i -> IO[(Int,i)]
дети:: ArrGraph i -> i -> IO[i]
вершины г =
делать { (ло, привет)
Преимущества представления графов в виде массивов
Недостатки представления графиков в виде массивов
- Требует, чтобы доступ к графу был командой, а не вычислением.

- Домен Vertices должен быть такого типа, который можно использовать в качестве индекса в массиве.
Алгоритмы на графиках
Алгоритмов на графах очень много. В этой заметке мы будем посмотрите на некоторые из них. Они включают:
- Поиск графиков
- Обнаружение циклов на графиках
- Алгоритмы кратчайшего пути
Вернемся к ежедневной записи.
Вернуться на страницу класса.
CSE 392 — Алгоритмы графов задач программирования (неделя 10)
CSE 392 — Алгоритмы графов задач программирования (неделя 10)Далее: Об этом документе… Вверх: Моя домашняя страница
Свойства графиков
Теория графов — это изучение свойств графовых структур. Он предоставляет нам язык, на котором можно говорить о графах.
Ключом к решению многих проблем является определение фундаментального теоретико-графового
понятие, лежащее в основе ситуации, а затем с использованием классического
алгоритмы решения возникшей проблемы.
Графы состоят из вершин и ребер. Простейшим свойством вершины является ее степень , число инцидентных ему ребер.
Сумма степеней вершин любого неориентированного графа вдвое больше ребер, так как каждое ребро вносит один вклад в степень обе смежные вершины.
Деревья — это неориентированные графы, не содержащие циклов. Степени вершин важны при анализе деревьев. лист дерева является вершиной степени 1. Каждое -вершинное дерево содержит ребра, поэтому все нетривиальные деревья содержат не менее двух листовых вершин.
Связь
Граф является 90 286 связным 90 287, если существует ненаправленный путь между каждой пары вершин.
Существование остовного дерева достаточно, чтобы доказать связность. Подключенные компоненты, основанные на поиске в ширину или в глубину. можно использовать алгоритм найти такое остовное дерево.
Однако существуют и другие понятия связности.
Наиболее интересен частный случай, когда имеется единственное слабое звено в
график. Единственная вершина, удаление которой разъединяет граф, называется артикуляция
вершина ; любой граф без такой вершины называется двусвязным .
Единственное ребро, удаление которого разъединяет граф, называется мостом .
Единственная вершина, удаление которой разъединяет граф, называется артикуляция
вершина ; любой граф без такой вершины называется двусвязным .
Единственное ребро, удаление которого разъединяет граф, называется мостом .
Проверить вершины артикуляции или мосты легко с помощью грубой силы. Для каждой вершины/ребра удалите ее из графа и проверьте, граф остается связным. Не забудьте добавить эту вершину/ребро перед выполнением следующее удаление!
В ориентированных графах нас часто интересуют сильно связанные компоненты , т.е. разбиение графа на куски такое, что между всеми парами вершин существуют направленные пути внутри заданного фрагмента. Дорожные сети должны быть сильно связаны, иначе будут места, которые вы может ехать, но не ехать домой извне нарушение односторонних знаков.
Циклы в графиках
Все графы, не являющиеся древовидными, содержат циклы.
Особенно интересны циклы, которые посещают все ребра или вершины. графика.
графика.
Эйлеров цикл — это обход всех ребер графа. ровно один раз. Маршрут почтальона в идеале является эйлеровым циклом, поэтому он может посетить все улица (край) по соседству один раз перед возвращением домой.
ненаправленный граф содержит эйлеров цикл, если он связен и каждая вершина четной степени. Почему? Цепь должна входить и выходить каждая вершина, с которой он сталкивается, подразумевая, что все степени должны быть четными.
Мы можем найти эйлеров цикл, построив его один цикл за раз. Мы можем найти простой цикл в графе, найдя заднее ребро с помощью ДФС. Удаление ребер в этом цикле оставляет каждую вершину с четной степенью. Как только мы разбили ребра на реберно-непересекающиеся циклы, мы можем объединить эти циклы произвольно в общих вершинах, чтобы построить эйлеров цикл.
Гамильтонов цикл — это тур, который посещает каждую вершину графа.
ровно один раз.
Задача коммивояжера требует кратчайшего такого путешествия на
взвешенный график.
К сожалению, не существует эффективного алгоритма для решения гамильтониана проблемы с циклом. Если граф достаточно мал, его можно решить с помощью поиска с возвратом.
Минимальные связующие деревья
Остовное дерево графа является подмножеством ребер из формирования дерева, соединяющего все вершины .
Для взвешенных по ребрам графов нас особенно интересует минимальное остовное дерево , остовное дерево, сумма весов ребер которого является минимально возможным.
Минимальные остовные деревья — это ответ, когда нам нужно соединиться набор точек (представляющих города, перекрестки или другие местоположения) самым маленьким количество проезжей части, провода или трубы.
Мы представим здесь алгоритм Прима, потому что мы думаем, что он проще программировать, и потому что это дает нам алгоритм кратчайшего пути Дейкстры с очень минимальными изменениями.
Мы обобщаем структуру данных графа для поддержки взвешенных по ребрам графов. Каждая запись ребра ранее содержала только другую конечную точку данного ребра.
Мы должны заменить это записью, позволяющей аннотировать ребро с помощью
веса:
Каждая запись ребра ранее содержала только другую конечную точку данного ребра.
Мы должны заменить это записью, позволяющей аннотировать ребро с помощью
веса:
структура typedef {
на телевидении; /* соседняя вершина */
инт вес; /* вес ребра */
} край;
структура typedef {
края края[MAXV+1][MAXDEGREE]; /* информация о соседстве */
целая степень[MAXV+1]; /* степень исхода вершины */
внутренние вершины; /* количество вершин */
внутренние ребра; /* количество ребер в графе */
} график;
Алгоритм Прима
Алгоритм Прима поэтапно выращивает минимальное остовное дерево. начиная с заданной вершины. На каждой итерации мы добавляем одну новую вершину в остовное дерево. Для корректности достаточно жадного алгоритма: мы всегда добавляем ребро с наименьшим весом, связывающее вершину дерева с вершина снаружи.
Наша реализация отслеживает самое дешевое ребро от любой вершины дерева до каждой вершины, не являющейся деревом. вершина в графе.
Самое дешевое ребро из всех оставшихся вершин, не являющихся деревьями, добавляется в каждую
итерация.
Мы должны обновить стоимость доступа к вершинам, не являющимся деревьями, после
каждая вставка.
вершина в графе.
Самое дешевое ребро из всех оставшихся вершин, не являющихся деревьями, добавляется в каждую
итерация.
Мы должны обновить стоимость доступа к вершинам, не являющимся деревьями, после
каждая вставка.
Само минимальное остовное дерево или его стоимость может быть реконструирован двумя различными способами. Простейшим методом было бы дополнить эту процедуру операторами которые печатают ребра по мере их нахождения или суммируют вес всех выбранных ребер в переменной для последующего возврата. С другой стороны, поскольку топология дерева кодируется родительским массивом это плюс исходный график говорит вам все о минимальном остовном дереве.
Реализация Прим
prim(график *g, int начало) {
интервал я, j; /* счетчики */
логическое внутреннее дерево[MAXV]; /* есть ли вершина в дереве? */
расстояние [MAXV]; /* расстояние вершины от начала */
на телевидении; /* текущая вершина для обработки */
инт ш; /* следующая вершина-кандидат */
инт вес; /* вес ребра */
внутр. расстояние; /* кратчайшее текущее расстояние */
for (i=1; i<=g->nвершин; i++) {
intree[i] = ЛОЖЬ;
расстояние[i] = MAXINT;
родитель [я] = -1;
}
расстояние[начало] = 0;
v = начало;
в то время как (intree[v] == FALSE) {
intree[v] = ИСТИНА;
for (i=0; i
расстояние; /* кратчайшее текущее расстояние */
for (i=1; i<=g->nвершин; i++) {
intree[i] = ЛОЖЬ;
расстояние[i] = MAXINT;
родитель [я] = -1;
}
расстояние[начало] = 0;
v = начало;
в то время как (intree[v] == FALSE) {
intree[v] = ИСТИНА;
for (i=0; iстепень[v]; i++) {
w = g->рёбра[v][i].v;
вес = g->ребра[v][i].вес;
if ((расстояние[w] > вес) && (intree[w]==FALSE)) {
расстояние[w] = вес;
родитель[ш] = v;
}
}
v = 1;
расстояние = MAXINT;
для (i=2; i<=g->nвершин; i++)
if ((intree[i]==FALSE) && (расстояние > расстояние[i])) {
расстояние = расстояние [я];
v = я;
}
}
}
Алгоритм Дейкстры для поиска кратчайших путей
BFS недостаточно , а не для поиска кратчайших путей во взвешенных графах,
потому что кратчайший взвешенный путь от до не обязательно
содержат наименьшее количество ребер.
Алгоритм Дейкстры является методом выбора для нахождения кратчайшего пути. путь между двумя вершинами в графе, взвешенном по ребрам и/или вершинам. Учитывая конкретную начальную вершину, он находит кратчайший путь из к каждой другой вершине графа, включая желаемый пункт назначения.
Основная идея очень похожа на алгоритм Прима. На каждой итерации мы будем добавлять ровно одну вершину к дереву. вершин, для которых мы знаем кратчайший путь из .
Разница между алгоритмами Дейкстры и Прима заключается в том, как они оценить желательность каждой внешней вершины. В кратчайший путь мы хотим включить ближайшую внешнюю вершину. (по кратчайшему пути) до начала. Это функция как нового веса ребра , так и расстояние от начало вершины дерева, к которой он примыкает.
На самом деле это изменение очень незначительное. Ниже мы приводим реализацию алгоритма Дейкстры, основанную на замене ровно три строки из реализации нашего Prim, одна из которых просто имя функции!
Реализация Дейкстры
dijkstra(graph *g, int start) /* БЫЛО prim(g,start) */
{
интервал я, j; /* счетчики */
логическое внутреннее дерево[MAXV]; /* есть ли вершина в дереве? */
расстояние [MAXV]; /* расстояние вершины от начала */
на телевидении; /* текущая вершина для обработки */
инт ш; /* следующая вершина-кандидат */
инт вес; /* вес ребра */
внутр. расстояние; /* кратчайшее текущее расстояние */
for (i=1; i<=g->nвершин; i++) {
intree[i] = ЛОЖЬ;
расстояние[i] = MAXINT;
родитель [я] = -1;
}
расстояние[начало] = 0;
v = начало;
в то время как (intree[v] == FALSE) {
intree[v] = ИСТИНА;
for (i=0; i
расстояние; /* кратчайшее текущее расстояние */
for (i=1; i<=g->nвершин; i++) {
intree[i] = ЛОЖЬ;
расстояние[i] = MAXINT;
родитель [я] = -1;
}
расстояние[начало] = 0;
v = начало;
в то время как (intree[v] == FALSE) {
intree[v] = ИСТИНА;
for (i=0; iстепень[v]; i++) {
w = g->рёбра[v][i].v;
вес = g->ребра[v][i].вес;
/* ИЗМЕНЕНО */ if (distance[w] > (distance[v]+weight)) {
/* ИЗМЕНЕНО */ Distance[w] = Distance[v]+Weight;
родитель[ш] = v;
}
}
v = 1;
расстояние = MAXINT;
для (i=2; i<=g->nвершин; i++)
if ((intree[i]==FALSE) && (расстояние > расстояние[i])) {
расстояние = расстояние [я];
v = я;
}
}
}
Как мы используем dijkstra найти длину кратчайшего пути от начала до заданного вершина? Это и есть значение расстояния[t]. Как мы можем восстановить реальный путь? Следуя обратным родительским указателям от до тех пор, пока мы не нажмем start (или -1, если такого пути не существует)
В отличие от Прима,
Алгоритм Дейкстры работает только с графами без ребер с отрицательной стоимостью. В большинстве приложений нет ребер с отрицательным весом, поэтому это обсуждение
академический.
В большинстве приложений нет ребер с отрицательным весом, поэтому это обсуждение
академический.
Кратчайший путь для всех пар
Многим приложениям необходимо знать длину кратчайшего пути между все пары вершин данного графа. Например, предположим, что вы хотите найти «центральную» вершину, тот, который минимизирует самое длинное или среднее расстояние до всех остальных узлы. Возможно, это лучшее место для начала нового бизнеса.
Мы могли бы решить эту проблему, вызывая алгоритм Дейкстры из каждого возможные начальные вершины. Но алгоритм поиска кратчайшего пути для всех пар Флойда удивительно ловок. способ построить эту матрицу расстояний от оригинала весовая матрица графа.
Алгоритм Флойда лучше всего использовать со структурой данных матрицы смежности, что не является экстравагантностью, так как мы все равно должны хранить все попарные расстояния. Наш тип adjacency_matrix выделяет место для максимально возможного матрица и отслеживает количество вершин в графе:
структура typedef {
целая масса[MAXV+1][MAXV+1]; /* информация о смежности/весе */
внутренние вершины; /* количество вершин в графе */
} adjacency_matrix;
Важным вопросом в любой реализации матрицы смежности является то, как мы обозначаем
ребер, которых нет в графе. Для невзвешенных графов принято обозначать ребра графа
по и неребер по .
Это дает совершенно неправильную интерпретацию, если числа обозначают ребро
веса, поскольку неребра интерпретируются как свободный проезд между вершинами.
Вместо этого мы должны инициализировать каждое неребро значением MAXINT.
Для невзвешенных графов принято обозначать ребра графа
по и неребер по .
Это дает совершенно неправильную интерпретацию, если числа обозначают ребро
веса, поскольку неребра интерпретируются как свободный проезд между вершинами.
Вместо этого мы должны инициализировать каждое неребро значением MAXINT.
initialize_adjacency_matrix(adjacency_matrix *g)
{
интервал я, j; /* счетчики */
г -> nвершин = 0;
для (i=1; i<=MAXV; i++)
для (j=1; j<=MAXV; j++)
g->вес[i][j] = MAXINT;
}
Алгоритм Флойда начинается с нумерации вершины графа от до , используя эти числа, чтобы не помечать вершины а заказать их.
Выполним итерации, где й итерация позволяет
только первые вершины как возможные промежуточные шаги на
путь между каждой парой вершин и .
При , нам не разрешены промежуточные вершины, так что единственный
разрешенные пути состоят из исходных ребер в графе.
Таким образом
исходная матрица кратчайших путей для всех пар состоит из начальной смежности
матрица. На каждой итерации мы допускаем более богатый набор возможных кратчайших путей.
Разрешение вершины th в качестве нового возможного посредника
помогает, только если есть короткий путь, который проходит, поэтому
На каждой итерации мы допускаем более богатый набор возможных кратчайших путей.
Разрешение вершины th в качестве нового возможного посредника
помогает, только если есть короткий путь, который проходит, поэтому
Реализация алгоритма Флойда
Правильность этого несколько тонка, и мы призываем вас чтобы убедить себя в этом. Но нет ничего тонкого в том, как коротка и приятна реализация. является:
Флойд (adjacency_matrix * g)
{
интервал я, j; /* счетчики размеров */
инт к; /* счетчик промежуточных вершин */
интервал_k; /* расстояние через вершину k */
для (k=1; k<=g->nвершин; k++)
для (i=1; i<=g->nвершин; i++)
for (j=1; j<=g->nвершин; j++) {
through_k = g->вес[i][k]+g->вес[k][j];
если (через_k вес[i][j])
g->weight[i][j] = through_k;
}
}
Переходное закрытие
Алгоритм Флойда имеет еще одно важное применение — вычисление транзитивное замыкание ориентированного графа. При анализе ориентированного графа нас часто интересует, какие вершины
достижимы из данного узла.
При анализе ориентированного графа нас часто интересует, какие вершины
достижимы из данного узла.
Например, рассмотрим граф шантажа , определенный на наборе людей, где есть направленное ребро, если имеет достаточно чувствительный личную информацию, чтобы заставить его делать все, что он хочет. Вы хотите нанять одного из этих людей в качестве своего личного представителя. Кто обладает наибольшей силой с точки зрения потенциала шантажа?
Упрощенным ответом будет вершина высшей степени, но даже лучшим представителем был бы человек, у которого есть цепи шантажа до самых другие партии. Стив может только напрямую шантажировать Мигеля, но если Мигель может шантажировать все остальные, то Стив — тот человек, которого вы хотите нанять.
Вершины, достижимые из любого отдельного узла, могут быть вычислены с помощью использования
поиск в ширину или в глубину.
Но всю партию можно вычислить как задачу поиска кратчайшего пути для всех пар.
Если кратчайший путь от до остается MAXINT после запуска
Алгоритм Флойда, вы можете быть уверены, что нет направленного пути от к . Любая пара вершин с весом меньше MAXINT должна быть достижима,
оба в
теоретико-графовый и шантажный смыслы этого слова.
Любая пара вершин с весом меньше MAXINT должна быть достижима,
оба в
теоретико-графовый и шантажный смыслы этого слова.
Двустороннее сопоставление и сетевой поток
Любой взвешенный по ребрам граф можно рассматривать как сеть труб, где вес ребра измеряет вместимость трубка. Для заданного взвешенного графа и двух вершин и , проблема сетевого потока запрашивает максимальный объем потока, который может быть отправлены из в, соблюдая максимальную пропускную способность каждой трубы.
Хотя проблема сетевого потока представляет самостоятельный интерес, ее первостепенное значение
заключается в том, чтобы иметь возможность решать другие важные задачи графа.
Классический пример — двудольное сопоставление.
А , соответствующее в графе, является подмножеством ребер
такое, что никакие два ребра в не имеют общей вершины.
Таким образом, паросочетание объединяет определенные вершины так, что каждая вершина находится в точке
максимум одна такая пара.
Граф двудольный или двухцветный , если вершины могут быть разделить на два множества, скажем, и , такие, что все ребра в имеют одна вершина в и одна вершина в . Многие естественно определенные графы являются двудольными. Например, предположим, что определенные вершины представляют рабочие места, сделано, а остальные вершины люди, которые потенциально могут их сделать. Существование края означает, что работа потенциально может быть выполнена человек . Или пусть некоторые вершины представляют мальчиков, а некоторые вершины — девочек, с ребрами представляющие совместимые пары. Соответствия на этих графиках имеют естественную интерпретацию как работу. назначения или как браки.
Максимально возможное двудольное соответствие может быть найдено с использованием сетевого потока. Подробности смотрите в учебнике.
Назначенные проблемы
111001 (Веснушки) — Соедините точки, используя как можно меньше чернил. Какой классической задаче с графами это соответствует?
111002 (Ожерелье) — Существует ли способ нанизывать двухцветные бусины так, чтобы каждая пара соседних граней бусинок имеет общий цвет? Какой классической задаче с графами это соответствует? Что эффективно вычисляет классическая задача с графом это тоже соответствует?
111006 (Туристический гид) —
Какие вершины в графе делят граф на две части,
т.

 Необходимо, начиная от одного из этих пунктов и побывав в каждом из пунктов только один раз, вернуться в исходный пункт. Какой маршрут надо выбрать, чтобы путь оказался кратчайшим?
Необходимо, начиная от одного из этих пунктов и побывав в каждом из пунктов только один раз, вернуться в исходный пункт. Какой маршрут надо выбрать, чтобы путь оказался кратчайшим?
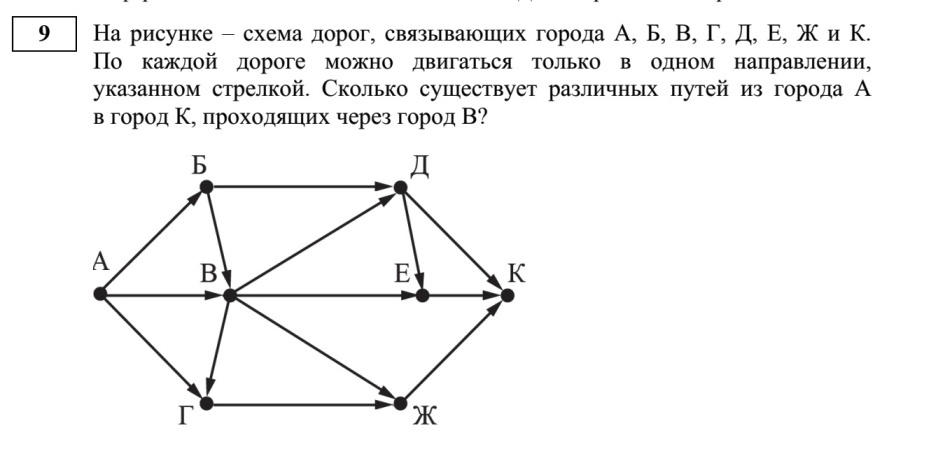 Некоторые города соединены дорогами. Император галактики Максимус принимает решение составить список этих дорог на планете. Но так как он слаб в математике, просит у вас помощи.
Некоторые города соединены дорогами. Император галактики Максимус принимает решение составить список этих дорог на планете. Но так как он слаб в математике, просит у вас помощи.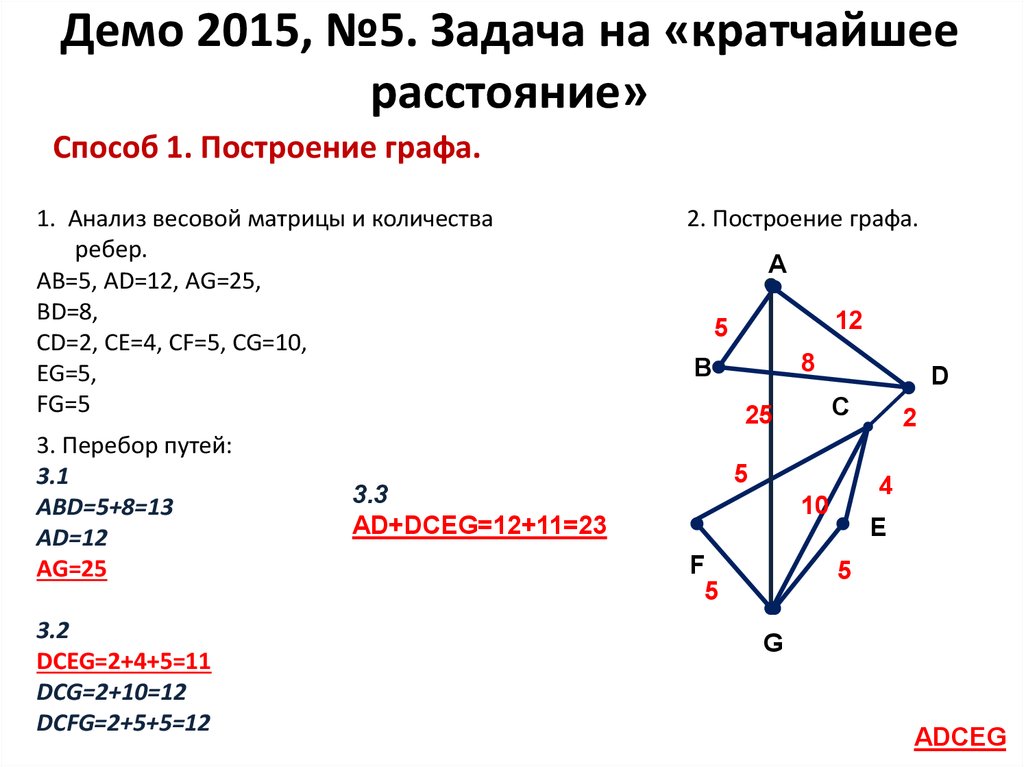 Если такая дорога имеется, следовательно, на пересечении j-го столбца и i-строки тоже будет 1. То есть если
Если такая дорога имеется, следовательно, на пересечении j-го столбца и i-строки тоже будет 1. То есть если
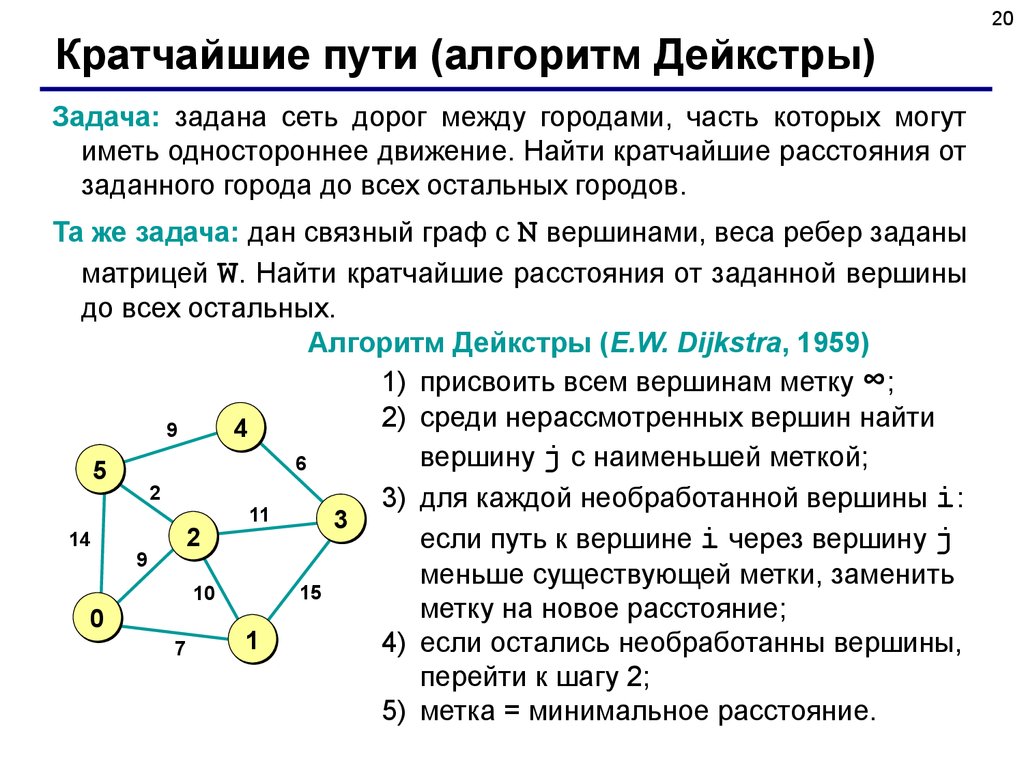
 Понятно, что при помощи этого графа нетрудно определить, с кем играли остальные участники соревнований.
Понятно, что при помощи этого графа нетрудно определить, с кем играли остальные участники соревнований. Есть дуга
между v1 и v2, если (v1,v2) является элементом множества ребер.
Есть дуга
между v1 и v2, если (v1,v2) является элементом множества ребер.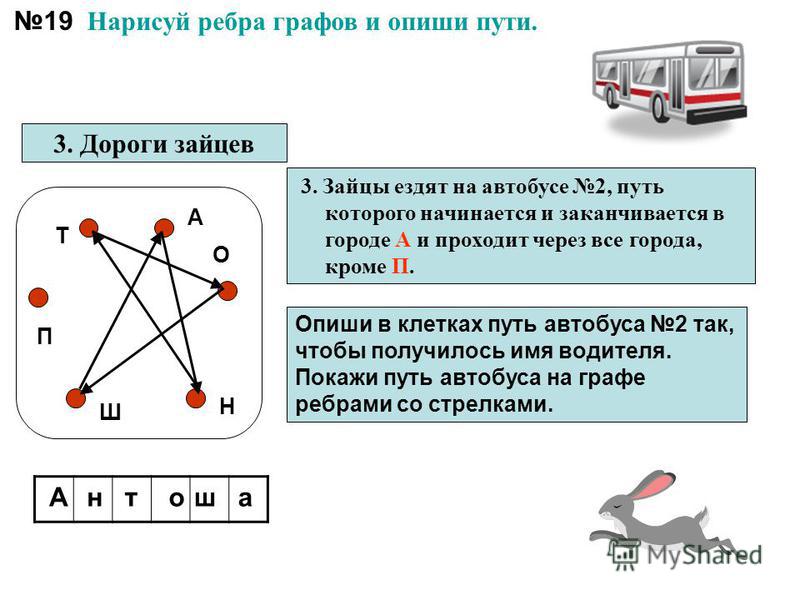
 В файле присутствуют только идентификационные данные.
пара в наборе Edge. Это относится к (ключевым, спутниковым) данным
различие для сортировки.
В файле присутствуют только идентификационные данные.
пара в наборе Edge. Это относится к (ключевым, спутниковым) данным
различие для сортировки.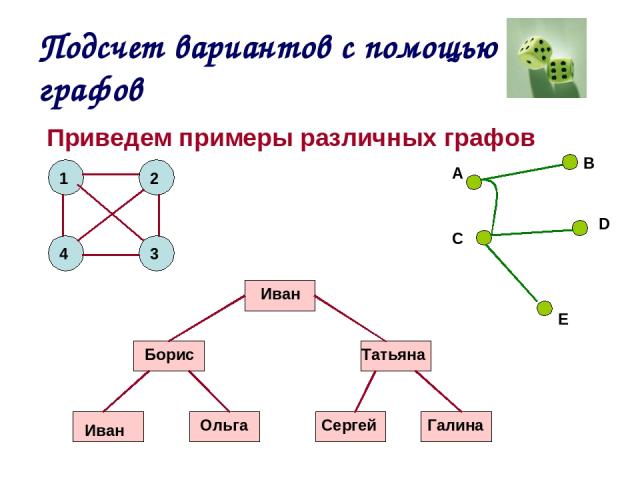
 На приведенном ниже графике, который представляет собой
неориентированный граф, веса рисуются рядом с
края и кажутся темно-фиолетовыми.
На приведенном ниже графике, который представляет собой
неориентированный граф, веса рисуются рядом с
края и кажутся темно-фиолетовыми.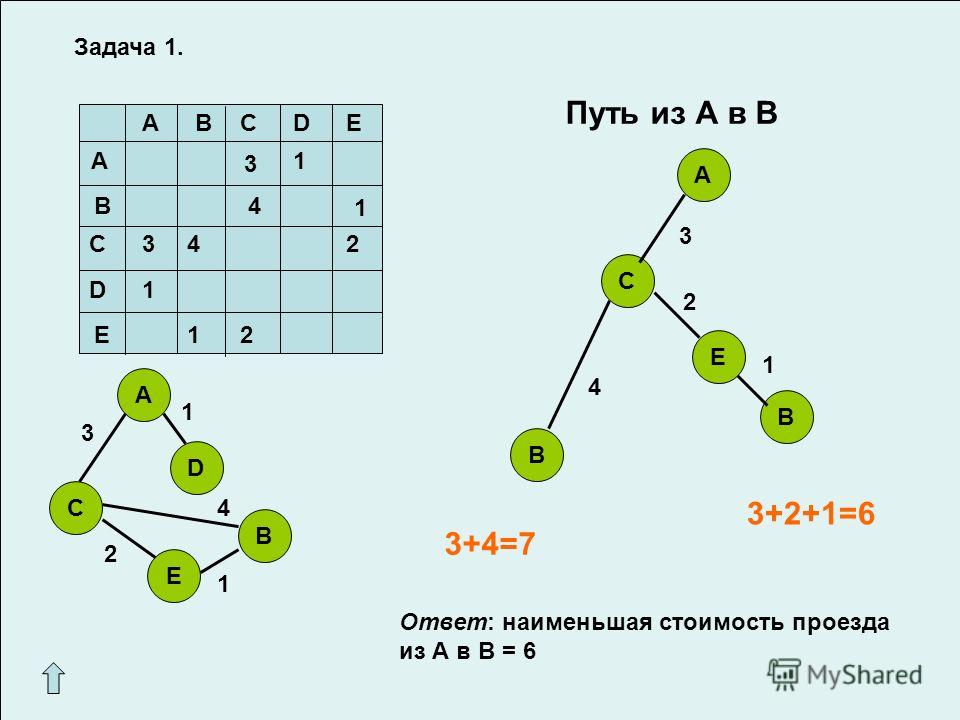 Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.
Граф может иметь несвязанные компоненты и даже одиночные вершины.
без единого подключения.