17. Вычисление двойного интеграла в декартовых координатах
Теорема 14.1 Если : 1) функция F(X,Y) интегрируема в правильной в направлении Oy области S: , т. е. существует двойной интеграл , 2) существует повторный интеграл , то
(2.3)
Теорема 14.2. Если :1) функция F(X,Y) интегрируема в правильной в направлении Ox области , т. е. существует двойной интеграл , 2) существует повторный интеграл , то
. (2.4)
Из вышеприведенных теорем следует, что При вычислении повторного интеграла можно изменять порядок интегрирования.
Пример 4. Изменить порядок интегрирования в интеграле .
|
Ñ Так как из (2.4) имеем , то правильная в направлении Ox область D ограничена линиями X=Y, X=2—Y, Y
 14.7). Эта область является правильной и в направлении Oy. Так как участок OAB Границы состоит из отрезков прямых и , то , где (см. (2.1)) ,
14.7). Эта область является правильной и в направлении Oy. Так как участок OAB Границы состоит из отрезков прямых и , то , где (см. (2.1)) ,. Итак, = = =.#
Пример 5. Вычислить по области D, ограниченной линиями и .
Ñ Изобразим область D. Для отыскания точек пересечения парабол и решаем уравнение , откуда имеем действительные корни , . Таким образом, параболы пересекаются в точках ( рис. 14.8). Рассматривая D как правильную в направлении Oy (рис.14.8а), имеем (см.(2.1)) . По формуле (2.3)
Рис.14.8 а)
=.
Если область D рассматривать как правильную в направлении Ox (рис.14.8б),
Рис.14.8.б
То (см. (2.2)) . По формуле (2.4)
=
. #
Задачи для самостоятельного решения
Изменить порядок интегрирования в следующих повторных интегралах:
8. . 9. .
10. . 11..
Перейти от двойного интеграла по конечной области D к повторному интегралу и расставить пределы интегрирования:
12.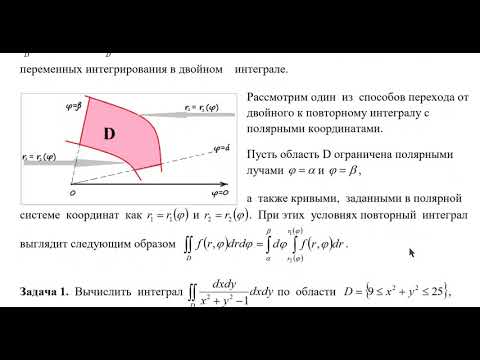 Область D – параллелограмм со сторонами .
Область D – параллелограмм со сторонами .
13. . 14. .
15. — треугольник со сторонами .
16. .
17. — треугольник с вершинами .
18. D – сегмент, ограниченный линиями .
Вычислить двойные интегралы:
19. . 20. — Круг .
21. — область, ограниченная линиями .
22. — область, ограниченная линиями .
23. — область, ограниченная линиями .
24.- четверть круга , лежащая в первом квадранте.
25. — область, ограниченная параболой и прямой .
26. , если D ограничена осью абсцисс и первой аркой циклоиды , , .
| Следующая > |
|---|
1.2 Вычисление двойного интеграла в декартовых координатах
Требуется вычислить
двойной интеграл
,
где функцияz=f(x,y)≥0 непрерывна в областиD . Как мы выяснили двойной интеграл
выражает объём цилиндрического тела,
ограниченного сверху поверхностьюz=f(x,y).
Как мы выяснили двойной интеграл
выражает объём цилиндрического тела,
ограниченного сверху поверхностьюz=f(x,y).
Согласно методу параллельных сечений , гдеS(x)-площадь сечения плоскостью, перпендикулярной осиОх ,х=а ,х=b — уравнение плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямымих=а ,х=b и кривыми,(рис. 4). Функцииинепрерывны идля всех.
Определение. Область Dназываетсяправильнойв направлении осиOy, если любая прямая параллельная осиOy , пересекает границу области не более, чем в двух точках.
Точка — точка входа,
— точка выхода.
Рис. 4
4
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох :х=const,. В сечении получим криволинейную трапециюABCD , ограниченную линиями, гдех=const,z=0 ,,(рис. 5).
Площадь S(x)этой трапеции находим с помощью определённого интеграла
Рис. 5
Т.о. согласно формуле (1.2.1) вычисления двойного интеграла сводятся к последовательному вычислению двух определённых интегралов.
Правую часть формулы (1.2.1) называют двукратным интегралом от функции f(x,y) по областиD. При этом называется внутренним интегралом.
Для
вычисления двукратного интеграла
сначала берём внутренний интеграл,
считаяx— постоянным,
затем берём внешний интеграл, т. е.
результат первого интегрирования
интегрируем поxв пределах отадоb .
е.
результат первого интегрирования
интегрируем поxв пределах отадоb .
Если область Dограничена прямымиy=c, y=d (c<d) , кривыми,причёмдля, т.е. областьD— правильная в направлении осиOx(рис. 6). То, рассекая тело плоскостьюy=const , аналогично получим
Рис. 6
(1.2.2)
Здесь при вычислении внутреннего интеграла считаем y—const
Замечания.
1) Формулы (1.2.1) и (1.2.2) справедливы в случае, когда f(x,y)<0 .
2) Если область Dправильная в обоих направлениях, то
двойной интеграл можно вычислять как
по формуле 1. 2.1, так и по формуле 1.2.2.
2.1, так и по формуле 1.2.2.
3) Если область D не является правильной ни поxни поy
4) Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны , а внутренние, как правило, переменные.
Пример:
Вычислить двойной интеграл ,,.
Решение:
Строим область интегрирования (рис. 7). В данном примере удобнее вычислять интеграл по формуле (1.2.2), в направлении оси Ох.
Рис. 7
Вычисляем внутренний интеграл, y—const
.
Полученную функцию интегрируем по х
Можно было
воспользоваться формулой (1. 2.1), но для
этого область D следует разбить на две областиD1иD2(рис. 8).
2.1), но для
этого область D следует разбить на две областиD1иD2(рис. 8).
Рис. 8
Вычислить самостоятельно двойные интегралы в правой части. Получить тот же результат 29/20.
Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводят новые переменные под знаком двойного интеграла.
Введём новые переменные , пусть и, функцииφиψимеют в некоторой областиплоскостиОuvнепрерывные частные производные.
Функциональный определитель
— называется определителем Якоби или якобианом.
Если функция непрерывна в областиD , а якобиан, то справедлива формула замены переменных в двойном интеграле
.
Рассмотрим частный случай: замену декартовых координат
 Прямоугольные
и полярные координаты связаны формулами
Прямоугольные
и полярные координаты связаны формулами.
В качестве uиvвозьмём полярные координатыr и φ. Составим Якобиан преобразованияu=r, v=φ.
Формула замены переменных x, y в полярных координатах будет иметь вид
— область в полярной системе координат, соответствует области Dв декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют тоже правило сведения его к двукратному интегралу
ЕРис. 9
сли область(рис.9) ограниченна лучамиφ=αиφ=β, гдеα<βи кривыми,, где, для любого, т.е. область-правильная: то двойной интеграл в полярной системе координат вычисляется по следующей формуле
Внутренний интеграл
берётся при условии, что φ- константа.
Замечание:
1) переход к полярным координатам полезен, когда подынтегральная функция имеет вид ; областьD — есть круг, кольцо или часть таковых;
2) на практике переход к полярным координатам осуществляется путём замены . Уравнения линий, ограничивающих областьD, так же преобразуются к полярным координатам.
Пределы интегрирования по rи φ находят, совместив декартову и полярную системы координат.
Пример: Вычислить
D:(рис. 10)
Решение:
Переходим к полярным координатам
Область D в полярной системе координат :
Рис. 10
Подынтегральная функция в полярной системе координат:
Вычисляем интеграл
python — Двойной интеграл в декартовых координатах вместо (R,Theta)
На самом деле, интегрирование в декартовых координатах довольно простое. Теперь, когда у вас есть функция интенсивности, вы должны выразить радиус
Теперь, когда у вас есть функция интенсивности, вы должны выразить радиус r координатами x и y . Тривиальная вещь, которую вы на самом деле сделали в своем вопросе.
Итак, функция, которую нужно интегрировать (без некоторых констант):
из scipy import special as sp
# Функция интенсивности Фраунгофера (сферическая апертура)
защита f(x,y):
г = np.sqrt (х ** 2 + у ** 2)
возврат (sp.j1(r)/r)**2
Или, используя тот факт, что 2 J1( x )/ x = J0( x ) + J2( x ) [спасибо, Хайме!]:
def f(x,y):
г = np.sqrt (х ** 2 + у ** 2)
возврат (sp.j0(r) + sp.jn(2,r))**2
Эта форма лучше в том смысле, что нигде не имеет особенности.
Теперь я не использую никаких постоянных коэффициентов. Вы можете добавить их, если хотите, но мне проще нормализовать результат интегрирования по бесконечной области. В противном случае слишком легко просто забыть какую-то константу (обычно я так и делаю).
Интеграцию можно выполнить с помощью scipy.integrate.nquad . Он принимает многомерную функцию для интеграции. Итак, в этом случае:
import scipy.integrate интеграл = scipy.integrate.nquad(f, ([-d/2, d/2], [-d/2, d/2]))[0]
Однако, поскольку ваша функция явно симметрична, вы можете рассмотреть возможность интегрирования только по одному квадранту, а затем умножить на четыре:
4. * scipy.integrate.nquad(f, ([0, d/2], [0 , д/2]))[0]
При их использовании полная интенсивность:
>>> 4. * scipy.integrate.nquad(f, [[0,inf],[0,inf]])[0] 12,565472446489999
(что очень похоже на 4 пи, кстати.) Конечно, вы также можете использовать полярные координаты для вычисления полного значения, поскольку функция имеет круговую симметрию (как описано в функции «Интеграл интенсивности» в python). Различные значения обусловлены разным масштабированием (2 pi опущены при полярном интегрировании, 2 потому что я использую здесь форму суммы функций Бесселя).
Например, для площади от -1 до 1 в обоих направлениях нормализованная (деленная на указанное выше значение полной мощности) мощность по площади равна:
>>> 4*scipy.integrate.nquad(f, [[0,1],[0,1]])[0] / 12,565472446489999 0,27011854108867
Итак, примерно 27 % падающего света попадает на квадратный фотоприемник.
Когда дело доходит до ваших констант, кажется, что чего-то (по крайней мере единиц) не хватает. Мое предположение:
- Длина волны: 550 нм
- диаметр круглого отверстия: 0,0055″ = 0,14 мм
- расстояние от отверстия до сенсора: 2,8 мм Размер квадратного сенсора
- 5,4 мкм x 5,4 мкм
Последнее, что я только что догадался по картинке. Поскольку размер датчика намного меньше расстояния, sin(ϴ) очень близок к y / d , где d — расстояние, а y — смещение от оптической оси. Используя эти числа, x = тыс. лет назад sin(ϴ) = тыс. лет назад / d ≈ 1,54. Для этого числа интеграл интенсивности дает примерно 0,52 (или 52 %).
лет назад / d ≈ 1,54. Для этого числа интеграл интенсивности дает примерно 0,52 (или 52 %).
Если вы сравниваете это с некоторым экспериментальным значением, помните, что существует множество источников ошибок. Изображение на плоскости изображения представляет собой преобразование Фурье апертуры. Если на краю диафрагмы есть небольшие дефекты, они могут изменить результирующее пятно. Воздушные кольца редко бывают такими красивыми, как думают астрономы…
Просто так:
Калькулятор двойных интегралов с шагом (прямоугольный и полярный)
Калькулятор двойных интегралов, который мы здесь представляем, является отличным инструментом для решения всех видов двойных интегралов в прямоугольных или полярных координатах.
Калькулятор двойных интегралов
| ∫ | ∫ | р др дт dxdydzdtdadbdcdfdhdldmdndodpdqdrdsdvdw | dxdydzdtdadbdcdfdhdldmdndodpdqdrdsdvdw | |
| Используйте inf для +∞ и -inf для -∞ |
| Координаты | Десятичные числа |
| RectangularPolars | 12345678910111213141516 |
Шаги 9
4 РешениеСодержание
- 1 Калькулятор двойных интегралов
- 2 Инструкции по использованию калькулятора двойных интегралов
- 3 Что такое двойной интеграл?
- 4 Свойства двойного интеграла
Инструкция по использованию Калькулятора двойных интегралов
Как видите, интерфейс калькулятора очень интуитивно понятен, что делает его простым в использовании. Чтобы использовать его, вам просто нужно выполнить следующие шаги:
Чтобы использовать его, вам просто нужно выполнить следующие шаги:
- Выберите тип координат, который вы будете использовать для вычисления двойного интеграла: выберите опцию «Прямоугольная», чтобы вычислить двойные интегралы по прямоугольным областям, или выберите опцию «Полярная», чтобы вычислить двойные интегралы в полярных координатах.
- Выберите дифференциал интегрирования: если вы выбрали прямоугольные координаты, у вас есть два выпадающих списка для этого. В случае, если вы выбрали полярные координаты, дифференциал интегрирования будет rdrdt , где переменная t относится к греческой букве тета.
- Введите в калькулятор функцию, которая будет подынтегральной функцией двойного интеграла. Для этого следует иметь в виду таблицу допустимых функций, представленную в этом разделе.
- Затем введите пределы интегрирования, которые могут быть числовыми или математическими выражениями, использующими переменные, присутствующие в дифференциале интегрирования.
 Обратите внимание, что для ввода числа пи вы должны написать пи , а если вы хотите написать ∞, вы должны написать inf .
Обратите внимание, что для ввода числа пи вы должны написать пи , а если вы хотите написать ∞, вы должны написать inf . - Выберите точность десятичных разрядов.
- Наконец, нажмите кнопку «Рассчитать», чтобы получить результат. Решение будет развернуто автоматически, показывая этапы процесса интеграции.
Для просмотра примеров двойных интегралов нажмите кнопку «Примеры».
| Допустимые функции и символы | Описание |
|---|---|
| квт() | Квадратный корень |
| лн() | Натуральный логарифм |
| лог() 9 | Экспоненты |
| абс() | Абсолютное значение |
| sin(), cos(), tan(), csc(), sec(), cot() | Основные тригонометрические функции |
| asin(), acos(), atan(), acsc(), asec(), acot() | Обратные тригонометрические функции |
| sinh(), cosh(), tanh(), csch(), sech(), coth() | Гиперболические функции |
| asinh(), acosh(), atanh(), acsch(), asech(), acoth() | Обратные гиперболические функции |
| число пи | PI-номер (π = 3,14159. ..) ..) |
| е | Число Непера (e= 2,71828...) |
| я | Для обозначения мнимой составляющей комплексного числа. |
| инф | ∞ |
Что такое двойной интеграл?
Двойные интегралы — это все интегралы функций от двух переменных по прямоугольной области R2.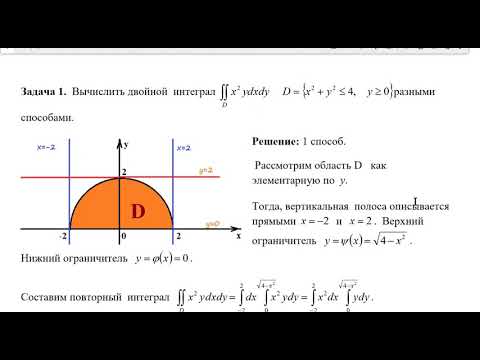

 Обратите внимание, что для ввода числа пи вы должны написать пи , а если вы хотите написать ∞, вы должны написать inf .
Обратите внимание, что для ввода числа пи вы должны написать пи , а если вы хотите написать ∞, вы должны написать inf .