определение и формулы для умножения частного, примеры решения задач
Содержание:
- Что такое логарифм произведения
- Логарифм произведения трех положительных чисел
- Логарифм произведения степени, частного
- Примеры решения задач на логарифмы
Содержание
- Что такое логарифм произведения
- Логарифм произведения трех положительных чисел
- Примеры решения задач на логарифмы
Что такое логарифм произведения
Определение
Логарифм числа по основанию определяется как показатель степени, в которую надо возвести основание, чтобы получить число.
Число а обычно называют основанием, а число b — аргументом логарифма.
Логарифм имеет следующий вид \(\log_a\left(b\right)\) и читается как «логарифм b по основанию a».
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Существуют логарифмы со специальными обозначениями. К ним относятся:
- Десятичный логарифм, который обозначается как lg и всегда имеет основание равное 10: \(\log_{10}=lg.\)
- Натуральный логарифм, который обозначается как ln и всегда имеет основание равное е = 2,718281… (это число иррационально, его невозможно вычислить точно), \(\log_e=ln.\)
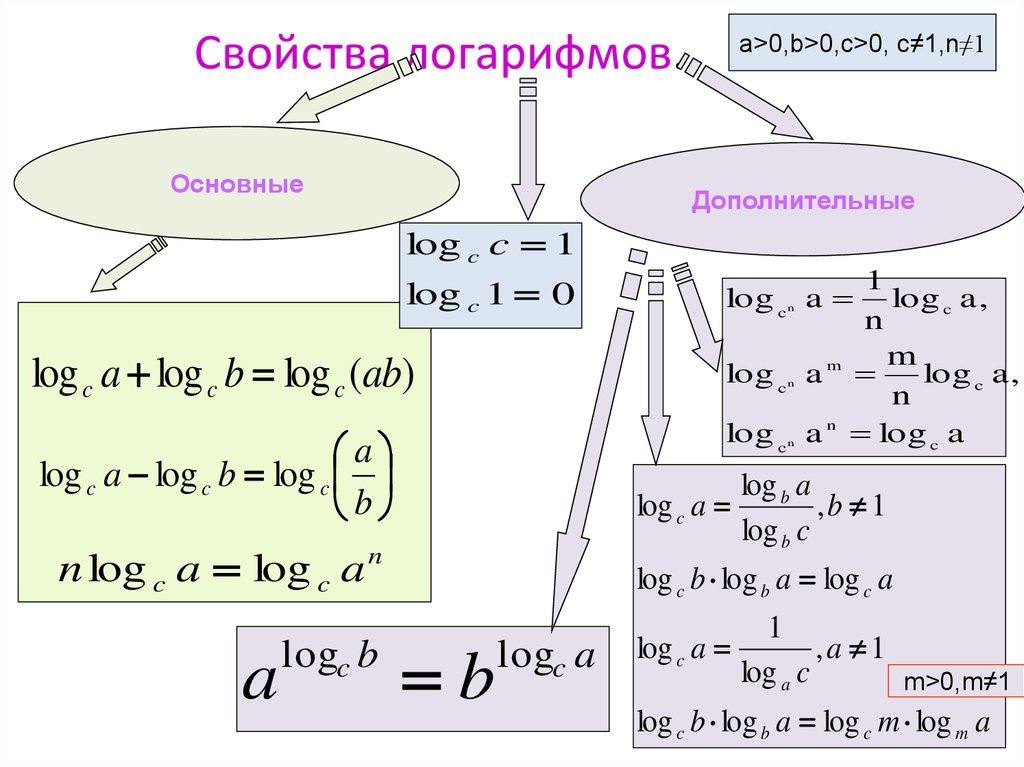
Логарифм также имеет основные свойства, которые необходимо помнить для решения примеров:
Теорема
Логарифм произведения двух чисел \(x\) и \(y\) равен сумме логарифмов этих чисел, если \(x\), \(y\), \(a\) — положительные числа, где \(a\) — основание и \(a\neq1\). {k+l}\) следует, что \(k+l=\log_a\left(x\times y\right).\)
{k+l}\) следует, что \(k+l=\log_a\left(x\times y\right).\)
Если \(k=\log_a\left(x\right)\) и \(l=\log_a\left(y\right)\), то \(\log_a\left(x\times y\right)=\log_a\left(x\right)+\log_a\left(y\right).\)
Логарифм произведения трех положительных чисел
Формула логарифма произведения применяется также и для нескольких положительных множителей. Возьмем для примера три числа и запишем формулу логарифма произведения в преобразованном виде.
\(\log_a\left(x_1\times x_2\times x_3\right)=\log_a\left(x_1\right)+\log_a\left(x_2\right)+\log_a\left(x_3\right)\)
где \(a\) — логарифмическое основание и \(a, x_1,\;x_2,\;x_3 > 0, a\neq0.\)
Логарифм произведения степени, частного
Помимо логарифма произведения, рассмотрим такие понятия как логарифм степени и частного. Они являются не менее важными для решения задач.
Определение
Логарифм степени с положительным основанием — это показатель степени, умноженный на логарифм ее основания.
Определение
Логарифм частного двух положительных чисел — это разность между логарифмом делимого и логарифмом делителя.
\(\log_a\left(\frac xy\right)=\log_a\left(x\right)-\log_a\left(y\right)\)
Примеры решения задач на логарифмы
Задача 1
Вычислить \(\log_{11}\left(21\right).\)
Решение
Разложим аргумент логарифма на более простые числа и применим формулу логарифма произведения. Получим:
\(\log_{11}\left(21\right)=\log_{11}\left(3\times7\right)=\log_{11}\left(3\right)+\log_{11}\left(7\right)\)
Задача 2
Вычислить \(\log_{1,8}\left(1,8\times\sqrt{11}\right).\)
Решение
Применим формулу логарифма произведения для нескольких множителей. Получим:
\(\log_{1,8}\left(1,8\times\sqrt{11}\right)=\log_{1,8}\left(1,8\right)+\log_{1,8}\left(\sqrt{11}\right)=1+\log_{1,8}\left(\sqrt{11}\right)\)
Задача 3
Вычислить \(\log_{12}\left(\frac8{13}\right).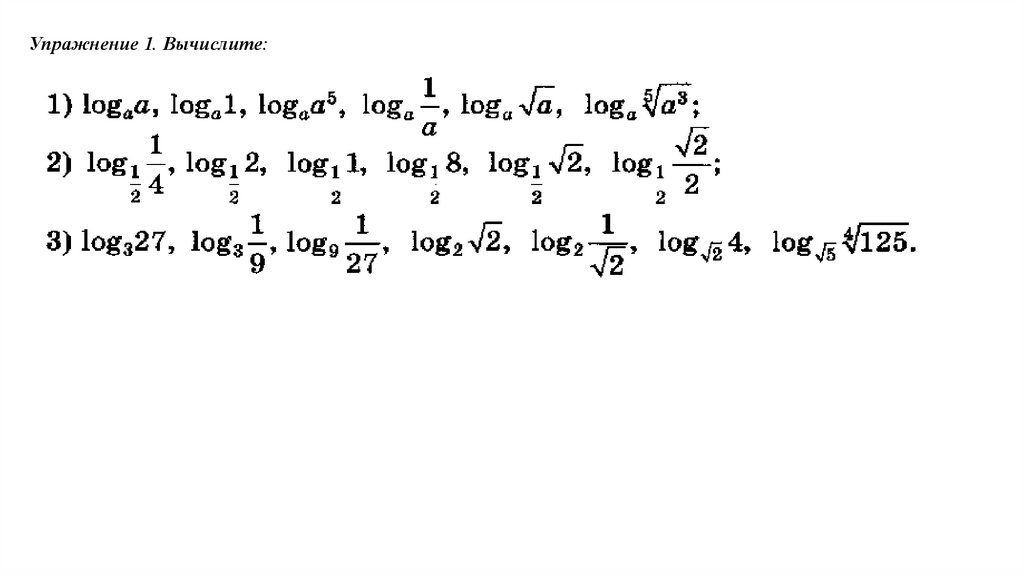 2\right)=2\times\log_4\left(5\right)\)
2\right)=2\times\log_4\left(5\right)\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Вычисление дискретного логарифма
Определение. Пусть G = < G; •, 1 > — конечная группа, а и b —элементы группы G; r = ordb. Натуральное число l называют дискретнымлогарифмом элемента а при основании b, если
(1.1)
Замечания.
а) В качестве группы G избираем мультипликативную группу из ненулевых элементов конечного поля Fr
б) Если q = р — простое
число и b — первообразный
корень по модулю р, то
число l,
определяемое условием (1. 1), называют индексом числа а при
основании b по
модулю р.
1), называют индексом числа а при
основании b по
модулю р.
в) Вместо термина «дискретный логарифм элемента а при основании b» употребляют также термин » индекс элемента а при основании b».
Обозначение. indba — дискретный логарифм элемента а при основании b. (Группа G обычно подразумевается из контекста.)
Задача
определения дискретного логарифма элемента конечной
группы может быть легко решена, если
порядок группы не слишком велик и для
этой группы составлена таблица индексов.
При отыскании логарифма положительного
действительного числа, если нет таблицы
логарифмов или она недоступна, можно
воспользоваться методом последовательного
приближения. Он состоит в следующем. На
каждом шаге применения этого метода
интервал границ значения арифметического
логарифма сужают вдвое. Так продолжая,
легко определить значение этого логарифма
с любой заранее объявленной точностью.
Алгоритм перебора — метод, который хотя
бы теоретически может всегда привести
к успеху. Он состоит в следующем. Пусть b —примитивный элемент
данного конечного поля и a — другой какой-нибудь
элемент того же поля. Чтобы найти indba,
начиная, например, с п = 0, сравниваем элемент а с
элементом bn, если a = bn,
то indba = п, в противном случае
находим bп+1 = bn • b и опять сравниваем
элемент а с
элементом bп+1 и т. д. Если число
элементов поля 2100 или больше, то количество операций
(умножений), необходимое для вычисления
дискретною логарифма произвольного
элемента конечного поля в приемлемое
время, чрезвычайно велико и находится
за пределами возможностей современных
вычислительных машин.
д. Если число
элементов поля 2100 или больше, то количество операций
(умножений), необходимое для вычисления
дискретною логарифма произвольного
элемента конечного поля в приемлемое
время, чрезвычайно велико и находится
за пределами возможностей современных
вычислительных машин.
Теорема 1. Пусть t, r — натуральные числа, r2 t . Для любого целого l можно указать целые числа х и у такие, что
Доказательство. Можем предполагать, что. Полагаем
Имеем
С другой стороны.
поэтому
или
Теорема 2. Пусть G = < G, , 1 > —конечная группа; а и b элементы группы G; t = ord b;
(1. 2)
2)
Тогда число l можно найти, выполнив не более чем операции умножения на элементы группы
G.Доказательство. Полагаем . Рассмотрим ряды
(1.3)
(1.4)
Если разрешимо относительно l, представим l ввиде
Так как t = ord b, то b‘ = bxr+y = а в том и только в том случае, когда
, (1.5)
т.е. когда найдется элемент ряда (1.3), который совпадет с каким-нибудь членом ряда (1.4).
Нетрудно сосчитать число операций, позволяющих установить равенство (1.2). При вычислении элементов ряда (1.3) потребуется выполнить не более r-2 умножений. Для вычисления в силу следующей леммы
логарифмический калькулятор с основанием 3 | Icalc – онлайн-калькуляторы
Log Base 3 Calculator (Калькулятор логарифма 3) находит результат функции логарифмирования по основанию 3; Вычислить логарифмическое основание 3 числа.
Что такое номер
Согласно Log Base 3 Calculator:
Список log 3 таблицы значений функций, log base 3 чисел.
Логарифмическая база 3 из 1 = логарифмическая 3 (1) = 0,0000000000
База 3 из 2 = 3 (2) = 0,6309297536
База 3 из 3 = 3 (3) = 1,00000000000 1 лог. (4) = 1,2618595071
Основание логарифма 3 из 5 = логарифм 3 (5) = 1,4649735207
Основание логарифма 3 из 6 = логарифм 3 (6) = 1,6309297536
7) = 1,7712437492
Логарифмическая база 3 из 8 = логарифм 3 (8) = 1,8927892607
Логарифмическая база 3 из 9 = логарифм 3 (9) = 2,0000000000
Основание логарифма 3 из 10 = 3 (10) = 2,095
Основание логарифма 3 из 11 = 3 (11) = 2,1826583386
Основание 3 из 120 2.2618595071
Bog Base 3 из 13 = log 3 (13) = 2,3347175195
Bog Base 3 из 14 = Log 3 (14) = 2,4021735027
BASE 3 из 15 = LOG 3 (15) = 2,4677735079679679679679677507967967967750796796679679679677507
967
9679679667
9679679679679679679679679679679679679667
79 Логарифмическая база 3 из 16 = логарифм 3 (16) = 2,52371
Логарифмическая база 3 из 17 = логарифм 3 (17) = 2,57832
Log Base 3 of 18 = log 3 (18) = 2.
 6309297536
6309297536 Log Base 3 of 19 = log 3 (19) = 2.6801438592
Log Base 3 of 20 = log 3 (20) = 2.7268330279
Основание логарифма 3 из 21 = логарифм 3 (21) = 2,7712437492
Основа логарифма 3 из 22 = логарифм 3 (22) = 2,8135880922
3 из 24 = log 3 (24) = 2,8927892607
Log Base 3 из 25 = log 3 (25) = 2,9299470414
Bog Base 3 из 26 = log 3 (26) = 2,9656472730
Bog Base 3 из 27 = log 3 (27) = 3,000000000000
Log Base 3 из 28 = log 3 (28) = 3,03310322563
66666 3 (28) = 3,0331032563
666666666666666669. База журнала 3 из 29 = логарифм 3 (29) = 3,0650447521
База логарифма 3 из 30 = логарифм 3 (30) = 3,09543
База логарифма 3 из 31 = логарифм 3 9057 9 лог. 3 из 32 = log 3 (32) = 3,1546487679
Log Base 3 из 33 = log 3 (33) = 3,1826583386
Bog Base 3 из 34 = log 3 (34) = 3,2098316767
Log Base 3 из 35 = log 3 (35) = 3,2362172699
Bog Base 3 из 36 = log 3 (36) = 3,2611859171
699 = log 3 (36) = 3,2611859171
6919
6919
66919 = log 3 (36) = 3,2611859171
919
6919.
 Основание 3 из 37 = log 3 (37) = 3,2867991282
Основание 3 из 37 = log 3 (37) = 3,2867991282 Основание 3 из 38 = log 3 (38) = 3,3110736128
из 40 = log 3 (40) = 3,3577627814
Log Base 3 из 41 = log 3 (41) = 3,3802389660
Bog Base 3 из 42 = log 3 (42) = 3,4021735027
Log Base 3 из 43 = log 3 (43) = 3,4235918845
. База 3 из 45 = log 3 (45) = 3,4649735207
Лог. База 3 из 46 = log 3 (46) = 3,4849795838
Лог. База 3 из 47 = log 3 (474) = 50 из 48 = log 3 (48) = 3,52371
Log Base 3 из 49 = log 3 (49) = 3,5424874983
Bog Base 3 из 50 = log 3 (50) = 3,5608767950
Log Base 3 из 51 = log 3 (51) = 3,57832
Bog Base 3 из 52 = log 3 (52) = 3,59657702669 3 . Основание 3 из 53 = log 3 (53) = 3,6139154409
Лог. База 3 из 54 = log 3 (54) = 3,6309297536
Лог.
 из 56 = log 3 (56) = 3,6640330099
из 56 = log 3 (56) = 3,6640330099 Log Base 3 из 57 = log 3 (57) = 3,6801438592
Bog Base 3 из 58 = log 3 (58) = 3,6959745057
Log Base 3 из 59 = log 3 (59) = 3,7115345295
Bog Base 3 из 60 = log 3 (60) = 3,726833333999
666666669
66666669
666669
66669
6669
69
669
669
69
69
69
69 3 (60). Основа журнала 3 из 61 = логарифм 3 (61) = 3,7418786469
3 из 64 = log 3 (64) = 3,7855785214
Log Base 3 из 65 = log 3 (65) = 3,7996
2
Bog Base 3 из 66 = log 3 (66) = 3,8135880922
Log Base 3 из 67 = log 3 (67) = 3,8272761581
. База 3 из 69 = log 3 (69) = 3,8540498302
Лог. База 3 из 70 = log 3 (70) = 3,8671470235
Лог. База 3 из 71 = log 3 906 30 Лог. из 72 = log 3 (72) = 3,8927892607
Log Base 3 из 73 = log 3 (73) = 3,44836
Bog Base 3 из 74 = log 3 (74) = 3,9177288818
Log Base 3 из 75 = log 3 (75) = 3,9299470414
Bog Base 3 из 76 = log 3 (76) = 3,94200336666 = log 3 (76) = 3,942003366666666666666 3 (76) = 3,94200366666. Основание 3 из 77 = log 3 (77) = 3,953
Основание 3 из 77 = log 3 (77) = 3,953
Лог. Основание 3 из 78 = log 3 (78) = 3,9656472730
Лог. из 80 = log 3 (80) = 3,9886925350
Log Base 3 из 81 = log 3 (81) = 4,0000000000
Bog Base 3 из 82 = log 3 (82) = 4,0111687196
Log Base 3 из 83 = log 3 (83) = 4,0222020574
Log Base 3 из 84 = log 3 (84) = 4,033113132563
66666666666666. База 3 из 85 = log 3 (85) = 4,0438754439
Лог. База 3 из 86 = log 3 (86) = 4,0545216381
Лог. База 3 из 87 = log 3
6 лог. из 88 = log 3 (88) = 4,0754475994
Log Base 3 из 89 = log 3 (89) = 4,0857328978
Bog Base 3 из 90 = log 3 (90) = 4,09543
Log Base 3 из 91 = log 3 (91) = 4,1059612686
. База 3 из 93 = log 3 (93) = 4,1257498573
Лог База 3 из 94 = log 3 (94) = 4,1354851290
Лог База 3 из 95 = log 35 (851) 70 из 96 = log 3 (96) = 4,1546487679
Log Base 3 из 97 = log 3 (97) = 4,1640813831
Bog Base 3 из 98 = log 3 (98) = 4,1734172519
Log Base 3 из 99 = log 3 (99) = 4,1826583386
Bog Base 3 из 100 = log 3 (100) = 4,191866486 2 3 (100) = 4,1918664869 29639963963 9000 3 .

Примеры расчетов, которые вы можете выполнить с помощью нашего калькулятора логарифмической базы 3:
Согласно калькулятору логарифмической базы 3 — логарифмическая база 3 из 7 равна 1,7712437492
Согласно логарифмической базе 3 калькулятора 1 логарифмическая база 3 составляет 2,57832
Согласно калькулятору логарифмической базы 3 — логарифмическая база 3 из 27 составляет 3,0000000000
Согласно калькулятору логарифмической базы 3 — логарифмическая база 3 из 37 равна 3,2867991282
Согласно калькулятору логарифмической базы 3 — логарифмическая база 3 из 47 равна 3,5045553754
© Get1, Nezikist Group Ltd.
Нажмите Enter для поиска
Войти
Запомнить меня
Нажмите Enter для поиска
- Калькуляторы
Калькулятор логарифмов
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Обычный логарифм — это логарифм с основанием 10, также известный как десятичный логарифм или десятичный логарифм. В то время как натуральный логарифм является основанием с математической константой «е», которая приблизительно равна 2,718281828459
Обычный логарифм — это логарифм с основанием 10, также известный как десятичный логарифм или десятичный логарифм. В то время как натуральный логарифм является основанием с математической константой «е», которая приблизительно равна 2,718281828459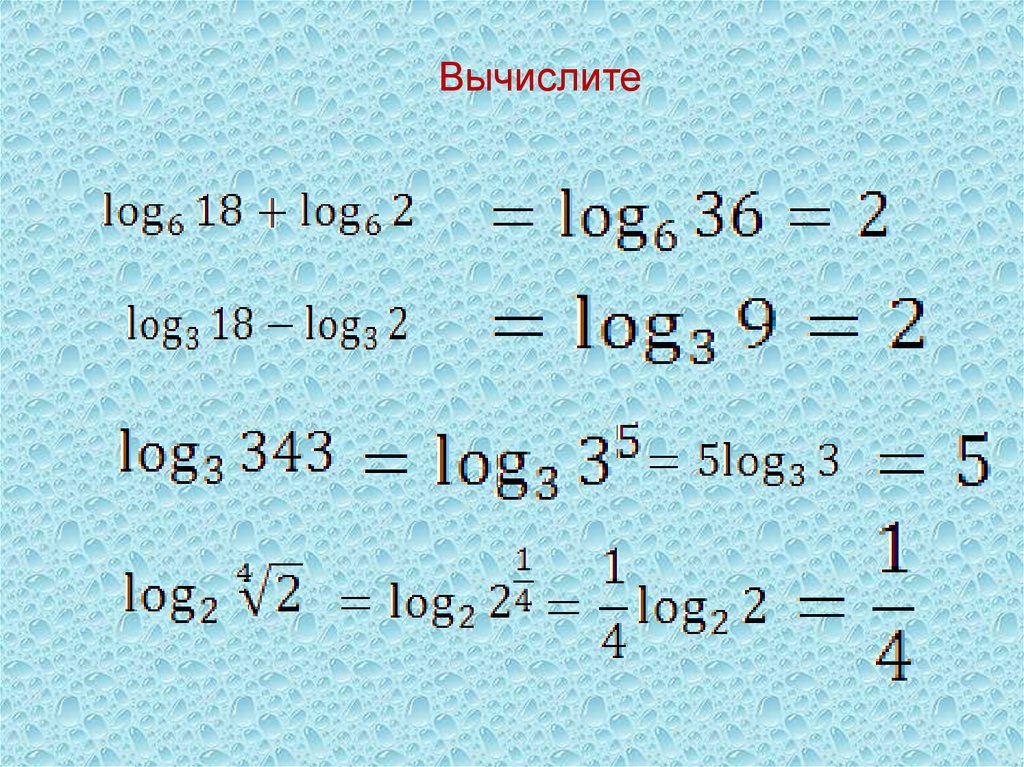 ..
.. Методы контроля над рождаемостью
Методы контроля над рождаемостью ..
.. ..
..
 Впрочем, об этом математическом понятии все слышали в средней школе (алгебре), если не раньше. В алгебре вы узнаете о логарифмических функциях. Например, давайте посмотрим на пример ниже:
Впрочем, об этом математическом понятии все слышали в средней школе (алгебре), если не раньше. В алгебре вы узнаете о логарифмических функциях. Например, давайте посмотрим на пример ниже: {y})
{y})
