Калькулятор среднего с шагами — онлайн и бесплатно!
Калькулятор среднего с шагами — онлайн и бесплатно!Рассчитать среднее Рассчитать медиану Рассчитать интеграл Рассчитать предел
Рассчитать среднее значение
Введите или вставьте сюда свой набор чисел
Неправильный ввод
Общее:
Иметь в виду:
Калькулятор среднего значения
Добавить в закладки
Добавьте калькулятор среднего значения в закладки вашего браузера
1. Для Windows или Linux — нажмите Ctrl + D .
2. Для MacOS — нажмите Cmd + D .
3. Для iPhone (Safari) : Нажмите и удерживайте , затем нажмите Добавить закладку .
4. Для Google Chrome : нажмите 3 точки в правом верхнем углу, затем нажмите знак звездочки .
Как использовать?
Как пользоваться калькулятором среднего значения
1Шаг 1
Введите на клавиатуре или вставьте из буфера обмена свой набор чисел. Цифры следует разделять запятыми.
2Шаг 2
Нажмите кнопку Рассчитать. Результат моментально отобразится на экране.
3Шаг 3
Теперь вы можете скопировать результат в буфер обмена.
Что такое среднее в математике
Среднее значение в математике — это, пожалуй, самый распространенный способ вычисления среднего значения. Его часто используют в статистических исследованиях, а также в повседневной жизни. Если вы спросите многих людей, как рассчитать среднее значение, большинство запомнит именно это.
Как рассчитать среднее значение. Это наиболее знакомый вам способ вычисления среднего значения комбинации чисел, который вы, вероятно, часто использовали в прошлом. Формула очень проста — вы складываете все заданные числа (вычисляете арифметическую сумму) и делите результат на количество чисел.
Пример расчета среднего
Возьмем следующий набор чисел: 3, 9, 2, 5, 7, 8. Чтобы найти среднее значение этого набора чисел, вам нужно применить простую формулу. Сначала вы суммируете все числа. 5 + 11 + 3 + 6 + 8 + 9 = 42. Теперь вам нужно посчитать, сколько чисел в строке: это 6. Последнее, что нужно сделать, это разделить сумму на количество чисел: 42 / 6 = 7. Итак, 7 — это Среднее значение текущего набора данных.
Почему вам может понадобиться вычислить среднее значение
Расчет среднего значения очень распространен и широко используется.
Как найти среднее арифметическое число в Excel
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:h2 и нажимаем ВВОД.
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
- Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:h2). Результат:
Формула: =СРЗНАЧ(A1:B1;F1:h2). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)
Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Вычислить среднее значение группы чисел
Excel
Формулы и функции
Формулы
Формулы
Вычислить среднее значение группы чисел
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно. .. Меньше
.. Меньше
Предположим, вы хотите найти среднее количество дней, затрачиваемое на выполнение задачи разными сотрудниками. Или вы хотите рассчитать среднюю температуру в определенный день за 10-летний период времени. Существует несколько способов вычисления среднего значения группы чисел.
Функция СРЗНАЧ измеряет центральную тенденцию, то есть положение центра группы чисел в статистическом распределении. Тремя наиболее распространенными мерами центральной тенденции являются:
Среднее Это среднее арифметическое, которое рассчитывается путем сложения группы чисел и последующего деления на количество этих чисел. Например, среднее число 2, 3, 3, 5, 7 и 10 равно 30, делённому на 6, что равно 5.
Медиана Среднее число группы чисел.
 Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы. Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.
Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы. Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.Режим Самое часто встречающееся число в группе чисел. Например, режим 2, 3, 3, 5, 7 и 10 равен 3.
Для симметричного распределения группы чисел все эти три меры центральной тенденции одинаковы. При асимметричном распределении группы чисел они могут быть разными.
Выполните следующие действия:
Щелкните ячейку ниже или справа от чисел, для которых вы хотите найти среднее значение.
На Вкладка Главная в группе Редактирование щелкните стрелку рядом с Автосумма , выберите Среднее и нажмите клавишу ВВОД.
Для выполнения этой задачи используйте функцию СРЗНАЧ . Скопируйте приведенную ниже таблицу на пустой рабочий лист.
Формула | Описание (Результат) |
=СРЕДНЕЕ(A2:A7) | Усредняет все числа в списке выше (9.5) |
=СРЕДНЕЕ(A2:A4,A7) | Усредняет первые три и последний номер в списке (7. |
=СРЗНАЧЕСЛИ(A2:A7, «<>0″) | Усредняет числа в списке, кроме тех, которые содержат ноль, например ячейка A6 (11.4) |
Для выполнения этой задачи используйте функции СУММПРОИЗВ и СУММ . vВ этом примере вычисляется средняя цена, уплаченная за единицу по трем покупкам, где каждая покупка предназначена для разного количества единиц по разной цене за единицу.
Скопируйте приведенную ниже таблицу на пустой рабочий лист.
|
|
Для выполнения этой задачи используйте функции СРЗНАЧ и ЕСЛИ . Скопируйте приведенную ниже таблицу и помните, что этот пример может быть легче понять, если вы скопируете его на пустой лист.
Скопируйте приведенную ниже таблицу и помните, что этот пример может быть легче понять, если вы скопируете его на пустой лист.
Формула | Описание (Результат) |
=СРЗНАЧЕСЛИ(A2:A7, «<>0″) | Усредняет числа в списке, кроме тех, которые содержат ноль, например ячейка A6 (11.4) |
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
СРЕДНИЙ
СРЕДНЕЕСЛИ
СУММА
СУММПРОДУКТ
Калькулятор средних значений
Создано Mateusz Mucha
Отзыв от Jack Bowater
Последнее обновление: 12 декабря 2022 г.
- Как рассчитать среднее
- Часто задаваемые вопросы
Калькулятор среднего вычисляет среднее значение до тридцати чисел . Интересным аспектом калькулятора является то, что вы можете видеть, как среднее значение изменяется по мере ввода дополнительных значений. Прежде чем использовать калькулятор, вы должны знать, как рассчитать среднее значение, на тот случай, если у вас нет Интернета и вы не можете получить доступ к этому калькулятору. Обратите внимание, что среднее значение такое же, как среднее , и мы можем использовать эти термины взаимозаменяемо.
🙋 Существуют также различные методы оценки среднего значения. Наш калькулятор среднего геометрического поможет вам понять концепцию среднего геометрического и оценить результат за секунду.
Как вычислить среднее значение
Среднее значение набора чисел — это просто сумма чисел, деленная на общее количество значений в наборе. Например, предположим, что нам нужно среднее 24 , 55 , 17 , 87 и 100 . Просто найдите сумму чисел:
Просто найдите сумму чисел: 24 + 55 + 17 + 87 + 100 = 283 и разделите на 5 , чтобы получить 56,6 . Простую задачу, подобную этой, можно решить вручную без особых проблем, но для более сложных чисел, включающих много знаков после запятой, удобнее использовать этот калькулятор. Обратите внимание, что калькулятор среднего рейтинга выполняет аналогичную математику — он вычисляет средний рейтинг, учитывая количество голосов со значениями от 1 до 5.
Аналогичные концепции, связанные со средними значениями
Калькулятор средневзвешенного значения позволяет присвоить вес каждому числу. Взвешивание числа является показателем его важности. Распространенным типом вычисляемого средневзвешенного значения является средний балл успеваемости (GPA). Проверьте наш специальный калькулятор GPA для получения более подробной информации. Чтобы сделать это вручную, выполните следующие действия:
- Умножьте значение буквенной оценки на количество кредитов в классе.

- Сделайте это для всех классов и подсчитайте сумму.
- Разделите сумму на общее количество кредитов.
Предположим, что оценки представляют собой A для кредитного класса 3 , две B для кредитного класса 4 и C для кредитного класса 2 . Используя стандартное значение 4 для A, 3 для B и 2 для C, средний балл составляет GPA = [4(3) + 3(4) + 3(4) + 2(2)]/(3 + 4 + 4 + 2) = 40/13 = 3,08
Обратите внимание, что калькулятор среднего вычисляет среднее значение для всех значений с одинаковым весом, в отличие от инструментов, связанных выше. В статистике мы рассматриваем среднее значение как меру центральной тенденции.
Часто задаваемые вопросы
Каковы 4 средние значения?
Четыре средних значения — это среднее значение, медиана, мода и диапазон . Среднее значение 90 328 — это то, что вы обычно считаете средним значением 90 329, найденное путем суммирования всех значений и деления суммы на количество значений. Медиана 90 328 — это среднее значение 90 329 набора (или среднее двух средних значений, если набор четный). Режим — это часть данных, которая встречается чаще всего , а диапазон — это разница между самым высоким и самым низким значениями .
Медиана 90 328 — это среднее значение 90 329 набора (или среднее двух средних значений, если набор четный). Режим — это часть данных, которая встречается чаще всего , а диапазон — это разница между самым высоким и самым низким значениями .
Почему мы считаем среднее?
Мы рассчитываем средние значения, потому что они очень полезны для представления большого количества данных . Вместо того, чтобы просматривать сотни или тысячи фрагментов данных, у нас есть одно число, которое кратко суммирует весь набор . Несмотря на некоторые проблемы со средними значениями, например выбросы, показывающие неточное среднее значение, они полезны для быстрого сравнения данных .
Почему средние значения вводят в заблуждение?
Средние значения могут вводить в заблуждение по ряду причин . Они лучше всего представляют равномерно распределенные кривые нормального распределения , где большинство результатов находятся в середине и несколько на концах. Но даже одна очень крайняя точка может резко изменить среднее , поэтому эти аномалии часто исключаются, но не всегда. Далее, люди склонны интерпретировать средние значения как идеальные представления , что приводит к отсутствию желания понимать нюансы данных. Наконец, мы часто используем средние значения для предсказания отдельных случаев, которые часто крайне неточны .
Но даже одна очень крайняя точка может резко изменить среднее , поэтому эти аномалии часто исключаются, но не всегда. Далее, люди склонны интерпретировать средние значения как идеальные представления , что приводит к отсутствию желания понимать нюансы данных. Наконец, мы часто используем средние значения для предсказания отдельных случаев, которые часто крайне неточны .
Как рассчитать средний балл?
Чтобы рассчитать среднюю оценку:
- Умножьте каждую оценку на кредиты или вес, присвоенный ей . Если ваши оценки не взвешены, пропустите этот шаг.
- Сложите вместе все взвешенные оценки (или только оценки, если взвешивания нет).
- Разделите сумму на количество сложенных оценок.
- Полученное частное является вашей окончательной средней оценкой.
Как рассчитать средневзвешенное значение?
Чтобы вычислить средневзвешенное значение:
- Умножьте каждое число на его вес .

- Сложите все взвешенные числа вместе.
- Разделите сумму на количество точек данных.
- Полученное частное является средневзвешенным.
Среднее лучше режима?
нет простого ответа на вопрос, лучше ли среднее значение, чем режим — это полностью зависит от данных установленных перед вами. Если данные нормально распределены и не имеют выбросов, то вам, вероятно, следует использовать среднее значение , так как оно представит вам наиболее репрезентативное значение. Однако режим более надежен, чем , и будет представлять наиболее распространенное значение независимо от каких-либо выбросов. Этот режим следует всегда использовать с категориальными данными, т. е. данными с отдельными группами, поскольку группы не являются непрерывными.
Как рассчитать средний процент в Excel?
Хотя проще использовать Omni Average Calculator, для расчета среднего процента в Excel:
- Введите нужные данные, например, из ячеек с A1 по A10.

- Выделите все ячейки, щелкните правой кнопкой мыши и выберите Формат ячеек .
- В поле Format Cells под Number выберите Percentages и укажите желаемое количество знаков после запятой.
- В другой ячейке введите =СРЗНАЧ(ячейка 1, ячейка 2,…) . В нашем примере это будет =СРЗНАЧ(A1:A10).
- Наслаждайтесь средними показателями!
Можете ли вы усреднить средние значения?
Вы можете усреднять средние значения, но это часто очень неточно и должно быть сделано осторожно. Допустим, у вас есть две страны: одна с населением 10 миллионов человек и ВВП 30 000 долларов, а другая — 10 000 человек и ВВП 2 000 долларов. Средний ВВП на страну составляет 16 000 долларов США, а средний ВВП на человека составляет ~ 30 000 долларов США, оба совершенно разные цифры, показывающие совершенно разные вещи — так что будьте осторожны.
Что лучше, среднее или медиана?
Следует ли вам использовать среднее значение или медиану, будет зависеть от данных, которые вы анализируете . Если данные имеют нормальное распределение и не имеют выбросов, то вам, вероятно, следует использовать среднее значение , хотя значение будет очень похоже на значение медианы. Если данные 90 328 сильно искажены, следует использовать медиану 90 329, поскольку выбросы меньше влияют на нее.
Является ли среднее значение точным?
Среднее из средних неточно — в большинстве случаев . Данные могут быть вводящими в заблуждение из-за двух основных факторов, скрытых переменных и средневзвешенных . Скрытые переменные — это то место, где при усреднении средних значений часть информации теряется , что обеспечивает более глубокое понимание рассматриваемой темы. Другая проблема заключается в том, что не взвешивает средние значения, когда это необходимо .

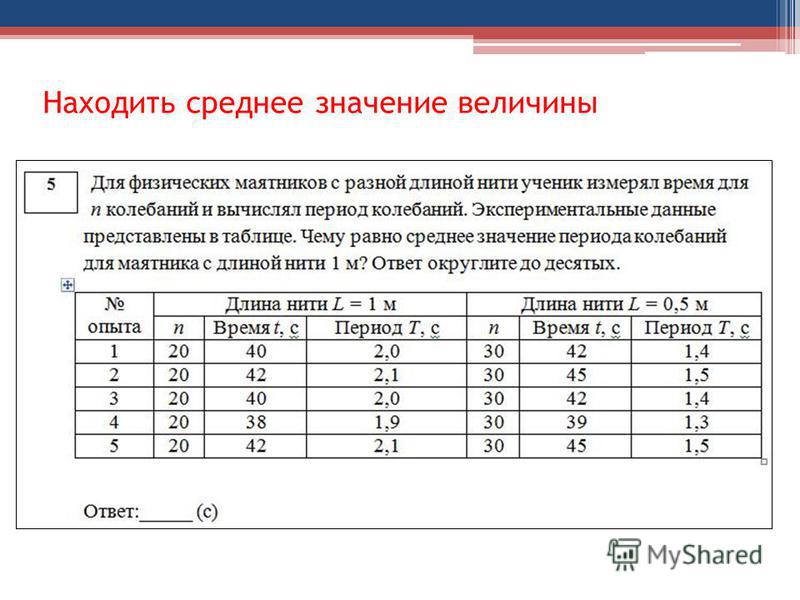 Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы. Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.
Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы. Например, медиана 2, 3, 3, 5, 7 и 10 равна 4. 5)
5)

