Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. 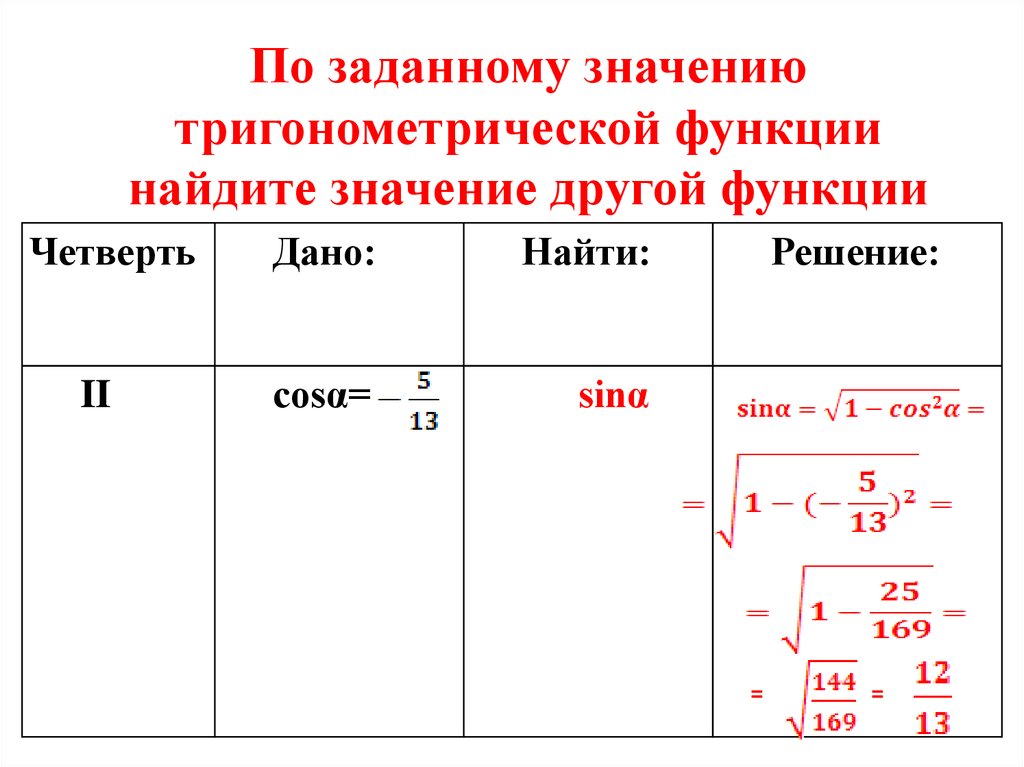 СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4.  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Выражение тригонометрических функций через тангенс половинного аргумента | План-конспект занятия:
Технологическая карта практического занятия
Название УД, ПМ, раздела, МДК: Математика
Специальность, группа: 09.02.07 Информационные системы и программирование, 14 группа
Тема занятия: Выражение тригонометрических функций через тангенс половинного аргумента
Цели занятия:
1) образовательная: организовать деятельность студентов по изучению и первичному закреплению основных формул суммы тригонометрических функций в произведение и произведения в сумму;
2) воспитательная: воспитывать самостоятельность, информационную компетентность;
3) развивающая: развивать внимание, память, познавательный интерес к учебной дисциплине.
Учебные цели:
• обеспечение сформированности представлений о социальных, культурных и исторических факторах становления математики;
• обеспечение сформированности логического, алгоритмического и математического мышления;
• обеспечение сформированности умений применять полученные знания при решении различных задач;
предметных:
сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;
сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
метапредметных:
умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
Умение организовать собственную деятельность, определение методов и способов выполнения профессиональных задач, оценивание их эффективности и качества.
Уровень освоения: 1,2.
Междисциплинарные связи: истоки, выход
Материально-техническое оснащение: ПК, презентация, проектор, интерактивна доска.
Учебно-методическое оснащение: рабочая программа, презентация, КТП, технологическая карта урока, практическая работа.
Этапы и хронология занятия (90 мин):
Этапы занятия | Время | Содержание занятия |
1.Организационный момент | 2 мин | Приветствие, отметка отсутствующих, контроль готовности аудитории и студентов к началу занятия. |
2. Проверка домашнего задания | 2 мин | Колмагоров 10-11 клас «Алгебра, начала математического анализа» 14 (в,г) |
3. | 1 мин | Сообщение темы, целей, хода занятия, указание на важность темы. |
4.Практическая работа | 40 мин | Задания Колмагоров 10-11 клас «Алгебра, начала математического анализа» |
5. Самостоятельная работа | 40 мин | Раздаточный материал |
6.Подведение итогов | 4 мин | Выставление оценок за выполнение практической работы. |
7.Задание на дом | 1 мин | № 20 |
Формулировка темы, ее мотивацияСписок использованной литературы и Интернет-ресурсов:
1.
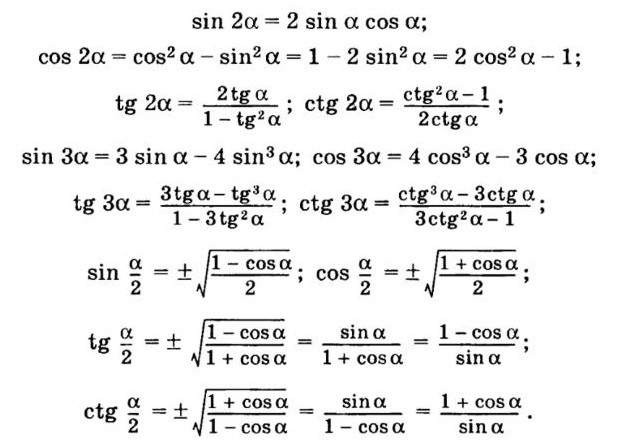Колмагоров А.Н. и др, Алгебра 10-11 класс. – М.: 2013 г.
2. Алимов Ш. А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10-11 классы. — М., 2014.
3. Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. — М., 2014.
4. Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. Пособие для студ. учреждений сред. проф. образования. — М., 2014.
5. Башмаков М. И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф.образования. — М., 2014.
ФИО и подпись преподавателя _____________ Дуракова Т.М.
Как использовать тождества половинного угла для оценки триггерной функции
Вы можете использовать тождества половинного угла для оценки триггерной функции угла, который не находится на единичной окружности, используя тот, который находится. Например, 15 градусов, не лежащие на единичной окружности, составляют половину от 30 градусов, лежащих на единичной окружности.
Разрезание пополам специальных углов на единичном круге дает множество новых углов, которые нельзя получить с помощью формул суммы и разности или формул двойного угла. Хотя формулы половинного угла не дадут вам всех углов единичного круга, они, безусловно, сделают вас ближе, чем вы были раньше.
Хитрость заключается в том, чтобы знать, какой тип удостоверения лучше всего подходит для вашей цели. Формулы половинного угла являются лучшим вариантом, когда вам нужно найти триггерные значения для любого угла, который может быть выражен как половина другого угла на единичной окружности. Например, чтобы вычислить триггерную функцию числа пи/8, можно применить формулу половинного угла к числу пи/4. Поскольку никакая комбинация сумм или разностей специальных углов не даст вам число пи/8, вы знаете, как использовать формулу половинного угла.
Вы также можете найти значения триггерных функций для таких углов, как pi/12, каждый из которых составляет ровно половину угла на единичной окружности.
Конечно, эти ракурсы — не единственные типы, для которых работают тождества. Вы можете продолжать делить пополам любой угол на единичной окружности до конца своей жизни (если вам больше нечем заняться) и брать триггерные функции этих углов. Например, 15 градусов — это половина 30 градусов, а 7,5 градуса — половина 15 градусов.
Формулы половинного угла для синуса, косинуса и тангенса следующие:
Обратите внимание, что в формуле половинного угла для синуса и косинуса перед каждым радикалом (квадратный корень) появляется знак плюс/минус. Будет ли ваш ответ положительным или отрицательным, зависит от того, в каком квадранте находится новый угол (половина угла). Формула половинного угла для тангенса не имеет знака плюс/минус впереди, поэтому вышеизложенное не относится к тангенсу. .
Например, чтобы найти sin 165º, выполните следующие действия:
Перепишите триггерную функцию и угол как половину значения единичного круга.
Сначала поймите, что 165 градусов — это половина от 330 градусов, поэтому вы можете переписать функцию синуса как sin(330/2).
Определите знак триггерной функции.
Поскольку 165 градусов находится в квадранте II координатной плоскости, его значение синуса должно быть положительным.
Подставьте значение угла в правильное тождество.
Значение угла 330 градусов подставляется для x в формуле положительного полуугла для синуса. Это дает вам
Замените cos x его фактическим значением.
Используйте единичный круг, чтобы найти cos 330 градусов. Подставив это значение в уравнение, вы получите
.Упростите формулу половинного угла для решения.
Этот подход состоит из трех шагов:
Найдите общий знаменатель двух верхних дробей (включая 1/1), чтобы получить
Используйте правила деления дробей, чтобы получить
Наконец, нижний квадрат упрощается до 2, и в итоге получается
.
Эту статью можно найти в категории:
- Предварительное вычисление,
Формулы половинного и двойного угла
Автор: преподаватель Майкл Б.
Цель
В этом разделе вы познакомитесь с формулами, устанавливающими взаимосвязь между основными тригонометрическими величинами
(sin, cos, tan) для конкретного угла и тригонометрические значения
для угла, который в два раза больше или в половину меньше первого угла. Эти соотношения могут быть очень полезны в доказательствах, а также при решении задач, поскольку их часто можно использовать для упрощения уравнения.
Формулы двойного угла
Имея тригонометрические значения угла α, мы хотели бы определить тригонометрические значения
для другого угла 2α: α, и используя тригонометрический
формулы суммирования. Вспомним три формулы суммирования:
Из них мы можем вывести формулы двойного угла для sin(2α), cos(2α) и tan(2α): Кроме того, формула cos(2α) имеет две альтернативные, но распространенные формы. Используя тождество sin 2 (α) + cos 2 (α) = 1, мы также можем вывести две формулы:
Также важно отметить, что следующие соотношения0079 НЕ верно:
Формулы половинного угла
Как и в случае с формулами двойного угла, при наличии тригонометрических значений угла α мы хотели бы иметь возможность определить тригонометрические значения
для другого угла α/2:
Находя sin и cos из альтернативных форм cos(2α), а затем подставляя α = α/2, мы получаем:
Обратите внимание на эти два уравнения.
Обычно, когда вы видите символ «±» в математических уравнениях, это обычно означает использование и положительный и отрицательный ответ. Например, в квадратном уравнении есть два ответа — один для положительной версии и один для отрицательной версии радикала. Однако в этом случае следует выбрать только один ответ (либо положительный , либо отрицательный ). Выбор не является произвольным — учащийся должен использовать информацию, доступную в заданной задаче, чтобы определить, какой ответ является правильным. Обычно это делается путем определения того, в каком квадранте находится угол α/2, поскольку знак каждой тригонометрической функции строго определяется квадрантом угла (ASTC).
Формула касательной половины угла также имеет три версии, которые могут быть полезны в различных сценариях:
Примеры
Пример #1
Дан угол, для которого sin(α) = -3/5 в квадранте III , определите значения для sin(2α), cos(2α), tan(2α), sin(α/2), cos(α/2) и tan(α/2).