404 Cтраница не найдена
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Python 3.
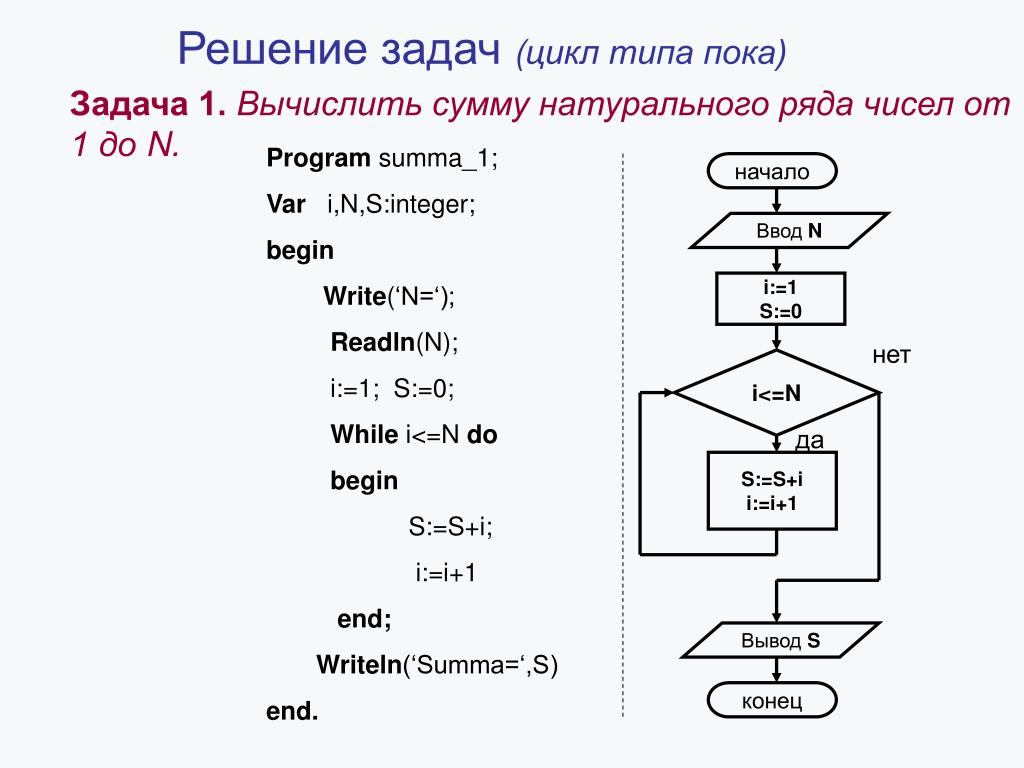 Организация циклов | Информационные технологии
Организация циклов | Информационные технологииУчебные программы » Информационные технологии » Программирование » Python 3. Организация циклов
Задача: Напишите программу, которая вводит два целых числа и находит их произведение, не используя операцию умножения. Учтите, что числа могут быть отрицательными.
Решение
a, b = map(int, input().split()) res, s = 0, 1 if bЗадача: Напишите программу, которая вводит натуральное число N и выводит первые N чётных натуральных чисел. Программа должна вывести в одну строчку N первых чётных натуральных чисел, разделив их пробелами.
Решение
n = int(input()) for i in range (1,2*n,2): print (i+1)Задача: Напишите программу, которая вводит натуральные числа a и b и выводит сумму квадратов натуральных чисел в диапазоне от a до b.
Решение
a, b = map(int, input().split()) if a > b: t = a a = b b = t s = 0 for i in range (a, b+1): s = s+i*i print (s)Задача: Напишите программу, которая вводит четыре натуральных числа (a, b, c и d) и находит все пятизначные числа, которые при делении на a дают в остатке b , а при делении на c дают в остатке d .
3
Напишите программу, которая находит все числа Армстронга на отрезке [a, b].Входные данные: Входная строка содержит два натуральных числа – значения a и b, разделённых пробелами. Гарантируется, что a ≤ b.
Выходные данные: Программа должна вывести в одну строчку все числа Армстронга на отрезке [a, b] , разделив их пробелами. Если таких чисел нет, программа должна вывести число -1.
Решение
x = input().split() a = int(x[0]) b = int(x[1]) ''' a = 100 b = 400 ''' if a > b: t = a a = b b = t if aЗадача: Напишите программу, которая считает количество чётных цифр введённого числа.
Решение
n = int(input()) n = int(n) k = 0 m = 0 while n>0: if n%2==0: k+=1 else: m+=1 n=n//10 print(k)Задача: Напишите программу, которая определяет, верно ли, что введённое число содержит две одинаковых цифры, стоящие рядом (как, например, 221).
Решение
n = int(input()) res = "NO" d1 = 0 d2 = 0 while n > 0: d1 = n%10 d2 = n//10%10 if d1 == d2: res = "YES" n = n//10 print (res)Задача: Напишите программу, которая определяет, верно ли, что введённое число содержит по крайней мере две одинаковых цифры, возможно, не стоящие рядом (как, например, 212).
Программа должна вывести слово 'YES', если в числе есть две одинаковые цифры, и слово 'NO', если такой пары цифр нет.
Решение
n = int(input()) res = "NO" d1 = 0 d2 = 0 while n>0: d1 = n%10 m = n//10 while m > 0: d2 = m%10 if d1 == d2: res = "YES" m = m//10 n = n//10 print (res)Задача: Модифицированный алгоритм Евклида для вычисления наибольшего общего делителя двух натуральных чисел, формулируется так: нужно заменять большее число на остаток от деления большего на меньшее до тех пор, пока остаток не станет равно нулю; тогда второе число и есть НОД. Напишите программу, которая реализует этот алгоритм.
Входные данные: Входная строка содержит два числа, разделённые пробелом – a и b .
Выходные данные: Программа должна вывести в одной строке два числа: сначала наибольший общий делитель двух введённых чисел, а затем – количество шагов цикла, которые были выполнены.
Решение
x = input().split() #Python 3.x a = int(x[0]) b = int(x[1]) n = 0 while a!=0 and b!=0: if a > b: a = a % b else: b = b % a n+=1 print (a+b, n)
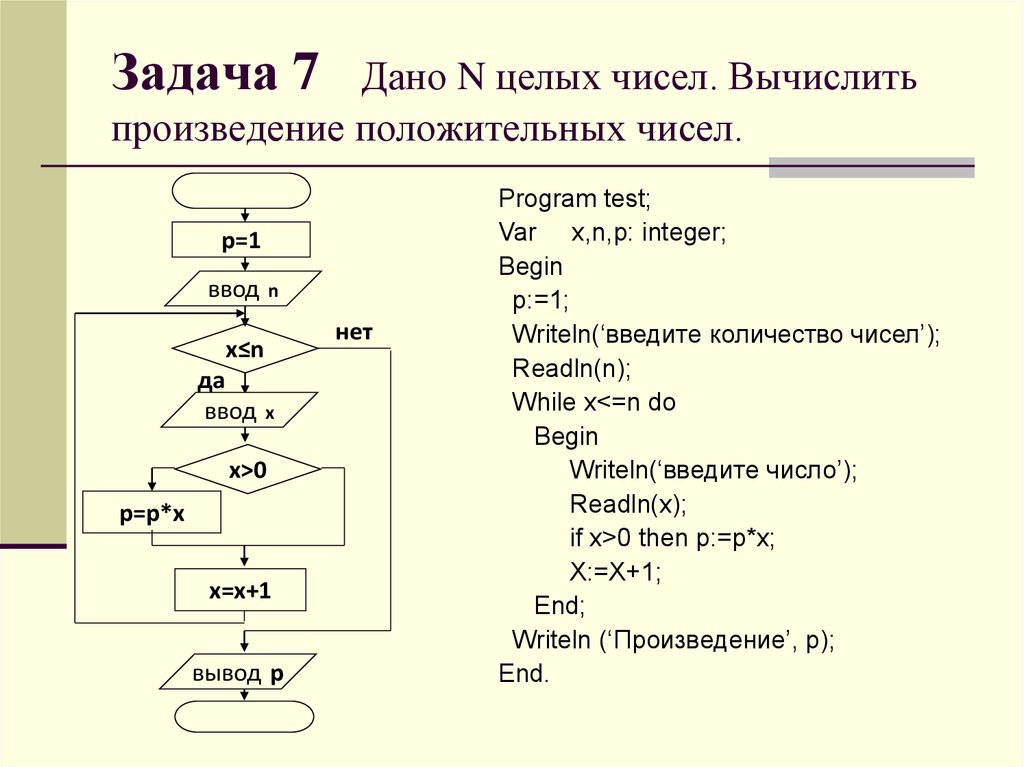
Задача: Напишите программу, которая вычисляет сумму и произведение целых чисел, поданных на её вход. Ввод заканчивается числом 0.
Входные данные: Во входных строках записаны целые числа, по одному в каждой строке. В последней строке записано число 0.
Выходные данные: Программа должна вывести в одной строке сумму и произведение введённых чисел (не считая завершающий 0), разделив их пробелом.
Решение
summ, mul = 0, 1 while 1: c = int(input()) if c == 0: break; summ += c mul *= c print (summ,mul)Задача: Напишите программу, которая вводит натуральное число N и определяет его факториал, то есть произведение натуральных чисел от 1 до N: N! = 1·2·{...}· N.
Решение
n = int(input()) f = 1 while n>1: f *= n n -= 1 print (f)Задача: Напишите программу, которая выводит на экран все цифры числа, начиная с первой.
Входные данные: Входная строка содержит натуральное число N.
Выходные данные: Программа должна вывести все цифры введённого числа в одной строке, начиная с первой. Цифры отделяются пробелами.
Решение
n = int(input()) res = "" while n>0: res = str(n%10)+ " " + res n = n//10 print (res.strip())Задача: Напишите программу, которая вводит натуральные числа a и b и выводит все простые числа в диапазоне от a до b. Входная строка содержит два натуральных числа: a и b. Гарантируется, что a ≤ b. Программа должна вывести в одной строке через пробел все простые числа на отрезке [a, b]. Если таких чисел нет, программа должна вывести 0.
Решение
x = input().split() a = int(x[0]) b = int(x[1]) if a == 0: a = 1 res = "" for i in range(a, b + 1): for j in range(2,i): if i%j == 0: break else: res = res + " " + str(i) if res != '': print (res) else: print (0)CC-BY-CA anonymous, 01.06.2017
|
ЗАДАЧИ ДЛЯ СРС 3Б курс. 
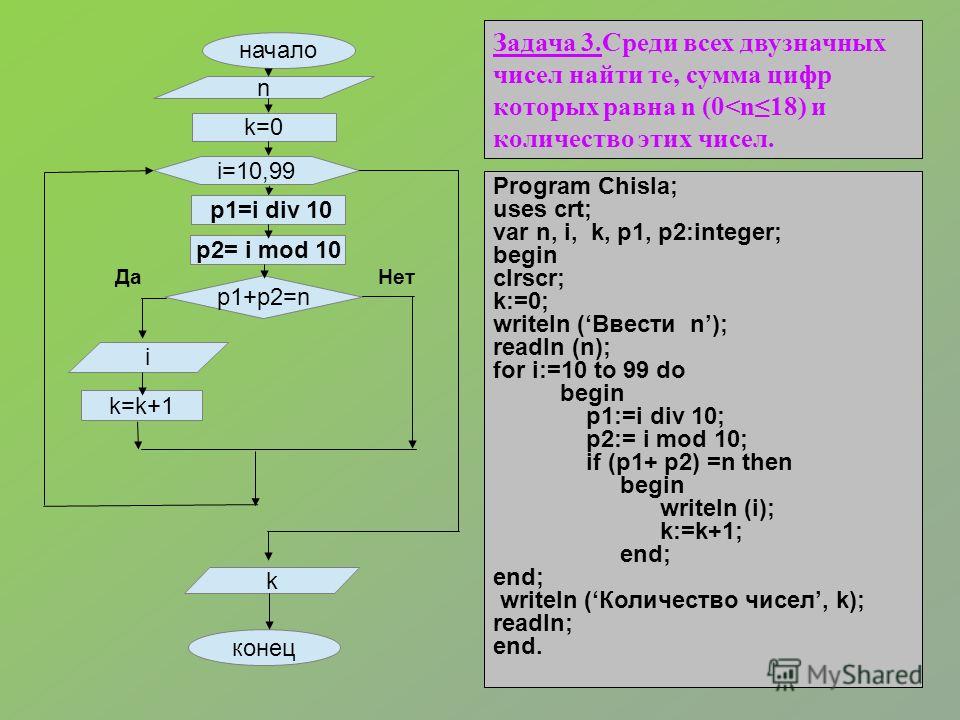
Найти двузначное число, равное сумме цифры его десятков и квадрата цифры единиц. Если к сумме цифр двузначного числа прибавить квадрат этой суммы, то снова получиться это двузначное число. Найти все такие числа. Квадрат трёхзначного числа оканчивается тремя цифрами, которые как раз составляют взятое число. Найти все такие числа. Найти четырёхзначное число, которое при делении на 133 даёт в остатке 125, а при делении на 134 даёт в остатке 111. Припишите к 523*** три такие цифры справа, чтобы полученное шестизначное число делилось на 7, на 8 и на 9 без остатка. Припишите к ***999 три такие цифры слева, чтобы полученное число делилось на 13, на 17 и на 19 без остатка. Найдите трёхзначное число, квадрат которого оканчивается тремя цифрами, отличными от нуля. Найдите четырёхзначное число, являющееся точным квадратом, у которого две первые цифры одинаковы и две последние тоже одинаковы. 
В магазине имеется мастика в ящиках по 16 кг, 17 кг, 21кг. Как некоторой организации получить 185 кг мастики, не вскрывая ящики? Найти все трёхзначные числа, равные сумме кубов своих цифр. В трёхзначном числе зачеркнули первую цифру слева; когда полученное число умножили на 7, получилось исходное трёхзначное число. Найдите его. В трёхзначном числе, все цифры которого нечетны, зачеркнули среднюю цифру. Оказалось, что полученное двузначное число является делителем исходного числа. Найдите всё такие трёхзначные числа. Сумма цифр трехзначного числа кратно 7. Найдите все такие числа. Четырехзначное число, а также число, записанное теми же цифрами в обратном порядке, оба являются точными квадратами. Найдите эти числа. Найдите все двузначные числа, сумма цифр которых не меняется при умножении числа на 2, 3, 4, 5, 6, 7, 8, 9.  2+n+41 является генератором простых чисел при целых n, кратных 41.Требуется доказать или опровергнуть это утверждение. 2+n+41 является генератором простых чисел при целых n, кратных 41.Требуется доказать или опровергнуть это утверждение.
26. Дано простое число. Найти и вывести на печать ближайшее к нему число. 27. Разработать программу поиска трех простых чисел, предшествующих числу М, заданному пользователем, причем М>= 10. 28. Разработать программу поиска и печати всех чисел – близнецов, принадлежащих заданному диапазону [N,M]. 29. Найти и вывести на экран 3 совершенных числа, больше некоторого М. 30. Дано натуральное число N. Найти и вывести на экран ближайшее к нему совершенное число. 31. Разработать программу поиска и печати всех пар дружественных чисел, меньших 10000. Примечание. Дружественными называются два натуральных числа, каждое из которых равно сумме делителей другого. Можно дать другое определение дружественных чисел: сумма всех делителей одного и другого такого числа равна сумме обоих чисел. 32. Найти и вывести на печать все четырехзначные, симметричные числа. Скачать 32,5 Kb. Поделитесь с Вашими друзьями: |
K-я сумма N чисел
| с0 | с1 | с2 | с3 | с4 | с5 | с6 | с7 | |
|---|---|---|---|---|---|---|---|---|
| р1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| р2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| р3 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
| р4 | 1 | 4 | 10 | 20 | 35 | 56 | 84 | 120 |
| р5 | 1 | 5 | 15 | 35 | 70 | 126 | 210 | 330 |
| р6 | 1 | 6 | 21 | 56 | 126 | 252 | 462 | 792 |
| р7 | 1 | 7 | 28 | 84 | 210 | 462 | 924 | 1716 |
| р8 | 1 | 8 | 36 | 120 | 330 | 792 | 1716 | 3432 |
| р9 | 1 | 9 | 45 | 165 | 495 | 1287 | 3003 | 6435 |
| р10 | 1 | 10 | 55 | 220 | 715 | 2002 | 5005 | 11440 |
С самого начала математики математики
интересует суммирование чисел. Для каждой заданной серии мы
может определить сумму этого определенного ряда. Изучая суммы рядов,
привел меня к некоторым довольно хорошим открытиям, которые я покажу в этом
статья.
Для каждой заданной серии мы
может определить сумму этого определенного ряда. Изучая суммы рядов,
привел меня к некоторым довольно хорошим открытиям, которые я покажу в этом
статья.
Одна из самых простых сумм — это сумма всех натуральных чисел. до $n$. Общеизвестно, что эта сумма может быть найдена формула: $$\frac{n(n+1)}{2}$$ Давайте проверим некоторые числа и посмотрим, работает:
$1+2+3+4=4(4+1)/2=20/2=10$
$1+2+3+4+5+6+7+8=8(8+ 1)/2=72/10=36$.
Эту формулу легко доказать по индукции (я оставлю это читателю).
Что, если мы возьмем ряды чисел, являющиеся суммами числа до определенного числа (они называются треугольными числа), или другими словами ряд:
$1$, $3$, $6$, $10$, $15$, $21$, $28$, $\ldots$ где $$a_n=\frac{n(n+1)}{2}$$ дает нам члены этого ряда. Как найдем ли мы сумму этого ряда?
Давайте посмотрим на полученные частичные суммы:
$1=1$
$1+3=4$
$1+3+6=10$
$1+3+6+10=20$
$1+3+6+10+15=35$
$1+3+6+10+15+21=56$
и так далее.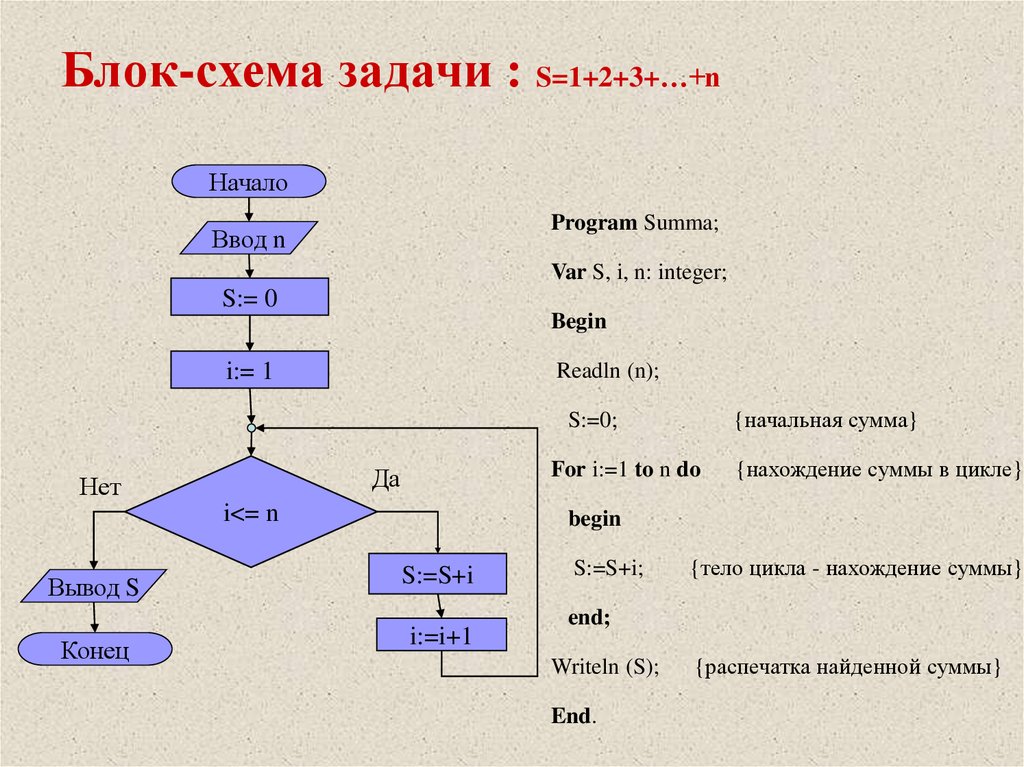 Есть ли какая-то общая формула для этой суммы? Давайте
присмотрись и попробуй узнать:
Есть ли какая-то общая формула для этой суммы? Давайте
присмотрись и попробуй узнать:
$1=1$
$4=2\умножить на 2$
$10=3\раз(3+1/3)$
$20=4\умножить на 5$
$35=5\умножить на 7$
$56 =6\times(9+1/3)$
Можно попытаться предположить, что они равны: $n\times$ (еще один число), но не все из них являются целыми числами. Мы можем предположить что те, которые не являются целыми числами, имеют дроби с знаменатель $3$. Если это правда, мы могли бы умножить все эти числа на $3$, и дроби исчезнут. Давай попробуем вышло:
$1\times 3=3=1\times 3$
$4\times 3=12=2\times 6$
$10\times 3=30=3\times 10$
$20\times 3=60= 4\times 15$
$35\times 3=105=5\times 21$
$56\times 3=168=6\times 28$
В этих продуктах $1$, $2$, $3$, $4$, $5$, $6$, $\ldots$
целые числа, а $3$, $6$, $10$, $15$, $21$, $28$, $\ldots$ — это
известные нам треугольные числа равны $$\frac{n(n+1)}{2}.$$
Назовем эту сумму $b_n$. Каждая частичная сумма является произведением $n$ и
треугольное число $(n+1)^{\textrm{th}}$, это дает
по следующей формуле: $$3b_n=n\times\frac{(n+1)(n+2)}{2}$$
$$b_n=\frac{n(n+1)(n+2)}{6}$$ Теперь докажем по индукции, что:
$$1+3+6+10+15+\ldots+\frac{n(n+1)}{2}=\frac{n(n+1)(n+2)}{6}$$ Первый
проверим, верно ли это при $n=1$. $$1=\frac{1(2)(3)}{6}=1$$
Предположение: утверждение верно для $n=k$, некоторого целого числа,
то есть:
$$1+3+6+10+15+\ldots+\frac{k(k+1)}{2}+\frac{k(k+1)(k+2)}{6}$$
докажите это для $n=k+1$, добавим следующее слагаемое в LHS и в
RHS: $$1+3+6+40+15+…+\frac{k(k+1)}{2}+\frac{(k+1)(k+2)}{2} $$ $$
=\frac{k(k+1)(k+2)}{6}+\frac{(k+1)(k+2)}{2} $$ $$
=\frac{k(k+1)(k+2)+3(k+1)(k+2)}{6} $$ $$ =\frac{(k+1)(k+2)( к+3)}{6}
$$ Доказано для всех $n$ по аксиоме индукции. 9{\textrm{th}}$ сумма
числа до $n$:
$$1=\frac{1(2)(3)}{6}=1$$
Предположение: утверждение верно для $n=k$, некоторого целого числа,
то есть:
$$1+3+6+10+15+\ldots+\frac{k(k+1)}{2}+\frac{k(k+1)(k+2)}{6}$$
докажите это для $n=k+1$, добавим следующее слагаемое в LHS и в
RHS: $$1+3+6+40+15+…+\frac{k(k+1)}{2}+\frac{(k+1)(k+2)}{2} $$ $$
=\frac{k(k+1)(k+2)}{6}+\frac{(k+1)(k+2)}{2} $$ $$
=\frac{k(k+1)(k+2)+3(k+1)(k+2)}{6} $$ $$ =\frac{(k+1)(k+2)( к+3)}{6}
$$ Доказано для всех $n$ по аксиоме индукции. 9{\textrm{th}}$ сумма
числа до $n$:
$$\frac{n(n+1)(n+2)…(n+k)}{k+1}= \frac{(n+k)!} {(n-1)!(k+1)!}= \left[\begin{массив}{c} n+k \\n-1 \end{массив}\right] = \left[\begin{array}{c} n+k \\k+1 \end{array}\right] $$ Что мы на самом деле получается, что сумму можно рассматривать как бином коэффициент!
Попробуем доказать эту формулу по индукции: $$
\left[\begin{массив}{c} k \\ k \end{массив}\right] +
\left[\begin{массив}{c} k+1 \\k \end{массив}\right] +
\left[\begin{массив}{c} k+2 \\k \end{массив}\right] +… +
\left[\begin{массив}{c} n+(k-1) \\k \end{массив}\right] =
\left[\begin{array}{c} n+k \\ k+1 \end{array}\right] $$ Проверка
для $n=1$: $$ \left[\begin{array}{c} k \\ k \end{array}\right] +
\left[\begin{array}{c} k \\k \end{array}\right] $$ Предположение:
утверждение верно для $n=m$, определенного целого числа, то есть: $$
\left[\begin{массив}{c} k \\ k \end{массив}\right] +
\left[\begin{массив}{c} k+1 \\k \end{массив}\right] +
\left[\begin{массив}{c} k+2 \\k \end{массив}\right] +. .. +
\left[\begin{массив}{c} m+(k-1) \\k \end{массив}\right] =
\left[\begin{array}{c} m+k \\ k+1 \end{array}\right] $$ Чтобы доказать это
для $n=m+1$ добавим следующий член к правой и левой сторонам: $$
\left[\begin{массив}{c} k \\ k \end{массив}\right] +
\left[\begin{массив}{c} k+1 \\k \end{массив}\right] +
\left[\begin{массив}{c} k+2 \\k \end{массив}\right] +… +
\left[\begin{массив}{c} m+(k-1) \\k \end{массив}\right] +
\left[\begin{array}{c} m+k \\ k \end{array}\right] $$
.. +
\left[\begin{массив}{c} m+(k-1) \\k \end{массив}\right] =
\left[\begin{array}{c} m+k \\ k+1 \end{array}\right] $$ Чтобы доказать это
для $n=m+1$ добавим следующий член к правой и левой сторонам: $$
\left[\begin{массив}{c} k \\ k \end{массив}\right] +
\left[\begin{массив}{c} k+1 \\k \end{массив}\right] +
\left[\begin{массив}{c} k+2 \\k \end{массив}\right] +… +
\left[\begin{массив}{c} m+(k-1) \\k \end{массив}\right] +
\left[\begin{array}{c} m+k \\ k \end{array}\right] $$
$$ = \left[\begin{массив}{c} m+k \\k+1 \end{массив}\right] + \left[\begin{array}{c} m+k \\ k \end{массив}\right] $$
$$ = (m+k)!({\frac{1}{(k+1) )!(m-1)!}} + {\frac{1}{k!m!}}) $$
$$ = (m+k)! (\frac{m+k+1}{(k+1)!m!}) $$
$$ = \frac{(m+k+1)!}{(k+1)!m!} $$
$$ = \left[\begin{массив}{c} m+k+1 \\k+1 \end{массив}\right] $$ Таким образом, доказано.
На самом деле, это очень известное биномиальное тождество.
Подстановкой $k=1$, $2$, $3$ $\ldots$ можно получить все формулы
для всех $k^{\textrm{th}}$ сумм чисел до $n$. Довольно
Круто.
Довольно
Круто.
На самом деле неудивительно, что мы получаем биномиальный коэффициент для описания такого рода сумм. Биномиальный коэффициент имеет сильную Связь с треугольником Паскаля. Натуральные числа – это частичные суммы $1$ во внешней строке, треугольные числа сформировать следующую строку и так далее. Читатель может записать Паскаля треугольник и убедитесь, что это правда. Чтобы найти частичную сумму все числа в любой строке, просто посмотрите на номер прямо на справа от последнего числа, подлежащего суммированию, а ниже в треугольный массив. Именно это мы и доказали по индукции. (Дополнительная информация о связи с треугольником Паскаля может быть в книге Мартина Гарднера «Математический карнавал»).
Читатель может попытаться найти такие суммы для других суммы ряда. Если вы найдете что-то интересное, я уверен, что я, и другим тоже будет интересно узнать об этом.
Ятиру Халеви 18 лет, он живет в Маккабиме, Израиль. ходит в среднюю школу Маккабим-Реут.
Программа Kotlin для нахождения суммы N натуральных чисел
В этом посте мы рассмотрим программу Kotlin для нахождения суммы n натуральных чисел.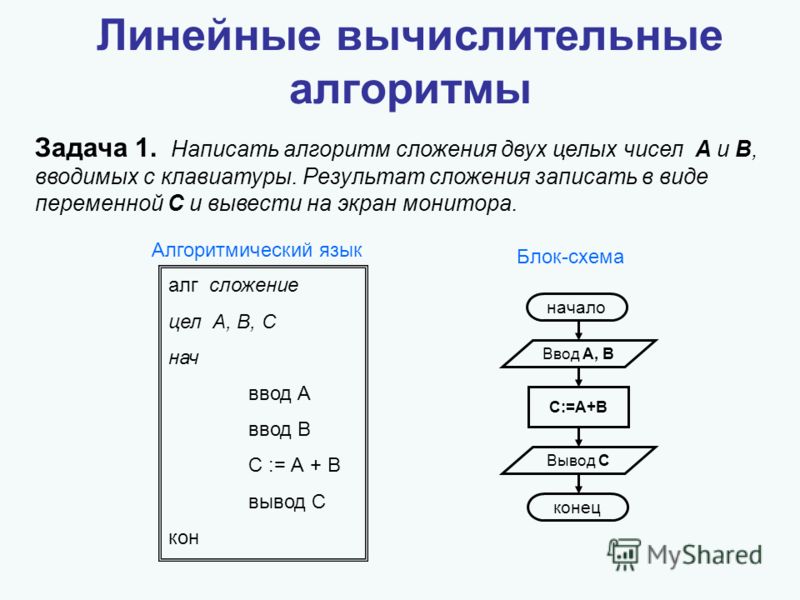
Что такое натуральное число?
Положительные числа, напр. 1,2,3,4,5,6… и т. д., известны как натуральные числа. Нам нужно найти сумму n натуральных чисел.
Другими словами, вы можете сказать, что мы найдем результат 1+2+3+4…..+n .
В этом посте мы найдем сумму натуральных чисел, используя
- For Loop
- Пока Цикл
- Формула: мы можем найти сумму n натуральных чисел, используя следующую формулу –
Сумма n натуральных чисел = (n * (n+1)) / 2, Где n - количество натуральных чисел, до которых вы хотите найти сумму.
1. Найти сумму натуральных чисел (используя цикл for)
Исходный код —
импортировать java.util.*
веселая главная () {
val read = Сканер (System.`in`)
println("Введите максимальное число:")
числовое значение = read.nextInt()
сумма переменных = 0
for(curNum в 1..numb) {
сумма += текущее число
}
println("Сумма натуральных чисел $numb равна $sum")
}
При запуске программы вывод будет
Введите максимальное количество: 20 Сумма 20 натуральных чисел равна 210
Здесь мы создали объект Scanner.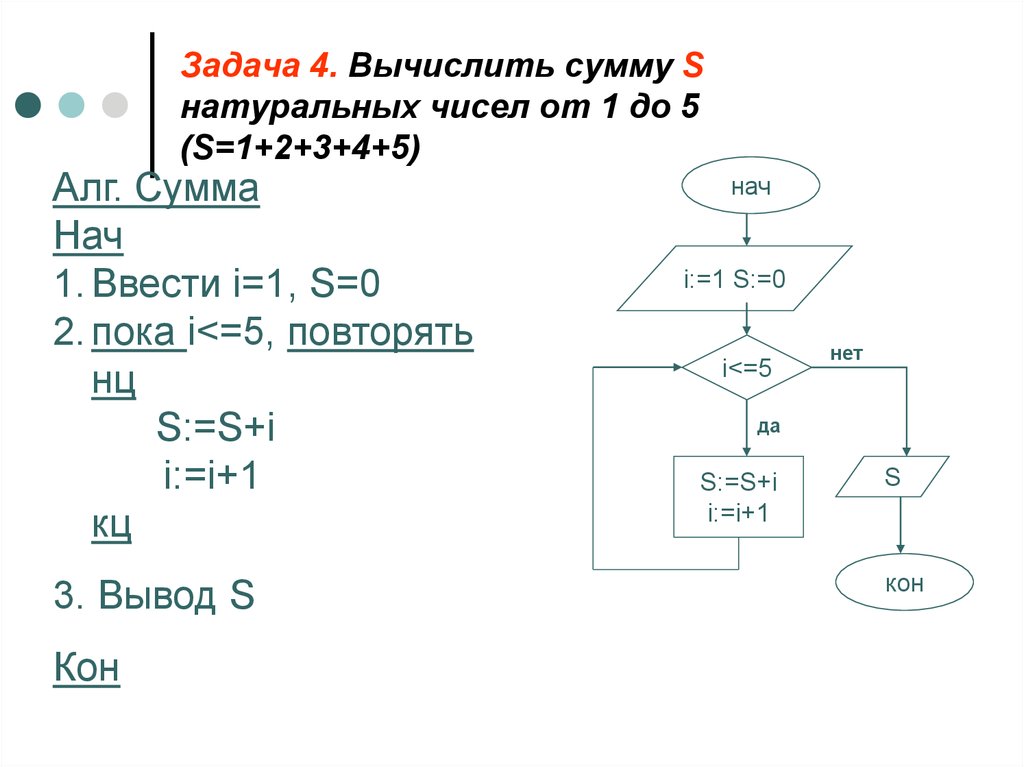 Сканер принимает аргумент, который говорит, откуда брать ввод.
Сканер принимает аргумент, который говорит, откуда брать ввод.
System.`in` означает ввод со стандартного ввода – Клавиатура.
read.nextIn() означает чтение всего, что вводится пользователем до пробела или разрыва строки из стандартного ввода – клавиатура.
Ввод, прочитанный сканером, затем сохраняется в переменной год
Мы используем цикл for, чтобы найти сумму натуральных чисел в kotlin. В цикле for мы запускаем цикл от 1 до максимального числа , т.е. numb .
Предположим, что максимальное число равно 3. Итак,
Для i = 1,
сумма += curNum
=> сумма = сумма + curNum
=> сумма = 0 + 1 сумма
4 =>
4 = 1
Для i = 2,
=> сумма = 1 + 2
=> сумма = 3
Для i = 3,
=> сумма = 3 + 3
=> сумма = 6
Таким образом, сумма трех натуральных чисел равна 6.
Наконец, мы печатаем результат, используя метод println() .
2. Найдите сумму натуральных чисел, используя блок while
Мы уже видели сумму натуральных чисел, используя цикл for. Теперь мы найдем сумму натуральных чисел, используя цикл while в Котлине.
импортировать java.util.*
веселая главная () {
val read = Сканер (System.`in`)
println("Введите максимальное число:")
числовое значение = read.nextInt()
сумма переменных = 0
переменная я = 1
в то время как (я <= онемение) {
сумма += я
я++
}
println("Сумма натуральных чисел $numb равна $sum")
}
При запуске программы вывод будет
Введите максимальное количество: 30 Сумма 30 натуральных чисел равна 465.
Здесь мы создали объект Scanner. Сканер принимает аргумент, который говорит, откуда брать ввод.
System.`in` означает ввод со стандартного ввода – Клавиатура.
read.nextIn() означает чтение всего, что вводится пользователем до пробела или разрыва строки из стандартного ввода – клавиатура.
Ввод, прочитанный сканером, затем сохраняется в переменной год
Мы используем цикл while для нахождения суммы натуральных чисел вместо цикла for. Он работает аналогично циклу for.
Предположим, что максимальное число равно 3. Итак,
Пока i = 1, (i сумма += i
=> сумма = сумма + i
=> сумма = 0 + 1
=> сумма = 1
Кроме того, i++ означает i = i + 1 . Значение i будет увеличено на 1. Итак, i = 2.
Пока i = 2, (2 сумма = 1 + 2
=> сумма = 3
Также значение i будет увеличено на 1. Итак, i = 3.
Пока i = 3, (3 сумма = 3 + 3
=> сумма = 6
Кроме того, значение i будет увеличено на 1.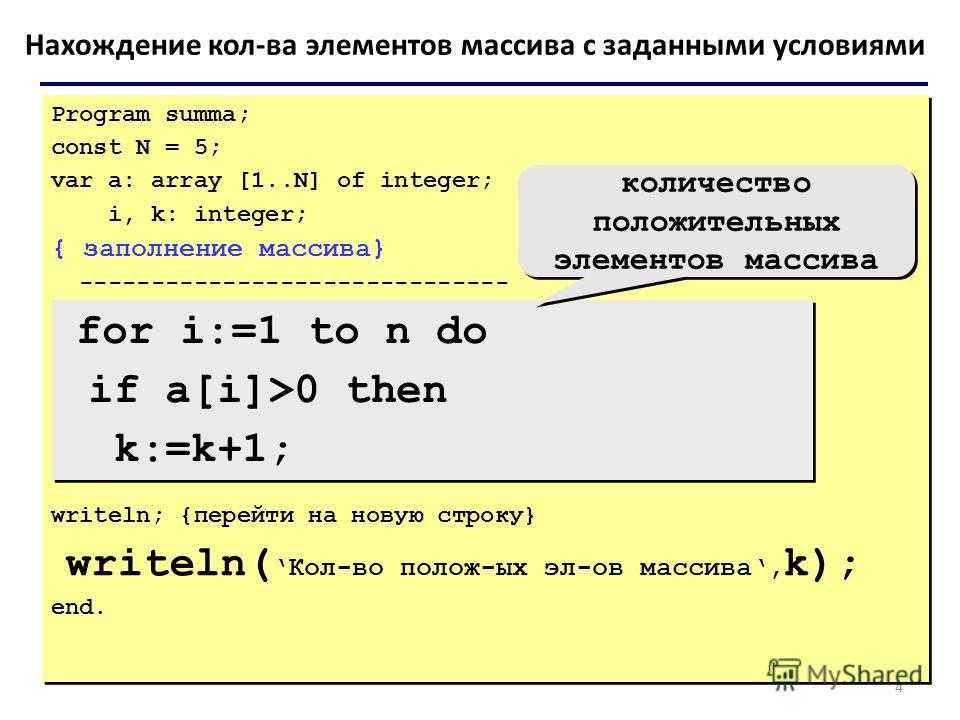 Таким образом, i = 4.
Таким образом, i = 4.
Пока i = 4, (4 метод println().
3. Сумма натуральных чисел с использованием формулы
Мы уже получили видел сумму натуральных чисел, используя цикл for и цикл while
Теперь мы найдем сумму натуральных чисел, используя формулу
Как мы уже обсуждали,
Формула для нахождения суммы = (n * (n+1)) / 2
Где n — количество натуральных чисел.
Исходный код —
импортировать java.util.*
веселая главная () {
val read = Сканер (System.`in`)
println("Введите максимальное число:")
числовое значение = read.nextInt()
сумма значений = (число * (число + 1)) / 2
println("Сумма натуральных чисел $numb равна $sum")
}
При запуске программы вывод будет
Введите максимальное количество: 30 Сумма 30 натуральных чисел равна 465.
Здесь мы использовали формулу для нахождения суммы n натуральных чисел. Остальные вещи такие же, как описано выше.
Итак, мы прошли программу Kotlin, чтобы найти сумму n натуральных чисел.
Beyond infinity - Curious
Это вторая тема в нашей серии из двух частей о бесконечности. Мы рекомендуем вам прочитать первую часть серии — «В бесконечность» — прежде чем читать эту.Ранее мы рассмотрели методы сравнения размеров множеств и обнаружили, что многие бесконечные множества можно точно спарить, например множество натуральные числа ГЛОССАРИЙ натуральных чисел Набор всех положительных целых чисел, которые можно использовать для подсчета отдельных объектов. В зависимости от того, какого математика вы спросите, этот набор может включать или не включать число 0. Примеры: 1, 2, 3, … и множество четных чисел. Оба эти множества имеют одинаковый размер, или «мощность», а именно ℵ 0 , знакомую нам «бесконечность».
Все ли бесконечные множества имеют одинаковый размер? Можно ли их всех точно совместить?
Несмотря на интуицию, мы можем считать и сравнивать размеры бесконечных множеств. Источник изображения: benjgibbs/Flickr.
Источник изображения: benjgibbs/Flickr.Долгое время казалось, что все бесконечные множества могут быть соединены друг с другом в пары — это означало, что все бесконечные множества имеют одинаковый размер, ℵ 0 . Эта интуитивная идея была разрушена в 1874 году открытием все больших и больших бесконечностей. В пятистраничной статье, которая потрясла математический мир (и породила в процессе теорию множеств), немецкий математик Георг Кантор изложил свое открытие новых горизонтов «за пределами бесконечности».
Как можно построить «большее» бесконечное множество, чем множество всех натуральных чисел? Очевидно, нам нужно будет добавить дополнительные ингредиенты в смесь.
Рациональное мышление
Первый способ расширить нашу систему счисления — ввести все отрицательные числа, образуя множество
целые числа ГЛОССАРИЙ целых чисел Набор всех целых чисел, как положительных, так и отрицательных. Число 0 определенно является частью этого множества. Натуральные числа являются частью целых чисел. Примеры: -2,-1,0,1,2, … , ℤ. Однако вскоре становится ясно, что это не поможет нам достичь большей кардинальности — мы фактически удвоили множество ℕ, добавив отрицательное число для каждого положительного числа, и мы знаем из нашего опыта объединения нечетных и четных чисел. что удвоение бесконечного множества не изменит его мощности.
Натуральные числа являются частью целых чисел. Примеры: -2,-1,0,1,2, … , ℤ. Однако вскоре становится ясно, что это не поможет нам достичь большей кардинальности — мы фактически удвоили множество ℕ, добавив отрицательное число для каждого положительного числа, и мы знаем из нашего опыта объединения нечетных и четных чисел. что удвоение бесконечного множества не изменит его мощности.
Следующее, что мы можем попробовать, это включить все числа, которые можно записать в виде дробей, создав множество рациональное число ГЛОССАРИЙ рациональных чисел Набор всех чисел, как положительных, так и отрицательных, которые можно записать в виде дроби. Эквивалентно, набор всех чисел, десятичные расширения которых либо заканчиваются, либо в конечном итоге повторяются. Натуральные и целые числа являются частью рациональных чисел. Примеры: -3, 1/3, 0,5, … , ℚ. Кажется, у нас ужасно много чисел в ℚ — для начала, между любыми двумя целыми числами бесконечно много дробей! Ясно, что спарить набор натуральных чисел будет сложно:
$$\mathbb{N}\text{ = \{0, 1, 2, 3, 4, 5, 6, … \}}$$
с набором рациональных чисел:
$$\mathbb {Q}\text{ = \{ 0,} \frac{1}{2},\frac{1}{3}, \frac{2}{3}, \frac{1}{4}, \frac {3}{4}, … , 1, \frac{11}{2}, \frac{11}{3} … \}$$
Сложно … но возможно. Кантор показал, как этого можно добиться, если подумать о вещах немного по-другому. Суть в том, чтобы понять, что для того, чтобы соединить рациональные числа с натуральными, нам просто нужно найти способ перечислить рациональные числа в каком-то порядке. Затем мы можем соединить первое рациональное число в нашем списке с натуральным числом 1, второе рациональное число в списке с 2 и так далее.
Кантор показал, как этого можно добиться, если подумать о вещах немного по-другому. Суть в том, чтобы понять, что для того, чтобы соединить рациональные числа с натуральными, нам просто нужно найти способ перечислить рациональные числа в каком-то порядке. Затем мы можем соединить первое рациональное число в нашем списке с натуральным числом 1, второе рациональное число в списке с 2 и так далее.
На первый взгляд, это кажется сложным — как мы можем перечислить рациональные числа, включающие в себя дроби, в таком порядке, чтобы охватить каждое из них? Начнем с того, что наименьшей дроби больше 0 не существует! Но, проделав несколько мысленных зигзагов, оказывается, что такой список можно составить.
Для начала заметим, что каждая дробь состоит из пары натуральных чисел — одного в верхней части дроби (числитель) и одного в нижней части (знаменатель). Есть два предостережения. Во-первых, у нас не может быть 0 в знаменателе дроби. Во-вторых, одну и ту же дробь можно записать бесконечно многими способами, используя разные пары чисел (например, 9).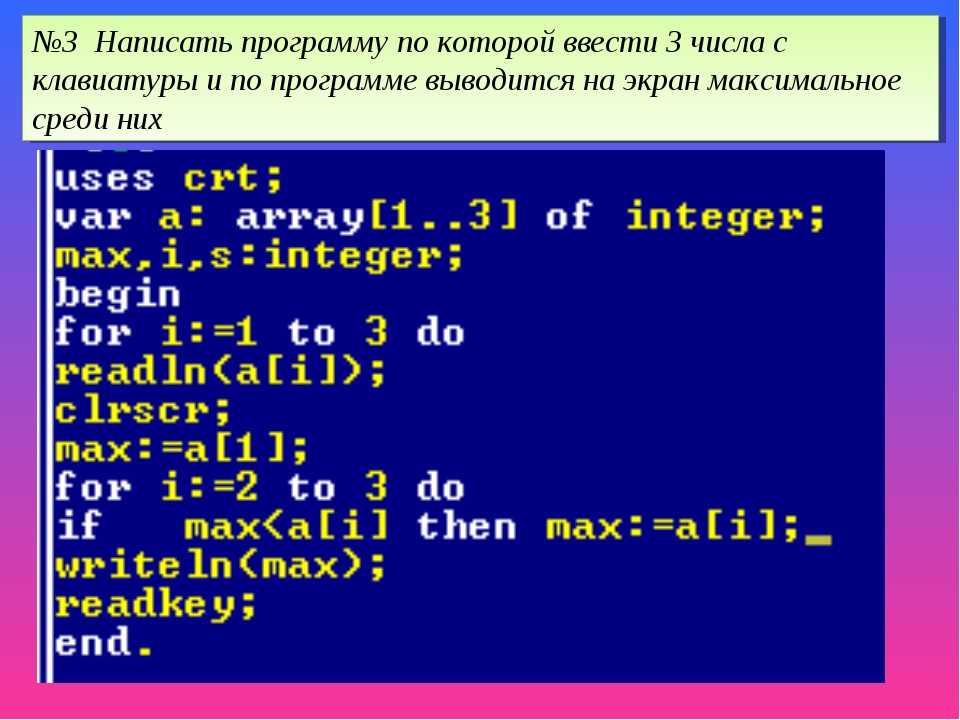 0528 1 ⁄ 2 совпадает с 2 ⁄ 4 и 3 ⁄ 6 и так далее).
0528 1 ⁄ 2 совпадает с 2 ⁄ 4 и 3 ⁄ 6 и так далее).
- Почему нельзя делить на ноль
Помимо калькуляторов, выдающих ошибки, и шуток о возгорании рабочих тетрадей и спонтанном образовании черных дыр, есть очень веская (и очень простая) причина, по которой мы не можем делить любое число на ноль.
Еще в школе мы узнаём, что в математике есть четыре основных действия: сложение, вычитание, умножение и деление. Однако для математиков есть только две основные операции: сложение и умножение. Мы получаем вычитание и деление бесплатно, как противоположности сложения и умножения.
В частности, каждый вопрос на вычитание можно рассматривать как вопрос на сложение, а каждый вопрос на деление можно рассматривать как вопрос на умножение. Например, типичный вопрос на умножение может выглядеть так:
$$\text{2 × 3 = ?}$$
Тогда как типичная задача на деление может выглядеть так:
$$\text{6 ÷ 2 = ?} $$
Но что это значит? Когда мы спрашиваем: «Сколько шесть разделить на два?», на самом деле мы спрашиваем: «На что умножить два, чтобы получить шесть?».
 Другими словами,
Другими словами,$$\text{6 ÷ 2 = ?}$$
та же проблема, что и:
$$\text{2 × ? = 6}$$
Итак, задача на деление — это на самом деле задача на умножение с неизвестным числом на другой стороне уравнения. Имея это в виду, давайте подумаем о делении на ноль.
$$\text{1 ÷ 0 = ?}$$
— это та же проблема, что и вопрос: «На что умножить ноль, чтобы получить единицу?».
$$\text{0 × ? = 1}$$
Но ни один номер не работает! На что бы мы ни умножали ноль, мы всегда будем получать ноль. Вот почему мы не можем делить ни одно, ни два, ни любое другое число на ноль — здесь нет разумного ответа, потому что нет числа, которое можно было бы умножить на ноль, чтобы получить единицу, или две, или что-то еще — кроме нуля.
Что приводит к последнему вопросу: как насчет деления нуля на ноль?
$$\text{0 ÷ 0 = ?}$$
— это та же проблема, что и вопрос: «На что умножить ноль, чтобы получить ноль?».
$$\text{0 × ? = 0}$$
На этот раз проблема не в том, что нет ни одного работающего числа, а в том, что работает каждое число! Поскольку умножение любого числа на ноль дает ноль, отсюда следует, что ноль, разделенный на ноль, может быть буквально любым числом.
 И по этой причине у него также нет разумного ответа.
И по этой причине у него также нет разумного ответа.Если бы мы попытались быть любезными и позволили бы 0 ÷ 0 быть любым числом по вашему выбору, то мы быстро столкнулись бы со следующей проблемой:
Поскольку 0 ÷ 0 = 1 и 0 ÷ 0 = 2, это означает, что 1 = 0 ÷ 0 = 2.
Поскольку 1 и 2 определенно не одно и то же число, мы не можем разумно определить 0 ÷ 0.
Поскольку каждое рациональное число можно рассматривать как пару натуральных чисел, мы можем составьте следующую бесконечную таблицу, чтобы зафиксировать все возможные рациональные числа:
Вверху: начало бесконечной таблицы, в которой перечислены все возможные дроби в самой упрощенной форме. Каждая дробь получается делением номера столбца (числителя) на номер строки (знаменатель).
Мы хотим, чтобы каждая дробь появлялась в таблице только один раз, и в данный момент эта таблица фиксирует каждую дробь снова и снова, бесконечно много раз. Поэтому мы позаботимся об исключении всех дубликатов, вычеркнув каждую запись в таблице, где дробь может быть упрощена (все записи, в которых числитель и знаменатель имеют общий множитель, удаляются).
Вверху: бесконечная таблица дробей с удаленными дубликатами.
Сделав это, теперь мы можем двигаться по таблице зигзагом, чтобы поймать каждую дробь, например так:
Вверху: обход таблицы дробей зигзагами, чтобы перечислить все возможные дроби в каком-то порядке (порядке, в котором мы встречаем их в наших зигзагах).
Тогда все, что нам нужно сделать, это перечислить каждую дробь в том порядке, в котором мы встречались с ней во время зигзага:
| Натуральное число | Рациональный номер |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 ⁄ 2 |
| 4 | 2 |
| 5 | 1 ⁄ 3 |
| … | … |
Вот так мы сделали биекцию между рациональными числами ℚ и натуральными числами ℕ! Мы можем проверить, что у каждого натурального числа есть партнер (список дробей никогда не заканчивается) и что у каждого рационального числа есть партнер (каждое рациональное число встречается в таблице ровно один раз, после того как мы тщательно удалим дубликаты). Хотя мы не зафиксировали все отрицательные рациональные числа в нашем отображении, ту же идею можно легко изменить, чтобы учесть их.
Хотя мы не зафиксировали все отрицательные рациональные числа в нашем отображении, ту же идею можно легко изменить, чтобы учесть их.
Получается, что множество рациональных чисел тоже счетно — его мощность ℵ 0 . Может показаться, что у нас закончились варианты; что на самом деле существует только один тип бесконечности. Но у Кантора был в рукаве последний трюк, который он опубликовал в своей знаменитой статье 1874 года. Есть еще один источник цифр, на который мы можем опираться.
Настоящий сюрприз
Помимо натуральных и рациональных чисел, есть еще один набор чисел, с которым знакомо большинство людей, — набор
вещественные числа ГЛОССАРИЙ Действительные числа Набор всех чисел, находящихся на числовой прямой. Натуральные числа, целые числа и рациональные числа являются частью действительных чисел, но к действительным числам также относятся числа, которые нельзя записать в виде дроби, например, π и квадратный корень из числа пи, чьи десятичные разложения никогда не заканчиваются и не повторяются. Примеры: -2, 0, 1/4, √3, log 2, … , ℝ. Множество действительных чисел включает в себя все целые числа и все дроби, а также множество других чисел, которые нельзя записать в виде дроби, например, π (пи) и квадратный корень из 2.
Примеры: -2, 0, 1/4, √3, log 2, … , ℝ. Множество действительных чисел включает в себя все целые числа и все дроби, а также множество других чисел, которые нельзя записать в виде дроби, например, π (пи) и квадратный корень из 2.
Кантор смог доказать, что невозможно создать биекцию между множеством действительных чисел ℝ и множеством натуральных чисел ℕ. Как бы вы ни старались, вы всегда в конечном итоге израсходуете все натуральные числа, а действительные числа останутся непарными. Математически точных чисел определенно больше, чем натуральных чисел.
Чтобы доказать это, Кантор использовал элегантную математическую технику, известную как «доказательство от противного». Кантор начал с предположения, что вы можете создать биекцию, перечислив все действительные числа в некотором порядке, точно так же, как мы сделали для рациональных чисел, чтобы сопоставить их с натуральными числами. Затем он показал, что независимо от того, как вы создали список, он сможет показать вам реальное число, которого нет в вашем списке, тем самым противореча вашему результату и доказав, что это невозможно.
Еще более невероятным является то, что «аргумент диагонализации» Кантора даже не требует учета всех действительных чисел. Оказывается, любой участок числовой прямой, каким бы крошечным он ни был, содержит «больше» чисел, чем все натуральные числа (и все рациональные тоже)! Чтобы проиллюстрировать аргумент Кантора, мы просто возьмем набор действительных чисел от 0 до 1 и покажем, что вы не можете сопоставить их с набором всех натуральных чисел.
Предположим, что мы создали биекцию, создав список, содержащий все действительные числа от 0 до 1 в некотором порядке. Затем Кантор дает нам другое действительное число от 0 до 1, которого не может быть в нашем списке. Чтобы создать это число, он берет первый десятичный разряд нашего первого числа в нашем списке и добавляет к нему 1, и использует результат в качестве первого десятичного разряда своего нового числа. (Если первый десятичный разряд нашего первого числа был 9, он меняет его на 0). Затем он берет второй десятичный разряд нашего второго числа и прибавляет к нему 1, используя результат как второй десятичный разряд своего нового числа. Этот процесс продолжается, в результате чего получается реальное число, которого, по утверждению Кантора, не будет в нашем списке.
Этот процесс продолжается, в результате чего получается реальное число, которого, по утверждению Кантора, не будет в нашем списке.
Интерактивный
Некоторые бесконечности больше других
Как бы вы их ни соединяли, всегда можно найти действительное число, которое не сочетается с натуральным числом. Это означает, что действительных чисел больше, чем натуральных, хотя и тех, и других бесконечное количество!
Используйте этот интерактив, чтобы соединить некоторые натуральные числа с началом действительных чисел. Мы всегда сможем сгенерировать новый номер, которого нет в вашем списке. Мы делаем это, беря по одной цифре от каждого действительного числа (по диагонали) и увеличивая ее на единицу.
| Натуральное число | Действительное число |
|---|---|
| 1 | 0. |
| 2 | 0. |
| 3 | 0. |
| 4 | 0. |
| 5 | 0. |
- Несопоставленный реальный номер
- 0,00000
- Вставьте цифры в каждую секцию, затем нажмите «обновить результат»
Сброс
Он прав? Что ж, давайте попробуем найти число Кантора в нашем списке. Это не может быть первое число, потому что первый десятичный разряд (по крайней мере) не совпадает. Это не может быть второе число в нашем списке, потому что второй десятичный разряд не совпадает. Это не может быть миллионное число в нашем списке, потому что не совпадает миллионный десятичный знак и так далее. Независимо от того, как мы будем составлять список, мы не сможем зафиксировать даже каждое действительное число от 0 до 1!
Аргумент Кантора работает для действительных чисел, потому что десятичное представление действительного числа не должно иметь шаблона. Это контрастирует с десятичными разложениями рациональных чисел, которые в конечном итоге должны повторяться.
Это контрастирует с десятичными разложениями рациональных чисел, которые в конечном итоге должны повторяться.
Итак, наконец, мы нашли бесконечность большую, чем ℵ 0 ! Возможно, неудивительно, что эта новая бесконечность — мощность множества действительных чисел ℝ — называется ℵ 1 . Это второе трансфинитное кардинальное число и наш первый пример большей бесконечности, чем бесконечность ℵ 0 , которую мы знаем и любим.
Заключение
Таким образом, хотя цели Базза Лайтера, заключающиеся в путешествии «в бесконечность и дальше», не имеют буквального смысла — бесконечность — это не место, не пункт назначения и не конечная точка, — можно утверждать, что математика позволяет нам исследовать бесконечность и за ее пределами. Различные бесконечные множества могут иметь разную мощность, и некоторые из них больше, чем другие. За пределами бесконечности, известной как ℵ 0 (мощность натуральных чисел) есть ℵ 1 (что больше) … ℵ 2 (что еще больше) … и, в самом деле, бесконечное множество различных бесконечностей.


 3
3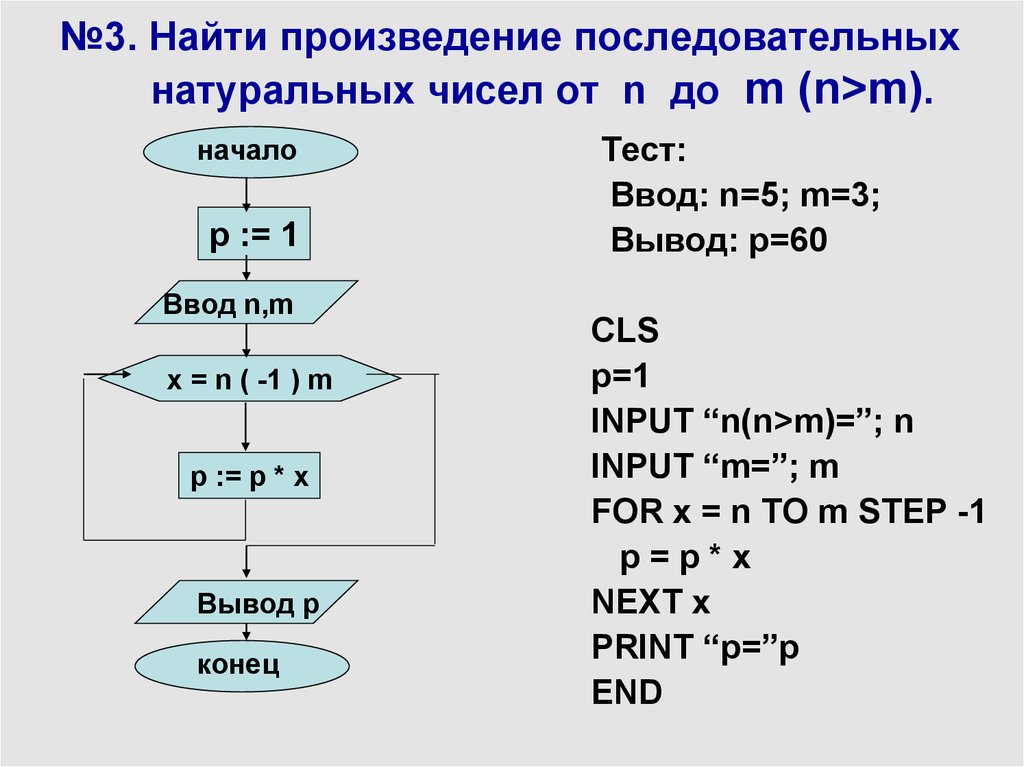 Программа должна вывести слово 'YES', если в числе есть две одинаковые цифры, и слово 'NO', если такой пары цифр нет.
Программа должна вывести слово 'YES', если в числе есть две одинаковые цифры, и слово 'NO', если такой пары цифр нет. x
a = int(x[0])
b = int(x[1])
n = 0
while a!=0 and b!=0:
if a > b:
a = a % b
else:
b = b % a
n+=1
print (a+b, n)
x
a = int(x[0])
b = int(x[1])
n = 0
while a!=0 and b!=0:
if a > b:
a = a % b
else:
b = b % a
n+=1
print (a+b, n)
 Дружественными числами являются, например 220 и 284.
Дружественными числами являются, например 220 и 284.
 Другими словами,
Другими словами, И по этой причине у него также нет разумного ответа.
И по этой причине у него также нет разумного ответа.