Её область определения – это все рациональные числа, т.к. её точки могут бесконечно уходить влево и вправо.
А её область значений – это все значения ординат больше или равные, чем –8, т.к. ниже этой точки данный график не существует.
Получаем, что \(D(y) = R,\ E(y) = (–8; + \infty)\)
ОГРАНИЧЕННОСТЬ:
Ограниченность – это свойство функции, которое описывает, с какой стороны может «расти» график.
Например, парабола, ветви которой направлены вверх, всегда будет ограничена снизу, как бы мы её не перемещали по координатной плоскости. Она всегда будет иметь минимальное значение функции, ниже которой не опустится. А вот линейная функций нигде не ограничена, т.к. её график – бесконечная прямая.
Примером ограниченной функции также является функция корня. Это функций ограничена сразу с нескольких сторон, т.к. может существовать только в одной четверти координатной плоскости:
НЕПРЕРЫВНОСТЬ:
Это свойство говорит нам о том, есть ли разрывы у функции.
Линейная, квадратичная функция и функция корня являются непрерывными, когда в свою очередь функция обратной пропорциональности имеет разрыв.
Прямая по которой проходит разрыв называется асимптотой.
Для графика функции \(y = \frac{k}{x}\) асимптотами являются прямые \(x = 0\) и \(y = 0\). На этих прямых данная функция не существует. Это влияет и на область допустимых значений, и на область допустимых определений:
МОНОТОННОСТЬ:
Монотонность – это характеристика графика функции, описывающая его промежутки возрастания и убывания.
Функция возрастает – если функция «поднимается» слева направо.
Функция убывает – если функция «падает» слева направо.
Математическим язык можно сказать так:
Функция возрастает, если при возрастании значения абсцисс возрастает значение ординат её точек.
{2}–8x\) возрастает при \(x \in (–\infty;2)\) и убывает при \(x \in (2; + \ \infty).\)
ТОЧКИ ЭКСТРЕМУМА:
Точка между промежутками возрастания и убывания функции называется экстремумом.
Если функция возрастает, а потом убывает, то точка между такими промежутками называется точкой максимума.
Если функция убывает, а потом возрастает, то точка между такими промежутками называется точкой минимума.
Например:
Данный график функций является немонотонным, и непрерывным, значит он имеет промежутки возрастания и убывания, между которые находятся точки экстремумов.
График возрастает при \(x \in (–\infty;0) \cup (3; + \infty)\) и убывает при \(x \in (0;3)\)
Точка минимум: \(x_{\min} = 3\)
Точка максимума: \(x_{\max} = 0\)
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ:
Наименьшее и наибольшее значение функции показывают, для каких аргументов значения функции наибольшие или наименьшие, например:
Это значит, что наименьшее значение наблюдается в конкретной точке x = 1.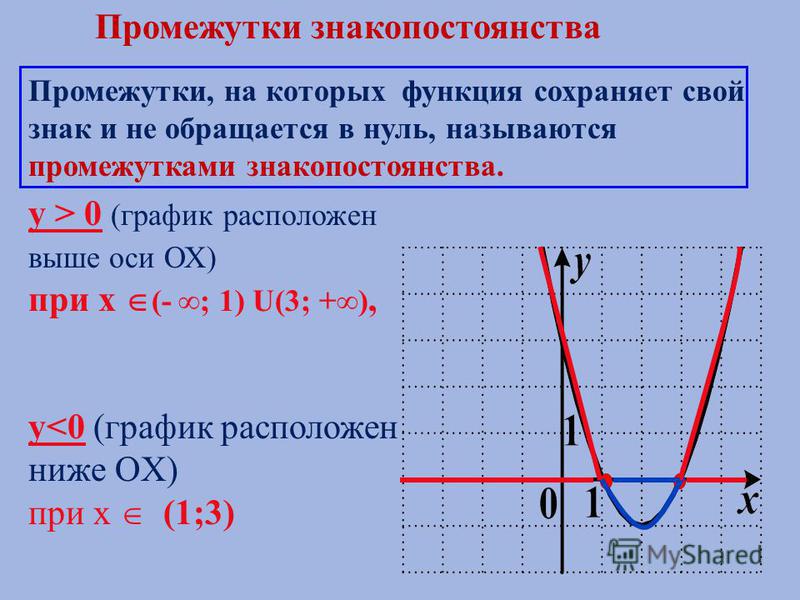
А наибольшее значение достигается, когда x стремить в положительную сторону бесконечно долго, в таких случаях говорят, что наибольшего значения функции не существует.
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:
Промежутки знакопостоянства показывают, на каких промежутках функция положительная, а на каких функция отрицательная.
Например:
\(y > 0\ при\ x \in \left( –\infty;0 \right) \cup \left( 4; + \infty \right)\)
\(y < 0\ при\ x \in (0;4)\)
ЧЕТНОСТЬ ФУНКЦИИ:
Четная функция – это функция, симметричная оси Оу. В таком случае \(f(–x) = f(x)\).
Нечетная функция – это функция, симметричная началу координат. В таком случае \(f(–x) = –f(x).\)
Примером четной функции может служить косинус или парабола, вершина которой находится на оси Оу. В таком случае её ветви симметричны оси Оу:
Можно определить четность визуально: мы видим, что для \(x = 1\) и \(x = –1\ \)значение функции одинаково\(\ y = 2\ \)– следовательно функция четная.
{2}\) четная.
Нечетной функцией является линейная функция, проходящая через начало координат, или функция обратной пропорциональности с асимптотами \(x = 0\) и \(y = 0:\)
Визуально нечетность выглядит как отражение графика на противоположную четверть – \(I\ \)отражается в \(\text{III}\) и наоборот и \(\text{II}\ \)отражается в \(\text{IV}\) и наоборот.
С помощью формулы аналогично можно определить и нечетность функции:
\(f\left( –x \right) = –f\left( x \right)\)
\(y\left( 3 \right) = 2 \bullet 3 = 6\)
\(y\left( –3 \right) = 2 \bullet \left( –3 \right) = \ –6\)
\(y(–3) = \ –y(3) = \ –6\)
следовательно функция нечетная.
Если для функции не соблюдается ни одно из этих условий четности, то ей называют ни четной, ни нечётной или функцией общего вида.
ПЕРИОДИЧНОСТЬ:
Периодичная функция – это функция, график которой визуально повторяется через определённый промежуток. Этот промежуток называется периодом.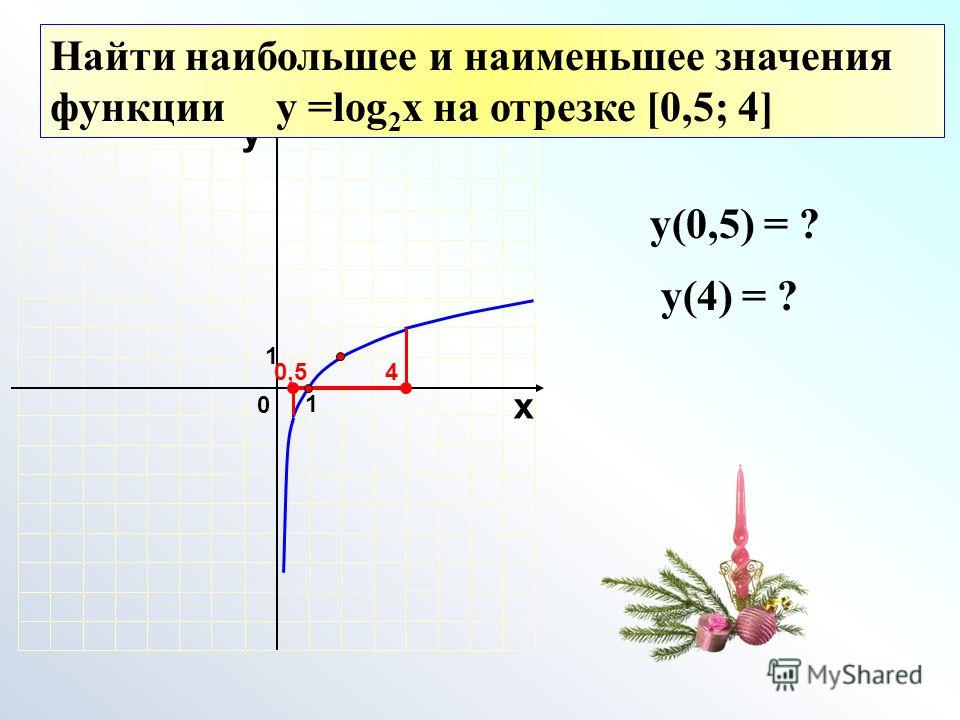
Примером периодичных функций являются тригонометрические функции.
Например, \(y = \sin(x)\) и \(y = \cos(x)\) имеют период\(\ 2\pi\), а функции \(y = \text{tg}(x)\ \)и \(y = \text{ctg}(x)\) имеют период π.
Различные графики имеют свой набор характеристик, поэтому, чтобы понять, как ведет себя конкретный график, нужно учитывать совокупность всех его свойств.
Функция нуля — значение, график, примеры
LearnPracticeDownload
Существуют различные виды функций, которые мы изучаем в математике. Функция — это отношение, которое отображает элементы в домене на элементы в совместном домене таким образом, что каждый элемент в домене отображается только в один элемент в совместном домене. Нулевая функция — это функция, область определения которой состоит из всех действительных чисел, а диапазон состоит из одного элемента, т. е. 0. Нулевая функция также является постоянной функцией, поскольку ее значение никогда не меняется при изменении входных данных.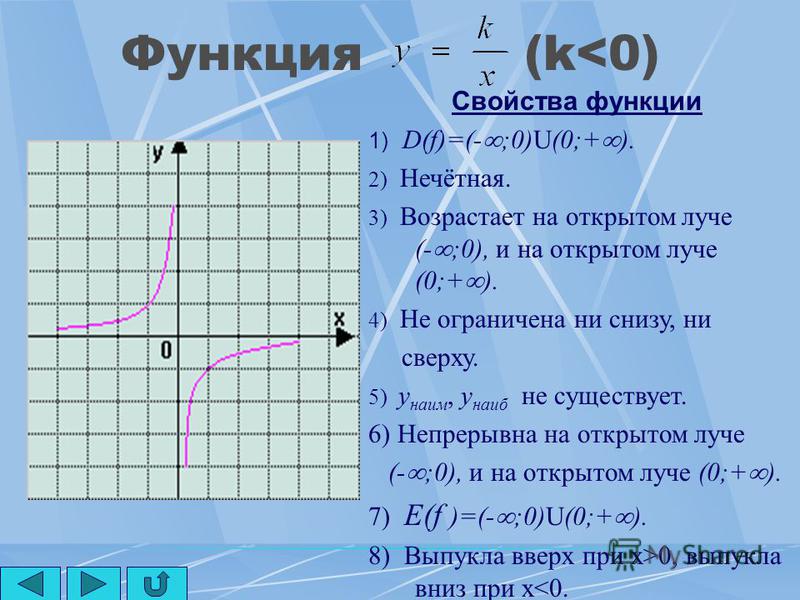
В этой статье мы исследуем свойства нулевой функции и ее природу.
| 1. | Что такое нулевая функция? |
| 2. | График нулевой функции |
| 3. | Характеристики нулевой функции |
| 4. | Нулевая функция четная или нечетная? |
| 5. | Часто задаваемые вопросы о нулевой функции |
Что такое нулевая функция?
Нулевая функция — это постоянная функция, для которой выходное значение всегда равно нулю, независимо от входных данных. Вход нулевой функции может принимать любое значение из действительных чисел, тогда как выход нулевой функции фиксирован, то есть 0. Поскольку изображение каждого элемента в области равно 0, поэтому нулевая функция не является однозначной. -одна функция.
Нулевая функция Значение
Функция f: R → R, определяемая как f(x) = 0 для всех значений x в R, называется нулевой функцией.
График нулевой функции
График нулевой функции f(x) = 0 аналогичен графикам других постоянных функций, которые параллельны оси x. Любую функцию можно рассматривать как постоянную, если она имеет вид y = k, где k — константа, а k — любое действительное число. Это также записывается как f(x) = k. Поскольку для нулевой функции диапазон равен нулю, а значение координаты y всегда равно нулю, поэтому график нулевой функции представляет собой саму ось X. Другими словами, можно сказать, что график нулевой функции является горизонтальной осью.
Характеристики нулевой функции
Функции имеют различные характеристики, такие как наклон, область определения, диапазон, дифференцируемость, предел и непрерывность.
- Функция наклона нуля: Функция нуля также может быть записана как y = 0x + 0. Сравнивая эту форму с формой пересечения наклона линии y = mx + b, где m — наклон линии и b — точка пересечения с осью y, мы получаем, что наклон нулевой функции равен 0,9.0070
- Домен и диапазон нулевой функции: Нулевая функция — это линейная функция, диапазон которой содержит только один элемент независимо от количества элементов в домене. Поскольку нулевая функция определена для всех значений x, поэтому областью определения являются все действительные числа R, а диапазон нулевой функции равен {0}.
- Производная нулевой функции: Дифференциация нуля любой постоянной функции. Производной считается наклон функции в любой заданной точке, а мы уже знаем, что наклон нулевой функции всегда равен 0.
Следовательно, производная нулевой функции равна 0,9.0070 - Предел нулевой функции: Согласно свойствам пределов предел постоянной функции равен той же константе. Следовательно, предел нулевой функции равен 0, .
- Непрерывность нулевой функции: Постоянные функции являются непрерывными, поскольку они представляют собой горизонтальные линии, непрерывно продолжающиеся в обе стороны без каких-либо разрывов. Поскольку нулевая функция является постоянной функцией, поэтому нулевая функция является непрерывной функцией без каких-либо разрывов во всей области.
Следовательно, производная нулевой функции равна 0,9.0070Нулевая функция четная или нечетная?
Функция f называется четной, если f(-x) = f(x) для всех значений x в области определения f, и функция называется нечетной, если f(-x) = -f(x ) для всех значений x в области определения f. Нулевая функция — единственная функция, которая удовлетворяет обоим этим условиям вместе для всех значений x в области определения f.
Важные замечания по функции установки нуля
- Выход (диапазон) функции установки нуля всегда равен 0.
- Функция нуля является как четной, так и нечетной.
- График нулевой функции представляет собой ось X и представляет собой непрерывную функцию.
Темы, связанные с функцией нуля
- Типы функций
- Постоянная функция
- Функция идентификации
- Нули квадратного полинома
Примеры нулевой функции
Пример 1: Определите, является ли функция f(x) = 6 нулевой функцией.
Решение: f(x) = 6 — постоянная функция, диапазон которой всегда равен 6, а 6 не равно 0. Для нулевой функции диапазон равен {0} и имеет вид f(x) = 0 для всех х.
Следовательно, f(x) = 6 не является нулевой функцией.Ответ: Нет, f(x) = 6 не является нулевой функцией.
Пример 2: Каков предел нулевой функции f(x) = 0 при стремлении x к бесконечности?
Решение: Предел постоянной функции всегда равен значению константы (выходу) при всех значениях x. Следовательно, предел нулевой функции f(x) = 0 равен 0, когда x стремится к бесконечности.
Ответ: Предел нулевой функции 0 при стремлении x к бесконечности.
Следовательно, f(x) = 6 не является нулевой функцией.перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по нулевой функции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по нулевой функции
Что такое нулевая функция в математике?
Функция f: R → R, определенная как f(x) = 0 для всех значений x в R, называется нулевой функцией.
Диапазон нулевой функции — это одноэлементный набор, то есть {0}. Нулевая функция — это постоянная функция, для которой выходное значение всегда равно нулю независимо от входных данных.
Что такое ненулевая функция?
Функция, выход которой не равен нулю при всех значениях входов, называется ненулевой функцией. Ненулевая функция может иметь 0 в качестве выхода для некоторых значений в домене, но если она равна нулю для всех элементов в домене, то это нулевая функция.
Является ли нулевая функция четной или нечетной?
Нулевая функция — это единственная функция, которая одновременно является четной и нечетной, поскольку она удовлетворяет обоим условиям f(-x) = f(x) и f(-x) = -f(x) для всех значений x в домен ф.
Что такое интеграл нулевой функции?
Интеграл нулевой функции f(x) = 0 – это произвольная константа C, которая может принимать любые значения действительных чисел. Поскольку производная любой константы равна нулю, следовательно, интеграл от нулевой функции является произвольной константой.
Как найти нули функции?
Нули функции можно вычислить с помощью различных методов, таких как квадратичная формула и разложение полинома на множители.
Рабочие листы по математике и 93
