Задачи линейного программирования в школьном курсе математики
Автор: Гребенникова Юлия Васильевна
Рубрика: Педагогика
Опубликовано в Молодой учёный №43 (281) октябрь 2019 г.
Дата публикации: 23.10.2019 2019-10-23
Статья просмотрена: 424 раза
Скачать электронную версию
Скачать Часть 4 (pdf)
Библиографическое описание: Гребенникова, Ю. В. Задачи линейного программирования в школьном курсе математики / Ю. В. Гребенникова. — Текст : непосредственный // Молодой ученый. — 2019. — № 43 (281). — С. 236-239. — URL: https://moluch.ru/archive/281/63249/ (дата обращения: 10.04.2023).
В. Задачи линейного программирования в школьном курсе математики / Ю. В. Гребенникова. — Текст : непосредственный // Молодой ученый. — 2019. — № 43 (281). — С. 236-239. — URL: https://moluch.ru/archive/281/63249/ (дата обращения: 10.04.2023).
Задачами линейного программирования называются задачи, в которых требуется найти наибольшее или наименьшее значение (или экстремум) некоторой линейной функции при наличии некоторых ограничений на переменные, причём все ограничения заданы в виде линейных равенств или неравенств.
Модель задачи линейного программирования имеет вид:
Функция называется целевой функцией, набор переменных , удовлетворяющий системе ограничений, называется допустимым решением (или планом). Множество всех допустимых решений называется областью допустимых решений (ОДР). Допустимое решение, при котором достигается экстремум целевой функции, называется оптимальным решением (оптимальным планом).
Применительно к школьному курсу математики можно рассматривать задачи линейного программирования, содержащие две переменные. Модель задачи в этом случае имеет вид:
В этом случае задачу можно решить графическим способом. Действительно, целевая функция является линейной, и её линией уровня будет прямая. Все неравенства в системе ограничений являются линейными, решение каждого неравенства можно изобразить на плоскости как полуплоскость, расположенную по одну сторону от некоторой прямой. Таким образом, пересечение всех полуплоскостей и будет являться областью допустимых решений. В школьном курсе математики рассматриваются методы решения системы линейных неравенств, основанные на геометрических построениях. Пересечение плоскостей обычно представляет собой некоторый выпуклый многоугольник, и его построение в прямоугольной системе координат не должно вызывать особых сложностей для учеников. Понятие линии уровня также встречается в школьном курсе, причём не только в математике, но и в физике, географии и других дисциплинах.
Проиллюстрируем на примере решение задачи с экономическим содержанием. Пусть швейная фабрика выпускает мужские и женские костюмы, и для их пошива использует ткани четырёх видов Известны величины расходов каждого вида ткани на производство одного мужского и одного женского костюма, а также имеющиеся запасы тканей, заданные в таблице:
Виды тканей | Расход ткани на изготовление одного костюма (условных единиц) | Запасы тканей (тыс. | |
Мужские костюмы | Женские костюмы | ||
A | 2 | 4 | 32 |
B | 3 | 2 | 24 |
C | 3 | 0 | 18 |
D | 0 | 4 | 28 |
Известно, что реализация одного мужского костюма приносит доход в 3 условных единиц, а одного женского — 4 условных единиц. Требуется составить оптимальный план выпуска товаров, то есть такой план, при котором с учётом имеющихся ресурсов тканей доход от реализации костюмов будет наибольшим.
Решение
Построим математическую модель задачи. Введём переменные — количество мужских и женских костюмов соответственно (тыс. шт.). Тогда суммарный доход от их реализации определяется выражением
,
которое нужно максимизировать. По имеющимся исходным данным определяем ограничения по ресурсам каждого вида тканей. Они определяются неравенствами:
— для тканей вида ;
— для тканей вида ;
— для тканей вида ;
— для тканей вида .
Количество выпускаемых костюмов есть величина неотрицательная, поэтому Таким образом, получаем:
Построим область допустимых решений. Заменив в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств на знаки точных равенств, построим по двум контрольным точкам прямые, соответствующие этим равенствам, и для удобства пронумеруем все прямые:
Построим полуплоскости с этими граничными прямыми и найдём их пересечение. Получим шестиугольник , который и представляет собой ОДР. Затем строим линию нулевого уровня она пройдёт через начало координат, построим также нормальный вектор Передвигая линию уровня в направлении вектора параллельно самой себе, найдём крайнюю точку выхода из ОДР, в которой линия уровня займёт положение опорной прямой. В нашем случае это будет точка , которая будет точкой максимума целевой функции. Найдём координаты точки как точки пересечения прямых и , решив систему уравнений:
Получим шестиугольник , который и представляет собой ОДР. Затем строим линию нулевого уровня она пройдёт через начало координат, построим также нормальный вектор Передвигая линию уровня в направлении вектора параллельно самой себе, найдём крайнюю точку выхода из ОДР, в которой линия уровня займёт положение опорной прямой. В нашем случае это будет точка , которая будет точкой максимума целевой функции. Найдём координаты точки как точки пересечения прямых и , решив систему уравнений:
В результате получим:
Значит, — точка максимума, и тогда
.
Таким образом, фабрике следует выпускать 4 тысячи мужских костюмов и 6 тысяч женских костюмов, при этом доход будет наибольшим и составит 36 тысяч условных единиц.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи рационального использования сырья и материалов; оптимизации раскроя; оптимизации производственной программы предприятий; оптимального размещения и концентрации производства; составления оптимального плана перевозок, работы транспорта; управления производственными запасами· и многие другие, принадлежащие сфере оптимального планирования.
Литература:
- Антонюк, Т. П. Задачи линейного программирования. Т. П. Антонюк // г. Ижевск. Ижевская областная типография, 2008–365с.

- Дорофеев, Г. В. Математика. 5 класс. Часть 1. Л. Г. Петерсон// М.: ООО «БИНОМ. Лаборатория знаний»
- Дорофеев, Г. В. Математика. 5 класс. Часть 2. Л. Г. Петерсон// М.: ООО «БИНОМ. Лаборатория знаний»
- Виленкин, А. Н. Математика 5 класс. Часть 1, А. Н. Виленкин., В. И. Жохов., А. С. Чесноков// М.: Просвещение
- Виленкин, А. Н. Математика 5 класс. Часть 2, А. Н. Виленкин., В. И. Жохов., А. С. Чесноков// М.: Просвещение
- Дорофеев, Г. В. Математика. 5 класс. Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова// Под ред. Г. В. Дорофеева, И. Ф. Шарыгина. — М.: Просвещение
- Дорофеев, Г. В. Математика. 6 класс. Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова// Под ред. Г. В. Дорофеева, И. Ф. Шарыгина. — М.: Просвещение
- Никольская, И. Л. Учимся рассуждать и доказывать. И. Л. Никольская, Е. Е. Семенов // Книга для учащихся 6–10 кл. сред.шк.-М.: Просвещение, 1989. –С. 192.
- Матюшкин, А. М. Проблемные ситуации в мышлении и обучении/ А.
 М. Матюшкин — М.:«Педагогика», 2007. — 198 с.
М. Матюшкин — М.:«Педагогика», 2007. — 198 с. - Атанасян, Л. С. Методика преподавания математики в средней школе. / Л. С. Атанасян, — М.: Просвещение, 2012. — 368 с.
Основные термины (генерируются автоматически): линейное программирование, целевая функция, линия уровня, вид, костюм, решение, допустимое решение, нормальный вектор, оптимальное решение, школьный курс математики.
Похожие статьи
Применение метода
линейногоПриложения линейного программирования к решению… допустимое базисное решение, целевая функция, функция, переменная
Пересечение области допустимых решений с линией уровня в том ее положении, когда дальнейшее перемещение линии уровня даст. ..
..
Приложения
линейного программирования к решению…допустимое базисное решение, целевая функция, функция, переменная, квадратичная
Решение задачи линейного программирования в Excel позволяет получить оптимальное
Задача линейного программирования характеризуется линейной целевой функцией…
Планирование производственного процесса при нарушении…
Основные термины (генерируются автоматически): целевая функция, линейное программирование, коэффициент, оптимальное
Задача линейного программирования характеризуется линейной целевой функцией. Задачи оптимального программирования в…
Задачи оптимального программирования в…
Роль графического метода в принятии управленческих
решений.После нахождения области допустимых решений производится поиск оптимального решения.
Пересечение области допустимых решений с линией уровня в том ее положении, когда дальнейшее перемещение линии уровня даст пустое пересечение (вниз для задачи на…
Решение многокритериальных задач линейного…Решение многокритериальных задач линейного программирования (ЗЛП) методом
Получим второе допустимое решение . Целочисленное решение задач линейного
Линейное программирование — это мощный инструмент для описания и решения задач оптимизации.
В данной статье рассматривается понятие линейного программирования, а также наиболее распространенная задача данного класса математического моделирования — транспортная задача.
Некоторые прикладные задачи целочисленного
программированияОбластью допустимых решений полученной исходной задачи является многоугольникOABEFD. Вточке Е(9,4) этого многоугольника целевая функция принимает максимальное значение. Так как координаты точки Е — целые числа и неизвестные принимают целочисленные значения…
Формирование компетенций при изучении дисциплины…
Построим линию уровня, отвечающую значению функции Z = 0 (4×1+3×2 = 0). Вектор-градиент , составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Передвинем линию уровня в направлении вектора параллельно самой себе до…
Вектор-градиент , составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Передвинем линию уровня в направлении вектора параллельно самой себе до…
Решение интервальной задачи дробно-линейного программирования сведением к задаче линейного программирования.
целевая функция, оптимальное решение задачи, ограничение, задача, сумма значений, значение переменных, оптимальное решение задач…
Похожие статьи
Применение метода
линейного программирования для решения.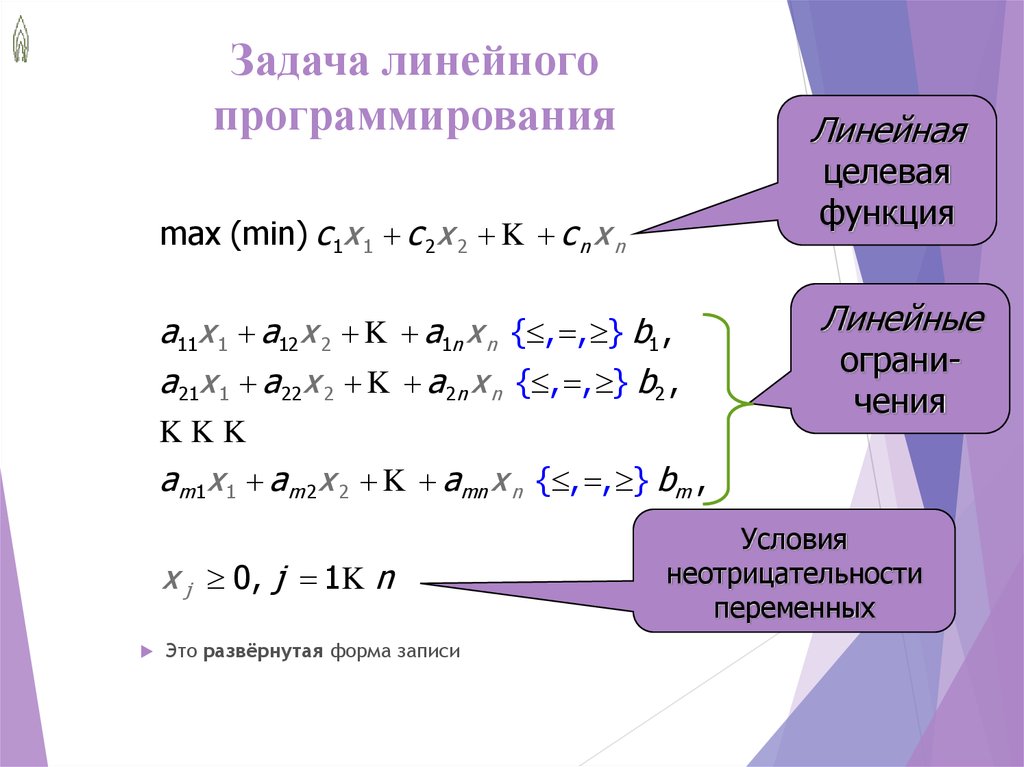 ..
..Приложения линейного программирования к решению… допустимое базисное решение, целевая функция, функция, переменная
Пересечение области допустимых решений с линией уровня в том ее положении, когда дальнейшее перемещение линии уровня даст…
Приложения
линейного программирования к решению…допустимое базисное решение, целевая функция, функция, переменная, квадратичная
Решение задачи линейного программирования в Excel позволяет получить оптимальное
Задача линейного программирования характеризуется линейной целевой функцией. ..
..
Планирование производственного процесса при нарушении…
Основные термины (генерируются автоматически): целевая функция, линейное программирование, коэффициент, оптимальное
Задача линейного программирования характеризуется линейной целевой функцией. Задачи оптимального программирования в…
Роль графического метода в принятии управленческих
решений.После нахождения области допустимых решений производится поиск оптимального решения.
Пересечение области допустимых решений с линией уровня в том ее положении, когда дальнейшее перемещение линии уровня даст пустое пересечение (вниз для задачи на. ..
..
Решение многокритериальных задач линейного программирования (ЗЛП) методом
Получим второе допустимое решение . Целочисленное решение задач линейного
Линейное программирование — это мощный инструмент для описания и решения задач оптимизации.
Решение транспортных задач с применением программирования…В данной статье рассматривается понятие линейного программирования, а также наиболее распространенная задача данного класса математического моделирования — транспортная задача.
Некоторые прикладные задачи целочисленного
программированияОбластью допустимых решений полученной исходной задачи является многоугольникOABEFD. Вточке Е(9,4) этого многоугольника целевая функция принимает максимальное значение. Так как координаты точки Е — целые числа и неизвестные принимают целочисленные значения…
Вточке Е(9,4) этого многоугольника целевая функция принимает максимальное значение. Так как координаты точки Е — целые числа и неизвестные принимают целочисленные значения…
Формирование компетенций при изучении дисциплины…
Построим линию уровня, отвечающую значению функции Z = 0 (4×1+3×2 = 0). Вектор-градиент , составленный из коэффициентов целевой функции, указывает направление максимизации Z(X). Передвинем линию уровня в направлении вектора параллельно самой себе до…
Решение интервальной задачи дробно-линейного…Решение интервальной задачи дробно-линейного программирования сведением к задаче линейного программирования.
целевая функция, оптимальное решение задачи, ограничение, задача, сумма значений, значение переменных, оптимальное решение задач…
Теория линейное программирование — тест с ответами
Математика дается не всем. Но сдавать её нужно чтобы получить за нее зачет или какую либо оценку. Сейчас чаще всего проводится проверка знаний в виде тестирования. Мы собрали частые вопросы встречающиеся в тестах на этой странице. Обратите внимание что правильные варианты ответов выделены символом [+].
Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная
[+] а) Неотрицательна
[-] б) положительна
[-] в) свободна от ограничений
[-] г) отрицательная
Транспортная задача является задачей …. Программирования
[-] а) динамического
[-] б) нелинейного
[+] в) линейного
[-] г) целочисленного
д) параметрического
Если в транспортной задаче объем спроса равен объему предложения, то такая задача называется
[-] а) замкнутой
[+] б) закрытой
[-] в) сбалансированной
[-] г) открытой
д) незамкнутой
Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят
[-] а) фиктивный пункт производства
[+] б) фиктивный пункт потребления
[-] в) изменения структуры не требуются
Методы теории игр предназначены для решения задач
[+] а) с конфликтными ситуациями в условиях неопределенности
[-] б) с полностью детерминированными условиями
[-] в) статистического моделирования
Стратегия игрока – это совокупность правил, определяющих выбор его действий при
[+] а) каждом ходе в зависимости от сложившейся ситуации в одном сеансе игры
[-] б) одном ходе игры
[-] в) всех сеансах игры
Нижняя цена игры – это
[+] а) максимин, т. е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
[-] б) гарантированный выигрыш одного из игроков при любой стратегии другого игрока
[-] в) минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
Верхняя цена игры – это
[+] а) минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
[-] б) гарантированный проигрыш одного из игроков при любой стратегии другого игрока
[-] в) максимин, т.е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
Решение игры в чистых стратегиях определяется
[-] а) ценой игры, равной нижней цене игры
[-] б) ценой игры, равной верхней цене игры
[-] в) наличием седловой точки
[+] г) всем перечисленным в ответах на это задание
Решение игры в смешанных стратегиях определяется
[+] а) вероятностью выбора каждой из активных (полезных) стратегий, совокупный выигрыш которых представляет случайную величину с математическим ожиданием равным цене игры
[-] б) ценой игры, равной нижней цене игры
[-] в) ценой игры, равной верхней цене игры
[-] г) наличием седловой точки
Задача, процесс нахождения решения которой является многоэтапным, относится к задачам
[-] а) линейного программирования
[-] б) теории игр
[+] в) динамического программирования
[-] г) нелинейного программирования
д) параметрического программирования
Определите, что включает симплексный метод решения задач линейного программирования:
[-] а) определение одного из допустимых базисных решений поставленной задачи (опорного плана)
[-] б) определение правила перехода к не худшему решению проверку оптимальности найденного решения
[+] в) определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения
Выберите правильный вариант. Задача линейного программирования не имеет конечного оптимума, если:
Задача линейного программирования не имеет конечного оптимума, если:
[-] а) в точке А области допустимых значений достигается максимум целевой функции F
[-] б) в точке А области допустимых значений достигается минимум целевой функции F
[-] в) система ограничений задачи несовместна
[+] г) целевая функция не ограничена сверху на множестве допустимых решений
Как называется модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений?
[-] а) стандартной
[+] б) канонической
[-] в) общей
[-] г) основной
д) нормальной
Что должно быть в линейных оптимизационных моделях, решаемых с помощью геометрических построений число переменных?
[+] а) не больше двух
[-] б) равно двум
[-] в) не меньше двух
[-] г) не больше числа ограничений +2
д) сколько угодно
Отметьте, какое максимальное значение может достигать задача линейного программирования?
[-] а) только в одной точке
[-] б) в двух точках
[+] в) во множестве точек
[-] г) в одной или двух точках
д) в одной или во множестве точек
Выберите верный вариант. Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная:
Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная:
[+] а) неотрицательна
[-] б) положительна
[-] в) свободна от ограничений
[-] г) отрицательная
Вставьте пропущенное слово. Транспортная задача является задачей ___________ программирования.
[-] а) динамического
[-] б) нелинейного
[+] в) линейного
[-] г) целочисленного
д) параметрического
Как называется задача, если в транспортной задаче объем спроса равен объему предложения:
[-] а) замкнутой
[+] б) закрытой
[-] в) сбалансированной
[-] г) открытой
д) незамкнутой
Выберите верный вариант. Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят:
[-] а) фиктивный пункт производства
[+] б) фиктивный пункт потребления
[-] в) изменения структуры не требуются
Lesson ПРОБЛЕМЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ И РЕШЕНИЯ 1
Этот урок (ПРОБЛЕМЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ И РЕШЕНИЯ 1) создан пользователем Theo(12639) : Посмотреть исходный код, Показать
00 2 О Theo 90:
ПРОБЛЕМА НОМЕР 1
Фермер может засеять до 8 акров земли пшеницей и ячменем сорта
. Он может заработать 5000 долларов за каждые
Он может заработать 5000 долларов за каждые
акров, которые он засеет пшеницей, и 3000 долларов за каждые
акров, которые он засеет ячменем. Использование им необходимого пестицида
ограничено федеральным законом 9.0007 правил до 10 галлонов на все его 8 акров.
Для пшеницы требуется 2 галлона пестицида на каждые
акров земли, а для ячменя требуется всего 1 галлон
на акр.
Какую максимальную прибыль он может получить?
РЕШЕНИЕ ПРОБЛЕМЫ НОМЕР 1
пусть x = количество акров пшеницы
пусть y = количество акров ячменя.
поскольку фермер зарабатывает 5000 долларов за каждый акр пшеницы и 3000 долларов за каждый акр ячменя, то общая прибыль, которую может получить фермер, равна 5000*x + 3000*y.
Пусть p = общая прибыль, которую можно получить. ваше уравнение для прибыли становится:
р = 5000х + 3000у
это ваша целевая функция. это то, что вы хотите максимизировать
ограничения:
количество акров должно быть больше или равно 0.
количество акров должно быть меньше или равно 8.
количество пестицида должно быть меньше или равно 10.
ваши уравнения ограничений:
x >= 0
y >= 0
х + у
2x + y
, чтобы изобразить эти уравнения, найти y в тех уравнениях, в которых есть y, а затем изобразить равенство частей этих уравнений.
х >= 0
г >= 0
г
y
x = 0 — вертикальная линия, совпадающая с осью y.
y = 0 — это горизонтальная линия, совпадающая с линией оси x.
область графа, удовлетворяющая всем ограничениям, является областью допустимости.
максимальное или минимальное решение задачи будет в точках пересечения линий, ограничивающих область допустимости.
график ваших уравнений выглядит следующим образом:
область выполнимости — заштрихованная область графика.
Из этого графика видно, что область допустимости ограничена следующими (x,y) координатными точками:
(0,0)
(0,8)
(2,6)
(5,0)
точка (0,0) является пересечением линии оси x с осью y.
точка (0,8) является пересечением прямой y = 8 — x с осью y.
точка (5,0) является пересечением линии y = 10 — 2x с осью x.
точка (2,6) является пересечением прямой y = 8 — x с прямой y = 10 — 2x.
точка (2,6) была решена следующим образом:
уравнений пересекающихся прямых:
y = 8 — x
y = 10 — 2x
вычесть первое уравнение из второго уравнения, и вы получите:
0 = 2 — x
добавьте x к обеим частям этого уравнения, и вы получите:
x = 2
замените x на 2 в любом уравнении, чтобы получить y = 6.
что делает точку пересечения (x,y) = ( 2,6).
целевое уравнение:
p = 5000x + 3000y
прибыль будет максимальной в точках пересечения области осуществимости на графике.
уравнение прибыли оценивается в каждой из этих точек, как показано в следующей таблице.
точка пересечения (x,y) p
(0,0) $0
(0,8) 24 000 долларов США
(2,6) 28 000 долларов *****
(5,0) 25 000 долларов США
максимальная прибыль возникает, когда фермер засевает 2 акра пшеницы и 6 акров ячменя.
количество акров пшеницы равно 2, а количество акров ячменя равно 6, что в сумме составляет 8 акров, что является максимальным количеством акров, доступных для посадки.
Количество галлонов пестицида, используемого для пшеницы, равно 4, а количество галлонов пестицида, используемого для ячменя, составляет 6, что в сумме составляет 10 галлонов пестицида, что является максимальным количеством пестицида, которое можно использовать.
ПРОБЛЕМА НОМЕР 2
У художника есть ровно 32 единицы желтого красителя и 54 единицы зеленого красителя.
Он планирует смешать как можно больше галлонов цвета A и цвета B.
На каждый галлон цвета A требуется 4 единицы желтой краски и 1 единица зеленой краски.
На каждый галлон цвета B требуется 1 единица желтого красителя и 6 единиц зеленого красителя.
Найдите максимальное количество галлонов, которое он может смешать.
РЕШЕНИЕ ПРОБЛЕМЫ НОМЕР 2
целевая функция состоит в том, чтобы определить максимальное количество галлонов, которое он может смешать.
используются цвета A и B.
пусть x = количество галлонов цвета A.
пусть y = количество галлонов цвета B.
Если мы допустим g = максимальное количество галлонов, которое может сделать маляр, то целевая функция примет вид:
г = х + у
Составьте таблицу для цвета A и цвета B, чтобы определить необходимое количество каждого красителя.
ваша таблица будет выглядеть так:
для каждого галлона цвета A или B потребуется:
единицы желтого красителя единицы зеленого красителя
цвет А 4 1
цвет В 1 6
Всего единиц желтого красителя: 32 Всего
единиц зеленого красителя: 54
ваши уравнения ограничений:
x >= 0
y >= 0
4x + y
x + 6y
x и y должны быть больше или равны 0, потому что количество галлонов не может быть отрицательным.
Чтобы построить эти уравнения в виде графика, вы решаете для y те уравнения, в которых есть y.
уравнения для построения графика:
х >= 0
г >= 0
г
y
x = 0 — вертикальная линия, совпадающая с осью y.
y = 0 — это горизонтальная линия, совпадающая с линией оси x.
график будет выглядеть следующим образом:
область осуществимости — заштрихованная область графика.
все точки в допустимой области удовлетворяют ограничениям задачи.
точками пересечения области осуществимости являются:
(0,0)
(0,9)
(6,8)
(8,0)
максимальное или минимальное значение целевой функции будет в этих точках пересечения.
Решите целевую функцию в каждой из этих точек пересечения, чтобы определить, какая точка содержит максимальное количество галлонов.
целевая функция:
g = x + y
таблица со значением g в каждой из этих точек пересечения показана ниже:
точка пересечения (x,y) галлонов краски (0,0) 0 (0,9) 9 (6,8) 14 ***** (8,0) 8
максимальное количество галлонов краски для цветов A и B, с учетом ограничений, равно 14.
состоит из 6 галлонов цвета A и 8 галлонов цвета B.
6 галлонов цвета A использует 24 галлона желтого красителя и 8 галлонов цвета B используется 8 галлонов желтого красителя, что в сумме дает 32 галлона желтого красителя, что является максимальным количеством желтого красителя, которое можно использовать.
6 галлонов цвета A Пользователь, использующий 6 галлонов зеленого красителя и 8 галлонов цвета B, использует 48 галлонов зеленого красителя, что в сумме дает 54 галлона зеленого красителя, что является максимальным количеством зеленого красителя, которое можно использовать.
ПРОБЛЕМА НОМЕР 3
Магазин бисера продает материалы для изготовления собственных украшений. Покупатель может выбрать бусины из различных корзин. Грейс хочет создать собственное ожерелье на Хэллоуин из оранжевых и черных бусин. Она хочет сделать ожерелье длиной не менее 12 дюймов, но не более 24 дюймов. Грейс также хочет, чтобы ее ожерелье состояло из черных бусин, которые по крайней мере в два раза длиннее оранжевых бусин. Наконец, она хочет, чтобы в ее ожерелье было не менее 5 дюймов черных бусин.
Найдите ограничения, зарисуйте задачу и найдите вершины (точки пересечения)
РЕШЕНИЕ ПРОБЛЕМЫ НОМЕР 3
Пусть x = количество дюймов черных бусин.
пусть y = количество дюймов оранжевых бусин.
целевая функция длина ожерелья
есть максимальная длина и минимальная длина.
Если принять n равным длине ожерелья, то целевая функция примет вид:
н = х + у
, поскольку задача заключается в поиске количества дюймов черных бусин и количества дюймов оранжевых бусин, допустим:
уравнения ограничений для этой задачи:
x >= 0
y >= 0
x + y >= 12
x + y
х >= 2г
х >= 5
x >= 0, потому что количество дюймов черных бусин не может быть отрицательным.
y >= 0, потому что количество дюймов оранжевых бусин не может быть отрицательным.
x + y >= 12, потому что общая длина ожерелья должна быть больше или равна 12 дюймам.
х + у
x >= 2y существует, потому что длина черных бусин должна быть больше или равна удвоенной длине оранжевых бусин.
x >= 5 существует, потому что количество дюймов черных бусин должно быть больше или равно 5.
чтобы построить эти уравнения, мы должны решить для y в каждом уравнении, в котором есть y, а затем изобразить часть равенства каждого из них.
Ваши уравнения для построения графика:
х >= 0
у >= 0
у >= 12 — х
г
у
х >= 5
x = 0 — это вертикальная линия, совпадающая с линией оси Y.
y = 0 — это горизонтальная линия, совпадающая с линией оси x.
х = 5 — это вертикальная линия в точке х = 5.
ниже показан график ваших уравнений:
область выполнимости – заштрихованная область графика.
все точки в области допустимости удовлетворяют ограничениям задачи.
точками пересечения, ограничивающими область осуществимости, являются:
(8,4)
(12,0)
(16,8)
(24,0)
(8,4) — это пересечение прямых y = x/2 и y = 12 — x
найти точку пересечения, приравнять x/2 и 12-x друг другу и найти xx.
получается:
x/2 = 12-x
умножьте обе части уравнения на 2, чтобы получить:
x = 24-2x
прибавьте 2x к обеим частям уравнения, чтобы получить:
3x = 24
разделите обе части уравнения на 3, чтобы получить:
x = 8.
подставьте 8 вместо x в любом уравнении, чтобы получить y = 4.
(12,0) — пересечение прямой y = 12 — x с осью x.
(24,0) — пересечение прямой y = 24 — x с осью x.
, чтобы найти точку пересечения, установите y равным 0 в каждом уравнении и найдите x.
(16,8) есть пересечение прямых y = x/2 и y = 24 — x.
, чтобы найти точку пересечения, приравняйте x/2 к 24-x и найдите x.
вы получаете:
x/2 = 24-x
умножьте обе части этого уравнения на 2, чтобы получить:
x = 48 — 2x
прибавьте 2x к обеим частям этого уравнения, чтобы получить:
3x = 48
разделите обе части этого уравнения на 3, чтобы получить:
x = 16
подставьте 16 вместо x в любом уравнении, чтобы получить:
y = 8.
максимальная/минимальная длина ожерелья будет в точках пересечения границ области возможной реализации.
оценка целевой функции на этих пересечениях дает следующее:
целевая функция:
x + y = n, где n — длина ожерелья в дюймах.
количество точек пересечения в дюймах (8,4) 12 (12,0) 12 (16,8) 24 (24,0) 24
количество дюймов черных бусин как минимум в два раза превышает количество дюймов оранжевых бусин.
количество дюймов черных бусин не менее 5.
общая длина ожерелья больше или равна 12 дюймам или меньше или равна 24 дюймам.
все ограничения соблюдены.
максимальная длина ожерелья, которая может соответствовать ограничениям, составляет 24 дюйма.
минимальная длина ожерелья, которая может соответствовать ограничениям, составляет 12 дюймов.
ПРОБЛЕМА НОМЕР 4
Садовый магазин желает подготовить запас специального удобрения с минимальными затратами путем смешивания двух удобрений, A и B.
Смесь должна содержать:
не менее 45 единиц фосфата
не менее 36 единиц нитрата
не менее 40 единиц аммония
Удобрение А стоит магазину 0,97 доллара за фунт.
Удобрение B стоит в магазине 1,89 доллара за фунт. Удобрение
Удобрение
А содержит 5 единиц фосфата, 2 единицы нитрата и 2 единицы аммония. Удобрение
B содержит 3 единицы фосфата, 3 единицы нитрата и 5 единиц аммония.
сколько фунтов каждого удобрения должен использовать магазин, чтобы минимизировать их стоимость.
РЕШЕНИЕ ПРОБЛЕМЫ НОМЕР 4
пусть x = количество фунтов удобрений A.
пусть y = количество фунтов удобрения B.
целевой функцией является минимизация затрат.
целевая функция принимает вид:
с = 0,97х + 1,89у
уравнения ограничений:
, так как количество фунтов каждого удобрения не может быть отрицательным, 2 уравнения ограничений принимают вид:
х >= 0
у >= 0
, поскольку количество единиц фосфата должно быть не менее 45, уравнение ограничения для фосфата принимает вид:
5x + 3y >= 45
, поскольку количество единиц нитратов должно быть не менее 36, уравнение ограничения для нитратов принимает вид:
2x + 3y >= 36
, поскольку количество единиц аммония должно быть не менее 40, уравнение ограничения для аммония принимает вид:
2x + 5y >= 40
уравнения ограничений для этой задачи принимают вид:
х >= 0
у >= 0
5х + 3у >= 45
2х + 3у >= 36
2x + 5y >= 40
Чтобы построить график этих уравнений, вы должны решить для y в каждом уравнении, в котором есть y, а затем построить график равенства частей этих уравнений.
уравнения для построения графика:
x >= 0
y >= 0
y >= (45-5x)/3
y >= (36 — 2x)/3
y >= (40-2x)/5
x = 0 — это вертикальная линия, совпадающая с линией оси Y.
y = 0 — это горизонтальная линия, совпадающая с линией оси x.
график вашего уравнения показан ниже:
область выполнимости – это заштрихованная область графика.
все точки в области допустимости удовлетворяют ограничениям задачи.
точками пересечения на границах области осуществимости являются:
(0,15) (3,10) (15,2) (20,0)
точки пересечения границ области допустимости содержат решение минимальной стоимости для целевой функции в этой задаче.
теперь, когда у вас есть точки пересечения, вы можете решить уравнение минимальной стоимости, которое является целевой функцией:
с = 0,97х + 1,89у
В следующей таблице показано значение уравнения стоимости в каждой из точек пересечения.
точки пересечения (x,y) c = 0,97x + 1,89y минимальное решение
(0,15) 28,35
(3,10) 21,81
(15,2) 18,33 *****
(20,0) 19. 40
40
таблица предполагает, что у нас есть решение с минимальной стоимостью, когда значение x равно 15, а значение y равно 2.
, когда x = 15 и y = 2, количество фунтов калия, нитратов и аммония составляет:
фосфат = 5x + 3y = 5*15 + 3*2 = 75 + 6 = 81
нитрат = 2x + 3y = 2*15 + 3*2 = 30 + 6 = 36
аммоний = 2x + 5y = 2* 15 + 5*2 = 30 + 10 = 40
соблюдены все ограничения, связанные с целью минимальной стоимости.
р — Как ускорить решение задачи линейного программирования?
Нижеследующее написано на python , но я думаю, что концепция передается очень легко и может быть переформулирована в r при желании.
В основном: Переформулируйте свою проблему. Вместо оптимизации длинного вектора бинарных переменных «отбора» все, что вам нужно, это 3 переменные, чтобы сформулировать это, а именно (целое) число 1, 2 и 3 для выбора.
Это решает почти мгновенно как IP.
импортировать pyomo.environ как pyo из случайного импорта randint п = 1000 к = 500 образец = [randint (1, 3) для t в диапазоне (n)] avail = {t : len([val для val в образце, если val==t]) для t в диапазоне (1, 4)} цель = 86/47 m = pyo.ConcreteModel() m.vals = pyo.Set (инициализация = [1,2,3]) m.pick = pyo.Var(m.vals, domain=pyo.NonNegativeIntegers) m.delta = pyo.Var() m.obj = pyo.Objective (expr = m.delta) # ограничить дельту абсолютным значением |sum(picks) - target| m.C1 = pyo.Constraint(expr=m.delta >= sum(m.pick[v]*v for v в m.vals)-target*k) m.C2 = pyo.Constraint(expr=m.delta >= -sum(m.pick[v]*v для v в m.vals)+target*k) # не используйте больше, чем доступно для каждого значения предел защиты (м, v): вернуть m.pick[v] <= avail[v] m.C3 = pyo.Constraint(m.vals, правило=лимит) soln = pyo.SolverFactory('glpk').solve(m) печать (солн) m.pick.display()
Выходы:
Решатель:
- Статус: ок
Условия окончания: оптимальные
Статистика:
Филиал и граница:
Количество ограниченных подзадач: 885
Количество созданных подзадач: 885
Ошибка rc: 0
Время: 0,358074
81592
Решение:
- количество решений: 0
количество отображаемых решений: 0
выбрать: размер = 3, индекс = значения
Ключ : Нижний : Значение : Верхний : Фиксированный : Устаревший : Домен
1 : 0 : 3. 0 : Нет : Ложь : Ложь : NonNegativeIntegers
2 : 0 : 0.0 : Нет : Ложь : Ложь : NonNegativeIntegers
3 : 0 : 304.0 : Нет : Ложь : Ложь : NonNegativeIntegers
0 : Нет : Ложь : Ложь : NonNegativeIntegers
2 : 0 : 0.0 : Нет : Ложь : Ложь : NonNegativeIntegers
3 : 0 : 304.0 : Нет : Ложь : Ложь : NonNegativeIntegers
Поймите, что вы также можете довольно эффективно атаковать это алгоритмически и получить (довольно просто) почти оптимальный ответ или, приложив немного усилий, также получить оптимальный ответ. Ниже приведена структура, с которой я возился. Ключевое наблюдение заключается в том, что вы можете «добавлять больше троек» к решению до тех пор, пока не достигнете точки, где сумма должна уйти (чтобы получить тыс. * цель может быть заполнена всеми единицами. Это очень близко к как-хорошо- как есть, за исключением случаев, когда вам лучше заменить пару двойок ближе к концу, я думаю, или сделать резервную копию, если у вас закончатся 1.
Приведенное ниже выполняется (в python ) и большую часть пути соответствует для хорошего приближения.
### Код:
# среднее попадание
из случайного импорта randint
п = 1000
к = 50
образец = [randint (1, 3) для t в диапазоне (n)]
доступный = {t : len([val для val в образце, если val==t]) для t в диапазоне (1, 4)}
цель = 86/47
print(f'доступно в начале: {доступно}')
сумма_цель = цель * k
раствор = []
выборки_оставшиеся = к
того = сумма_цель - сумма (солн)
для выбора в диапазоне (k):
если togo > k - выбрать и available[3] > 0:
раствор.

 усл. ед.)
усл. ед.)
 М. Матюшкин — М.:«Педагогика», 2007. — 198 с.
М. Матюшкин — М.:«Педагогика», 2007. — 198 с. 40
40
 environ как pyo
из случайного импорта randint
п = 1000
к = 500
образец = [randint (1, 3) для t в диапазоне (n)]
avail = {t : len([val для val в образце, если val==t]) для t в диапазоне (1, 4)}
цель = 86/47
m = pyo.ConcreteModel()
m.vals = pyo.Set (инициализация = [1,2,3])
m.pick = pyo.Var(m.vals, domain=pyo.NonNegativeIntegers)
m.delta = pyo.Var()
m.obj = pyo.Objective (expr = m.delta)
# ограничить дельту абсолютным значением |sum(picks) - target|
m.C1 = pyo.Constraint(expr=m.delta >= sum(m.pick[v]*v for v в m.vals)-target*k)
m.C2 = pyo.Constraint(expr=m.delta >= -sum(m.pick[v]*v для v в m.vals)+target*k)
# не используйте больше, чем доступно для каждого значения
предел защиты (м, v):
вернуть m.pick[v] <= avail[v]
m.C3 = pyo.Constraint(m.vals, правило=лимит)
soln = pyo.SolverFactory('glpk').solve(m)
печать (солн)
m.pick.display()
environ как pyo
из случайного импорта randint
п = 1000
к = 500
образец = [randint (1, 3) для t в диапазоне (n)]
avail = {t : len([val для val в образце, если val==t]) для t в диапазоне (1, 4)}
цель = 86/47
m = pyo.ConcreteModel()
m.vals = pyo.Set (инициализация = [1,2,3])
m.pick = pyo.Var(m.vals, domain=pyo.NonNegativeIntegers)
m.delta = pyo.Var()
m.obj = pyo.Objective (expr = m.delta)
# ограничить дельту абсолютным значением |sum(picks) - target|
m.C1 = pyo.Constraint(expr=m.delta >= sum(m.pick[v]*v for v в m.vals)-target*k)
m.C2 = pyo.Constraint(expr=m.delta >= -sum(m.pick[v]*v для v в m.vals)+target*k)
# не используйте больше, чем доступно для каждого значения
предел защиты (м, v):
вернуть m.pick[v] <= avail[v]
m.C3 = pyo.Constraint(m.vals, правило=лимит)
soln = pyo.SolverFactory('glpk').solve(m)
печать (солн)
m.pick.display()
 0 : Нет : Ложь : Ложь : NonNegativeIntegers
2 : 0 : 0.0 : Нет : Ложь : Ложь : NonNegativeIntegers
3 : 0 : 304.0 : Нет : Ложь : Ложь : NonNegativeIntegers
0 : Нет : Ложь : Ложь : NonNegativeIntegers
2 : 0 : 0.0 : Нет : Ложь : Ложь : NonNegativeIntegers
3 : 0 : 304.0 : Нет : Ложь : Ложь : NonNegativeIntegers
