Y 1 3x 1 график – Mathway | Популярные задачи — Таловская средняя школа

Содержание

График функции y = 3^x+1

Решение

$$f{\left (x \right )} = 3^{x} + 1$$

График функции

[LaTeX]

Точки пересечения с осью координат X

[LaTeX]

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$3^{x} + 1 = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X Точки пересечения с осью координат Y

[LaTeX]

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в 3^x + 1.
$$3^{0} + 1$$
Результат:
$$f{\left (0 \right )} = 2$$
Точка:

(0, 2)

Экстремумы функции

[LaTeX]

Для того, чтобы найти экстремумы, нужно решить уравнение
$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$3^{x} \log{\left (3 \right )} = 0$$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет Точки перегибов

[LaTeX]

Найдем точки перегибов, для этого надо решить уравнение
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Вторая производная
$$3^{x} \log^{2}{\left (3 \right )} = 0$$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет Горизонтальные асимптоты

[LaTeX]

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$\lim_{x \to -\infty}\left(3^{x} + 1\right) = 1$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты слева:
$$y = 1$$
$$\lim_{x \to \infty}\left(3^{x} + 1\right) = \infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существует Наклонные асимптоты

[LaTeX]

Наклонную асимптоту можно найти, подсчитав предел функции 3^x + 1, делённой на x при x->+oo и x ->-oo
$$\lim_{x \to -\infty}\left(\frac{1}{x} \left(3^{x} + 1\right)\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой справа
$$\lim_{x \to \infty}\left(\frac{1}{x} \left(3^{x} + 1\right)\right) = \infty$$
Возьмём предел
значит,
наклонной асимптоты справа не существует Чётность и нечётность функции

[LaTeX]

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$3^{x} + 1 = 1 + 3^{- x}$$
— Нет
$$3^{x} + 1 = -1 — 3^{- x}$$
— Нет
значит, функция
не является
ни чётной ни нечётной

www.kontrolnaya-rabota.ru

Как построить график линейной функции y=1/3x-1 Дайте пример решения

Заходишь на <a rel=»nofollow» href=»https://www.wolframalpha.com» target=»_blank»>https://www.wolframalpha.com</a>, пишешь свою ф-ю,… всё, любуешься диаграммой

первый по 2 точкам, прдставь 2 значения и соедини линию, а второй это парабола, соприкасаетсяс осью Х в точке (-1,0) и имеет в ней вершину, а дальше также 2 точки посчитай и соединяй

во как хорошо то объяснили.

линейной? у тебя нам Х умноженное на 1/3 или 1 делённое на 3Х?

Если у тебя 1/3x, то это не лийнейная. Это обратная пропорциональность. Строишь гиперболу, находишь асимптоты и строишь схематически. Если 1\3 умножить на х, то по правилам построения линейной функции — берешь аргумент, умножаешь на треть прибавляешь единицу и отображаешь координаты на плоскости. Вторая функция строится чисто по правилам преобразования графиков функции. Строишь параболу и сдвигааешь ее на модуль (1) влево ( все точки, которые выбрал на основной параболе).

Для построение прямой достаточно двух точек. В твоем случае проще всего выбрать точки на коорд. осях: (0;-1) и (3;0). Параболу у=х^2 сдвинь на единицу влево (вдоль ОХ).

y=(x+1)^2 <img src=»//otvet.imgsmail.ru/download/43387438_40a835b3f4affe6269506d1c90d824fd_800.png» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/43387438_40a835b3f4affe6269506d1c90d824fd_120x120.png» data-big=»1″>

touch.otvet.mail.ru

Постройте график функций y = 3/x + 1

Задание.
Постройте график функции y = 3/x + 1.

Решение.
В уравнении данной функции находится дробь, в знаменателе которой стоит переменная х. Как известно, дробь не может существовать при знаменателе, равном нулю. Следовательно, и функция также не будет существовать при х = 0. Получается, что график функции не будет пересекаться с осью Оу.
Исследуем функцию на четность. Для этого вместо переменной х подставим переменную, противоположную ей, —х:

Получили, что функция ни четная, ни нечетная.
Далее пойдем простым путем — путем подбора точек через произвольный выбор значений переменной х. Проще говоря, выберем несколько положительных и отрицательных значений переменной х, высчитаем для них значение функции и получим координаты точек, через которые будет проходить функция.

Запишем координаты полученных точек:

Отметим эти точки на координатной плоскости и проведем через них кривую, не забывая, что функция не будет пересекать ось Оу.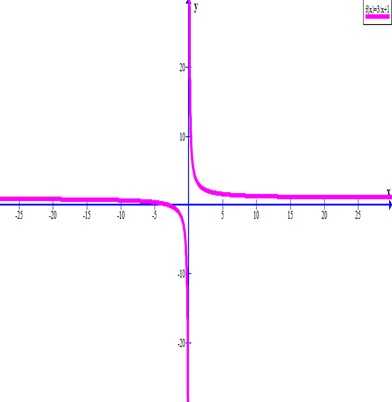

ru.solverbook.com

График функции y = 3^x+1

Решение

Как построить график линейной функции y=1/3x-1 Дайте пример решения

Постройте график функций y = 3/x + 1

Добавить комментарий Отменить ответ