Y 1 4×2: «Построить график функции y=-1/4×2(в квадрате)+x-1?»

Оч надо решение! 90 Алгебра 9 класс Макарычев – Рамблер/класс

Оч надо решение! 90 Алгебра 9 класс Макарычев – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Постройте график функции y=1/4x².
Найдите:
а)   значение у при х = -2,5; —1,5; 3,5;
б)  значения х, при которых у = 5; 3; 2;

в)   промежуток возрастания и промежуток убывания функции.
 

ответы

а) При х = -2,5; у = 1,5625. При х = -1,5; у = 0,5625. При х = 3,5; у = 3,0625;     

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

150 Алгебра 9 класс Макарычев Помогите решить графически

Решите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.
 

ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)

ГДЗ11 классКолмогоров А.Н.Алгебра

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 13 ОГЭ Русский язык 9 класс Однородное подчинение придаточных

     Среди предложений    21-29:  
      (21) И Митрофанов услышал в этом смехе и прощение себе, и даже какое-то (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые).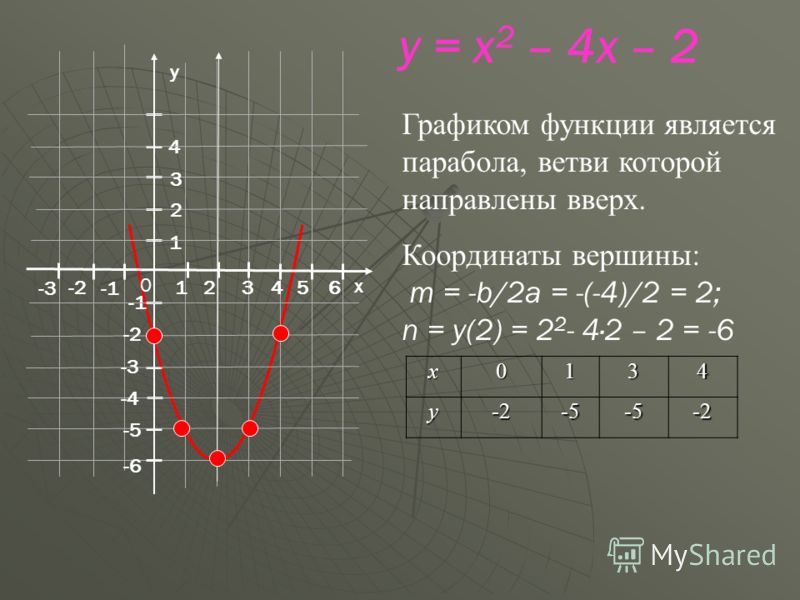 (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Алгебра 8 Мордкович (упр. 19.1

Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 19. Функция у = kх², её свойства и график. ОТВЕТЫ на упражнения 19.1 — 19.66. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.

§ 19. Функция у = kх², её свойства и график

Найдите значение коэффициента k для заданной функции у = kx²:
Задание № 19.1.   а) у = 2х²;   б) у = –8x²;   в) у = 7х²;   г) у = –х².

Смотреть ответы на № 19.1

Задание № 19.2.   а) у = 0,2x²;   б) у = –x²/8;   в) у = –1,85x²;   г) у = –x²/37.

Смотреть ответы на № 19.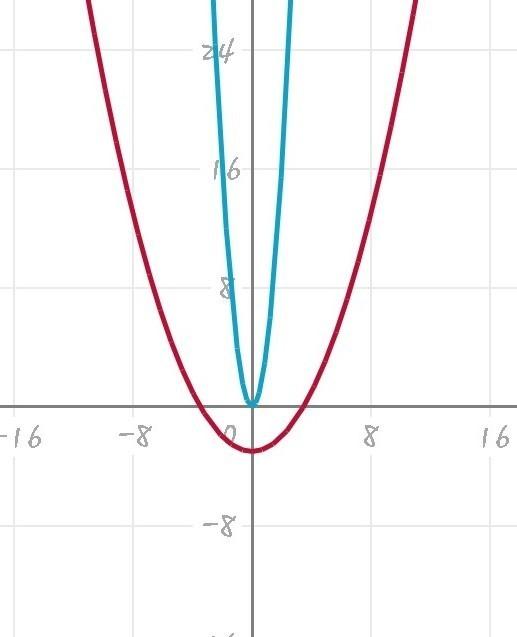

2

Задание № 19.3.   Изобразите схематически график функции:
а) у = –0,2х²;   б) у = 10x²;   в) г/ = –1,8x²;   г) у = ³/₅ • x².

Смотреть ответы на № 19.3

Постройте график функции и укажите, где она убывает, где возрастает:
Задание № 19.4.  а) у = 3х²;   б) y = –4x²;   в) y = –2x²;   г) y = 5x².

Смотреть ответы на № 19.4

Задание № 19.5.  а) у = –1,5x²;   б) y = ¹/₄ • x²;   в) y = 2,5x²;   г) у = –¹/₂ • x².

Смотреть ответы на № 19.5

Постройте в одной системе координат графики заданных функций и сделайте вывод о взаимном расположении построенных графиков:
Задание № 19.6.  а) у = х² и у = –х²;   б) у = 0,5x² и y = –0,5x²;   в) у = 3,5х

2 и у = –3,5х²;   г) у = x²/5 и у = –x²/5.

Смотреть ответы на № 19.6

Задание № 19.7.  

Смотреть ответы на № 19.7

Задание № 19.8.  Не выполняя построения графиков функций, ответьте на вопрос, как расположены в одной системе координат и по отношению друг к другу графики функций:   а) у = 105x² и у = –105x²;   б) у = –3,165x² и у = 3,165x².

Смотреть ответы на № 19.8

Задание № 19.9.  Постройте график функции:
а) у = 2х²;   б) y = 0,5х²;   в) у = 3х²;   г) у = 0,2х².
Что можно сказать о взаимном расположении построенного графика и графика функции у = х²?

Смотреть ответы на № 19.9

Задание № 19.10.   Постройте график функции:
а) у = –1,5х²;   б) у = –3х²;   в) у = –2,5х

2;   г) у = –0,5х².
Что можно сказать о взаимном расположении построенного графика и графика функции у = –х² ?

Смотреть ответы на № 19. 10

Задание № 19.11.  Задайте число k так, чтобы график функции у = kx² был расположен:
а) в первой и второй четвертях;
б) в третьей и четвертой четвертях.

Смотреть ответы на № 19.11

Задание № 19.12.

Смотреть ответы на № 19.12

Задание № 19.13.

Смотреть ответы на № 19.13

Задание № 19.14.

Смотреть ответы на № 19.14

Задание № 19.15.

Смотреть ответы на № 19.15

Задание № 19.16.

Смотреть ответы на № 19.16

Задание № 19.17.

Смотреть ответы на № 19.17

Задание № 19.18.

Смотреть ответы на № 19.18

Задание № 19.19.

Смотреть ответы на № 19.19

Задание № 19.20.

Смотреть ответы на № 19.20

Задание № 19.21.

Смотреть ответы на № 19.21

Задание № 19.22.

Смотреть ответы на № 19.22

Задание № 19.23.

Смотреть ответы на № 19.23

Задание № 19.24.

Смотреть ответы на № 19.24

Задание № 19.25.

Смотреть ответы на № 19.25

Задание № 19.26.

Смотреть ответы на № 19.26

Задание № 19.27.

Смотреть ответы на № 19.27

Задание № 19.28.

Смотреть ответы на № 19.28

Задание № 19.29.

Смотреть ответы на № 19.29

Задание № 19.30.

Смотреть ответы на № 19.30

Задание № 19.31.

Смотреть ответы на № 19.31

Задание № 19.32.

Смотреть ответы на № 19.32

Задание № 19.33.

Смотреть ответы на № 19.33

Задание № 19.34.

Смотреть ответы на № 19.34

Задание № 19.35.

Смотреть ответы на № 19.35

Задание № 19.36.

Смотреть ответы на № 19.36

Задание № 19.37.

Смотреть ответы на № 19.37

Задание № 19.38.

Смотреть ответы на № 19.38

Задание № 19.39.

Смотреть ответы на № 19.39

Задание № 19. 40.

Смотреть ответы на № 19.40

Задание № 19.41.

Смотреть ответы на № 19.41

Задание № 19.42.

Смотреть ответы на № 19.42

Задание № 19.43.

Смотреть ответы на № 19.43

Задание № 19.44.

Смотреть ответы на № 19.44

Задание № 19.45.

Смотреть ответы на № 19.45

Задание № 19.46.

Смотреть ответы на № 19.46

Задание № 19.47.

Смотреть ответы на № 19.47

Задание № 19.48.

Смотреть ответы на № 19.48

Задание № 19.49.

Смотреть ответы на № 19.49

Задание № 19.50.

Смотреть ответы на № 19.50

Задание № 19.51.

Смотреть ответы на № 19.51

Задание № 19.52.

Смотреть ответы на № 19.52

Задание № 19.53.

Смотреть ответы на № 19.53

Задание № 19.54.

Смотреть ответы на № 19.54

Задание № 19.55.

Смотреть ответы на № 19.55

Задание № 19. 56.

Смотреть ответы на № 19.56

Задание № 19.57.

Смотреть ответы на № 19.57

Задание № 19.58.

Смотреть ответы на № 19.58

Задание № 19.59.

Смотреть ответы на № 19.59

Задание № 19.60.

Смотреть ответы на № 19.60

Задание № 19.61.

Смотреть ответы на № 19.61

Задание № 19.62.

Смотреть ответы на № 19.62

Задание № 19.63.

Смотреть ответы на № 19.63

Задание № 19.64.

Смотреть ответы на № 19.64

Задание № 19.65.

Смотреть ответы на № 19.65

Задание № 19.66.

Смотреть ответы на № 19.66

 

---

Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 19. Функция у = kх², её свойства и график. ОТВЕТЫ на упражнения 19.1 — 19.66. Вернуться в ОГЛАВЛЕНИЕ.

Просмотров: 73 941

РЕШЕНО: Найти два решения степенного ряда дифференциального уравнения Глвена относительно обыкновенной точки x = 0.

y» + 8xy’ + 8y = 0 0 Y1 = 1 — 4×2 + 8×4 32 Y1 = 1 — 4×2 8×4 32 3*6 Y1 = 1 — 4×2 + 8×4 32 8x» 32 Y1 = 1 + 4×2 32 Y1 = 1 и Yz = х + 3 64 15 503 и Y2 = X 3* 55*s+ 503 и Y2 65 503 и Y2 Ss 503 и Y2 65 512 105

Вопрос

Пошаговый ответ

Найдите два решения степенного ряда дифференциального уравнения Гвена относительно обычной точки x = 0. у» + 8xy’ + 8y = 0 0 Y1 = 1 — 4×2 + 8×4 32 Y1 = 1 — 4×2 _ 8×4 _ 32 3*6…

Найдите два решения степенного ряда дифференциального уравнения Гвена относительно обычной точки x = 0. y» + 8xy’ + 8y = 0 0 Y1 = 1 — 4×2 + 8×4 32 Y1 = 1 — 4×2 _ 8×4 _ 32 3*6 Y1 = 1 — 4×2 + 8×4 32 8x» 32 Y1 = 1 + 4x2_ 32 Y1 = 1 — 4×2 _ 8×4 и Yz = х + 3 64 15 503 и Y2 = X 3* 55*s+ 503 и Y2 65 503 и Y2 Ss 503 и Y2 65 512 105

---

Видеоответ:

Решено проверенным экспертом

Вопрос о наилучшем совпадении:

Найдите решения двух степенных рядов дифференциального уравнения glven относительно обыкновенной точки x = 0. y» + 8xy’ + 8y = 0 0 Y1 = 1 — 4×2 + 8×4 32 Y1 = 1 — 4×2 _ 8×4 _ 32 3*6 Y1 = 1 — 4×2 + 8×4 32 8x» 32 Y1 = 1 + 4x2_ 32 Y1 = 1 — 4×2 _ 8×4 и Yz = х + 3 64 15 503 и Y2 = X 3* 55*s+ 503 и Y2 65 503 и Y2 Ss 503 и Y2 65 512 105

Рекомендуемые видеоролики

Стенограмма

Нам дано дифференциальное уравнение y двойной штрих плюс 8 x y штрих плюс 8 y равно 0. Нам нужно определить 2 степенных ряда данного дифференциального уравнения относительно обычной точки x , равный 0, теперь с использованием степенного ряда y, равного суммированию n, равного 0 до бесконечности, a n x n y тире, равного суммированию n, равного 1 до бесконечности, A n x, возведенного в степень n минус 1, и двойного тире y, равного суммированию и равного 2. До бесконечности n раз n минус 1, n x возводится в степень n минус 2 пи, теперь помещая эти значения в данное дифференциальное уравнение. Получаем суммирование n равное 2 до бесконечности n раз n минус 1 и x, возведение в степень минус 2 плюс 8 x раз, суммирование n равное 1 до бесконечности и умножение на n x возведение в степень n минус 1 плюс 8 суммирование и равно 0 до бесконечности n x возвести в степень, равную 0, что подразумевает суммирование, равное 2 до бесконечности n раз n минус 1, n x возвести в степень и минус 2 плюс 8 суммирование n равно 1 до бесконечности n n x возвести в степень n плюс 8 суммирование n равно от 0 до бесконечности a n x, возведем в степень n, равной 0, теперь приравняем степени x. Мы получаем суммирование n равное 0 до бесконечности n плюс 2 умноженное на n плюс 1. n плюс 2 x возведение в степень n плюс 8 умноженное на суммирование n равное 1 до бесконечности a n x возведение в степень n плюс 8 суммирование n равное 0 до бесконечности и x возведите в степень, равную 0. Теперь начните каждый член с n. Равно 0, получаем суммирование n равное 0 до бесконечности n плюс 2 умноженное на n плюс 1 умноженное на n плюс 2 х возведение в степень n плюс 8 суммирование n равное 0 до бесконечности n, n х возведенное в степень n плюс 8 суммирование N, равно 0 до бесконечности a n x, возведем в степень, равную 0. Теперь установив коэффициенты равными 0 po, мы получим n плюс 2, умноженное на n плюс 1, n плюс 2 плюс n плюс 18 равно 0. Это означает, что n плюс 2 равно до минус 8, а n при n плюс 2, теперь положим n равным 0, а 2 равно минус 8, а не при 2 равно минус 4, а не и при n равно 1, а 3 равно минус 8, при 3, a не равно минус 4. Следовательно, решение равно y равно a не плюс a 1 x минус 4, a не x квадрат минус 8.