Y 5x 2 график: Mathway | Популярные задачи

2

Алгебра 7 Макарычев КР-3 В3

10/09/202029/06/2021 Администратор

Контрольная работа № 3 «Функции и их графики. Линейная функция» по алгебре в 7 классе с ответами и решениями Вариант 3. Представленные ниже работа ориентирована на учебник «Алгебра 7 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Алгебра 7 Макарычев КР-3 В3.

Другие варианты:  КР-3 Вариант 1 КР-3 Вариант 2 КР-3 Вариант 4

Алгебра 7 класс (Макарычев)

Контрольная работа № 3. Вариант 3

КР-3 «Функции и их графики. Линейная функция» (транскрипт заданий)

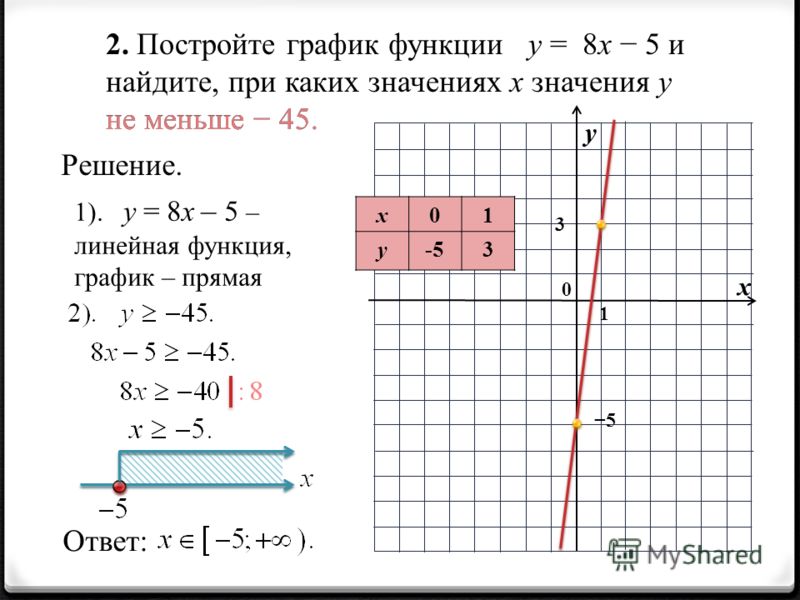
1. Функция задана формулой y = 5x + 18. Определите:
   а) значение y, если x = 0,4;  б) значение x, при котором у = 3;  в) проходит ли ее график через точку С(–6; –12).
2. а) Постройте график функции у = 2x + 4.
   б) Укажите с помощью графика, чему равно значение у при х = –1,5.
3. В одной и той же системе координат постройте графики функций: а) y = –0,5x;   б) у = 5.
4. Найдите координаты точки пересечения графиков функций у = –14x + 32 и у = 26x – 8.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат.

 

ОТВЕТЫ на контрольную работу

№1. Функция задана формулой y = 5x + 18. Определите: а) значение y, если x = 0,4;  б) значение x, при котором у = 3;  в) проходит ли ее график через точку С(–6; –12).
Правильный ответ: а) у = 20;  б) х = –3;  в) 5 • (–6) + 18 = –12. Верно, график проходит через С(–6; –12).

№2. а) Постройте график функции у = 2x + 4. б) Укажите с помощью графика, чему равно значение у при х = –1,5.
Правильный ответ: а) см. построение графика в спойлере;

б) 2 • (–1, 5) + 4 = 1.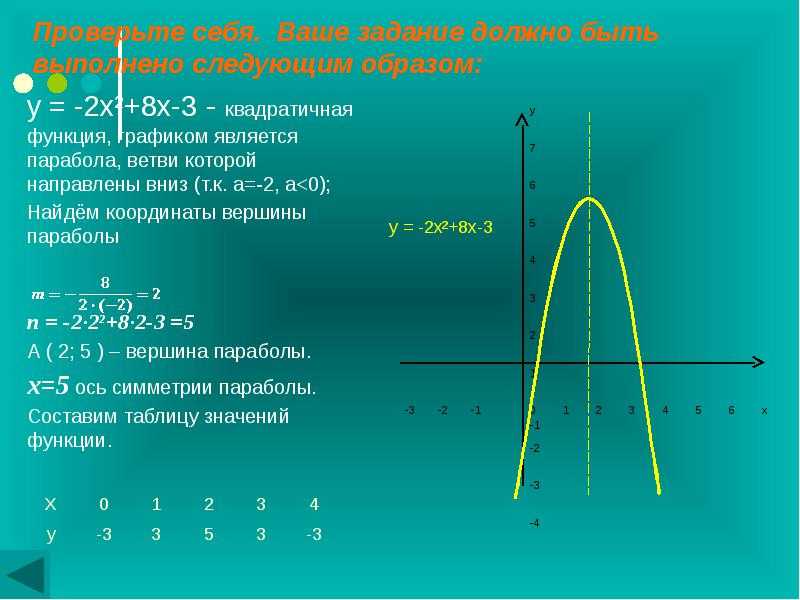

№3. В одной и той же системе координат постройте графики функций: а) y = –0,5x;   б) у = 5.
Правильный ответ: а) у = –0.5х;   б) у = 5.

№4. Найдите координаты точки пересечения графиков функций у = –14x + 32 и у = 26x – 8.
Правильный ответ: –14х + 32 = 26х – 8; х = 1; у = 18; А(1; 18).

№5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат.
Подсказка: b = 0. Правильный ответ: у = 2х.

   Нажмите на спойлер ниже, чтобы увидеть решения всех заданий в тетради.

Смотреть подробные РЕШЕНИЯ заданий

 

Другие варианты:  КР-3 Вариант 1 КР-3 Вариант 2 КР-3 Вариант 4

Вернуться на страницу: КОНТРОЛЬНЫЕ РАБОТЫ по алгебре в 7 классе (Макарычев).

 

---

Вы смотрели: Алгебра 7 Макарычев КР-3 В3. Контрольная работа по алгебре 7 класс «Уравнения с одной переменной» для УМК Макарычев и др.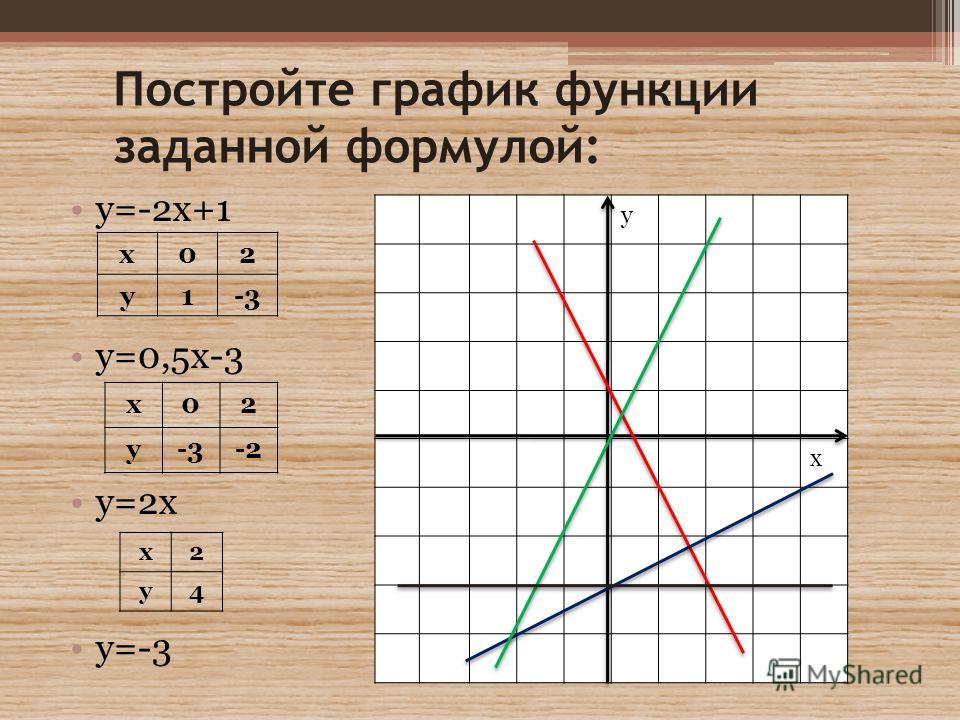 Цитаты из учебного пособия «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение» использованы в учебных целях. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий.

Ответы

Вас могут заинтересовать…

2-3x-11=0 Tiger Algebra Solver

Пошаговое решение :

Шаг 1 :

Уравнение в конце шага 1 :

 (5x  2  - 3x) - 11 = 0
 

Шаг 2 :

Попытка разложить средний член на множители.

Средний член равен  -3 x , его коэффициент равен -3 .
Последний член, «константа», равен  -11 

Шаг-1: Умножьте коэффициент первого члена на константу   5 • -11 = -55 

Шаг-2: Найдите два множителя -55 , сумма которых равна коэффициенту среднего члена, который равен   -3 .

	-55	+	1	=	-54
	-11	+	5	=	-6
	-5	+	11	=	6
	-1	+	55	=	54

Observation : No two такие факторы можно найти!!
Заключение: Трехчлен нельзя разложить на множители

Уравнение в конце шага 2 :

 5x  2  - 3x - 11 = 0
 

Шаг 3 :

Парабола, нахождение вершины :

 3. 1      Найдите вершину     y = 5x ² -3x-11

Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как нанесем на график «у», потому что коэффициент первого члена, 5 , положителен (больше нуля).

 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.

 Параболы могут моделировать многие реальные жизненные ситуации, например, высоту над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую ​​информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

 Для любой параболы, Ax ² +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна  0,3000  

Подключение к формуле параболы 0,3000 для x Мы можем рассчитать y -координату:
y = 5,0 * 0,30 * 0,30 -3,0 * 0,30 -11,0
или y = -11,450

Parabola, график вершина и X -Intercess:

.

Корневой график для:  y = 5x ² -3x-11
Ось симметрии (штриховая)  {x}={ 0,30} 
Вершина в  {x,y} = {0,30,-11,45} 
 x -Перехваты (корни ) :
Корень 1 в точке {x,y} = {-1,21, 0,00}
Корень 2 в точке {x,y} = {1,81, 0,00}

Решите квадратное уравнение, заполнив квадрат

 3.2     Решение   5x ² -3x-11 = 0, заполнив квадрат .

 Поделите обе части уравнения на 5, чтобы получить 1 в качестве коэффициента при первом члене:
   x ² -(3/5)x-(11/5) = 0

Прибавьте 11/5 к обеим частям уравнения:
   x ² -(3/5)x = 11/5

Теперь немного хитрости: возьмем коэффициент при x, равный 3/5, разделим на два, получим 3/10, и, наконец, возвести в квадрат это дает 9/100

Прибавьте 9/100 к обеим частям уравнения:
/100) дает 229/100 
  Таким образом, прибавив к обеим частям, мы окончательно получим:
   x ² -(3/5)x+(9/100) = 229/100

Добавление 9/100 завершило левую часть в полный квадрат:
   x ² -(3/5)x+(9/100)  =
   (x-(3/10)) • (x-(3/10))  =
  (x-(3 /10)) ²
Вещи, равные одной и той же вещи, также равны друг другу. Так как
   x ² -(3/5)x+(9/100) = 229/100 и
   x ² -(3/5)x+(9/100) = (x-(3/10)) ²
тогда, согласно закону транзитивности,
   (x-(3/10)) ² = 229/100

Мы будем называть это уравнение уравнением #3.2.1  

Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.

Обратите внимание, что квадратный корень из
   (x-(3/10)) ²  is
   (x-(3/10)) ^2/2  =
 (x-(3/10)) ¹  =
   x-(3/ 10)

Теперь, применяя принцип квадратного корня к уравнению. #3.2.1  получаем:
   x-(3/10) = √ 229/100

Добавьте 3/10 к обеим частям, чтобы получить:
   x = 3/10 + √ 229/100

Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное/100
или
x = 3/10 — √ 229/100

Обратите внимание, что √ 229/100 можно записать как
√ 229/√ 100, что является √ 229/10

Уравнение квадратично

 3. 3     Решение    5x ² -3x-11 = 0 по квадратичной формуле .

 Согласно квадратичной формуле,  x  , решение для   Ax ² +Bx+C  = 0  , где A, B  и C – числа, часто называемые коэффициентами, определяется следующим образом:
                        
-B ± √ B ² -4AC
x = ————————
2A

В нашем случае A = 5
B = -3
C = -11

Соответственно, b ² -4AC =
9-(-220) =
229

Применение квадратичной формулы:

3 ± √ 229
x = ————
10

√ 229, округленная до 4 десятичных цифр, составляет 15,1327
, так что теперь мы рассмотрим:
x = (3 ± 15,133)/10

Два реальных решения:

x = (3+√229)/10 = 1,813

или:

 x = (3-√229)/10=-1,213

Два решения были найдены: √229)/10= 1,813

11.4: Графики линейных уравнений (Часть 2)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

21783

• OpenStax
• OpenStax

Вертикальные и горизонтальные линии на графике

Можем ли мы изобразить уравнение только с одной переменной? Просто х и без у, или просто у без х? Как мы составим таблицу значений, чтобы получить точки для построения?

Рассмотрим уравнение x = −3. Уравнение говорит, что x всегда равно −3, поэтому его значение не зависит от y. Независимо от того, что такое y, значение x всегда равно −3.

Чтобы составить таблицу решений, мы пишем -3 для всех значений x. Затем выберите любые значения для y. Поскольку x не зависит от y, вы можете выбирать любые числа. Но чтобы соответствовать размеру нашего графика координат, мы будем использовать 1, 2 и 3 для координат y, как показано в таблице.

х = -3
х	у	(х, у)
-3	1	(-3, 1)
-3	2	(-3, 2)
-3	3	(-3, 3)

Затем нанесите точки и соедините их прямой линией.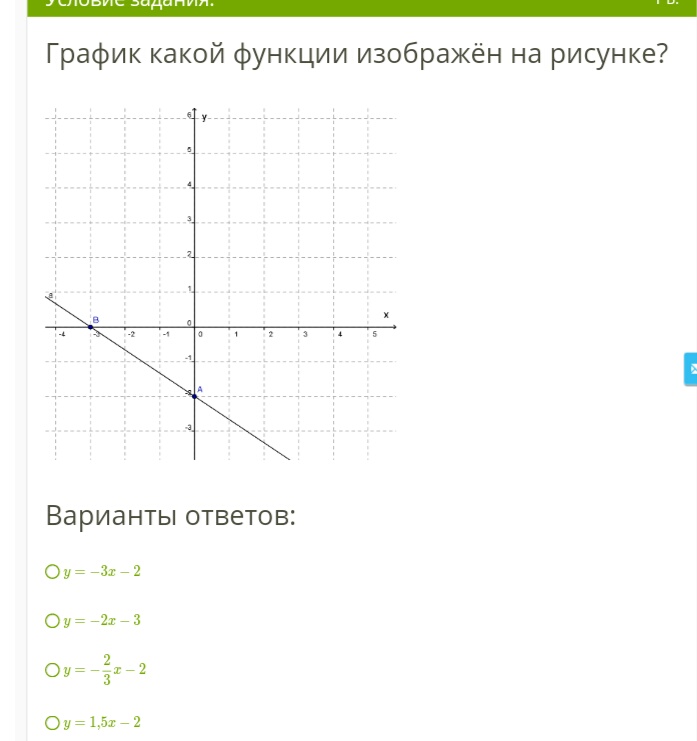 Обратите внимание на рисунок \(\PageIndex{5}\), что диаграмма представляет собой

вертикальная линия .

Рисунок \(\PageIndex{5}\)

Определение: Вертикальная линия

Вертикальная линия — это график уравнения, которое можно записать в виде x = a. Линия проходит через ось x в точке (a, 0).

Пример \(\PageIndex{6}\):

Изобразите уравнение x = 2. Какой тип линии оно образует?

Решение

В уравнении есть только переменная x, а x всегда равен 2. Мы составляем таблицу, где x всегда равно 2, и вводим любые значения y.

х = -3
х	у	(х, у)
2	1	(2, 1)
2	2	(2, 2)
2	3	(2, 3)

Нанесите точки и соедините их, как показано.

График представляет собой вертикальную линию, проходящую через ось x в точке 2.

Упражнение \(\PageIndex{10}\):

Нарисуйте уравнение: x = 5.

Ответ

Упражнение \(\PageIndex{11}\):

Нарисуйте уравнение: x = −2.

Ответить

Что, если в уравнении есть y, но нет x? Давайте нарисуем уравнение y = 4. На этот раз значение y является константой, поэтому в этом уравнении y не зависит от x.

Чтобы составить таблицу решений, напишите 4 для всех значений y, а затем выберите любое значение для x.

Мы будем использовать 0, 2 и 4 для значений x.

х = -3
х	у	(х, у)
0	4	(0, 4)
2	4	(2, 4)
4	4	(4, 4)

Нанесите точки и соедините их, как показано на рисунке \(\PageIndex{6}\). Этот график представляет собой горизонтальную линию, проходящую через ось Y в точке 4.

Рисунок \(\PageIndex{6}\)

Определение: Горизонтальная линия

Горизонтальная линия представляет собой график уравнения, которое можно записать в виде у = b. Линия проходит через ось y в точке (0, b).

Пример \(\PageIndex{7}\):

Нарисуйте уравнение y = −1.

Решение

Уравнение y = −1 имеет только переменную y. Значение у является постоянным. Все упорядоченные пары в таблице имеют одну и ту же координату y, −1. Мы выбираем 0, 3 и −3 в качестве значений x.

х = -3
х	у	(х, у)
-3	-1	(-3, -1)
0	-1	(0, -1)
3	-1	(3, -1)

График представляет собой горизонтальную линию, проходящую через ось Y в точке –1, как показано.

Упражнение \(\PageIndex{12}\):

Нарисуйте уравнение: y = −4.

Ответить

Упражнение \(\PageIndex{13}\):

Нарисуйте уравнение: y = 3.

Ответ

Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения вида y = 4x. В чем разница между уравнениями y = 4x и y = 4?

Уравнение y = 4x содержит и x, и y. Значение у зависит от значения х. Координата y изменяется в соответствии со значением x.

Уравнение y = 4 имеет только одну переменную. Значение у является постоянным. Координата y всегда равна 4. Она не зависит от значения x.

у = 4х
х	у	(х, у)
0	0	(0, 0)
1	4	(1, 4)
2	8	(2, 8)

\(\textcolor{red}{y = 4}\)
х	у	(х, у)
0	4	(0, 4)
1	4	(1, 4)
2	4	(2, 4)

На графике показаны оба уравнения.

Обратите внимание, что уравнение y = 4x дает наклонную линию, тогда как y = 4 дает горизонтальную линию.

Пример \(\PageIndex{8}\):

График y = −3x и y = −3 в одной и той же прямоугольной системе координат.

Решение

Найдите три решения для каждого уравнения. Обратите внимание, что в первом уравнении есть переменная x, а во втором нет. Решения для обоих уравнений перечислены.

\(\textcolor{red}{y = -3x}\)
х	у	(х, у)
0	0	(0, 0)
1	-3	(1, -3)
2	-6	(2, -6)

у = -3
х	у	(х, у)
0	-3	(0, -3)
1	-3	(1, -3)
2	-3	(2, -3)

На графике показаны оба уравнения.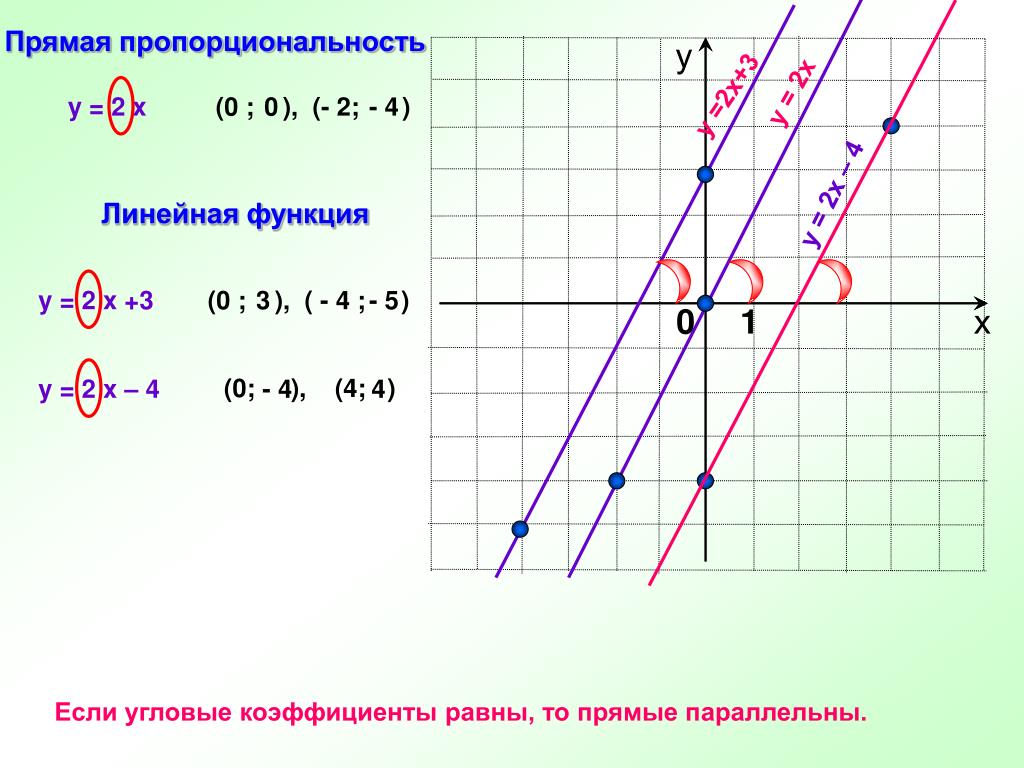

Упражнение \(\PageIndex{14}\):

Нарисуйте уравнения в той же прямоугольной системе координат: y = −4x и y = −4.

Ответить

Упражнение \(\PageIndex{15}\):

Нарисуйте уравнения в той же прямоугольной системе координат: y = 3 и y = 3x.

Ответить

ДОСТУП К ДОПОЛНИТЕЛЬНЫМ ОНЛАЙН-РЕСУРСАМ

Использование таблицы значений

График линейного уравнения, содержащего дроби

График горизонтальных и вертикальных линий

Практика делает решение уравнения на графике идеальным

Распознавание соотношения0222

Для каждой упорядоченной пары решите, а) является ли упорядоченная пара решением уравнения? б) находится ли точка на прямой?

39. у = х + 2
    1. (0, 2)
    2. (1, 2)
    3. (− 1, 1)
    4. (- 3, 1)
40. у = х — 4
    1. (0, − 4)
    2. (3, − 1)
    3. (2, 2)
    4. (1, − 5)
41. у = \ (\ dfrac {1} {2} \) х — 3
    1. (0, − 3)
    2. (2, − 2)
    3. (- 2, — 4)
    4. (4, 1)
42. у = \(\dfrac{1}{3}\)х + 2
    1. (0, 2)
    2. (3, 3)
    3. (- 3, 2)
    4. (− 6, 0)

Построение графика линейного уравнения по точкам

В следующих упражнениях построение графика по точкам.

43. у = 3х — 1
44. у = 2х + 3
45. у = -2х + 2
46. у = -3х + 1
47. у = х + 2
48. у = х — 3
49. у = — х — 3
50. у = — х — 2
51. г = 2 х
52. г = 3 х
53. г = -4x
54. г = -2x
55. у = \(\dfrac{1}{2}\)х + 2
56. у = \(\dfrac{1}{3}\)х — 1
57. у = \(\dfrac{4}{3}\)х — 5
58. у = \(\dfrac{3}{2}\)х — 3
59. у = \(- \dfrac{2}{5}\)х + 1
60. у = \(- \dfrac{4}{5}\)х — 1
61. у = \(- \dfrac{3}{2}\)х + 2
62. у = \(- \dfrac{5}{3}\)х + 4
63. х + у = 6
64. х + у = 4
65. х + у = -3
66. х + у = -2
67. х — у = 2
68. х — у = 1
69. х — у = -1
70. х — у = -3
71. -х + у = 4
72. −х + у = 3
73. -х — у = 5
74. -х — у = 1
75. 3x + у = 7
76. 5х + у = 6
77. 2х + у = -3
78. 4х + у = -5
79. 2х + 3у = 12
80. 3х — 4у = 12
81. \(\dfrac{1}{3}\)х + у = 2
82. \(\dfrac{1}{2}\)х + у = 3

График вертикальных и горизонтальных линий

В следующих упражнениях начертите вертикальные и горизонтальные линии.

83. х = 4
84. х = 3
85. х = −2
86. х = −5
87. г = 3
88. г = 1
89. г = -5
90. г = -2
91. х = \(\dfrac{7}{3}\)
92. х = \(\dfrac{5}{4}\)

В следующих упражнениях постройте график каждой пары уравнений в одной и той же прямоугольной системе координат.

93. y = \(− \dfrac{1}{2}\)x и y = \(− \dfrac{1}{2}\)
94. y = \(− \dfrac{1}{3}\)x и y = \(− \dfrac{1}{3}\)
95. у = 2х и у = 2
96. у = 5х и у = 5

Смешанная практика

В следующих упражнениях постройте график каждого уравнения.

97. у = 4x
98. г = 2 х
99. у = \(- \dfrac{1}{2}\)х + 3
100. у = \(\dfrac{1}{4}\)х — 2
101. у = — х
102. у = х
103. х — у = 3
104. х + у = — 5
105. 4x + у = 2
106. 2х + у = 6
107. г = -1
108. г = 5
109. 2х + 6у = 12
110. 5х + 2у = 10
111. х = 3
112. х = -4

Математика на каждый день

113. Стоимость дома на колесах Робинсоны арендовали дом на колесах на неделю, чтобы поехать в отпуск. Аренда дома на колесах обошлась им в 594 доллара плюс 0,32 доллара за милю, поэтому линейное уравнение y = 594 + 0,32x дает стоимость y для проезда x миль. Подсчитайте стоимость аренды за проезд в 400, 800 и 1200 миль, а затем нарисуйте линию.
114. Еженедельный заработок В художественной галерее, где он работает, Сальвадор получает 200 долларов в неделю плюс 15% от продаж, которые он делает, поэтому уравнение y = 200 + 0,15x дает сумму y, которую он зарабатывает за продажу x долларов произведений искусства. Подсчитайте сумму, которую Сальвадор зарабатывает на продаже 9 долларов.00, 1600 и 2000 долларов, а затем начертите линию.

Письменные упражнения

115. Объясните, как вы выберете три значения x, чтобы составить таблицу для построения графика линии y = \(\dfrac{1}{5}\)x − 2.
116. В чем разница между уравнениями вертикальной и горизонтальной прямой?

Самопроверка

(a) После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.