Graph equations with Step-by-Step Math Problem Solver
The language of mathematics is particularly effective in representing relationships between two or more variables. As an example, let us consider the distance traveled in a certain length of time by a car moving at a constant speed of 40 miles per hour. We can represent this relationship by
- 1. A word sentence:
The distance traveled in miles is equal to forty times the number of hours traveled. - 2. An equation:
d = 40r. - 3. A tabulation of values.
- 4. A graph showing the relationship between time and distance.
We have already used word sentences and equations to describe such relationships; in this chapter, we will deal with tabular and graphical representations.
7.1 SOLVING EQUATIONS IN TWO VARIABLES
ORDERED PAIRS
The equation d = 40f pairs a distance d for each time t. For example,
if t = 1, then d = 40
if t = 2, then d = 80
if t = 3, then d = 120
and so on.
The pair of numbers 1 and 40, considered together, is called a solution of the equation d = 40r because when we substitute 1 for t and 40 for d in the equation, we get a true statement. If we agree to refer to the paired numbers in a specified order in which the first number refers to time and the second number refers to distance, we can abbreviate the above solutions as (1, 40), (2, 80), (3, 120), and so on. We call such pairs of numbers ordered pairs, and we refer to the first and second numbers in the pairs as components. With this agreement, solutions of the equation d — 40t are ordered pairs (t, d) whose components satisfy the equation. Some ordered pairs for t equal to 0, 1, 2, 3, 4, and 5 are
(0,0), (1,40), (2,80), (3,120), (4,160), and (5,200)
Such pairings are sometimes shown in one of the following tabular forms.
In any particular equation involving two variables, when we assign a value to one
of the variables, the value for the other variable is determined and therefore
dependent on the first.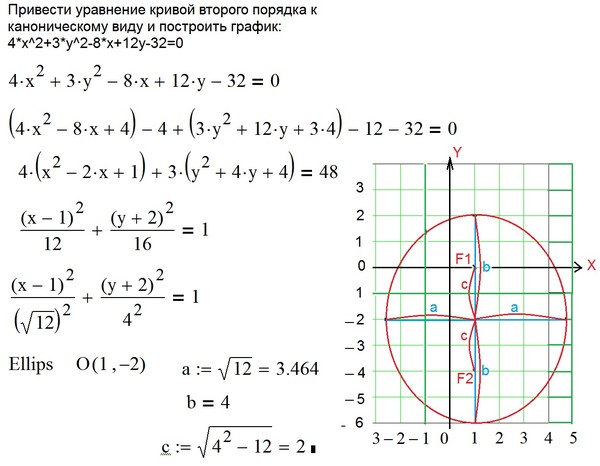
by substituting a particular value of one variable into Equation (1) and solving for the other variable.
Example 1
Find the missing component so that the ordered pair is a solution to
2x + y = 4
a. (0,?)
b. (1,?)
c. (2,?)
if x = 0, then 2(0) + y = 4
y = 4
if x = 1, then 2(1) + y = 4
y = 2
if x = 2, then 2(2) + y = 4
y = 0
The three pairings can now be displayed as the three ordered pairs
(0,4), (1,2), and (2,0)
or in the tabular forms
EXPRESSING A VARIABLE EXPLICITLY
We can add -2x to both members of 2x + y = 4 to get
-2x + 2x + y = -2x + 4
y = -2x + 4
In Equation (2), where y is by itself, we say that y is expressed explicitly in terms
of x. It is often easier to obtain solutions if equations are first expressed in such form
because the dependent variable is expressed explicitly in terms of the independent
variable.
It is often easier to obtain solutions if equations are first expressed in such form
because the dependent variable is expressed explicitly in terms of the independent
variable.
For example, in Equation (2) above,
if x = 0, then y = -2(0) + 4 = 4
if x = 1, then y = -2(1) + 4 = 2
if x = 2 then y = -2(2) + 4 = 0
We get the same pairings that we obtained using Equation (1)
(0,4), (1,2), and (2,0)
We obtained Equation (2) by adding the same quantity, -2x, to each member of Equation (1), in that way getting y by itself. In general, we can write equivalent equations in two variables by using the properties we introduced in Chapter 3, where we solved first-degree equations in one variable.
Equations are equivalent if:
- The same quantity is added to or subtracted from equal quantities.
- Equal quantities are multiplied or divided by the same nonzero quantity.
Example 2
Solve 2y — 3x = 4 explicitly for y in terms of x and obtain solutions for x = 0,
x = 1, and x = 2.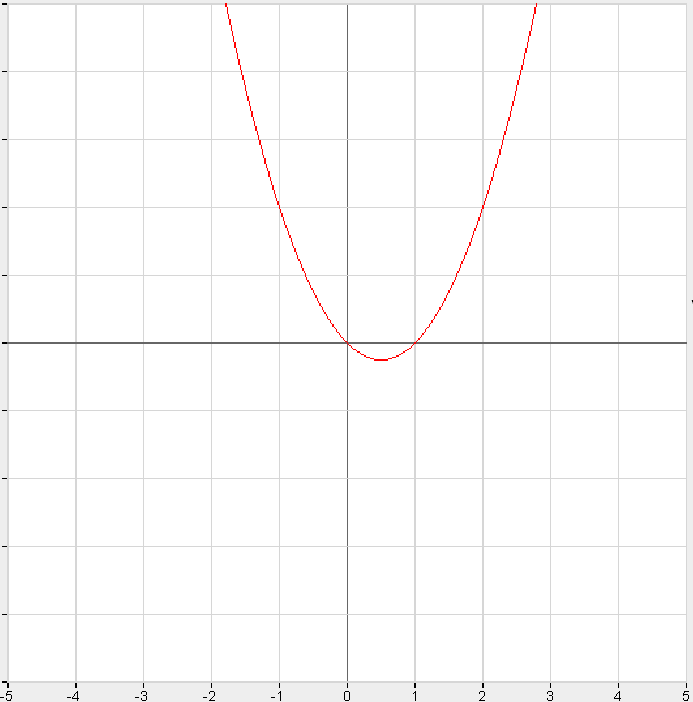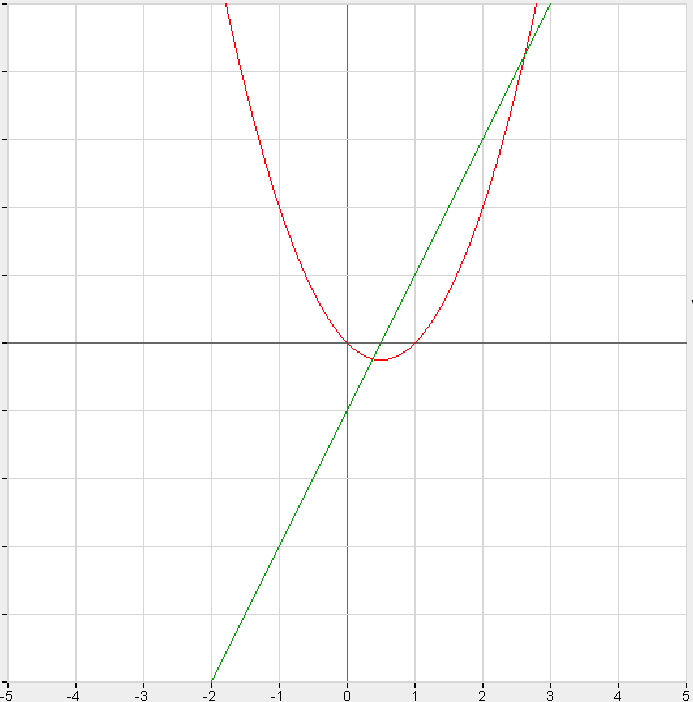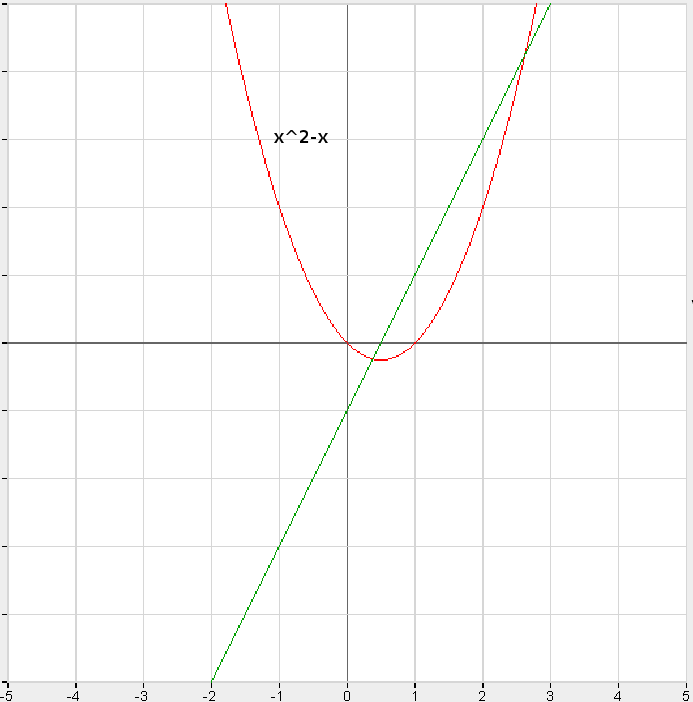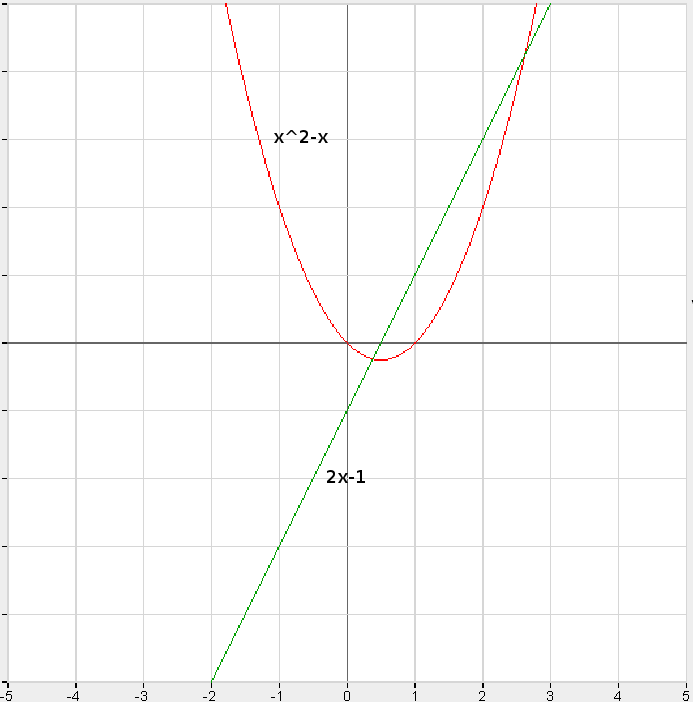
Solution
First, adding 3x to each member we get
2y — 3x + 3x = 4 + 3x
2y = 4 + 3x (continued)
Now, dividing each member by 2, we obtain
In this form, we obtain values of y for given values of x as follows:
In this case, three solutions are (0, 2), (1, 7/2), and (2, 5).
FUNCTION NOTATION
Sometimes, we use a special notation to name the second component of an ordered pair that is paired with a specified first component. The symbol f(x), which is often used to name an algebraic expression in the variable x, can also be used to denote the value of the expression for specific values of x. For example, if
f(x) = -2x + 4
where f{x) is playing the same role as y in Equation (2) on page 285, then f(1) represents the value of the expression -2x + 4 when x is replaced by 1
f(l) = -2(1) + 4 = 2
Similarly,
f(0) = -2(0) + 4 = 4
and
f(2) = -2(2) + 4 = 0
The symbol f(x) is commonly referred to as function notation.
Example 3
If f(x) = -3x + 2, find f(-2) and f(2).
Solution
Replace x with -2 to obtain
f(-2) = -3(-2) + 2 = 8
Replace x with 2 to obtain
f(2) = -3(2) + 2 = -4
7.2 GRAPHS OF ORDERED PAIRS
In Section 1.1, we saw that every number corresponds to a point in a line. Simi- larly, every ordered pair of numbers (x, y) corresponds to a point in a plane. To graph an ordered pair of numbers, we begin by constructing a pair of perpendicular number lines, called axes. The horizontal axis is called the x-axis, the vertical axis is called the y-axis, and their point of intersection is called the origin. These axes divide the plane into four quadrants, as shown in Figure 7.1.
Now we can assign an ordered pair of numbers to a point in the plane by referring
to the perpendicular distance of the point from each of the axes. If the first
component is positive, the point lies to the right of the vertical axis; if negative, it
lies to the left. If the second component is positive, the point lies above the
horizontal axis; if negative, it lies below.
If the second component is positive, the point lies above the
horizontal axis; if negative, it lies below.
Example 1
Graph (3, 2), (-3, 2), (-3, -2), and (3, -2) on a rectangular coordinate system.
Solution
The graph of (3, 2) lies 3 units to the right of
the y-axis and 2 units above the x-axis;
the graph of (-3,2) lies 3 units to the left of the
y-axis and 2 units above the x-axis;
the graph of (-3, -2) lies 3 units to the left of
the y-axis and 2 units below the x-axis;
the graph of (3, -2) lies 3 units to the right of
the y-axis and 2 units below the x-axis.
The distance y that the point is located from the x-axis is called the ordinate of the point, and the distance x that the point is located from the y-axis is called the abscissa of the point. The abscissa and ordinate together are called the rectan- gular or Cartesian coordinates of the point (see Figure 7.2).
7.3 GRAPHING FIRST-DEGREE EQUATIONS
In Section 7.1, we saw that a solution of an equation in two variables is an ordered
pair.
y = x + 2
by letting x equal 0, -3, -2, and 3. Then,
for x = 0, y=0+2=2
for x = 0, y = -3 + 2 = -1
for x = -2, y = -2 + 2 — 0
for x = 3, y = 3 + 2 = 5
and we obtain the solutions
(0,2), (-3,-1), (-2,0), and (3,5)
which can be displayed in a tabular form as shown below.
If we graph the points determined by these ordered pairs and pass a straight line through them, we obtain the graph of all solutions of y = x + 2, as shown in Figure 7.3. That is, every solution of y = x + 2 lies on the line, and every point on the line is a solution of y = x + 2.
The graphs of first-degree equations in two
variables are always straight lines; therefore,
such equations are also referred to as linear
equations.
In the above example, the values we used for x were chosen at random; we could have used any values of x to find solutions to the equation. The graphs of any other ordered pairs that are solutions of the equation would also be on the line shown in Figure 7.3. In fact, each linear equation in two variables has an infinite number of solutions whose graph lies on a line. However, we only need to find two solutions because only two points are necessary to determine a straight line. A third point can be obtained as a check.
To graph a first-degree equation:
- Construct a set of rectangular axes showing the scale and the variable repre- sented by each axis.
- Find two ordered pairs that are solutions of the equation to be graphed by assigning any convenient value to one variable and determining the corre- sponding value of the other variable.
- Graph these ordered pairs.
- Draw a straight line through the points.
- Check by graphing a third ordered pair that is a solution of the equation and
verify that it lies on the line.

Example 1
Graph the equation y = 2x — 6.
Solution
We first select any two values of x to find the associated values of y.
We will use 1 and 4 for x.
If x = 1, y = 2(1) — 6 = -4
if x = 4, y = 2(4) — 6 = 2
Thus, two solutions of the equation are
(1, -4) and (4, 2).
Next, we graph these ordered pairs and draw a straight line through the points as shown
in the figure. We use arrowheads to show that
the line extends infinitely far in both directions.
Any third ordered pair that satisfies the
equation can be used as a check:
We then note that the graph of (5, 4) also lies on the line
To find solutions to an equation, as we have noted it is often easiest to first solve explicitly for y in terms of x.
Example 2
Graph x + 2y = 4.
Solution
We first solve for y in terms of x to get
We now select any two values of x to find the associated values of y. We will use
2 and 0 for x.
We will use
2 and 0 for x.
Thus, two solutions of the equation are (2, 1) and (0, 2).
Next, we graph these ordered pairs and pass a straight line through the points, as shown in the figure.
Any third ordered pair that satisfies the equation can be used as a check:
We then note that the graph of (-2, 3) also lies on the line.
SPECIAL CASES OF LINEAR EQUATIONS
The equation y = 2 can be written as
0x + y = 2
and can be considered a linear equation in two variables where the coefficient of x is 0. Some solutions of 0x + y = 2 are
(1,2), (-1,2), and (4,2)
In fact, any ordered pair of the form (x, 2) is a solution of (1). Graphing the solutions yields a horizontal line as shown in Figure 7.4.
Similarly, an equation such as x = -3 can be written as
x + 0y = -3
and can be considered a linear equation in two variables where the coefficient of y is 0.
Some solutions of x + 0y = -3 are
(-3, 5), (-3, 1), and (-3, -2). In fact, any
ordered pair of the form (-3, y) is a solution
of (2). Graphing the solutions yields a vertical
line as shown in Figure 7.5.
In fact, any
ordered pair of the form (-3, y) is a solution
of (2). Graphing the solutions yields a vertical
line as shown in Figure 7.5.
Example 3
Graph
a. y = 3
b. x=2
Solution
a. We may write y = 3 as Ox + y =3.
Some solutions are (1, 3), (2,3), and (5, 3).
b. We may write x = 2 as x + Oy = 2.
Some solutions are (2, 4), (2, 1), and (2, -2).
7.4 INTERCEPT METHOD OF GRAPHING
In Section 7.3, we assigned values to x in equations in two variables to find the corresponding values of y. The solutions of an equation in two variables that are generally easiest to find are those in which either the first or second component is 0. For example, if we substitute 0 for x in the equation
3x + 4y = 12
we have
3(0) + 4y = 12
y = 3
Thus, a solution of Equation (1) is (0, 3). We can also find ordered pairs that are
solutions of equations in two variables by assigning values to y and determining the
corresponding values of x. In particular, if we substitute 0 for y in Equation (1), we
get
In particular, if we substitute 0 for y in Equation (1), we
get
3x + 4(0) = 12
x = 4
and a second solution of the equation is (4, 0). We can now use the ordered pairs (0, 3) and (4, 0) to graph Equation (1). The graph is shown in Figure 7.6. Notice that the line crosses the x-axis at 4 and the y-axis at 3. For this reason, the number 4 is called the x-intercept of the graph, and the number 3 is called the y-intercept.
This method of drawing the graph of a linear equation is called the intercept method of graphing. Note that when we use this method of graphing a linear equation, there is no advantage in first expressing y explicitly in terms of x.
Example 1
Graph 2x — y = 6 by the intercept method.
Solution
We find the x-intercept by substituting 0 for y in the equation to obtain
2x — (0) = 6
2x = 6
x = 3
Now, we find the y-intercept by substituting for x in the equation to get
2(0) — y = 6
-y = 6
y = -6
The ordered pairs (3, 0) and (0, -6) are solutions of 2x — y = 6. Graphing these
points and connecting them with a straight line give us the graph of 2x — y = 6.
If the graph intersects the axes at or near the origin, the intercept method is not
satisfactory. We must then graph an ordered pair that is a solution of the equation
and whose graph is not the origin or is not too close to the origin.
Graphing these
points and connecting them with a straight line give us the graph of 2x — y = 6.
If the graph intersects the axes at or near the origin, the intercept method is not
satisfactory. We must then graph an ordered pair that is a solution of the equation
and whose graph is not the origin or is not too close to the origin.
Example 2
Graph y = 3x.
Solution
We can substitute 0 for x and find
y = 3(0) = 0
Similarly, substituting 0 for y, we get
0 = 3.x, x = 0
Thus, 0 is both the x-intercept and the y-intercept.
Since one point is not sufficient to graphy = 3x, we resort to the methods outlined in Section 7.3. Choosing any other value for x,say 2, we get
y = 3(2) = 6
Thus, (0, 0) and (2, 6) are solutions to the equation. The graph of y = 3x is shown at the right.
7.5 SLOPE OF A LINE
SLOPE FORMULA
In this section, we will study an important property of a line. We will assign a
number to a line, which we call slope, that will give us a measure of the «steepness»
or «direction» of the line.
It is often convenient to use a special notation to distinguish between the rectan- gular coordinates of two different points. We can designate one pair of coordinates by (x1, y1 (read «x sub one, y sub one»), associated with a point P1, and a second pair of coordinates by (x2, y2), associated with a second point P2, as shown in Figure 7.7. Note in Figure 7.7 that when going from P1 to P2, the vertical change (or vertical distance) between the two points is y2 — y1 and the horizontal change (or horizontal distance) is x2 — x1.
The ratio of the vertical change to the horizontal change is called the slope of the line containing the points P1 and P2. This ratio is usually designated by m. Thus,
Example 1
Find the slope of the line containing the two
points with coordinates (-4, 2) and (3, 5) as
shown in the figure at the right.
Solution
We designate (3, 5) as (x2, y2) and (-4, 2)
as (x1, y1). Substituting into Equation (1)
yields
Note that we get the same result if we subsitute -4 and 2 for x2 and y2 and 3 and 5 for x1 and y1
Lines with various slopes are shown in Figure 7.8 below. Slopes of the lines that go up to the right are positive (Figure 7.8a) and the slopes of lines that go down to the right are negative (Figure 7.8b). And note (Figure 7.8c) that because all points on a horizontal line have the same y value, y2 — y1 equals zero for any two points and the slope of the line is simply
Also note (Figure 7.8c) that since all points on a vertical have the same x value, x2 — x1 equals zero for any two points. However,
is undefined, so that a vertical line does not have a slope.
PARALLEL AND PERPENDICULAR LINES
Consider the lines shown in Figure 7. 9. Line l1 has slope m1 = 3, and line l2 has
slope m2 = 3. In this case,
9. Line l1 has slope m1 = 3, and line l2 has
slope m2 = 3. In this case,
These lines will never intersect and are called parallel lines. Now consider the lines shown in Figure 7.10. Line l1, has slope m1 = 1/2 and line l2 has slope m2 = -2. In this case,
These lines meet to form a right angle and are called perpendicular lines.
In general, if two lines have slopes and m2:
- a. The lines are parallel if they have the same slope, that is,
if m1 = m2.
b. The lines are perpendicular If the product of their slopes is -1, that is, if m1 * m2 = -1.
7.6 EQUATIONS OF STRAIGHT LINES
POINT-SLOPE FORM
In Section 7.5, we found the slope of a straight line by using the formula
Let us say we know that a line goes through the point (2, 3) and has a slope of 2.
If we denote any other point on the line as P(x, y) (See Figure 7. 1 la), by the slope
formula
1 la), by the slope
formula
Thus, Equation (1) is the equation of the line that goes through the point (2, 3) and has a slope of 2.
In general let us say we know a line passes through a point P1(x1, y1 and has slope m. If we denote any other point on the line as P(x, y) (see Figure 7.11 b), by the slope formula
Equation (2) is called the point-slope form for a linear equation. In Equation (2), m, x1 and y1 are known and x and y are variables that represent the coordinates of any point on the line. Thus, whenever we know the slope of a line and a point on the line, we can find the equation of the line by using Equation (2).
Example 1
A line has slope -2 and passes through point (2, 4). Find the equation of the line.
Solution
Substitute -2 for m and (2, 4) for (x1, y1) in Equation (2)
Thus, a line with slope -2 that passes through the point (2, 4) has the equation
y = -2x + 8. We could also write the equation in equivalent forms y + 2x = 8,
2x + y = 8, or 2x + y — 8 = 0.
We could also write the equation in equivalent forms y + 2x = 8,
2x + y = 8, or 2x + y — 8 = 0.
SLOPE-INTERCEPT FORM
Now consider the equation of a line with slope m and y-intercept b as shown in Figure 7.12. Substituting 0 for x1 and b for y1 in the point-slope form of a linear equation, we have
y — b = m(x — 0)
y — b = mx
or
y = mx + b
Equation (3) is called the slope-intercept form for a linear equation. The slope and y-intercept can be obtained directly from an equation in this form.
Example 2 If a line has the equation
then the slope of the line must be -2 and the y-intercept must be 8. Similarly, the graph of
y = -3x + 4
has a slope -3 and a y-intercept 4; and the graph of
has a slope 1/4 and a y-intercept -2.
If an equation is not written in x = mx + b form and we want to know the slope
and/or the y-intercept, we rewrite the equation by solving for y in terms of x.
Example 3
Find the slope and y-intercept of 2x — 3y = 6.
Solution
We first solve for y in terms of x by adding -2x to each member.
2x — 3y — 2x = 6 — 2x
— 3y = 6 — 2x
Now dividing each member by -3, we have
Comparing this equation with the form y = mx + b, we note that the slope m (the coefficient of x) equals 2/3, and the y-intercept equals -2.
7.7 DIRECT VARIATION
A special case of a first-degree equation in two variables is given by
y = kx (k is a constant)
Such a relationship is called a direct variation. We say that the variable y varies directly as x.
Example 1
We know that the pressure P in a liquid varies directly as the depth d below the surface of the liquid. We can state this relationship in symbols as
P = kd
In a direct variation, if we know a set of conditions on the two variables, and if
we further know another value for one of the variables, we can find the value of
the second variable for this new set of conditions.
In the above example, we can solve for the constant k to obtain
Since the ratio P/d is constant for each set of conditions, we can use a proportion to solve problems involving direct variation.
Example 2
If pressure P varies directly as depth d, and P = 40 when d = 10, find P when d = 15.
Solution
Since the ratio P/d is constant, we can substitute values for P and d and obtain the
proportion
Thus, P = 60 when d = 15.
7.8 INEQUALITIES IN TWO VARIABLES
In Sections 7.3 and 7.4, we graphed equations in two variables. In this section we will graph inequalities in two variables. For example, consider the inequality
y ≤ -x + 6
The solutions are ordered pairs of numbers that «satisfy» the inequality. That is, (a, b) is a solution of the inequality if the inequality is a true statement after we substitute a for x and b for y.
Example 1
Determine if the given ordered pair is a solution of y = -x + 6.
a. (1, 1)
(1, 1)
b. (2, 5)
Solution
The ordered pair (1, 1) is a solution because, when 1 is substituted for x and 1 is
substituted for y, we get
(1) = -(1) + 6, or 1 = 5
which is a true statement. On the other hand, (2, 5) is not a solution because when 2 is substituted for x and 5 is substituted for y, we obtain
(5) = -(2) + 6, or 5 = 4
which is a false statement.
To graph the inequality y = -x + 6, we first graph the equation y = -x + 6
shown in Figure 7.13. Notice that (3, 3), (3, 2), (3, 1), (3, 0), and so on, associated
with the points that are on or below the line, are all solutions of the inequality
y = -x + 6, whereas (3,4), (3, 5), and (3,6), associated with points above the
line are not solutions of the inequality. In fact, all ordered pairs associated with
points on or below the line are solutions of y = — x + 6. Thus, every point on or
below the line is in the graph. We represent this by shading the region below the
line (see Figure 7.14).
In general, to graph a first-degree inequality in two variables of the form Ax + By = C or Ax + By = C, we first graph the equation Ax + By = C and then determine which half-plane (a region above or below the line) contains the solutions. We then shade this half-plane. We can always determine which half- plane to shade by selecting a point (not on the line of the equation Ax + By = C) and testing to see if the ordered pair associated with the point is a solution of the given inequality. If so, we shade the half-plane containing the test point; otherwise, we shade the other half-plane. Often, (0, 0) is a convenient test point.
Example 2
Graph 2x+3y = 6
Solution
We first graph the line 2x + 3y = 6 (see graph a). Using the origin as a test point,
we determine whether (0, 0) is a solution of 2x + 3y ≥ 6. Since the statement
2(0) + 3(0) = 6
is false, (0, 0) is not a solution and we shade the half-plane that does not contain
the origin (see graph b).
When the line Ax + By = C passes through the origin, (0, 0) is not a valid test point since it is on the line.
Example 3
Graph y = 2x.
Solution
We begin by graphing the line y = 2x (see graph a). Since the line passes through
the origin, we must choose another point not on the line as our test point. We will
use (0, 1). Since the statement
(1) = 2(0)
is true, (0, 1) is a solution and we shade the half-plane that contains (0, 1) (see graph b).
If the inequality symbol is ‘ , the points on the graph of Ax + By = C are not solutions of the inequality. We then use a dashed line for the graph of Ax + By = C.
CHAPTER SUMMARY
A solution of an equation in two variables is an ordered pair of numbers. In the ordered pair (x, y), x is called the first component and y is called the second component. For an equation in two variables, the variable associated with the first component of a solution is called the independent variable and the variable associated with the second component is called the dependent variable.
 Function notation f(x) is used to name an algebraic expression in x. When x in
the symbol f(x) is replaced by a particular value, the symbol represents the value
of the expression for that value of x.
Function notation f(x) is used to name an algebraic expression in x. When x in
the symbol f(x) is replaced by a particular value, the symbol represents the value
of the expression for that value of x.The intersection of the two perpendicular axes in a coordinate systemis called the origin of the system, and each of the four regions into which the plane is divided is called a quadrant. The components of an ordered pair (x, y) associated with a point in the plane are called the coordinates of the point; x is called the abscissa of the point and y is called the ordinate of the point.
The graph of a first-degree equation in two variables is a straight line. That is, every ordered pair that is a solution of the equation has a graph that lies in a line, and every point in the line is associated with an ordered pair that is a solution of the equation.
The graphs of any two solutions of an equation in two variables can be used to obtain the graph of the equation.
 However, the two solutions of an equation in two
variables that are generally easiest to find are those in which either the first or
second component is 0. The x-coordinate of the point where a line crosses the x-axis
is called the x-intercept of the line, and the y-coordinate of the point where a line
crosses the y-axis is called they-intercept of the line. Using the intercepts to graph
an equation is called the intercept method of graphing.
However, the two solutions of an equation in two
variables that are generally easiest to find are those in which either the first or
second component is 0. The x-coordinate of the point where a line crosses the x-axis
is called the x-intercept of the line, and the y-coordinate of the point where a line
crosses the y-axis is called they-intercept of the line. Using the intercepts to graph
an equation is called the intercept method of graphing.The slope of a line containing the points P1(x1, y1) and P2(x2, y2) is given by
Two lines are parallel if they have the same slope (m1 = m2).
Two lines are perpendicular if the product of their slopes is — l(m1 * m2 = -1).
The point-slope form of a line with slope m and passing through the point (x1, y1) is
y — y1 — m(x — x1)
The slope-intercept form of a line with slope m and y-intercept b is
y = mx + b
A relationship determined by an equation of the form
y = kx (k a constant)
is called a direct variation.

A solution of an inequality in two variables is an ordered pair of numbers that, when substituted into the inequality, makes the inequality a true statement. The graph of a linear inequality in two variables is a half-plane. The symbols introduced in this chapter appear on the inside front covers.
4.4 Solving simultaneous equations | Equations and inequalities
Previous 4.3 Solving quadratic equations | Next 4.5 Word problems |
4.4 Solving simultaneous equations (EMA38)
Up to now we have solved equations with only one unknown variable. When solving for two unknown variables,
two equations are required and these equations are known as simultaneous equations. The solutions are the
values of the unknown variables which satisfy both equations simultaneously. In general, if there are \(n\)
unknown variables, then \(n\) independent equations are required to obtain a value for each of the \(n\)
variables.
The solutions are the
values of the unknown variables which satisfy both equations simultaneously. In general, if there are \(n\)
unknown variables, then \(n\) independent equations are required to obtain a value for each of the \(n\)
variables.
An example of a system of simultaneous equations is:
\begin{align*} x + y & = -1 \\ 3 & = y — 2x \end{align*}We have two independent equations to solve for two unknown variables. We can solve simultaneous equations algebraically using substitution and elimination methods. We will also show that a system of simultaneous equations can be solved graphically.
Solving by substitution (EMA39)
Use the simplest of the two given equations to express one of the variables in terms of the other.
Substitute into the second equation.
 By doing this we reduce the number of equations and the
number of variables by one.
By doing this we reduce the number of equations and the
number of variables by one.We now have one equation with one unknown variable which can be solved.
Use the solution to substitute back into the first equation to find the value of the other unknown variable.
The following video shows how to solve simultaneous equations using substitution.
Video: 2FD5
Worked example 6: Simultaneous equations
Solve for \(x\) and \(y\):
\begin{align*} x — y & =1 \qquad \ldots\left(1\right) \\ 3 & = y — 2x \qquad \ldots\left(2\right) \end{align*}
Use equation \(\left(1\right)\) to express \(x\) in terms of \(y\)
\[x=y+1\]Substitute \(x\) into equation \(\left(2\right)\) and solve for \(y\)
\begin{align*} 3 & = y — 2\left(y + 1\right) \\ 3 & = y — 2y — 2 \\ 5 & = -y \\ \therefore y & = -5 \end{align*}Substitute \(y\) back into equation \(\left(1\right)\) and solve for \(x\)
\begin{align*} x & = \left(-5\right) + 1 \\ \therefore x & = -4 \end{align*}Check the solution by substituting the answers back into both original equations
Write the final answer
\begin{align*} x & = -4 \\ y & = -5 \end{align*} temp textWorked example 7: Simultaneous equations
Solve the following system of equations:
\begin{align*} 4y + 3x & = 100 \qquad \ldots\left(1\right) \\ 4y — 19x & = 12 \qquad \ldots \left(2\right) \end{align*}
Use either equation to express \(x\) in terms of \(y\)
\begin{align*} 4y + 3x & = 100 \\ 3x & = 100 — 4y \\ x & = \frac{100 — 4y}{3} \end{align*}Substitute \(x\) into equation \(\left(2\right)\) and solve for \(y\)
\begin{align*} 4y — 19\left(\frac{100 — 4y}{3}\right) & = 12 \\ 12y — 19\left(100 — 4y\right) & = 36 \\ 12y — \text{1 900} + 76y & = 36 \\ 88y & = \text{1 936} \\ \therefore y & =22 \end{align*}Substitute \(y\) back into equation \(\left(1\right)\) and solve for \(x\)
\begin{align*} x & = \frac{100 — 4\left(22\right)}{3} \\ & = \frac{100 — 88}{3} \\ & = \frac{12}{3} \\ \therefore x & = 4 \end{align*}Check the solution by substituting the answers back into both original equations
Write the final answer
\begin{align*} x & = 4 \\ y & = 22 \end{align*} temp textSolving by elimination (EMA3B)
Worked example 8: Simultaneous equations
Solve the following system of equations:
\begin{align*} 3x + y & = 2 \qquad \ldots \left(1\right) \\ 6x — y & = 25 \quad \ldots \left(2\right) \end{align*}
Make the coefficients of one of the variables the same in both equations
The coefficients of \(y\) in the given equations are \(\text{1}\) and \(-\text{1}\). Eliminate
the variable \(y\) by adding equation \(\left(1\right)\) and equation \(\left(2\right)\)
together:
Eliminate
the variable \(y\) by adding equation \(\left(1\right)\) and equation \(\left(2\right)\)
together:
\[\begin{array}{cccc} & 3x + y & = & 2 \\ + & 6x — y & = & 25 \\ \hline & 9x + 0 & = & 27 \end{array}\]
Simplify and solve for \(x\)
\begin{align*} 9x & = 27 \\ \therefore x & = 3 \end{align*}Substitute \(x\) back into either original equation and solve for \(y\)
\begin{align*} 3\left(3\right) + y & = 2 \\ y & = 2 — 9 \\ \therefore y & = -7 \end{align*}Check that the solution \(x=3\) and \(y=-7\) satisfies both original equations
Write the final answer
\begin{align*} x & =3 \\ y & =-7 \end{align*} temp textWorked example 9: Simultaneous equations
Solve the following system of equations:
\begin{align*} 2a — 3b & = 5 \qquad \ldots \left(1\right) \\ 3a — 2b & = 20 \qquad \ldots\left(2\right) \end{align*}
Make the coefficients of one of the variables the same in both equations
By multiplying equation \(\left(1\right)\) by \(\text{3}\) and equation \(\left(2\right)\) by
\(\text{2}\), both coefficients of \(a\) will be \(\text{6}\).
\[\begin{array}{cccc} & 6a — 9b & = & 15 \\ — & (6a — 4b & = & 40) \\ \hline & 0 — 5b & = & -25 \end{array}\]
(When subtracting two equations, be careful of the signs.)
Simplify and solve for \(b\)
\begin{align*} b & = \frac{-25}{-5} \\ \therefore b & = 5 \end{align*}Substitute value of \(b\) back into either original equation and solve for \(a\)
\begin{align*} 2a — 3\left(5\right) & = 5 \\ 2a — 15 & = 5 \\ 2a & = 20 \\ \therefore a & = 10 \end{align*}Check that the solution \(a=10\) and \(b=5\) satisfies both original equations
Write the final answer
\begin{align*} a & = 10 \\ b & = 5 \end{align*} temp textSolving graphically (EMA3C)
This section can be included in the chapter on functions and graphs with graphs of linear equations. Before beginning this section it may be necessary to revise plotting graphs of linear equations with
your learners.
Before beginning this section it may be necessary to revise plotting graphs of linear equations with
your learners.
It is also important that learners are either given the graphs or are encouraged to draw accurate graphs on graph paper to help them solve simultaneous equations graphically. Graph sketching software can be used in this section to ensure that graphs are accurate.
Simultaneous equations can also be solved graphically. If the graphs of each linear equation are drawn, then the solution to the system of simultaneous equations is the coordinates of the point at which the two graphs intersect.
For example:
\begin{align*} x & = 2y \qquad \ldots \left(1\right) \\ y & = 2x — 3 \qquad \ldots \left(2\right) \end{align*}The graphs of the two equations are shown below.
The intersection of the two graphs is \((2;1)\). So the solution to the system of simultaneous equations is \(x=2\) and \(y=1\). We can also check the solution using algebraic methods.
Substitute equation \((1)\) into \((2)\):
\begin{align*} x & = 2y \\ \therefore y & = 2(2y) — 3 \end{align*}Then solve for \(y\):
\begin{align*} y — 4y & = -3 \\ -3y & = -3 \\ \therefore y & = 1 \end{align*}Substitute the value of \(y\) back into equation \((1)\):
\begin{align*} x & = 2(1) \\ \therefore x & = 2 \end{align*}Notice that both methods give the same solution.
You can use an online tool such as graphsketch to draw the graphs and check your solution.
Worked example 10: Simultaneous equations
Solve the following system of simultaneous equations graphically:
\begin{align*} 4y + 3x & = 100 \qquad \ldots \left(1\right) \\ 4y — 19x & = 12 \qquad \ldots \left(2\right) \end{align*}
Write both equations in form \(y=mx + c\)
\begin{align*} 4y + 3x & = 100 \\ 4y & = 100 — 3x \\ y & = -\frac{3}{4}x + 25 \end{align*}\begin{align*} 4y — 19x & = 12 \\ 4y & = 19x + 12 \\ y & = \frac{19}{4}x + 3 \end{align*}Sketch the graphs on the same set of axes
Find the coordinates of the point of intersection
The two graphs intersect at \(\left(4;22\right)\)
Write the final answer
\begin{align*} x & = 4 \\ y & = 22 \end{align*} temp textTextbook Exercise 4. 3
3
Look at the graph below
Solve the equations \(y = 2x + 1\) and \(y = -x — 5\) simultaneously
From the graph we can see that the lines intersect at \(x = -2\) and \(y = -3\)
Look at the graph below
Solve the equations \(y = 2x — 1\) and \(y = 2x + 1\) simultaneously
The lines are parallel. Therefore there is no solution to \(x\) and \(y\).
Look at the graph below
Solve the equations \(y = -2x + 1\) and \(y = -x — 1\) simultaneously
From the graph we can see that the lines intersect at \(x = 2\) and \(y = -3\)
\(- 10 x = -1\) and \(- 4 x + 10 y = -9\).
Solve for \(x\):
\begin{align*} — 10x = -1\\ \therefore x = \frac{1}{10} \end{align*}
Substitute the value of \(x\) into the second equation and solve for \(y\):
\begin{align*} -4x + 10y & = -9 \\ -4\left(\frac{1}{10}\right) + 10y & = -9 \\ \frac{-4}{10} + 10y & = -9 \\ 100y & = -90 + 4 \\ y & = \frac{-86}{100} \\ & = \frac{-43}{50} \end{align*}
Therefore \(x = \frac{1}{10} \text{ and } y = — \frac{43}{50}\).
\(3x — 14y = 0\) and \(x — 4y + 1 = 0\)
Write \(x\) in terms of \(y\):
\begin{align*} 3x — 14y & = 0 \\ 3x & = 14y \\ x & = \frac{14}{3}y \end{align*}
Substitute value of \(x\) into second equation:
\begin{align*} x — 4y + 1 & = 0 \\ \frac{14}{3}y — 4y + 1 & = 0 \\ 14y — 12y + 3 & = 0 \\ 2y & = -3 \\ y & = -\frac{3}{2} \end{align*}
Substitute value of \(y\) back into first equation:
\begin{align*} x & = \frac{14\left(-\frac{3}{2}\right)}{3} \\ & = -7 \end{align*}
Therefore \(x = -7 \text{ and } y = -\frac{3}{2}\).
\(x + y = 8\) and \(3x + 2y = 21\)
Write \(x\) in terms of \(y\):
\begin{align*} x + y & = 8 \\ x & = 8 — y \end{align*}
Substitute value of \(x\) into second equation:
\begin{align*} 3x + 2y & = 21 \\ 3(8 — y) + 2y & = 21 \\ 24 — 3y + 2y & = 21 \\ y & = 3 \end{align*}
Substitute value of \(y\) back into first equation:
\[x = 5\]
Therefore \(x = 5 \text{ and } y = 3\).
\(y = 2x + 1\) and \(x + 2y + 3 = 0\)
Write \(y\) in terms of \(x\):
\[y = 2x + 1\]
Substitute value of \(y\) into second equation:
\begin{align*} x + 2y + 3 & = 0 \\ x + 2(2x + 1) + 3 & = 0 \\ x + 4x + 2 + 3 & = 0 \\ 5x & = -5 \\ x & = -1 \end{align*}
Substitute value of \(x\) back into first equation:
\begin{align*} y & = 2(-1) + 1 \\ & = -1 \end{align*}
Therefore \(x = -1 \text{ and } y = -1\).
\(5x-4y = 69\) and \(2x+3y = 23\)
Make \(x\) the subject of the first equation:
\begin{align*} 5x-4y &= 69 \\ 5x &= 69+4y \\ x &= \frac{69+4y}{5} \end{align*}
Substitute value of \(x\) into second equation:
\begin{align*} 2x+3y &= 23 \\ 2 \left(\frac{69+4y}{5} \right) +3y &= 23 \\ 2(69+4y) +3(5)y &= 23(5) \\ 138+8y+15y &= 115\\ 23y &= -23 \\ \therefore y &= -1 \end{align*}
Substitute value of \(y\) back into first equation:
\begin{align*} x &= \frac{69+4y}{5} \\ &= \frac{69+4(-1)}{5} \\ &= 13 \end{align*}
Therefore \(x =13 \text{ and } y = -1\).
\(x + 3y = 26\) and \(5x + 4y = 75\)
Make \(x\) the subject of the first equation:
\begin{align*} x + 3y &= 26 \\ x &= 26 — 3y \end{align*}
Substitute value of \(x\) into second equation:
\begin{align*} 5x+4y &= 75 \\ 5(26 — 3y) + 4y &= 75 \\ 130 — 15y + 4y &= 75 \\ -11y &= -55 \\ \therefore y &= 5 \end{align*}
Substitute value of \(y\) back into first equation:
\begin{align*} x &= 26 — 3y \\ &= 26 — 3(5) \\ &= 11 \end{align*}
Therefore \(x =11 \text{ and } y = 5\).
\(3x — 4y = 19\) and \(2x — 8y = 2\)
If we multiply the first equation by 2 then the coefficient of \(y\) will be the same in both equations:
\begin{align*} 3x — 4y &= 19 \\ 3(2)x — 4(2)y & = 19(2) \\ 6x — 8y & = 38 \end{align*}
Now we can subtract the second equation from the first:
\[\begin{array}{cccc} & 6x — 8y & = & 38 \\ — & (2x — 8y & = & 2) \\ \hline & 4x + 0 & = & 36 \end{array}\]
Solve for \(x\):
\begin{align*} \therefore x &= \frac{36}{4} \\ & = 9 \end{align*}
Substitute the value of \(x\) into the first equation and solve for \(y\):
\begin{align*} 3x-4y &= 19 \\ 3(9)-4y &= 19\\ \therefore y &= \frac{19-3(9)}{-4} \\ &= 2 \end{align*}
Therefore \(x = 9 \text{ and } y = 2\).
\(\dfrac{a}{2} + b = 4\) and \(\dfrac{a}{4} — \dfrac{b}{4} = 1\)
Make \(a\) the subject of the first equation:
\begin{align*} \frac{a}{2} + b & = 4 \\ a + 2b & = 8 \\ a & = 8 — 2b \end{align*}
Substitute value of \(a\) into second equation:
\begin{align*} \frac{a}{4} — \frac{b}{4} & = 1 \\ a — b & = 4 \\ 8 — 2b — b & = 4 \\ 3b & = 4 \\ b & = \frac{4}{3} \end{align*}
Substitute value of \(b\) back into first equation:
\begin{align*} a & = 8 — 2\left(\frac{4}{3}\right) \\ & = \frac{16}{3} \end{align*}
Therefore \(a = \frac{16}{3} \text{ and } b = \frac{4}{3}\).
\(-10x + y = -1\) and \(-10x — 2y = 5\)
If we subtract the second equation from the first then we can solve for \(y\):
\[\begin{array}{cccc} & -10x + y & = & -1 \\ — & (-10x — 2y & = & 5) \\ \hline & 0 + 3y & = & -6 \end{array}\]
Solve for \(y\):
\begin{align*} 3y & = -6 \\ \therefore y &= -2 \end{align*}
Substitute the value of \(y\) into the first equation and solve for \(x\):
\begin{align*} -10x + y &= -1 \\ -10x — 2 &= -1\\ -10x &= 1 \\ x &= \frac{1}{-10} \end{align*}
Therefore \(x = \frac{-1}{10} \text{ and } y = -2\).
\(- 10 x — 10 y = -2\) and \(2 x + 3 y = 2\)
Make \(x\) the subject of the first equation:
\begin{align*} — 10 x — 10 y = -2\\ 5x + 5y & = 1 \\ 5x & = 1 — 5y \\ \therefore x = -y + \frac{1}{5} \end{align*}
Substitute the value of \(x\) into the second equation and solve for \(y\):
\begin{align*} 2x + 3y & = 2 \\ 2\left(-y + \frac{1}{5}\right) + 3y & = 2 \\ -2y + \frac{2}{5} + 3y & = 2 \\ y & = \frac{8}{5} \end{align*}
Substitute the value of \(y\) in the first equation:
\begin{align*} 5x + 5y & = 1 \\ 5x + 5\left(\frac{8}{5}\right) & = 1 \\ 5x + 8 & = 1 \\ 5x & = -7 \\ x &= \frac{-7}{5} \end{align*}
Therefore \(x = — \frac{7}{5} \text{ and } y = \frac{8}{5}\).
\(\dfrac{1}{x} + \dfrac{1}{y} = 3\) and \(\dfrac{1}{x} — \dfrac{1}{y} = 11\)
Rearrange both equations by multiplying by \(xy\):
\begin{align*} \frac{1}{x} + \frac{1}{y} & = 3 \\ y + x & = 3xy \\\\ \frac{1}{x} — \frac{1}{y} & = 11 \\ y — x & = 11xy \end{align*}
Add the two equations together:
\[\begin{array}{cccc} & y + x & = & 3xy \\ + & (y — x & = & 11xy) \\ \hline & 2y + 0 & = & 14xy \end{array}\]
Solve for \(x\):
\begin{align*} 2y & = 14xy \\ y & = 7xy \\ 1 & = 7x \\ x & = \frac{1}{7} \end{align*}
Substitute value of \(x\) back into first equation:
\begin{align*} y + \frac{1}{7} & = 3\left(\frac{1}{7}\right)y \\ 7y + 1 & = 3y \\ 4y & = -1 \\ y & = -\frac{1}{4} \end{align*}
Therefore \(x = \frac{1}{7} \text{ and } y = -\frac{1}{4}\). 2 &= 3 — ab
\end{align*}
2 &= 3 — ab
\end{align*}
Note that this is the same as the second equation
\(a\) and \(b\) can be any real number except for \(\text{0}\).
\(y + 2x = 0\) and \(y — 2x — 4 = 0\)
First write the equations in standard form:
\begin{align*} y + 2x & = 0 \\ y & = -2x \\\\ y — 2x — 4 & = 0 \\ y & = 2x + 4 \end{align*}
Draw the graph:
The graphs intersect at \((-1;2)\) so \(x = -1\) and \(y=2\).
Checking algebraically we get:
\[y = -2x\]
Substitute value of \(y\) into second equation:
\begin{align*} y — 2x — 4 & = 0 \\ -2x — 2x — 4 & = 0 \\ -4x & = 4 \\ x & = -1 \end{align*}
Substitute the value of \(x\) back into the first equation:
\begin{align*} y & = -2(-1) \\ y & = 2 \end{align*}
\(x + 2y = 1\) and \(\dfrac{x}{3} + \dfrac{y}{2} = 1\)
First write the equations in standard form:
\begin{align*} x + 2y & = 1 \\ 2y & = -x + 1\\ y & = -\frac{1}{2}x + \frac{1}{2} \\ \\ \frac{x}{3} + \frac{y}{2} & = 1 \\ y & = -\frac{2}{3}{x} + 2 \end{align*}
Draw the graph:
The graphs intersect at \((9;-4)\) so \(x = 9\) and \(y=-4\).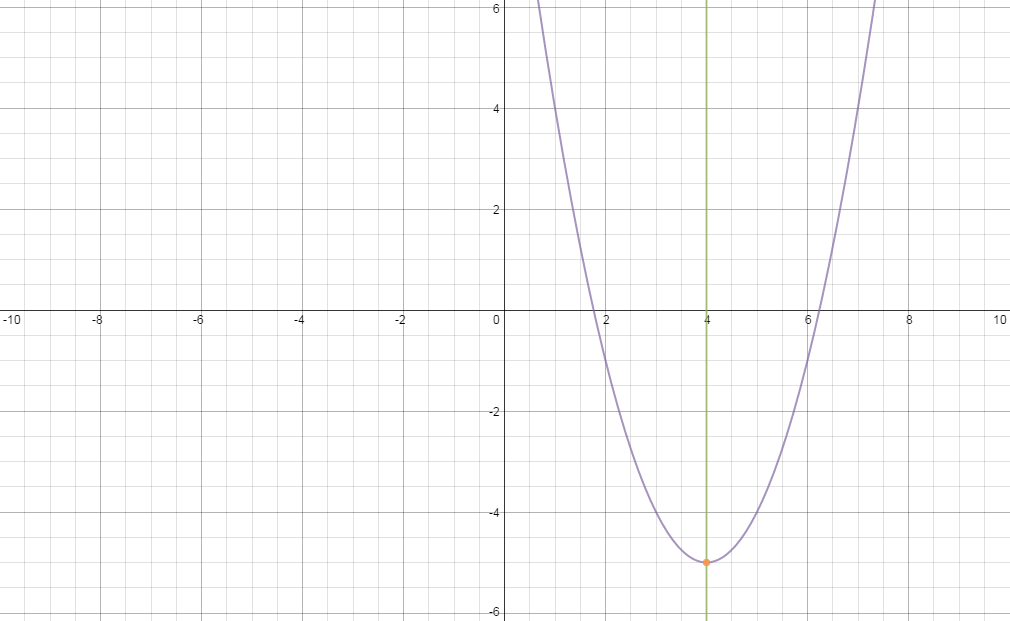
Checking algebraically we get:
\[x = -2y + 1\]
Substitute value of \(x\) into first equation:
\begin{align*} \frac{-2y + 1}{3} + \frac{y}{2} & = 1 \\ -4y + 2 + 3y & = 6 \\ y & = -4 \end{align*}
Substitute the value of \(y\) back into the first equation:
\begin{align*} x + 2(-4) & = 1 \\ x — 8 & = 1 \\ x & = 9 \end{align*}
\(y — 2 = 6x\) and \(y — x = -3\)
First write the equations in standard form:
\begin{align*} y — 2 & = 6x \\ y & = 6x + 2\\\\ y — x & = -3 \\ y & = x — 3 \end{align*}
Draw the graph:
The graphs intersect at \((-1;-4)\) so \(x = -1\) and \(y=-4\).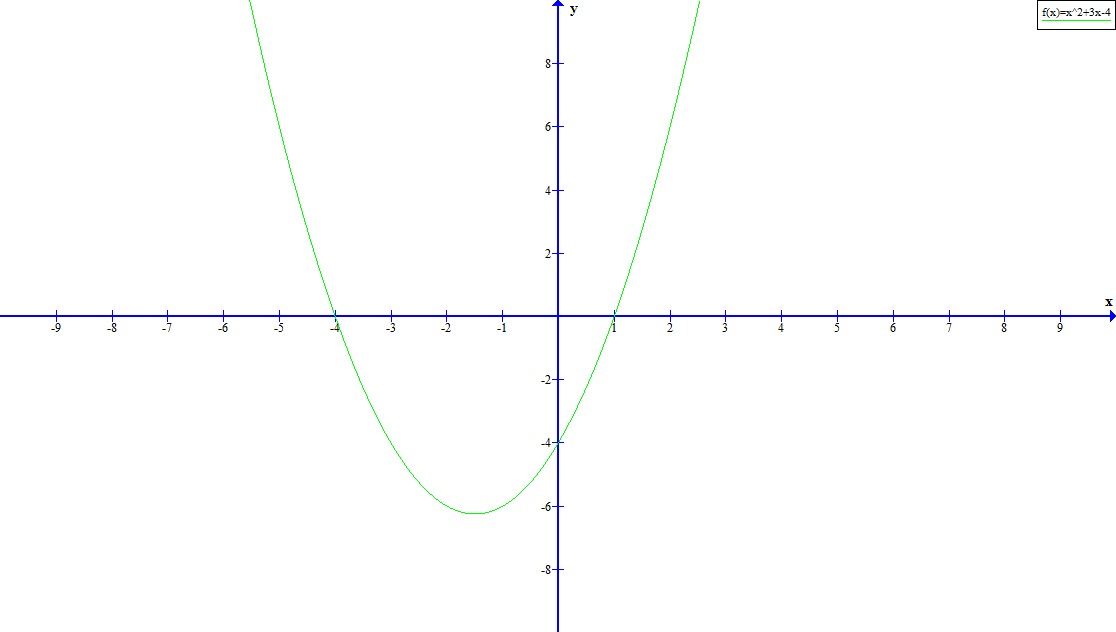
Checking algebraically we get:
\[y = 6x + 2\]
Substitute value of \(y\) into first equation:
\begin{align*} 6x + 2 & = x — 3 \\ 5x & = -5 \\ x & = -1 \end{align*}
Substitute the value of \(x\) back into the first equation:
\begin{align*} y & = 6(-1) + 2 \\ y & = -4 \end{align*}
\(2x + y = 5\) and \(3x — 2y = 4\)
First write the equations in standard form:
\begin{align*} 2x + y & = 5 \\ y & = -2x + 5\\ \\ 3x — 2y & = 4 \\ 2y & = 3x — 4 \\ y & = \frac{3}{2}x — 2 \end{align*}
Draw the graph:
The graphs intersect at \((2;1)\) so \(x = 2\) and \(y=1\).
Checking algebraically we get:
\[y = -2x + 5\]
Substitute value of \(y\) into first equation:
\begin{align*} -2x + 5 & = \frac{3}{2}x — 2 \\ -4x + 10 & = 3x — 4 \\ 7x & = 14 \\ x & = 2 \end{align*}
Substitute the value of \(x\) back into the first equation:
\begin{align*} x & = -2(2) + 5 \\ y & = 1 \end{align*}
\(5 = x + y\) and \(x = y — 2\)
First write the equations in standard form:
\begin{align*} 5 & = x + y \\ y & = -x + 5\\ \\ x & = y — 2 \\ y & = x + 2 \end{align*}
Draw the graph:
The graphs intersect at \((\text{1,5};\text{3,5})\) so \(x = \text{1,5}\) and
\(y=\text{3,5}\).
Checking algebraically we get:
\[y = -x + 5\]
Substitute value of \(y\) into second equation:
\begin{align*} x & = -x + 5 — 2 \\ 2x & = 3 \\ x & = \frac{3}{2} \end{align*}
Substitute the value of \(x\) back into the first equation:
\begin{align*} 5 & = \frac{3}{2} + y \\ y & = \frac{7}{2} \end{align*}
Previous 4.3 Solving quadratic equations | Table of Contents | Next 4. |
Draw the graph of the equation y 3x 4 Find graphically i the value of y when x 1 ii the value of x w…
Jump to
- Coordinate Geometry Exercise 19.1
- Coordinate Geometry Exercise 19.2
- Coordinate Geometry Exercise 19.3
- Coordinate Geometry Exercise 19.4
- Rational and Irrational Numbers
- Compound Interest
- Expansions
- Factorization
- Simultaneous Linear Equations
- Problems on Simultaneous Linear Equations
- Quadratic Equations
- Indices
- Logarithms
- Triangles
- Mid Point Theorem
- Pythagoras Theorem
- Rectilinear Figures
- Theorems on Area
- Circle
- Mensuration
- Trigonometric Ratios
- Trigonometric Ratios and Standard Angles
- Coordinate Geometry
- Statistics
Home >
ML Aggarwal Solutions
Class 9
Mathematics
>
Chapter 19 — Coordinate Geometry
>
Coordinate Geometry Exercise 19. 2
>
Question 5
2
>
Question 5
Question 5 Coordinate Geometry Exercise 19.2
Draw the graph of the equation y = 3x – 4. Find graphically.
(i) the value of y when x = -1
(ii) the value of x when y = 5.
Answer:
y = 3x-4
when x = 0,
y = 3×0-4 = 0-4 = -4
when x = 1,
y = 3×1-4 = 3-4 = -1
when x = 2,
y = 3×2-4 = 6-4 = 2
(i) x = -1:
Draw a line parallel to Y axis from x = -1. It meets the graph at y = -7.
So when x = -1, the value of y is -7.
(ii) y = 5
Draw a line parallel to X-axis from y = 5. It meets the graph at x = 3.
So when y = 5, the value of x is 3.
Video transcript
m-bb-mlaggarwal9-ch29-ex19p2-q5 «hi guys welcome to lido q a video
i am vineet your leader tutor bringing
you this question on your screen
question is draw the graph of the
equation
y is equal to 3x minus 4 find
graphically
the value of y when x equals to minus 1
and the value of y when x when y equal
to 5
again y equal to
3x minus 4.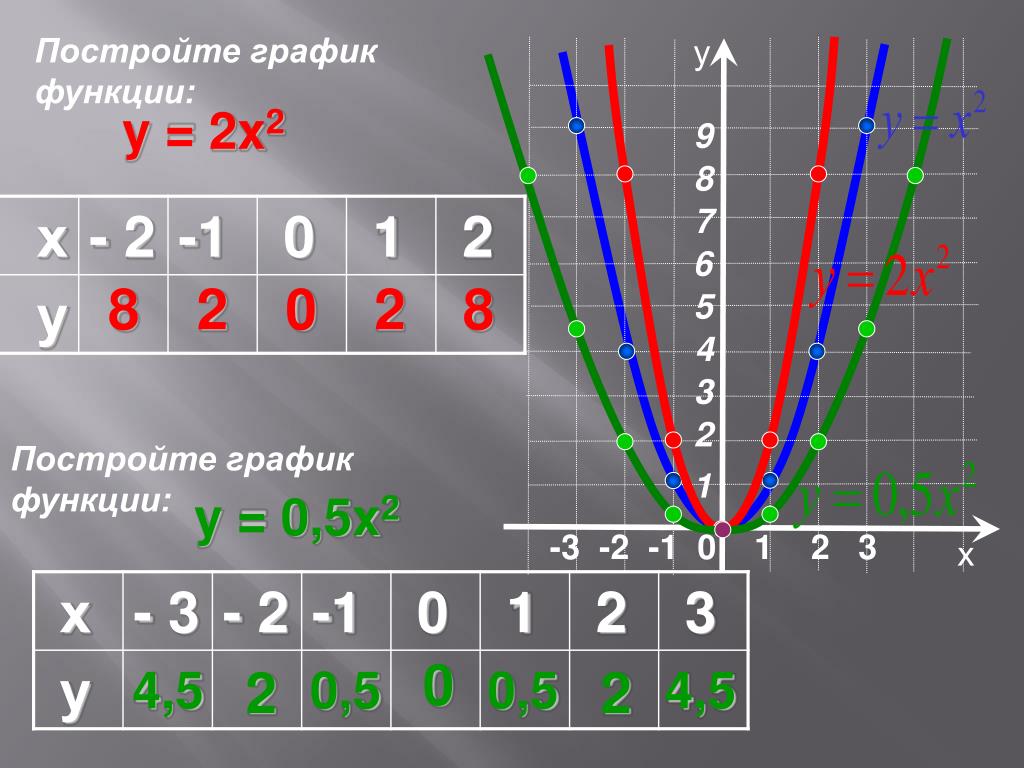 so then we find the
corresponding values of y for some
values of x
right so let us do that first
so let us take x as minus 1 0
and 2 and y will be
minus 7
so
so that is what we have to find
graphically so what we are going to do
is we are going to take 0
1 and 2 right
so we get y is equal to minus 1
minus 1 here minus 4 here
and minus 2 here
right so now let us plot the graph
so plus 2 here sorry right so 2 2
so taking the points 0 minus 4 1 minus 1
and 2
2 we plot the graph
okay and this is the graph
now this is the graph from the graph
what we can see is when x is equal to
minus 1
right the value of y will be
minus 7
and when y is equal to 5
is here x is equal to
3 right
so when x is equal to minus 1
y is equal to minus 7 and
when y is equal to 5 x will be equal to
3 isn’t that easy guys
if you still have a doubt please leave a
comment below do like the video and
subscribe to our channel
i’ll see you in our next video until
then bye guys
keep practicing»
so then we find the
corresponding values of y for some
values of x
right so let us do that first
so let us take x as minus 1 0
and 2 and y will be
minus 7
so
so that is what we have to find
graphically so what we are going to do
is we are going to take 0
1 and 2 right
so we get y is equal to minus 1
minus 1 here minus 4 here
and minus 2 here
right so now let us plot the graph
so plus 2 here sorry right so 2 2
so taking the points 0 minus 4 1 minus 1
and 2
2 we plot the graph
okay and this is the graph
now this is the graph from the graph
what we can see is when x is equal to
minus 1
right the value of y will be
minus 7
and when y is equal to 5
is here x is equal to
3 right
so when x is equal to minus 1
y is equal to minus 7 and
when y is equal to 5 x will be equal to
3 isn’t that easy guys
if you still have a doubt please leave a
comment below do like the video and
subscribe to our channel
i’ll see you in our next video until
then bye guys
keep practicing»
Related Questions
Draw the graphs of the following linear equations :(i) 2x +y+ 3 = 0(ii) x- 5y- 4 = 0
Draw the graph of 3y = 12-2x. Take 2cm = 1 unit on both axes.
Take 2cm = 1 unit on both axes.
Draw the graph of 5x+6y-30 = 0 and use it to find the area of the triangle formed by the line and th…
Draw the graph of 4x-3y+12 = 0 and use it to find the area of the triangle formed by the line and th…
The graph of a linear equation in x and y passes through (4, 0) and (0, 3). Find the value of k if t…
Use the table given alongside to draw the graph of a straight line. Find, graphically the values of …
Facebook Whatsapp
Copy Link
Was This helpful?
Exercises
Coordinate Geometry Exercise 19. 1
1
Coordinate Geometry Exercise 19.2
Coordinate Geometry Exercise 19.3
Coordinate Geometry Exercise 19.4
Chapters
Rational and Irrational Numbers
Compound Interest
Expansions
Factorization
Simultaneous Linear Equations
Problems on Simultaneous Linear Equations
Quadratic Equations
Indices
Logarithms
Triangles
Mid Point Theorem
Pythagoras Theorem
Rectilinear Figures
Theorems on Area
Circle
Mensuration
Trigonometric Ratios
Trigonometric Ratios and Standard Angles
Coordinate Geometry
Statistics
Courses
Quick Links
Terms & Policies
Terms & Policies
2022 © Quality Tutorials Pvt Ltd All rights reserved
Mathematics Part I Solutions for Class 10 Math Chapter 1
- Textbook Solutions
- Class 10
- Math
- linear equations in two variables
Mathematics Part I Solutions Solutions for Class 10 Math Chapter 1 Linear Equations In Two Variables are provided here with simple step-by-step explanations. These solutions for Linear Equations In Two Variables are extremely popular among Class 10 students for Math Linear Equations In Two Variables Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Mathematics Part I Solutions Book of Class 10 Math Chapter 1 are provided here for you for free. You will also love the ad-free experience on Meritnation’s Mathematics Part I Solutions Solutions. All Mathematics Part I Solutions Solutions for class Class 10 Math are prepared by experts and are 100% accurate.
These solutions for Linear Equations In Two Variables are extremely popular among Class 10 students for Math Linear Equations In Two Variables Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Mathematics Part I Solutions Book of Class 10 Math Chapter 1 are provided here for you for free. You will also love the ad-free experience on Meritnation’s Mathematics Part I Solutions Solutions. All Mathematics Part I Solutions Solutions for class Class 10 Math are prepared by experts and are 100% accurate.
Page No 4:
Question 1:
Complete the following activity to solve the simultaneous equations.
5x + 3y = 9 ——(I)
2x + 3y = 12 —— (II)
Answer:
Disclaimer: There is error in the Q. In (II) there should have been 2x — 3y = 12
5x + 3y = 9 ——(I)
2x — 3y = 12 —— (II)
Add (I) and (II)
7x = 21
x = 3
Putting the value of x = 3 in (I) we get
53+3y=9⇒15+3y=9⇒3y=9-15=-6⇒y=-2
Thus, (x, y) = (3, -6).
Page No 5:
Question 2:
Solve the following simultaneous equations.
(1) 3a + 5b = 26; a + 5b = 22
(2) x + 7y = 10; 3x – 2y = 7
(3) 2x – 3y = 9; 2x + y = 13
(4) 5m – 3n = 19; m – 6n = –7
(5) 5x + 2y = –3; x + 5y = 4
(6) 13x+y=103; 2x+14y=114
(7) 99x + 101y = 499; 101x + 99y = 501
(8) 49x – 57y = 172; 57x – 49y = 252
Answer:
(1) 3a + 5b = 26; …..(I)
a + 5b = 22 …..(II)
Subtracting (II) from (I)
2a = 4
⇒ a = 2
Putting the value of a = 2 in (II)
5b = 22 — 2 = 20
⇒b = 205=4
Thus, a = 2 and b = 4.
(2) x + 7y = 10; . ….(I)
….(I)
3x – 2y = 7 …..(II)
Multiplying (I) with 3
3x + 21y = 30; …..(III)
3x – 2y = 7 …..(IV)
Subtracting (IV) from (III) we get
23y = 23
⇒y = 1
Putting the value of y in (IV) we get
3x – 2 = 7
⇒3x = 7 + 2 = 9
⇒3x = 9
⇒x = 3
Thus, (x, y) = (3, 1)
(3) 2x – 3y = 9 …..(I)
2x + y = 13 …..(II)
Subtracting (II) from (I) we get
– 3y − y = 9 − 13
⇒-4y=-4⇒y=1
Putting this value in (I) we get
2x-31=9⇒2x=9+3=12⇒x=122=6
Thus, (x, y) = (6, 1)
(4) 5m – 3n = 19 …..(I)
m – 6n = –7 …..(II)
Multiplying (I) with 2 we get
10m – 6n = 38 . ….(III)
….(III)
m – 6n = –7 …..(IV)
Subtracting (IV) from (III) we get
10m-m-6n—6n=38—7⇒9m=45⇒m=459=5
Putting the value of m = 5 in (II) we get
5-6n=-7⇒-6n=-7-5⇒-6n=-12⇒n=-12-6=2
Thus, (m, n) = (5, 2).
(5) 5x + 2y = –3 …..(I)
x + 5y = 4 …..(II)
Multiply (II) with 5 we get
5x + 25y = 20 …..(III)
Subtracting (III) from (I) we get
5x-5x+2y-25y=-3-20⇒-23y=-23⇒y=-23-23=1
Putting the value of y = 1 in (II) we get
x+51=4⇒x+5=4⇒x=4-5=-1
Thus, (x, y) = (−1, 1)
(6)
13x+y=103 …..I2x+14y=114 …..(II)
Multiply (I) with 3 and (II) with 4
x+3y=10 …..III8x+y=11 …..IV
Multiply (IV) with 3
24x + 3y = 33 …..(V)
Subtracting (V) from (III)
x-24x+3y-3y=10-33⇒-23x=-23⇒x=1
Putting the value of x = 1 in (III)
1+3y=10⇒3y=10-1=9⇒y=93=3
Thus, (x, y) = (1, 3)
(7) 99x + 101y = 499 . ….(I)
….(I)
101x + 99y = 501 …..(II)
Adding (I) and (II)
200x+200y=1000⇒x+y=5 …..(III)
Subtracting (II) from (I)
99x-101x+101y-99y=499-501⇒-2x+2y=-2⇒-x+y=-1 …..IV
Adding (III) and (IV)
x+y=5-x+y=-1⇒2y=4⇒y=2
Putting the value of y = 2 in (III) we get
x+2=5⇒x=5-2=3
Thus, (x, y) = (3, 2)
(8) 49x – 57y = 172 …..(I)
57x – 49y = 252 …..(II)
Adding (I) and (II)
49x+57x-57y-49y=172+252⇒106x-106y=424⇒x-y=4 …..III
Subtracting (II) from (I) we have
49x-57y-57y—49y=252-172⇒-8x-8y=-80⇒-x-y=-10 ⇒x+y=10 …..IV
Adding (III) and (IV)
x-y=4x+y=10⇒2x=14⇒x=7
Putting the value of x = 7 in (IV) we get
7+y=10⇒y=10-7⇒y=3
Thus, (x, y) = (7, 3).
Page No 8:
Question 1:
Complete the following table to draw graph of the equations–
(I) x + y = 3 (II) x – y = 4
|
|
Answer:
| x | 3 | -2 | 0 |
| y | 0 | 5 | 3 |
| (x, y) | (3, 0) | -2, 5 | (0, 3) |
| x | 4 | –1 | 0 |
| y | 0 | -5 | –4 |
| (x, y) | 4,0 | -1,-5 | (0, –4) |
Page No 8:
Question 2:
Solve the following simultaneous equations graphically.
(1) x + y = 6 ; x – y = 4
(2) x + y = 5 ; x – y = 3
(3) x + y = 0 ; 2x – y = 9
(4) 3x – y = 2 ; 2x – y = 3
(5) 3x – 4y = –7 ; 5x – 2y = 0
(6) 2x – 3y = 4 ; 3y – x = 4
Answer:
(1) x + y = 6;
| x | 0 | 6 | 2 |
| y | 6 | 0 | 4 |
x – y = 4
| x | 4 | 5 | 0 |
| y | 0 | 1 | −4 |
Point of intersection of the two lines is (5, 1).
(2) x + y = 5
| x | 0 | 5 | 2 |
| y | 5 | 0 | 3 |
x – y = 3
| x | 3 | 0 | 5 |
| y | 0 | −3 | 2 |
Point of intersection of the two lines is (4, 1)
(3) x + y = 0
| x | 3 | 1 | 2 |
| y | −3 | −1 | −2 |
2x – y = 9
| x | 3 | 0 | 1 |
| y | −3 | −9 | −7 |
Point of intersection of the two lines is (3, −3).
(4) 3x – y = 2
| x | 0 | 1 | 2 |
| y | −2 | 1 | 4 |
2x – y = 3
| x | 0 | 1 | 2 |
| y | −3 | −1 | 1 |
Point of intersection of the two lines is (−1, −5).
(5) 3x – 4y = –7
| x | 1 | 0 | −2.3 |
| y | 2.5 | 1.75 | 0 |
5x – 2y = 0
| x | 0 | 2 | 4 |
| y | 0 | 5 | 10 |
Point of intersection of the two lines is (1, 2. 5).
5).
(6) 2x – 3y = 4
| x | 2 | 3.5 | 1 |
| y | 0 | 1 | −0.6 |
3y – x = 4
| x | −4 | 2 | −1 |
| y | 0 | 2 | 1 |
Point of intersection of the two lines is (8, 4).
Page No 16:
Question 1:
Fill in the blanks with correct number
3 24 5=3× – ×4= –8=
Answer:
3 24 5=35-24=15-8=7
Thus, we have
3 24 5=3× 5 – 2 ×4= 15 –8= 7
Page No 16:
Question 2:
Find the values of following determinants.
(1) -1 7 2 4
(2) 5 3-7 0
(3) 73533212
Answer:
(1) -1 7 2 4
= -14-72=-4-14=-18
(2) 5 3-7 0=5×0-3×-7=0+21=21
(3) 73533212=73×12-53×32=76-52=7-156=-86=-43
Page No 16:
Question 3:
Solve the following simultaneous equations using Cramer’s rule.
(1) 3x – 4y = 10 ; 4x + 3y = 5
(2) 4x + 3y – 4 = 0 ; 6x = 8 – 5y
(3) x + 2y = –1 ; 2x – 3y = 12
(4) 6x – 4y = –12 ; 8x – 3y = –2
(5) 4m + 6n = 54 ; 3m + 2n = 28
(6) 2x+3y=2 ; x-y2=12
Answer:
(1) 3x – 4y = 10
4x + 3y = 5
D=3-443=3×3—4×4=9+16=25Dx=10-453=10×3—4×5=30+20=50Dy=31045=3×5-10×4=15-40=-25
x=DxD=5025=2y=DyD=-2525=-1x,y=2,-1
(2) 4x + 3y – 4 = 0 ; 6x = 8 – 5y
D=4365=4×5-6×3=20-18=2Dx=4385=4×5-3×8=20-24=-4Dy=4468=4×8-6×4=32-24=8
x=DxD=-42=-2y=DyD=82=4x,y=-2,4
(3) x + 2y = –1 ; 2x – 3y = 12
D=122-3=1×-3-2×2=-3-4=-7Dx=-1212-3=-1×-3-2×12=3-24=-21Dy=1-1212=1×12—1×2=12+2=14
x=DxD=-21-7=3y=DyD=14-7=-2x,y=3,-2
(4) 6x – 4y = –12 ; 8x – 3y = –2
D=6-48-3=6×-3—4×8=-18+32=14Dx=-12-4-2-3=-12×-3—4×-2=36-8=28Dy=6-128-2=6×-2—12×8=-12+96=84
x=DxD=2814=2y=DyD=8414=6x,y=2,6
(5) 4m + 6n = 54 ; 3m + 2n = 28
D=4632=4×2-6×3=8-18=-10Dx=546282=54×2-6×28=108-168=-60Dy=454328=4×28-54×3=112-162=-50
x=DxD=-60-10=6y=DyD=-50-10=5x,y=6,5
(6) 2x+3y=2 ; x-y2=12
D=231-12=2×-12-3×1=-1-3=-4Dx=2312-12=2×-12-3×12=-1-32=-52Dy=22112=2×12-2×1=1-2=-1
x=DxD=-52-4=58y=DyD=-1-4=14x,y=58,14
Page No 19:
Question 1:
Solve the following simultaneous equations.
1 2x-3y=15; 8x+5y=772 10x+y+2x-y=4; 15x+y-5x-y=-23 27x-2+31y+3=85; 31x-2+27y+3=894 13x+y+23x-y=34; 123x+y-123x-y=-18
Answer:
1 2x-3y=15; 8x+5y=77
Let 1x=u and 1y=v
So, the equation becomes
2u-3v=15 …..I8u+5v=77 …..II
Multiply (I) with 4 we get
8u-12v=60 …..III
(II) − (III)
8u-8u+5v—12v=77-60⇒17v=17⇒v=1Putting the value of v in I2u-31=15⇒2u=15+3=18⇒u=9
Thus,
1x=u=9⇒x=191y=v=1⇒y=1x,y=19,1
2 10x+y+2x-y=4; 15x+y-5x-y=-2
Let 1x+y=u and 1x-y=v
So, the equation becomes
10u+2v=4 …..I15u-5v=-2 …..II
Multiplying (I) with 5 and (II) with 2 we get
50u+10v=20 …..III30u-10v=-4 …..IV
Adding (III) and (IV) we get
u=1680=15
Putting this value in (I)
10×15+2v=4⇒2+2v=4⇒v=1
1x+y=15 and 1x-y=1⇒x+y=5 and x-y=1Solving these equations we getx=3 and y=2
3 27x-2+31y+3=85; 31x-2+27y+3=89
Let 1x-2=u and 1y+3=v
27u+31v=85 . ….I31u+27v=89 …..IIAdding I and II58u+58v=174u+v=3 …..IIISubtracting II from I4u-4v=4⇒u-v=1 …..IV
….I31u+27v=89 …..IIAdding I and II58u+58v=174u+v=3 …..IIISubtracting II from I4u-4v=4⇒u-v=1 …..IV
Adding (III) and (IV) we get
2u=4⇒u=2
Putting the value of u in III
2+v=3⇒v=1
1x-2=u=2⇒x-2=12⇒x=52
1y+3=1⇒y+3=1⇒y=-2
x,y=52,-2
4 13x+y+23x-y=34; 123x+y-123x-y=-18
Let 13x+y=u and 13x-y=v
u+2v=34 and 12u-12v=-18
So, the equations become
4u+4v=3 …..I4u-4v=1 …..II
Adding (I) and (II)
8u=4⇒u=12
Putting the value of u in (I)
12+2v=34⇒v=14
13x+y=u and 13x-y=v⇒13x+y=123x+y=2 …..IIIAlso, 13x-y=14⇒3x-y=4 …..IV
(III) + (IV) we get
6x=6⇒x=1y=-1
Page No 26:
Question 1:
Two numbers differ by 3. The sum of twice the smaller number and thrice the greater number is 19. Find the numbers.
Answer:
Let the smaller number be x and the larger number be y.
Given that the two numbers differ by 3 so,
y-x=3 …..(I)
Also, sum of twice the smaller number and thrice the greater number is 19
So, 2x+3y=19 ……(II)
The two equations obtained are
y-x=3
2x+3y=19
Multiplying (I) by 3 we get
3y-3x=9 …..(III)
Adding (III) and (II) we have
4y = 28
⇒y=284=7
Putting the value of y = 7 in (I) we get
7-x=3⇒-x=3-7⇒-x=-4⇒x=4
Thus, the two numbers are 4 and 7.
Page No 26:
Question 2:
Complete the following.
Answer:
The length of the given rectangle is 2x+y+8 and 4x-y
2x+y+8=4x-y⇒y+y+8=4x-2x⇒8+2y=2x⇒2x-2y=8Dividing by 2x-y=4 …..I
Breadth of the rectangle is 2y and x + 4.
2y=x+4⇒x-2y=-4 …..II
Subtracting (II) from (I)
x-x-y—2y=4—4⇒-y+2y=8⇒y=8Putting the value of y=8 in (I) we getx-8=4⇒x=4+8=12
Length = 4x-y=412-8=40
Breadth = 2×8=16
Perimeter = 2length+breadth=240+16=112 units
Area = length×breadth=40×16=640 unit2
Page No 26:
Question 3:
The sum of father’s age and twice the age of his son is 70. If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages.
If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages.
Answer:
Let the father’s age be x years and son’s age be y years.
Sum of father’s age and twice the age of his son is 70 so,
x+2y=70 ……(I)
Double the age of the father added to the age of his son the sum is 95
2x+y=95 …..(II)
Adding (I) and (II) we get
3x+3y=165Dividing by 3x+y=55 …..III
Subtracting (I) from (II)
2x-x+y-2y=95-70⇒x-y=25 …..IV
Adding (III) and (IV) we get
2x=80⇒x=40Putting the value of x=40 in III40+y=55⇒y=55-40⇒y=15
Thus, the age of the father is 40 years and age of his son is 15 years.
Page No 26:
Question 4:
The denominator of a fraction is 4 more than twice its numerator. Denominator becomes 12 times the numerator, if both the numerator and the denominator are reduced by 6. Find the fraction.
Find the fraction.
Answer:
Let the fraction be xy.
Denominator of a fraction is 4 more than twice its numerator.
So,
y=4+2x⇒2x-y=-4 …..I
Also, denominator becomes 12 times the numerator, if both the numerator and the denominator are reduced by 6.
So,
y-6=12x-6⇒y-6=12x-72⇒12x-y=72-6=66⇒12x-y=66 …..II
Subtracting (I) from (II)
12x-2x-y—y=66—4⇒10x=70⇒x=7010=7⇒x=7
Putting the value of x = 7 in (I)
27-y=-4⇒14-y=-4⇒y=14+4=18
Thus, the fraction obtained is 718.
Page No 26:
Question 5:
Two types of boxes A, B are to be placed in a truck having capacity of 10 tons. When 150 boxes of type A and 100 boxes of type B are loaded in the truck, it weighes 10 tons. But when 260 boxes of type A are loaded in the truck, it can still accommodate 40 boxes of type B, so that it is fully loaded. Find the weight of each type of box.
Answer:
Let the weight of box A be x and that of box B be y.
When 150 boxes of type A and 100 boxes of type B are loaded in the truck, it weighes 10 tons i.e 10000 kg.
So,
150x+100y=10000⇒15x+10y=1000⇒3x+2y=200 …..I
When 260 boxes of type A are loaded in the truck, it can still accommodate 40 boxes of type B, so that it is fully loaded.
260x+40y=10000⇒26x+4y=1000⇒13x+2y=500 …..II
Subtracting (I) from (II) we get
13x-3x+2y-2y=500-200⇒10x=300⇒x=30Putting the value of x=30 in I330+2y=200⇒90+2y=200⇒2y=200-90=110⇒y=1102=55
Thus, weight of box A = 30 kg and that of box B = 55 kg.
Page No 26:
Question 6:
Out of 1900 km, Vishal travelled some distance by bus and some by aeroplane. Bus travels with average speed 60 km/hr and the average speed of aeroplane is 700 km/hr. It takes 5 hours to complete the journey. Find the distance, Vishal travelled by bus.
Answer:
We know speed=distancetime
Average speed of bus = 60km/h.
Let the time taken in bus be x hours.
Average speed of bus = 700km/h.
Let the time taken in bus be y hours.
Total distance covered = 1900 km
60x+700y=1900⇒6x+70y=190⇒3x+35y=95 …..I
It takes 5 hours to complete the journey so,
x+y=5 …..II
Multiplying (II) with 3
3x+3y=15 …..III
Subtracting (III) from (I) we get
3x-3x+35y-3y=95-15⇒32y=80⇒y=2.5
Putting the value of y = 2.5 in (II) we get
x+2.5=5⇒x=2.5
Distance travelled by Vishal by bus = speed×time=60×2.5=150 km.
Page No 27:
Question 1:
Choose correct alternative for each of the following questions
(1) To draw graph of 4x +5y = 19, Find y when x = 1.
| A) 4 | (B) 3 | (C) 2 | (D) –3 |
(2) For simultaneous equations in variables x and y, Dx = 49, Dy = –63, D = 7 then what is x ?
| A) 7 | (B) –7 | (C) 17 | (D) -17 |
(3) Find the value of 53-7-4
| A) –1 | (B) –41 | (C) 41 | (D) 1 |
(4) To solve x + y = 3 ; 3x – 2y – 4 = 0 by determinant method find D.
| A) 5 | (B) 1 | (C) –5 | (D) –1 |
(5) ax + by = c and mx + ny = d and an ≠ bm then these simultaneous equations have —
| (A) | Only one common solution. | (A) | No solution. |
| (C) | Infinite number of solutions. | (D) | Only two solution. |
Answer:
(1) 4x +5y = 19
When x = 1, then y will be
41+5y=19⇒4+5y=19⇒5y=19-4=15⇒5y=15⇒y=155=3
Hence, the correct answer is option (B).
(2) x=DxD=497=7
Hence, the correct answer is option (A).
(3) 53-7-4=5×-4-3×-7=-20+21=1
Hence, the correct answer is option (D).
(4) x + y = 3 ; 3x – 2y – 4 = 0
D=113-2=1×-2-1×3=-2-3=-5
Hence, the correct answer is option (C).
(5) ax + by = c and mx + ny = d
D=abmn=an-bm
an ≠ bm
So, D ≠ 0.
So, the given equations have a unique solution or only one common solution.
Hence, the correct answer is option A.
Page No 27:
Question 2:
Complete the following table to draw the graph of 2x – 6y = 3
| x | –5 | x |
| y | x | 0 |
| (x, y) | x | x |
Answer:
2x – 6y = 3
| x | –5 | 32 |
| y | -136 | 0 |
| (x, y) | -5,-136 | 32,0 |
Page No 27:
Question 3:
Solve the following simultaneous equations graphically.
(1) 2x + 3y = 12 ; x – y = 1
(2) x – 3y = 1 ; 3x – 2y + 4 = 0
(3) 5x – 6y + 30 = 0 ; 5x + 4y – 20 = 0
(4) 3x – y – 2 = 0 ; 2x + y = 8
(5) 3x + y = 10 ; x – y = 2
Answer:
(1) 2x + 3y = 12
| x | 0 | 6 | 3 |
| y | 4 | 0 | 2 |
x – y = 1
| x | 0 | 1 | 3 |
| y | −1 | 0 | 2 |
The solution of the given equations is the point of intersection of the two line i. e(3, 2).
e(3, 2).
(2) x – 3y = 1
| x | 1 | 4 | 7 |
| y | 0 | 1 | 2 |
3x – 2y + 4 = 0
| x | 0 | 2 | 4 |
| y | 2 | 5 | 8 |
The solution of the given equations is the point of intersection of the two line i.e (-2,-1).
(3) 5x – 6y + 30 = 0
| x | 0 | –6 |
| y | 5 | 0 |
5x + 4y – 20 = 0
| x | 0 | 4 |
| y | 5 | 0 |
The solution of the given equations is the point of intersection of the two line i. e (0, 5).
e (0, 5).
(4) 3x – y – 2 = 0
| x | 0 | 1 |
| y | –2 | 1 |
2x + y = 8
| x | 0 | 4 |
| y | 8 | 0 |
The solution of the given equations is the point of intersection of the two line i.e (2, 4).
(5) 3x + y = 10
| x | 0 | 1 |
| y | 10 | 7 |
x – y = 2
| x | 0 | 2 |
| y | –2 | 0 |
The solution of the given equations is the point of intersection of the two line i. e (3, 1).
e (3, 1).
Page No 27:
Question 4:
Find the values of each of the following determinants.
| (1) 4327 | (2) 5-2-31 | (3) 3-114 |
Answer:
(1) 4327=4×7-3×2=28-6=22
(2) 5-2-31=5×1—2×-3=5-6=-1
(3) 3-114=3×4—1×1=12+1=13
Page No 28:
Question 5:
Solve the following equations by Cramer’s method.
(1) 6x – 3y = –10 ; 3x + 5y – 8 = 0
(2) 4m – 2n = –4 ; 4m + 3n = 16
(3) 3x – 2y = 52 ; 13x+3y=-43
(4) 7x + 3y = 15 ; 12y – 5x = 39
(5) x+y-82=x+2y-143=3x-y4
Answer:
(1) 6x – 3y = –10 ; 3x + 5y – 8 = 0
D=6-335=6×5—3×3=30+9=39Dx=-10-385=-10×5—3×8=-50+24=-26Dy=6-1038=6×8—10×3=48+30=78x=DxD=-2639=-23y=DyD=7839=2x,y=-23,2
(2) 4m – 2n = –4 ; 4m + 3n = 16
D=4-243=4×3—2×4=12+8=20Dx=-4-2163=-4×3—2×16=-12+32=20Dy=4-4416=4×16—4×4=64+16=80x=DxD=2020=1y=DyD=8020=4x,y=1,4
(3) 3x – 2y = 52 ; 13x+3y=-43
D=3-2133=9+23=293Dx=52-2-433=152-83=296Dy=35213-43=-4-56=-296x=DxD=296293=12y=DyD=-296293=-12x,y=12,-12
(4) 7x + 3y = 15 ; 12y – 5x = 39
D=73-512=7×12—5×3=84+15=99Dx=1533912=15×12-39×3=180-117=63Dy=715-539=7×39—5×15=273+75=348x=DxD=6399=711y=DyD=34899=11633x,y=711,11633
(5) x+y-82=x+2y-143=3x-y4
x+y-82=x+2y-143⇒3x+3y-24=2x+4y-28⇒x-y=-4 . ….Iand x+2y-143=3x-y4⇒4x+8y-56=9x-3y⇒5x-11y=-56 …..II
….Iand x+2y-143=3x-y4⇒4x+8y-56=9x-3y⇒5x-11y=-56 …..II
From (I) and (II)
D=1-15-11=-11×1—1×5=-11+5=-6Dx=-4-1-56-11=-11×-4—1×-56=44-56=-12Dy=1-45-56=-56×1—4×5=-56+20=-36x=DxD=-12-6=2y=DyD=-36-6=6x,y=2,6
Page No 28:
Question 6:
Solve the following simultaneous equations.
(1) 2x+23y=16 ; 3x+2y=0
(2) 72x+1+13y+2=27 ; 132x+1+7y+2=33
(3) 148x+231y=527xy ; 231x+148y=610xy
(4) 7x-2yxy=5 ; 8x+7yxy=15
(5) 123x+4y+152x-3y=14 ; 53x+4y-22x-3y=-32
Answer:
(1) 2x+23y=16 ; 3x+2y=0
Let 1x=u and 1y=v
2u+23v=16 12u+4v=1 …..I3u+2v=0 …..II
Multiply (II) with 2
6u+4v=0 …..III
I-III
6u=1⇒u=16
Putting the value of u in II.
3×16+2v=0⇒12+2v=0⇒v=-14
1x=u⇒x=61y=v⇒y=-4x,y=6,-4
(2) 72x+1+13y+2=27 ; 132x+1+7y+2=33
Let 12x+1=u and 1y+2=v
7u+13v=27 …..I13u+7v=33 . ….II
….II
(I) + (II)
20u+20v=60u+v=3 …..III
(II) − (I)
6u-6v=6 u-v=1 …..IV
(III) + (IV)
2u=4⇒u=2Putting the value of u in (IV) 2-v=1⇒v=1
12x+1=u=2 ⇒2x+1=12⇒x=-14and 1y+2=v=1⇒y+2=1⇒y=-1x,y=-14,-1
(3) 148x+231y=527xy ; 231x+148y=610xy
Multiply by xy
148y+231x=527 …..I 231y+148x=610 …..IIAdding I and II 379y+379x=1137⇒x+y=3 …..IIIII-I83y-83x=83⇒y-x=1 …..IVIII+IV2y=4⇒y=2
Putting the value of y in (IV)
2-x=1⇒x=1x,y=1,2
(4) 7x-2yxy=5 ; 8x+7yxy=15
⇒7y-2x=5 and 8y+7x=15
Let 1x=u,1y=v
7v-2u=5 …..I8v+7u=15 …..II
Multiply (I) with 7 and (II) with 2
49v-14u=35 …..III16v+14u=30 …..IV
Adding (III) and (IV)
65v=65⇒v=1And 1y=v=1⇒y=1
Putting the value of v in (I)
71-2u=5⇒u=11x=u=1⇒x=1x,y=1,1
(5) 123x+4y+152x-3y=14 ; 53x+4y-22x-3y=-32
13x+4y=u,12x-3y=v12u+15v=14 ⇒10u+4v=5 . ….I5u-2v=-32⇒10u-4v=-3 …..II
….I5u-2v=-32⇒10u-4v=-3 …..II
(I) + (II)
20u=2⇒u=110
Putting the value of u in (II)
10×110-4v=-3⇒1+3=4v⇒v=1
13x+4y=u=110⇒3x+4y=10 …..III12x-3y=v=1⇒2x-3y=1 …..IV
Multiply (III) with 2 and (IV) with 3
6x+8y=20 …..V6x-9y=3 …..VI
(V) − (VI)
17y=17⇒y=1
Putting the value of y in (VI)
6x-9=3⇒6x=12⇒x=2x,y=2,1
Page No 28:
Question 7:
Solve the following word problems.
(1) A two digit number and the number with digits interchanged add up to 143. In the given number the digit in unit’s place is 3 more than the digit in the ten’s place. Find the original number.
(2) Kantabai bought 112 kg tea and 5 kg sugar from a shop. She paid Rs 50 as return fare for rickshaw. Total expense was Rs 700. Then she realised that by ordering online the goods can be bought with free home delivery at the same price. So next month she placed the order online for 2 kg tea and 7 kg sugar. She paid Rs 880 for that. Find the rate of sugar and tea per kg.
She paid Rs 880 for that. Find the rate of sugar and tea per kg.
(3) To find number of notes that Anushka had, complete the following activity.
(4) Sum of the present ages of Manish and Savita is 31. Manish’s age 3 years ago was 4 times the age of Savita. Find their present ages.
(5) In a factory the ratio of salary of skilled and unskilled workers is 5 : 3. Total salary of one day of both of them is Rs 720. Find daily wages of skilled and unskilled workers.
(6) Places A and B are 30 km apart and they are on a st raight road. Hamid travels from A to B on bike. At the same time Joseph starts from B on bike, travels towards A. They meet each other after 20 minutes. If Joseph would have started from B at the same time but in the opposite direction (instead of towards A) Hamid would have caught him after 3 hours. Find the speed of Hamid and Joseph.
Answer:
(1) Let the number at the unit’s place be x and the digit at the ten’s place be y.
The number is thus 10y + x
After interchanging the digits the number becomes 10x + y.
Given that two digit number and the number with digits interchanged add up to 143.
So, 10y + x + 10x + y = 143
⇒11x+11y=143⇒x+y=13 …..I
Also, in the given number the digit in unit’s place is 3 more than the digit in the ten’s place.
So, x-y=3 …..II
Adding (I) and (II) we get
2x=16⇒x=8
Putting the value of x in (I) we get
8+y=13⇒y=13-8=5
Thus, the number is 58.
(2) Let the rate of tea be x Rs per kg and that of sugar be y Rs per kg.
When Kantabai bought the items by going to the shop,
32x+5y+50=700⇒3x+10y=1300 …..I
When Kantabai bought the items online then
2x+7y=880 …..II
Multiplying (I) with 2 and (II) with 3 we get
6x+20y=2600 …..III6x+21y=2640 …..IV
(IV) — (III)
y=40
Putting the value of y = 40 in (II)
2x+740=880⇒2x=880-280=600⇒x=300
Thus, tea is at 300 Rs per kg and sugar is 40 Rs per kg.
(3) Disclaimer: There is error in the question given. Instead of Rs 10 notes there should be Rs 100 notes.
Let the number of notes of Rs 100 be x and that of Rs 50 be y.
100x+50y=2500⇒2x+y=50 …..I
When number of notes is interchanged so,
50x+100y=2000⇒x+2y=40 …..II
Multiply (I) with 2
4x+2y=100 …..III
Subtracting (III) from (II) we get
3x=60⇒x=203x=60⇒x=20
Putting the value of x in (I) we get
y=10
Thus, there are 20 Rs 100 notes and 10 Rs 50 notes.
(4) Let the present age of Manish be x years and that of Savita be y years.
Sum of their present ages = 31
x+y=31 …..I
Their age 3 years ago was
Manish’s age = x-3
Savita’s age = y-3
Manish’s age 3 years ago was 4 times the age of Savita.
x-3=4y-3⇒x-3=4y-12⇒x-4y=-9 …..II
(I) — (II) we get
5y=40⇒y=8
Putting the value of y in (I) we get
x+8=31⇒x=23
Thus, age of Manish is 23 years and age of Savita is 8 years.
(5) Ratio of salary of skilled to unskilled workers = 5 : 3
Let one day salary of skilled person be x and that of unskilled person be y.
Their total one day salary Rs 720
x+y=720 …..I
Also,
xy=53⇒3x=5y⇒3x-5y=0 …..II
Multiplying (I) with 3 we get
3x+3y=2160 …..III
(III) — (II)
8y=2160⇒y=270
Putting value of y in (I) we get
x=450
One day salary of skilled person Rs 450 and that of unskilled person Rs 270.
(6) Let the speed of Hamid be x km/h and that of Joseph be y km/h.
When both travel in same direction so, the distance covered by them together will be 30 km.
We know Speed=DistanceTime
They meet each other after 20 min = 2060=13 hours
x3+y3=30⇒x+y=90 …..I
When Joseph started from point B but moved in opposite direction.
Distance travelled by Hamid — Distance travelled by Joseph = 30
⇒3x-3y=30⇒x-y=10 . ….II
….II
Adding (I) and (II) we get
2x=100⇒x=50
Putting the value of x in (II) we get
50-y=10⇒y=40
Thus, speed of Hamid is 50 km/h and that of Joseph is 40 km/h.
Page not found | Lebyazhevsky Agro-Industrial College (Cossack Cadet Corps)
Use the search.
Dear applicants!
reception campaign 2022-2023 academic year started on June 1, 2022. Acceptance of applications for training in professional programs is carried out until August 15, 2022 inclusive, and subject to availability will last until November 25, 2022. Information about the work of the admissions committee is located in the «Applicant» section http://lebpu.ru/pravila-priyoma-v-lapt/
Admissions committee telephone: 8(35 2 909) 9-18-23
IMPORTANT INFORMATION
Dear students and parents!
According to the decision of the Commission of the Government of the Kurgan Region for the Prevention and Elimination of Emergencies and Ensuring Fire Safety and the Operational Headquarters for the Prevention of the Importation and Spread of a New Coronavirus Infection in the Kurgan Region, training sessions for technical school students are held in accordance with the schedule. posted in the «Distance Learning» section for students of the Mokrousovsky branch in accordance with the schedule posted in the «Mokrousovsky branch» section on the technical school website. The interaction of teachers and students is carried out through e-learning and distance learning technologies.
posted in the «Distance Learning» section for students of the Mokrousovsky branch in accordance with the schedule posted in the «Mokrousovsky branch» section on the technical school website. The interaction of teachers and students is carried out through e-learning and distance learning technologies.
The sections «News» and «Information for students» contain informative information. All services of professional educational organizations work as usual, teachers work according to the schedule. We also recommend not to visit public places: parks, cafes, shopping centers. This will help protect against infection. College hotline — 8(35-237) 9-18-23, E-mail — [email protected].
Visually impaired version
Acting Directors Lopareva Natalya Aleksandrovna 8-919-580-62-87
Educational building: 8-35-237-9-18-23
Additional numbers:
Reception 909 909
Head of the educational service: 200948
Accounting: 204
hostel: 8-327-9-18-21
9090EV number: 205
Mokrousovsky branch:
Head Novopashina Galina Fedorovna
phone: 8 (35234) 9-80-78
Site search
Find:Useful links
USE-2016
Helpline
Public services
«>
Recent entries
- Sports — yes! No alcohol!
- Harvest
- “It’s not for nothing that the whole of Russia remembers!”
- «Conversations about the important»
- Again memory opens its diary
Weather
Recording calendar
| Mon | W | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|
| Jul | ||||||
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | ||
Job Information Portal
SAFE SUMMER 2020
45PROFOR
Recent records
- Sports — yes! No alcohol!
- Harvest
- “It’s not for nothing that the whole of Russia remembers!”
- «Conversations about the important»
- Again memory opens its diary
Categories
- «Initiation into cadets-2016»
- Antiterrorism
- Video footage
- Information Security
- News
- Anti-corruption
- Photo gallery
Function properties
Function zerosThe zero of the function is the value x at which the function becomes 0, i.
 e. f(x)=0.
e. f(x)=0. Zeros are points of intersection of the graph of the function with the axis Ox.
Function parity
A function is called even if for any x from the domain of definition f(-x) = f(x)
Even function is symmetrical about the axis Oy
Odd function
A function is called odd if for any x from the domain of definition the equality f(-x) = -f(x) is satisfied.
The odd function is symmetrical with respect to the origin.
A function that is neither even nor odd is called a general function.
Function increase
The function f(x) is called increasing if the larger value of the argument corresponds to the larger value of the function, i.e. x 2 >x 1 → f(x 2 )>f(x 1 )
Descending function
The function f(x) is called decreasing if the larger value of the argument corresponds to the smaller value of the function, i. e. x 2 >x 1 → f(x 2 )
e. x 2 >x 1 → f(x 2 )
Intervals on which the function either only decreases or only increases are called intervals of monotonicity . Function f(x) has 3 intervals of monotonicity:
(-∞ x 1 ), (x 1 , x 2 ), (x 3 ; +∞)
Find intervals of monotonicity using the service Intervals of increasing and decreasing function
Local maximum
The point x 0 is called a local maximum point if for any x from the neighborhood of the point x 0 the following inequality holds: f(x 0 ) > f(x)
Local minimum
Point x 0 is called a local minimum point if for any x from the neighborhood of the point x 0 the following inequality holds: f(x 0 ) < f(x).
Local maximum points and local minimum points are called local extremum points.
x 1 , x 2 — local extremum points.
Function periodicity
Function f(x) is called periodic, with period T , if for any x the equality f(x+T) = f(x) is true.
Constancy intervals
Intervals on which the function is either only positive or only negative are called intervals of constancy.
f(x)>0 for x∈(x 1 , x 2 )∪(x 2 , +∞), f(x)<0 for x∈(-∞,x 1 )∪(x 1 , x 2 )
Continuity of function
The function f(x) is called continuous at the point x 0 if the limit of the function as x → x 0 is equal to the value of the function at this point, i.e. .
Break points
Points where the continuity condition is violated are called break points of the function.
x 0 — break point.

2. Find the intersection points of the graph of functions with the coordinate axes.
3. Investigate the function for even or odd.
4. Investigate the function for periodicity.
5. Find intervals of monotonicity and extremum points of the function.
6. Find the intervals of convexity and inflection points of the function.
7. Find the asymptotes of the function.
8. Based on the results of the study, build a graph.
Example: Investigate and plot a function: y = x 3 – 3x
Solution can be found online:
1) The function is defined on the entire real axis, i.e. its domain of definition is D(y) = (-∞; +∞).
2) Find the points of intersection with the coordinate axes:
with the OX axis: solve the equation x 3 — 3x = 0
.
with the OY axis: y(0) = 0 3 – 3*0 = 03) Find out if the function is even or odd:
y(-x) = (-x) 3 – 3(-x) = -x 3 + 3x = — (x 3 – 3x) = -y(x)
It follows that the function is odd.

4) The function is not periodic.
5) Find intervals of monotonicity and extremum points of the function: y′ = 3x 2 — 3.
Critical points: 3x 2 – 3 = 0, x 2 =1, x= ±1. y(-1) = (-1) 3 – 3(-1) = 2
y(1) = 1 3 – 3*1 = -2
6) Find the convex intervals and inflection points of the function: y″ = 6x
Critical points: 6x = 0, x = 0.
y(0) = 0 3 – 3*0 = 0
7) The function is continuous, it has no asymptotes.
8) According to the results of the study, we will plot the function:
Solution of equations, inequalities and their systems. Task #21
1. Solving equations, inequalities and their systems Task #21
1 21. Solve the equation 2 3 0.
x
x
Solution. We reduce to a common denominator:
2
1 2 x 3x
0
2
x
1 2 x 3 x 2 0 ,
3 x 2 2 x 1 0 ,
x 0;
x0;
x 1,
x 1,
1
x ;
1
x .

3
3
x 0;
1
Answer: ; 1.
3
2. Solve the equation x x 2 x 1 2 x 1 .
2
Solution.
x x 2 2 x 1 2 x 1
2
x x 1 2 x 1 0
x 1 x x 1 2 0
x 1 x 2 x 2 0
x 1
x 1 0
x 1
2
x x twenty;
x 2.
Answer: 2; one; 1.
3. Solve the equation x 2 4 x 2 5 0.
Solution.
4
2
x 2 4 x 2 5 0
2
Let’s go back to the original variable:
x 2 2 5
x 5 2,
x 2 5 ,
x 5 2.
x25;
4
Answer : 2 5 .
2
.
12
4. Solve the inequality 2
0.
x 7x 8
Solution.
12
T .c . 12 0 , x 7 x 8 0 , then 2
0
x
7
x
8
provided that x 2 7 x 8 0
x2 7x 8 0
x 1 x 8 0
x 1,
x 8 ;
x
8
1
x 1; 8
2
Answer: 1 x 8.
12
5. Solve the inequality 2
0.
x 7x 8
Solution.
12
T .c .
 12 0 , x 7 x 8 0 , then 2
12 0 , x 7 x 8 0 , then 2 0
x 7x 8
2
provided that x 7 x 8 0
x2 7x 8 0
x 1 x 8 0
x 1,
x 8;
x
8
2
1
x ; eighteen;
Answer :
; eighteen; .
12
0.
6. Solve the inequality
2
x 1 2
Solution.
12
T .c . 12 0 , x 1 2 0 , then
0
2
x
1
2
2
provided that x 1 2 0
2
x2 2x 1 0
D 2 2 4 18 3 x 20 9123 1 2
1 2
x 1 2;1 2
x
2 8
1 2 ,
x
2
2 8
1 2;
x
2
Answer: 1 2 x 1 2 .
7. Solve the inequality
Solution.
x 4 3 x 4
2
x 4 3 x 4 0
x 4 x 4 3 0
x 4 2
3 x 4 .
2
4 3
4
x 4 x 4
x 4; 4 3
x
x40,
x430;
x 4,
x 4 3;
Answer: 4 x 4 3 .
3 0
8. Solve the system of inequalities
Solution.
2 x
1
0
2
2 3 x
2 x
0,
2
2 3 x
6 9 x 31 4 x.

T .c . 3 x 0 , then 3 x 2 2 0 for any x;
2
2
2 x
then
0 provided that 2 x 0.
2
2 3 x
x 2,
x 2 x 2.
3
x 5;
2 6 9 x 31 4 x
5
2
9 x 4 x 31 6
5 x 25
x 5; 2
x 5.
Answer: 5 x 2.
x
9. Solve the inequality 3 x 7 2 7 x 3 2 .
Solution. 1 way
3x 7 7 x 3
2
2
3x 7 7 x 3 0 (Using the difference of squares formula)
3x 7 7 x 3 3x 7 7 x 3 0
4 x 4 10 x 10 0
40 x 1 x 1 0
x 1 x 1 0
x 1 x 1 0
2
2
1
x 1; 1
1
x
x 1,
x 1;
Answer: 1 x 1.
9. Solve the inequality 3 x 7 2 7 x 3 2 .
Solution. 2 way
3x 7
2
7 x 3
2
9 x 2 42 x 49 49 x 2 42 x 9
40 40 x 2 : 40
x2 1
x 1
1 x 1 91
10. Solve the inequality x 2 x 2 9 9 x 2 9 .
Solution. 1 way
x 2 x 2 9 9 x 2 9
x 2 x 2 99 x 2 9 0
x 2 9 x 2 9 0 1
2
2
2
2
T
.

to
.
x
0
,
then
x
9 9 0 for any x;
x 9 x 9 0
So x 2 9 x 2 9 0 is satisfied under the condition 3 3;
x3,
x3;
Answer: x 3; x 3.
10. Solve the inequality x 2 x 2 9 9 x 2 9 .
Solution. 2 way
x 2 x 2 9 9 x 2 9
x 2 0 , then x 2 0 x 2 9 9 0 for any x;
x2 x2 9 9 x2 9
x2 9
x 3
: x
2
9 0
x 3,
x 3;
Answer: x 3; x 3.
11. Solve the system of inequalities 7 3 x 2 3 7 x 2 2 x ,
x 4 x 8 0.
Solution.
1 7 3 x 2 3 7 x 2 2 x
21x 14 21x 6 2 x
8 2 x x 4.
2 x 4 x 8 0
x 4 x 8 0
4
8
x 8; 4
x
x 4,
x 8;
x 4,
3
8 x 4.
8 x 4;
Answer: 8 x 4.
1
1
12. Find the value of the expression a 3 16a
a 4 a 4
at a 45.
Solution.
1
a 4 a 4
1
2
1 a 16a
a a 16
a 4 a 4
a 4 a 4
3
a a 2 16
8
2 8
1
a 16
2 If a 45, then 8 45 360.

Answer: 360.
4x 9 y
13. Find the value of the expression
y
2 x 3 y
if x y 7.
2
2
2 x 3 y
4x 9 y
1
y
y
2 x 3 y
2 x 3 y x y
2 If
y 2 x 3 y y
x y 7 , then 2 x y 2 7
3x
x 9 27 x 3 x 9 27 x 6 27
13.5.
10
4
6
6
x 2x
2x
2x
2
3
Answer: 13.5.
15. Find the value of the expression
b 6 b
.
if p b
b 3
Solution.
p a
p 6 a
a 6 a
1 p a
;
a 3
6 a 6 6 a 6 a a
2p6a
;
6 a 3
3 a
p a
a 6 a 6 a a a 6 a 3 a 1
p
a
16. Find the value of the expression
3
1
if p b b 3b .
b
b
Solution.
2
2
2
2
3
1
a
3
3
a
2
a
a
a
a
a
2
2
1 1 3 1 1 1
3
1 3a 3 a
2 p
3
3a a
;
2
A
A 1 A 1 A
A
A
A
P A
A 2 3 3A 2 1 3A 2 3 A 2
3
:
1.

2
2
A
A
1
PU
a
Answer: 1.
17. Find the value of the expression 61a 11b 50
2 a 7b 5
9.
if
7 a 2b 5
Solution.
2 a 7b 5 9
7 a 2b 5 1
2a 7b 5 63a 18b 45
0 63a 2a 18b 7b 45 5
61a 11b 40 0 10
61a 11b 50 10
Answer: 10.
18. Find
f 3 if f x 1 7 6 x .
Solution.
f 3 f 4 1 7 6 4 7 2 49.
Answer: 49.
19. Solve the equation
Solution.
x 7 3 49 x 7
3
x 7 49 x 7 0
2
x 7 x 7 49 0
x 7 x 2 14 x 0
x 7 x x 14 0
x 7 0,
x 14 28 x0;
x 7
3
49 x 7 .
x 7,
x 14,
x 0.
Answer: 14; 7; 0.
20. Solve the equation x 3 x 2 9 x 9.
Decision.
x3 x 2 9 x 9
2
x x 1 9 x 1
x 2 x 1 9 x 1 0
x 1 x 2 9 0
x 1 x 3 x 3 0
x 1 0. x 3 0;
x 1,
x 3,
x 3.
Answer: 3; one; 3.
21. Solve the equation x 3 4 x 2 5 x.

Solution.
x3 4 x 2 5x
x3 4 x 2 5x 0
x x2 4x 5 0
x 0,
2
x 4 x 5 0;
x 0,
x 1,
x 5.
Answer: 1; 0; 5.
22. Solve the equation x 3 3 x 2 x 3 0.
Solution.
x 3 3x 2 x 3 0
2
x x 3 x 3 0
x 3 x 2 1 0
x 3 x 1 x 1 0
x 3 0,
x 3,
x 1 0 , x 1,
x 1 0;
x 1.
Answer: 3; one; 1.
23. Solve the equation x 2 2 x 3 12 x 2 .
Solution.
2
x 2 x 3 12 x 2
x 2 2 x 3 12 x 2 0
x 2 x 2 x 3 12 0
x 2 x 2 5 x 6 0
x 2 0,
x 2,
2
x 1,
x 5 x 60;
x 6.
Answer: 1; 2; 6.
24. Solve the equation
x 2 x 3 x 4 x 2 x 3 x 5 .
Solution.
x 2 x 3 x 4 x 2 x 3 x 5
x 2 x 3 x 4 x 2 x 3 x 5 0
x 2 x 3 x 4 x 5 0
x 2 x 3 1 0
x 2 0,
x 2,
x 3 0;
x 3.
Answer: 2; 3.
25. Solve equation
2 x 3 x 3 2 x 3 x 3 .
2
Solution.
2 x 3 2 x 3 2 x 3 x 3 2
2
2
2 x 3 x 3 2 x 3 x 3 0
2 x 3 x 3 2 x 3 x 3 0
2 x 3 x 3 x 0
x 1.
 5,
5, 2 x 3 0 ,
x 3 0 , x 3,
x 0;
x 0.
Answer: 0; 1.5; 3.
2
26. Solve the equation x x 20 .
4
2
Solution.
2
x 4 x 20
x x 20
2 2
2
x 2 x 20 ,
2
x x 20;
x , because . D 0
x x 20 0 ,
x 5,
x 5,
2
x 4.
x x 20 0;
x 4.
2
Answer: 5; 4.
27. Solve the equation x x 5 .
6
3
Solution.
3
x 6 x 5
x x 5
2 3
3
x x 5
x2 x 5 0
No real roots because . D 0
2
Answer: x.
28. Solve the equation 2 x 7 x 3 1.
x2 9
Solution.
2×2 7x 3
1
2
x 9
2 x 2 7 x 3 x 2 9 ,
2
x 9 0;
x3,
2
x7x120,
x4; x 4.
2
x 9;
x3;
2
Answer: 4.
29. Solve the equation x 2 6 x 6 x 6 x 7.
Solution.
x 6x 6 x 6 x 7
x 2 6 x 7,
6 x 0;
x 2 6 x 7 0,
x 1,
x 7;
x6;
x6;
2
Answer: 1.

x 1.
30. Solve the equation
x
2
2
Solution. 1 way
x 25 x 3x 10 0
x250,
x3x100;
x 5,
2
2
2
2
2
2
25 x 3 x 100.
2
2
2
2
x 25 38 x 5;
2
x 3 x 10 0;
x5,
x2;
Answer: 5.
2
x 5.
30. Solve the equation 2 way
x
2
2
25 x 3 x 10 0
x 5 x 5 2 x 5 x 2 2 0
2
2
x 5 x 5 x 2 0
2
x 5 x 2 x 10 x 2 2 4 x 4 0
2
x 5 2 x 2 14 x 29 0
2
2
2
x 5 0,
x 5,
2
x , because . D 0.
2x14x290;
Answer: 5.
x 5.
31. Solve the system of equations
Solution.
3 x 2 y 4 ,
2
2 x y 1;
x 1,
y 1;
2
3 x 2 y 4 ,
2
2 x y 1.
5 x 2 5,
x 2 1,
2
2 x 1 y ;
2 1 1 y ;
x 1,
x 1;
at 1;
Answer:
x 1,
y 1;
x 1,
y 1.
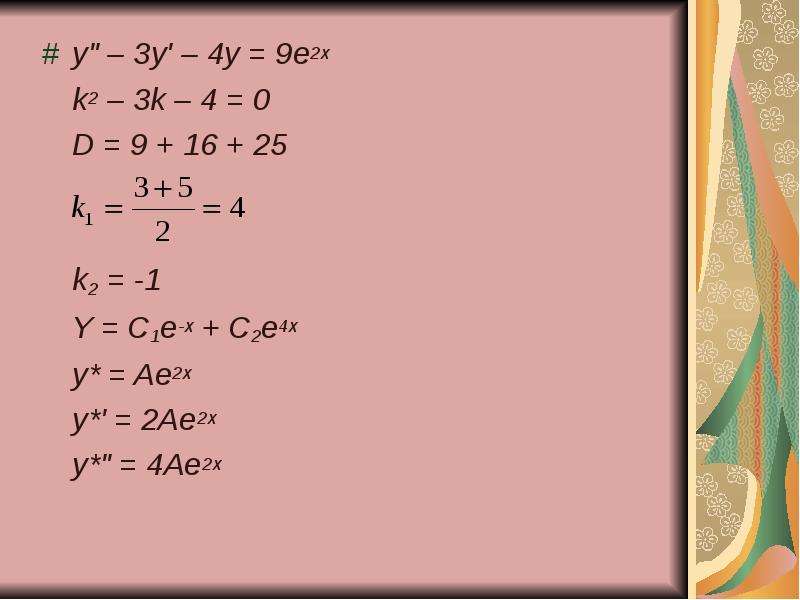
1; one ; one; one .
2 x 2 3 y 2 11,
32. Solve the system of equations
4 x 2 6 y 2 11x.
Solution.
2 x 2 3 y 2 11,
2
4 x 2 6 y 2 22 ,
2
2
4 x 6 y 2 11x;
4 x 6 y 2 11x;
2 x 2 3 y 2 11,
2 2 2 3 y 2 11,
0 11x 22;
x2;
y1 1,
y 1,
y2 1;
x2;
x2;
2
Answer:
x1 2,
y1 1;
x 2,
2
y2 1.
2; one ; 2; one .
33. Solve the system of equations
x 6 y 2 7 y ,
x 6 y 2 7 x.
Decision.
x 6 y 2 7 y ,
0 7 y 7 x ,
2
2
x 6 y 7 x;
x6y7x;
x y ,
x y ,
x y ,
2
2
7 x 7 x 1 0;
49x7x;
x6x7x;
x y
x1 0 ,
x 1 ;
2 7
1
x2 ,
x1 0 ,
7
or
y1 0;
at 1 .
2 7
1 1
Answer: 0; 0; ; .
7 7
34. Solve the system of equations
Solution.
2 x 3 2 5 y ,
3 x 2 2 5 y .

2 x 3 2 5 y ,
2 x 3 2 3 x 2 2 ,
2
2
3 x 2 5 y ;
3 x 2 5 y ;
x1 1,
2 x 3 3 x 2 ,
2 x 3 3 x 2; x2 1;
2
2
3
x
2
5 y;
3x25y;
x2 1,
x1 1,
or
1
y1 5;
y2 5 .
Answer:
1; 5 ; one; 0.2 .
35. Solve the system of equations
Solution.
x 2 y 2 37 ,
2
xy 6;
x 2 y 2 37 ,
xy 6.
x 2 y 2 37 ,
2 xy 12;
x y 7 ,
x 2 xy y 49 ,
x y 49 ,
x y 7;
xy6;
xy 6;
xy6;
x 7 y ,
x 7 y ,
2
y 7 y 6 0;
7 y 6;
x 7 y ,
x 7 y ,
2
y 7 y 6 0;
7 y 6;
2
2
2
35. Solve the system of equations
Solution. (continued)
x 2 y 2 37 ,
xy 6.
x 7 y ,
x 7 y ,
y1 1 ,
2
y 6;
2
y 7 y 6 0;
x 7 y ,
x 7 y ,
2
y 7 y 6 0;
y 1,
y 6;
Answer:
x1 6 ,
y1 1;
x 1,
2
y 2 6;
x3 6 ,
y 1;
3
x4 1,
y4 6.

6; one ; one; 6; 6; one ; one; 6.
36. Solve the system of equations
x 2 4 y 1,
2
x 3 4 y y 2 .
Solution.
x 2 4 y 1,
x 2 4 y 1,
2
2
x 3 4 y y ;
4 y 1 3 4 y y 2 ;
2
2
x 4 y 1,
x 4 y 1,
2
x 4 y 1,
2
y1 2 ,
y1 2 ,
y 4;
y2;
y2;
2
2
x 2 9 ,
x1 3,
y1 2;
y1 2;
x 3,
2
not
has
meanings
x 7 ,
2
y 2 2;
y2 2;
Answer: 3; 2; 3; 2.
37. Solve the system of equations
Solution.
x 6 y 7 0 ,
y 4
x y 10 3.
x 6 ,
x 6 0 ,
y 4
3;
x 6 y 7 0 ,
6 y 10
y 7 0;
y 4
x y 10 3;
y 4 3;
y 7 ,
x y 10
7 4
3;
x 7 10
37. Solve the system of equations
Solution. (continued)
x 6 ,
y 4 3;
6 y 10
y 7 ,
7 4
3;
x 7 10
x 6 y 7 0 ,
y 4
x y 10 3
y 4;
y 7,
y 7,
3 3 x 3,
x 4,
x 3;
x3;
x4;
y 7.

Answer:
4; 7.
Find the largest value of the function
Learn how to solve USE problems in a couple of minutes!
DO YOU HAVE BACK PAIN?
Alexander | 2014-06-20
In the last article, we considered tasks for determining the maximum (minimum) points of a power function. Here are 7 examples with a power function. It is required to determine the largest (or smallest) value of the function on the interval. The blog has already considered similar examples of functions with the number e, logarithmic, trigonometric, rational.
The standard algorithm for solving such tasks involves, after finding the zeros of the function, the determination of the signs of the derivative on the intervals. Then the calculation of the values at the found points of the maximum (or minimum) and on the border of the interval, depending on what question is in the condition.
I advise you to do things a little differently. Why? Wrote about it here.
I propose to solve such tasks as follows:
1. Find the derivative.
2. Find the zeros of the derivative.
3. Determine which of them belong to the given interval.
4. Calculate the values of the function on the boundaries of the interval and points of item 3.
5. Draw a conclusion (answer the question).
In the course of solving the presented examples, the solution of quadratic equations is not considered in detail, you should be able to do this. You should also know the derivatives of elementary functions.
Consider the following examples:
77422. Find the maximum value of the function y=x 3 -3x+4 on the segment [-2;0].
Find the derivative of the given function:
Find the zeros of the derivative:
The point x = –1 belongs to the interval specified in the condition.
Calculate the values of the function at points -2, -1 and 0:
The largest value of the function is 6.
Answer: 6
77425. Find the smallest value of the function y \u003d x 3 3 90 + 2 on the segment [1;4].
We will find a derivative of a given function:
We find zeros derivative:
The point indicated in the condition of the interval belongs to the point x = 2.
We calculate the values of the function 1, 2 and 4:
907 907 907 907 907 907 907 907 907 907 907 907 907 907 907 907 907 907 -2.Answer: -2
77426
Find the derivative of the given function:
Find the zeros of the derivative:
The point x = 0 belongs to the interval specified in the condition. 0
77429. Find the smallest value of the function y \u003d x 3 — 2x 2 + x +3 on the segment [1; 4].
Find the derivative of the given function:
Find the zeros of the derivative, solve the quadratic equation:
3x 2 — 4x + 1 = 0
We get the roots: x 1 = 1 x 1 = 1/3.
Only x = 1 belongs to the interval specified in the condition.
Let’s find the values of the function at points 1 and 4:
functions y \u003d x 3 + 2x 2 + x + 3 on the interval [- 4; -one].
Find the derivative of the given function:
Find the zeros of the derivative, solve the quadratic equation:
3x 2 + 4x + 1 = 0
Get the roots:
The root = 1 belongs to the interval specified in the conditions.
We find the values of the function at points -4, -1, -1/3 and 1:
We found that the largest value of the function is 3.
Answer: 3
77433. Find the smallest value of the function y \u003d x 3 – x 2 — 40x +3 on the interval [0;4].
We will find a derivative of a given function:
We find zero derivatives, solve the square equation:
3x 2 — 20 = 0
We get the roots:
.
We find the values of the function at points 0 and 4:
We found that the smallest value of the function is -109.
Answer: -109
Consider a method for determining the largest and smallest values of functions without a derivative. This approach can be used if you have big problems with the definition of the derivative. The principle is simple — we substitute all integer values from the interval into the function (the fact is that in all such prototypes the answer is an integer).
77437. Find the smallest value of the function y=7+12x–x 3 on the segment [–2;2].
Substituting points from -2 to 2:
y(-2)=7+12 (-2) — (-2) 3 = – 9
7
y(1)=7+12∙1 – 1 3 = 18
y(2)=7+12∙2 – 2 3 = 23
The smallest value is –9.
Answer: –9
77441
Insert points from -2 to 2:
y(-2)=9 (-2) 2 — (-2) 3 = 44
0
y(1)=9∙1 2 – 1 3 = 8
y(2)=9∙2 2 – 2 3 = 28
is equal to .


 Function notation f(x) is used to name an algebraic expression in x. When x in
the symbol f(x) is replaced by a particular value, the symbol represents the value
of the expression for that value of x.
Function notation f(x) is used to name an algebraic expression in x. When x in
the symbol f(x) is replaced by a particular value, the symbol represents the value
of the expression for that value of x. However, the two solutions of an equation in two
variables that are generally easiest to find are those in which either the first or
second component is 0. The x-coordinate of the point where a line crosses the x-axis
is called the x-intercept of the line, and the y-coordinate of the point where a line
crosses the y-axis is called they-intercept of the line. Using the intercepts to graph
an equation is called the intercept method of graphing.
However, the two solutions of an equation in two
variables that are generally easiest to find are those in which either the first or
second component is 0. The x-coordinate of the point where a line crosses the x-axis
is called the x-intercept of the line, and the y-coordinate of the point where a line
crosses the y-axis is called they-intercept of the line. Using the intercepts to graph
an equation is called the intercept method of graphing.
 By doing this we reduce the number of equations and the
number of variables by one.
By doing this we reduce the number of equations and the
number of variables by one. 5 Word problems
5 Word problems