Квадратичная функция: ее график и свойства 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 1: Функции и их свойства
- Видео
- Тренажер
- Теория
Заметили ошибку?
Тема 4.
Всем привет! Сегодня мы поговорим об одной из самых важных функций, о квадратичной функции.
Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.
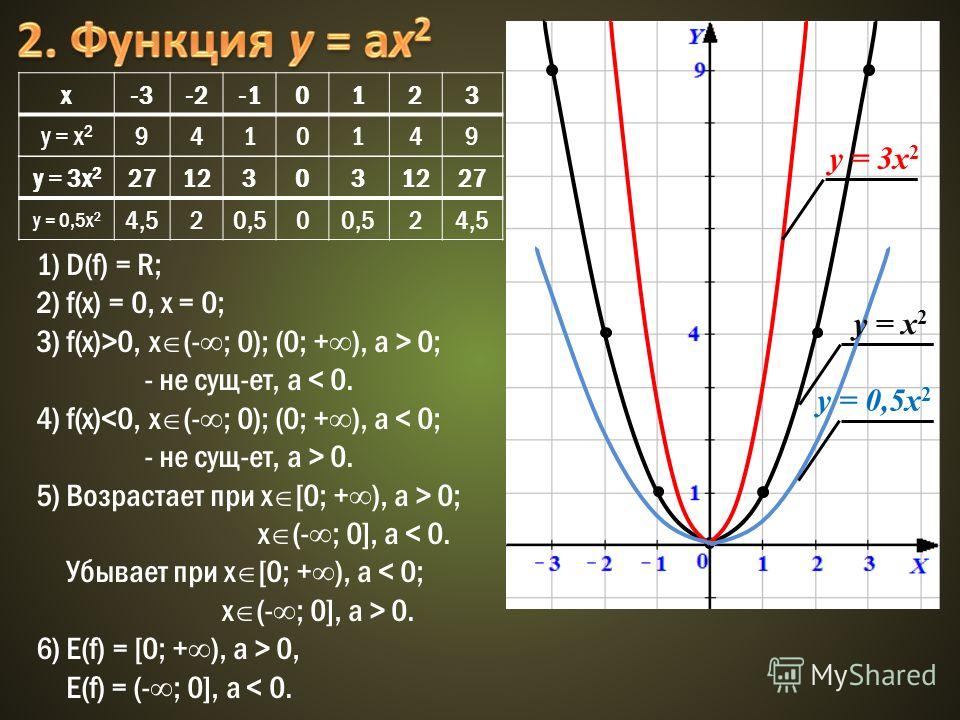
Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.
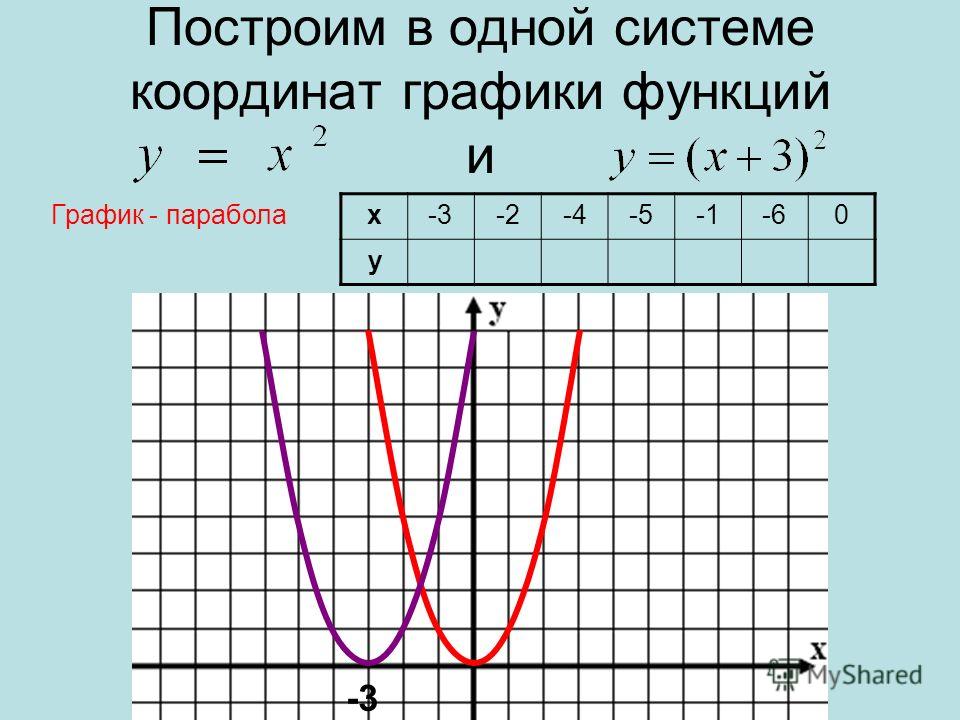
Построим в одной системе координат
y = x2; y = 2x2; y = 3x
y = x2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
y = 2x2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
18 |
8 |
2 |
0 |
2 |
8 |
18 |
При любом x ≠ 0 значение функции y = x2 в 2 раза больше соответствующих значений функции y = x2.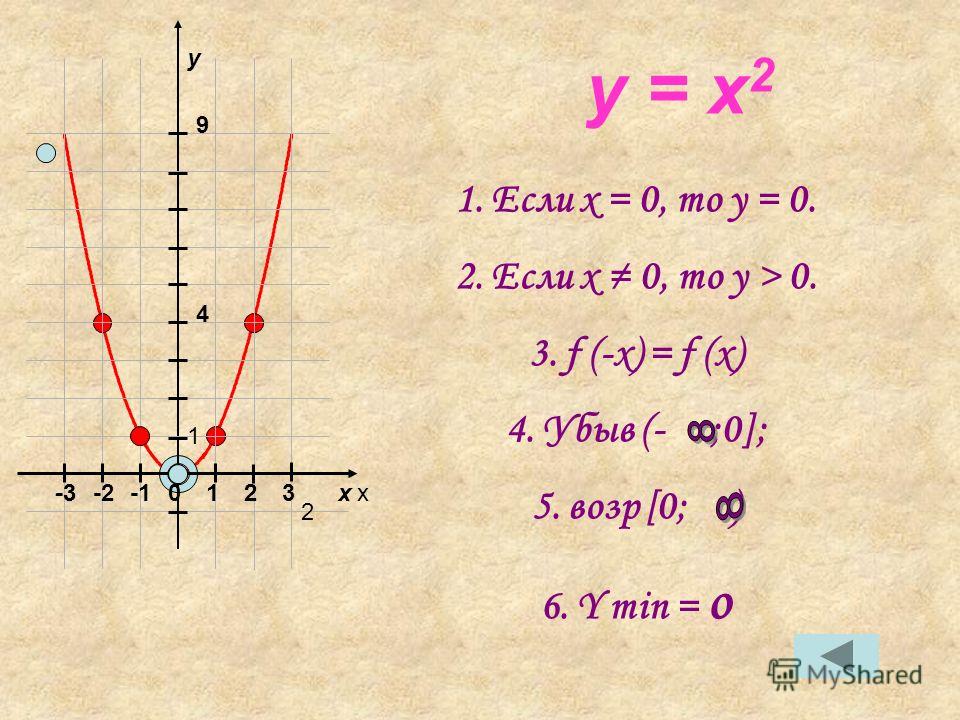 То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
Аналогично, график функции y = 3x2 можно получить из графика функции y = x2 растяжением от оси x в 3 раза.
Построим теперь в одной системе координат графики функции y = x2, y=12×2, y=13×2.
y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Заметим, что при любом 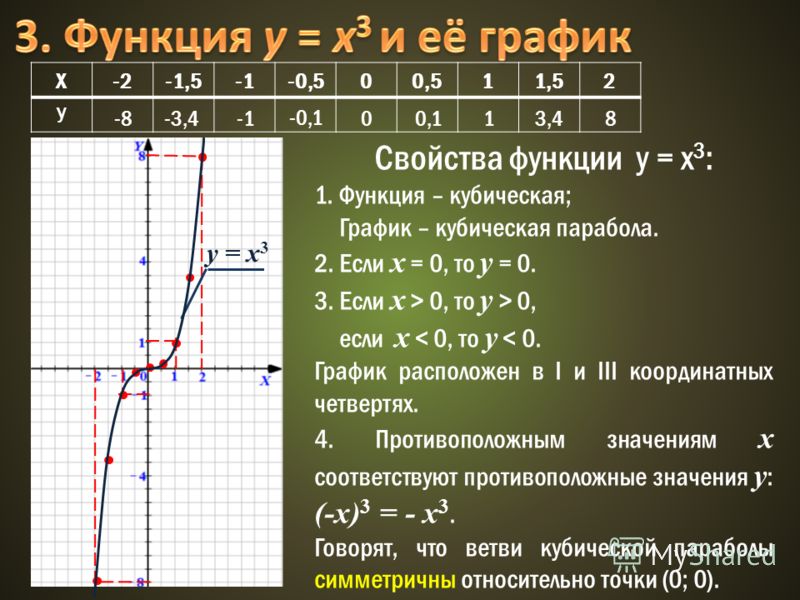
Таким образом, график функции y=12×2 можно получить из параболы y = x2 сжатием к оси x в 2 раза.
y=13×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
3 |
43 |
13 |
0 |
13 |
43 |
3 |
Аналогично график функции y=13×2 можно получить из графика функции = x2 сжатием к оси x в 3 раза.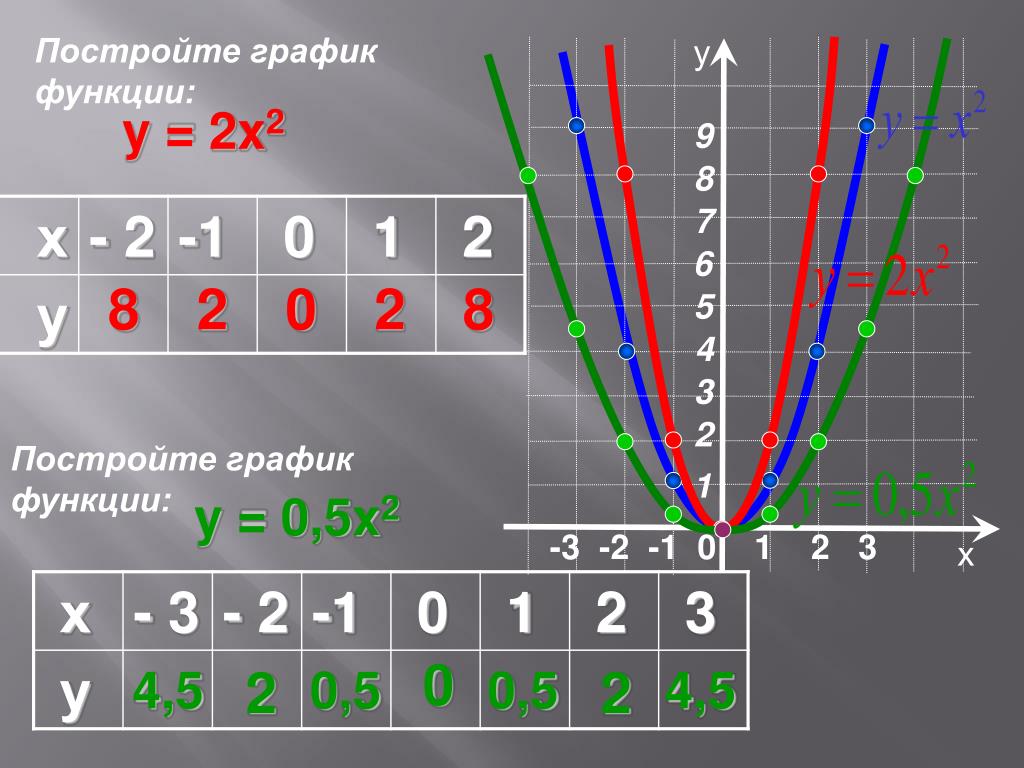
Давай сделаем вывод:
График функции y = ax2 можно получить из параболы y = x2 растяжением от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0 a
Рассмотрим теперь случай, когда a y=-13×2. Составим таблицу значений:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-3 |
-43 |
-13 |
0 |
-13 |
-43 |
-3 |
Сравним графики функций y=13×2 и y=-13×2. При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
То есть графики функций y = ax2 и y = —ax2 при a ≠ 0 симметричны относительно оси x. Графиком функции y = ax2, как и графиком функции y = x2 является парабола
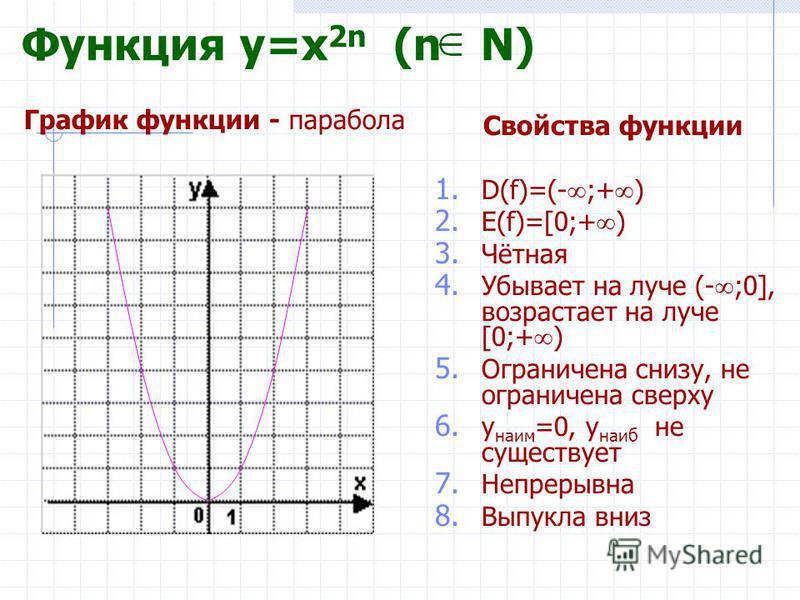
Сформулируем свойства функции y = ax2 при a > 0.
- Область определения -∞;+∞;
- Область значений функций 0;+∞
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
-
График функции симметричен относительно оси y.

- Функция убывает в промежутке -∞;0 и возрастает в промежутке 0;+∞.
- При x = 0 функция принимает наименьшее значение, равное 0. Наибольшего значения функции нет.
Сформулируем свойства функции y = ax2 при a
- Область определения -∞;+∞;
- Область значений функций -∞;0
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y
- График функции симметричен относительно оси y.
- Функция убывает в промежутке 0;+∞ и возрастает в промежутке -∞;0.
- При x = 0 функция принимает наибольшее значение, равное 0. Наименьшего значения функции нет.
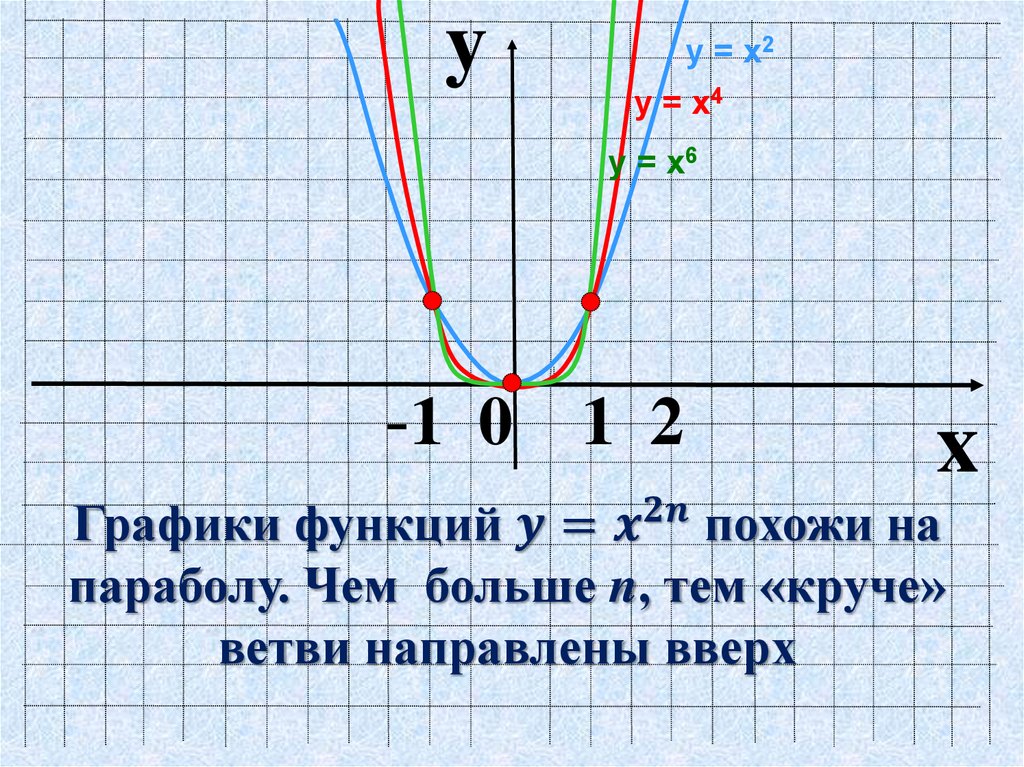
От коэффициента a зависит направление ветвей параболы.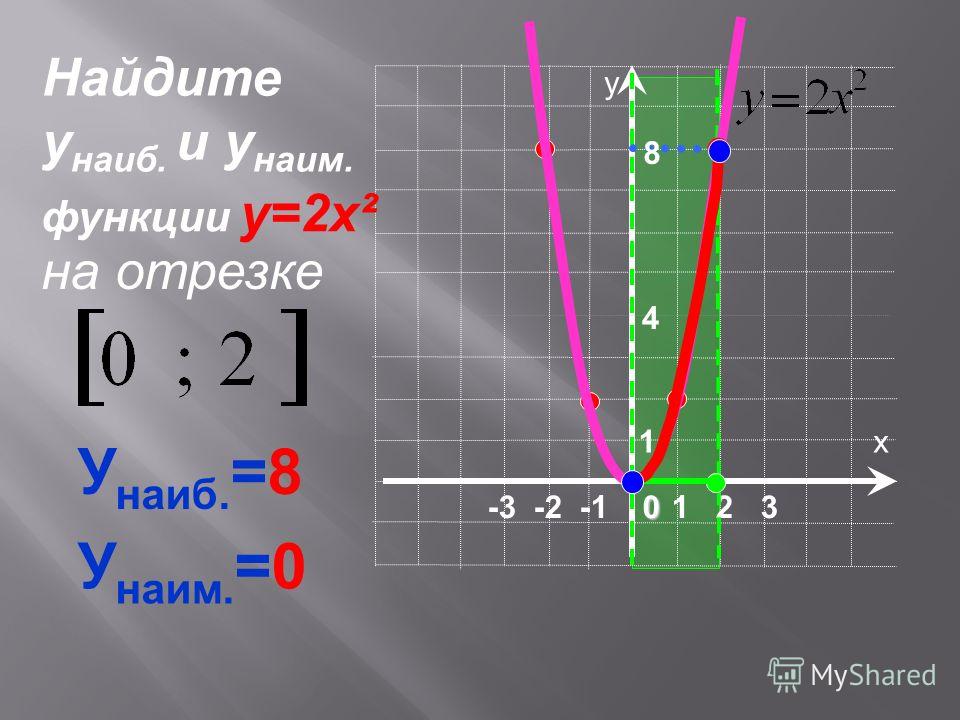 Если a > 0, то ветви параболы направлены вверх, если a
Если a > 0, то ветви параболы направлены вверх, если a
Построение графика, симметричного данному относительно оси x, или сжатие к оси x – различные виды преобразований графиков функций. Преобразования графиков функции, рассмотренные нами сегодня для функций y = ax2, применимы к любой функции.
График функции y=-fx можно получить из графика функции y=fx с помощью симметрии относительно оси абсцисс.
График функции y=afx можно получить из графика функции y=fx с помощью растяжения от оси
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Урок 5. функция y=х² и её график — Алгебра — 8 класс
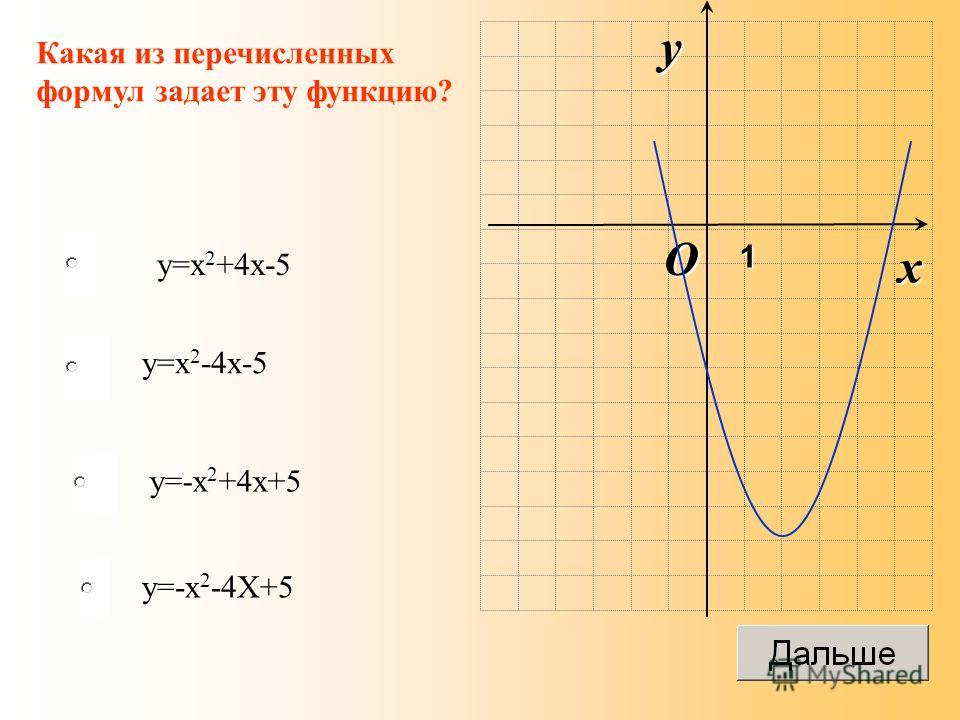
Выберите верные равенства.
Дана функция y = x2.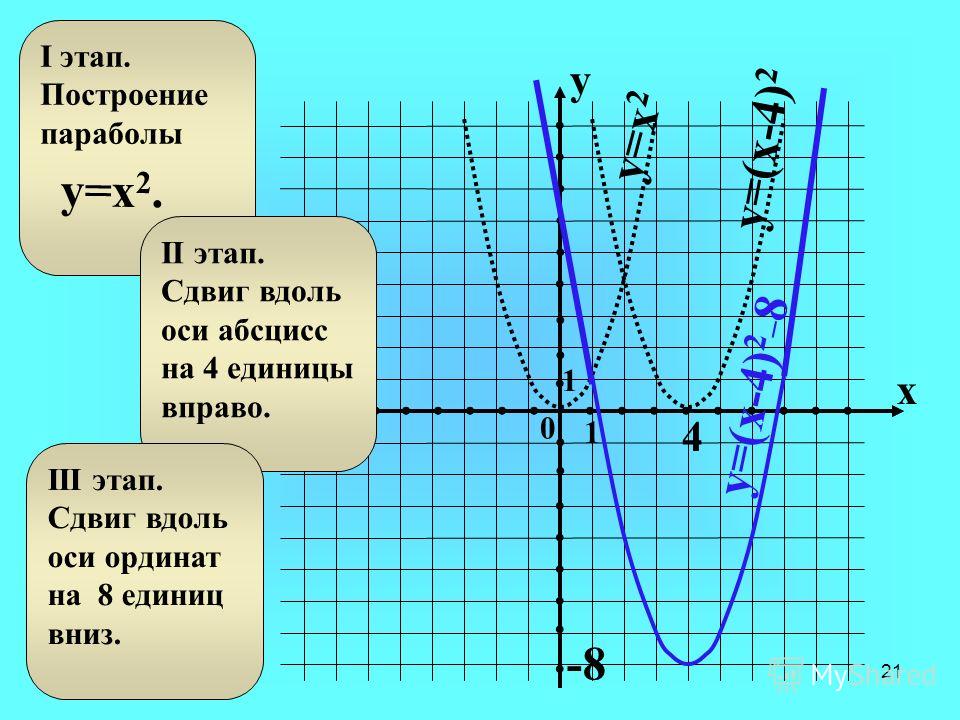
y (2,5) = 6,25
y (–8) = 8
y (0) = 0
y (–2,5) = 625
y (–2) = –4
y (10) = 1000
y (–2) = 4
y (2) = 8
y (–10) = –100
Впишите пропущенные числа.
Для функции y = x2 впишите значения абсцисс и ординат на отрезке x ∈ [–1,5; 2,5]
при изменении x через 0,5.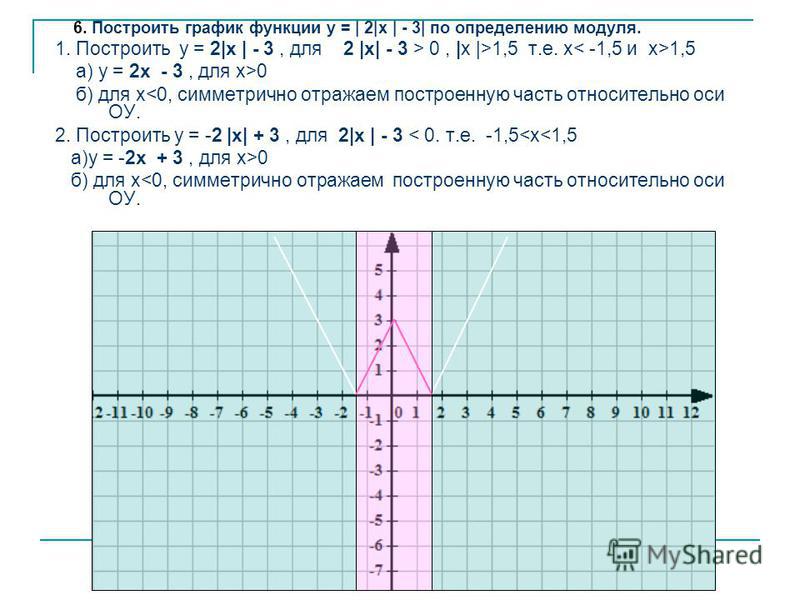
Для вписывания десятичной запятой используйте обычную запятую с клавиатуры. Между знаком минус и числом, а также перед и после десятичной запятой пробел ставить не нужно. Для вписывания знака «минус» используйте символ минус на клавиатуре (расположен над знаком «+»).
x = –1,5; y =
x =
; y =
x =
; y =
x =
; y =
x =
; y =
x =
; y =
x =
; y =
x =
; y =
x = 2,5; y =
Заполните пропуски.
Дана функция y = x2. Сравните значения функции и подберите подходящий знак в каждой паре значений. >
=
=
>
=
>
>
=
Укажите все правильные ответы.
На каких промежутках функция y = x2 только возрастает?
(–1; –0,5)
[–10; 7)
[–3; 3]
[–9; 0]
(4; 7]
[0; 9]
Укажите все правильные ответы.
На каких промежутках функция y = x2 только убывает?
[–1,9; 0)
[–16; 2]
[–10; 17)
(–1; –0,5)
(2; 8]
[10; 19]
Укажите все правильные ответы.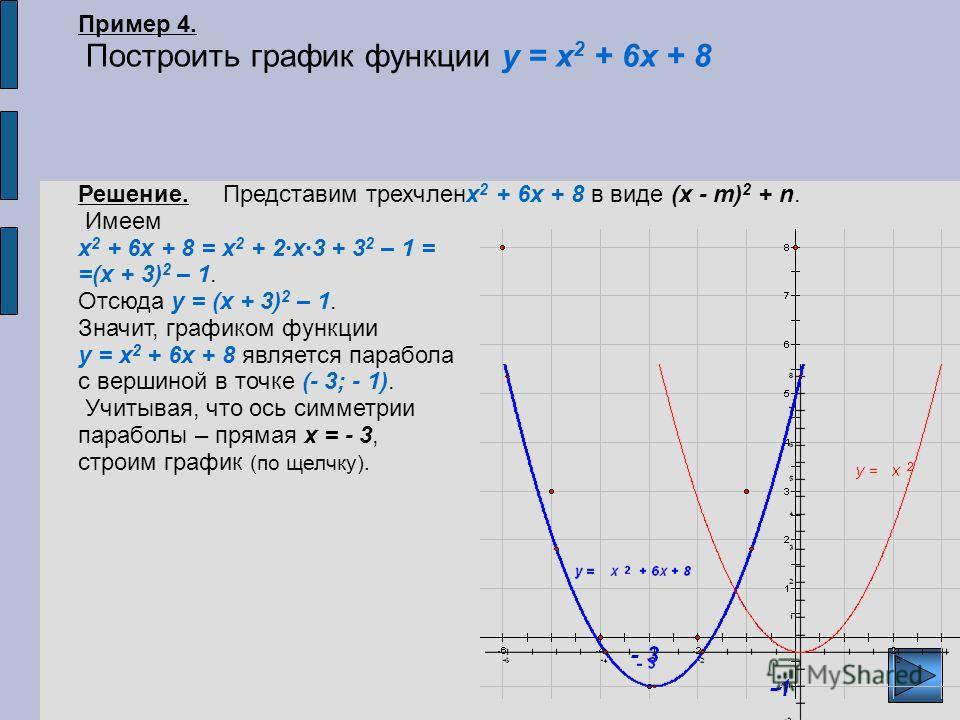
Выберите верные утверждения, относящихся к функции y = x2.
График функции симметричен относительно начала координат.
Вершина параболы – это точка с наибольшими значениями абсциссы и ординаты.
Вершина параболы – это точка с наименьшими координатами абсцисс и ординаты.
График функции симметричен относительно оси абсцисс.
График функции симметричен относительно оси ординат.
Вершина параболы – это начало координат (на координатной плоскости xOy).
Точка с координатами (0; 0) не принадлежит графику функции.
Точка с координатами (0; 0) принадлежит графику функции.
Линия, представляющая собой график функции, называется параболой.
Укажите все правильные ответы.
В каких координатных четвертях расположен график функции y = x2?
III
IV
I
II
Укажите все правильные ответы.
Какие точки принадлежат графику функции y = x2?
C (–4; 16)
B (0; 9)
E (0,125; 0,125)
O (0;0)
D (–0,4; 0,16)
A (–3; –9)
Установите соответствие между названием точки на графике и её координатами.
(3; 9)
(1,5; 6,25)
(–3; 9)
(1,5; –2,25)
(–1,5; 2,25)
(1,5; 2,25)
(9; 3)
(–1,5; 6,25)
(–1,5; –2,25)
Сбросить ответы Сохранить и перейти к следующему Проверить
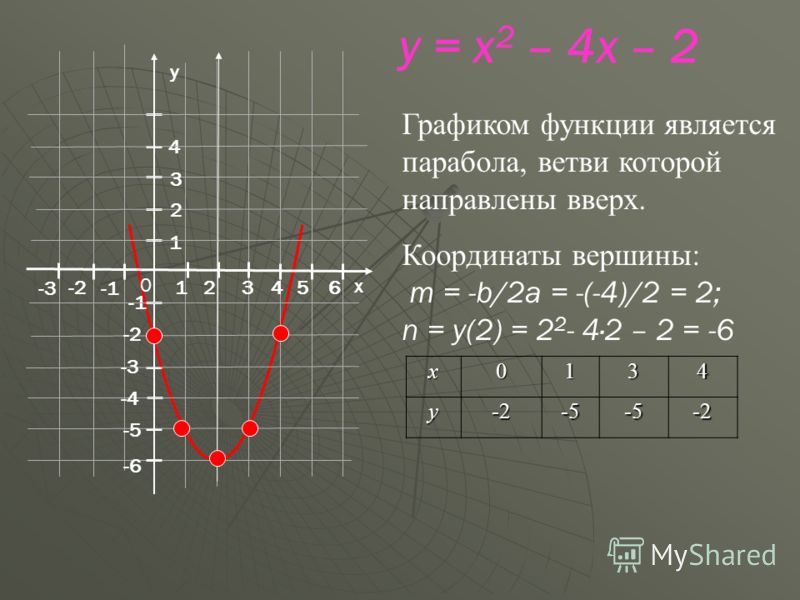
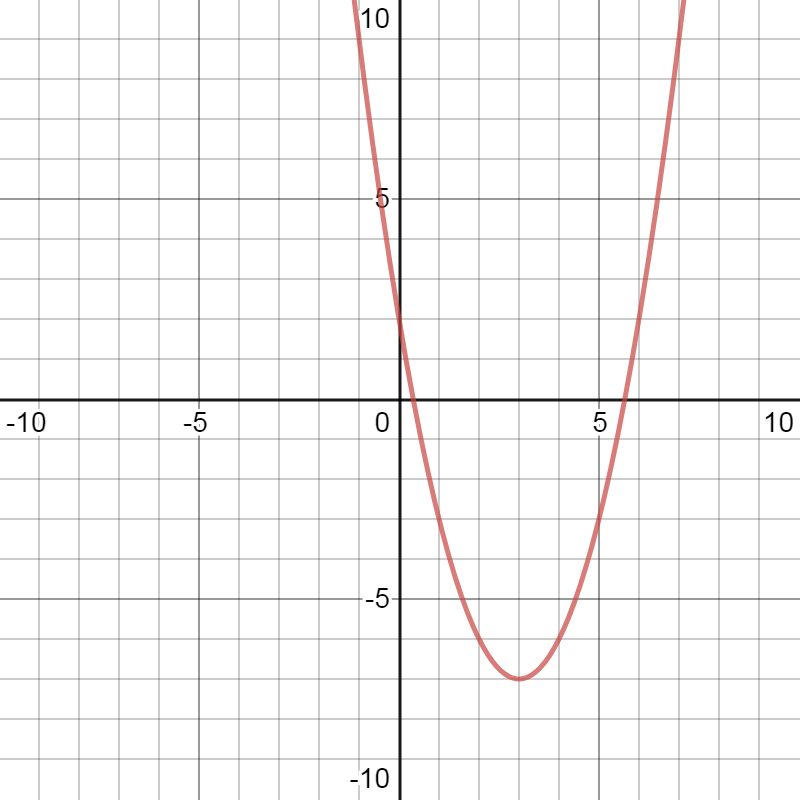
График функции y x 2 6x 4.
 Функции и графики
Функции и графикиВ золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.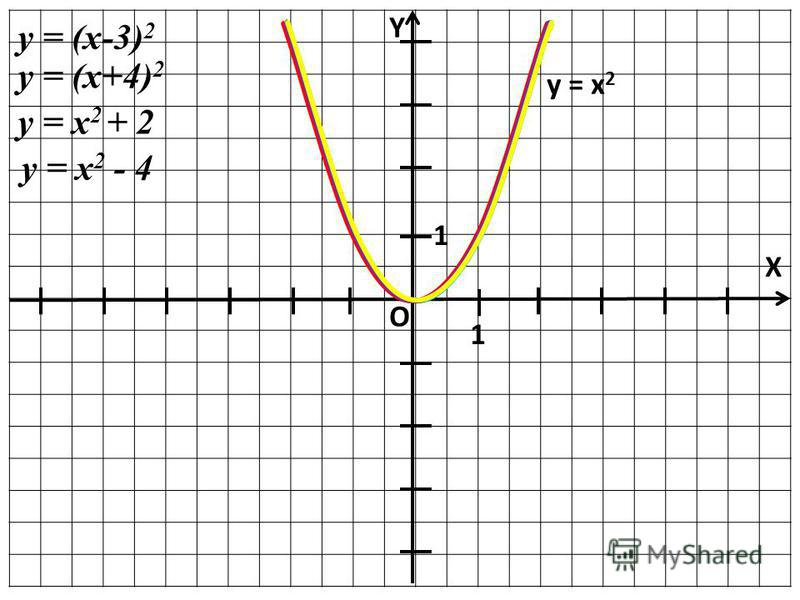
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
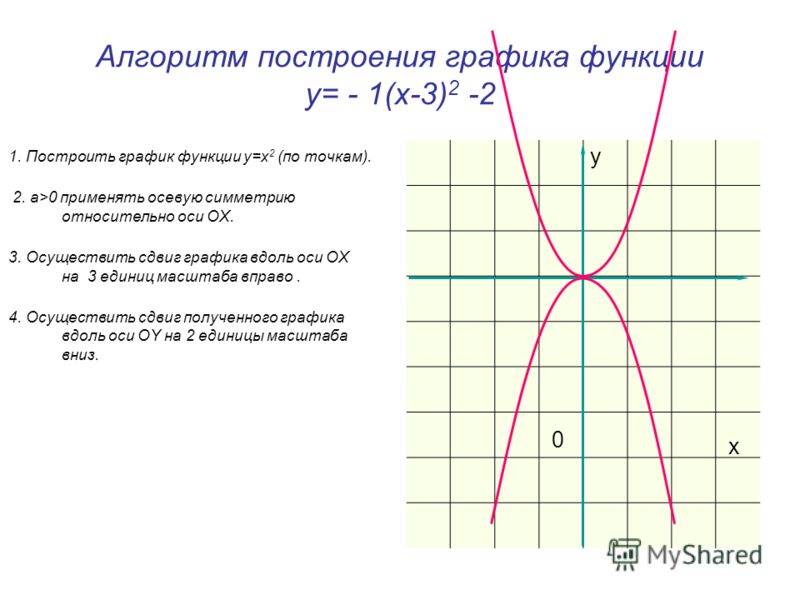
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
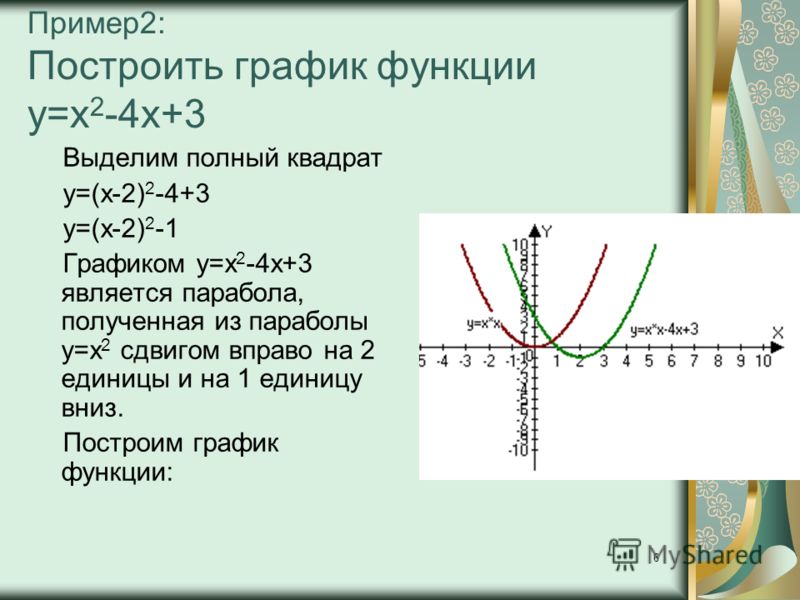
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4.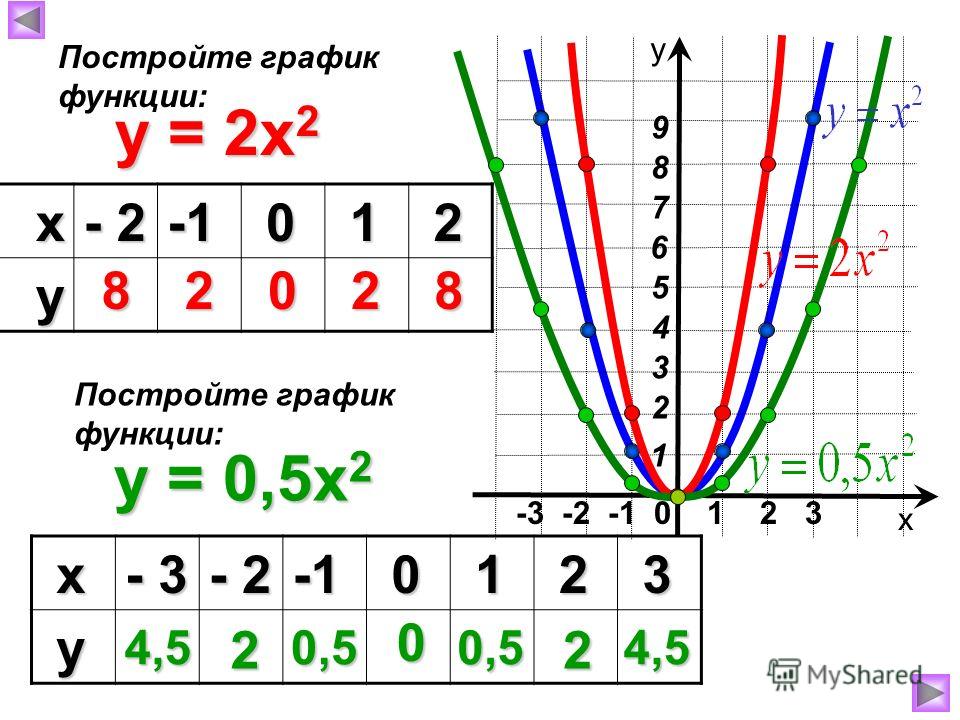 Изобразить график функции y = |-x 2 + 2|x| – 1|.
Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т.
 д.
д. - Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
 2-4 а)составьте уравнение касательной к графику данн… — Учеба и наука
2-4 а)составьте уравнение касательной к графику данн… — Учеба и наукаЛучший ответ по мнению автора
02.  05.16
05.16Лучший ответ по мнению автора Ответ понравился автору вопроса
Михаил Александров
Читать ответы Андрей Андреевич
Читать ответы Eleonora Gabrielyan
Читать ответы Посмотреть всех экспертов из раздела Учеба и наука > Математика
Похожие вопросы Решено
в зоопарке живут крокодилы и страусы.
 2)<=8
2)<=8Пользуйтесь нашим приложением
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.Функция вида , где называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как ,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:
,
3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2.
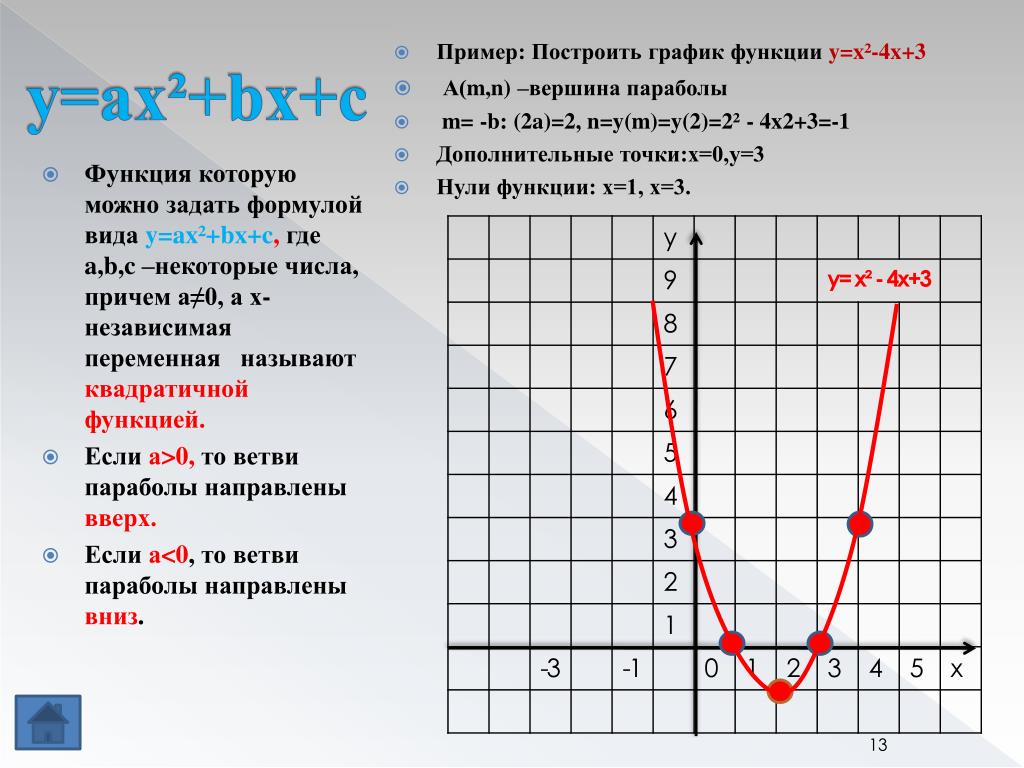
 Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболыили в уравнении квадратичной функции , и второй коэффициент — четное число.
Построим для примера график функции .
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно
- сначала построить график функции ,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.
Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1.
 Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
3-89 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Преобразования квадратичных функций | Колледж Алгебра
Результаты обучения
- График вертикальных и горизонтальных сдвигов квадратичных функций
- График вертикального сжатия и растяжения квадратичных функций
- Напишите уравнение преобразованной квадратичной функции, используя вершинную форму
- Определите вершину и ось симметрии для данной квадратичной функции в форме вершины 92 [/latex]
Величина [latex]a[/latex] указывает на растяжение графика.
 Если [latex]|a|>1[/latex], точка, связанная с конкретным [latex]x[/latex]-значением, смещается дальше от оси [latex]x[/latex] – , поэтому график кажется, становится уже, и есть вертикальное растяжение. Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]
Если [latex]|a|>1[/latex], точка, связанная с конкретным [latex]x[/latex]-значением, смещается дальше от оси [latex]x[/latex] – , поэтому график кажется, становится уже, и есть вертикальное растяжение. Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]Однако на практике обычно легче запомнить, что [latex]h[/latex] – это выходное значение функции, когда входное значение [ латекс]h[/латекс], поэтому [латекс]f\left(h\right)=f\left(-\dfrac{b}{2a}\right)=k[/latex].
Попробуйте
Координатная сетка наложена на квадратичную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение траектории мяча. Стрелок попадает в корзину?
(кредит: модификация работы Дэна Мейера)
Показать решение
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее
Квадратичные функции
Квадратичные функцииГрафер
Калькулятор
Возврат
Справка
Точечная диаграмма
Содержание : Эта страница соответствует § 3.1 (стр. 244) текста.
Предполагаемые проблемы из текста:
р. 251 #1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
г.
Графики
Стандартная форма
приложений
Графики
Квадратичная функция имеет вид f(x) = ax 2 + bx + c , где a , b и c — это числа, где a не равны нулю.

График квадратичной функции представляет собой кривую, называемую параболой . Параболы могут раскрываться вверх или вниз и различаются по «ширине» или «крутизне», но все они имеют одинаковую основную форму «U». На рисунке ниже показаны три графика, и все они являются параболами.
г.Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекается его ось симметрии в точке, называемой вершиной параболы.
Вы знаете, что две точки определяют прямую. Это означает, что если вам даны любые две точки на плоскости, то существует одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать о точках и квадратичных функции.
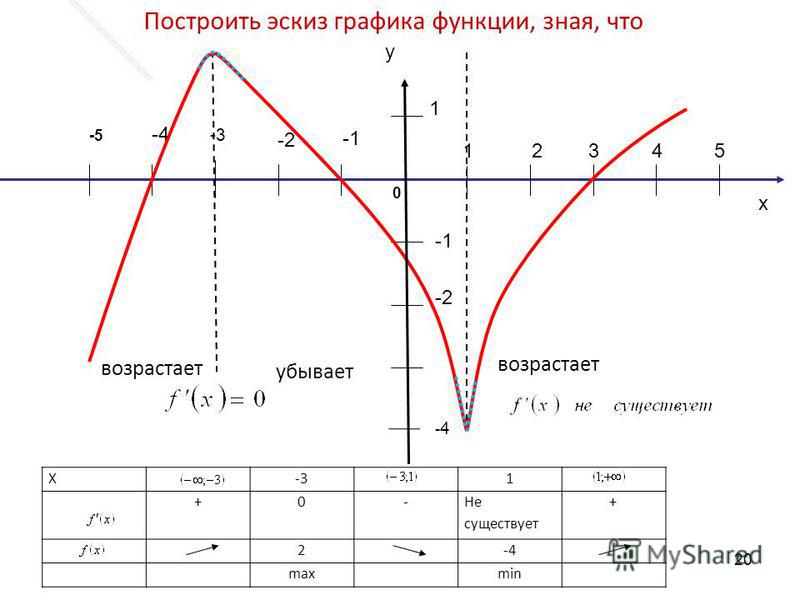
г.Даны три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой, существует ровно одну квадратичную функцию f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт. График содержит три точки и параболу, проходящую через все три.
 Соответствующая функция показана в тексте
поле под графиком. Если перетащить любую из точек, то функция и парабола обновятся.
Соответствующая функция показана в тексте
поле под графиком. Если перетащить любую из точек, то функция и парабола обновятся.г. Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения/сжатия и сдвига. (перевод) парабола y = x 2 . (См. раздел об управлении графики.)
Пример 1 .
Нарисуйте график y = x 2 /2. Начиная с графика y = x 2 , мы уменьшаем его в множитель из одной половины. Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем 5 единиц вниз.
Упражнение 1 :
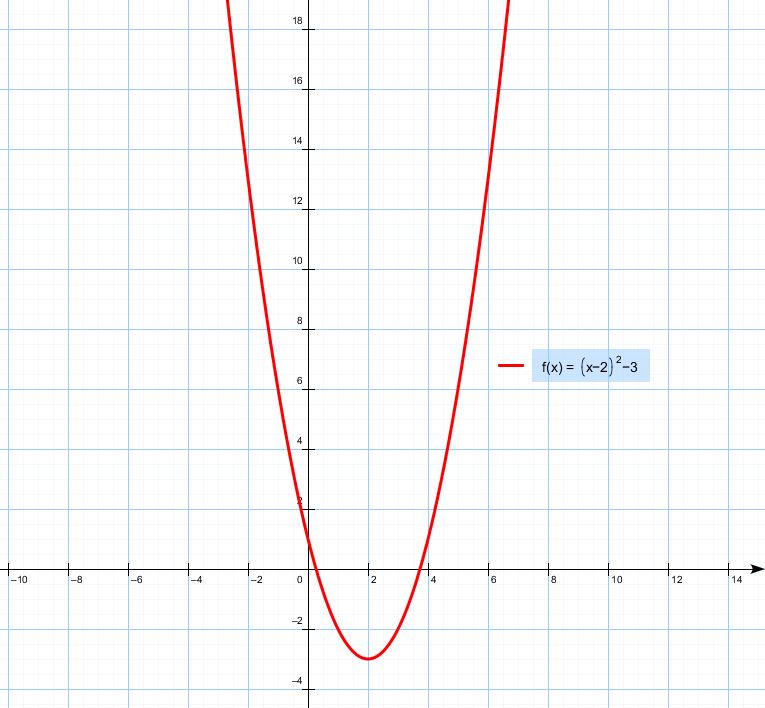
(a) Нарисуйте график y = (x + 2) 2 — 3. Ответ
(b) Нарисуйте график y = -(x — 5) 2 + 3. Ответ
Вернуться к содержанию
Стандартная форма
г.
Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме . Когда квадратичная функция имеет стандартную форму, ее график легко начертить, отражая, сдвигая и растяжение/сжатие параболы y = x 2 .
Говорят, что квадратичная функция f(x) = a(x — h) 2 + k, не равная нулю, находится в стандартной форме . Если а положительное, то график открывается вверх, а если а отрицательное, то открывается вниз. линия симметрии – вертикальная линия x = h, а вершина – точка (h,k).
Любая квадратичная функция может быть переписана в стандартной форме с помощью , дополняющего квадрат . (см. раздел о решая уравнения алгебраически, чтобы просмотреть завершение квадрата.) Шаги, которые мы используем в этом разделе для заполнения квадрата, будут выглядеть немного иначе, потому что наш главный цель здесь не решение уравнения.
г.
Обратите внимание, что, когда квадратичная функция находится в стандартной форме, также легко найти ее нули по квадратному корню. принцип.
Пример 3 .
Запишите функцию f(x) = x 2 — 6x + 7 в стандартной форме. Нарисуйте график функции f и найдите ее нули. и вершина.
f(x) = x 2 — 6x + 7.
= (x 2 — 6x )+ 7. Сгруппируйте x 2 и х слагаемых и затем завершите квадрат на этих условиях.
= (х 2 — 6х + 9 — 9) + 7.
Нам нужно прибавить 9, потому что это квадрат половины коэффициента x, (-6/2) 2 = 9. Когда мы решали уравнение, мы просто прибавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9 так что мы не меняем функцию.
= (х 2 — 6x + 9) — 9 + 7. Мы видим, что x 2 — 6x + 9 — полный квадрат, а именно (x — 3) 2 .

f(x) = (x — 3) 2 — 2. Это стандартная форма .
Из этого результата легко найти вершину графа функции f (3, -2).
Чтобы найти нули f, мы приравняем f к 0 и найдем x.
(х — 3) 2 — 2 = 0,
(х — 3) 2 = 2.
(х — 3) = ± кв. м (2).
х = 3 ± квадрат (2).
Чтобы начертить график f, сдвинем график y = x 2 на три единицы вправо и на две единицы вниз.
Если коэффициент при x 2 не равен 1, то мы должны вынести этот коэффициент из x 2 и x условий, прежде чем продолжить.
г.Пример 4 .
Запишите f(x) = -2x 2 + 2x + 3 в стандартной форме и найдите вершину графика f.
f(x) = -2x 2 + 2x + 3.
= (-2x 2 + 2x) + 3.

= -2(х 2 — х) + 3.
= -2(х 2 — х + 1/4 — 1/4) + 3.
Мы прибавляем и вычитаем 1/4, потому что (-1/2) 2 = 1/4, а -1 — коэффициент при x.
= -2(х 2 — х + 1/4) -2(-1/4) + 3.
Обратите внимание, что все в скобках умножается на -2, поэтому, когда мы удаляем -1/4 из скобок, мы надо умножить на -2.
= -2(х — 1/2) 2 + 1/2 + 3.
= -2(х — 1/2) 2 + 7/2.
Вершина — это точка (1/2, 7/2). Поскольку график открывается вниз (-2 < 0), вершина является самой высокой точкой на графике.
г.Упражнение 2 :
Запишите f(x) = 3x 2 + 12x + 8 в стандартной форме. Нарисуйте график функции f, найдите его вершину и найдите нули f. Ответ
Альтернативный метод нахождения вершины
В некоторых случаях завершение квадрата — не самый простой способ найти вершину параболы.
г. Если график
квадратичная функция имеет две точки пересечения с х, тогда линия симметрии — это вертикальная линия, проходящая через середину
x-перехватов.
Если график
квадратичная функция имеет две точки пересечения с х, тогда линия симметрии — это вертикальная линия, проходящая через середину
x-перехватов.Точки пересечения по оси X на приведенном выше графике находятся в точках -5 и 3. Линия симметрии проходит через -1, что является средним из -5 и 3. (-5 + 3)/2 = -2/2 = -1. Как только мы знаем, что линия симметрии равна x = -1, мы знаем первую координату вершины равно -1. Вторую координату вершины можно найти, вычислив функцию при x = -1.
Пример 5 .
г.Найдите вершину графика функции f(x) = (x + 9)(х — 5).
Поскольку формула для f факторизуется, нули легко найти: -9 и 5.
Среднее значение нулей равно (-9 + 5)/2 = -4/2 = -2. Итак, линия симметрии равна x = -2, а первая координата вершины равно -2.
Вторая координата вершины: f(-2) = (-2 + 9)(-2 — 5) = 7*(-7) = -49.
Следовательно, вершина графика функции f равна (-2, -49).

Вернуться к содержанию
приложений
Пример 6 .
Владелец ранчо имеет 600 метров забора, чтобы оградить прямоугольный загон с другим забором, разделяющим его посередине. как на схеме ниже.
Как показано на схеме, четыре горизонтальные секции забора будут иметь длину по x метров, а три каждая вертикальная секция будет иметь длину y метров.
г.Цель владельца ранчо — использовать весь забор и ограждать как можно большую площадь .
Каждый из двух прямоугольников имеет площадь xy, поэтому у нас есть
общая площадь: A = 2xy.
Мы мало что можем сделать с величиной А, пока она выражается как произведение двух переменных. Однако, тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому x и y должны удовлетворять.
3у + 4х = 1200.

3г = 1200 — 4х.
г = 400 — 4x/3.
Теперь у нас есть выражение y как функция x, и мы можем подставить это выражение вместо y в формулу для общего район А.
А = 2xy = 2x (400 -4x/3).
Нам нужно найти значение x, при котором A будет как можно больше. A является квадратичной функцией x, и график открывается вниз, поэтому самая высокая точка на графике A является вершиной. Поскольку A факторизуется, самый простой способ найти вершина состоит в том, чтобы найти x-перехваты и среднее значение.
г.2x (400 -4x/3) = 0,
2x = 0 или 400 -4x/3 = 0.
х = 0 или 400 = 4х/3.
х = 0 или 1200 = 4х.
х = 0 или 300 = х.
Следовательно, линия симметрии графика А равна х = 150, среднему значению 0 и 300.
Теперь, когда мы знаем значение x, соответствующее наибольшей площади, мы можем найти значение y, вернувшись назад. к уравнению, связывающему x и y.
г.
у = 400 — 4х/3 = 400 -4(150)/3 = 200.
Вернуться к содержанию
Графер
Калькулятор
Возврат
Справка
Точечная диаграмма
Определение области определения и области значений квадратичных функций
Давайте начнемИсследование области и диапазона с помощью графиковИсследование области и диапазона с помощью вербальных описанийСловарный запас Журнал активности
Учитывая ситуацию, которую можно смоделировать с помощью квадратичной функции или графика квадратичной функции, определите область определения и область значений функции.
Стандарты TEKS и ожидания учащихся
A(6) Квадратичные функции и уравнения.
 Учащийся применяет стандарты математического процесса при использовании свойств квадратичных функций для написания и представления квадратными уравнениями различными способами, с технологией и без нее. Ожидается, что учащийся:
Учащийся применяет стандарты математического процесса при использовании свойств квадратичных функций для написания и представления квадратными уравнениями различными способами, с технологией и без нее. Ожидается, что учащийся:A(6)(A) определит область определения и область значений квадратичных функций и представит область определения и область значений с помощью неравенств
Ресурс Цель(и)
Определить область определения и область значений квадратичной функции по заданному оператору или графику.
Основные вопросы
Как определить область определения и область значений квадратичной функции, зная ее график?
Как определить область определения и область значений квадратичной функции, если задано вербальное утверждение?
Словарь
- Квадратное уравнение
- Парабола г.
- Домен
- Диапазон
Мы собираемся изучить различные представления квадратичных функций, включая графики, словесные описания и таблицы.
 Мы определим область определения и область значений квадратичной функции с помощью этих представлений.
Мы определим область определения и область значений квадратичной функции с помощью этих представлений.Давайте сначала рассмотрим графики квадратичных функций и узнаем, как определить область определения и область значений квадратичной функции по графику.
Квадратное уравнение — это любое уравнение/функция со степенью 2, которая может быть записана в форме y = a x 2 + b x + c, где a, b и c — действительные числа, а a не равно 0. Его график называется параболой. Константы a, b и c называются параметрами уравнения. Значения a, b и c определяют форму и положение параболы.
Область определения – это набор всех действительных значений x , которые дают действительные значения для y . Диапазон функции – это набор всех действительных значений числа 9.1871 y , которые можно получить, подставив действительные числа в x.
Пример 1
Квадратичная родительская функция равна y = x 2 .
 График этой функции показан ниже.
График этой функции показан ниже.Пример 2
График y = — x 2 + 5 показан ниже. Определите домен и диапазон функции и проверьте, правильно ли вы интерпретировали график.
Пример 3
График y = 25 x 2 + 4 показан ниже. Определите область определения и диапазон этой функции. Перетащите соответствующие значения в поля под графиком.
Практическое задание — Проводник квадратичных функций
1. Используя приведенную выше интерактивную ссылку, переместите ползунки, чтобы отрегулировать значения коэффициентов: a, b и c. Обратите внимание, как меняется график при перемещении этих ползунков.
2. Продолжайте корректировать значения коэффициентов до тех пор, пока график не будет соответствовать значениям домена и диапазона, указанным ниже. Запишите функцию и соответствующий ей домен и диапазон в своих заметках.

Область: –∞ < x < ∞, Диапазон: y ≥ 0
Область: –∞ < x < ∞, Диапазон: y ≤ -5
Область: –1817 < 81 < 9 ∞, Диапазон: г ≥ 2Иногда проблема будет представлена в словесной, а не в символической форме. Чтобы определить область определения и диапазон квадратичной функции из вербального утверждения, часто проще использовать вербальное представление — или словесную задачу — для построения графика. Используя эту словесную задачу, вы можете более удобно находить домен и диапазон на графике.
Нажмите на изображение, чтобы открыть видео и следуйте инструкциям:
- Посмотрите видео. Когда вас попросят определить истинное утверждение относительно независимой и зависимой переменных, выберите A, B или C.
- Запишите пример задачи и таблицу значений для t и h .
- После построения графика определите домен и диапазон функции и запишите их в своих заметках.
 Оцените максимальное значение t для домена. г.
Оцените максимальное значение t для домена. г.
Используйте свой графический калькулятор или онлайн-калькулятор для следующих примеров. Постройте график функций, чтобы определить область определения и диапазон квадратичной функции.
Пример 4
Птица строит гнездо на дереве на высоте 36 футов над землей. Птица роняет палку из гнезда. Функция f( x ) = -16 x 2 + 36 описывает высоту палки в футах через x секунды. График этой функции показан ниже. Определите домен и диапазон этой функции, используя действие перетаскивания ниже.
Пример 5
Семья ДеВинд живет в доме прямоугольной формы длиной 45 футов и шириной 35 футов. Мистер ДеВинд планирует постелить ковры во всех комнатах дома, за исключением квадратной кухни. Кухня имеет длину стороны x футов. Функция y = 1575 — x 2 описывает площадь дома в квадратных футах без кухни.
 Определите домен и диапазон этой функции.
Определите домен и диапазон этой функции.- Печать
- Поделиться
VCE Mathematical Methods — Units 1 and 2 — 4G
Цели обучения:
В этом разделе мы рассмотрим:
- Преобразования квадратичной функции в виде1872) 2 + к .
- Графики квадратичных функций в любой форме (общая, факторизованная или точка поворота).
- Обозначение основных элементов параболы.
Transformations of the quadratic function
A quadratic function can exist in three forms:
- The general (polynomial) form: y = ax 2 + bx + c
- The turning point форма: у = а ( х — ч ) 2 + k
- Факторизованная форма: y = a ( x — m )( x — n )
 Рассмотрим форму точки поворота:
Рассмотрим форму точки поворота:Мы можем рассмотреть влияние каждого параметра ( a, h и k ) на графике параболы.
- a вызовет расширение в a раз от x -ось.
- h приведет к горизонтальному перемещению h единиц.
- k приведет к вертикальному перемещению k единиц.
Прежде чем обсуждать преобразования квадратного числа, всегда проверяйте, что оно находится в форме точки поворота. Если он не в форме точки поворота, заполните квадрат на общей форме.
Изучение индивидуальных эффектов a , h и k
Влияние параметра a
Динамический рабочий лист GeoGebra иллюстрирует влияние a на график y = ax 2 .
- Пожалуйста, нажмите кнопку воспроизведения в левом нижнем углу, чтобы оживить !
График ниже показывает влияние a на график y = ax 2 .

Рисунок 1 — Влияние a на график y = ax 2 .
Из приведенного выше графика видно, что:
- Когда a > 0 (положительно), парабола вогнута вверх .
- Если 0 < a < 1 парабола вогнута вверх и поднимается медленно (график шире ).
- Если а > 1, то график вогнут вверх и поднимается вверх круто (график уже ).
- Когда a < 0 (отрицательное) парабола вогнута вниз .
- Если — 1 < a < 0 парабола вогнута вниз и падает медленно (график шире ).
- Если a < - 1, то парабола вогнута вниз и падает круто (график уже ).
a вызывает расширение в a раз от оси x .

Влияние параметра h
Динамический рабочий лист GeoGebra иллюстрирует влияние h на график y = ( x — h ) 2 9 .
- Пожалуйста, нажмите кнопку воспроизведения в левом нижнем углу, чтобы оживить !
На графике ниже показано влияние ч на графике у = ( х — ч ) 2 . Рисунок 2
Из приведенного выше графика видно, что:
- Когда h > 0 (положительное) парабола переместила ч единиц в отрицательном направлении — 4
4
- Когда ч < 0 (отрицательное) парабола, переведенная на ч единиц в положительном x -направлении.
Влияние параметра k
Динамический рабочий лист GeoGebra иллюстрирует влияние k на график y = x + 2
5 25- Пожалуйста нажмите кнопку воспроизведения в нижнем левом углу, чтобы оживить !
График ниже показывает влияние k на график y = x 2 + k .

Рисунок 2 — Влияние k на график y = x 2 + k .
Из приведенного выше графика видно, что:
- Когда k > 0 (положительное) парабола перевела ч единицы в положительное г -направление.
- Когда k < 0 (отрицательное) парабола переместила ч единиц в отрицательном y -направлении.
Изучение комбинированных эффектов A , H и K
.181822
911822 и - 1872 и K
Рабочий лист Dynamic Geogebra. = ( х + ч ) 2 + к .
- Пожалуйста, используйте ползунки для настройки параметров и наблюдения за преобразованиями.

Построение графика квадратичных функций
При построении графика квадратичных функций (парабол) необходимо четко показать:
- x -пересечения (если они есть).
- и -перехваты.
- Поворотный момент.
Рисунок 1 — График y = x 2 + 2x — 8 с отмеченными ключевыми функциями.
Метод: График квадратика
Шаг 1: Найдите Y -интерцепт
- Если уравнение находится в общем ( AX 2 9197. перехват (0 , c ).
- Если уравнение , а не в общем виде, пусть x = 0 и решите для y .
Шаг 2: Найдите точку пересечения x затем использовать для решения квадратного уравнения для x .
- Пожалуйста, используйте ползунки для настройки параметров и наблюдения за преобразованиями.
- Если уравнение нельзя легко разложить на множители, то можно использовать общую квадратичную формулу для нахождения x -перехватов.
 Когда уравнение имеет общий вид ( ax 2 + bx + c ), общая квадратичная формула гласит:
Когда уравнение имеет общий вид ( ax 2 + bx + c ), общая квадратичная формула гласит:
- Помните: вы можете использовать дискриминант (Δ), чтобы определить, сколько существует x -отрезков:
- Самый простой способ найти точку поворота — это когда квадратичная функция находится в форме точки поворота ( y = a ( x — h ) 2 2 + k ), где ( ч, к ) является поворотным моментом. Чтобы получить квадратное выражение в форме точки поворота, вам нужно завершить квадрат.
- В противном случае можно использовать ось симметрии для определения координаты x точки поворота, координату y можно найти, подставив координату x в квадратное уравнение. Ось симметрии определяется как:
- Наконец, вы можете использовать дифференциальное исчисление, чтобы определить стационарную точку квадратичного уравнения, которая является поворотной точкой параболы.

Шаг 4: Проведите параболу через точки (1) — (3) на наборе осей
- Найдите каждую из точек, найденных на шаге (1) , (2) и (3) на комплект осей.
- Определите, является ли парабола положительной или отрицательной, по значению a в общей форме
Рисунок 2 — Общая форма положительной и отрицательной параболы.
- Три точки, построенные на шаге (1) , (2) и (3) должны указать вам общую форму параболы; однако всегда полезно знать, какой формы вы должны ожидать.
Шаг 5: Пометьте все точки их координатами
Наконец, и самое главное, убедитесь, что все важные функции графика были помечены их координатами . Помните, что важными функциями являются:
- x г. -перехваты (если они есть).

- и -перехваты.
- Поворотный момент.
4G — Видео Пример 1 :
График Следующее квадратичное уравнение:
4G — Видео Пример 2 :
. Пример. :
Нарисуйте следующее квадратное уравнение:
Критерии успеха:
Вы добьетесь успеха, если сможете:
- Определить y -отрезок квадратичной функции.


 д.
д.
 2-4 а)составьте уравнение касательной к графику данн… — Учеба и наука
2-4 а)составьте уравнение касательной к графику данн… — Учеба и наука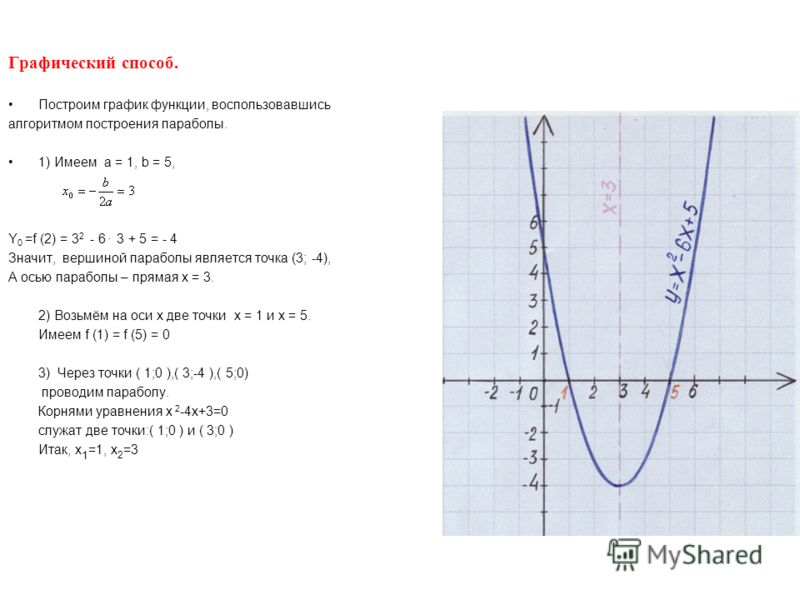 05.16
05.16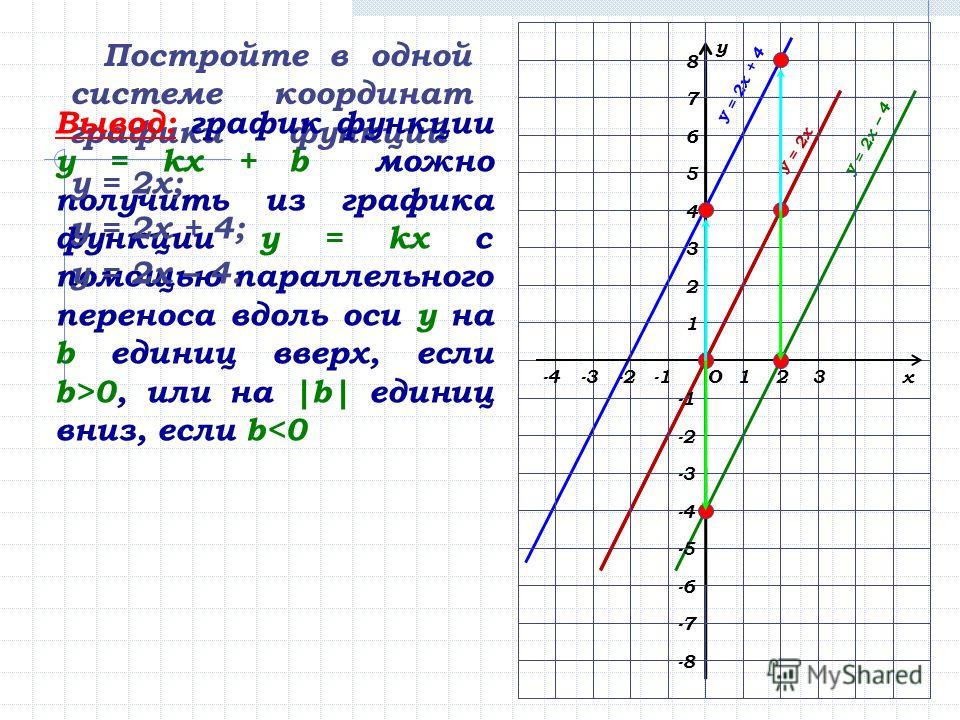 2)<=8
2)<=8

 Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы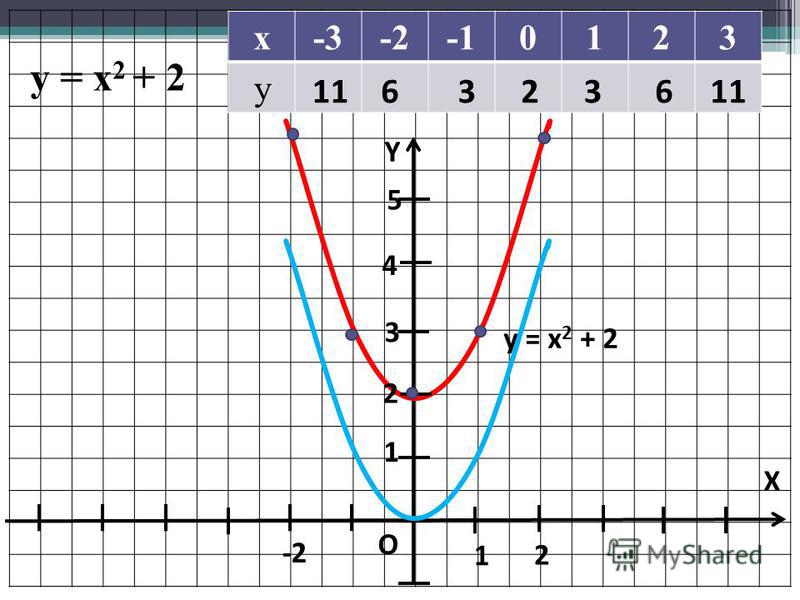 Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ: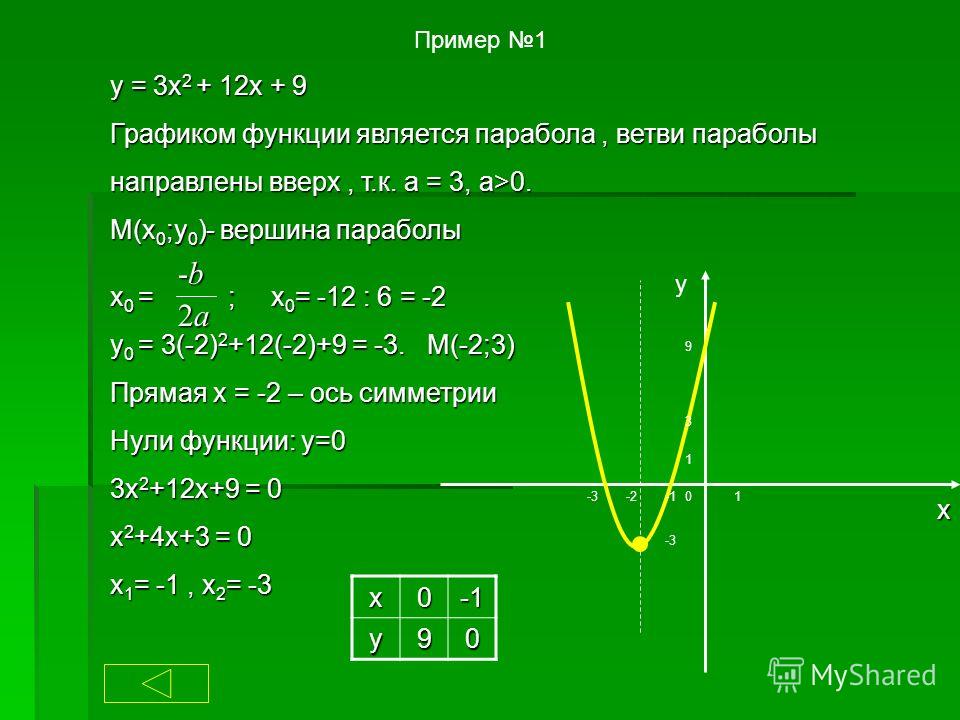 Если [latex]|a|>1[/latex], точка, связанная с конкретным [latex]x[/latex]-значением, смещается дальше от оси [latex]x[/latex] – , поэтому график кажется, становится уже, и есть вертикальное растяжение. Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]
Если [latex]|a|>1[/latex], точка, связанная с конкретным [latex]x[/latex]-значением, смещается дальше от оси [latex]x[/latex] – , поэтому график кажется, становится уже, и есть вертикальное растяжение. Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]

 Соответствующая функция показана в тексте
поле под графиком. Если перетащить любую из точек, то функция и парабола обновятся.
Соответствующая функция показана в тексте
поле под графиком. Если перетащить любую из точек, то функция и парабола обновятся.
 Если график
квадратичная функция имеет две точки пересечения с х, тогда линия симметрии — это вертикальная линия, проходящая через середину
x-перехватов.
Если график
квадратичная функция имеет две точки пересечения с х, тогда линия симметрии — это вертикальная линия, проходящая через середину
x-перехватов.

 Учащийся применяет стандарты математического процесса при использовании свойств квадратичных функций для написания и представления квадратными уравнениями различными способами, с технологией и без нее. Ожидается, что учащийся:
Учащийся применяет стандарты математического процесса при использовании свойств квадратичных функций для написания и представления квадратными уравнениями различными способами, с технологией и без нее. Ожидается, что учащийся: Мы определим область определения и область значений квадратичной функции с помощью этих представлений.
Мы определим область определения и область значений квадратичной функции с помощью этих представлений. График этой функции показан ниже.
График этой функции показан ниже.
 Оцените максимальное значение t для домена.
Оцените максимальное значение t для домена. Определите домен и диапазон этой функции.
Определите домен и диапазон этой функции. Рассмотрим форму точки поворота:
Рассмотрим форму точки поворота:

 Когда уравнение имеет общий вид ( ax 2 + bx + c ), общая квадратичная формула гласит:
Когда уравнение имеет общий вид ( ax 2 + bx + c ), общая квадратичная формула гласит: