Y x в кубе график функции: Функция игрек равен икс в кубе. Свойства функции игрек равен икс в кубе. График функции игрек равен икс в кубе

Свойства и графики основных элементарных функций

• Свойства и график линейной функции
• Свойства и график степенной функции с целым показателем
• Свойства и график степенной функции с любым рациональным показателем
• Свойства и графики функции корень
• Свойства и графики тригонометрических функций
• Свойства и графики обратных тригонометрических функций
• Свойства и график показательной функции
• Свойства и графики логарифмической функции

Основные свойства и графики элементарных функций — фундаментальные сведения, на базе которых строится исследование любых, как простых, так и сложных функций, рассматриваемых в курсе математического анализа в высшей математике.

Элементарные функции называются элементарными, потому что они заданы элементарными, то есть не сложными выражениями, например, 1/x, x², sinx и другими, рассматриваемыми в курсе школьной математики.

На основе элементарных функций строятся сложные функции, являющиеся комбинациями элементарных функций.

Если вы намерены серьезно подойти к изучению высшей математики и сдать этот предмет, то основные свойства и графики элементарных функций желательно запомнить наизусть, хотя бы до экзамена.

График элементарной функции, впрочем, как и любой функции (множество точек, составляющих определенную линию) строится в прямоугольной декартовой системе координат, где Ox — ось абсцисс, а Oy — ось ординат. На оси Ox по точкам графика получаем область определения функции, на оси Oy — область значений функции.

Область определения — одно из основных свойств элементарных функций. Областью определения функции служит некоторое множество чисел, при значениях которых выражение, с помощью которого задана функция, имеет смысл.

Областью определения многих элементарных функций служит

множество всех действительных чисел R, а областями определениях некоторых из них — множество положительных действительных чисел R или множество отрицательных действительных чисел R.

Кроме области определения будут даны следующие основные свойства элементарных функций.

Область значений функции. Это множество всех элементов, которые заданной функцией поставлены в соответствие элементам из её области определения. Иначе говоря, область значений функции является образом её области определения.

Чётность или нечетность функции. Четная функция удовлетворяет условию: f(−x)=f(x) для всех x из её области определения. Область определения чётной функции симметрична относительно точки x=0. Нечётная функция удовлетворяет условию:

f(−x)=−f(x) для всех x из её области определения. Область определения нечётной функции также симметрична относительно точки x=0. Если область определения функции не симметричная относительно этой точки, то функция не является ни чётной, ни нечётной.

Промежутки возрастания и убывания функции.

Выпуклость и вогнутость функции.

Является ли функция периодической. Периодическая функция — функция, значения которой не изменяются при добавлении к значениям его аргумента некоторого не равного нулю числа T, которое называется периодом функции. Для построения графика периодической функции достаточно построить её график на отрезке [0;T], тогда весь график получается сдвигом построенной части вдоль оси абсцисс на ±T, ±2T и так далее.

Линейной функцией называется функция, заданная формулой y=kx+b, где k и b — некоторые числа.

Область определения линейной функции — множество всех действительных чисел R.

Область значений линейной функции — также множество всех действительных чисел R.

Линейная функция является чётной, если k=0, нечётной, если b=0, и ни чётной, ни нечётной, если k≠0 и b≠0.

Линейная функция возрастает, если k>0, убывает, если k<0, если же k=0, то линейная функция является постоянной.

Линейная функция является одновременно выпуклой и вогнутой.

Линейная функция не является периодичной.

График линейной функции y=kx+b есть прямая линия. Для построения такого графика достаточно двух точек, например, A(0;b) и B(−b/k;0)

На рисунке синим цветом изображён график функции y=2x+3, красным — y=5x+2, зелёным — y=-x/2+4.

Если k=0, то имеет место частный случай линейной функции — постоянная функция, называемая также константой. Она задается формулой y=b.

Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат.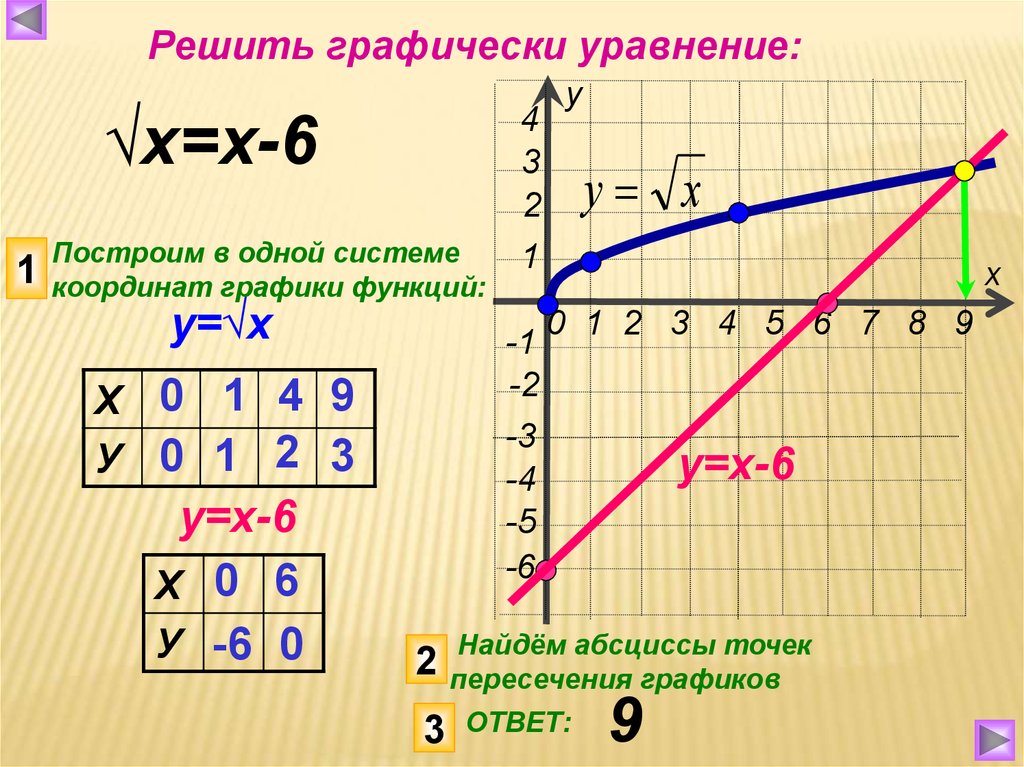 В частности, графиком функции y=0 является ось абсцисс.

На рисунке синим цветом изображён график функции

y=3, красным — y=-2.

В общем случае речь пойдет о функции вида , где m — целое число.

Степенная функция с чётным натуральным показателем

Рассмотрим сначала функцию (игрек равен икс в квадрате).

Область определения этой функции — множество всех действительных чисел R

Область значения функции — множество положительных действительных чисел: y∈[0;+∞).

Эта функция не является ни чётной, ни нечётной.

Функция возрастает на промежутке [0;+∞) и убывает на промежутке ]−∞;0].

Эта функция — вогнутая на всей области определения.

Эта функция — непериодическая.

График функции называется параболой.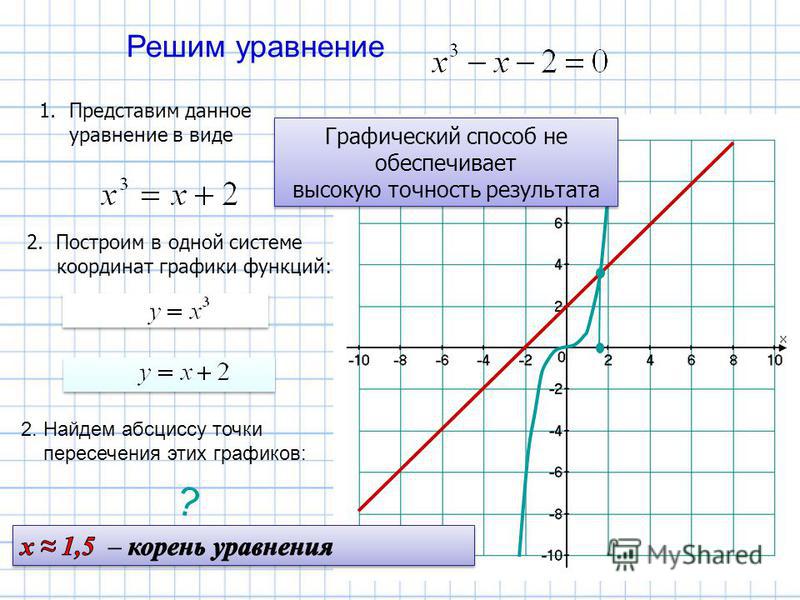

Теперь перейдём к степенным функциям, в которых показатель степени — произвольное чётное натуральное число, большее двух: 4, 6, 8 и так далее. В этом случае степенная функция обладает теми же свойствами, что и функция (игрек равен икс в квадрате). График такой функции похож на параболу, только ветви графика тем круче идут вверх, чем больше показатель степени.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

Степенная функция с нечётным натуральным показателем

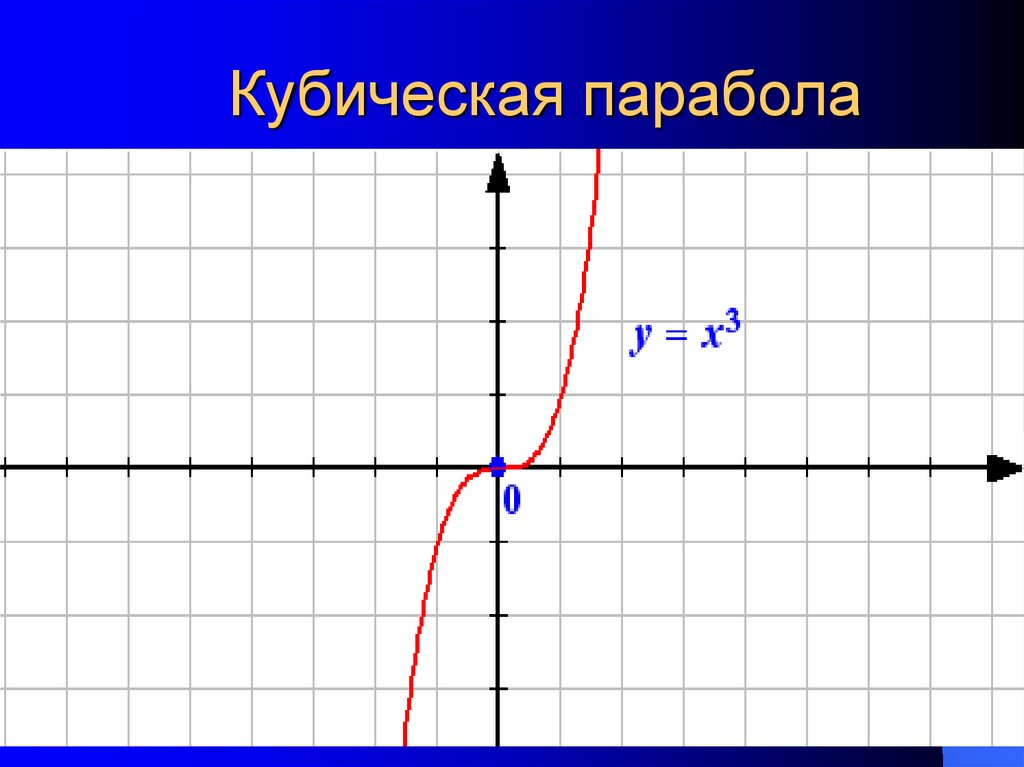
Рассмотрим сначала функцию (игрек равен икс в кубе).

Область определения этой функции — множество всех действительных чисел R.

Область значений этой функции — также множество всех действительных чисел R.

Это нечётная функция.

Функция возрастает на всём множестве R.

Эта функция выпуклая при x∈(−∞;0] и вогнутая при x∈[0;+∞].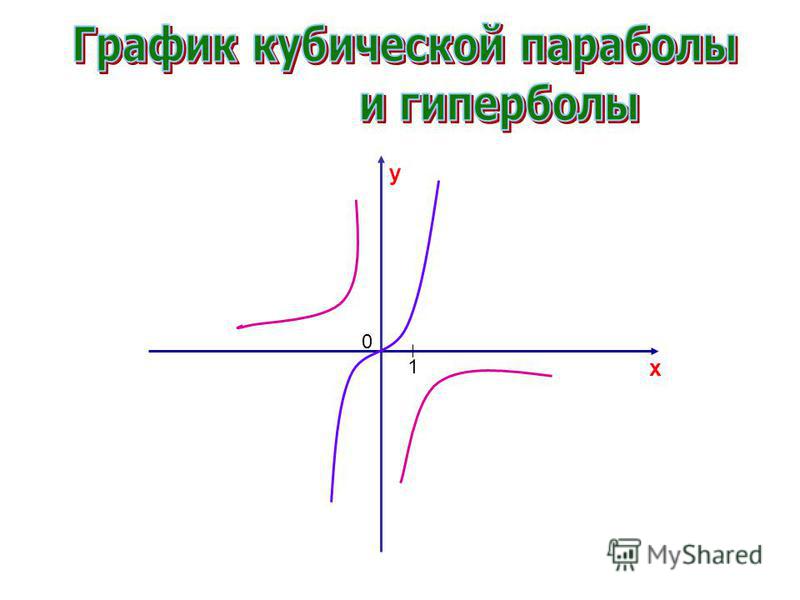

Это непериодическая функция.

График функции называется кубической параболой.

Рассмотрим теперь степенные функции, в которых показатель степени — произвольное нечётное натуральное число, большее трёх: 5, 7, 9 и так далее. В этом случае степенная функция обладает теми же свойствами, что и функция (игрек равен икс в кубе). График такой функции также похож на кубическую параболу, только ветви графика тем круче идут вверх и вниз, чем больше показатель степени.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

Степенная функция с чётным отрицательным показателем

В общем виде это функция , где n — чётное число. Если, например, n=2, то эту функцию можно представить также как .

Область определения: .

Область значений: .

Функция возрастает при и убывает при .

Это чётная функция.

Функция является вогнутой при .

Функция непериодическая.

Ветви графика функции расположены в первом и втором квадрантах координатной плоскости. Они неограниченно (асимптотически) приближаются к осям координат.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

Степенная функция с нечётным отрицательным показателем

В общем виде это функция , где n — нечётное число. Если, например, n=1, то эту функцию можно представить также как .

Область определения: .

Область значений:

Функция убывает при .

Это нечётная функция.

Функция является выпуклой при и вогнутой при .

Это непериодическая функция.

Ветви графика функции расположены в первом и третьем квадрантах координатной плоскости.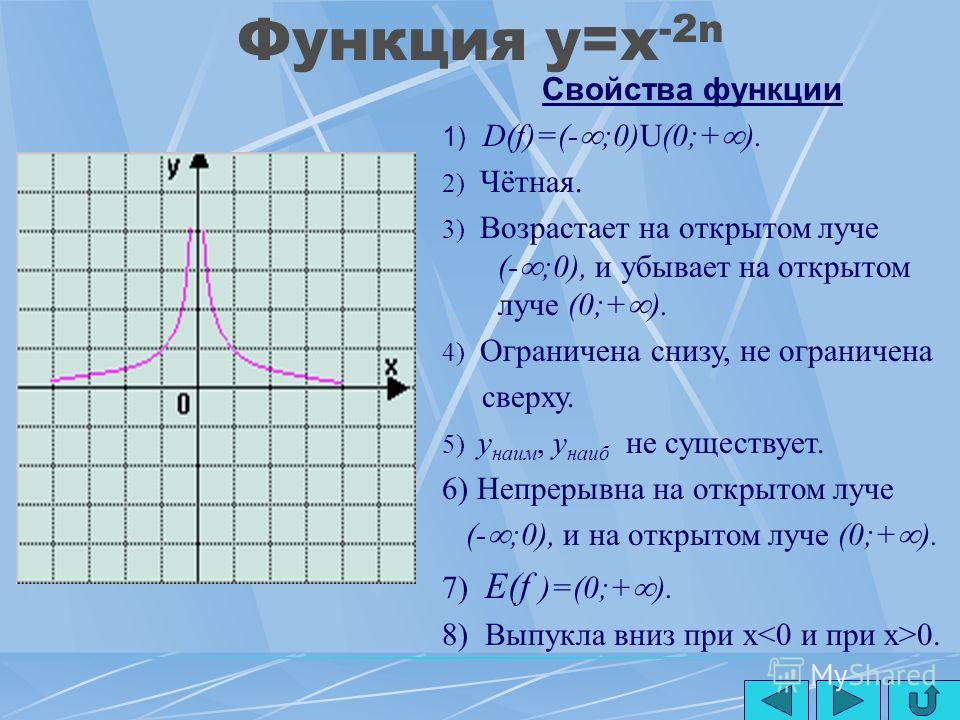 График функции называется гиперболой. Её ветви неограниченно (асимптотически) приближаются к осям координат.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

В общем виде это функция (показатель степени принадлежит множеству рациональных чисел).

Могут представиться три случая:

• r>1;
• 0<r<1;
• r<0.

Показатель степени больше единицы

Область определения: .

Область значений: .

Функция возрастает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция является вогнутой при , если 1<r<2 и при , если

r>2.

Это непериодическая функция.

На рисунке синим цветом изображён график функции , красным — , зелёным — , фиолетовым — .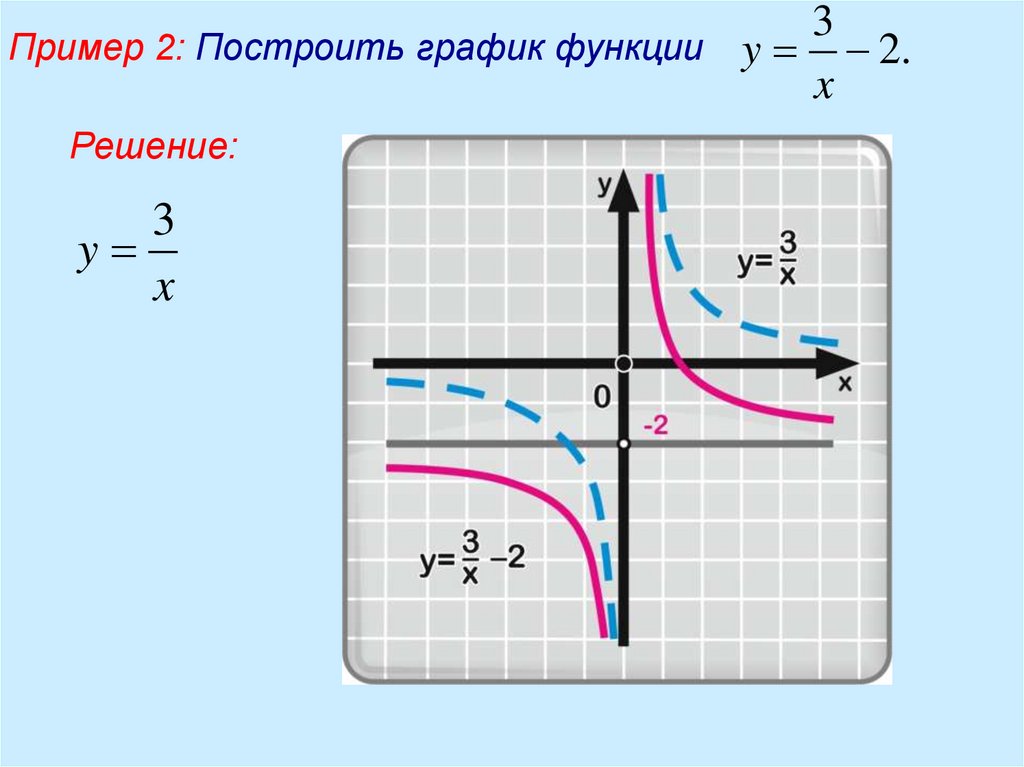 Чем больше показатель степени, тем круче вверх идёт ветвь графика.

Показатель степени больше нуля и меньше единицы

Область определения: .

Область значений: .

Функция возрастает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция является выпуклой при .

Это непериодическая функция.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

Показатель степени меньше нуля

Область определения: .

Область значений: .

Функция убывает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция является вогнутой при .

Это непериодическая функция.

На рисунке синим цветом изображён график функции , красным — , зелёным — .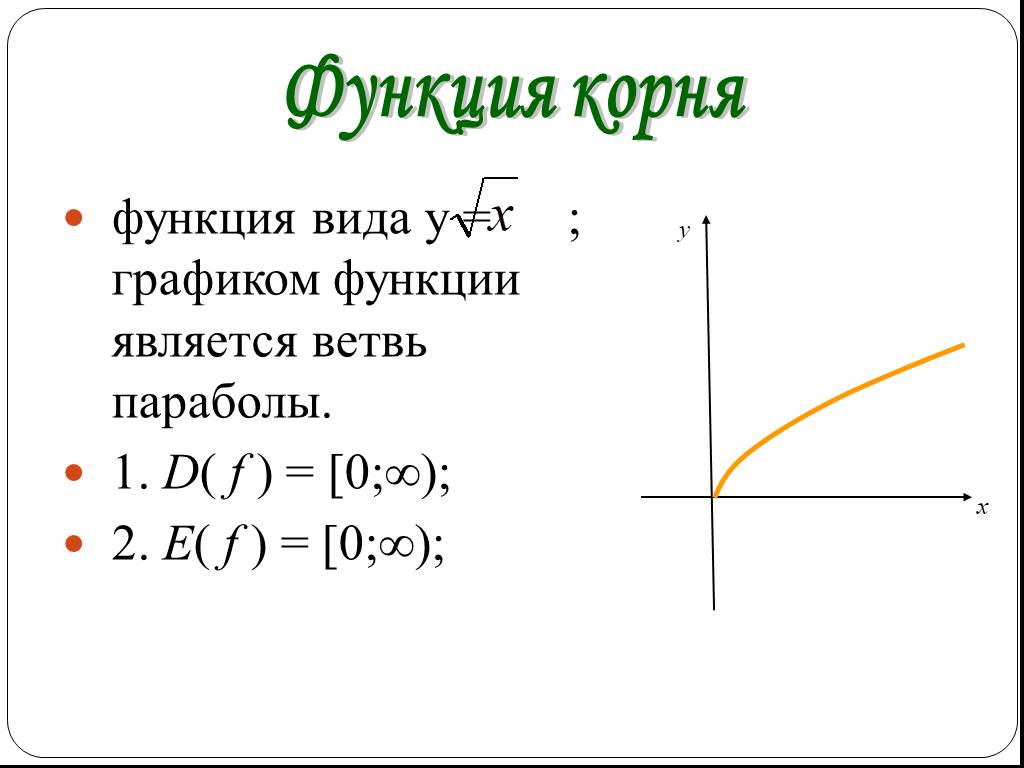 Ветви графика такой функции неограниченно (асимптотически) приближаются к осям координат.

В общем виде это функция , где n — натуральное число больше единицы.

Корень

n-й степени, n — чётное число

Область определения: .

Область значений: .

Функция возрастает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция выпуклая на всей области определения.

Это непериодическая функция.

График функции полностью расположен в первом квадранте координатной плоскости.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

Корень

n-й степени, n — нечётное число

Область определения: множество всех действительных чисел R.

Область значений: множество всех действительных чисел R.

Функция возрастает на всей области определения.

Функция является нечётной.

Функция выпуклая на и вогнутая на .

Это непериодическая функция.

Ветви графика функции расположены в первом и третьем квадрантах координатной плоскости.

На рисунке синим цветом изображён график функции , красным — , зелёным — .

Функция

y=sinx

Область определения множество всех действительных чисел R.

Область значений — отрезок y∈[−1;1]

Функция возрастает при , (принадлежит множеству целых чисел) убывает при .

Это нечётная функция.

Функция является выпуклой при , вогнутой при .

Это периодическая функция с основным периодом 2π

График функции синус называется синусоидой, он показан на рисунке ниже.

Функция

y=cosx

Область определения множество всех действительных чисел R.

Область значений — отрезок y∈[−1;1]

Функция возрастает при , убывает при .

Это чётная функция.

Функция является выпуклой при и вогнутой при .

Это периодическая функция с основным периодом 2π.

График функции косинус называется косинусоидой, он показан на рисунке ниже.

Функция

y=tgx

Область определения: .

Область значений: множество всех действительных чисел R.

Функция возрастает при .

Это нечётная функция.

Функция является выпуклой при и вогнутой при .

Это периодическая функция с основным периодом π.

График функции тангенс называется тангенсоидой, он показан на рисунке ниже.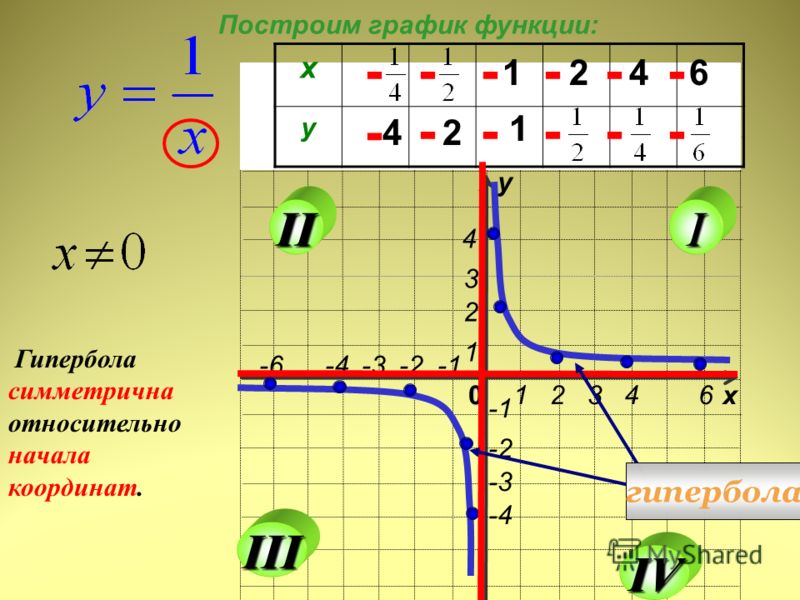

Функция

y=ctgx

Область определения: .

Область значений: множество всех действительных чисел R.

Функция убывает при .

Это нечётная функция.

Функция является выпуклой при и вогнутой при .

Это периодическая функция с основным периодом π.

График функции котангенс называется котангенсоидой, он показан на рисунке ниже.

Функция

y=arcsinx

Область определения: x∈[−1;1]

Область значений: y∈[−π/2;π/2]

Функция возрастает на всей области определения.

Это нечётная функция.

Функция является выпуклой при x∈[−1;0] и вогнутой при x∈[0;1]

Функция

y=arccosx

Область определения: x∈[−1;1].

Область значений: y∈[0;π].

Функция убывает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция является выпуклой при x∈[0;1] и вогнутой при x∈[−1;0]

Функция

y=arctgx

Область определения: множество всех действительных чисел R.

Область значений:

Функция возрастает на всей области определения.

Функция является нечётной.

Функция является выпуклой при и вогнутой при .

Функция

y=arcctgx

Область определения: множество всех действительных чисел R.

Область значений: y∈(0;π)

Функция убывает на всей области определения.

Функция не является ни чётной, ни нечётной.

Функция является выпуклой при и вогнутой при .

Показательная функция — функция вида , где a — некоторое число, x — переменная.

Область определения: множество всех действительных чисел R.

Область значений: множество положительных действительных чисел.

Показательная функция при (основание меньше единицы) убывает на всей области определения. Показательная функция при (основание больше единицы) возрастает на всей числовой прямой.

На рисунке синим цветом изображён график функции , красным — .

Функция не является ни чётной, ни нечётной.

Функция является вогнутой на всей числовой прямой.

Функция не обладает периодичностью.

Логарифмическая функция с основанием a — функция, заданная формулой . При этом .

Область определения: .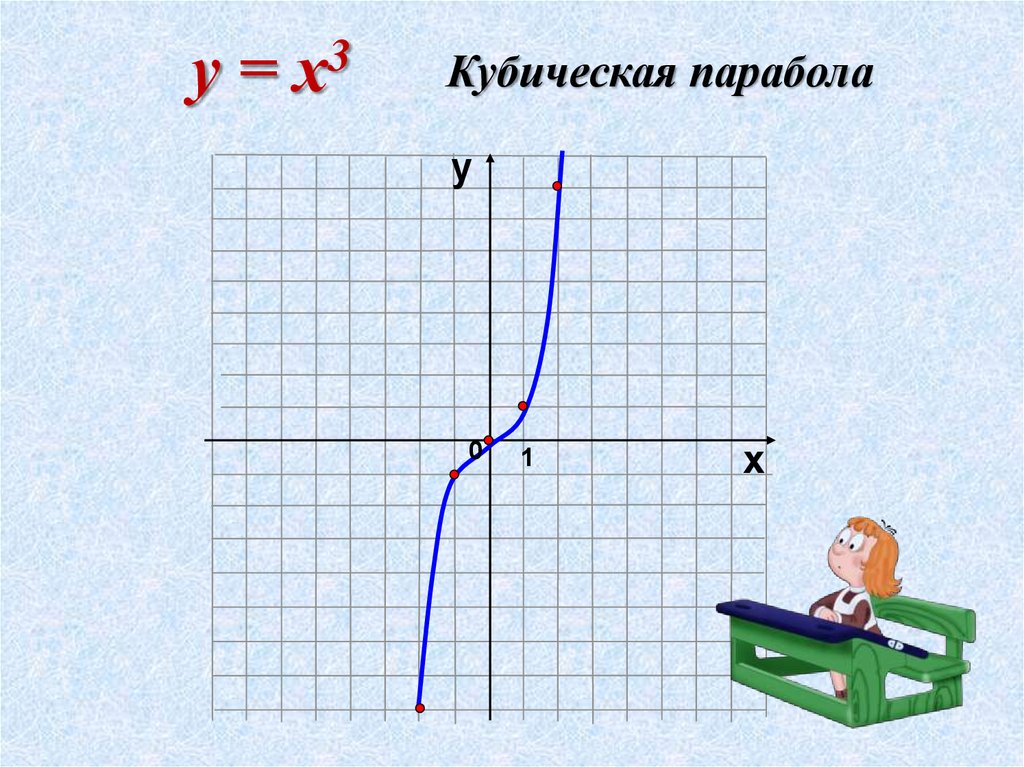

Область значений: множество всех действительных чисел R.

При (основание больше единицы) функция возрастает на всей области определения. При (основание меньше единицы) функция убывает на всей области определения.

Функция не является ни чётной, ни нечётной.

При (основание больше единицы) функция является выпуклой на всей области определения. При (основание меньше единицы) функция является вогнутой на всей области определения.

Функция не обладает периодичностью.

На рисунке ниже — график логарифмической функции с основанием больше единицы.

На следующем рисунке — график логарифмической функции с основанием меньше единицы.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Другие темы в блоке «Школьная математика»

Действия со степенями и корнями

Решение квадратных уравнений

Решение дробных уравнений с преобразованием в квадратное уравнение

График х в кубе 1 – Telegraph

График х в кубе 1

Скачать файл — График х в кубе 1

Соответственно, область определения данной функции — вся числовая прямая.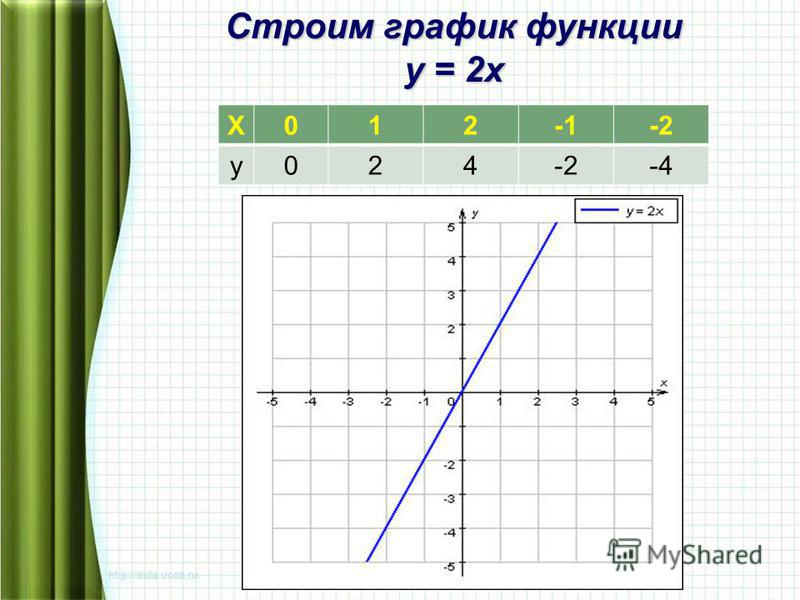 Соответственно, область значений — также вся числовая прямая. На небольшом корабле полностью закончилась пресная вода. Необходимо привезти достаточное количество воды из города. Вода заказывается заранее и оплачивается за полный куб, даже если залить её чуть меньше. Сколько кубов надо заказать, что бы не переплачивать за лишний куб и полностью заполнить цистерну? Известно, что цистерна имеет одинаковые длину, ширину и высоту, которые равны 1,5 м. Решим эту задачу, не выполняя вычислений. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 см. Значит надо заказать 4 куба. Мы видим, что эти точки симметричны относительно точки с координатами 0,1. В итоге получаем кубическую параболу, смещенную вверх по оси OY см. Материалы сайта — оригинальные, не скопированы из других источников учебников, задачников, сайтов, ресурсов и т. Они разработаны в строгом соответствии с ФГОС конкретного автора или темы. Запрещено любое копирование материалов сайта без письменного согласия владельцев ресурса! Номер свидетельства о регистрации СМИ: ДЕТСКИЙ САД Задания для детей Задания для детей 2 лет Задания для детей 3 лет Задания для детей 4 лет Задания для детей 5 лет Задания для детей 6 лет Задания для детей 7 лет Тесты для детей и дошкольников Тесты для детей 2 лет Тесты для детей 3 лет Тесты для детей от 4 лет Тесты для детей 5 лет Тесты для детей 6 лет Тесты для детей 7 лет Математика для малышей Математика для детей 2 лет Математика для детей 3 лет Математика для детей 4 лет Математика в 5 лет Математика в 6 лет Математические игры для дошкольников и малышей Количественный счет в детском саду, развивающие задачи Занимательная математика Картинки, цифры, шаблоны для скачивания 1 КЛАСС Контрольные работы Входная Петерсон Л. 3$

Кедр авто 10 инструкция по применению

Черная маска сделать самой

Функция y = x³ и ее график

Уголовный кодекс рф последняя редакция

Полиняло платье что делать сине белое

Поезд чудово москва расписание

Паук узор спицами

7.2.6. Кубическая функция

Стихи выпускнице начальной школы

Статьи затрат организации

Товароведная характеристика бытовой химии

Построить график функции онлайн. Построить график функции с параметрами. График Функции. функция, график онлайн, график, построить график, построить график функции, y=, построить график,построить график функции,построить график y,x построить график,постройте график функции y,построить график онлайн,y x построить график,постройте график функции y x,построить график функции онлайн,постройте график функции, build function graph online, build function graph, build graph online, исследовать функцию и построить ее график онлайн

Презентация коттеджного поселка

Рыболовная карта реки дон

Грейпфрут для лица

Параболы и кубики

Параболы и кубики

На этом уроке мы познакомимся с графиками уравнений вида y   =  x ² и y   =  ax ³ . Мы видели ранее, что график y   = m x + b — это график линии. Что произойдет, если там является членом x ² в этом выражении? Давайте сначала посмотрим на простейшее уравнение, которое имеет х ² срок.

---

Пример 1

Что такое график

y   =  x ²

Раствор

Чтобы нарисовать это, мы можем придумать несколько точек. Давайте сделаем T-таблицу с значения -3,-2,-1,0,1,2 для х .

У нас есть

(-3) ²   =  9    (-2) ²   = 4    (-1) ²   =  1

        (0) ² =  0      (1) ²   =  1 (2) ²   =  4    (3) ²   = 9

Мы можем поместить их в Т-таблицу.

х	г
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Эта таблица дает нам баллы (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4) и (3,9). Затем мы нанесем эти точки на плоскость xy . Обратите внимание, что все эти точки имеют неотрицательное и -координата.

Наконец, на графике мы можем соединить точки плавной кривой. график показан ниже.

Обратите внимание, что график остается над осью x . Если вы думаете о ось y как зеркало, то правая часть графика такая же, как левая часть графика отражена через y -ось. Мы видим что форма немного похожа на улыбку. Он круче вдали от истока и менее крутой вблизи начала координат. Мы называем этот тип графа парабола.

---

Теперь давайте рассмотрим другой пример построения графика уравнения, содержащего х ² .

Пример 2

Нарисуйте график

        у   =  — x ²

Раствор

Мы следуем тому же процессу, что и в примере 1.

Создадим Т-таблицу со значениями -3,-2,-1,0,1,2 для х .

У нас есть

-(-3) ²   =  -9    -(-2) ²   = -4    -(-1) ²   =  -1

-(0) ²   =  -0      -(1) ² =  -1     -(2) ²   =  -4 -(3) ²   =  -9

Мы можем поместить их в Т-таблицу.

х	г
-3	-9
-2	-4
-1	-1
0	-0
1	-1
2	-4
3	-9

Эта таблица дает нам баллы (-3,-9), (-2,-4), (-1,-1), (0,-0), (1,-1), (2,-4) и (3,-9). Затем мы наносим эти точки на плоскость xy . и соедините точки плавной кривой. Обратите внимание, что все эти точки имеют неположительную координату y .

Мы видим, что эта кривая имеет ту же форму, но перевернута, как хмурый взгляд. Небрежно мы называем это «параболой хмурого взгляда».

---

Получается, что все графики уравнений вида

        у   = ах ²

, где a — ненулевое число, имеют форму парабола. Чтобы определить, похоже ли это на улыбку или хмурый взгляд, следуйте принцип:

Если a > 0, то парабола выглядит как улыбка

Если a < 0, то парабола выглядит как хмурый взгляд

 

Пример 3

Графики, показанные ниже, представляют собой графики парабол. Обратите внимание, что уравнения, которые включают отрицательный знак, имеют графики, которые «хмурятся», в то время как те без «смайлов»

 

---

Теперь попробуйте сами.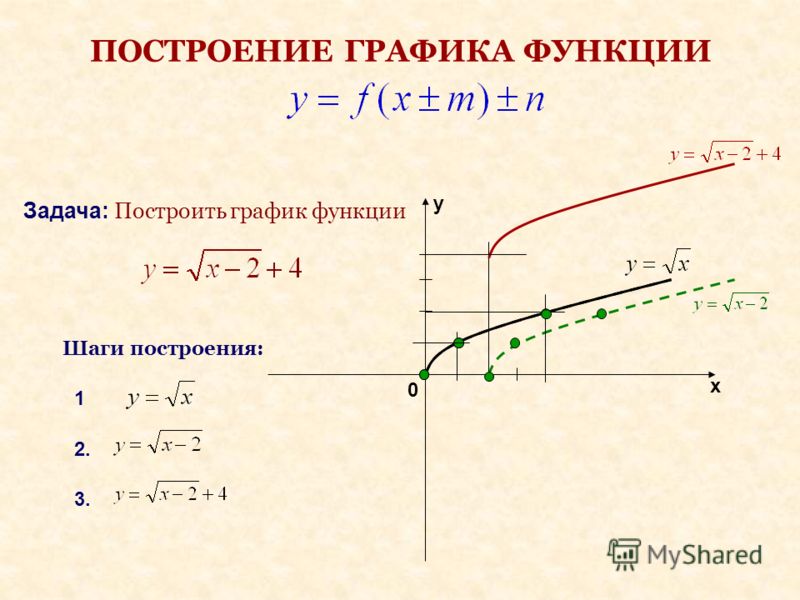 Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.

Упражнение 1

Что из следующего может быть графиком y   =  -0,4 x ² для положительных значений х ?

Ответ

---

Теперь, когда мы понимаем, как распознавать графики y   =  ax ² , посмотрим когда будем иметь мощность 3 вместо мощности 2. Эти графики называются кубические кривые и имеют уравнение

        у   =  ах ³

Пример 4

График y   =  x ³ показан ниже.

Обратите внимание, что этот график начинается снизу слева, резко движется вверх, становится плоским. в начале координат, а затем снова резко поднимается вверх. Это описание будет применяться ко всем графикам уравнений г   = ax ³ с положительными значениями a .

---

Пример 5

График y   =  -x ³ показан ниже.

Обратите внимание, что этот график совпадает с графиком и . = x ³ , но в перевернутом виде. В частности, слева начинается высоко. Затем она резко падает, пока не выравнивается в начале координат. Затем он возобновляет крутой спуск вправо от начала координат. Этот описание будет применяться ко всем графикам уравнений г =  x ³ с отрицательными значениями и .

---

Пример 6

Ниже приведены еще несколько кубических графиков.

Обратите внимание, что при появлении отрицательного знака график идет сверху слева к Нижний правый. В противном случае он идет снизу слева вверх справа.

---

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.

Упражнение 2

Сопоставьте уравнение с его графиком.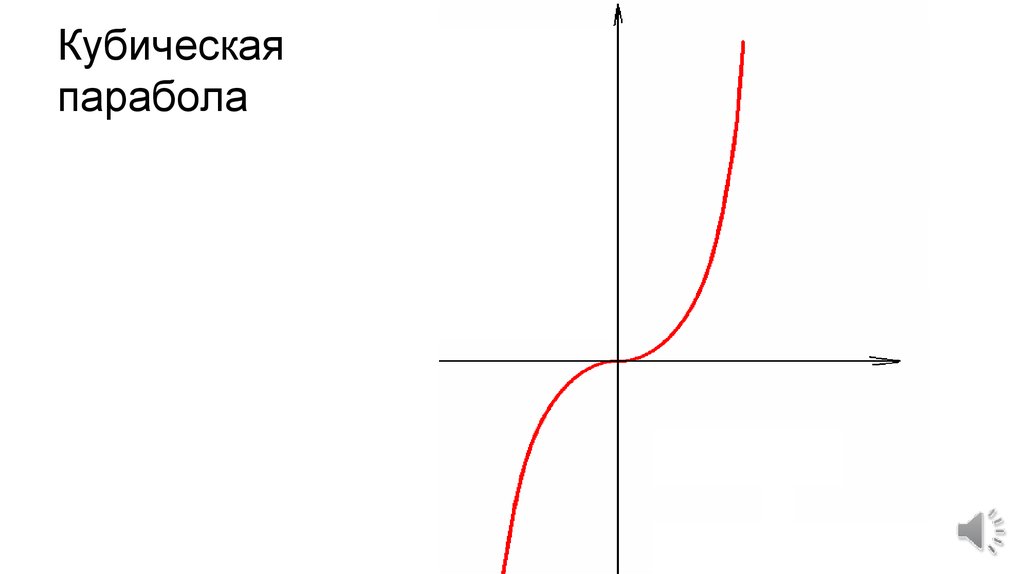

A.   y   =  1/3 x ² Б.   y   =  1/3 х ³   

C.     y   =  -1/3 x ² Д.   г =  -1/3 x ³                  

Ответ

 

Графики кубических полиномов: примеры, функции и уравнения

До сих пор мы рассматривали решение и построение графиков квадратичных полиномов. Напомним, что это полиномы второй степени x ² . Мы заметили, что такие уравнения создают кривую в форме колокола. Мы также знаем, что по основной теореме алгебры квадратичные многочлены имеют два корня. А что, если у нас есть многочлен третьей степени x ³ ? По основной теореме алгебры такое уравнение должно иметь не менее трех корней.

Такие многочлены называются кубическими. Как в этом случае будет выглядеть график кубического уравнения по сравнению с квадратичным? В этом уроке мы рассмотрим построение графиков кубических многочленов. Сначала установим приведенные ниже определения.

Кубический многочлен является многочленом третьей степени. Стандартная форма кубического многочлена:

, где a, b, c и d — константы, а a ≠ 0. A кубический граф является графическим представлением кубического многочлена.

Прежде чем перейти к этой теме, давайте сравним кубические графы и квадратичные графы. Начнем с того, что отметим следующие определения.

Ось симметрии параболы (кривой) представляет собой вертикальную линию, которая делит параболу на две конгруэнтные (одинаковые) половины.

Точкой симметрии параболы называется центральная точка, в которой

1. кривая делится на две равные части (находящиеся на равном расстоянии от центральной точки)
2. обе части обращены в разные стороны

Кубические графы против. Квадратичные графы

Мы начнем эту тему с рассмотрения различий в свойствах кубического графа и квадратичного графа.

Напомним, что квадратное выражение является полиномом второй степени и имеет стандартную форму ax ² + bx + c = 0, a ≠ 0. х ²

Cubic Graph, y = x ³

Basic Graph

The axis of symmetry is about the origin (0,0)

Точка симметрии относительно начала координат (0,0)

Количество корней (согласно основной теореме алгебры)

2 решения 6 9 9 9008

005

Domain

Set of all real numbers

Set of all real numbers

Range

Set of all real numbers

Set всех действительных чисел

Тип функции

Четный

Нечетный

6 5098930483 Axis of Symmetry

Present

Absent

Point of Symmetry

Absent

Present

Turning Points

Один : может быть либо максимальным, либо минимальным значением, в зависимости от коэффициента x корень x = 0 имеет кратность три, x ³ = 0)

OR

Two : this indicates that the curve has exactly one minimum value and one maximum value

Sketching Cubic Functions

При построении кубических функций следует учитывать три метода:

1. преобразование,

2. факторизацию и

3. построение таблицы значений.

Мы рассмотрим каждый метод по очереди вместе с некоторыми примерами работы, чтобы всесторонне продемонстрировать эти методы.

Трансформация

В геометрии трансформация — это термин, используемый для описания изменения формы. Точно так же мы можем применить эту концепцию при построении графиков. Изменяя коэффициенты или константы в заданном кубическом многочлене, мы можем изменить набросок кривой. Как и прежде, ниже показан график базовой кубической функции y = x ³ .

Граф кубического полинома, Айша Амри — StudySmarter Originals

Существует три способа преобразования этого графика. Это показано в таблице ниже.

Форма кубического полинома	Изменение значения	. (> 1) график становится круче (красная линия) Если a малы (0 < a < 1), график становится более плоским (синяя линия) Если a отрицателен, график становится инвертированным (зеленая линия)	Варьирование a меняет кубическую функцию в направлении y, то есть коэффициент a влияет на крутизну графика0757 Если k отрицательное, график смещается вниз на k единиц по оси Y (синяя линия) Если k положительное, график смещается вверх на k единиц по оси Y (зеленая линия)
Varying k shifts the cubic function up or down the y-axis by k units
y = (x — h ) 3	Если ч отрицательный, график смещается на h единиц влево от оси x (синяя линия) Если h положительный, график смещается на h единиц вправо от оси x (зеленая линия)
Вариация ч изменяет кубическую функцию по оси x на ч единицы.

Постройте график y = – 3x ³ – 5.

Шаг 1 : Коэффициент x ³ отрицательна и имеет коэффициент 3. Таким образом, мы ожидаем, что базовая кубическая функция будет обращенной и более крутой по сравнению с исходным эскизом.

Шаг 2 : Термин –5 указывает, что график должен сместиться на 5 единиц вниз по оси Y. Таким образом, взяв наш эскиз из шага 1, мы получим график y = – 3x ³ – 5 как:

Построим график y = (x + 4) ³ + 2.

Шаг 1: Член (х + 4) ³ указывает, что базовый кубический граф смещается на 4 единицы влево от оси x.

Шаг 2 : Наконец, член +2 говорит нам, что график должен сместиться на 2 единицы вверх по оси Y. Следовательно, взяв наш набросок из шага 1, мы получим график y = (x + 4) ³ + 2 как:

С помощью этих преобразований мы можем обобщить изменение коэффициентов a, k и h на кубический многочлен

y = a(x – h) ³ + k

Это известно как вершинная форма кубических многочленов. Напомним, что это похоже на вершинную форму квадратичных многочленов. Обратите внимание, что изменение a, k и h в этом случае следует одной и той же концепции. Единственная разница здесь в том, что степень (x – h) равна 3, а не 2!

Факторизация

Для этого метода графического изображения кубических многочленов мы выполним следующие шаги:

Шаг 1: Факторизация заданного кубического многочлена

Если уравнение имеет вид y = (x – a) (x – b) (x – c), мы можем перейти к следующему шагу.

Шаг 2: Определите точку пересечения по оси X, установив y = 0

Шаг 3: Определите точку пересечения по оси Y, установив x = 0

Шаг 4: Нанесите точки и начертите кривую На шаге 1 мы будем использовать методы факторинга, представленные в предыдущих темах.

Постройте график зависимости y = (x – 1) (x – 2) (x + 5).

Решение

Заметим, что данная функция полностью разложена на множители. Таким образом, мы можем пропустить Шаг 1.

Шаг 2 : Найдите точки пересечения x

Полагая y = 0, мы получаем (x – 1) (x – 2) (x + 5) = 0.

Решение таким образом, мы получаем три корня, а именно x = –5, x = 1 и x = 2.

Шаг 3 : Найдите точку пересечения y

Подставив x = 0, мы получим y = (0 – 1) ( 0 – 2) (0 + 5) = (–1) (–2) (5) = 10

Таким образом, точка пересечения y равна y = 10,

Шаг 4 : Нарисуйте график

Поскольку мы определили точки пересечения x и y, мы можем нанести их на график и нарисовать кривую, чтобы соединить эти точки вместе.

Обратите внимание, что на этом графике мы получаем две поворотные точки:

1. максимальное значение между корнями x = –5 и x = 1
2. минимальное значение между корнями x = 1 и x = 2.

Постройте график y = (x + 1) (x ² – 6x + 9).

Решение

Шаг 1: Обратите внимание, что член x ² – 6x + 9 можно дополнительно разложить на множители в квадрат двучлена.

Используя формулу для этой формы специальных продуктов, мы получаем (x – 3) ² .

Таким образом, заданный кубический многочлен принимает вид y = (x + 1) (x – 3) ²

Шаг 2 : Полагая y = 0, получаем (x + 1) (x – 3) ² = 0.

Решив это, мы получим единственный корень x = –1 и повторяющийся корень x = 3.

Заметим здесь, что x = 3 имеет кратность 2.

Шаг 3: Подставляя x = 0, получаем y = (0 + 1) (0 – 3) ² = (1) (9) = 9

Таким образом, точка пересечения у равна y = 9.

Шаг 4: Нанеся эти точки и соединив кривую, мы получим следующий график.

Опять же, мы получаем две поворотные точки для этого графика:

1. максимальное значение между корнями x = –1 и x = 3
2. минимальное значение при x = 3,

В этом случае, поскольку у нас есть повторяющийся корень при x = 3, минимальное значение известно как точка перегиба.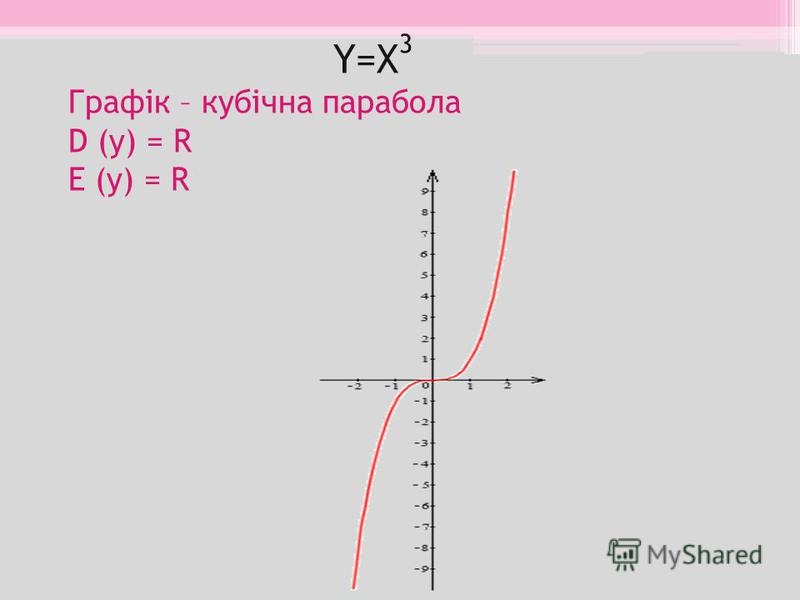 Обратите внимание, что слева от x = 3 график движется вниз, что указывает на отрицательный наклон, а справа от x = 3 график движется вверх, что указывает на положительный наклон.

Точка перегиба — это точка на кривой, где она меняется с наклона вверх на вниз или вниз на вверх.

Постройте график зависимости y = x ³ – 7x – 6, учитывая, что x = –1 является решением этого кубического многочлена.

Решение

Шаг 1: Согласно теореме о факторах, если x = -1 является решением этого уравнения, то (x + 1) должен быть фактором. Таким образом, мы можем переписать функцию как y = (x + 1) (ax ² + bx + c).

Обратите внимание, что в большинстве случаев нам может не быть дано никаких решений заданного кубического многочлена. Следовательно, нам нужно провести пробы и ошибки, чтобы найти значение x, при котором остаток равен нулю при решении для y. Обычные значения x, которые можно попробовать: 1, –1, 2, –2, 3 и –3.

Чтобы найти коэффициенты a, b и c в квадратном уравнении ax ² + bx + c, мы должны провести синтетическое деление, как показано ниже.

Глядя на первые три числа в последней строке, мы получаем коэффициенты квадратного уравнения и, таким образом, наш заданный кубический многочлен становится y = (x + 1) (x ² – x – 6).

Далее мы можем разложить выражение x ² – x – 6 как (x – 3) (x + 2).

Таким образом, полная факторизованная форма этой функции есть y = (x + 1) (x – 3) (x + 2)

Шаг 2: Полагая y = 0, получаем (x + 1) (x – 3) (x + 2) = 0,

Решая это, получаем три корня: x = –2, x = – 1 и x = 3.

Шаг 3: Подставляя x = 0, получаем y = (0 + 1) (0 – 3) (0 + 2) = (1) (–3) (2) = – 6

Таким образом, точка пересечения с осью y равна y = –6.

Шаг 4: График для данного кубического многочлена показан ниже.

Еще раз получаем две поворотные точки для этого графика:

1. максимальное значение между корнями x = –2 и x = –1
2. минимальное значение между корнями x = –1 и x = 3.

Постройте график зависимости y = — (2x – 1) ( х ² – 1).

Решение

Во-первых, обратите внимание, что перед приведенным выше уравнением стоит знак минус. Это означает, что граф примет форму перевернутого (стандартного) кубического полиномиального графа. Другими словами, эта кривая сначала откроется вверх, а затем откроется вниз.

Шаг 1: Сначала заметим, что двучлен (x ² – 1) является примером идеально квадратного двучлена. По принципу специальных продуктов мы можем дополнительно разложить это выражение на множители как (x + 1) (x – 1). Таким образом, полная факторизованная форма этого уравнения имеет вид y = – (2x – 1)(x + 1) (x – 1).

Шаг 2: Полагая y = 0, получаем

Решая это, получаем три корня: x = –1, x = и x = 1

Шаг 3: Подставляя x = 0, получаем получить

Таким образом, точка пересечения с осью y равна y = –1.

Шаг 4: График для данного кубического многочлена показан ниже. Будьте осторожны и помните знак минус в нашем исходном уравнении! Кубический граф будет здесь перевернутым.

В этом случае мы получаем две поворотные точки для этого графика:

1. минимальное значение между корнями x = –1 и x =
2. максимальное значение между корнями x = и x = 1

Составление таблицы значений

Прежде чем мы начнем этот метод построения графиков, мы познакомимся с принципом местоположения.

Принцип местоположения

Предположим, что y = f(x) представляет полиномиальную функцию.

Пусть a и b — два числа в области определения f такие, что f(a) < 0 и f(b) > 0.

Тогда функция имеет по крайней мере один действительный нуль между a и b.

Принцип местоположения, Glencoe McGraw-Hill, Algebra 2 (2008)

Принцип местоположения поможет нам определить корни данной кубической функции, поскольку мы не разлагаем выражение на множители явно.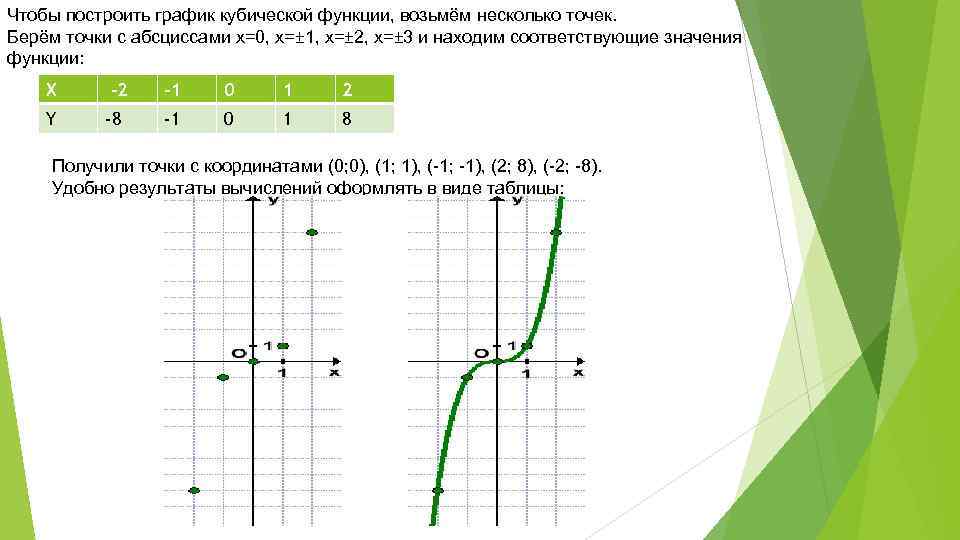 Для этой техники мы будем использовать следующие шаги.

Шаг 1: Вычислите f(x) для области значений x и создайте таблицу значений (мы будем рассматривать только целые значения)

Шаг 2: Найдите нули функции

Шаг 3 : Определите максимальную и минимальную точки

Шаг 4: Нанесите точки и нарисуйте кривую

Этот метод построения графика может быть несколько утомительным, так как нам нужно оценить функцию для нескольких значений x. Однако этот метод может быть полезен при оценке поведения графа на определенных интервалах.

Обратите внимание, что в этом методе нам не нужно полностью решать кубический многочлен. Мы просто рисуем выражение, используя построенную таблицу значений. Хитрость здесь заключается в том, чтобы вычислить несколько точек из заданной кубической функции и нанести ее на график, который затем соединим вместе, чтобы сформировать гладкую непрерывную кривую.

Нарисуйте график кубической функции f(x) = x ³ – 3x ² + 5.

Шаг 1: Оценим эту функцию между областью значений x = –2 и x = 4. Составим таблицу значений, мы получаем следующий диапазон значений для f(x).

x	f(x)
–2	–15
–1	1
	5
1	3
2	1
3	5
4	21

Шаг 2: Обратите внимание, что между x = –2 и x = –1 значение f(x) меняет знак. Принцип местоположения указывает, что между этими x-значениями есть ноль.

Шаг 3: Сначала мы наблюдаем интервал между x = –1 и x = 1. Значение f(x) при x = 0 кажется большим по сравнению с соседними точками.