Y x2 3x график: y=x^2-3x. построить график функции. желательно с рисунком и таблицей

Функция состоит из трех квадратных трехчленов. разложим их на множители по формуле

ax² + bx + c = a(x — x₁)(x — x₂), где х₁ и х₂ — корни квадратных уравнений.

Все три квадратных уравнения приведенные. Это значит, что можно найти их корни по теореме Виета. Именно поэтому я сразу напишу разложения этих трехчленов на множители. Конечно, решать через дискриминант никто не запрещал и ошибкой это не будет.

Итак, после разложения на множители функция примет такой вид:

Видно невооруженным глазом, что скобки из знаменателя сокращаются со скобками из числителя. Это просто супер-пупер! Но надо обязательно оговориться, что знаменатель не может быть равен нулю, а значит, что x ≠ -1 и x ≠ 3. Эти исключения подразумевают выколотые точки на нашем будущем графике.

После сокращения раскрываем оставшиеся скобки.

О, чудо! Это квадратичная функция! График — парабола!

Ищем ее вершину О (m; n).

Первая координата m, которую мы будем отмечать на оси Ох, находится по формуле.

А чтобы найти вторую координату надо m подставить в упрощенную ранее функцию и посчитать.

В общем, вершина параболы имеет координаты (-0,5; -2,25).

Чертим координатную плоскость и отмечаем вершину.

Мастера по рисованию парабол могут ее начертить, не прибегая к таблице по нахождению координат других точек. А вот тем, кто не в очень теплых отношениях с параболами, придется ее рисовать.

Поскольку я мастер — обойдусь без таблицы 🙂

Не забываем про выколотые точки!

В условии задачи сказано, что некоторая прямая y = m должна иметь одну общую точку с параболой. Эта прямая будет параллельна оси Ох и одну общую точку она будет иметь в выколотых точках и вершине параболы.

Ответ: 10; -2; -2,25.

P.S. Бывает так, что график нарисован очень криво. Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).

Построение и решение графиков Функций

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.

Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x).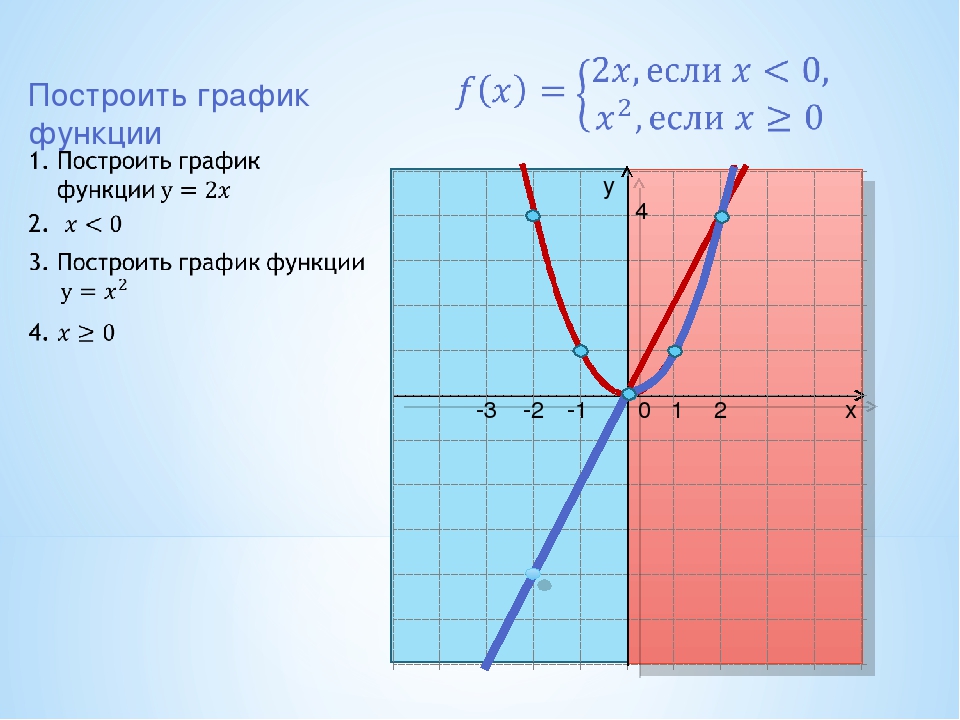 Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.


2. Найти область допустимых значений функции.


3. Проверить не является ли функция четной или нечетной.


4. Проверить не является ли функция периодической.


5. Найти нули функции.


6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.


7. Найти асимптоты графика функции.


8. Найти производную функции.


9. Найти критические точки в промежутках возрастания и убывания функции.


10. На основании проведенного исследования построить график функции.

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Как решаем:

Упростим формулу функции:

Задача 2.

Как решаем:

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Как решаем:

Вспомним, как параметры a, b и c определяют положение параболы.

1. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины




2. Ветви вверх, следовательно, a > 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.




3. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c > 0.

   Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.

Задача 4. Построить графики функций:

а) y = 3x — 1

б) y = -x + 2

в) y = 2x

г) y = -1

Как решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) y = 3x — 1

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

б) y = -x + 2

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

в) y = 2x

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

г) y = -1

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Как решаем:

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

а) y = x² + 1

б)

в) y = (x — 1)² + 2

г)

д)

Как решаем:

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

y = x²

Сдвигаем график вверх на 1:

y = x² + 1

б)

Преобразование в одно действие типа f(x — a).

y = √x

Сдвигаем график вправо на 1:

y = √x — 1

в) y = (x — 1)² + 2

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

y = x²

Сдвигаем график вправо на 1:

y = (x — 1)²

Сдвигаем график вверх на 2:

y = (x — 1)² + 2

г)

Преобразование в одно действие типа

y = cos(x)

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.

Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.

Параграф 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

Работу выполнил: Косярский А.А. студент группы 45.2

Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

1. Понятие числовой функции

Числовой функцией с областью определения D называется зависимость, при которой каждому числу x
из множества D (области определения) ставится в соответствие единственное число y.
Записывается это соотвествие так: y=f(x)
Обозначения и термины
D(f) — область определения
E(f) — область значений
x — аргумент (независимая переменная)
y — функция (зависимая переменная)
f — функция
f(x0) — значение функции f в точке x0

2. График функции

Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x
«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x

3. Возрастающие и убывающие функции

Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2) < f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

4. Чётные и нечётные функции

Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy

Функция f(x) нечётная:
если f(-x) = -f(x)
для любых x из области определения.
График нечётной функции симметричен относительно начала координат

Объяснение и обоснование

1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.

Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.

Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).

Область определения функции f — это множество тех значений, которые
может принимать аргумент x. Она обозначается D(f).

Область значений функции f — это множество, состоящее из всех чисел
f(x), где x принадлежит области определения. её обозначают E(f).

Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.

Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).

Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]

2. График функции. Напомним, что
графиком функции y = f(x) называется множество точек
координатной плоскости с координатами (x;f(x)), где первая координата
x «пробегает» всю область определения функции, а вторая координата —
это соответствующее значение функции f точке x.

На рисунках к пункту 4 табицы 2 приведены графики функций y = x²
и y = 1/x, а на рисунке 11 — график функции y = |x|.

Приведём также график функции y = [x], где [x] — обозначение
целой части числа x, то есть наибольшего целого числа,
не превосходящего x (рис. 12). Область определения этой функции
D(y) = R — множество всех действительных чисел, а область
значений E(y) = Z — множество всех целых чисел.

На рисунке 13 приведён график ещё одной числовой функции y = {x},
где {x} — обозначение дробной части числа x ( по определению
{x} = x — [x]).

3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.

Функция f(x) называется возрастающей на множестве P, если
большему значению аргумента из этого множества соответствует
большее значение функции.

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) > f(x1).
Например, функция f(x) = 2x возрастающая ( на всей области
определения — на множестве R), поскольку при x2 > x1 имеем
2⋅ > 2⋅, то есть f(x2) > f(x1). У возрастающей
функции при увеличении аргумента соотвествующие точки графика
поднимаются (рисунок 14).

На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).

Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.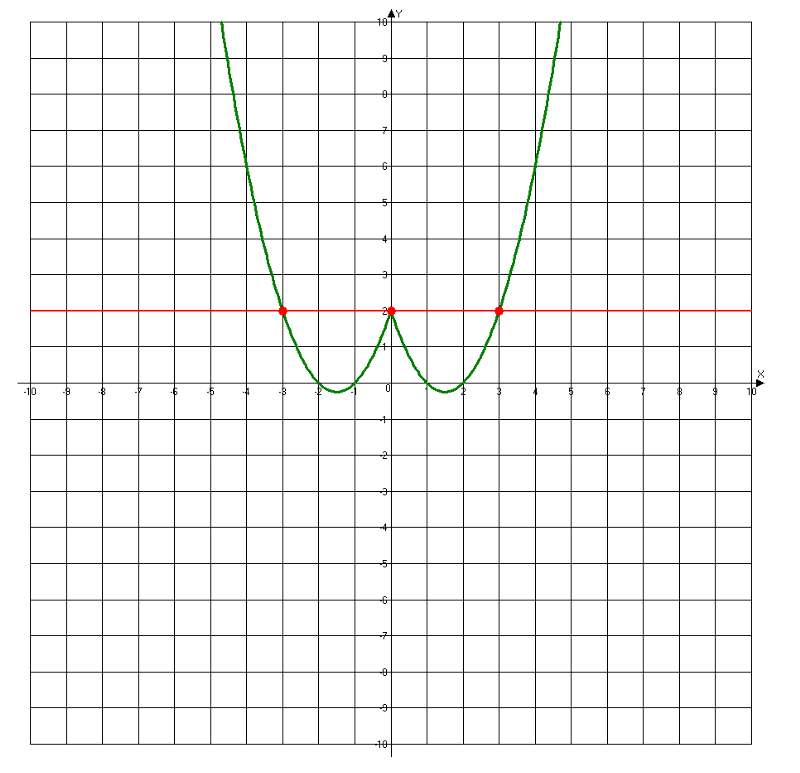

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) < f(x1).

Например, функция f(x) = -2x убывающая ( на всей области
определения — на множестве R), поскольку при x2 > x1 имеем
-2⋅ < -2⋅, то есть f(x2) < f(x1). У убывающей
функции при увеличении аргумента соотвествующие точки графика
опускаются (рисунок 16).

Рассматривая график функции y = x² (рис. 17), видим, что
на всей области определения эта функция не является ни возрастающей,
ни убывающей. Однако можно выделить промежутки области определения,
где эта функция возрастает и где убывает. Так как на промежутке
(-∞;0] — убывает, а на промежутке [0;+∞) функция
y = x² возрастает.(Докажите самостоятельно).

отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.

Если функция возрастает, то большему значению функции
соответствует большее значение аргумента.
Если функция убывает, то большему значению функции
соответствует меньшее значение аргумента.

Обоснуем первое из этих свойств методом от противного. Пусть
функция f(x)возрастает и f(x2) > f(x1). Допустим, что
аргумент x2 не больше аргумента x1, то есть x2≤x1.
Из этого предположения получаем: если x2≤x1 и f(x)
возрастает, то f(x2)≤f(x1), что противоречит
условию f(x2) > f(x1). Таким образом, наше предположение
неверно, и если f(x2) > f(x1), то x2 > x1, ч.т.д.
Аналогично обосновывается и второе свойство.

Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.

4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).

Например, функция y = x² (то есть функция f(x) = x²) —
чётная, поскольку f(-x) = (-x)² = x² = f(x).

Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.

Например, график четной функции y = x² (рис. 17)
симметричен относительно Oy.
Функция f называется нечётной, если для любого x из её области определения
f(-x) = -f(x).
Например, функция y = 1/x ( то есть функция f(x) = 1/x) — нечётная,
поскольку f(-x) = 1/(-x) = -1/x = -f(x).

Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.

Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ:

1. Что называется числовой функцией? Приведите примеры таких функций.
2. На примерах объясните, что такое область определния функции и область
значений функции. Какие ограничения необходимо учесть при нахождении
области определения функции y = √x/x ? Найдите её область определения.
3. Что называется графиком функции y = f(x)? Приведите примеры.
4. Какая функция называется возрастающей? Приведите примеры.
5. Какая функция называется убывающей? Приведите примеры.
6. Какая функция называется чётной? Приведите примеры. Как расположен
график чётной функции на координатной плоскости? Приведите примеры.
7. Какая функция называется нечётной? Как расположен график нечётной
функции на координатной плоскости? Приведите примеры.

УПРАЖНЕНИЕ 1. Найдите область определения функции: 1.y = x² + x         2.y = x/(x² + x)          3. y= √(x+5)
РЕШЕНИЕ 1) Ограничений для нахождения значений выражения x² + x нет, таким образом D(y) = R. 2) Область определения функции y = x/(x² + x) задаётся ограничением x² + x ≠ 0, поскольку знаменатель не может быть равным нулю. Выясним, когда x² + x = 0. Имеем x(x + 1) = 0, x = 0 или x = -1. Тогда область определения можно задать ограничениями x ≠ 0, x ≠ -1 или записать так: D(y) = (-∞;-1) ∪ (-1;0) ∪ (0;+∞) 3) Область определения функции y= √(x+5) задаётся ограничением x + 5 ≥ 0, то есть x ≥ -5, поскольку под знаком квадратного корня должно стоять неотрицательное выражение. Таким образом, D(y) = [-5;+∞)	КОММЕНТАРИЙ Поскольку все функции заданы формулами, то их области определения — это множество всех значений переменной x, при которых формула имеет смысл, то есть имеет смысл выражение, которое стоит в правой части формулы y = f(x). В курсе алгебры встречались только два ограничения, которые необходимо учитывать при нахождении области определения: 1)если выражение записано в виде дроби A/B, то знаменатель B ≠ 0 2)если запись выражения содержит квадратный корень √ A, то подкоренное выражение A ≥ 0. В других случаях, которые вам приходилось рассматривать, областью определения выражения были все действительные числа.
УПРАЖНЕНИЕ 2. Найдите область определения функции: y = x² — 3
РЕШЕНИЕ Составим уравнение x² — 3 = a. Оно равносильно уравнению x² = a +3, которое имеет решения, если a + 3 ≥ 0, то есть при a ≥-3. Все эти числа и составят область значений функции. Таким образом, область значений заданной функции E(f) = [-3;+∞), то есть y ≥ -3.	КОММЕНТАРИЙ Обозначим значение заданной функции f(x) ( то есть x² — 3) через a и выясним, для каких a можно найти соответствующее значение x ( при этом значении x значение f(x) = a). Тогда все числа a, для которых существует хотя бы один корень уравнения f(x) = a, войдут в область значений функции f(x). Множество всех таких a и составит область значений функции.
УПРАЖНЕНИЕ 3. Докажите, что при k ≠ 0 областью значений линейной функции y = kx + b является множество всех действительных чисел.
ДОКАЗАТЕЛЬСТВО Если kx + b = a (где k ≠ 0), то решение этого уравнения x = (a — b)/k существует для любого a ∈ R (k ≠ 0 по условию). Таким образом, значением заданной функции может быть любое действительное число. Итак, ее область значений E(f) = R.	КОММЕНТАРИЙ Обозначим значение заданной функции f(x), то есть kx + b, через a и выясним, для каких a можно найти соответствующее значение x, такое, что f(x) = a. Множество всех таких значений a и будет составлять область значений функции f(x).
УПРАЖНЕНИЕ 4. Докажите, что линейная функция y = kx + b при k > 0 является возрастающей, а при k < 0 — убывающей.
ДОКАЗАТЕЛЬСТВО Пусть x2 > x1 (тогда x2 — x1 >0). Рассмотрим разность f(x2) — f(x1) = kx2 + b — (kx1 + b) = k(x2 — x1). Поскольку x2 — x1 > 0, то при k > 0 имеем f(x2) — f(x1) > 0, таким образом, f(x2) > f(x1) и, значит, функция возрастает. При k < 0 имеем f(x2) — f(x1) < 0, таким образом, f(x2) < f(x1), значит, функция убывает.	КОММЕНТАРИЙ Для обснования возрастания или убывания функцииполезно помнить, что для доказательства неравенсства f(x2) > f(x1) или f(x2) < f(x1) достаточно найти знак разноссти f(x2) — f(x1). Функция f(x) = kx + b будет возрастающей, если из неравенства x2 > x1 будет следовать неравенство f(x2) > f(x1), а для доказательства последнего неравенства достаточно найти знак разности f(x2) — f(x1) (аналогичные рассуждения применимы и для убывания функции)
УПРАЖНЕНИЕ 5. Докажите, что: 1.Сумма двух возрастающих на множестве P функций всегда является возрастающей функцией на этом множестве. 2.Сумма двух убывающих на множестве P функций всегда является убывающей функцией на этом множестве.
ДОКАЗАТЕЛЬСТВО 1) Пусть функции f(x) и g(x) являются возрастающими на одном и том же множестве P. Если x2 > x1, то f(x2) > f(x1) и g(x2) > g(x1). Складывая почленно эти нервенства, получаем: f(x2) + g(x2) > f(x1) + g(x1) Это и означает, что сумма двух возрастающих функций есть функция возрастающая. 2) Пусть функции f(x) и g(x) являются убывающими на одном и том же множестве P. Если x2 > x1, то f(x2) < f(x1) и g(x2) < g(x1). Складывая почленно эти нервенства, получаем: f(x2) + g(x2) < f(x1) + g(x1) Это и означает, что сумма двух убывающих функций есть функция убывающая.	КОММЕНТАРИЙ Для доказательства того, что сумма двух возрастающих функций f(x) и g(x) является возрастающей функцией, достаточно доказать, что на множестве P из неравенства x2 >x1 следует неравенство: f(x2) + g(x2) > f(x1) + g(x1) Аналогино, для доказательства того, что сумма двух убывающих функций f(x) и g(x) является убывающей функцией, достаточно доказать, что на множестве P из неравенства x2 > x1 следует неравенство: f(x2) + g(x2) < f(x1) + g(x1)
УПРАЖНЕНИЕ 6. Докажите, что возрастающая или убывающая функция принимает каждое свое значение только в одной точке её области определения.
ДОКАЗАТЕЛЬСТВО Пусть функция f(x) является возрастающей и f(x1) = f(x2) (1) Допустим x1 ≠ x2. Если x1 ≠ x2, то x1 > x2 или x1 x2 имеем f(x1) > f(x2), что противоречит равенству (1). Таким образом, наше предположение неверно, и равенство f(x1) = f(x2) возможно только при x1 = x2. То есть возрастающая функция принимает каждое свое значение только в одной точке её области определения. Аналогично доказывается утверждение и для убывающей функции.	КОММЕНТАРИЙ Докажем это утверждение методом от противного. Для этого достаточно допустить, что выполняется противоположное утверждение (функция может принимать одно и то же значение хотя бы в двух точках), и получить противоречие. Это будет означать, что наше предположение неверно, а верно данное утверждение.
УПРАЖНЕНИЕ 7. Исследуйте, какие из данных функций являются четными, какие нечётными, а какие ни чётными, ни нечётными. 1. y = 1/(x + 1)      2. y = x²      3. y = x³ + x
РЕШЕНИЕ 1) Область определения функции y = 1/(x+1): x ≠ -1, то есть она не симметрична относительно точки O (точка x = 1 принадлежит области определения, а точка x = -1 — нет). Таким образом, заданная функция не является ни чётной, ни нечётной. 2) Область определения функции y = x²: D(y) = R, то есть она симметрична относительно точки O. f(-x)=(-x) ² = x ²$; = f(x), следовательно, функция чётная. 3) Область определения функции y = x³ + x: D(y) = R, то есть она симметричная относительно точки . f(-x)=(-x)² + (-x) = — (x³ + x) = -f(x), значит функция нечётная.	КОММЕНТАРИЙ Для исследования функции y = f(x) на чётность или нечётность достаточно, во-первых, убедиться, что область опредления этой функции симметричная относительно точки O ( вместе с каждой точкой x содержит и точку -x), и, во-вторых, сравнить значения f(-x) и f(x).

5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x⁵ 5) y = √(x)

6. Докажите, что на заданном промежутке функция возрастает:
1) y = -2/x, где x > 0 2) y = 1/x, где x < 0

7. Обоснуйте, что заданная функция является убывающей (на её области определения):
1) y = -3x 2) y = -x -1 3) y = -x³ 4) y = -x⁵

8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x < 0 2) y = 5/x, где x > 0

9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.

10. Используя утверждения, приведённые в примере 5, укажите какие из данных функций являются возрастающими, а какие — убывающими.
1) y = x³ + x 2) y = -x -x⁵ 3) y = x + √ (x) 4) y = -x³-x⁵

11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.

12. Обоснуйте, что заданная функция является чётной:
1) y = x⁶ 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x⁴)

13. Обоснуйте, что заданная функция является нечётной:
1) y = x⁵ 2) y = -1/x³ 3) y = x |x| 4) y = x³ — x

Как зависит парабола от коэффициента

☰

Графиком функции y = x² является парабола. Данная функция является функцией вида y = kx², в которой k = 1. Однако какими будут графики функций такого вида при других значениях k?

Графиками всех функций вида y = kx² также будут являться параболы, но измененные по сравнению с y = x². При k > 0 чем больше его значение, тем больше значение функции при том же аргументе. Например, при x = 2 функция y = x² принимает значение y = 4, в то время как значение функции y = 3x² равно 12, а функции y = 0.5x² равно 2.

Это значит, что с увеличением значения k (при k > 0) график функции быстрее устремляется вверх, как бы становится круче. Вводят такое понятие как «степень крутизны» параболы.
Если нарисовать графики функций вида y = kx² при различных значениях k, то возрастание крутизны параболы с возрастанием k можно увидеть наглядно:

На графике также отмечены точки соответствующие значению функции, равному 4. Видно, что чем меньше k, тем модуль координаты x больше. Так функция y = 0,1x² принимает значение, равное 4, при x равном по модулю немного больше 6. А вот функция y = 20x² принимает то же значение при x равном по модулю меньше 0,5.

Сохранится ли такая же зависимость между коэффициентом k и изменением параболы, если рассматривать функцию вида y = –kx²?

Как известно, функции y = x² и y = –x² симметричны друг другу относительно оси x. Поэтому графики функций y = kx² и y = –kx² при одинаковых по модулю k также симметричны. Убедимся на графиках:

Однако здесь мы не можем сказать, что с увеличением значения k возрастает степень крутизны параболы. Наоборот, она возрастает с уменьшением значения k. Ведь, например, –10 < –1.

Если же говорить о графиках функций вида y = kx при любом значении k (где k — действительное число), то можно сказать, что парабола имеет большую крутизну при большем значении k по модулю (|k|).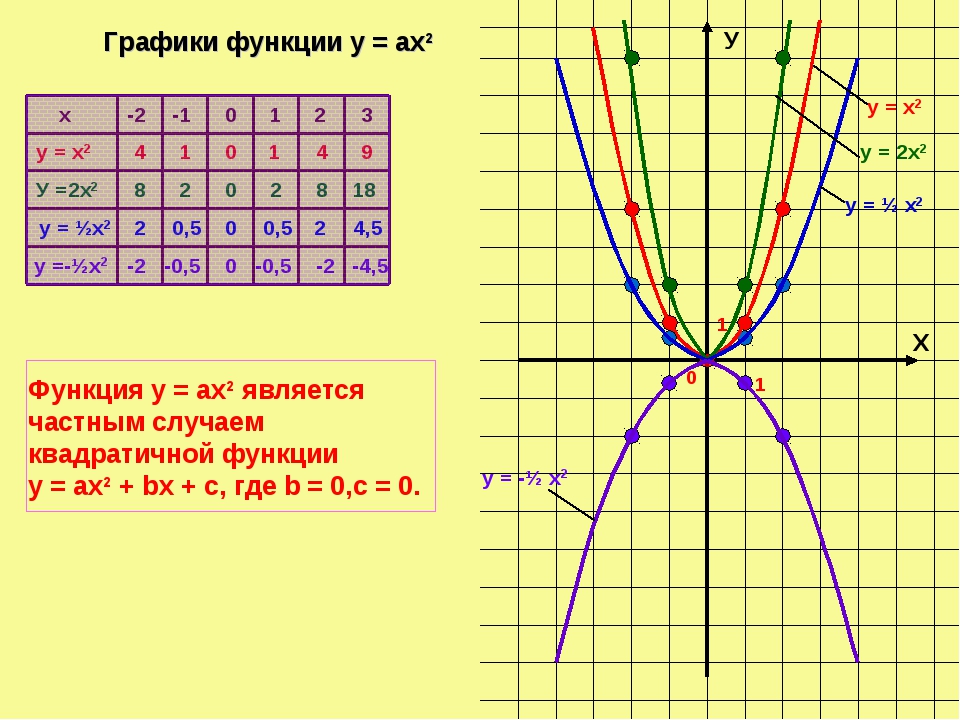 2+q $$

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные. 2 \)

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

Координатные плоскости и графики, функции.

Прямоугольная система координат это пара перпендикулярных координатных линий, называемых осями координат, которые размещены так, что они пересекаются в их начале.

Обозначение координатных осей буквами х и у является общепринятым, однако буквы могут быть любые. Если используются буквы х и у, то плоскость называется xy-плоскость. В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости и ts-плоскости.

Упорядоченная пара

Под упорядоченной парой действительных чисел мы имеем в виду два действительных чисел в определённом порядке. Каждая точка P в координатной плоскости может быть связана с уникальной упорядоченной парой действительных чисел путём проведения двух прямых через точку P: одну перпендикулярно оси Х, а другую — перпендикулярно оси у.

Например, если мы возьмём (a,b)=(4,3), тогда на координатной полоскости

Построить точку Р(a,b) означает определить точку с координатами (a,b) на координатной плоскости. Например, различные точки построены на рисунке внизу.

В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке

Определение графика

Графиком уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения

Пример: нарисовать график y = x²

Это приближении к графику y = x²

Пример: нарисовать график y = 1/x

Из-за того, что 1/x не определено, когда x=0, мы можем построить только точки, для которых x ≠0

Пример: Найдите все пересечения с осями
(a) 3x + 2y = 6
(b) x = y²-2y
(c) y = 1/x

Решение:

Пусть y = 0, тогда 3x = 6   or   x = 2

является искомой точкой пересечения оси x.

Установив, что х=0, найдем что точкой пересечения оси у является точка у=3.

Таким эе образом вы можете решить уравнение (b), а решения для (c) приведено ниже

y = 1/x

x-пересечение

Пусть y = 0

1/x = 0 => x не может быть определено, то есть нет пересечения с осью у

Пусть x = 0

y = 1/0 => y также не определено, => нет пересечения с осью y

На рисунке внизу точки (x,y), (-x,y),(x,-y) и (-x,-y) обозначают углы прямоугольника.

• график симметричен относительно оси х, если для каждой точки (x,y) графика, точка (x,-y) есть также точкой на графике.

• график симметричен относительно оси y, если для каждой точки графика (x,y) точка (-x,y) также принадлежит графику.

• график симметричен относительно центра координат, если для каждой точки (x,y) графика, точка (-x,-y) также принадлежит этому графику.

Определение:

График функциина координатной плоскости определяется как график уравнения y = f(x)

Пример 1

Постройте график f(x) = x + 2

y = x + 2

Пример 2. Постройте график f(x) = |x|

y = |x|

График совпадает с линией y = x         для x> 0 и с линией y = -x

для x < 0 .

graph of f(x) = -x

Соединяя эти два графика, мы получаем

график f(x) = |x|

Пример 3. Постройте график

t(x) = (x²— 4)/(x — 2) =

= ((x — 2)(x + 2)/(x — 2)) =

= (x + 2)       x ≠ 2

Следовательно, эта функция может быть записана в виде

y = x + 2            x ≠ 2

График h(x)= x² — 4 Or                     x — 2

график y = x + 2 x ≠ 2

Пример 4. Постройте график

Графики функций с перемещением

— Предположим, что график функции f(x) известен

— Тогда мы можем найти графики

y = f(x) + c

y = f(x) — c

y = f(x + c)

y = f(x — c)

y = f(x) + c          — график функции f(x), перемещённый

ВВЕРХ на c значений

y = f(x) — c          — график функции f(x), перемещённый

ВНИЗ на c значений

y = f(x + c)          — график функции f(x), перемещённый

ВЛЕВО на c значений

y = f(x — c)          — график функции f(x), перемещённый

Вправо на c значений

Пример 5. Постройте

график y = f(x) = |x — 3| + 2

Переместим график y = |x| на 3 значения ВПРАВО, чтобы получить график

y = |x-3|

Переместим график y = |x — 3| на 2 значения ВВЕРХ, чтобы получить график y = |x — 3| + 2

Пример 8

Постройте график

y = x² — 4x + 5

Преобразуем заданное уравнение следующим образом, прибавив к обеим частям 4:

y + 4 = (x² — 4x + 5) + 4 y = (x² — 4x + 4) + 5 — 4

y = (x — 2)² + 1

Здесь мы видим, что этот график может быть получен перемещением графика y = x² вправо на 2 значения, потому что x — 2, и вверх на 1 значение, потому что +1.

y = x² — 4x + 5

Отражения

(-x, y) есть отражением (x, y) относительно оси y

(x, -y) есть отражением (x, y) относительно оси x

Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y

Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x

График может быть получен отражением и перемещением:

— Нарисуйте график

— Найдём его отражение относительно оси y, и получим график

— Переместим этот график вправо на 2 значения и получим график

Вот искомый график

Если f(x) умножена на положительною постояную c, то

график f(x) сжимается по вертикали, если 0 < c < 1

график f(x) растягивается по вертикали, если c > 1

Кривая не является графиком y = f(x) для любой функции f

Логарифмическая функция, ее свойства и график

Слайды и текст этой онлайн презентации

Слайд 1

Подготовила: Коровашкова А. Д. учитель математики
Логарифмическая функция,
её свойства и график.

Слайд 2

№1.Какие из данных графиков являются графиками функций?
тест
д
ж
о
н
к
л

Слайд 3

Решить уравнение: Л)2 Н) log3 6 П)log6 3 А)нет решений

Слайд 4

1. На одном из рисунков изображен график функции . Укажите букву этого рисунка.
К)
К)
О)
Е)
Ц)

Слайд 5

На одном из рисунков изображен график функции . Укажите букву этого рисунка
п
е
щ
о

Слайд 6

Функция задана графиком. Укажите множество всех значений аргумента, при которых она возрастает.
Е)
Ц)
В)
М)
Нет решений

Слайд 7

На каком из указанных ниже рисунков изображен график монотонной функции?
А)
Н)
Ч)
Р)

Слайд 8

Джон Непер
Шотландский математик -изобретатель логарифмов. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд “Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году. Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
(1550 г.— 4 апреля 1617г.)

Слайд 9

Y=
Показатель степени
X=log a y
Y=log a x
Функция y=Log aX Где а>o, а ≠ 1 называется логарифмической

Слайд 10

Слайд 11

Свойства функции.
4.На промежутке x>0 функция является
Возрастающей убывающей
5. Функция принимает положительные значения(y>0)
Х>1 06.Функция принимает отрицательные значения(y01
1.Область определения-
Множество всех положительных чисел(x>0)
2.Множество значений-
Множество всех действительных чисел
3.График функции проходит через точку-
(1;0)

Слайд 12

Слайд 13

x
x
Сравнить:
log 4 и log 3

Слайд 14

Выяснить положительное или отрицательное число
y
x
Log3 4,5
Log3 0,45
Log 2
Log 0,5
>0
>0
y
x
1
1
y=log1/3 X
y=log3X

Слайд 15

Построение графиков логарифмической функции
Построить график функции y= log3(x-2)
График получается Параллельным переносом Кривой y=log3 X Вдоль оси X на 2 единицы вправо
Область определения Данной функции –это множество (2;+∞)
1
1
2
3
y=log3 X
y=log3(x-2)

Слайд 16

Построить график y= log1/3x-2
Log x
Log x-2
2
y
x
1
Сдвиг по оси оу на 2 вниз
Область определения (0;+ ∞)
Множество значений функции (- ∞;+ ∞)

Слайд 17

Построение графиков логарифмической функции
Построить график функции y= log1/3/x/
Cначала строим график y=log 1/3 X ,при x>0
Потом отображаем Его относительно Оси ОУ на промежутке (- ∞;0)
1
1
-1
y=log1/3 X
y=log1/3 /x/
Область определения заданной функции является множество (- ∞;0)U(0;+ ∞)

Слайд 18

y
x
1
Y=log 3 (x+2)-3
-1
-2
y=log 3 x
-3
y=log3 (x+2)-3
Область определения (-2;+ ∞) Множество значений (- ∞;+ ∞)

Слайд 19

Логарифмическая функция определена при любом х
нет
Областью значений логарифмической функции является любое действительное число
да
Функция y=log5 x является возрастающей
да
График функции пересекается с осью Ох
да
Существует логарифм отрицательного числа
нет

Слайд 20

Слайд 21

Какое из указанных ниже чисел не принадлежит области определения
А)
Н)
Х)
Р)
1
5
-8
0
Log5(36-x2)

Графические квадратичные функции: примеры

Решение линейно-квадратичных систем

Вы, наверное, решили системы линейных уравнений. Но как насчет системы двух уравнений, в которой одно уравнение является линейным, а другое — квадратичным?

Мы можем использовать версию метода подстановки для решения систем этого типа.

Помните, что уравнение прямой имеет вид y = mx + b, а стандартная форма уравнения параболы с вертикальной осью симметрии — y = ax2 + bx + c, a 0.

Чтобы избежать путаницы с переменными, запишем линейное уравнение в виде y = mx + d, где m наклон и d Y-пересечение линии.

Подставляем выражение для y из линейного уравнения в квадратное уравнение. То есть подставляем mx + d для тебя в y = ax2 + bx + c .

mx + d = ax2 + bx + c

Теперь перепишите новое квадратное уравнение в стандартной форме.

Вычесть mx + d с обеих сторон.

(mx + d) — (mx + d) = (ax2 + bx + c) — (mx + d) 0 = ax2 + (b − m) x + (c − d)

Теперь у нас есть квадратное уравнение с одной переменной, решение которого можно найти с помощью формулы корней квадратного уравнения.

Решения уравнения ax2 + (b − m) x + (c − d) = 0 даст x-координаты точек пересечения графиков прямой и параболы.Соответствующие координаты y можно найти с помощью линейного уравнения.

Другой способ решения системы — построить график двух функций на одной и той же координатной плоскости и определить точки пересечения.

Пример 1:

Найдите точки пересечения прямой y = 2x + 1 и парабола y = x2−2.

Замена 2x + 1 для y в y = x2−2.

2x + 1 = x2−2

Напишите квадратное уравнение в стандартной форме.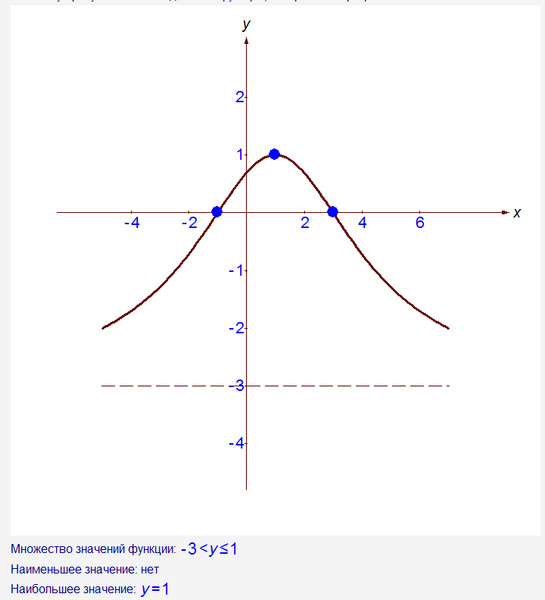

2x + 1−2x − 1 = x2−2−2x − 10 = x2−2x − 3

Используйте формулу корней квадратного уравнения, чтобы найти корни квадратного уравнения.

Здесь a = 1, b = −2, c = −3.

x = — (- 2) ± (−2) 2-4 (1) (- 3) 2 (1) = 2 ± 4 + 122 = 2 ± 42 = 3, −1

Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.

x = 3⇒y = 2 (3) +1 = 7x = −1⇒y = 2 (−1) +1 = −1
Следовательно, точки пересечения равны (3,7) и (−1, −1).

Постройте параболу и прямую линию на координатной плоскости.

Аналогичный метод можно использовать для поиска точек пересечения прямой и окружности.

Пример 2:

Найдите точки пересечения прямой y = −3x и окружность x2 + y2 = 3.

Заменитель −3x для тебя в x2 + y2 = 3 .

x2 + (- 3x) 2 = 3

Упростить.

x2 + 9×2 = 310×2 = 3×2 = 310
Извлечение квадратного корня, x = ± 310.

Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
x = 310⇒y = −3 (310) = −3310x = −310⇒y = −3 (−310) = 3310

Следовательно, точки пересечения (310, −3310) и (-310, 3310).

Постройте окружность и прямую линию на координатной плоскости.

… или линия и эллипс.

Пример 3:

Решите систему уравнений y = −5 и x29 + y24 = 1.

Заменитель −5 для тебя в −5.

x29 + (- 5) 24 = 1

Упростить.

x29 + (- 5) 24 = 14×236 + 9 (25) 36 = 14×2 + 225 = 364×2 = −189×2 = −1894

Здесь у нас есть отрицательное число как квадрат числа. Итак, два уравнения не имеют реальных решений.

Постройте эллипс и прямую линию на координатной плоскости.

Мы видим, что два не пересекаются.

ПРИМЕР 1 Построение квадратичного неравенства График y> x 2 + 3x — 4. РЕШЕНИЕ ШАГ 1 График y = x 2 + 3x — 4. Поскольку символ неравенства>, создайте параболу.

Презентация на тему: «ПРИМЕР 1 Построение квадратичного неравенства График y> x 2 + 3x — 4.

1

2 ПРИМЕР 1 Построение квадратичного неравенства График y> x 2 + 3x — 4.РЕШЕНИЕ ШАГ 1 График y = x 2 + 3x — 4. Поскольку символ неравенства>, сделайте параболу пунктирной. Проверьте точку внутри параболы, например (0, 0). ШАГ 2 y> x 2 + 3x — 4 0> 0 2 + 3 (0) — 4? 0> — 4

3 ПРИМЕР 1 Построение квадратичного неравенства Итак, (0, 0) является решением неравенства. ШАГ 3 Заштрихуйте область внутри параболы.

4 ПРИМЕР 2 Использование квадратичного неравенства в реальной жизни Манильская веревка, используемая для спуска со скалы, может безопасно выдерживать вес W (в фунтах) при условии, что Rappelling W ≤ 1480d 2, где d — диаметр веревки (в дюймах).Изобразите неравенство. РЕШЕНИЕ График W = 1480d 2 для неотрицательных значений d. Поскольку символ неравенства равен ≤, сделайте параболу твердой. Проверьте точку внутри параболы, например (1, 2000).

5 ПРИМЕР 2 Используйте квадратичное неравенство в реальной жизни W ≤ 1480d 2 2000 ≤ 1480 Поскольку (1, 2000) не является решением, заштрихуйте область ниже параболы. 2000 ≤ 1480 (1) 2?

6

7 ПРИМЕР 3 Построить график системы квадратичных неравенств. Построить график системы квадратичных неравенств.y <–x 2 + 4 Неравенство 1 y> x 2 — 2x — 3 Неравенство 2 РЕШЕНИЕ ШАГ 1 График y ≤ –x 2 + 4. График представляет собой красную область внутри параболы y = –x 2 + 4, включая параболу.

8 ПРИМЕР 3 Постройте систему квадратичных неравенств. ШАГ 2. График y> x 2 — 2x — 3. На графике изображена синяя область внутри (но не включая) параболы y = x 2 — 2x — 3. Найдите фиолетовую область, где находятся два графики перекрываются.Этот регион является графиком системы. ШАГ 3

9 РЕКОМЕНДУЕМЫЕ ПРАКТИКИ для примеров 1, 2 и 3 Изобразите неравенство. 1. y> x 2 + 2x — 8y <2x 2 - 3x + 1 2.

10 РЕКОМЕНДУЕМЫЕ ПРАКТИКИ для примеров 1, 2 и 3 Изобразите неравенство. y <–x 2 + 4x + 23. 4. Изобразите систему неравенств, состоящую из y ≥ x 2 и y <–x 2 + 5.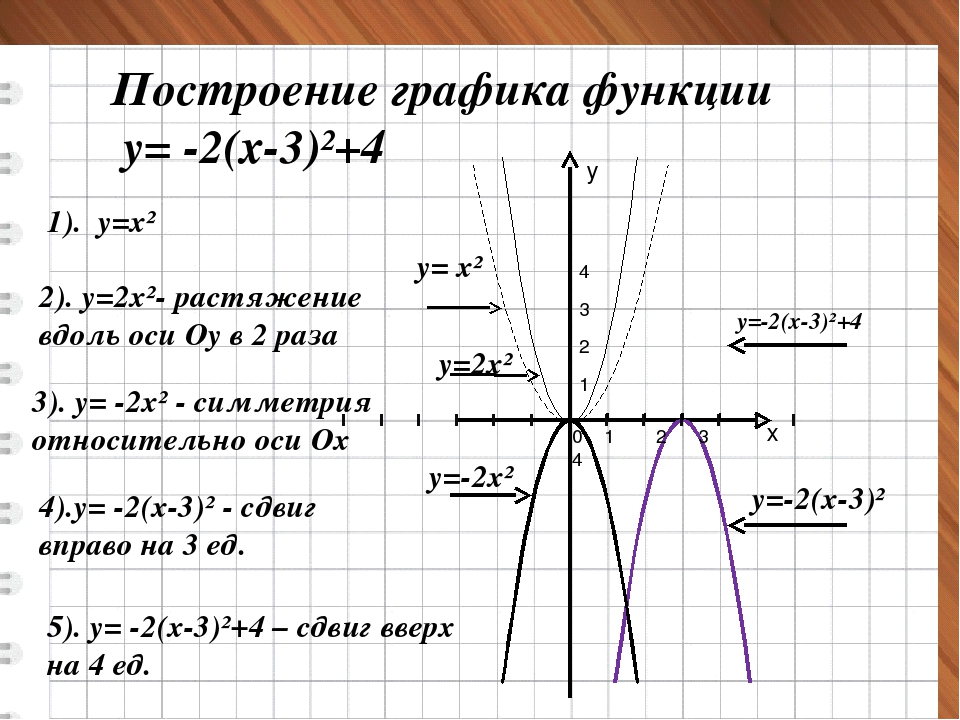

11 ПРИМЕР 4 Решите квадратное неравенство с помощью таблицы. Решите x 2 + x ≤ 6 с помощью таблицы. РЕШЕНИЕ Перепишем неравенство как x 2 + x — 6 ≤ 0. Затем составьте таблицу значений. Обратите внимание, что x 2 + x — 6 ≤ 0, когда значения x находятся между –3 и 2 включительно. Решение неравенства –3 ≤ x ≤ 2. ОТВЕТ

12 ПРИМЕР 5 Решите квадратное неравенство, построив график. Решите 2x 2 + x — 4 ≥ 0, построив график.РЕШЕНИЕ Решение состоит из значений x, для которых график y = 2x 2 + x — 4 лежит на оси x или выше нее. Найдите пересечение графика по x, положив y = 0 и используя формулу корней квадратного уравнения, чтобы найти x. 0 = 2x 2 + x — 4 x = –1+ 1 2 — 4 (2) (- 4) 2 (2) x = –1+ 33 4 x 1,19 или x –1,69

13 ПРИМЕР 5 Решите квадратное неравенство, построив Sketch на графике параболы, которая раскрывается и имеет 1,19 и –1,69 в качестве x -перехвата. График лежит на оси x или выше нее слева от x = –1,69 (включительно) и справа от x = 1,19 (включительно). Решение неравенства приблизительно равно x ≤ –1,69 или x ≥ 1,19. ОТВЕЧАТЬ

14 РЕКОМЕНДУЕМЫЕ ПРАКТИКИ для примеров 4 и 5 Решите неравенство 2x 2 + 2x ≤ 3, используя таблицу и график. 5. –1,8 ≤ x ≤ 0,82 ОТВЕТ

15 ПРИМЕР 6 Использование квадратичного неравенства в качестве модели. Число T команд, которые участвовали в соревновании по сборке роботов для старшеклассников, можно смоделировать с помощью робототехники T (x) = 7.51x 2 –16,4x + 35,0, 0 ≤ x ≤ 9 Где x — количество лет, прошедших с 1992 года. В течение каких лет количество команд превышало 100?

16 ПРИМЕР 6 Использование квадратичного неравенства в качестве модели T (x)> 100 7,51x 2 — 16,4x + 35,0> 100 7,51x 2 — 16,4x — 65> 0 График y = 7,51x 2 — 16,4x — 65 в области 0 ≤ x ≤ 9. Перехват графа по x составляет около 4,2. График лежит выше оси x, когда 4,2

17 ПРИМЕР 7 Решите квадратное неравенство алгебраически. Решите x 2 — 2x> 15 алгебраически. РЕШЕНИЕ Сначала напишите и решите уравнение, полученное заменой> на =. x 2 — 2x = 15 x 2 — 2x — 15 = 0 (x + 3) (x — 5) = 0 x = –3 или x = 5 Запишите уравнение, соответствующее исходному неравенству.Пишите в стандартной форме. Фактор. Свойство нулевого продукта

18 ПРИМЕР 7 Решите квадратное неравенство алгебраически. Числа –3 и 5 являются критическими значениями x неравенства x 2 — 2x> 15. Постройте –3 и 5 на числовой прямой, используя открытые точки, потому что значения не удовлетворяют неравенству. . Критические значения x делят числовую прямую на три интервала. 2 «.

Пошаговое решение:

Шаг 1:

Попытка разложить на множители путем разделения среднего члена

1,1 Факторинг x ² -3x-7

Первый член, x ² , его коэффициент равен 1.
Средний член равен -3x, его коэффициент равен -3.
Последний член, «константа», равен -7

Шаг-1: Умножьте коэффициент первого члена на константу 1 • -7 = -7

Шаг-2: Найдите два множителя -7, сумма которых равен коэффициенту среднего члена, который равен -3.

 x  2  - 3x - 7 = 0
 

 Парабола, поиск вершины: 
 2.1 Найдите вершину y = x  2  -3x-7
 Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения.
 Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
 Для любой параболы Ax  2  + Bx + C координата x вершины задается как -B / (2A).В нашем случае координата x равна 1,5000
 Подставив в формулу параболы 1,5000 для x, мы можем вычислить координату y: 
 y = 1,0 * 1,50 * 1,50 — 3,0 * 1,50 — 7,0 
 или y = -9,250
 Парабола, Графики вершин и пересечений X: 
 Корневой график для: y = x  2  -3x-7 
 Ось симметрии (пунктирная линия) {x} = {1,50} 
 Вершина в точке {x, y} = {1,50, — 9.25} 
 x -Перехват (корни): 
 Корень 1 при {x, y} = {-1,54, 0,00} 
 Корень 2 при {x, y} = {4.54, 0.00}
 Решите квадратное уравнение, заполнив квадрат 
 2.2 Решение x  2  -3x-7 = 0, заполнив квадрат.
 Добавьте 7 к обеим сторонам уравнения: 
 x  2  -3x = 7
 Теперь умный бит: возьмите коэффициент при x, равный 3, разделите его на два, получив 3/2, и возведите его в квадрат. давая 9/4
 Добавьте 9/4 к обеим частям уравнения: 
 В правой части мы имеем: 
 7 + 9/4 или, (7/1) + (9/4) 
 Общий знаменатель две дроби равны 4. Сложение (28/4) + (9/4) дает 37/4 
 Таким образом, сложив обе стороны, мы, наконец, получаем: 
 x  2  -3x + (9/4) = 37/4
 Сложение 9/4 превратило левую часть в полный квадрат: 
 x  2  -3x + (9/4) = 
 (x- (3/2)) • (x- (3/2)) = 
 ( x- (3/2))  2  
 Вещи, которые равны одному и тому же, также равны друг другу.Так как 
 x  2  -3x + (9/4) = 37/4 и 
 x  2  -3x + (9/4) = (x- (3/2))  2  
 то по закону транзитивности, 
 (x- (3/2))  2  = 37/4
 Мы будем называть это уравнение уравнением. # 2.2.1
 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
 Обратите внимание, что квадратный корень из 
 (x- (3/2))  2  равен 
 (x- (3/2))  2/2  = 
 (x- (3/2))  1  = 
 x- (3/2)
 Теперь, применяя принцип квадратного корня к уравнению.# 2.2.1 получаем: 
 x- (3/2) = √ 37/4
 Добавьте 3/2 к обеим сторонам, чтобы получить: 
 x = 3/2 + √ 37/4
 Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 
 x  2  — 3x — 7 = 0 
 имеет два решения: 
 x = 3/2 + √ 37/4 
 или 
 x = 3/2 — √ 37/4
 Обратите внимание, что √ 37/4 можно записать как 
 √ 37 / √ 4, что равно √ 37/2 
 Решите квадратное уравнение с помощью квадратичной формулы 
 2.3 Решение x  2  -3x-7 = 0 по квадратичной формуле.
 Согласно квадратичной формуле, x, решение для Ax  2  + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, определяется по формуле: 
   
 — B ± √ B  2  -4AC 
 x = ———————— 
 2A
 В нашем случае A = 1 
 B = -3 
 C = -7
 Соответственно B  2  — 4AC = 
 9 — (-28) = 
 37
 Применяя квадратную формулу:
 3 ± √ 37 
 x = ————— 
 2
 √ 37, округленное до 4 десятичных цифр, равно 6.0828 
 Итак, теперь мы смотрим на: 
 x = (3 ± 6,083) / 2
 Два реальных решения:
 x = (3 + √37) / 2 = 4,541
 или:
 x = (3- √37) /2=-1,541
 Было найдено два решения: 
 x = (3-√37) /2=-1,541
 x = (3 + √37) / 2 = 4,541
 Quadratics 
 Квадратики — многочлены степени 2.
 Они бывают разных форм, но всегда имеют квадрат.
 Примеры
 Квадратичное выражение:
 Квадратное уравнение:
 Квадратичная функция:
 Квадратичный график:
 Квадратичное неравенство:
 Квадратичное отображение:
 Квадратичные графики 
 Квадратичные графики имеют отличительную U-образную форму 
 называется параболой.
 Улыбка положительной параболы:
 у = ах  2 
 Отрицательные параболы нахмурились!
 у = — ах  2 
 Рисование парабол вида y = ax 
 2 
 Выберите значения для x и поместите их в таблицу.
 Разработать соответствующий для y.
 Постройте эти точки и соедините их плавной кривой.
 Пример
 Заполните таблицу значений для 
 уравнение y = x  2 
 Построение этих точек и объединение их плавной кривой дает
 Обратите внимание, насколько симметричен график!
 Пример
 Заполните таблицу значений для 
 уравнение y = -5x  2 
 Построение этих точек и объединение их плавной кривой дает
 Снова обратите внимание на симметричность графика!
 Работа назад 
 Пример
 Найдите уравнение следующей параболы 
 вида y = ax  2  
 График имеет вид y = ax  2  
 Данная координата (2, 1) 
 Итак, x = 2 и y = 1 находятся на кривой
.
 Подставить и решить
 Параболы вида y = a (x-b) 
 2 
 Пример
 Заполните таблицу значений для 
 уравнение y = (x-2)  2 
 Нанесение этих точек и объединение их плавной кривой дает
 
 
 На этот раз график симметричен, когда x = 2
 Точка поворота (2,0)
 Ось симметрии b 
 в уравнении y = a (x-b)  2 
 Пример
 Найдите уравнение следующей параболы 
 вида y = a (x-b)  2 
 График имеет вид y = a (x-b)  2  
 Данная координата (2, 3) 
 Итак, x = 2 и y = 3 находятся на кривой 
.
Подставляем и решаем
 Параболы вида y = a (x-b) 
 2  + c
 Пример
 Заполните таблицу значений уравнения 
 у = -2 (х + 3)  2  + 2
 Обратите внимание, что ось симметрии x = — 3
 Работа в обратном направлении 
 Пример
 Найдите уравнение следующей параболы 
 вида y = a (x-b)  2  + c
 График имеет вид y = a (x-b)  2  + c
 Данная координата (-3, -2) 
 Итак, x = -3 и y = -2 находятся на кривой
.
 
 На графике b = -2, поскольку это ось симметрии.
 Заменить x = -3, y = -2 и b = -2
 Точка (-2, -5) также находится на кривой.
 Итак, c = -5
 Заменить на -2 = a + c
 Подставляя a, b и c в исходное уравнение 
 у = а (х-б)  2  + с
 Ось симметрии 
 Это квадрат в законченной квадратной форме. 
 Завершение площади
 Параболы формы y = ax 
 2  + bx + c
 Пример
 Заполнить таблицу значений 
 для уравнения y = 2x  2  + 3x — 2
 
 Поворотные моменты 
 Положительные параболы имеют минимальную точку поворота.
 Пример
 Найдите точку поворота квадратичной
 y = x  2  + 3x + 2
 Точка поворота находится на оси симметрии.
 Отрицательные параболы имеют максимальную точку поворота.
 Корни 
 Корень уравнения — это значение, которое удовлетворяет условию 
 уравнение, когда его выражение установлено равным нулю.
 Например, 0 = x  2  + 2x -3
 Максимально возможное количество корней 
 совпадает со степенью многочлена, 
 поэтому у квадратичной может быть не более двух корней.
 Не все квадраты имеют корни.
 Чтобы найти корни квадратичной, 
 Нарисуйте график и посмотрите, где он пересекает ось x.
 или
 Установить y = 0 и разложить на множители (если возможно)
 Пример 
 На графике видно, что уравнение y = x  2  + 2x –3 имеет корни 
 х = -3 и х = 1
 Это то же самое, что установить y на ноль и разложить на множители: —
 Любая скобка может равняться 0, поэтому необходимо учитывать обе:
 Таблица Excel
 Построение парабол 
  Чтобы нарисовать график  
  y = ax  2  + bx + c  
  
 Укажите форму как U (a> 0) или ∩ (a <0)
 Найдите корни уравнения.
 (ах  2  + bx + c = 0)
 Отметьте корни на вашей оси.
 Отметьте точку (0, c) на вашей оси.
 Найдите ось симметрии.
 (½ пути между корнями)
 Используйте это значение x, чтобы найти точку поворота.
 Соедините значения плавной кривой.
 Пример
 Эскиз y = x  2  — 2x — 3
 Это будет U-образная форма, так как a = 1
 Он обрежет ось Y в точке (0, -3)
 Пример
 Эскиз y = 3-2x-x  2 
 Это будет форма, так как a = -1
 Он обрежет ось Y в точке (0,3)
 Квадратные уравнения 
 Стандартная форма Квадратные уравнения имеют вид
 Чтобы найти решение квадратного уравнения:
 Записать выражение в стандартной квадратичной форме
 Факторизуйтесь, если можете:
 {Не забудьте найти общие множители и разницу двух квадратов}
 Используйте квадратные формулы
 Примеры
 Решить 3x — 6x  2  = 0
 Решить 49 — 9x  2  = 0
 Решить 15x  2  — x — 6 = 0
 Решить 15x  2  — x + 1 = 7
 Факторизация квадратичных расчетов
 Квадратичная формула 
 Если квадратичная величина не факторизуется,
 попробуйте квадратичную формулу:
 Пример
 Решить 2 + 4x -5x  2  = 0
 Дайте свой ответ в виде сурда.
 Пример
 Найдите корни 2 + 4x -5x  2 
 Ответьте правильно с точностью до двух десятичных знаков.
 Не все квадраты разложить на множители
 Дискриминант 
 Примеры
 
 Дискриминант 
 б  2  — 4ac 
 = 3  2  — 4x1x4 
 = 9–16 
 = — 7
 b  2  — 4ac <0 
 Нет настоящих корней
 б  2  — 4ac 
 = 3  2  — 4x1x (-2) 
 = 9 +8 
 = 17
 b  2  — 4ac> 0 
 Два отличных настоящих корня
 б  2  — 4ac 
 = 6  2  — 4x1x9 
 = 36–36 
 = 0
 b  2  — 4ac = 0 
 Корни равные и настоящие
 Работа назад
 Пример 
 
 Корни (x — 1) (x + k) = -4 равны.
 Найдите значения k.
 Сначала разложить скобки
 Касание 
 Касательная к кривой касается кривой только в одной точке. 
 Чтобы проверить касание, установите две функции равными друг другу 
 и найдем получившийся дискриминант.
 Если b  2  — 4ac> 0, линия обрывается в двух разных точках.
 Это не касательная.
 Если b  2  — 4ac <0, линия не касается кривой. 
 Это не касательная.
 Если b  2  — 4ac = 0, линия касается кривой только в одной точке. 
 Это касательная.
 Примеры 
 © Александр Форрест
 Как построить график параболы y x2 3x + 8 с использованием математики класса вершин 11 CBSE 
  Подсказка:  Эта проблема связана с коническими сечениями.2} = 4ay \], то вершиной этой параболы является начало координат $ \ left ({0,0} \ right) $, и для этой параболы нет пересечения, поскольку нет членов x или y. Если уравнение параболы включает какие-либо члены линейных x или y, то вершина параболы не является началом координат, вершина должна быть найдена путем упрощения ее до конкретной стандартной формы. 
 Вы в одном шаге от ответа!
 Подпишитесь бесплатно!
 Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин 
 и загружаемым PDF-файлам!
 Преобразования квадратичных функций | Колледж алгебры 
 Результаты обучения 
 График вертикальных и горизонтальных сдвигов квадратичных функций
 График вертикального сжатия и растяжения квадратичных функций
 Напишите уравнение преобразованной квадратичной функции, используя форму вершин
 Определить вершину и ось симметрии для данной квадратичной функции в форме вершины
 Стандартная форма  квадратичной функции  представляет функцию в форме
 [латекс] f \ left (x \ right) = a {\ left (x-h \ right)} ^ {2} + k [/ latex]
 где [латекс] \ left (h, \ text {} k \ right) [/ latex] — вершина.2 [/ латекс]
 Величина [латекс] а [/ латекс] указывает на растяжение графика. Если [latex] | a |> 1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается дальше от оси [latex] x [/ latex] –, поэтому график кажется, становится уже, и появляется вертикальная растяжка. Но если [latex] | a | <1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается ближе к оси [latex] x [/ latex] –, поэтому график кажется шире, но на самом деле есть вертикальное сжатие.{2}} {4a} \ end {align} [/ latex]
 На практике, однако, обычно легче запомнить, что [latex] h [/ latex] является выходным значением функции, когда входным значением является [latex] h [/ latex], поэтому [latex] f \ left (h \ right) = f \ left (- \ dfrac {b} {2a} \ right) = k [/ latex].
 Попробуй 
 Сетка координат наложена на квадратную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение пути мяча. Стрелок забивает корзину?
 (кредит: модификация работы Дэна Мейера)
 Показать решение
 Путь проходит через начало координат и имеет вершину в [latex] \ left (-4, \ text {} 7 \ ​​right) [/ latex], поэтому [latex] \ left (h \ right) x = — \ frac { 7} {16} {\ left (x + 4 \ right)} ^ {2} +7 [/ латекс].
No related posts.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя * 
Email * 
Сайт