Крутейшие задачи на комбинаторику — Журнал «Код» программирование без снобизма
Подобрали для вас самые интересные задачи на комбинаторику — когда решение кроется в том, как мы сочетаем, группируем и комбинируем данные. Очень приятные задачки для крутых разработчиков и очень полезные — для начинающих.
Все эти задачки мы уже загадывали вам в 2019 году, пора их собрать в одном месте для удобства и кайфа.
Представьте, что вы работаете в лаборатории, которая ищет средство от смертельной болезни. Вам на испытание пришла партия из 1 000 пробирок с лекарством, которое нужно опробовать на людях. Проверка санкционирована Минздравом, у вас имеются все лицензии, но есть проблема. Вы узнаёте, что одну пробирку перепутали и по ошибке отправили вместо лекарства ядовитый реактив. Внешне он ничем не отличается от медикамента.
Вам нужно как можно скорее передать пробирки в больницы для запуска клинического теста, но отправлять отравленную пробирку нельзя: погибнут люди. Тесты всех пробирок займут месяцы, это очень долго.
Но у вас есть лабораторные мыши. Вы знаете, что лекарство безвредно для них, но даже капля яда убьёт мышь за сутки. У вас 10 мышей, а пробирок — 1 000.
Как вычислить пробирку с ядом как можно быстрее? За какое время можно гарантированно найти пробирку с ядом?
Сначала кажется, что решить задачу нереально — мышей в 100 раз меньше, чем пробирок. Значит, нам нужно как-то научиться быстро сокращать количество элементов, которые нужно проверить.
Мы знаем, что даже капля яда убьёт мышь за сутки. Значит, если мы смешаем эту каплю с настоящим лекарством, яд тоже сработает. Воспользуемся этим так:
Разделим все пробирки на равные группы — по 100 пробирок в каждой.
В каждой группе возьмём по капле из каждой пробирки и смешаем их. Получим 10 смесей, одна из которых отравлена, и дадим каждой мыши свою смесь. Через сутки мы увидим, какой грызун погиб, и поймём, где конкретно был яд.
Теперь у нас осталось 100 пробирок и девять мышей. Видите, мы за сутки сократили количество пробирок в 10 раз.
Будем использовать этот же приём и дальше: делить сосуды на равные группы и делать смеси. На второй день разделим 100 пробирок на девять групп:
Восемь групп по 11 пробирок и одна группа из 12 пробирок.
Как видите, на совсем равные части поделить не получилось, но это не критично — задача всё равно решается. Теперь даём смеси мышам и через сутки смотрим, какое животное погибнет на этот раз.
Предположим самый сложный случай — яд был в смеси из 12 пробирок. У нас остаётся восемь мышей и 12 пробирок. Их тоже делим на восемь групп:
Четыре группы по две пробирки и четыре группы по одной пробирке.
Снова даём вещество мышам и через сутки смотрим на результат. Если погибла особь, которая пила только из одной пробирки, — то она и была отравлена, а значит, мы нашли яд за три дня. Если эта мышь дегустировала смесь из двух сосудов, то на следующий день мы берём эти две пробирки, две мыши из тех, что остались, и обеим даём попробовать своё лекарство.
Через сутки узнаем, где был яд.
В итоге за три или за четыре дня мы точно сможем сказать, какая пробирка в партии была перепутана.
Ответ: максимум за четыре дня мы найдём яд.
Сторож проверял инвентарь и заметил, что у него не работает фонарик. Он пошарил в тумбочке и вытащил 8 батареек. Насколько он помнил, половина из них — свежие, потому что он совсем недавно покупал в магазине батарейки по акции. А вот ещё четыре точно разряжены: сторож планировал их утилизировать, но оказалось, что сделать это в России не так просто. В общем, теперь сторожу нужно вставить батарейки в фонарик, чтобы проверить, какие из них ещё не разряжены.
Чтобы фонарик заработал, в него должны быть вставлены две заряженные батарейки. Сколько максимально пар батареек нужно перебрать сторожу, чтобы фонарик точно заработал?
Назовём каждую батарейку отдельной буквой — А, Б, В, Г, Д, Е, Ж, З. Это позволит нам не перепутать батарейки, когда мы будем менять их местами.
Теперь разобьём батарейки на пары и проверим в фонарике каждую из них:
(А Б) (В Г) (Д Е) (Ж З) — это четыре первые пары.
Если фонарик заработал на какой-то из них — отлично, мы нашли нужную пару.
Если лампочка так и не загорелась, значит, в каждой паре у нас оказалась одна хорошая батарейка и одна плохая. Давайте подумаем, почему.
Если бы в одной паре было две нерабочие батарейки, то на остальные три пары приходилось бы две нерабочие и четыре рабочие батарейки. Неизбежно одна из пар подобралась бы с двумя рабочими батарейками.
Следовательно, раз ни одна из пар не включила фонарь, в любой из них есть одна рабочая и одна нерабочая батарейка.
Теперь возьмём любые две пары — например (А Б) и (В Г) — и поменяем в них первые батарейки местами. Получим:
(В Б) и (А Г) — в этот момент мы проверили уже шесть пар.
Если фонарик не заработал и после этой перестановки, значит, мы поменяли местами одинаковые батарейки: хорошую заменили на хорошую или плохую — на плохую. Выходит, нужно взять вторую батарейку из первой пары и поменять её с первой батарейкой из второй пары:
Берём пару (В Б), достаём оттуда вторую батарейку Б и ставим её на первое место в паре (А Г), получаем (Б Г) — это седьмая пара.
Если фонарик загорелся, значит, второй мы поставили хорошую батарейку. Если фонарик всё ещё не светит, получается, в этой паре у нас две плохих батарейки, а две хороших остались в другой — (В А). Ставим их в фонарик, и готово!
Получается, что нам понадобится проверить максимум 7 пар.
Представьте, что вы затеяли переезд, сложили все вещи по ящикам и коробкам и отвезли их в новое место. В новом доме пока что беспорядок: коробки лежат друг на друге, что-то свалено в углу и до некоторых ящиков сложно добраться. В одном из таких ящиков вперемешку лежат носки разного цвета: пять синих, шесть жёлтых, семь красных и восемь чёрных. Так уж получилось.
Вам нужно выйти на улицу в носках одинакового цвета, но из-за беспорядка сложно достать сам ящик — можно вытаскивать оттуда только по одному предмету. В ящике щель, в которую вы можете засунуть руку, но не можете увидеть, за каким носком потянулись.
Вопрос: сколько максимально нужно достать носков из ящика, чтобы получить пару одинакового цвета? А что, если требуется взять с собой запасной комплект и он тоже должен быть одного цвета?
Для одной пары
Давайте возьмём самый неудачный случай и каждый раз будем вытаскивать носок нового цвета.
Например, мы сначала вытягиваем жёлтый носок, затем красный, потом синий и чёрный. Получилось четыре экземпляра без пары, в них на улицу не уйдёшь.
А теперь какой бы носок мы ни вытащили следующим, его цвет в любом случае совпадёт с тем, что у нас уже есть в руках. Например, пятым оказался жёлтый — а он у нас уже есть. Всё, пара готова, мы направляемся к выходу, и для этого нам потребовалось вытащить максимально пять носков. Это было легко.
Для двух пар
Две пары могут быть разного цвета — давайте это учтём при решении.
В первой части мы нашли комплект за пять попыток. В итоге у нас есть одна пара жёлтых носков и три одиноких носка: синий, красный и чёрный. Давайте подберём пару к ним.
Снова рассмотрим вариант, когда всё идёт не так быстро, как бы нам хотелось. Допустим, шестой носок, который мы вытащили, — опять жёлтый. Теперь у нас снова четыре предмета разного цвета, как в первом примере. Поэтому мы уже знаем, что любой следующий носок даст нам пару, а значит, для двух пар понадобится максимально семь попыток.
В одном городе ограбили магазин, и дело поручили инспектору — бывшему программисту. Он опросил трёх свидетелей преступления и выяснил, что преступники скрылись на машине. Но все три свидетеля говорили разные вещи:
Инспектору показалось подозрительным такое несоответствие в показаниях, поэтому он проверил свидетелей на старом детекторе лжи. Но детектор был настолько старый, что лишь показал, что каждый из свидетелей соврал про марку или цвет. Все думали, что найти машину не получится, но инспектор смог вычислить автомобиль преступников.
На удивление, эта задача решается простым алгоритмом с элементами перебора: берём высказывание первого свидетеля, предполагаем, что первая часть верная, а вторая — нет. После этого проверяем, насколько это совпадает с остальными условиями задачи и высказываниями других свидетелей.
1-й вариант: допустим, первый свидетель сказал правду про цвет, но наврал про марку. Получается, что цвет машины — синий, и это точно не «Жигули».
Тогда второй свидетель, который сказал про чёрную «Волгу», наврал про цвет, а это значит, что про марку он сказал правду. Получается, что машина была — синяя «Волга».
Теперь проверим показания третьего свидетеля. Он тоже один раз сказал правду, но его ответ был — «точно не синий „Мерседес“». Выходит, что он наврал и про цвет, и про марку, а по условиям задачи такого не может быть: каждый хоть раз сказал правду.
Получается, что первый свидетель наврал про цвет, а значит, про марку он сказал правду. Проверим это.
2-й вариант: допустим, первый свидетель сказал правду про марку — «Жигули», но наврал про цвет. Получается, что у нас есть «Жигули» точно не синего цвета.
Второй свидетель сказал, что это была чёрная «Волга», но мы уже поняли, что это были «Жигули», а значит, второй наврал про марку и сказал правду про цвет. А цвет у второго свидетеля — чёрный. Получились чёрные «Жигули». Проверим показания третьего.
Третий свидетель сказал, что это был «точно не синий „Мерседес“», но мы-то уже знаем про «Жигули», поэтому третий с маркой тоже наврал.
Всё сходится: преступники уехали на чёрных «Жигулях». Хотя лучше бы на «Мерседесе».
В пацанских пабликах пишут так: Джейсон Стэйтем использовал эту задачу, чтобы находить людей, способных мыслить логически на одном с ним уровне. Возможно, это был Альберт Эйнштейн. Но даже если это не он, задача всё равно чертовски интересная.
В целях ясности следует добавить, что каждый из пяти домов окрашен в свой цвет, а их жители — разных национальностей, владеют разными животными, пьют разные напитки и майнят разные криптовалюты. Ещё одно замечание: в утверждении 6 «справа» означает справа относительно вас.
Суть решения сводится к следующему: мы шаг за шагом будем брать данные из условий, чтобы найти неизвестные пока значения, а все результаты вписывать в такую таблицу:
| Дом | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Цвет | жёлтый | синий | ? | ? | ? |
| Национальность | норвежец | ? | ? | ? | ? |
| Напиток | вода | ? | ? | ? | ? |
| Криптовалюта | Ethereum | ? | ? | ? | ? |
| Животное | ? | ? | ? | ? | ? |
Затем мы будем брать новые результаты, смотреть, как их можно совместить с условиями, также занесём в таблицу и станем так делать до тех пор, пока не заполним все ячейки.
Разбираемся с первым домом
В п. 10 явно сказано, что норвежец живёт в первом доме, а если добавить сюда п. 15 (
Теперь разберёмся с цветом первого дома. Мы уже знаем, что рядом с первым домом стоит синий дом, а значит это единственный дом, который стоит рядом с первым. Из пункта 6 (зелёный дом стоит сразу справа от белого дома) следует, что первый дом не может быть зелёным или белым — зелёный и белый должны стоять рядом, а у нас рядом с первым домом стоит синий. Остаются красный или жёлтый. Но в красном доме живёт англичанин — так написано в п. 2, поэтому остаётся только жёлтый. Первый дом — жёлтый.
Смотрим, что говорят нам условия задачи про жёлтый дом:
п. 8 — в жёлтом доме майнят Ethereum;
п. 12 — в доме по соседству с тем, в котором держат лошадь, майнят Ethereum.
Но у нас рядом с домом, где майнят Ethereum, стоит только второй дом, поэтому лошадь держат во втором доме.
Переходим к напиткам. Мы уже знаем, что в первом жёлтом доме живёт норвежец, который майнит Ethereum. Вот как это влияет на условия:
- Норвежец не пьёт чай, потому что это делает украинец в п. 5.
- Норвежец не пьёт кофе, потому что по п. 4 кофе пьют в зелёном доме.
- Норвежец также не пьёт молоко, потому что в п. 9 написано, что в центральном доме пьют молоко. Но так как первый дом — не центральный, то и молоко в первом доме не пьют.
- Норвежец не пьёт апельсиновый сок, потому что согласно п. 13 апельсиновый сок пьёт тот, кто майнит IOTA.
Поэтому единственное, что остаётся пить норвежцу, — это вода. Отлично, мы нашли ответ на первый вопрос. Не забудем занести всю найденную информацию в таблицу:
| Дом | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| жёлтый | синий | ? | ? | ? | |
| Национальность | норвежец | ? | ? | ? | ? |
| Напиток | вода | ? | молоко | ? | ? |
| Криптовалюта | Ethereum | ? | ? | ? | ? |
| Животное | ? | лошадь | ? | ? | ? |
Всё о втором доме
Начнём с криптовалюты.
Мы точно знаем, что это не Ethereum, потому что её майнит норвежец в первом доме. А ещё, раз у жильца синего дома есть лошадь, то он точно не майнит Bitcoin — в п. 7 написано, что тот, кто майнит Bitcoin, разводит улиток. Давайте поработаем с предположениями и проверим, насколько верное каждое из них.
Допустим, что во втором доме майнят IOTA. По п. 13 (тот, кто майнит IOTA, пьёт апельсиновый сок) жилец пьёт апельсиновый сок, а это значит, что тут живёт не украинец, потому что он пьёт чай (п. 5). Это также не англичанин, который живёт в красном доме (п. 2), и не испанец, потому что по п. 3 у испанца есть собака. Японец тоже тут жить не может, потому что по п. 14 японец майнит Monero, а не IOTA. Норвежец же, напомним, живёт в первом доме. Получается, что во втором доме никто не живёт, а такого не может быть, следовательно, наше предположение, что во втором доме майнят IOTA, неверное.
Идём дальше и предположим, что во втором доме майнят Monero, а значит, из п.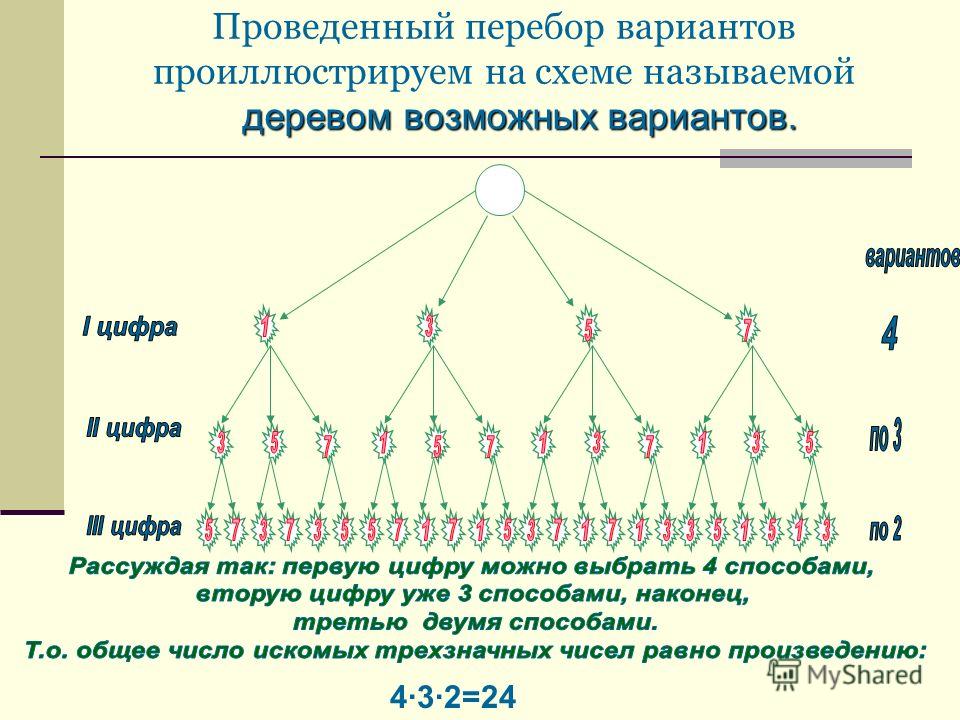
14 видно, что тут живёт японец (японец майнит Monero). Поэтому во втором доме не пьют чай, потому что чай пьёт украинец (п. 5), не пьют кофе, потому что
Давайте выясним национальность, зная название криптовалюты. Это не англичанин, который живёт в красном доме (п. 2), и не испанец с собакой (п. 3), потому что во втором доме держат лошадь. Ещё это не японец, который майнит Monero (п. 14), и не норвежец из первого дома. Получается, что во втором доме живёт украинец, а согласно п.
Занесём новые данные в таблицу:
| Дом | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Цвет | жёлтый | синий | ? | ? | ? |
| Национальность | норвежец | украинец | ? | ? | ? |
| Напиток | вода | чай | молоко | ? | ? |
| Криптовалюта | Ethereum | Stellar | ? | ? | ? |
| Животное | ? | лошадь | ? | ? | ? |
Где живёт лиса
Исходя из п. 11 (сосед того, кто майнит Stellar, держит лису), мы понимаем, что раз Stellar майнят во втором доме, то лиса живёт или в первом, или в третьем доме.
Допустим, что лиса — в третьем доме. Теперь делаем внезапный поворот и зададимся вопросом: а что тогда пьёт человек из п.
А раз так, то получается, что в зелёном доме живёт человек, который разводит улиток, майнит Bitcoin и пьёт кофе. Он точно не норвежец или украинец — мы это выяснили раньше. И это точно не англичанин, который живёт в красном доме (п. 2), не испанец, у которого собака (п. 3), и не японец, который майнит Monero (п. 14). Мы исключили все национальности, а такого не может быть, поэтому наше исходное предположение о том, что лиса живёт в третьем доме — неверное.
Получается, что лиса живёт в первом доме. Добавим это в табличку:
| Дом | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Цвет | жёлтый | синий | ? | ? | ? |
| Национальность | норвежец | украинец | ? | ? | ? |
| Напиток | вода | чай | молоко | ? | ? |
| Криптовалюта | Ethereum | Stellar | ? | ? | ? |
| Животное | лиса | лошадь | ? | ? | ? |
Третий дом
У нас осталось два свободных напитка — кофе и апельсиновый сок, которые пьют в четвёртом и пятом доме.
Тот, кто майнит Bitcoin и разводит улиток, не живёт в доме, где пьют сок, потому что его пьёт любитель IOTA (п. 13). Значит, делаем предположение, что любитель улиток живёт в доме, где пьют кофе, а по п. 4 кофе пьют в зелёном доме. А мы только что разобрали в разделе про лису именно ту ситуацию, когда жилец зелёного дома разводит улиток и пьёт кофе. Тогда мы пришли к выводу, что это невозможно, а значит, любитель улиток не может пить кофе или сок, поэтому он не живёт в четвёртом или пятом доме.
Получается, что любитель улиток, который майнит Bitcoin, живёт в третьем доме.
| Дом | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Цвет | жёлтый | синий | ? | ? | ? |
| Национальность | норвежец | украинец | ? | ? | ? |
| Напиток | вода | чай | молоко | ? | ? |
| Криптовалюта | Ethereum | Stellar | BitCoin | ? | ? |
| Животное | лиса | лошадь | улитки | ? | ? |
Четвёртый и пятый дома
В зелёном доме пьют кофе (п.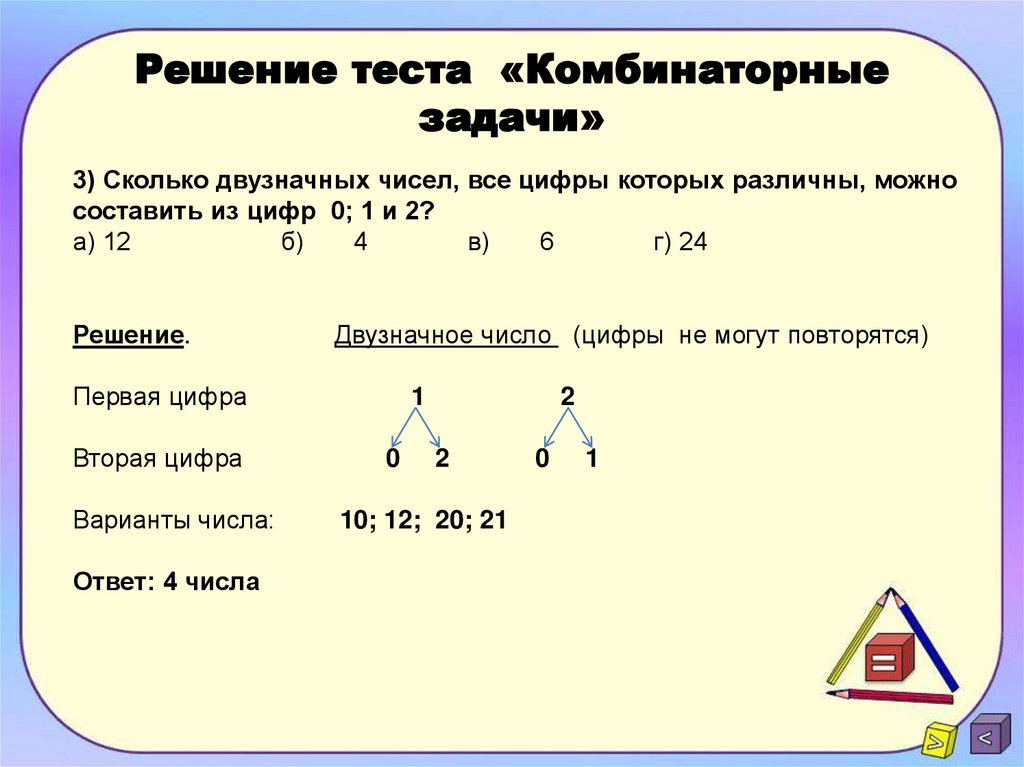
4), а любитель IOTA пьёт сок (п. 13), поэтому он не может жить в зелёном доме. Получается, что в зелёном доме майнят Monero, а раз так, то это — японец (п. 14).
Это означает, что в оставшемся доме пьют сок и майнят IOTA, и дом этот на 3-м или на 4-м месте (по п. 6 — зелёный дом стоит сразу справа от белого дома). Допустим, в третьем доме живёт испанец, у которого должна быть собака (п. 3), но в таблице в третьем доме уже есть улитки, а значит, испанец с собакой живёт в четвёртом доме, и как раз именно он пьёт сок и майнит IOTA.
Третий дом методом исключения остаётся англичанину, а это значит, что третий дом — красный (п. 2). Получается, что у испанца белый дом.
Запишем всё в таблицу:
| Дом | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Цвет | жёлтый | синий | красный | белый | зелёный |
| Национальность | норвежец | украинец | англичанин | испанец | японец |
| Напиток | вода | чай | молоко | сок | кофе |
| Криптовалюта | Ethereum | Stellar | BitCoin | IOTA | Monero |
| Животное | лиса | лошадь | улитки | собака | ? |
Зебра
У нас осталась одна незаполненная клетка в таблице, которая тоже методом исключения достаётся зебре.
Теперь мы можем ответить на вопросы по задаче: воду пьёт норвежец, а зебру держит японец.
Задачи по комбинаторике, комбинаторика
Задачи по комбинаторике, комбинаторика
Комбинаторика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике). Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов. |
Марки и конвертыКомбинаторика В киоске продают 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт и марку? Ответ
Замки и ключи.Комбинаторика Перед нами 10 закрытых замков и 10 похожих ключей к ним. К каждому замку подходит только один ключ, но ключи смешались. Возьмем один из замков, назовем его первым и попробуем открыть его каждым из 10 ключей. В лучшем случае он откроется первым же ключом, а в худшем — только десятым. Сколько нужно в худшем случае произвести проб, чтобы открыть все замки? Ответ
Сколько переводчиков?Комбинаторика На международную конференцию приехали 10 делегатов, не понимающих языка друг друга. Какое минимальное число переводчиков потребуется для обслуживания конференции при условии, что каждый переводчик знает только два языка? Ответ
70 шаров. Комбинаторика В ящике лежат 70 шаров: 20 красных, 20 синих, 20 желтых, остальные черные и белые. Какое наименьшее число шаров надо взять, не видя их, чтобы среди них было не меньше 10 шаров одного цвета? Ответ
Задача про шашки.Комбинаторика На пустую шашечную доску надо поместить две шашки разного цвета. Сколько различных положений могут они занимать на доске? Ответ
|
| Страница 2 из 3 |
Последние добавленные
- Как найти работу?
- Сколько ступеней на эскалаторе?
- Как купить книжку?
- Время на обратный путь.
- Задача про пятерки.
- Про шпионов
- Мальчик и дерево
- Любовный треугольник
- Контролер
- Хамелеоны
- 6 квадратов.
- Вишенка в бокале.
- Три квадрата.
- Уберите 6 спичек.
- Уберите 8 спичек.
- Уберите 4 спички
- Уберите 6 спичек.
- Переложите 12 спичек.
- Стрела.
- Уберите 4 спички.
- Уберите 8 спичек.
- Переложите 4 спички
- Переложите 3 спички.
Пословицы и поговорки
© 2020 Загадки, шарады, ребусы, головоломки, пословицы и поговорки — Лого-Рай.
Карта сайта
rieltorspb.ru
Комбинаторика | математика | Британика
Комбинаторика
Просмотреть все СМИ
- Ключевые люди:
- Пол Эрдёш Андрей Окуньков
- Похожие темы:
- теория графов перестановки и комбинации проблема с ожерельем Теорема Эйлера о многогранниках Числа Рэмси
Просмотреть весь связанный контент →
комбинаторика , также называемая комбинаторной математикой , область математики, связанная с проблемами выбора, расположения и работы в конечной или дискретной системе.
Включена тесно связанная область комбинаторной геометрии.
Одной из основных задач комбинаторики является определение числа возможных конфигураций ( например, графов, рисунков, массивов) данного типа. Даже когда правила, определяющие конфигурацию, относительно просты, перечисление иногда может представлять огромные трудности. Математику, возможно, придется довольствоваться приближенным ответом или, по крайней мере, хорошей нижней и верхней оценкой.
В математике обычно говорят, что объект «существует», если математический пример удовлетворяет абстрактным свойствам, определяющим этот объект. В этом смысле может быть неочевидно, что существует хотя бы одна конфигурация с определенными заданными свойствами. Эта ситуация порождает проблемы существования и построения. Снова имеется важный класс теорем, гарантирующих существование определенного выбора при соответствующих гипотезах. Помимо их внутреннего интереса, эти теоремы могут быть использованы как теоремы существования в различных комбинаторных задачах.
Наконец, есть проблемы с оптимизацией. Например, функция f , экономическая функция, присваивает числовое значение f ( x ) любой конфигурации x с определенными заданными свойствами. В этом случае проблема состоит в том, чтобы выбрать конфигурацию x 0 , которая минимизирует f ( x ) или делает его ε = минимальным, то есть для любого числа ε > 0 f ( x 0 ) ф ( x ) + ε, для всех конфигураций x с указанными свойствами.
Викторина «Британника»
Числа и математика
История
Ранние разработки
Некоторые типы комбинаторных задач привлекали внимание математиков с древних времен. Магические квадраты, например, квадратные массивы чисел со свойством, что строки, столбцы и диагонали в сумме дают одно и то же число, встречаются в И Цзин, китайская книга, датируемая 12 веком до н.
э. Биномиальные коэффициенты, или целые коэффициенты в разложении ( a + b ) n , были известны индийскому математику XII века Бхаскаре, который в своей книге Līlavati («Изящный») посвященный красивой женщине, дал правила их расчета вместе с наглядными примерами. «Треугольник Паскаля», треугольный массив биномиальных коэффициентов, преподавал персидский философ 13-го века Насир ад-Дин ах-Туси.
На Западе можно считать, что комбинаторика началась в 17 веке с Блеза Паскаля и Пьера де Ферма, оба из Франции, которые открыли многие классические комбинаторные результаты в связи с развитием теории вероятностей. Термин «комбинаторный» впервые был использован в современном математическом смысле немецким философом и математиком Готфридом Вильгельмом Лейбницем в его Dissertatio de Arte Combinatoria («Диссертация о комбинированных искусствах»). Он предвидел применение этой новой дисциплины ко всему спектру наук. Швейцарский математик Леонард Эйлер, наконец, стал ответственным за развитие школы подлинной комбинаторной математики, начиная с 18 века.
Он стал отцом теории графов, когда решил проблему Кенигсбергского моста, а его знаменитая гипотеза о латинских квадратах не была решена до 19 века.59.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
В Англии Артур Кейли в конце 19 века внес важный вклад в перечислительную теорию графов, а Джеймс Джозеф Сильвестр открыл множество комбинаторных результатов. Британский математик Джордж Буль примерно в то же время использовал комбинаторные методы в связи с развитием символической логики, а также комбинаторные идеи и методы Анри Пуанкаре, получившие развитие в начале ХХ века в связи с проблемой n тел привели к возникновению дисциплины топологии, которая занимает центральное место в математике. Многие комбинаторные задачи ставились в XIX веке как чисто развлекательные задачи и получили такие названия, как «задача восьми ферзей» и «задача Киркмана о школьницах». С другой стороны, изучение тройных систем, начатое Томасом П.
Киркманом в 1847 году и продолженное Якобом Штайнером, немецким математиком швейцарского происхождения, в 1850-х годах, стало началом теории дизайна. К числу самых ранних книг, посвященных исключительно комбинаторике, относятся «9» немецкого математика Ойгена Нетто.0027 Lehrbuch der Combinatorik (1901; «Учебник комбинаторики») и Combinatory Analysis (1915–16) британского математика Перси Александра Мак-Магона, которые дают представление о комбинаторной теории в том виде, в каком она существовала до 1920 года. век
Многие факторы способствовали ускорению темпов развития комбинаторной теории с 1920 г. Одним из них было развитие статистической теории планирования экспериментов английскими статистиками Рональдом Фишером и Фрэнком Йейтсом, давшее начало многим проблемы комбинаторного интереса; методы, изначально разработанные для их решения, нашли применение в таких областях, как теория кодирования. Теория информации, возникшая примерно в середине века, также стала богатым источником комбинаторных задач совершенно нового типа.
Другим источником возрождения интереса к комбинаторике является теория графов, важность которой заключается в том, что графы могут служить абстрактными моделями для многих различных схем отношений между наборами объектов. Его приложения распространяются на исследование операций, химию, статистическую механику, теоретическую физику и социально-экономические проблемы. Теорию транспортных сетей можно рассматривать как главу теории ориентированных графов. Одна из самых сложных теоретических задач, задача четырех цветов (см. ниже), относится к области теории графов. У него также есть приложения к таким другим разделам математики, как теория групп.
Развитие вычислительной техники во второй половине 20 века является главной причиной интереса к конечной математике вообще и комбинаторной теории в частности. Комбинаторные задачи возникают не только при численном анализе, но и при проектировании вычислительных систем и при применении компьютеров к таким задачам, как хранение и поиск информации.
Статистическая механика — один из старейших и наиболее продуктивных источников комбинаторных задач. С середины 20 в. прикладными математиками и физиками проделана большая важная комбинаторная работа, например, работа над моделями Изинга (см. ниже «Проблема Изинга»).
В чистой математике комбинаторные методы успешно использовались в таких различных областях, как вероятность, алгебра (конечные группы и поля, теория матриц и решеток), теория чисел (разностные множества), теория множеств (теорема Шпернера) и математическая логика. (теорема Рамзи).
В отличие от широкого круга комбинаторных задач и множества методов, разработанных для их решения, отсутствует центральная объединяющая теория. Однако объединяющие принципы и перекрестные связи стали появляться в различных областях комбинаторной теории. Поиск лежащего в основе паттерна, который может каким-то образом указывать на то, как переплетаются различные части комбинаторики, является задачей, стоящей перед математиками в последней четверти 20-го века.
Комбинаторика | Открытый Проблемный Сад
Главная » Тема
См. также: Теория графов » Гиперграфы
| Тема » Подтема | |||||
|---|---|---|---|---|---|
| Длинные радужные арифметические прогрессии | Fox; джунгский; Махдиан; несетрил; Radoicic | ✭✭ | 0 | vjungic | |
| Rainbow AP(4) in an almost equinumerous coloring | Conlon | ✭✭ | 0 | vjungic | |
| Монотонные 4-членные арифметические прогрессии | Дэвис; Участник; Грэм; Simmons | ✭✭ | 0 | vjungic | |
| Четные и нечетные латинские квадраты | Alon; Tarsi | ✭✭✭ | 0 | mdevos | |
| 2-доступность простых чисел | Landman; Робертсон | ✭✭ | 0 | вьюнгич | |
| 3-доступность чисел Фибоначчи | Ландман; Робертсон | ✭✭ | 0 | vjungic | |
| Гипотеза о широком разделении | Чоу; Taylor | ✭✭ | 0 | tchow | |
| Гипотеза о случайном обмене | Бенеш; Фольклор; Стоун | ✭✭✭ | 0 | Вадим Любимов | |
| Гипотеза Бенеша | Бенеш | ✭✭✭ | 0 | Вадим Любимов | |
| Разделение неограниченных перегородок | David S. 9012; Newman | ✭✭ | 0 | DavidSNewman | |
| Sequence defined on multisets | Erickson | ✭✭ | 1 | Martin Erickson | |
| Square achievement game on an n x n grid | Эриксон | ✭✭ | 1 | Martin Erickson | |
| Transversal achievement game on a square grid | Erickson | ✭✭ | 1 | Martin Erickson | |
| Length of surreal product | Гоншор | ✭ | 1 | Лукаш Лански | |
| Варианты американских горок | Ахмед; Сневелий | ✭✭✭ | 0 | Tanbir Ahmed | |
| The Double Cap Conjecture | Kalai | ✭✭ | 0 | Jon Noel | |
| Saturation in the Hypercube | Morrison; Ноэль; Скотт | ✭✭ | 0 | Джон Ноэль | |
| Экстремальный $4$-Neighbour Bootstrap Перколяция в гиперкубе | Моррисон; Ноэль | ✭✭ | 0 | Jon Noel | |
| Turán Problem for $10$-Cycles in the Hypercube | Erdos | ✭✭ | 0 | Jon Noel | |
Perfect 2-error-correcting codes over arbitrary finite alphabets. | ✭✭ | 0 | Коды | davidcullen | |
| Комбинаторные покрытия | Gordon; Мельницы; Рёдль; Шёнхайм | ✭ | 0 | Designs | Pseudonym |
| A nowhere-zero point in a linear mapping | Jaeger | ✭✭✭ | 0 | Matrices | mdevos |
| The additive basis conjecture | Jaeger; Линиал; Паян; Tarsi | ✭✭✭ | 0 | Matrices | mdevos |
| The permanent conjecture | Kahn | ✭✭ | 0 | Matrices | mdevos |
| Базисная гипотеза Алона-Тарси | Алона; Линиал; Meshulam | ✭✭ | 0 | Matrices | mdevos |
| Rota’s unimodal conjecture | Rota | ✭✭✭ | 0 | Matroid Theory | mdevos |
| Bases of many weights | Schrijver ; Сеймур | ✭✭✭ | 0 | Теория матроидов | mdevos |
| Гипотеза Аарони-Бергера | Аарони; Berger | ✭✭✭ | 0 | Матроидная теория | mdevos |
| Равенство в матроидальной окружности, связанной | Оксли; Royle | ✭✭ | 0 | Matroid Theory | Gordon Royle |
Ding’s tau_r vs. |