Круги Эйлера – понятие, 12+ примеров задач для детей
- Примеры задач для детей 2-3 лет
- Примеры задач, которые помогут понять детям 4-5 лет что значит круги Эйлера
При помощи геометрической схемы, которая и именуется круги Эйлера, можно наглядно установить связи между понятиями. Кроме того, наглядно видно, какое отношение существует между частью множества и им самим.
Достоинство кругов Эйлера в том, что они помогают упростить рассуждения и получить наглядный ответ. Сам Леонард Эйлер, придумавший данный метод, так и объяснял его значимость. Несмотря на то, что учёный предложил свой способ 3 столетия назад, он и сегодня актуален, так как помогает наглядно увидеть задачу и способ её решения.
Круги могут пересекаться или не пересекаться, а также один круг может быть вложен в другой.
Практическое значения метода в том, что он помогает решать сложные задачи, когда объединяются или пересекаются множества.
- анализ, когда ребята умеют выделять главные и второстепенные признаки представленных предметов;
- синтез, когда учатся объединять предметы по какому-либо признаку;
- классификация, сравнение, умение достраивать недостающие элементы, установление причинно-следственных связей.
Применяются круги Эйлера для решения простейших задач уже в детском саду. Ребята учатся мыслить логически, а также применяют простейшие математические знания. В дальнейшем приобретённые навыки понадобятся детям для подготовки к школе и решения более сложных задач.
Примеры задач для детей 2-3 лет
Знакомства с кругами Эйлера можно начинать в раннем возрасте. Конечно, предложенные задания будут элементарными.
Например, можно попросить малыша положить в круг (его роль выполняет обыкновенный обруч) мяч. Второй мяч надо положить вне круга. После этого два обруча надо наложить один на второй и предложить ребёнку положить мяч так, чтобы он оказался сразу в двух кругах.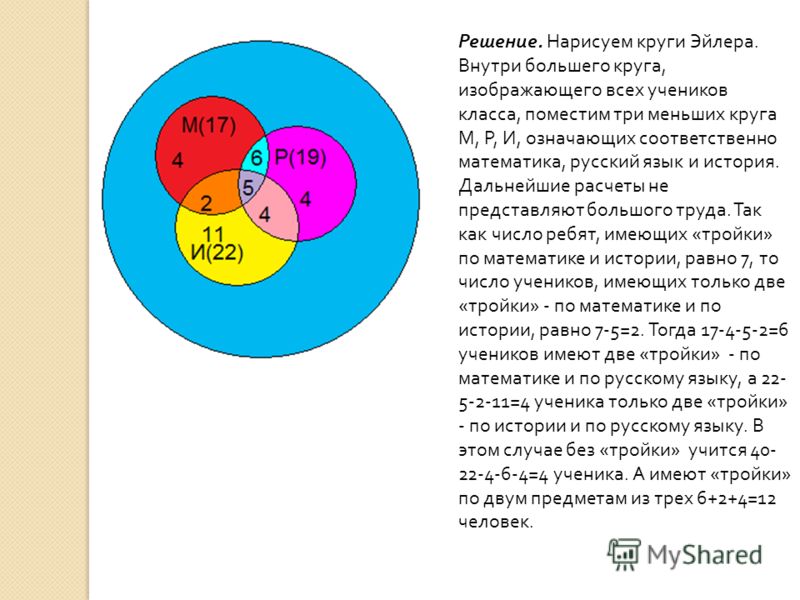
Усвоим элементарные понятия, можно приступать к более сложному – выполнению некоторых задач, которые в состоянии решить ребёнок. Конечно, подбирать задания необходимо в соответствии с возрастом и умениями конкретного ребёнка.
Примеры задач, которые помогут понять детям 4-5 лет что значит круги Эйлера
Ребятам в таком возрасте под силу решить следующие задачи. Начинаются они простого уровня сложности идут по возрастанию.
Простой уровень
Найти предмет по двум свойствам
Дети видят 3 карточки, где изображены кубик Рубика, пирамидка и мячик. В двух кругах задано условие: надо выбрать предмет квадратной формы и разноцветный. Подходит только кубик.
Найти животное
Задача аналогична предыдущей. Дети должны выбрать зелёное маленькое животное из предлагаемых. Это заяц, лягушка и хомяк. Параметры заданы снова в кругах. Под описание подходит только лягушка.
Найти фрукты
И это задание построено по аналогии с предыдущим. Из фруктов (предложена клубника, лимон и жёлтая груша) необходимо выбрать жёлтый, но при этом сладкий.
Ответ очевиден – это груша.
Средний уровень
Больше множеств
Детям предлагается найти предмет из трёх предложенных (солнце, фонарь и цыплёнок), который описан в кругах как яркий, тёплый и жёлтый. Здесь надо применить сразу 3 характеристики. И подходят они солнцу.
По аналогии можно предложить дать ответ относительно одежды или любых других предметов.
Выбрать круг с неправильной характеристикой
Можно пойти от обратного и попросить найти описание, которое совсем не подходит к предмету. Например, предлагается изображение чипсов, а затем их свойства: полезные, вкусные, картофельные, хрустящие. Слово «полезные» окажется лишним.
Разложить предметы в два круга
Нескольким детям предлагается разложить предметы, лежащие на столе. В одном кругу должны оказаться кукла, мячик, пирамидка, кораблик, самолётик и машинка. К слову, мячик, машинка и кукла жёлтого цвета.
Сначала ребятам предлагается положить транспорт в один круг, а игрушки в другой.
Обычно такое задание не вызывает труда и выполняется быстро.
Задание усложняется. Детям предлагается положить в один круг предметы, относящиеся к транспорту, а во второй поместить предметы жёлтого цвета. Тогда и возникнет вопрос: куда надо поместить машинку? Одна и транспорт, и в то же время имеет жёлтый цвет.
В результате разгоревшейся дискуссии дети приходят к выводу: машинка должна быть сразу в двух кругах. Значит, их надо наложить один на другой так, чтобы получилось общее.
Задача про друзей
Ребятам предлагается следующая задача. У Васи несколько друзей. 5 из них любят заниматься спортом, а 4 предпочитают читать книги. 2 друга и читают, и занимаются спортом.
Дети в один круг вписывают цифру 5, во второй – 4, а на пересечении кругов оказывается 2. Таким образом, наглядно видно, что у Васи всего 11 друзей.
Примеры задач для детей школьного возраста
Школьники быстро усваивают разницу между геометрическими фигурами при помощи кругов Эйлера.
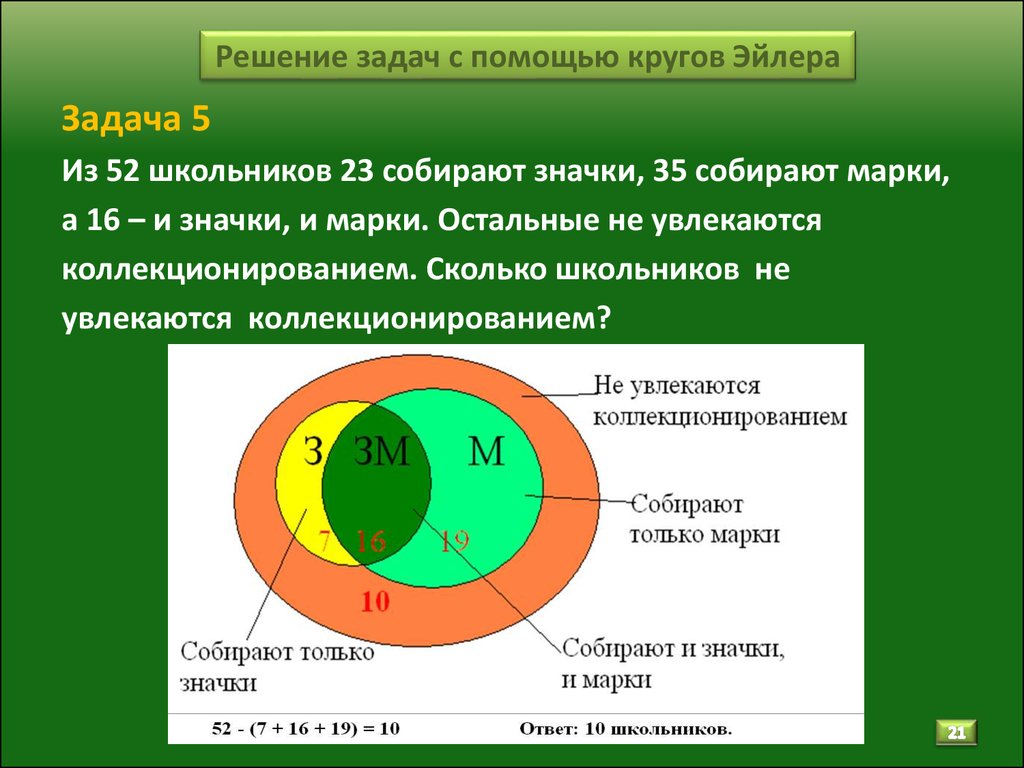
Задача 1
Дети решают задачу. Бассейн посещают 45 школьников. Из них 35 постоянно ходят в школьный бассейн, а 20 – регулярно в городской. Предлагается ответить на вопросы:
Сколько школьников:
- Посещают как школьный, так и городской бассейн?
- Не ходят в городской бассейн?
- Не ходят в школьный бассейн?
- Посещают только школьный бассейн?
- Посещают только городской бассейн?
Решение.
Чтобы определить, сколько школьников посещают оба бассейна, необходимо выполнить следующее действие: (35 + 20) – 45 = 10
В городской бассейн не ходят 25 учащихся, так как 45 – 20 = 25
В школьный бассейн не ходят 10 учащихся, так как 45 – 35 = 10
Только в городской бассейн ходят 10 школьников: 45 – 35 =10
Только в школьный бассейн ходят 15 школьников: 45 – 20 = 15
Задача 2
Предлагается ещё одна задача. Надо узнать, количество рабочих, которые строят магазин и фабрику, если известно, что всего рабочих 30, из них 16 – заняты на строительстве магазина, а 20 – на строительстве фабрики.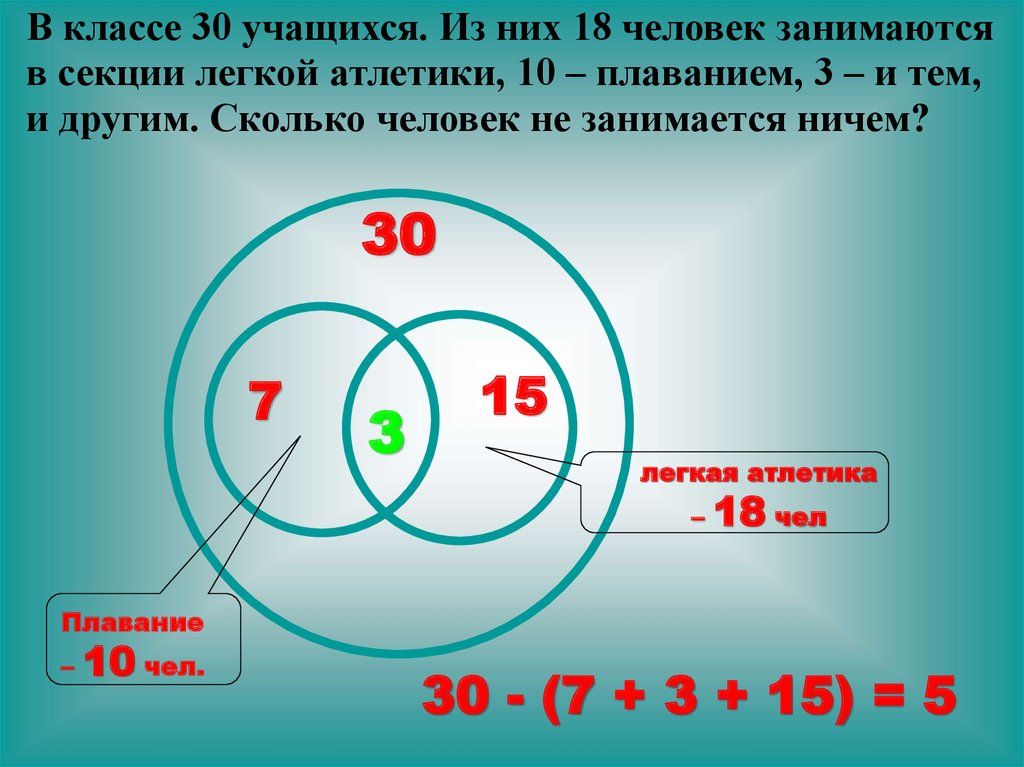
Для решения сначала надо узнать, сколько человек строят только магазин. Для этого от 30 необходимо отнять 16. В результате получится 14. Затем выполняется следующее действие: 20- 14 = 6. Получается, что 6 рабочих трудятся сразу на двух объектах.
Круги Эйлера помогают наглядно увидеть условие задачи, а также найти способ решения. В этом и заключается практическая ценность данного метода.
Автор публикации
- Наталья Степанова
Последние статьи
Решение задач с помощью кругов Эйлера: pol_ektof — LiveJournal
?- Дети
- Кино
- Cancel
Вот на этом сайте — http://logika.
vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
Выходит, что:
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».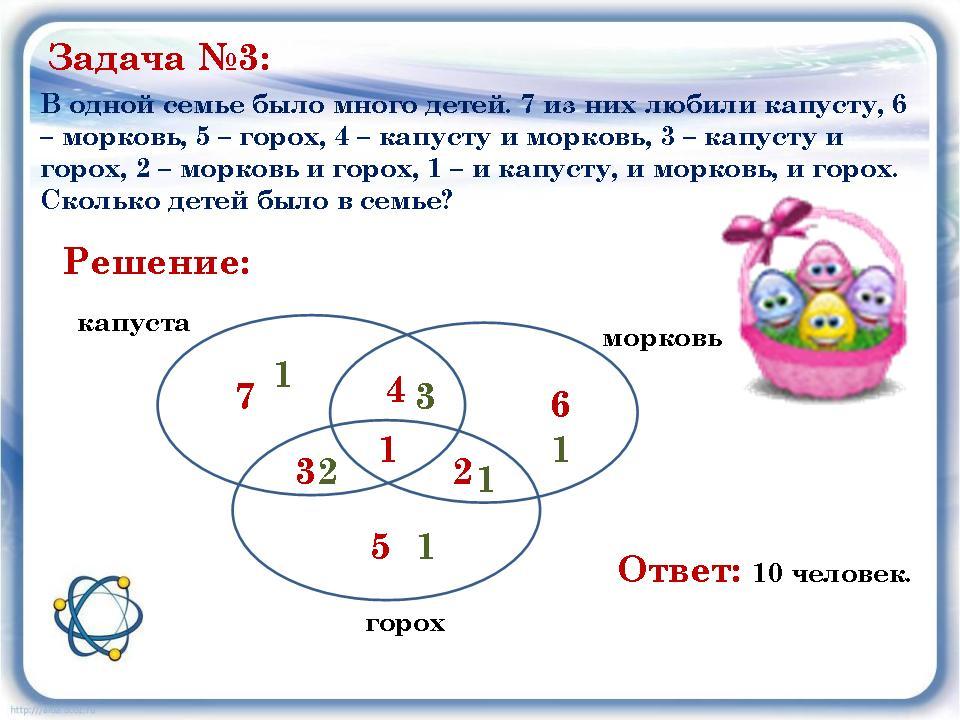
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
Tags: logos, логика
Subscribe
К расплывчатости МАТЕРИИ и недоказанности ЭНЕРГИИ
В философии. Мы примерно знаем — что такое материя (зависит от того, кто объясняет, ибо у всех по-разному). И верим, что…
Париж, Paris, Парыж (9)
9 Paris, Париж! Может Парис надо говорить.
Там же «S» в конце, а не «Ж». Не понимать. Нихт ферштее!…Капитальный сдвиг в сознании!
Обожаю одного человека! Это лингвист и историковед А.А. Зализняк. Внизу вырезки из его выступления о капитальном сдвиге в сознании людей:…
в OZONе
Два года назад, а то и три… ай, ай, ай, как бежит время, из центра нашего города (лишь из вежливости к прошлому…
Там же «S» в конце, а не «Ж». Не понимать. Нихт ферштее!…Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Математический кружок Колорадо
Заинтересованы в расширении своих математических знаний и оттачивании аналитического мышления? Присоединяйтесь к Colorado Math Circle для увлекательных математических бесед и занятий по решению задач, организованных Колорадским университетом в Боулдере. Темы будут включать теорию чисел, комбинаторику, вероятность и геометрию.
Euler Group предназначен для старшеклассников.
Новое в 2022-2023 : группа Euler AMC будет собираться удаленно по четвергам во второй половине дня, чтобы попрактиковаться в задачах на уровне AMC, AIME и ARML. Эта программа предназначена для старшеклассников, у которых уже есть опыт участия в математических конкурсах. Более подробную информацию можно найти на странице регистрации.
Модель Galois Group предназначена для продвинутых учащихся средней школы. Он соберется в январе и феврале для практики AMC 8 и MATHCOUNTS.
Кроме того, Galois MATHCOUNTS 9Группа 0008 будет собираться удаленно по четвергам во второй половине дня, чтобы попрактиковаться в решении математических задач.
Более подробную информацию можно найти на странице регистрации.
Рекомендуемая подготовка: алгебра средней школы. (Примечание: младшие школьники должны подождать до шестого класса, прежде чем посещать занятия, даже если в настоящее время они изучают математику в средней или старшей школе.)
Вы можете посетить любое собрание без предварительной регистрации, но если вы хотите добавить свое имя в список рассылки Колорадского математического кружка, пожалуйста, заполните эту регистрационную форму.
Ознакомьтесь с расписанием встреч на 2022–2023 годы в нашем календаре.
В 2022-2023 учебном году мы планируем проводить встречи математических кружков лично в кампусе Университета Колорадо в Боулдере (см. указания), за исключением еженедельных собраний Galois MathCounts и Euler AMC, которые будут проходить удаленно в Zoom.
июнь 2022
Поздравляем команду Colorado ARML, которая заняла 9-е место в дивизионе A за пределами площадки ARML Competition ! В конкурсе приняли участие более 110 команд из пятнадцати человек и 1600 участников со всей страны.
В этом году половина команд соревновалась на одной из четырех региональных площадок, а другая половина (включая команду Колорадо) соревновалась лично на местном уровне.
Особые поздравления Jackson Dryg из Fossil Ridge HS, который занял 9-е место среди всех участников за пределами площадки и выиграл приз в размере 500 долларов!
Май 2022
Поздравляем Шрути Арун из Campus MS, занявший 10-е место в Национальном соревновании по математическим вычислениям 2022 года , которое проходило 7-9 мая в Вашингтоне, округ Колумбия!
Апрель 2022
Поздравляем Srinivas Arun из Cherry Creek HS и Jackson Dryg из Fossil Ridge HS с результатами олимпиады по математике в США и олимпиады по математике среди юниоров США ! Шринивас был награжден бронзовой наградой USAMO , а Джексон был назван победителем USAJMO , получив одну из самых высоких оценок.
У обоих будет возможность принять участие в Летней программе математической олимпиады (MOSP), в рамках которой будут обучаться и отбираться члены сборной США по математической олимпиаде. Поздравляем Шриниваса и Джексона!!
Апрель 2022
В местном соревновании ARML 2022 приняли участие 117 команд из шести человек со всей страны. Поздравляем следующие команды Колорадо!
Кроме того, Сринивас Арун из Cherry Creek HS занял 8-е место в общем зачете в индивидуальном раунде, став одним из 12 участников, получивших высший балл.
Апрель 2022
Объявлено о вручении наград и сертификатов AMC для молодых женщин по математике .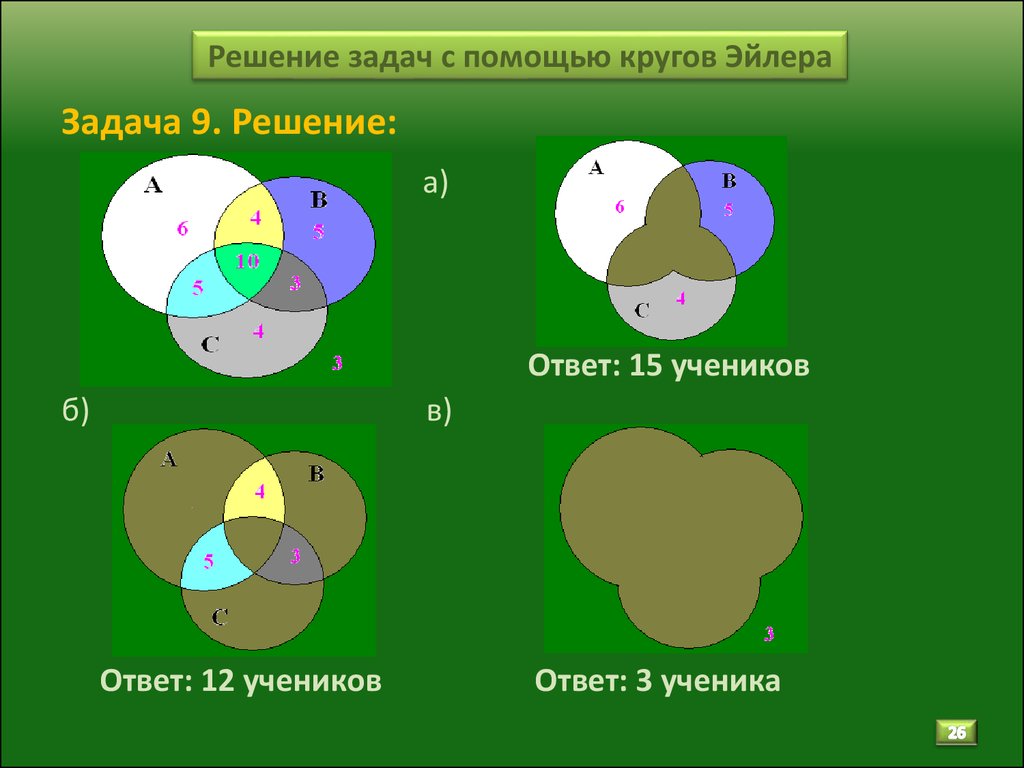
Поздравляем следующих членов математического кружка, которые стали обладателями сертификатов!
| AMC 8 | Одри Хаас, Эллисон Дуан | ||||
| AMC 10A | Shruti Arun, Valerie Xin, Alicia Tan, Pei Xiao (Mia) Wu, Emma Russell, Kelly Yang | ||||
| AMC 10B | Kelly Young, Shruti Arun, Valerie Xin | ||||
| AMC 12A | Элли Грейсон, Эмили Чжан, Майя Вендхан, Танишка Пухан | ||||
| AMC 12B | TANISHQA PUHAN, Maylia Vendies vendies vendies.0005Апрель 2022Поздравляем членов математического кружка, прошедших квалификацию 2022 США Математическая олимпиада (USAMO):
и Юношеская математическая олимпиада США (USAJMO):
Март 2022Математический кружок Колорадо занял 10-е место в конкурсе ARML Power Contest 2021-2022 ! Поздравляем всех, кто принял участие! Старые новости… В течение года мы будем готовиться к командным соревнованиям по математике. Читать далее … Нас поддерживает Департамент прикладной математики CU-Boulder. Если вы хотите сделать не облагаемое налогом пожертвование в пользу Колорадского математического кружка, посетите нашу страницу пожертвований. Спасибо за Вашу поддержку! Ответы на часто задаваемые вопросы см. в разделе часто задаваемых вопросов. Ресурсы | Математический кружок Сан-Хосе Основная цель программы BAMA (Математические приключения в районе залива) состоит в том, чтобы бросить вызов учащимся и мотивировать их к математическому мышлению. Математический спор — это соревнование, похожее на дебаты между двумя командами. Вот некоторые ресурсы для математических споров:
Ежегодно проводится ряд интересных олимпиад и конкурсов.
Вот поддерживаемый ИИГС веб-сайт математических кружков по всей стране. Если вам неудобно посещать наш кружок, попробуйте другие в Bay Area:
Вот веб-страницы некоторых математических кружков, не принадлежащих Bay Area. |
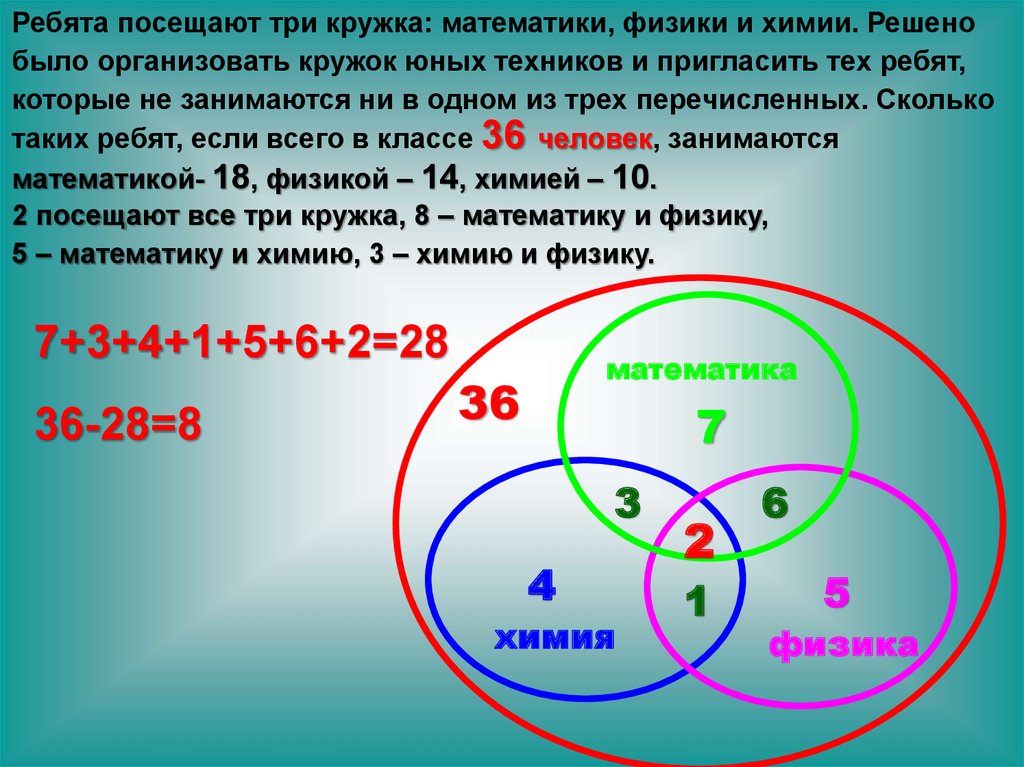В конце года мы примем участие в конкурсе ARML , который пройдет 2–4 июня 2023 года. В 2022 году тридцать пять учеников из пятнадцати разных школ были выбраны для представления Колорадо на национальном конкурсе. За прошедшие годы команда Колорадо пять раз завоевывала национальные награды в дивизионе B, в том числе первое место в 2021 году. Студенты Колорадо входили в десятку лучших участников соревнований за шесть разных лет.
Спикеры представят настоящую математику и поделятся с аудиторией современными взглядами на математику. Некоторые доклады предоставят учащимся связанные проблемы или позволят учителям позже расширить темы со своими учениками.
Вот ссылки на некоторые из них: