Решение задач по теме «площади фигур». 9 класс (подготовка к ОГЭ)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ
«ПЛОЩАДИ ФИГУР»
9 КЛАСС
(ПОДГОТОВКА К ОГЭ)
ЗАДАЧА №1.
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник. Найдите
его площадь.
ЗАДАЧА №2.
На клетчатой бумаге с размером
клетки 1×1 изображена трапеция. Найдите её
площадь.
ЗАДАЧА №3.
На клетчатой бумаге с размером
Найдите его площадь.
ЗАДАЧА №4.
На клетчатой бумаге с размером
клетки 1×1 изображён ромб.
Найдите площадь этого ромба.
ЗАДАЧА №5.
Периметр квадрата равен
160. Найдите площадь этого
квадрата.
ЗАДАЧА №6.
Найдите площадь квадрата,
описанного около окружности
радиуса 40.
ЗАДАЧА №7.
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник. Найдите
его площадь.
ЗАДАЧА №8.
На клетчатой бумаге с размером
клетки 1×1 изображена трапеция. Найдите её
площадь.
ЗАДАЧА №9.
На клетчатой бумаге с размером
клетки 1×1 изображён параллелограмм.
Найдите его площадь.
ЗАДАЧА №10.
Найдите площадь параллелограмма,
изображённого на рисунке.
ЗАДАЧА №11.
Два катета прямоугольного
треугольника равны 6 и 7.
Найдите площадь этого
треугольника.
ЗАДАЧА №12.
Найдите площадь ромба, если
его диагонали равны 14 и 6.
ЗАДАЧА №13.
Сторона треугольника равна 24, а
высота, проведённая к этой стороне,
равна 19. Найдите площадь этого
треугольника.
ЗАДАЧА №14.
Основания трапеции равны
4 и 10, а высота равна 5.
Найдите площадь этой трапеции.
ЗАДАЧА №15.
Найдите площадь параллелограмма,
изображённого на рисунке.
ЗАДАЧА №16.
Сторона квадрата равна 5√3.
Найдите площадь этого
квадрата.
ЗАДАЧА №17.
Сторона ромба равна 10, а
расстояние от точки пересечения
диагоналей ромба до неё равно 3.
Найдите площадь этого ромба.
ЗАДАЧА №19.
Периметр ромба равен 36, а один
из углов равен 30°. Найдите
площадь этого ромба.
ЗАДАЧА №20.
Площадь
параллелограмма ABCD равна 180.
Точка E — середина стороны AB.
Найдите площадь трапеции DAEC.
ЗАДАЧА №21.
В равнобедренной трапеции основания
боковой стороной и основанием
равен 45°. Найдите площадь этой
трапеции.
ЗАДАЧА №22.
На стороне AC треугольника ABC отмечена
точка D так, что AD=5, DC=7. Площадь
треугольника ABC равна 60. Найдите площадь
треугольника ABD.
ЗАДАЧА №23.
Площадь параллелограмма равна 40, а
две его стороны равны 5 и 10. Найдите
его высоты. В ответе укажите большую
высоту.
ЗАДАЧА №24.
НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА
ЗАДАЧА №25.
НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА
ЗАДАЧА №26.
ЗАДАЧА №27.
ЗАДАЧА №28.
ЗАДАЧА №29.
ЗАДАЧА №30.
ЗАДАЧА №31.
ЗАДАЧА №32.
85
?
40
ЗАДАЧА №33.
ЗАДАЧА № 34
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ. ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ. ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ.
ОТВЕТ ДАЙТЕВ КВАДРАТНЫХ САНТИМЕТРАХ.
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ. ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.
English Русский Правила
Геометрия. Задачи на клетчатой бумаге и площади фигур
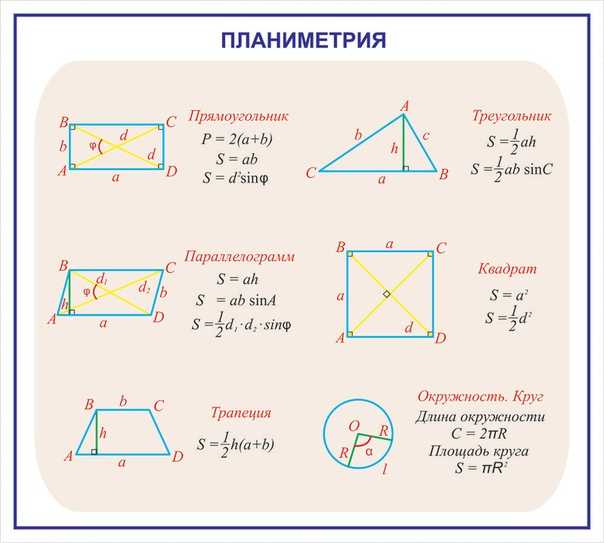
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике.
Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда
Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.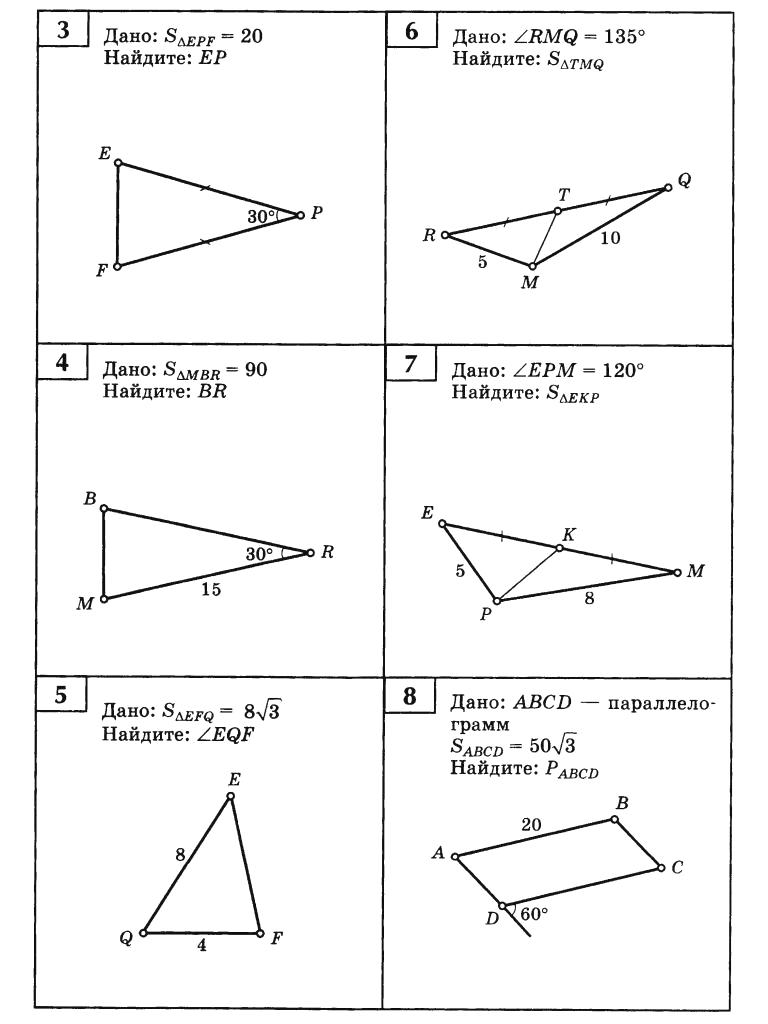
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
, где и — диагонали.
Получим:
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.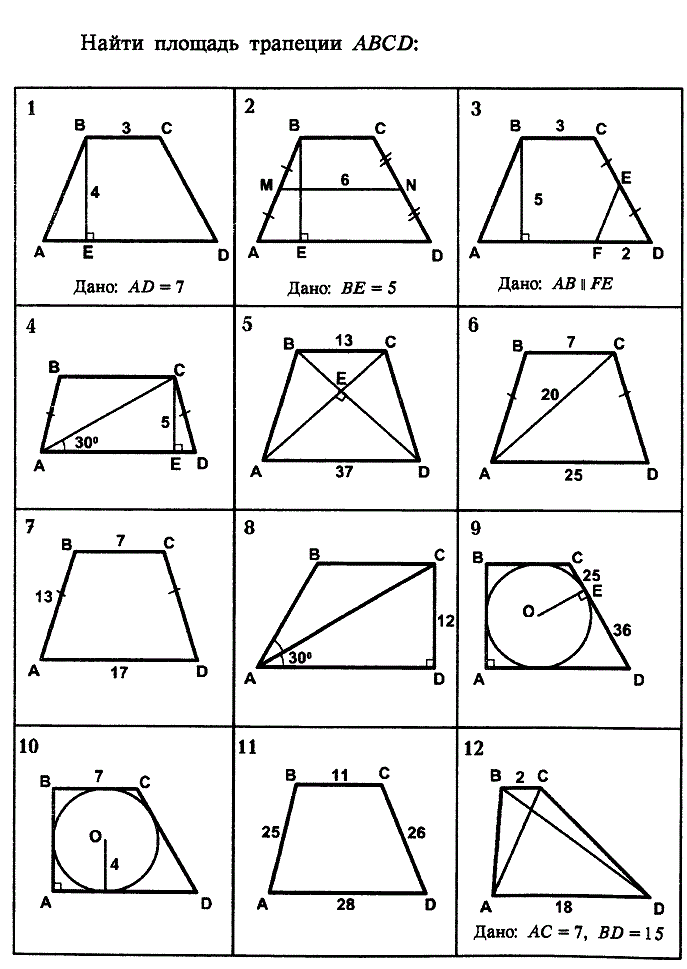
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов).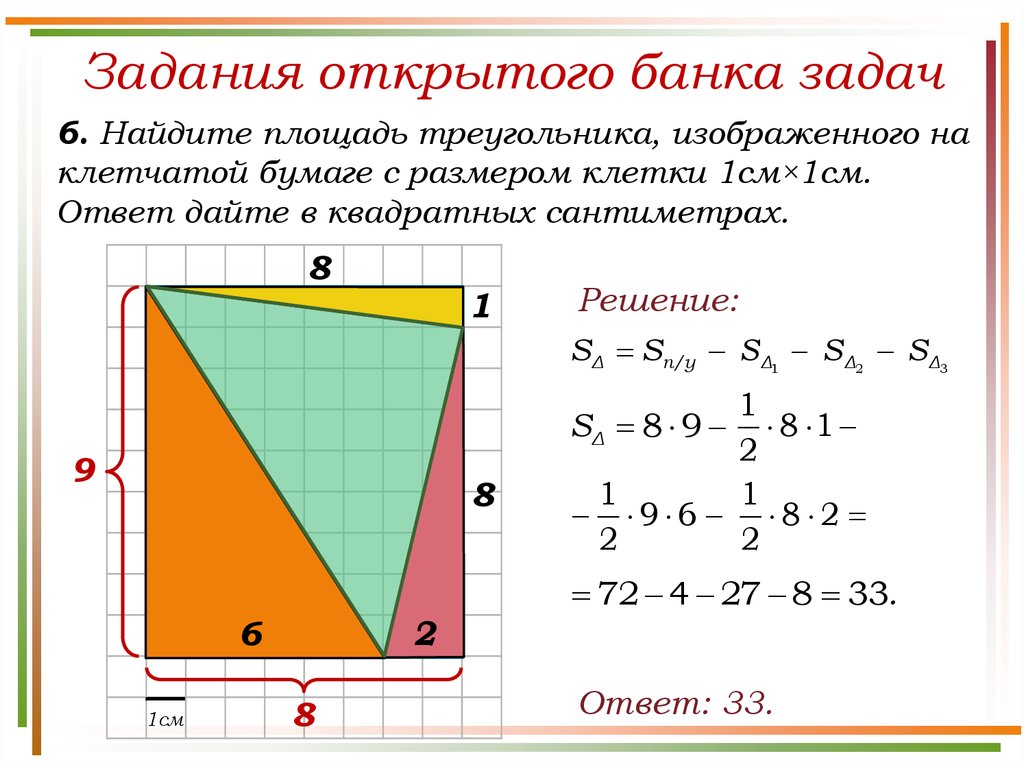
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13.
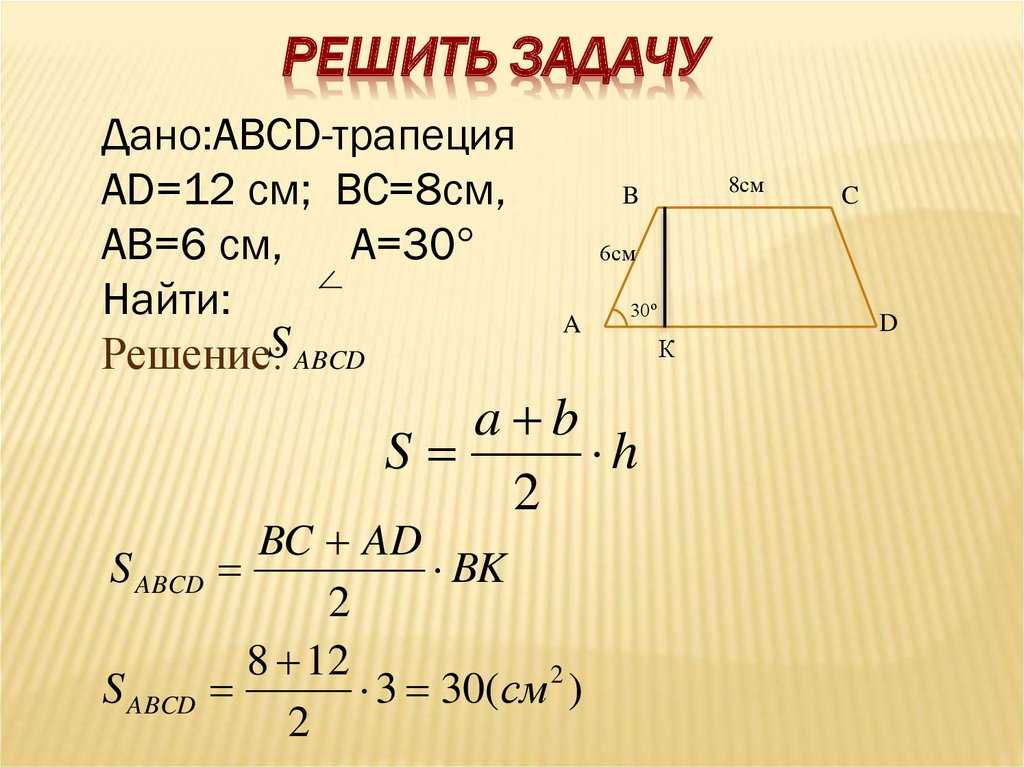Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.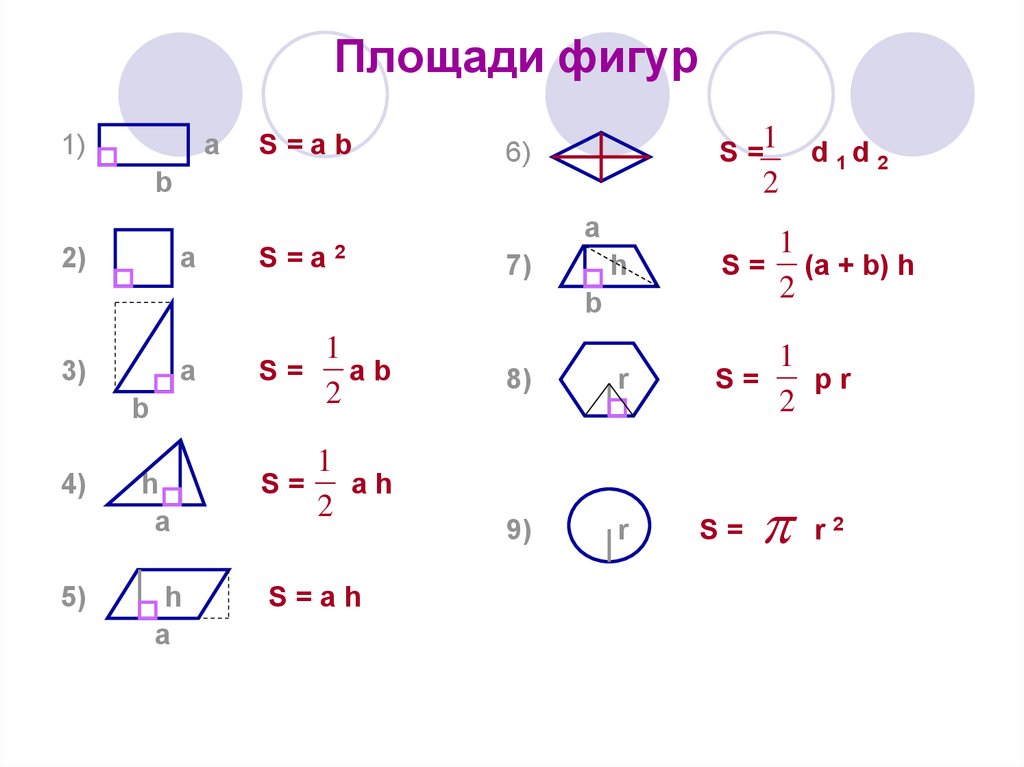
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.04.2023
Найдите с помощью палитры равную площади. Метод поиска областей с помощью палитры
.
Цель:
Задачи урок:
учебный :
познакомить с методом измерения площади криволинейных форм; с приспособлением для измерения площадей — палитрой; закреплять умение находить площади прямолинейных фигур.
развивающая :
развивать внимание, наблюдательность, способность рассуждать, обобщать и делать выводы.
учебная :
воспитывать познавательный интерес к предмету;
поощрять инициативу и самостоятельность в познавательной деятельности.
Во время занятий
1. Организационный момент.
Что самое ценное на земле?
Этот вопрос волнует человечество уже не одну тысячу лет.
Вот ответ известного ученого Аль-Бируни: «Знание — самое превосходное из владений. Все к этому стремятся, а оно не приходит.
У нас урок математики — урок открытия новых знаний.
2. Актуализация знаний и фиксация затруднений в пробном учебном действии.
— На столе каждой карточки с названными цифрами, которые необходимо расположить в порядке возрастания ( единиц площади ).
Самопроверка:
Если вы выполнили задание правильно, то, перевернув карты, вы получите предложение: Есть желание, есть способ!
Пусть эти слова станут девизом нашего урока.
Что вы расположили в порядке возрастания? (единицы площади).
О чем будет разговор на уроке? (о площади фигур)
Какие знания вы уже имеете по этой теме?
(Слышны ответы нескольких учеников.)
Расскажите нам о районе.
Что еще вы хотели бы узнать о площади?
Нахождение площади фигур (работа в парах)
Проверка выполненных заданий.
Какова площадь первой фигуры? (18 см 2).
Кто вычислил площадь второй фигуры?
Почему нельзя?
3. Выявление причин затруднений.
В чем проблема? (мы не знаем, как найти площадь фигуры неопределенной формы)
Определить тему урока (Нахождение площади криволинейной фигуры ).
Какова цель нашего урока? (Узнать, как найти площадь криволинейных фигур).
4. Выход из затруднения.
Как мы решим эту проблему? Как вы нашли площадь прямоугольника, если еще не знали формулы его площади? (Площадь прямоугольника мы измерили меркой)
А для криволинейной фигуры можно попробовать этот способ? (Да.)
Как узнать площадь криволинейной фигуры с помощью одноклеточного измерения? (Разделить по меркам, продолжая ряд измерительных ячеек)
Что вы сделаете, разбив фигуру на мерки, чтобы узнать площадь фигуры? (Рассчитаем количество мерок на рисунке)
Работа в группах.
Представители групп записывают свои ответы на доске. Ответы разные.
Почему ответы были разными? (Группа с меньшим количеством измерений поясняет: «Нецелочисленные измерения мы не считали»)
Что делать с неполными измерениями, ребята? Как их посчитать? (Сложите в два такта.)
Еще раз посчитайте количество полных тактов. Неполные измерения.
Учащиеся работают в группах.
Сколько квадратных мер составляет размер фигуры? (Представители групп называют ответы. Все сверяются со своими ответами.)
Подумайте, удобно ли каждый раз отмечать цифру? (Нет)
Как вы думаете, какой выход из этой проблемы нашли математики? (Есть специальная заготовка, разделенная на квадраты) — Да, для ускорения работы люди придумали прибор для определения площади фигур. (Воспитатель раздает детям диапозитивы, разложенные на квадратные сантиметры, и карточки с цифрами.)
Перед вами такое устройство.
Откройте учебники на странице 45 и прочитайте, как это называется.
Палитра — прозрачная пленка, разделенная на равные квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры.
5. Вывод алгоритма измерение площади фигур палитрой.
«Алгоритм измерения площади фигур с помощью палитры».
6. Первичная консолидация.
Работа по учебнику (с комментированием)
№ 208 (зеленая цифра)
7. Самостоятельная работа с самопроверкой.
Самостоятельная практическая работа в парах.
8. Подведение итогов, самооценка.
9. Конспект урока.
В школе вы изучаете предметную область. Как вы считаете, нужны ли эти знания в жизни?
Донецкая общеобразовательная школа I-III ступеней №97
Министерство образования и науки
Донецкая Народная Республика
УРОК МАТЕМАТИКА
Тема: Измерение площади фигур палитрой 900 04 .
подготовлено и проведено
учитель начальных классов
Кисенко Н.В.
Метод нахождения площадей с помощью палитры. На начальном курсе математики учащиеся измеряют площади фигур с помощью палитры таким образом: считают количество квадратов, лежащих внутри фигуры, и количество квадратов, через которые проходит контур фигуры. Затем второе число делится пополам и прибавляется к первому. Полученную сумму считают площадью фигуры. Палитра позволяет с определенной точностью измерить площадь фигуры. Для получения более точного результата нужно взять палитру с меньшими квадратами.
Слайд 9 из презентации «Квадраты в геометрии» . Размер архива с презентацией 1561 КБ.
Геометрия 9 класс
конспект других презентаций
«Геометрия вокруг нас» — Границы. Предполагаемый результат изучения элективного курса. Реализация задачи внутрипредметных и межпредметных связей.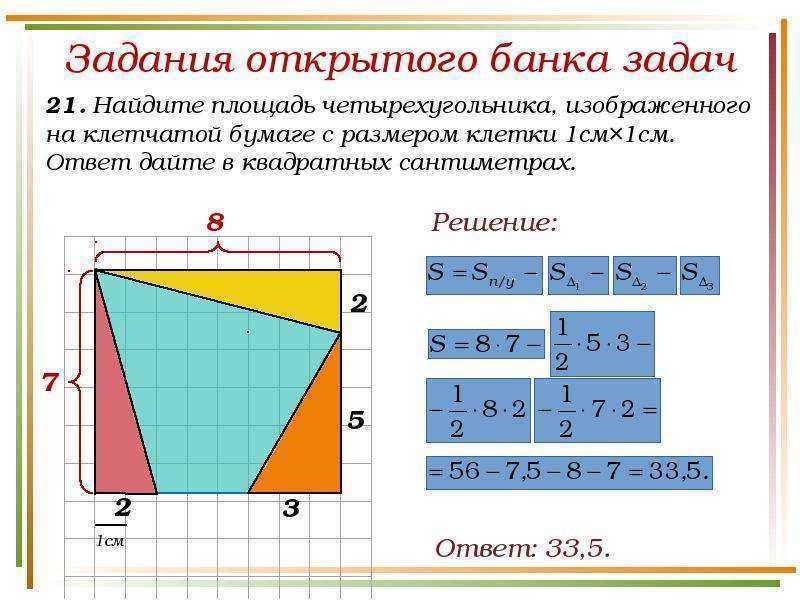
Практическая часть. Математик. Построить бордюр типа «параллельный перенос». Зеркальное отражение и параллельный перенос. Различные способы построения границ. Геометрия вокруг нас. Способы построения границ. Теоретическая часть программы. Алмаз.
Золотое сечение в жизни — Золотое сечение в архитектуре и искусстве. Золотая спираль в природе. Золотая спираль. Архитектор М.Ф. казаки. Путешествие в историю математики. Холст. Золотое сечение заключается в пропорциях человеческого тела. Что такое золотое сечение. Золотое сечение в природе. Разделение сегмента. Научный аппарат. Золотая спираль в искусстве. Концепция золотого сечения. Золотое сечение. Валуйки. Живопись и золотое сечение.
«Метод золотого сечения» — Золотое сечение в математике. Проект. Золотое сечение в архитектуре. Принцип гармонии. Гармоничны ли люди? Пейзажная фотография. Наши задачи. Рамка выглядит более выигрышно, если вы поместите композицию или предмет не в центр кадра. Золотой прямоугольник. Широкие плечи почти равны высоте тела.
Деление прямой по золотому сечению. «Золотая пропорция» в человеке. Золотое сечение в искусстве. Золотая спираль в природе.
«Понятие вектора в геометрии» — Откладывание вектора от заданной точки. Ненулевые векторы. Назовите все изображенные векторы. Длина вектора. Что такое коллинеарные векторы? Определение Физминутка. Шарада. Проверь себя. Векторы называются равными, если они сонаправлены и их длины равны. Коллинеарные векторы. Сегодня на уроке. Понятие вектора. Что называется вектором. Любая точка на плоскости является нулевым вектором. Прямоугольная коробка.
««Координатный метод» 9 класс» — Задача. Равнобедренный прямоугольный треугольник. Уравнение первой степени. Уравнение окружности. Формула. Координаты точки. Докажем формулу. Два противоположных луча. Воспользуемся формулой, чтобы найти расстояние. В скобках указаны координаты точки М. Абсцисса. Отрезок AB параллелен оси OY. Координатный метод. Воспользуемся равенствами. Координаты середины отрезка. Точка M1 (x1; y1) не принадлежит окружности.
«Определение многоугольника» — Ход урока. Полигоны. Вещь. Ломаная линия называется простой, если она не имеет точек самопересечения. Сумма любых n несмежных углов описанного четырехугольника. Какой из них называется закрытым. Вокруг четырехугольника можно описать окружность. Произведение диагоналей произвольного четырехугольника. Определение сломанного. Определение многоугольника. Какой из них называется простым. Какова общая формула суммы углов многоугольника?
План урока открытого урока
Предмет: математика.
Тема: «Измерение площади фигуры. Палитра.»
Цели:
· Познакомить детей со способом нахождения площади фигур различной формы с помощью палитры.
· Научитесь анализировать геометрические фигуры.
· Развивать логическое мышление учащихся, умение точно и аргументировано рассуждать, выделять те стороны наблюдаемых явлений, которые необходимы для изучения и понимания проблемы.
· Улучшить способность решать проблемы.
· Воспитывать интерес к предмету, любознательность, доброжелательное отношение к одноклассникам в сотрудничестве.
Цели урока: Создать условия для самостоятельного поиска знаний.
Оборудование: «Измерение площади фигуры с помощью палитры», презентация
Учебно-методические материалы к занятию:
Учебный курс
1.Организационный момент :
Давай проверим, мой друг,
Ты готов начать урок?
Все на месте
Все в порядке
Ручка, книга и блокнот?
Все правильно сидят?
Все внимательно смотрят?
Все хотят получить
Только оценку «5»?
2. Тема урока пост
Учитель: Ребята, мы снова погружаемся в мир скучной математики. Сегодня мы познакомимся с геометрическими фигурами, площадь которых находим по-новому. А как, узнаем на уроке. Мы можем сделать это.
3. Оформление работ в тетрадях.
Математика — королева всех наук.
Он нужен в любой науке, в любой профессии, например, археологи. Вы знаете, кто такие археологи? Давайте посмотрим презентацию «Кто такие археологи».
7. Работа по индивидуальным карточкам.
Нахождение площади фигур прямоугольной и квадратной формы.
Давайте поиграем в эту профессию. Вы пришли на место раскопок. Вам нужно определить, какова площадь прямоугольной или квадратной земли, на которой вы будете что-то искать. (У каждого карточка с рисунком, данными. Дети по формуле находят площадь, делают рисунок и записывают в тетрадь.) Один ученик у доски.
S = 5 * 9 = 45 м2
ЧЕК. Воспитатель раздает карточки с указанием правильного ответа, дети зачитывают свои ответы — Сложите ответы и вы увидите археологов, которых вы откопали. Динозавры..jpg «width=»45″ height=»59 src=»>.jpg» width=»49″ height=»65 src=»>
8 . Физминута
Вы, наверное, устали?
-Да!
«И так все встали».
Дружелюбные вытянули шеи
как динозавры зашипели: зарычали.
Шипели, молчали
как динозавры, скакали.
Поскакал, поскакал
И скрылся за кустом.
9. Знакомство с новой темой.
Я нашел такого динозавра. (На доске вывешен плакат.)
— Можно ли найти его площадь по формуле? Почему?
Существует способ нахождения площади неправильных форм с помощью палитры — прозрачной пленки с нанесенными на нее квадратными сантиметрами.
10. Ознакомление с презентацией «Палитра» 11. Работа по теме урока
Нахождение области динозавра по алгоритму . использование большой палитры. Учитель комментирует.
Алгоритм площади поддона
1. Поставить палитру.
2. Сосчитайте количество
полных квадратов на рисунке.
3. Подсчитайте количество неполных квадратов и разделите это число на 2:
4. Сложите количество полных квадратов и количество неполных квадратов, деленное на 2.
Дети делают запись в тетради.
12. Физминутка. (Парный танец)
Давай, Дино, прыгай, прыгай. мы прыгаем.
И ногами прыгаем, прыгаем, прыгаем .
13. Самостоятельная работа. Найдите площадь яйца с помощью палитры.
Знаете ли вы, как рождаются маленькие динозавры? Из яиц. Продолжаем наши археологические раскопки. Тот, кто найдет яйцо динозавра в пределах квадратного метра, нарисованного на полу, имеет право посмотреть на него.
(Дети находят «яйцо» от киндера, внутри каждого – палитра и надпись «палитра»)
Воспитатель раздает рисунки яйца, просит найти его площадь. Дети самостоятельно находят площадь яйца с помощью палитры.
14. Тестирование.
Мы проверим наши знания. В тесте обведите правильный ответ.
ТЕСТ по теме «Палитра»
1. Прямоугольник, у которого все стороны равны, называется
Треугольник
2. Чтобы найти площадь квадрата или прямоугольника, нужно
Умножить длина по ширине
Найдите сумму всех сторон.
3. С помощью палитры площадь находится следующим образом:
Сложите количество полных квадратов и количество неполных квадратов, деленное на 2. 915 . РЕЗЕРВ .
Работа в группах.
1 группа записывает наименования предметов, площадь которых удобно найти по формуле
2. группа записывает наименования предметов, площадь которых удобно находить с помощью палитры.
16. Конспект урока. Комментирование оценок.
Узнали ли вы что-то новое на уроке?
Что понравилось?
17. Домашнее задание.
Используйте палитру для нахождения площади мелких предметов, рисунков.
Для определения площадей малых участков с криволинейными контурами на плане применяют палитры, чаще прямолинейные. К прямым поддонам относятся известные и наиболее распространенные квадратные и параллельные поддоны.
Квадратная палитра представляет собой сеть взаимно перпендикулярных линий, проведенных через 1-2 мм на прозрачном целлулоиде, оргстекле, фотопленке, стекле или кальке.
Площадь фигуры определяется простым подсчетом ячеек палитры, наложенных на фигуру. Доли клеток, расчлененных контуром на части, учитывают на глаз (рис. 13). Квадратную палитру не рекомендуется определять на плане площадей больше 2 см 2 . Недостаток его применения (помимо того, что площади рассекаемых контуром долей клеток приходится оценивать на глаз) состоит в том, что подсчет числа целых клеток часто сопровождается грубыми ошибками.
Таких недостатков не наблюдается при определении участков параллельной палитрой, представляющей собой лист прозрачного целлулоида, оргстекла или кальки, на котором проведены параллельные линии преимущественно на расстоянии 2 мм друг от друга. Область контура определяется по этой палитре следующим образом. Разложите его по контуру так, чтобы крайние точки a и b расположились посередине между параллельными линиями палитры. Тогда весь контур оказывается разделенным параллельными прямыми на фигуры, близкие к трапециям, с одинаковыми высотами, а отрезки параллельных прямых внутри контура являются средними линиями трапеции (рис.
14). Штриховыми линиями показаны основания этих трапеций.
Сумма площадей трапеций, т.е. площадь контура равна
Следовательно, чтобы получить площадь контура, надо взять сумму средних прямых, т.е. сумму отрезков параллельных линии внутри контура, и умножить на расстояние между ними.
Для упрощения определения площади в раствор компаса последовательно вычерчивают сумму средних линий, которую определяют по масштабной линейке и полученную длину умножают на ч , м (рис. 15). Чтобы не производить таких расчетов, для каждой шкалы строят специальную шкалу, по которой отсчитывают площадь контура, зная сумму средних линий.
Расчет масштаба: М 1:10000, h = 2 мм, при длине шкалы 1 см площадь равна (0,2 см 100 м) (1 см 100 м) = 2000 м 2 = 0,2 га. Параллельная палитра не должна определять на плане участки площадью более 10 см 2 .
4.5. Точность расчета площадей графически и с помощью палитры
При делении сечения на простые фигуры точность расчета для разных вариантов будет неодинаковой.
Площадь треугольника графически вычисляется точнее, чем площадь других фигур. Поэтому площадь при делении площади на треугольники вычисляется точнее, чем при делении на другие фигуры (трапеции, прямоугольники). При делении площади на треугольники из всех вариантов лучшим будет тот, в котором треугольники равносторонние или высота. h примерно равно основанию a .
Ошибка уменьшается, если площадь треугольника вычисляется не как
, и по формуле Герона
где
. Это дает уточнение до 13% даже для равностороннего треугольника. Основание треугольника может быть во много раз меньше высоты, если измерять его на местности, а не на плане.
При делении площади на треугольники ошибка площади участка
,
где М — знаменатель числового масштаба плана. Если вычислить дважды, то
.
Количество треугольников, на которые разбит участок, не влияет на ошибку площади. Поэтому при делении участка на треугольники не нужно стремиться к тому, чтобы их было меньше.
Точность однократного определения площади квадратных и параллельных поддонов, а также ротометра характеризуется эмпирической формулой
.
«Расчет площади плоских изделий с помощью интеграла синга». Вычислите площадь фигуры Отримана по формуле
На эту тему есть три урока, каждый урок разный.
Цели занятия:
Закрепление и разрушение знаний о певческом интеграле и його дополнить знания области фигур;
Формирование умін сходо застосування знаний и способов изменения этих новых исходных ситуаций; — развитие информационно-коммуникативной культуры студентов;
Проведение познавательной деятельности, вминня деятельности в коллективе, зазятти что достигают мети.
Задание на уроке:
Повторить таблицу и правила определения начальных, понимание криволинейной трапеции, алгоритм определения площади криволинейной трапеции; — необходимо помнить о том, что важно знать, что площадь плоской фигуры.
Формы организации роботов и учащихся: работа в группах.
Принадлежит играемым программам: интерактивная доска Smart Board, «Математика жива».
Выигрышные функции программного обеспечения интерактивной доски:
Функция — шторка:
Функция — клонирование объекта:
Функция — повторная затяжка объекта;
Функция — интеллектуальное перо.
Zavantage:
Вид спереди:
Занятие на тему: «Вычисление площадей фигур для дополнительного интегрирования»
В 11 классе.
Урок Скрыть:
- Организационный момент ((проверяется готовность перед занятием, озвучивается тема и цель занятия, записывается номер).906:20
Урок проходить под нос: Скажи мне, и я забуду, Покажи мне, и я запомню, Дай мне дышать самостоятельно, я научусь.
Конфуций.
- Этап актуализации предыдущих знаний(Мета этого этапа: повторение таблицы и правил распознавания примитивов, понимание криволинейной трапеции, алгоритм распознавания площади криволинейной трапеции).
Учитель: На предыдущих уроках мы узнали о понятиях первых, из таблицы и правилах их значения.
Питание 1 : Что называется первичным для функции y = f(x) на некотором интервале? Еда 2: Как установить все первичные функции y = f(x), чтобы F(x) была одной из них? Питание 3: Отмените правила познания первого. Как только открывается 2-я горка, открывается занавес, после чего прикрепляется еда для учеников. Голова 1: Знайте одну из первых функций для назначения. (изучение функции — перетаскивание, чтобы установить первую функцию на первую). Менеджер 2: Для назначенной функции узнайте одну из первых строк графика, чтобы пройти через эту точку. (Учащиеся на заданиях самостоятельно выступают, один из учниверя выдается, отвешивая экран).
А) Функции: 2х5 — 3х2; 3 cos x — 4 sin x; 3е х + 5 х — 2; е 2х — cos3x; 1/х + 1/sin 2 х — х.
Первичный: пер | х | -ctgx-х 2/2; 1/2e 2x — 1/3 sin 3x; х 6/3 — х 3; 3 sin x + 4 cos x; 3x + 5x/1n5.
B) Для функции f(x) = 2x + 3, чтобы узнать первую, график должен пройти через точку M(1; 2).
Питание 4: Какую фигуру называют криволинейной трапецией? Задание 3: Запишите мнение назначенной женщины, зафиксированное на слайде. Задание 4: Напишите формулу Ньютона Лейбница.
Задача 5: Вычислить интеграл. (Учащиеся рассчитывают самостоятельно, с повторной проверкой наступления). А) х 2 — 2х) дх; б)
Задача 6: Вычислить площадь фигуры, окруженной линиями у = 0, х = е, у = 1/х. (Учитесь самостоятельно считать задание с дальнейшей перепроверкой, открывая экраны на дощах).
- Этап лепки и повторения, убавления и начала при выполнении разных заданий по теме «Расчет площади фигур для дополнительного интегрирования» 906:20
1. Учить определять мощность площади
и указывать торец фигуры, площадь которой можно вычислить по формуле S = Вычислить площадь фигуры, окруженной строки у = 0, у = х 2 — 4. (Один урок по дополнительным функциям — смарт-ручкой писать решения на интерактивном планшете).
2.
Учащиеся обсуждают план вычисления площади фигуры, окруженной линиями у = х 2
— 6х +11 я у = х +1.
Кожаная сцена сопровождается занавесом.
- Групповая работа. Класс заздалэгід подразделяется на группы. Три ученика практикуются у доски, и решают ученики по трем вариантам (группам разбиений вариантов) на задания: Вычислить площадь фигуры, окруженной линиями: Вариант 1 — у = (х — 3) 2 , у = 0, х = 1, х = 4. Вариант 2 — у = х — 2, у = х 2 — 4х+2. 3 вариант — у = х, у = 5 — х, х = 1, х = 2.
- Групповая работа. Для кожных поражений 8 предметных стекол необходимо рассчитать площадь рисунка. У учеников в группах есть набор этих малышек. Научитесь выбирать формулу, по которой можно узнать площадь. Показан слайд, правое кресло показывает формулы, на него наложена функция клонирования. После обсуждения в группах по очереди изучите тип группы и перенесите выбранную формулу или напишите свою, так как на дощах такого нет. Дали следующую дискуссию: — Почему была выбрана именно эта формула? — Чьи є ще способы знаходження площади цієї фигури? — Яка с формулами найзручніша застосуванни 906:20
Домашнее задание.
Подсумок урока. Учний ответит на вопрос: — Что было собрано под часовым уроком? — Какая новая вонь обнаружилась на уроке? — Как он работал с этой группой?
Практическая работа на тему: «Вычисление площади плоских предметов с помощью интеграла синга»
Метароботы: освоить задачу вычисления площади криволинейной плоской фигуры с помощью интеграла синг.
Право собственности: учебная карта, таблица интегралов, лекционный материал на тему: «Одинарный интеграл. Геометрический смысл интеграла.
Методические положения:
1) Ознакомиться с лекционными материалами: «Поющий интеграл. Геометрический смысл интеграла.
Краткие теоретические положения
Единый интеграл функции на відрізку — це границу, до
, к которому pragne интегральная сумма при pragnnn_ ноль является суммой наибольшей части счета.
Нижняя граница интегрирования – это верхняя граница интегрирования.
Для вычисления единого интеграла подайте Формулу Ньютона-
Лейбница:
Геометрический смысл линейного интеграла . Как интегрируется на
Поскольку функция неотрицательна, то численно более ценная площадь криволинейной трапеции равна:
Криволинейная трапеция — фигура, окруженная графиком функции
Ось абсцисс и прямые, .
Возможность различных типов плоских форм, образующих координатную плоскость:
Подобно криволинейной трапеции с основанием, окруженным кривой внизу , то из зеркального отражения симметрии видно, что площадь фигуры больше или меньше.
Как будто фигура окружена кривой, как бы заполнена положительными и отрицательными значениями . Таким образом, чтобы вираховать квадрат фигуры шукано, необходимо разбить ее на части, затем
Как плоскую фигуру в окружении двух кривых , то її площадь можно узнать дополнительной площади двух криволинейных трапеций:
стыка.
Вычислить площадь фигуры, окруженной линиями:
Раствор. 1) Сделаем параболу прямой в координатной плоскости (Малюнок до встречи).
2) Мы видим (заштриховали) фигуру, обведенную этими линиями.
Малышка до завдання
3) Мы знаем точку абсцисс перекладины параболита и прямой. Для кого мы видим
систему в способе поринга:
Площадь фигуры известна как разность площадей криволинейных трапеций,
окружен параболой и прямой линией.
5) Видповид.
Алгоритм решения задач на вычисление площади фигуры, окруженной заданными линиями:
Оставаться в одной координатной плоскости заданной линии.
Заштрихуйте фигуру, окруженную этими линиями.
Определить интеринтеграцию (узнать точку абсцисс линии кривых).
Рассчитайте площадь фигуры, составив необходимую формулу.
Написать записку
2) Виконаите взять задание по одному из вариантов:
Менеджер.
Вычислить площади фигур, окруженных линиями (корректировать алгоритм решения задач на вычисление площадей фигур):
Усна робот 1. Проверить с помощью интеграла площади фигур, изображенных на рисунках:
2. Вычислить интегралы:
Найдите площадь фигуры:
5) 1/3; log2 ;√2
Троки истории
«Интеграл» придумав Яков Бернулли (1690р.)
«изобретать» от латинского интегро
«цилий» как латинское целое число
«Примитивная функция»,
9 0002 Латинскийпримитивный — Коб,
Жозеф Луи Лагранж
Интеграл давно
Первый известный способ розрахунку итеграів є Евдоксов наместный метод ( примерно 370 к св. е.), пытавшийся узнать площадь той обсяги, розрываючи їх на несшитых обезличенных частях , мы покрываем площадь чи обсяг вже відомы.
Цей метод був пидопления та розвинены Архимеда , и выкористовувався за параболическую площадь розраговки и площадку кола, примыкающую к розгонке.
Евдокс Книдский
Исаак Ньютон (1643-1727)
Самый последний вывод дифференциального и интегрального расчета в
Переменные величины — свободно
Изменение скорости свободно — поток (дополнительно)
Лейбниц Готфрид Вильгельм (1646-1716)
9 0028Символ скрытия от букв
S — короткое слово
сумма (Сума)
Формулы расчета площади фигур, заштрихованных на младших
Алгоритм расчета площади плоской фигуры :
- За головой ума добавьте схематическое кресло.
- Покажите нужную вам функцию, например сумму или разность криволинейных площадей трапеции, выберите правильную формулу.
- Знать между интеграцией (и тем, что б) помыть завдання или стул, потому что вони не дано.
- Рассчитать площадь кожной криволинейной трапеции и площадь фигуры шукано.
ЗАДАНИЕ
Перед школьной кабиной соорудили клумбу. Эль, форма клумбы может быть круглой, квадратной или прямоугольной. Она виновна в мести своим прямым и кривым линиям. Пусть она будет плоской фигурой, обведенной линиями
Y = 4/X + 2; Х=4; Y = 6.
Рассчитаем площадь снятой фигуры по формуле:
de f(x)=6 , a г(х)=4/х +2
Итак, так как за квадратный метр кожи платят 50 рублей, то доход составит:
6,4 * 50 \u003 д 320 (руб. ).
Домашние задания:
1125 Вычисление площадей плоских фигур с помощью интеграла Рыбина, Н.В. Федотова 0 Минобрнауки РФ СПО Укладычи С.Л. Рыбина, Н.В. Федотова Воронеж 2015 1 Вычисление площади плоских фигур для дополнительного интеграла: Методические введения к самостоятельной работе по математике для студентов 1 курса СПО/Воронежка ДАГУ; сост.
: С.Л. Рыбина, Н.В. Федотов. – Воронеж, 2015. – с. Даны теоретические сведения о том, как вычислить площади плоских фигур для дополнительного интеграла, приведены приложения задач, даны задания для самостоятельной работы. Возможен выигрыш за подготовку индивидуальных проектов. Предназначен для студентов 1 курса факультета среднего профессионального образования. Ил. 18. Библиография: 5 наименований. УДК 51:373(07) ББК 22.1й721 Стремиться к решениям на исходно-методической основе ради Воронежского ДАСУ Рецензент – Глазкова Мария Юрьевна, к.т.н. физ.-мат. наук, доцент, Вкладч кафедры высшей математики Воронежского ДАГУ В пункте 1 выполнены теоретические расчеты для вычисления площади плоских фигур для дополнительного интеграла, в пункте 2 дано приложение задач, а в пункте 3 предлагаются задания для самостоятельной работы. Основной позицией самостоятельной работы студентов является такая же роботизация, так как они одерживают победу над главой произведения, без какого-либо опосредованного участия (але под керівнитством) в специальных представлениях на этот час.
Цели и задачи самостоятельной работы: систематизация и закрепление знаний и практических знаний и умений студентов; разрушение этого расширения теоретических и практических знаний; формирование ума к подборке специальной, справочной литературы, Интернета; развитие учебных достижений и активности обучающихся, творческой инициативы, самостоятельности, жизнеспособности и организованности; формирование самостоятельности мышления, стремления к саморазвитию, саморазвитию и самореализации; развитие новейших знаний. базовые знания для профессиональной подготовки аспиранта соответствуют требованиям ФГОС; формирование и развитие глобальных компетенций, закрепленных в ФГОС среднего профессионального образования; подготовка к формированию и развитию профессиональных компетенций, что способствует систематизации основных видов профессиональной деятельности, закреплению, разрушению и расширению теоретических знаний и практических знаний обучающихся; развитие учебных достижений и активности студентов: творческой инициативы, самостоятельности, жизнеспособности и организованности; формирование самостоятельности мышления: построение на саморазвитие, саморазвитие и самореализацию; володиння практический новичок застосування информационно-коммуникационных технологий в профессии ияльности; развитие последних смертей.
Критериями оценки результатов самостоятельной работы студента на уроке являются усвоение студентом основного материала; 3 умных студента, чтобы выиграть теоретические знания в конце дня; обґрунтованість и читкість відповіді відповіді; оформление материала понятно требованиям ФГОС. 4 1. Расчет площади плоских изделий с помощью интегрального 1. Доводочный материал. 1.1. Криволинейной трапецией называется фигура, окруженная графиком непрерывной и неотрицательной функции y=f(x), снизу от оси Ox, а по бокам прямыми линиями x=a, x=b ( Рис. 1) 1 Площадь криволинейной трапеции можно вычислить с помощью дополнительного интеграла: b S f x dx F x b a F b (1) F a a 1.2. Пусть функция y=f(x) непрерывна с другой стороны и принимает положительные значения с другой стороны (рис. 2). Затем необходимо разбить валки на части, затем вычислить по формуле (1) общую площадь до этих частей, а площадь сложить. S = S1 + S2 c S b f x d x f x d x a (2) c 2 1.3. Для этого, если функция f (x) непрерывна g(x) на всем интервале (a; b).
Для какого направления площади цифры рассчитываются по формуле y b S = (f (x) g (x)) dx y = f (x) (4) a 1 -1 O -1 b 1 y = g (х) х Рис. 4 1.5. Задание на расчет площади плоских изделий можно выполнить по такому плану: 1) для задания на ум — эскизное кресло; 2) представить фигуру шукана в виде суммы или разности площадей криволинейных трапеций. Завдання, что кресло обозначают взаимосвязью для обшивки склада криволинейной трапеции; 3) записать скин-функцию как f x ; 4) рассчитать площадь кожной криволинейной трапеции и фигуры шукано. 6 2. Применить разбивку задач 1. Вычислить площадь криволинейной трапеции, окруженной линиями у = х + 3, у = 0, х = 1 и х = 3. . САБСД = В_дпов_д: 10. 2. Фигура, окруженная линиями у = -2х + 8, х = -1, у = 0, разделена линией у = х2 — 4х + 5 на две части. Знать площадь участка кожи. Решение: Давайте посмотрим на функцию y = x2 — 4x +5. у = х2 — 4х + 5 = (х2 — 4х + 4) — 4 + 5 = (х — 2) 2 + 1, т.е. график функции представляет собой параболу с вершиной K(2; 1). САБК = .
7 САБКМЭ = С1 = САБКМЭ + СЭМК, С1 = С2 = САБК — С1, С2 = Видповид: i = . . 3. Задания для самостоятельной работы Обычный тест 1. Какую фигуру называют криволинейной трапецией? 2. Как узнать площадь криволинейной трапеции? 4. Найдите площадь заштрихованной фигуры: 8 5. Назовите формулу вычисления площади изображения фигур: Письменный тест 1. На какой фигурке изображена фигура, а не криволинейная трапеция? 2. Для дополнительных формул Ньютона-Лейбница вычислите: A. Первичную функцию; Б. Площадь криволинейной трапеции; Б. Интеграл; Г. Отпусти. 3. Знайте площадь заштрихованной фигуры: 9А. 0; БИ 2; В 1; Д. 2. 4. Найдите площадь фигуры с бахромчатым небом О и параболой у = 9 — х2 А. 18; Б. 36; ст. 72; Д. Не подсчитывается. 5. Найдите площадь фигуры, окруженной графиком функции у = sin х, прямыми х = 0, х = 2 и всеми абсциссами. А. 0; Пчела. 2; В 4; Д. Не подсчитывается. Вариант 1 Вычислите площадь фигуры, окруженной линиями: а) у х2, б) у х2 в) у cos х, г) у 1, х3 у 0, х у 0; х, у 0, 0, 4; х х 1, х 0, х 6; 2.
10 Вариант 2 Вычислите площадь фигуры, окруженной линиями: б) у 1 2 х, у 2 х2 2 х, в) у sin х, г) у 1, х2 а) у 0, х у 0 ; 0, х 0, х 3; 3 2; х 1. Вариант 3 Вычислите площадь фигуры, окруженной линиями: а) у = 2 — х3, у = 1, х = -1, х = 1; б) у = 5 — х2, у = 2х2 + 1, х = 0, х = 1; в) у = 2sin х, х = 0, х = р, у = 0; г) у = 2х — 2, у = 0, х = 3, х = 4. Вариант 4 Вычислите площадь фигуры, окруженной линиями: а) у = х2 + 1, у = 0 , х = — 1, х = 2; б) у = 4 — х2 i у = х + 2; в) у = х2 + 2, у = 0, х = — 1, х = 2; г) у = 4 — х2 i у = 2 — х. Вариант 5 Вычислите площадь фигуры, окруженной линиями: а) 7 х, х=3, х=5, у=0; б) у в) у г) у 8, х = — 8, х = — 4, у = 0; х 0,5 х 2 4 х 10, у х 2; х 2, у х 6, х = -6 и оси координат. 11 Вариант 6 Вычислите площадь фигуры, обведенной линиями а) у 4 х 2, у=0; б) у cos х, х, х в) у х 2 8 х 18, у г) у х, у 2, у = 0; 2х 18; 1 х = 4. х Вариант 7 Вычислить площадь фигуры, окруженной линиями а) у х 2 6 х, х = -1, х = 3, у = 0; б) у=-3х, х=1, х=2, у=0; в) у х 2 10 х 16, у = х + 2; г) у 3 х, у = -х + 4 и оси координат.
Вариант 8 Вычислите площадь фигуры, окруженной линиями а) y sin x, x 3, x, y = 0; б) у х 2 4 , х=-1, х=2, у=0; в) у х 2 2 х 3, у 3 х 1; г) у х 2, у х 4 2, у = 0, Вариант 1 1. Вычислить площадь фигуры, окруженной линиями: а) у = х2, х = 1, х = 3, у = 0; б) у = 2cos х, у = 0, х = — Вт ш, х =; 2 2 в) у = 2х2, у = 2х. 2. (дополнительно) Найти площадь фигуры, окруженной графиком функции у = х2 — 2х + 3, так, чтобы график был проведен в його точке с абсциссой 2 и прямой х = -1. 12 Вариант 2 1. Вычислите площадь фигуры, окруженной линиями: а) у = х3, х = 1, х = 3, у = 0; б) у = 2cos х, у = 0, х = 0, х = W; 2 в) у = 0,5 х2, у = х. 2. (дополнительно) Найти площадь фигуры, окруженной графиком функции у = 3 + 2х — х2, так, чтобы график располагался в точке у-о с абсциссой 3 и прямой х = 0. Вариант 3 1. Вычислить площадь фигуры, обведенной линиями: а) у = х, х=1, х=2, у=0; б) y = 2cos x, y = 0, x = W 3W , x = ; 2 2 в) у = х2, у = -х2 + 2. 2. (дополнительно) Найти площадь фигуры, окруженной графиком функции у = 2х — х2, так что график построен в точке y-o-t от оси абсцисс 2 и оси y.
Вариант 4 1. Вычислить площадь фигуры, окруженной линиями: а) у = 0,5 х, х = 1, х = 2, у = 0; б) y = 2cos x, y = 0, x = W W , x = ; 4 2 в) у = 9- х2, у = 2х + 6. 2. (дополнительно) Найти площадь фигуры, окруженной графиком функции у = х2 + 2х, так, чтобы график был проведен в у-о -точка от оси абсцисс -2 и оси у. Задания для работы в парах: 1. Вычислить площадь заштрихованной фигуры 2. Вычислить площадь заштрихованной фигуры 13 3. Вычислить площадь заштрихованной фигуры 14 5. Вычислить площадь заштрихованной фигуры 14 заштрихованная фигура 6. Представьте площадь в виде трапеций кругов. 7. Покажите площадь заштрихованной фигуры как сумму разности хи площадей криволинейных трапеций, окруженных графиками, которые показывают вам линии. 15 Библиографический список 1. Шарыгин И. Ф. Математика: алгебра и основы математического анализа, геометрия. Геометрия. Базовый уровень. 10 — 11 класс: тьютор / И.Ф. Шарыгин. — 2-й вид., стерт. – Москва: Дрофа, 2015. – 238 с. 2. Муравин Г.К. Математика: алгебра и основы математического анализа, геометрия.
Базовый уровень. 11 класс: ассистент / Г. К. Муравин, О. В. Муравина — 2-й вид, стер. – Москва: Дрофа, 2015. – 189 с.п. 3. Муравин Г.К. Математика: алгебра и основы математического анализа, геометрия. Базовый уровень. 10 класс: ассистент / Г. К. Муравин, Муравина О. В. — 2-й вид., стерт. — Москва: Дрофа, 2013. — 285 с. 4. Преподавание геометрии в 10-11 классах: Метод. рекомендации к навч.: Кн. для учителя / С. М. Саакян, В. Ф. Бутузов. — 2-й вид. — М.: Просвитництво, 2014. — 222 с.: ил. 5. Изучение алгебры и начало анализа в 10-11 классах: Учеб. для учителя / Н.Я. Федорова, М. В. Ткачева. — 2-й вид. — М.: Просвитництво, 2014. — 205 с.: ил. 6. Алгебра и анализ в початке. 10-11 кл.: На две части. Часть 1: Учебник для глобального образования. установка / Мордкович А.Г. — 5 род. – М.: Мнемозина, 2014. – 375 с.: ил. Интернет-ресурсы: 1. http://www.exponenta.ru/educat/links/l_educ.asp#0 – корисн_ сообщение на сайте математической и светотехнической направленности: Исходные материалы, тесты 2.
http://www.fxyz. ru/ — Интерактивный справочник по формулам и сведениям из алгебры, тригонометрии, геометрии, физики. 3. http://maths.yfa1.ru — Справочник по извлечению материала из математики (арифметика, алгебра, геометрия, тригонометрия). 4. allmatematika.ru — Основные формулы алгебры и геометрии: те же преобразования, прогрессии, изменения, стереометрии и другие. 5. http://mathsun.ru/ — История математики. Биографии великих математиков. 16 бесплатных интро. …………………………………………. . ………………………………………… .. …………………………… 3 Вычисление площадей плоских фигур с помощью интеграла…. …………………………………………….. .. 5 1. Заключительный материал …………………………………. ………………………………………………….. …………. 5 2. Применить развязку задач …………………. …………….. .. …………………………. …………….. .. .. .. 7 3.