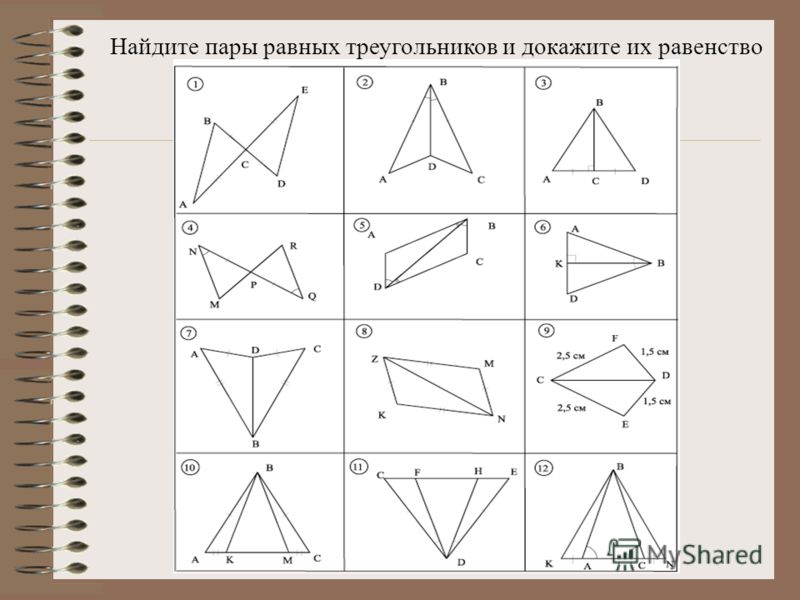
Задачи на готовых чертежах. Признаки равенства треугольников
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Геометрия 7 класс
Признаки равенства треугольников
Задача 1
В
С
О
А
Д
Доказать: Δ ВОС=Δ АОД
Задача 1
В
С
А
Д
Доказать: Δ АВС=Δ АДС
Задача 3
1
А
В
С
Д
2
Доказать: Δ АВД=Δ ВСД
Задача 2
В
А
С
Д
Доказать:
Д= В
Задача 3
C
В
D
А
Доказать: АВ=ВС
А
С
2
1
В
О
Д
Доказать: АО=СО
Задача 5
В
1
А
Д
2
С
Доказать: АВ=ВС
В
А
Д
Задача 6
С
Доказать: Δ ДВС=Δ ДАС
Задача 7
В
А
О
C
Д
Доказать:
А= В
Задача 8
Д
С
А
К
В
Найти: равные треугольники
Задача 9
В
С
О
А
Д
Доказать:
Д= В
В
О
А
Задача 9
С
Доказать: АО=СО
Задача 3
В
А
С
Д
Доказать: АВ=СД
Задача 4
В
С
А
Д
К
Р
Доказать:
Р= В
Задача 5
А
Д
В
С
К
Найти: равные треугольники
Задача 6
В
Д
А
С
Доказать: АВ=СД
С
В
Задача 7
О
А
1
2
Д
Доказать:
С= В
С
Задача 8
В
Д
А
H
K
Найти равные треугольники
Задача 9
В
Р
К
А
О
С
Доказать: АК=СР
Задача 10
В
Д
О
А
С
Найти: равные треугольники
Задача 11
В
Д
С
О
А
Найти: равные треугольники
Задача 12
С
В
А
Д
Доказать:
Д= В
Задача 13
В
А
Д
С
Доказать: Δ АВД=Δ ВСД
Задача 14
Р
Д
В
S
К
А
Доказать:
Р= К
Задача 15
В
К
А
Н
С
Доказать: АН=НС
Задача 16
В
А
Н
C
Д
Доказать: ВН=НД
В
А
Д
Задача 17
С
АД=СВ
Доказать:
А= В
Задача 18
В
С
Р
А
К
Д
Найти: равные треугольники
Задача 19
В
А
О
Найти:
С
АОВ
Задача 20
В
С
А
Р
К
Д
Найди: равные треугольники
Задача 21
В
А
С
О
Д
Найти: все пары
равных треугольников
1.
 Ершова А.П., Голобородько В.В, Ершова А.С
Ершова А.П., Голобородько В.В, Ершова А.ССамостоятельные и контрольные работы по алгебре
и геометриидля 7 класса.-М:Илекса, 2004.-176с.
Упражнения по планиметрии на готовых чертежах.М.: просвещение, 1987.-112 с.: ил.
3. Зив Б.Г. и др.
Задачи по геометрии: Пособие для учащихся 7-11 кл.
общеобразоват.учреждений.-М.:Просвещение, 2000.-271 с.: ил.
4. Рабинович Е.М.
Сборник задач на готовых чертежах.-К.:1996.-56с.
5. Гаврилова Н.Ф.
Поурочные разработки по геометрии: 7 класс.-2-е изд.,
перераб. и доп.-М.: ВАКО,2009.-304 с.
English Русский Правила
Задания на определение признаков равенства треугольников по готовым чертежам | Тест по геометрии (7 класс):
Опубликовано 22.11.2020 — 5:41 — Пономаренко Екатерина Ивановна
Тестирование
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
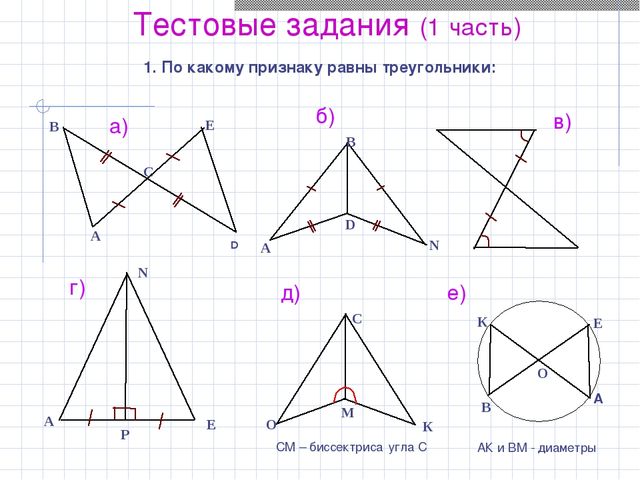
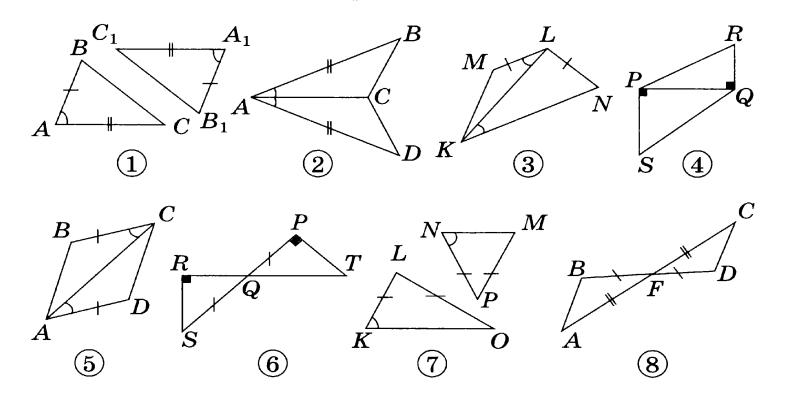
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 2
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 3
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 4
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 5
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 6
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 7
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
Слайд 8
По какому признаку равны треугольники? а) первый b) второй c) третий d) треугольники не равны
По теме: методические разработки, презентации и конспекты
Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Признаки равенства треугольников
Задания по теме «Признаки равенства прямоугольников» предназначены, прежде всего, для обучения школьников решению задач по только что изученному материалу, а также при повторении курса геометрии 7 кл. ..
..
Задачи в готовых чертежах по теме:»Признаки равенства треугольников»
Презентация , которую можно использовать на уроках геометрии в 7 классе по теме: «Признаки равенства треугольников»…
Использование заданий по готовым чертежам для детей с ограниченными возможностями здоровья при изучении темы «Признаки равенства треугольника»
Использование упражнений по готовым чертежам способствует формированию у школьников с ОВЗ полноценных образов геометрических объектов, так как ученики видят различное простр…
Технологическая карта урока по теме «Равенство треугольников. Первый признак равенства треугольников». 7 класс
Технологическая карта урока по теме «Равенство треугольников. Первый признак равенства треугольников». Геометрия 7 класс. Тип урока: урок освоения новых знаний. УМК: Геометрия 7, авторы В.Ф.Буту…
7 класс. Домашнее задание к теме: «Признаки равенства треугольников_1».
7 класс. Домашнее задание к теме: «Признаки равенства треугольников_1».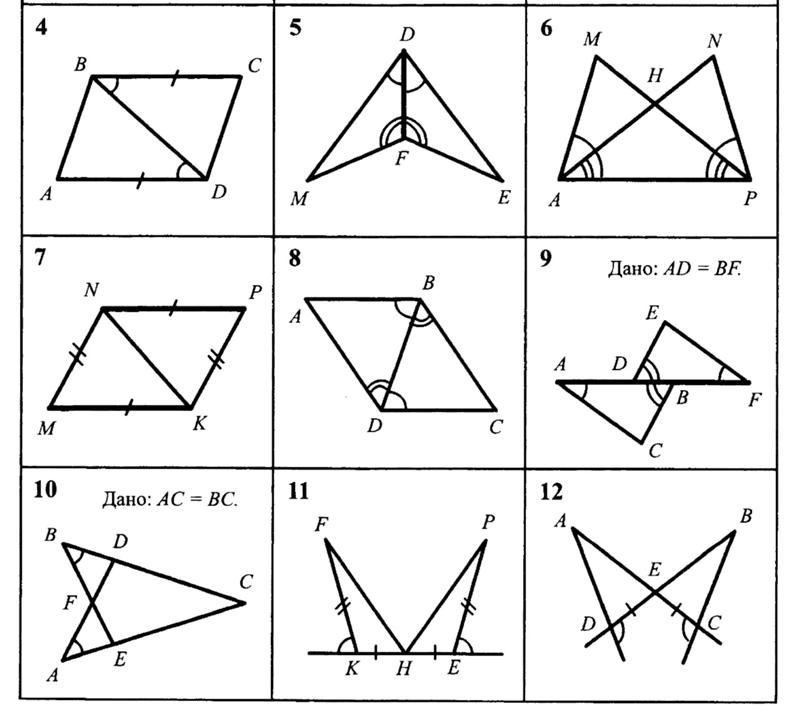 Геометрия. Задачи на готовых чертежах, 7-9 классы…
Геометрия. Задачи на готовых чертежах, 7-9 классы…
7 класс. Домашнее задание к теме: «Признаки равенства треугольников_2».
7 класс. Домашнее задание к теме: «Признаки равенства треугольников_2». Геометрия. Задачи на готовых чертежах, 7-9 классы…
Первый признак равенства треугольников. Решение задач по готовым чертежам.
Презентация. Первый признак равенства треугольников. 7 класс.Решение задач по готовым чертежам….
Поделиться:
Треугольники и четырехугольники – Математика для учителей начальных классов
Геометрия
Подумай / Соедини / Поделись
Самостоятельно следуйте этим указаниям:
- Нарисуйте любой треугольник на бумаге.
- Нарисуйте второй треугольник, который чем-то отличается от первого. Запишите предложение или два, чтобы сказать, как это отличается.
- Нарисуйте третий треугольник, отличный от двух других.
 Опишите, чем он отличается.
Опишите, чем он отличается. - Нарисуйте еще два треугольника, отличных от всех предыдущих.
Сравните свои треугольники и описания с партнером. Чтобы сделать «другие» треугольники, вам нужно изменить некоторые свойства треугольника. Составьте список функций, которые вы или ваш партнер изменили.
Треугольники классифицируются по разным свойствам. Цель изучения геометрии не в том, чтобы выучить много словарного запаса, а в том, чтобы использовать правильные термины для объектов, чтобы мы могли ясно общаться. Вот краткий словарь некоторых типов треугольников.
Классификация по сторонам
| разносторонний | равнобедренный | равносторонний |
|---|---|---|
| все стороны имеют разную длину | две стороны имеют одинаковую длину | все три стороны имеют одинаковую длину |
Классификация по углам
| острый | тупой |
|---|---|
| все внутренние углы меньше 90° | один внутренний угол больше 90° ° |
| справа | равноугольный |
| один внутренний угол равен 90 ° | все внутренние углы имеют одинаковую меру |
Помните, что «геометрия — это искусство делать хорошие выводы из плохих рисунков».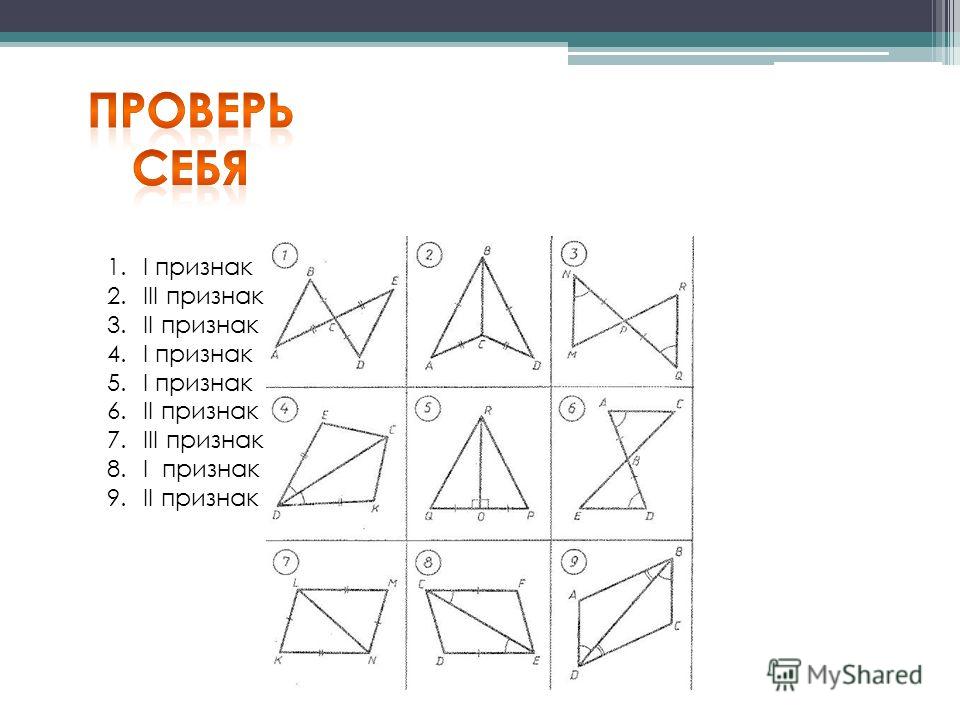
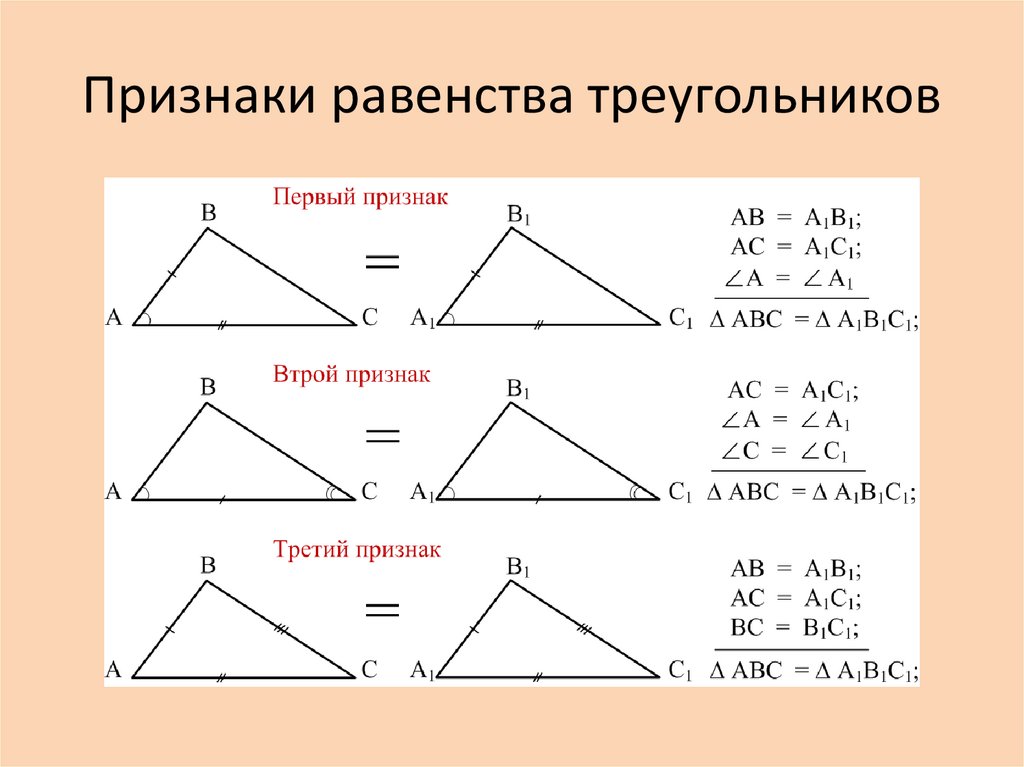
Обозначение: засечки
Математики либо записывают измерения, либо используют засечки, чтобы указать, когда стороны и углы должны быть равны.
Если две стороны имеют одинаковый размер или одинаковое количество делений, вы должны поверить, что они равны, и решить задачу соответствующим образом, даже если это не выглядит так на ваш взгляд .
Примеры можно увидеть на некоторых рисунках выше. Другим примером является маленький квадрат, используемый для обозначения прямого угла на изображении прямоугольного треугольника.
СамостоятельноВыполните следующие упражнения самостоятельно или с партнером.
1. Какие стороны на рисунке ниже понимаются как имеющие одинаковую длину (даже если на рисунке это не выглядит так)?
2. Какие углы на рисунке ниже понимаются как имеющие одинаковую меру (даже если на рисунке это не выглядит так)?
Какие углы на рисунке ниже понимаются как имеющие одинаковую меру (даже если на рисунке это не выглядит так)?
3. Вот разносторонний треугольник. Нарисуйте еще два разносторонних треугольника, каждый из которых чем-то отличается от показанного здесь.
4. Вот остроугольный треугольник. Нарисуйте еще два остроугольных треугольника, каждый из которых чем-то отличается от показанного здесь.
5. Вот тупоугольный треугольник. Нарисуйте еще два тупоугольных треугольника, каждый из которых чем-то отличается от показанного здесь.
6. Вот прямоугольный треугольник. Нарисуйте еще два прямоугольных треугольника, каждый из которых чем-то отличается от показанного здесь. Обязательно укажите, какой угол равен 90°.
7. Вот равнобедренный треугольник. Нарисуйте еще два равнобедренных треугольника, каждый из которых чем-то отличается от показанного здесь. Используйте галочки, чтобы указать, какие стороны равны.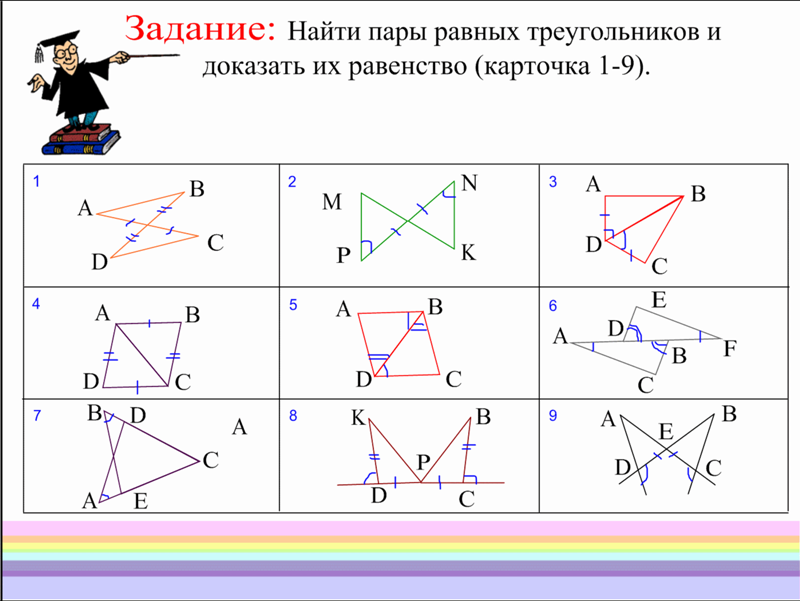
Подумай / Соедини / Поделись
К настоящему времени вы нарисовали на бумаге несколько разных треугольников. Выберите один из треугольников и следуйте этим указаниям:
- Используя ножницы, вырежьте треугольник.
- Оторвите (не срезайте) углы и соедините три вершины вместе. У вас должно получиться что-то похожее на эту картинку:
Что вы заметили? Что это говорит об углах треугольника?
Возможно, вы помните, что сумма углов любого треугольника равна 180°. В вашем классе теперь есть много примеров треугольников, в которых сумма углов равна 180°. Но помните, наши рисунки не точны. Как мы можем быть уверены, что наши глаза нас не обманывают? Как мы можем быть уверены, что сумма углов в треугольнике не равна 181° или 178°, а действительно равна 180° на носу в каждом случае?
Подумай / Соедини / Поделись
Что убедит вас вне всяких сомнений в том, что сумма углов любого треугольника равна 180°? Будет ли достаточно тестирования множества случаев? Сколько достаточно? Сможете ли вы когда-нибудь протестировать каждый возможный треугольник?
Часто школьные учителя геометрии доказывают, что сумма углов треугольника равна 180°, обычно используя некоторые факты о параллельных прямых. Но (может быть, это удивительно?) столь же хорошо принять это как аксиому , как данный факт о том, как работает геометрия, и двигаться дальше. Возможно, это менее удовлетворительно, чем доказательство из какого-либо другого утверждения, и если вам интересно, вы наверняка найдете доказательство или ваш инструктор может поделиться им с вами.
Но (может быть, это удивительно?) столь же хорошо принять это как аксиому , как данный факт о том, как работает геометрия, и двигаться дальше. Возможно, это менее удовлетворительно, чем доказательство из какого-либо другого утверждения, и если вам интересно, вы наверняка найдете доказательство или ваш инструктор может поделиться им с вами.
Около 300 г. до н.э., Евклид [1] был первым математиком (насколько нам известно), который попытался тщательно записать аксиомы, а затем построить из этих аксиом строгие доказательства математических истин.
ЕвклидУ Евклида было пять аксиом геометрии, первые четыре из которых казались математикам довольно очевидными. Люди считали, что это разумные предположения, из которых можно построить геометрические истины:
1. Имея две точки, вы можете соединить их отрезком прямой линии.
2. Получив отрезок, вы можете продлить его как угодно далеко в любом направлении, образуя линию.
3. Имея отрезок прямой, вы можете нарисовать окружность, используя этот отрезок в качестве радиуса.
4. Все прямые углы равны.
Немного больше беспокоил людей пятый постулат. Первоначально это было сказано более цветистым языком, но это было эквивалентно этому утверждению:
5. Сумма углов треугольника равна 180°.
Легко понять, почему эта пятая аксиома вызвала такой шум в математике. Это казалось гораздо менее очевидным, чем остальные четыре, и математики чувствовали, что они каким-то образом обманывают, если они просто предполагают это, а не доказывают, что это должно быть правдой. Многие математики потратили много-много лет, пытаясь доказать эту пятую аксиому из других аксиом, но им это не удалось. И не без оснований: есть и другие виды геометрий, в которых первые четыре аксиомы верны, а пятая — нет!
Например, если вы выполняете геометрию на сфере — например, на баскетбольном мяче или, что более важно, на поверхности Земли — а не на плоской плоскости, первые четыре аксиомы верны. Но треугольники немного странные на поверхности земли. Каждый треугольник, который вы можете нарисовать на поверхности земли, имеет сумму углов строго на больше, чем 180°. На самом деле, вы можете нарисовать на Земле треугольник с тремя прямыми углами [2] , что дает сумму углов 270°.
На самом деле, вы можете нарисовать на Земле треугольник с тремя прямыми углами [2] , что дает сумму углов 270°.
На сфере, подобной Земле, сумма углов не постоянна среди всех треугольников. У больших треугольников сумма углов больше, а у меньших треугольников сумма углов меньше, но даже у крошечных треугольников сумма углов больше 180°.
Геометрия, которую вы изучаете в школе, называется Евклидова геометрия ; это геометрия плоской плоскости, плоского мира. Это довольно хорошее приближение для маленького кусочка Земли, который мы видим в любой момент времени, но это не единственная существующая геометрия!
Сделайте копию этих полосок бумаги и вырежьте их. Они имеют длину от 1 единицы до 6 единиц. Вы можете раскрасить полоски, написать на них цифры или сделать что-то, что позволит легко отслеживать разную длину.
Проблема 3
Повторите следующий процесс несколько раз (не менее 10) и отслеживайте результаты (для вас была запущена таблица).
- Возьмите три полоски бумаги. (Длины не обязательно должны отличаться друг от друга, поэтому у вас есть несколько копий каждой длины.)
- Попробуйте сделать из этих трех полос треугольник и решите, возможно ли это, или нет. (Не накладывайте полоски друг на друга, не обрезайте и не сгибайте их. Длина полосок должна быть равна длине сторон треугольника.)
| Длина 1 | Длина 2 | Длина 3 | Треугольник? |
|---|---|---|---|
| 4 | 3 | 2 | да |
| 4 | 2 | 1 | нет |
| 4 | 2 | 2 | ?? |
Ваша цель — составить правило , описывающее, когда три длины образуют треугольник , а когда нет. Запишите правило своими словами.
Подумай / Соедини / Поделись
Сравните свое правило с другими учащимися. Затем используйте свое правило, чтобы ответить на следующие вопросы.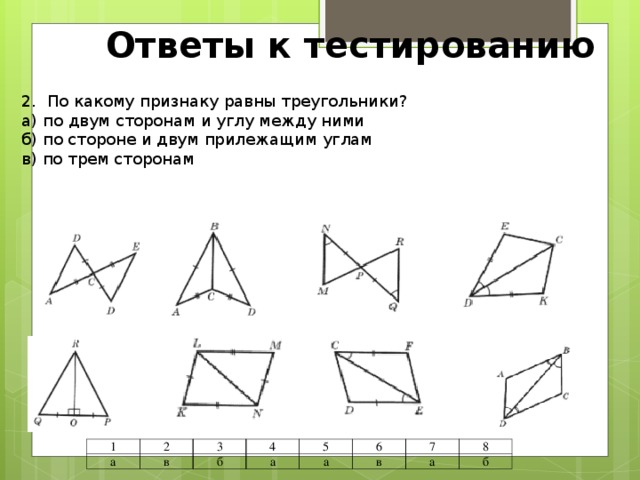 Имейте в виду, что цель состоит не в том, чтобы попытаться построить треугольник, а в том, чтобы предсказать результат на основе вашего правила.
Имейте в виду, что цель состоит не в том, чтобы попытаться построить треугольник, а в том, чтобы предсказать результат на основе вашего правила.
- Предположим, вас попросили построить треугольник со сторонами 40 единиц, 40 единиц и 100 единиц длины. Как вы думаете, вы могли бы это сделать? Поясните свой ответ.
- Предположим, вас попросили построить треугольник со сторонами 2,5 единицы, 2,6 единицы и длиной 5 единиц. Как вы думаете, вы могли бы это сделать? Поясните свой ответ.
Вероятно, вы придумали какую-то версию этого утверждения:
Теорема: неравенство треугольника
Сумма длин двух сторон треугольника больше длины третьей стороны.
Конечно, мы знаем, что в геометрии нельзя верить своим глазам. Вам нужно искать объяснение . Почему ваше утверждение имеет смысл?
Помните, что «геометрия — это искусство делать хорошие выводы из плохих рисунков». Наши материалы были не очень точными, так как же мы можем быть уверены, что это правило, которое мы придумали, верно?
Что ж, в этом случае правило точно такое же, как и поговорка «Кратчайшее расстояние между двумя точками — прямая».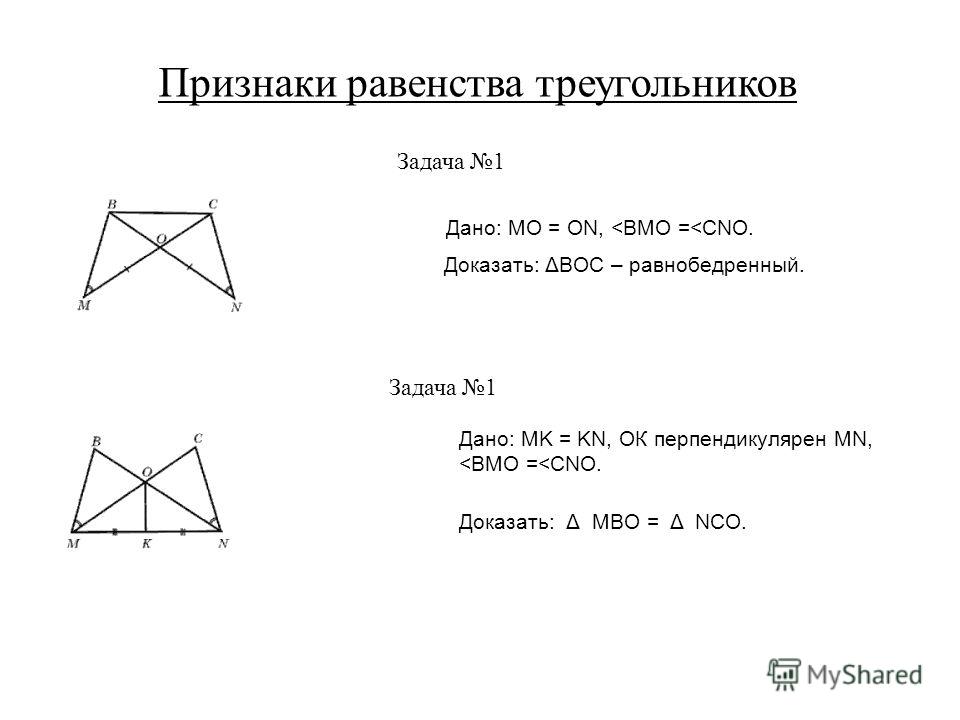 Собственно, это именно то, что мы подразумеваем под словами прямая в геометрии.
Собственно, это именно то, что мы подразумеваем под словами прямая в геометрии.
Мы говорим, что два треугольника (или любые два геометрических объекта) конгруэнтны , если они имеют одинаковую форму и одинаковый размер. Это означает, что если бы вы могли взять одну из них и переместить ее, чтобы положить на другую, они точно перекрылись бы.
Проблема 4
Повторите следующий процесс несколько раз и отслеживайте результаты.
- Выберите три полоски бумаги, которые обязательно образуют треугольник.
- Попробуйте сделать два различных (неконгруэнтных) треугольников из одинаковых трех полосок бумаги. Запишите, смогли ли вы это сделать.
Проблема 5
Повторите следующий процесс несколько раз и отслеживайте результаты.
- Возьмите четыре полоски бумаги и сформируйте из них четырехугольник. (Если ваши четыре полоски не образуют четырехугольник, возьмите еще четыре полоски.
 )
) - Попробуйте составить два различных (неконгруэнтных) четырехугольников из одних и тех же четырех полосок бумаги. Запишите, смогли ли вы это сделать.
Подумай / Соедини / Поделись
Что вы заметили в задачах 4 и 5? Можете ли вы сделать общее заявление, чтобы описать, что происходит? Можете ли вы объяснить, почему ваше утверждение имеет смысл?
Вероятно, вы придумали какую-то версию этого утверждения:
Теорема: SSS (сторона-сторона-сторона) Конгруэнтность
Если два треугольника имеют одинаковые длины сторон, то эти треугольники конгруэнтны.
Это, безусловно, неверно для четырехугольников. Например, если вы выберете четыре полоски одинаковой длины, вы можете сделать квадрат:
Но вы также можете раздавить этот квадрат в неквадратном ромбе. (Попробуйте!)
Если вы не выберете четыре одинаковые длины, помимо «сжатия» формы, вы можете переставить стороны, чтобы получились разные (неконгруэнтные) формы.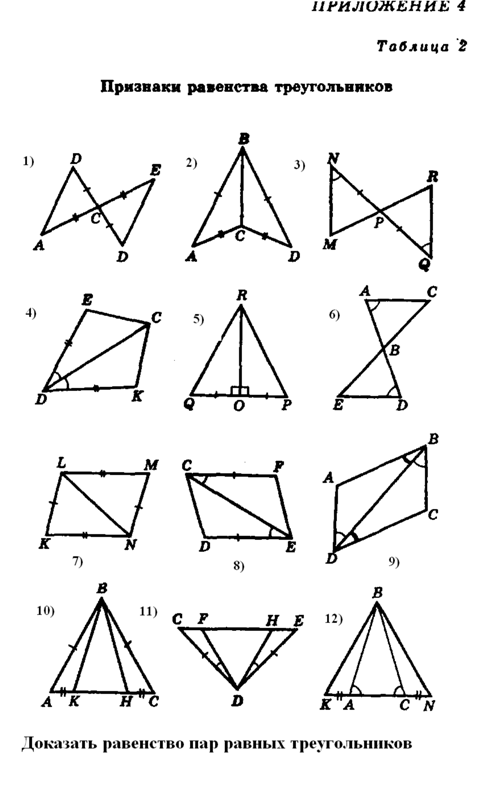 (Попробуйте!)
(Попробуйте!)
| Эти два четырехугольника имеют одинаковые длины четырех сторон в том же порядке. | |
|---|---|
Эти два четырехугольника имеют те же четыре длины сторон, что и два приведенных выше, , но стороны в другом порядке. | |
|---|---|
Но с треугольниками такого не может быть. Почему бы и нет? Ну уж точно три стороны не переставишь. Это было бы то же самое, что вращать треугольник или переворачивать его, но не создавать новую форму.
Почему треугольники не могут «сжиматься», как четырехугольник (и другие фигуры)? Вот один из способов понять это. Представьте, что вы выбираете две из трех длин и кладете их друг на друга, закрепив их в одном углу.
Здесь показан более длинный фиолетовый пунктирный сегмент и более короткий зеленый сегмент. Два сегмента шарнирно соединены с красной точкой слева. |
Теперь представьте, что шарнир открывается понемногу.
Когда петля открывается, две нешарнирные конечные точки отдаляются все дальше и дальше друг от друга. Какова бы ни была ваша третья длина (при условии, что вы действительно можете построить треугольник из ваших трех длин), есть ровно одно положение шарнира, где он будет точно соответствовать треугольнику. Никакая другая позиция не подойдет.
- Портрет Евклида из Викисклада, под лицензией Creative Commons Attribution 4.0 International. ↵
- Изображение предоставлено Coyau / Wikimedia Commons, через Wikimedia Commons, под лицензией Creative Commons Attribution-Share Alike 3.0 Unported. ↵
Какие есть примеры конгруэнтных треугольников в реальной жизни?
Амина Решма
Чтение за 4 мин
Что такое конгруэнтность?
Конгруэнтность относится к двум фигурам или объектам, которые являются точными копиями друг друга. Конгруэнтные фигуры перекрываются точка-точка, когда они сложены одна поверх другой. Даже если фигуры могут находиться в разных плоскостях, они все равно будут конгруэнтными, если их стороны, площади покрытия и объем одинаковы. 1
Значение конгруэнтности
Построение нашего понимания структур требует изучения конгруэнтности в цифрах. Благодаря развитию пространственного интеллекта вы можете иногда обнаружить две структуры, предметы или продукты, полностью идентичные друг другу. Конгруэнтные фигуры — это понятие, которое лучше понимается с одинаковым интеллектом.
Концепция конгруэнтности полезна в области архитектуры, ландшафтного дизайна, моделирования продуктов и производства для бизнеса. Помимо практической пользы, конгруэнтность укрепляет основу учащихся и помогает им сформировать более гибкое понимание понятий площади и объема.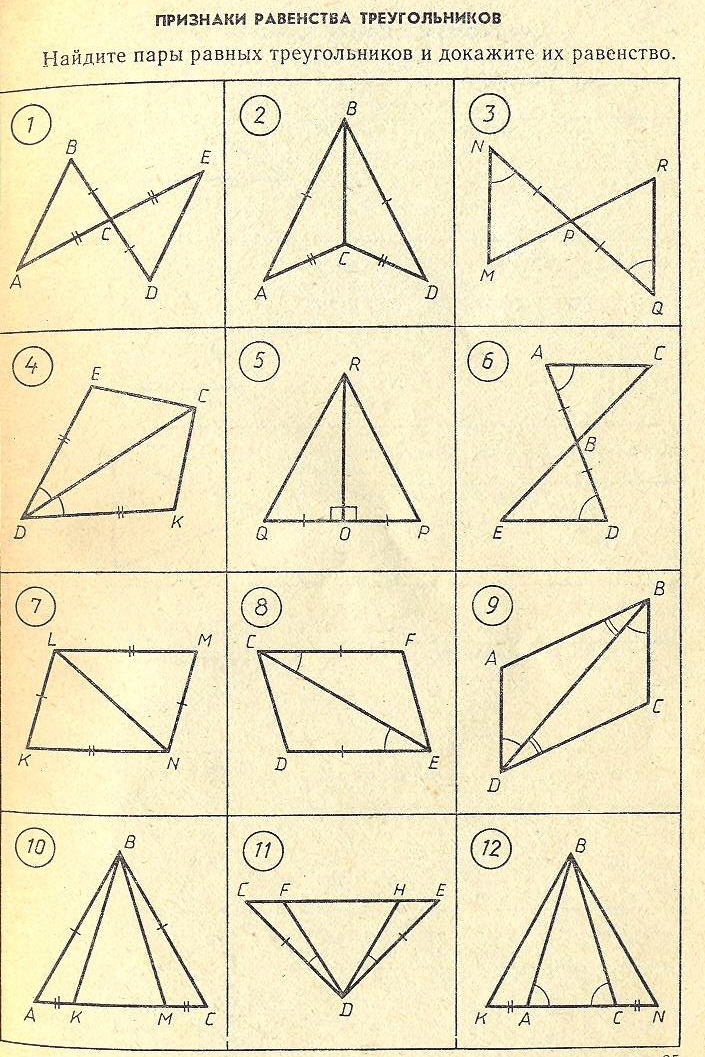 На уроке геометрии мы сравниваем две фигуры и сталкиваемся с конгруэнтностью, точно так же, как мы читаем о равенстве чисел на уроке элементарной математики. 1
На уроке геометрии мы сравниваем две фигуры и сталкиваемся с конгруэнтностью, точно так же, как мы читаем о равенстве чисел на уроке элементарной математики. 1
Что такое треугольник?
Одной из первых фигур, которую мы изучаем, является треугольник. Треугольник — это двумерная фигура с тремя сторонами, тремя углами и тремя вершинами. 2 Треугольники представляют собой трехсторонние замкнутые фигуры, которые можно разделить на различные типы в зависимости от их сторон и углов. Равнобедренные треугольники, равнобедренные треугольники и разносторонние треугольники являются распространенными вариантами.
Итак, что же тогда такое конгруэнтный треугольник?
Конгруэнтные треугольники — это треугольники, у которых три стороны и три угла совпадают с соответствующими сторонами и углами другого треугольника. Другими словами, мы можем сказать, что конгруэнтные треугольники имеют равные соответствующие стороны и углы.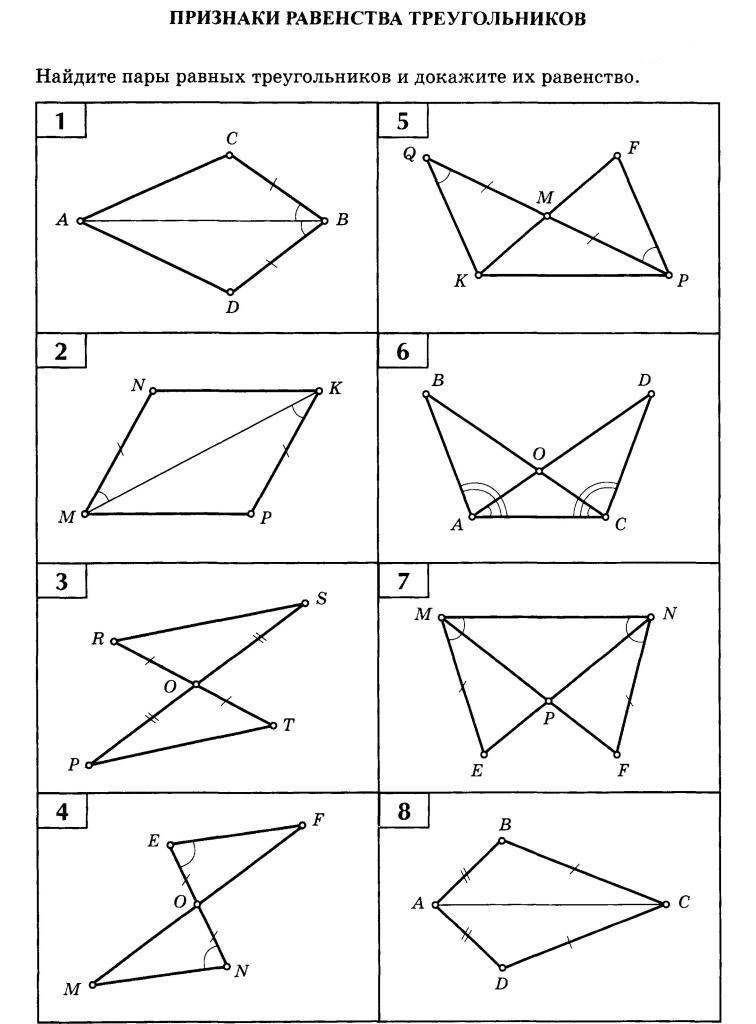 Чтобы треугольники выглядели одинаково, их можно вращать, переворачивать, поворачивать или сдвигать. Треугольники совпадают друг с другом и могут быть наложены друг на друга, если их переставить. 3
Чтобы треугольники выглядели одинаково, их можно вращать, переворачивать, поворачивать или сдвигать. Треугольники совпадают друг с другом и могут быть наложены друг на друга, если их переставить. 3
«Символ конгруэнтности равен ≅. Два треугольника равны, если три стороны и три угла одного треугольника имеют те же размеры, что и три стороны и три угла другого треугольника». 4
Конгруэнтные треугольникиПрименение конгруэнтности треугольников в реальном мире
Инженерное дело и архитектура
Конгруэнтные треугольники используются в процессе строительства для укрепления каркаса. Это гарантирует жесткость и прочность конструкций. В результате на них не влияют сильные ветры или другие погодные условия. Без них невозможно построить большие искусственные сооружения. Учитывая, что треугольник является одной из самых стабильных форм, а конгруэнтность необходима для создания ровных поверхностей, это так. В геометрическом искусстве, рисунках ковров, узорах ступеней и архитектурных проектах также часто используются конгруэнтные треугольники. 3
В геометрическом искусстве, рисунках ковров, узорах ступеней и архитектурных проектах также часто используются конгруэнтные треугольники. 3
Двумя наиболее распространенными примерами могут быть:
- Ферменный мост: Равносторонние треугольники используются для создания ферменных мостов с обеих сторон. Все эти треугольники соответствуют критерию конгруэнтности SSS, который гласит, что если длина трех сторон одного треугольника равна длине трех сторон другого треугольника, то говорят, что два треугольника конгруэнтны. Это связано с тем, что ферменный мост требует одинаковой длины для контроля веса, чтобы поддерживать конструкцию и предотвращать обрушение. 3
- Геодезический купол: это обычное игровое оборудование. Углы и длины сторон должны быть созданы такими, чтобы все задействованные треугольники были конгруэнтны по правилу SAS. Правило SAS гласит, что если две стороны треугольника и угол между ними равны двум сторонам и углу другого треугольника, то эти два треугольника конгруэнтны.
 Если не быть осторожным, одна ошибка с точки зрения угла, длины стороны или конгруэнтности может быть настолько опасной, что может стать фатальной. 3
Если не быть осторожным, одна ошибка с точки зрения угла, длины стороны или конгруэнтности может быть настолько опасной, что может стать фатальной. 3
Легенда
Знаете ли вы, что существует известная легенда, связанная с использованием конгруэнтных треугольников? Легенда гласит, что один из офицеров Наполеона вычислил ширину реки с помощью равных треугольников. Офицер опускал козырек фуражки до тех пор, пока край противоположного берега не стал самой дальней вещью в поле его зрения, когда он стоял прямо на берегу реки. После этого он повернулся и отметил место на своей стороне реки, которое было параллельно его глазу и кончику визора. Затем офицер измерил расстояние до этой точки и объявил, что это ширина реки. Если вы хотите подтвердить, что он был прав, вы можете использовать конгруэнтные треугольники. 5
Конгруэнтность — интригующая идея, которая помогает нам развивать и укреплять наши способности к математическому мышлению.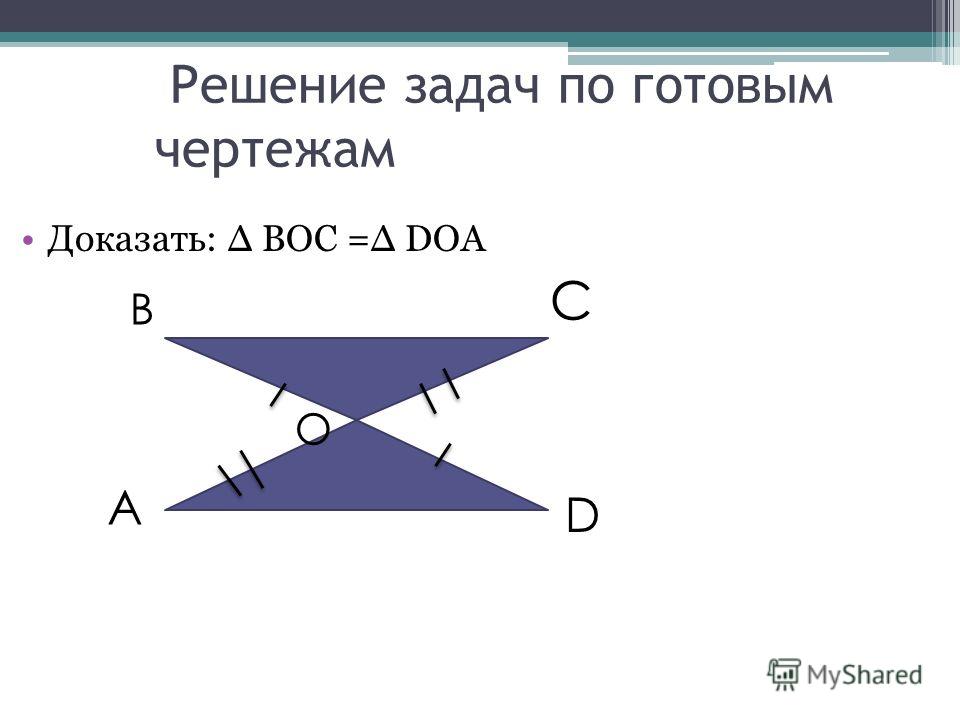 Время от времени он может служить мерилом совершенства и быть важным компонентом обеспечения качества. Путь к пониманию сложных концепций геометрии становится немного легче после достижения этой вехи в изучении формы. 1 После прочтения приведенных выше примеров, если вы чувствуете вдохновение искать конгруэнтность в своем окружении, сделайте это. Вы также можете прочитать о более интересных формах, таких как радиальные формы в природе и симметрия в пространстве. Вы также можете посетить блог BYJU’s FutureSchool, чтобы прочитать больше таких увлекательных статей.
Время от времени он может служить мерилом совершенства и быть важным компонентом обеспечения качества. Путь к пониманию сложных концепций геометрии становится немного легче после достижения этой вехи в изучении формы. 1 После прочтения приведенных выше примеров, если вы чувствуете вдохновение искать конгруэнтность в своем окружении, сделайте это. Вы также можете прочитать о более интересных формах, таких как радиальные формы в природе и симметрия в пространстве. Вы также можете посетить блог BYJU’s FutureSchool, чтобы прочитать больше таких увлекательных статей.
Ссылки:
- 20 реальных примеров конгруэнтных чисел – цифровая дислексия . (н.д.). Получено 5 июля 2022 г. с https://numberdyslexia.com/real-life-examples-of-congruent-figures/
- Конгруэнтные треугольники — объяснение и примеры . (н.д.). Получено 5 июля 2022 г. с https://www.storyofmathematics.com/congruent-triangles/
- 3 лучших применения конгруэнтных треугольников в реальной жизни .


 Опишите, чем он отличается.
Опишите, чем он отличается. )
)
 Если не быть осторожным, одна ошибка с точки зрения угла, длины стороны или конгруэнтности может быть настолько опасной, что может стать фатальной. 3
Если не быть осторожным, одна ошибка с точки зрения угла, длины стороны или конгруэнтности может быть настолько опасной, что может стать фатальной. 3