Задать вектор: с примерами. Просто и понятно!

Для того, чтобы задать вектор, необходимо указать:

1) прямую, на которой лежит вектор или которой он параллелен;

2) направление (ориентацию) вектора на этой прямой;

3) длину вектора.

Один и тот же вектор может быть отложен от любой точки пространства при помощи параллельного переноса, при этом сохраняются все три указанные характеристики этого вектора.

• Вектор называется нулевым, если его начало и конец совпадают:

• Векторы называются коллинеарными, если они лежат на параллельных или совпадающих прямых, обозначают  .

• Векторы называются сонаправленными, если они коллинеарны и одинаково направлены.

• Векторы называются равными, если они сонаправлены и имеют одинаковую длину, обозначают .

Заметим, что от любой точки пространства можно отложить вектор , равный данному, и при этом только один.

5.2. Операции над векторами

Из правила треугольника сложения векторов следует правило их вычитания: действительно, если , то .

• Произведением вектора на число  называется вектор , коллинеарный вектору , длиной , который сонаправлен с вектором , если >0 и противоположно направлен, если <0.

• Любому ненулевому вектору можно поставить в соответствие орт , имеющий единичную длину и направление которого совпадает с направлением вектора .

Свойства:

1)

2)

3)

4)

5)

Теорема 5.1. Векторы коллинеарны тогда и только тогда, когда для некоторого

.

Пример. В треугольнике АВС точки M, N, K – середины сторон АВ, АС, ВС соответственно. Найти векторы , если .

Р ешение: По условию, . Применяя правило вычитания, находим:

, .

Далее, AK — половина диагонали параллелограмма, сторонами которого являются отрезки АВ и АС (так как диагонали параллелограмма точкой пересечения делятся пополам). Следовательно, по правилу параллелограмма сложения векторов, имеем .

5 .3. Координаты векторов

Рассмотрим трехмерное пространство.

• О

  y

  y

  ртонормированным репером в трехмерном пространстве называется совокупность начальной точки О и векторов , таких, что:

1) (единичные векторы),

2) (попарно перпендикулярные),

3) векторы образуют правую тройку векторов, то есть из конца вектора поворот от вектора к вектору виден в положительном направлении – против часовой стрелки.

В таком случае обычная декартова система координат соответствует заданному ортонормированному реперу, так что направления осей Ох, Оу, Oz совпадают с направлениями базисных векторов .

Р ассмотрим теперь произвольный вектор в трехмерном пространстве.

Отметим, что если вектор отложен от начала координат, то его координаты совпадают с координатами конца этого вектора.

Применив дважды правило параллелограмма, замечаем, что

.

Свойства:

Пусть , . Тогда

1)

2)

3)

4 )

Теорема 5.2. Пусть точка А имеет координаты (x_A, y_A, z_A), точка В(x_В, y_В, z_В). Тогда

.

Для доказательства достаточно заметить, что , причем .

Замечание. Координаты вектора не изменятся, если этот вектор отложить от любой другой точки пространства.

Доказательство этого факта предоставим читателю.

Многие геометрические задачи на плоскости и в пространстве легко решаются с помощью векторов. При этом надо все условия задачи, сформулированные для точек и отрезков (а в дальнейшем – и углов) переформулировать для векторов, а затем перевести в координатную форму. Если рассматривается задача на плоскости, то и точки, и векторы имеют 2 координаты, и все сформулированные выше свойства имеют место для первых двух координат.

Пример 1: Точка М делит пополам отрезок АВ, где А(x_A, y_A, z_A),

В(x_В, y_В, z_В). Найти координаты точки М.

Решение: Для решения этой задачи используем векторы.

Точка М лежит на отрезке АВ   , причем эти векторы сонаправлены.

Кроме того, по условию, . Следовательно, .

Обозначим координаты точки М (x_М, y_М, z_М). Тогда , .

Используя свойство 2) координат, имеем:

, откуда выражаем

.

Пример 2. Даны точки: A(1; 0), B(4; 2), C(2; 5). Найти точку пересечения медиан треугольника АВС.

Р ешение: Как известно, все медианы треугольника пересекаются в одной точке. Обозначим эту искомую точку К(x_K, y_K) и рассмотрим две медианы: BN и CM.

Найдем сначала координаты точек N и M как середин сторон АВ и АС (см. Пример 1).

Точка М – середина отрезка АВ  . Аналогично, .

Следовательно, можем найти координаты векторов:

Точка КСМ    (свойство 4).

Аналогично,

точка КBN    .

Таким образом, мы получили два линейных уравнения с двумя неизвестными – координатами точки К. Решаем полученную систему:

 .

Таким образом, искомая точка .

Настройка ориентации образцов Векторной или Символьной Штриховки

Настройка ориентации образцов Векторной или Символьной Штриховки

Настройка ориентации образцов Векторной или Символьной Штриховки

Элементы управления Ориентацией Штриховки позволяют вручную настраивать направление векторной или символьной штриховки.

Настройка варианта Ориентации Штриховки Элемента

•Для настройки ориентации векторной или символьной Штриховки поверхностей можно воспользоваться параметрами “Способ Построения”, находящимися в панели Общих Параметров диалога Параметров Штриховки.

 

•Для настройки ориентации векторной или символьной штриховки Зон можно воспользоваться переключателем, находящимся в панели План Этажа диалога Параметров Зоны.

 

•Для настройки ориентации Штриховки Поверхностей Балок, Колонн, 3D-сеток, Перекрытий, Крыш, Оболочек, Отверстий или Морфов можно воспользоваться элементами управления Штриховкой Поверхностей, присутствующими в диалогах Параметров этих элементов.

 

См. также Назначение Штриховки Поверхности.

•Для штриховок сечений, используемых в компонентах сложных или многослойных элементов, Ориентация Штриховки определяется их Строительными Материалами.

Варианты Ориентации Штриховки

От Начала Проектных Координат

По Указанному Вектору

Создание элемента Штриховки По Указанному Вектору

3D-деформация

Специальная Деформация

Деформируемая Штриховка для Крыш

Применение Символьных Штриховок для Многослойных Элементов: По размеру слоя.

Радиальная Деформация (только для Символьных Штриховок)

От Начала Проектных Координат

Если выбран этот вариант, то штриховка всегда располагается ортогонально, а ее начало находится в Начале Проекта независимо от трансформаций элемента.

 

По Указанному Вектору

Этот вариант позволяет задать угол поворота образца штриховки.

Вектор, появляющийся при выборе штриховки, служит для графической настройки места ее начала и ориентации.

Примечание: Для постоянного показа векторов штриховки на экране (а не только при ее выборе) воспользуйтесь переключателем Векторы Штриховки в меню Вид > Параметры Вывода на Экран.

 

Чтобы изменить место начала штриховки, переместите вектор ее ориентации. При этом убедитесь, что в Локальной Панели выбран вариант Перемещение Подэлемента.

    

Создание элемента Штриховки По Указанному Вектору

При создании элемента Штриховки:

1.В диалоге Параметров Штриховки выберите вариант По Указанному Вектору.

 

2.Начертите многоугольник штриховки.

В результате курсор примет форму стрелки вектора штриховки.

 

3.Двумя щелчками задайте начало вектора и его направление.

     

Обратите внимание, что вектор может располагаться и за пределами многоугольника штриховки. Создав вектор штриховки, вы в любой момент можете переместить его в любое место на экране.

3D-деформация

Доступно для Балок, Колонн, Оболочек и Морфов.

Этот вариант позволяет искажать штриховки поверхностей, имитируя объемное отображение криволинейных поверхностей на Плане Этажа.

 

Специальная Деформация

При выборе этого варианта в точке начала штриховки располагается двойной вектор.

Перемещение начала и концов этого вектора дают возможность смещать образец штриховки и углы штрихов.

 

Деформируемая Штриховка для Крыш

Выберите для параметра Ориентации штриховки поверхностей Крыши вариант Привязать к Уклону Крыши с Деформацией.

В результате штриховка поверхностей будет автоматически деформироваться в соответствии с углами наклона скатов.

 

Применение Символьных Штриховок для Многослойных Элементов: По размеру слоя.

Если для слоев многослойных элементов применяется символьная штриховка, определяемая назначенными Строительными Материалами, то для нее можно использовать опцию “По размеру слоя”. Это оказывается особенно полезным при моделировании любой направленной штриховки, например, мягкой изоляции, клееной фанеры, металлической отделки и т. д.

 

Эти настройки присутствуют в диалоге Строительных Материалов (Параметры > Реквизиты Элементов > Строительные Материалы.)

1.Откройте диалог Строительных Материалов и выберите реквизит, который хотите отредактировать.

2.Для параметра Ориентации Штриховки примените вариант По Размеру Слоя.

В результате образец символьной штриховки будет масштабироваться по толщине слоя.

 

Радиальная Деформация (только для Символьных Штриховок)

Вариант Радиальной Деформации, присутствующий в диалоге Параметров Штриховки, служит для искажения штриховок по радиальному вектору. Этот вариант появляется при выборе символьной штриховки и только если:

•символьная штриховка использовалась в качестве слоя многослойной конструкции; И

•Ориентация штриховки слоя была установлена По размеру слоя в параметрах Строительного материала; И

•Вы выбрали эту символьную штриховку после декомпозиции криволинейной многослойной/сложной стены.

См. Декомпозиция в Текущем Виде.

Примечание: Использование в проекте многих радиальных деформируемых штриховок может снизить производительность работы с проектом.

На рисунке ниже приведена криволинейная многослойная стена с одним из слоев в виде символьной штриховки (ориентация: По размеру слоя) после ее декомпозиции. В результате декомпозиции каждый слой можно выбирать самостоятельно. Символьная штриховка имеет манипулятор штриховки, причем при ее выборе становится доступным способ построения Радиальная деформируемая штриховка. С помощью манипулятора штриховки можно изменить деформирование штриховки и место расположения начала образца штриховки.

 

Документация JDK 19 — Главная

1. Главная
2. Ява
3. Java SE
4. 19

Обзор

• Прочтите меня
• Примечания к выпуску
• Что нового
• Руководство по миграции
• Загрузить JDK
• Руководство по установке
• Формат строки версии

Инструменты

• Технические характеристики инструментов JDK
• Руководство пользователя JShell
• Руководство по JavaDoc
• Руководство пользователя средства упаковки

Язык и библиотеки

• Обновления языка
• Основные библиотеки
• HTTP-клиент JDK
• Учебники по Java
• Модульный JDK
• Руководство программиста API бортового регистратора
• Руководство по интернационализации

Технические характеристики

• Документация API
• Язык и ВМ
• Имена стандартных алгоритмов безопасности Java
• банок
• Собственный интерфейс Java (JNI)
• Инструментальный интерфейс JVM (JVM TI)
• Сериализация
• Проводной протокол отладки Java (JDWP)
• Спецификация комментариев к документации для стандартного доклета
• Прочие характеристики

Безопасность

• Руководство по безопасному кодированию
• Руководство по безопасности

Виртуальная машина HotSpot

• Руководство по виртуальной машине Java
• Настройка сборки мусора

Управление и устранение неполадок

• Руководство по устранению неполадок
• Руководство по мониторингу и управлению
• Руководство по JMX

Client Technologies

• Руководство по специальным возможностям Java

Clojure — Структуры данных

Содержание

• нет
• Числа
• Струны
• символов
• Ключевые слова
• Символы
• Коллекции
• Списки (IPersistentList)
• векторов (IPersistentVector)
• Карты (IPersistentMap)
• Структурные карты
• ArrayMaps
• Наборы

Clojure имеет богатый набор структур данных. У них общий набор свойств:

• Они неизменны

• Они читаемы

• Они поддерживают правильную семантику равенства значений в своей реализации equals

• Они обеспечивают хорошие значения хеш-функции

• Кроме того, коллекции:

  • Управление осуществляется через интерфейсы.

  • Поддержка секвенирования

  • Поддержка постоянных манипуляций.

  • Поддержка метаданных

  • Реализовать java.lang.Iterable

  • Реализовать необязательную (только для чтения) часть java.util.Collection или java.util.Map

nil

nil — возможное значение любого типа данных в Clojure. nil имеет то же значение, что и Java null. Условная система Clojure основана на nil и false, где nil и false представляют значения логической ложности в условных проверках — все остальное является логической истиной. Кроме того, nil используется в качестве сигнального значения конца последовательности в протоколе последовательности.

Numbers

Clojure по умолчанию обеспечивает полную поддержку примитивных значений JVM, что позволяет использовать высокопроизводительный идиоматический код Clojure для числовых приложений.

Clojure также поддерживает типы упакованных чисел Java, производные от java.lang.Number, включая BigInteger и BigDecimal, а также свой собственный тип Ratio. Существует специальная обработка:

Longs

По умолчанию Clojure работает с натуральными числами как экземплярами примитивного типа long в Java. Когда примитивная целочисленная операция приводит к значению, которое слишком велико, чтобы содержаться в примитивном значении, генерируется исключение java.lang.ArithmeticException. Clojure предоставляет набор альтернативных математических операторов, заканчивающихся апострофом: +’, -‘, *’, inc’ и dec’. Эти операторы автоматически повышают уровень до BigInt при переполнении, но они менее эффективны, чем обычные математические операторы.

Соотношение

Представляет отношение между целыми числами. Деление целых чисел, которые не могут быть сведены к целому числу, дает отношение, то есть 22/7 = 22/7, а не число с плавающей запятой или усеченное значение.

Заражение

BigInts и типы с плавающей запятой «заразны» для операций. То есть любая целочисленная операция, включающая BigInt, приведет к BigInt, а любая операция, включающая двойное число или число с плавающей запятой, приведет к двойному значению.

Литералы BigInt и BigDecimal

Числовые литералы для BigInt и BigDecimal указываются с использованием постфикса N и M соответственно.

Пример выражения	Возвращаемое значение
(== 1 1,0 1M)	правда
(/ 2 3)	2/3
(/ 2,0 3)	0,6666666666666666
(карта №(Math/abs %) (диапазон -3 3))	(3 2 1 0 1 2)
(класс 36786883868216818816N)	clojure. lang.BigInt
(класс 3.14159265358М)	java.math.BigDecimal

Вычисление: + — * / inc dec quot rem min max
Автоматическое продвижение вычисления: +’ -‘ *’ inc’ dec’
Сравнение: == < > >= ноль? поз? отрицательный?
Побитовые операции: бит-и бит-или бит-исключающее бит-не-бит-сдвиг-вправо бит-сдвиг-влево
Соотношения: числитель знаменатель
Приведения: int bigdec bigint double float long num short Java-строки. См. также Печать.

 user=> (map (fn [x] (.toUpperCase x)) (.split "Dasher Dancer Prancer" " "))
("ДАШЕР" "ТАНЦЕР" "ПРАНЦЕР") 

стр строка? pr-str prn-str print-str println-str with-out-str

Символы

Символы Clojure — это символы Java.

char char-name-string char-escape-string

Ключевые слова

Ключевые слова — это символические идентификаторы, которые оцениваются сами по себе. Они обеспечивают очень быстрые тесты на равенство. Как и у символов, у них есть имена и необязательные пространства имен, оба из которых являются строками. Ведущий «:» не является частью пространства имен или имени.

Ключевые слова реализуют IFn для вызова() одного аргумента (карты) с необязательным вторым аргументом (значение по умолчанию). Например (:mykey my-hash-map :none) означает то же, что и (получить my-hash-map :mykey :none) . Смотрите получить.

ключевое слово ключевое слово?

Символы

Символы — это идентификаторы, которые обычно используются для обозначения чего-то другого. Их можно использовать в формах программы для ссылки на параметры функций, привязки let, имена классов и глобальные переменные. У них есть имена и необязательные пространства имен, оба из которых являются строками. Символы могут иметь метаданные (см. with-meta).

Символы, как и ключевые слова, реализуют IFn для вызова() одного аргумента (карты) с необязательным вторым аргументом (значение по умолчанию). Например ('mysym my-hash-map :none) означает то же, что и (get my-hash-map 'mysym :none) . Смотрите получить.

символ символ? gensym (см. также макрос #-suffix reader)

Коллекции

Все коллекции Clojure являются неизменяемыми и постоянными. В частности, коллекции Clojure поддерживают эффективное создание «модифицированных» версий, используя совместное использование структур, и гарантируют все свои ограничения производительности для постоянного использования. Коллекции эффективны и по своей сути потокобезопасны. Коллекции представлены абстракциями, и может быть одна или несколько конкретных реализаций. В частности, поскольку операции «модификации» дают новые коллекции, новая коллекция может не иметь того же конкретного типа, что и исходная коллекция, но будет иметь тот же логический (интерфейсный) тип.

Все коллекции поддерживают count для получения размера коллекции, conj для «добавления» в коллекцию и seq для получения последовательности, которая может пройти по всей коллекции, хотя их конкретное поведение немного отличается для разных типов коллекций.

Поскольку коллекции поддерживают функцию seq, все функции последовательности можно использовать с любой коллекцией.

Хэши коллекции Java

Интерфейсы коллекции Java определяют алгоритмы для списков, наборов и карт при вычислении значений hashCode(). Все коллекции Clojure соответствуют этим спецификациям в своих реализациях hashCode().

Хэши коллекций Clojure

Clojure предоставляет свои собственные хеш-вычисления, которые обеспечивают лучшие свойства хеш-функций для коллекций (и других типов), известные как значение hasheq .

Интерфейс IHashEq помечает коллекции, которые предоставляют функцию hasheq() для получения значения hasheq. В Clojure хэш-функцию можно использовать для вычисления значения hasheq.

Упорядоченные коллекции (вектор, список, последовательность и т. д.) должны использовать следующий алгоритм для вычисления хэш-функции (где хэш вычисляет хэш-код). Обратите внимание, что unchecked-add-int и unchecked-multiply-int используются для вычисления целочисленного переполнения.

 (по определению хеш-упорядоченный [коллекция]
  (-> (reduce (fn [acc e] (unchecked-add-int
                            (unchecked-multipli-int 31 acc)
                            (Неужели он)))
              1
              коллекция)
      (mix-collection-hash (коллекция-коллекция)))) 

Неупорядоченные коллекции (карты, наборы) должны использовать следующий алгоритм вычисления hasheq. Запись карты рассматривается как упорядоченный набор ключей и значений. Обратите внимание, что unchecked-add-int используется для вычисления целочисленного переполнения.

 (определение хэш-неупорядоченный [коллекция]
  (-> (уменьшить unchecked-add-int 0 (коллекция хэшей карты))
      (смешанный-коллекция-хэш (коллекция-коллекция)))) 

Алгоритм смешанный-коллекция-хеш — это деталь реализации, которая может быть изменена.

Списки (IPersistentList)

Списки представляют собой коллекции. Они напрямую реализуют интерфейс ISeq.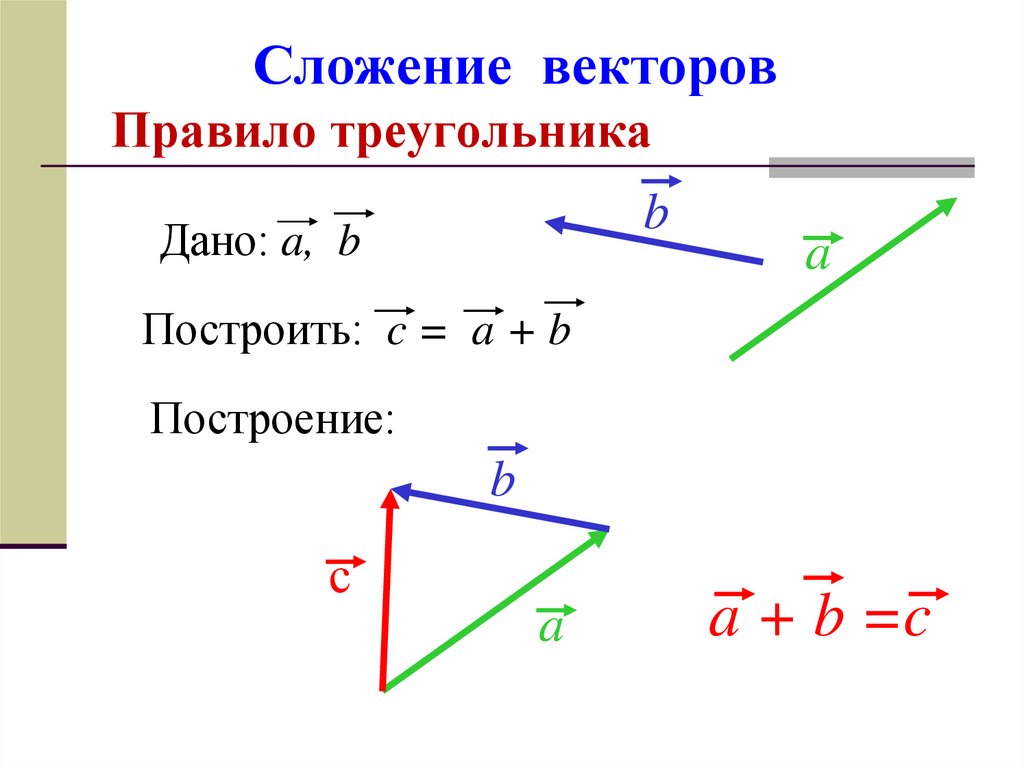 (Обратите внимание, что пустой список также реализует ISeq, однако функция seq всегда будет возвращать nil для пустой последовательности.) count равен O(1). conj помещает элемент в начало списка.

Создать список: list list*
Обрабатывать список как стопку: peek pop
Проверить список: list?

Векторы (IPersistentVector)

Вектор — это набор значений, индексированных смежными целыми числами. Векторы поддерживают доступ к элементам по индексу в прыжках log32N. количество равно O (1). conj помещает элемент в конец вектора. Векторы также поддерживают rseq, который возвращает элементы в обратном порядке. Векторы реализуют IFn для вызова() одного аргумента, который они считают индексом, и ищут в себе как бы по n-му, т.е. векторы являются функциями своих индексов. Векторы сравниваются сначала по длине, затем каждый элемент сравнивается по порядку.

Создать вектор: vector vec vector-of
Проверить вектор: получить n-й пик rseq vector?
‘изменить’ вектор: assoc pop subvec replace

См. также застежки-молнии

Карты (IPersistentMap)

Карта — это набор, который сопоставляет ключи со значениями. Предусмотрено два разных типа карт — хешированные и отсортированные. Для хеш-карт требуются ключи, которые правильно поддерживают hashCode и equals. Для отсортированных карт требуются ключи, реализующие Comparable, или экземпляр Comparator. Хэш-карты обеспечивают более быстрый доступ (log32N переходов) по сравнению с (logN переходов), но отсортированные карты, ну, в общем, отсортированы. количество равно O (1). conj ожидает другую карту (возможно, с одной записью) в качестве элемента и возвращает новую карту, которая представляет собой старую карту плюс записи из новой, что может перезаписать записи старой. conj также принимает MapEntry или вектор из двух элементов (ключ и значение). seq возвращает последовательность записей карты, которые представляют собой пары ключ/значение. Отсортированная карта также поддерживает rseq, который возвращает записи в обратном порядке. Карты реализуют IFn, для вызова() одного аргумента (ключа) с необязательным вторым аргументом (значение по умолчанию), т.е. карты являются функциями своих ключей. нулевые ключи и значения в порядке.

Создать новую карту: hash-map sorted-map sorted-map-by
‘изменить’ карту: assoc dissoc select-keys merge merge-with zipmap
Изучить карту: получить содержит? найти ключи vals карту?
Проверка записи карты: key val

StructMaps

Большинство применений StructMaps теперь лучше обслуживать записями.

Часто многие экземпляры карт имеют одинаковый базовый набор ключей, например, когда карты используются в качестве структур или объектов на других языках. StructMaps поддерживает этот вариант использования, эффективно обмениваясь информацией о ключах, а также предоставляя дополнительные средства доступа с повышенной производительностью к этим ключам. Структурные карты во всех отношениях являются картами, поддерживающими один и тот же набор функций, совместимыми со всеми другими картами и постоянно расширяемыми (т. е. карты структур не ограничиваются своими базовыми ключами). Единственное ограничение состоит в том, что вы не можете отделить карту структуры от одного из ее базовых ключей. Структурная карта сохранит свои базовые ключи по порядку.

StructMaps создаются путем создания базового объекта структуры с помощью create-struct или defstruct, а затем создания экземпляров с помощью struct-map или struct.

 (дефструктировать десилу: фред: рикки)
(def x (map (fn [n]
              (struct-map desilu
                :fred н
                : Рикки 2
                :люси 3
                :этель 4))
             (диапазон 100000)))
(def fred (аксессор desilu: fred))
(уменьшить (fn [n y] (+ n (:fred y))) 0 x)
 -> 4999950000
(уменьшить (fn [n y] (+ n (fred y))) 0 x)
 -> 4999950000 

Настройка StructMap: средство доступа create-struct defstruct
Создание отдельной структуры: struct-map struct

ArrayMaps

При выполнении манипуляций с кодовой формой часто желательно иметь карту, которая поддерживает порядок ключей.