Значения синуса, косинуса и тангенса для углов 30, 45 и 60
Урок 26. Геометрия 8 класс ФГОС
В этом уроке мы повторим определение синуса, косинуса, тангенса острого угла прямоугольного треугольника. Покажем способы нахождения значений синуса, косинуса, тангенса острых углов прямоугольного треугольника с помощью таблиц Брадиса и калькулятора. Найдем значения синуса, косинуса, тангенса для углов в 30°, 45° и 60°. Занесем полученные результаты в таблицу. На конкретных примерах покажем пользу использования таблицы. Рассмотрим способ легкого запоминания табличных значений.
Конспект урока «Значения синуса, косинуса и тангенса для углов 30, 45 и 60»
Прежде чем приступить к изучению нового материала, давайте вспомним, что синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом
острого угла прямоугольного треугольника называется
отношение прилежащего катета к гипотенузе.
Тангенсом острого угла
Тангенс острого угла прямоугольного треугольника можно записать и так
Синус и косинус одного и того же угла связаны между собой основным тригонометрическим тождеством: .
Посчитать значения синусов, косинусов, тангенсов, для всех острых углов прямоугольного треугольника очень трудно. Для этого существуют специальные таблицы Брадиса, названные так в честь Владимира Модестовича Брадиса, российского и советского математика.
Современные калькуляторы также помогают вычислить синусы, косинусы, тангенсы произвольных острых углов.
Но значения синуса, косинуса, тангенса для некоторых острых углов прямоугольного треугольника найти нетрудно.
Давайте рассмотрим прямоугольный треугольник, острые углы которого равны 30º и 60º соответственно.
Запишем
формулу, для нахождения синуса 30º: .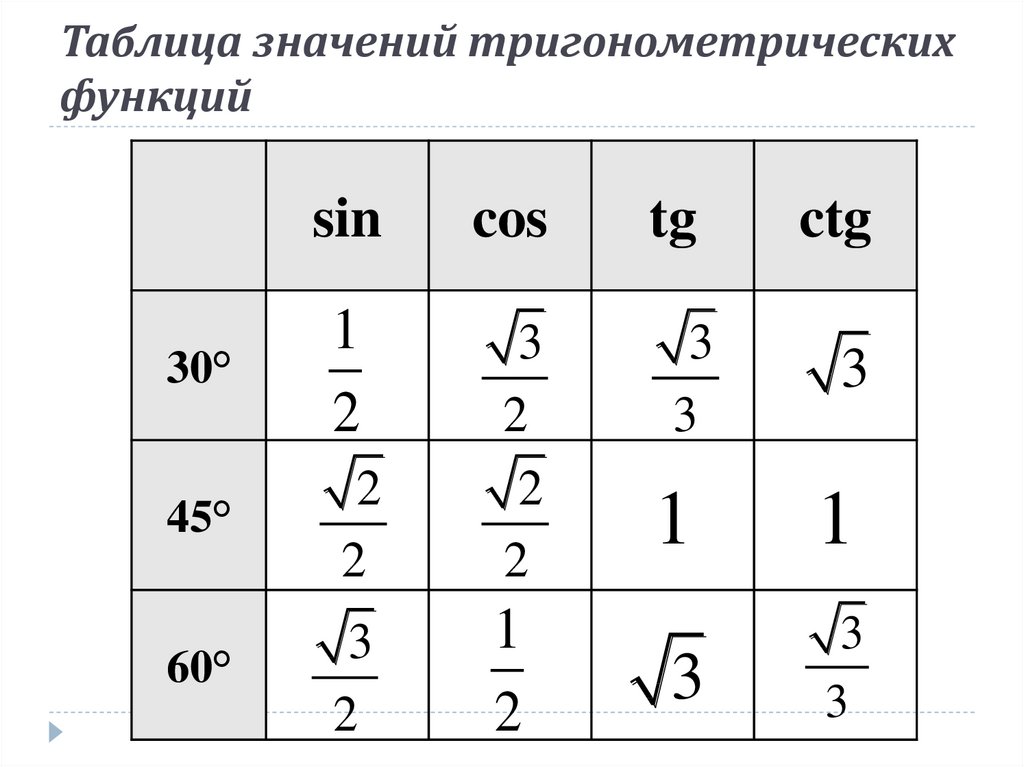
Но это же отношение равно косинусу 60º: , то есть косинус шестидесяти градусов равен одной второй.
Воспользовавшись основным тригонометрическим тождеством
, получим, что
Для вычисления тангенса, воспользуемся формулой:
; .
Еще раз обратите внимание, что из-за того, что сумма острых углов прямоугольного треугольника равна девяноста градусам
и .
Теперь давайте рассмотрим равнобедренный прямоугольный треугольник ABC с прямым углом C.
В этом треугольнике Ac= BC и острые углы равны по 45º. Запишем теорему Пифагора для этого треугольника.
.
Для удобства, занесем полученные нами значения для синуса, косинуса, тангенса в таблицу.
Теперь,
давайте на одной задаче попробуем показать пользу использования таблицы,
которую мы с вами составили.
Задача. Найти если .
Решение.
Сначала будем решать эту задачу, пользуясь только формулами для вычисления синуса, косинуса, тангенса.
По теореме Пифагора найдем, что гипотенуза равна двум.
Подставим полученные значения в формулы для вычисления синуса и косинуса и получим:
А теперь давайте решим эту задачу с помощью таблицы. Посмотрим на строку тангенс и найдем клеточку, в которой записан . Получим, что тангенс равен для угла в 60º. Тогда мы сразу можем записать, что синус 60º=, а косинус 60º=.
Ответ:
То есть, пользоваться табличными значениям гораздо удобнее, чем каждый раз вычислять синус, косинус и тангенс для этих углов.
Задача. В прямоугольном треугольнике . Вычислить длины катетов прямоугольного треугольника.
Решение.
Ответ: .
Задача.
Найти углы ромба с диагоналями и .
Решение.
Ответ: .
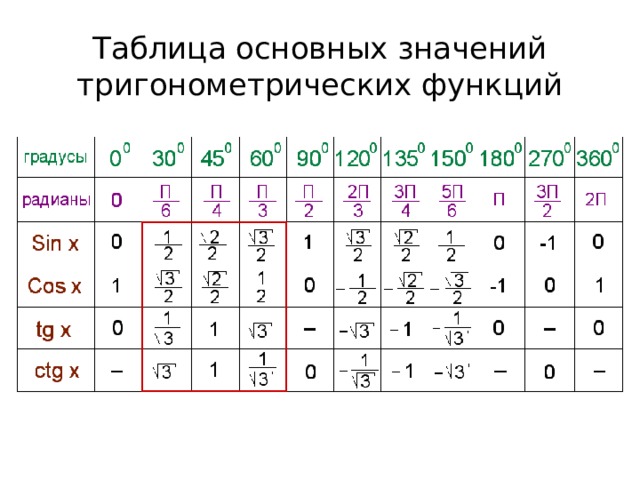
Давайте еще раз повторим таблицу значений для синуса, косинуса, тангенса углов 30º, 45º, 60º.
А запомнить эту таблицу несложно. Давайте посмотрим на строки, в которых записаны синусы и косинусы углов. Там записаны одни и те же значения, только в строке синусов они записаны в порядке возрастания, а в строке косинус – в порядке убывания. Тангенсы не надо заучивать, достаточно знать, что тангенс – отношение синуса к косинусу.
Предыдущий урок 25 Синус, косинус и тангенс острого угла прямоугольного треугольника
Следующий урок 27 Взаимное расположения прямой и окружности
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 8 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Синус — что это такое
Обновлено 21 июля 2021 Просмотров: 192 850 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.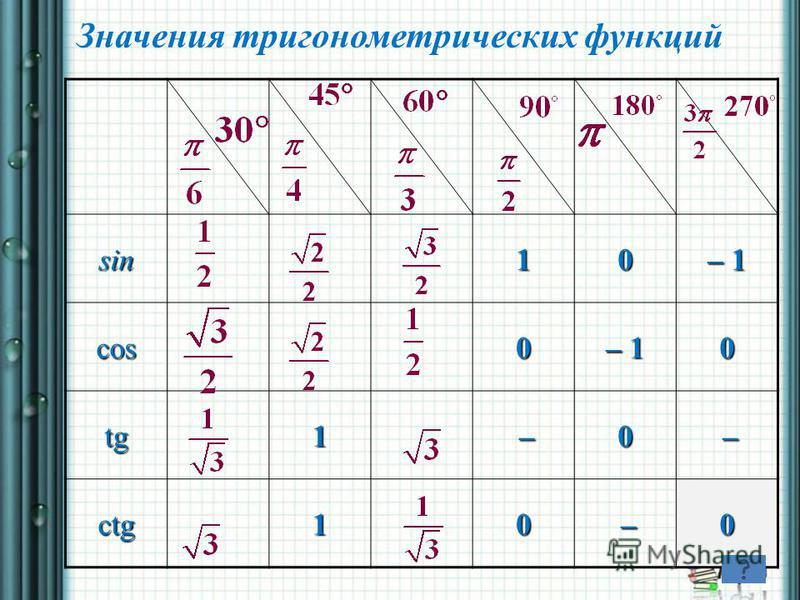 ru. Сегодня мы поговорим о том, что такие СИНУС.
ru. Сегодня мы поговорим о том, что такие СИНУС.
Наверняка многие знают, что это понятие относится к математике. Все мы учились в школе и проходили тригонометрию.
С понятиями СИНУС, КОСИНУС, ТАНГЕНС и КОТАНГЕНС школьники знакомятся в 8 классе.
И сейчас без этих знаний не обойтись на ЕГЭ. И задачки по тригонометрии обязательно входят в программу тестов единого государственного экзамена.
Так что эта статья будет в первую очередь полезна старшеклассникам. А читателям более старшего возраста будет полезно лишний раз освежить давно забытые знания.
Что такое тригонометрия
Но давайте начнем совсем с азов. Раз уж мы сказали, что СИНУС – это некая тригонометрическая функция, давайте расскажем и что такое тригонометрия.
Тригонометрия – это раздел математики, который был основан еще в Древней Греции. Само слово состоит из двух половин «τρίγωνον» и «μετρέω», что можно дословно перевести как «изучение треугольников».
Впервые нечто похожее на тригонометрические функции появилось в Древней Греции. Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.
Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.
Хотя ученые не исключают, что похожими вычислениями пользовались и при строительстве Египетских пирамид. А это уже 2-2,5 тысячи лет до нашей эры.
И опять же, пирамиды ведь имеют треугольную форму (в плоскости). И тригонометрия связана напрямую с треугольниками. Возможно совпадение, а возможно и нет.
Правда, в тригонометрии рассматривают конкретные треугольники – прямоугольные. Напомним, это такие фигуры, у которых две стороны из трех пересекаются друг с другом под углом 90 градусов.
Выглядит такой треугольник вот так:
У такого треугольника стороны имеют определенные названия:
КАТЕТЫ – это стороны, которые пересекаются под прямым углом.
В нашем случае это стороны АВ и ВС. Это название также имеет древнегреческие корни. Так, слово «káthetos» переводится как «перпендикуляр, опущенный, ответственный».ГИПОТЕНУЗА – сторона, которая идет под наклоном и соединяет между собой два катета.
В нашем случае это отрезок АС. Слово также родом из Древней Греции, «ὑποτείνουσα» означает «натянутая». И это очень хорошо характеризует этот отрезок, ведь он действительно выглядит как натянутая струна между двух опор. И даже если перевернуть треугольник, это ощущение не изменится.
Синус — это …
А вот теперь мы подобрались к самому главному, определению СИНУСА. Это величина не существует сама по себе. Она имеет отношение к какому-то углу треугольника. А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.
А вот теперь долгожданное определение:
СИНУС угла – это отношение противолежащего катета к гипотенузе.
Чтобы было понятно, о чем речь, взгляните еще раз на наш рисунок прямоугольного треугольника. В данном случае, противолежащим катетом к углу α будет сторона ВС. А противолежащим катетом к углу β будет сторона АС.
Соответственно, катет ВС для угла α будет прилежащим.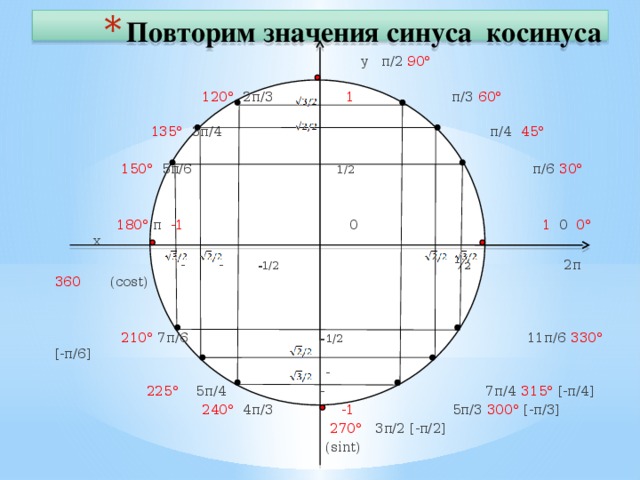 И точно таким же будет катет ВС для угла β.
И точно таким же будет катет ВС для угла β.
Конкретные формулы синусов будут такими:
Значения синусов
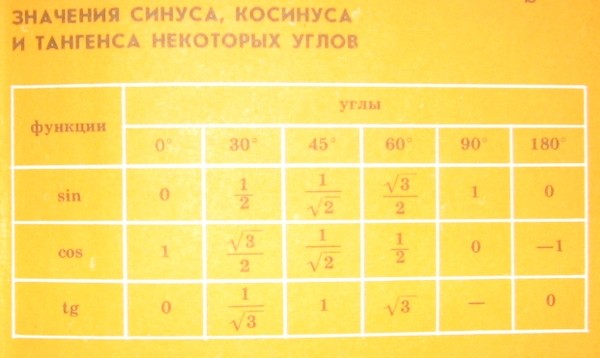
Чаще всего школьники имеют дело с определенными углами. Например, 30, 45, 60, 90 градусов и так далее. И чтобы не высчитывать каждый раз значение тригонометрических функций через стороны треугольника, есть уже готовые таблицы:
- 0 градусов — SIN = 0;
- 30 градусов — SIN = ½;
- 45 градусов — SIN = √2/2;
- 60 градусов – SIN = √3/2;
- 90 градусов – SIN = 1;
- 180 градусов – SIN = 0;
- 270 градусов – SIN = -1;
- 360 градусов – SIN = 0.
Вместо заключения
СИНУС – это не единственная тригонометрическая функция, которую проходят в школе. Есть еще и другие, и все они также связаны с прямоугольным треугольником.
А называются они вот так:
- КОСИНУС – это обратная синусу величина (даже в переводе с латыни это слово означает «перевернутый синус»). Косинус равен отношению прилежащего катета к гипотенузе.

- ТАНГЕНС – это отношение противолежащего катета к прилежащему. Или отношение синуса к косинусу.
- КОТАНГЕНС – это отношение прилежащего катета к противолежащему. Или отношение косинуса к синусу.
Вот и все, что мы хотели рассказать о тригонометрической функции СИНУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
7.3 Определение значений синусов углов
Для направления орудия в цель приходится определять значения синусов углов. Для их определения на угломерной шкале нанесены точки.
Для углов 0 и 30-00 синус равен нулю, поэтому против этих штрихов никаких точек нет.
Для углов 15-00 и 45-00 синус равен единице и это его значение условно отмечено тремя точками. Остальные
значения синуса расположены через
0,1 в промежутках вышеупомянутых углов,
причем четные значения 0,2; 0,4 и т. д.
указаны двумя точками, а нечетные 0,1;
0,3 и т. д. — одной точкой.
Остальные
значения синуса расположены через
0,1 в промежутках вышеупомянутых углов,
причем четные значения 0,2; 0,4 и т. д.
указаны двумя точками, а нечетные 0,1;
0,3 и т. д. — одной точкой.Шкала синусов не имеет оцифровки, так что при пользовании ею следует отсчитывать число мест точек, начиная от штрихов 0 или 30 до риски «у» индекса, причем каждое место считать за 0,1.
Отсчет от «О» ведется для углов, лежащих в пределах от 45-00 до 60-00 (нуля) и от 60-00 (нуля) до 15-00: отсчет от «30» — для углов в пределах от 15-00 до 30-00 и от 30-00 до 45-00.
Для определения значения синуса угла необходимо:
навести перекрестие сетки на цель;
установить на шкалах отсчет 30-00 для чего, нажав на рукоятку, подвести деление 30 шкалы под риску «у» индекса, а затем, нажав на кнопку и вращая шкалу, установить отсчет ноль;
вращая рукоятки, навести перекрестие сетки на батарею;
отсчитать число мест точек от деления «О» или «30» угломерной шкалы до риски «у» индекса; полученное число мест точек соответствует числу десятых синуса угла.

Отсчет мест точек начинать от «О» или «30» угломерной шкалы, в зависимости от того, откуда будет ближе до риски «у» индекса. Следует иметь в виду, что полученное значение синуса не может быть больше единицы.
8. Определение магнитного азимута и дальностей с помощью буссоли.
Для определения магнитного азимута необходимо:1. Подготовить буссоль к работе.
2. Сориентировать буссоль по магнитному меридиану (магнитной стрелке).
3. Определить магнитный азимут по удаленной точке. Для чего:
навести вертикальную линию перекрестия сетки на выбранный предмет с помощью отводки и маховичка отсчетного механизма;
снять отсчет по буссольному кольцу и барабанчику;
повторить не менее 3-4 раз измерения магнитного азимута, каждый раз заново ориентируя буссоль по магнитной стрелке и за окончательный результат взять среднее из числа произведенных измерений.

8.1 Определение поправки буссоли
Поправка буссоли m, позволяющая переходить от измеренной буссоли к дирекционному углу по формуле
Для определения поправки буссоли используется направление, дирекционный угол которого:
известен из каталога (списка) координат опорной сети;
получен вычислением по координатам точек сети, взаимно удаленных не менее чем на 2 км;
определен по Солнцу или звездам.
В крайнем случае, дирекционный угол может быть получен вычислением по координатам контурных точек, снятых с карты, расстояние между которыми на карте должно быть не менее 10 см.
Поправки буссолей
определяются заблаговременно и
одновременно для всех приборов
подразделения на основе одного
ориентирного направления.
Порядок определения поправок буссолей следующий:
На точке А ориентирного направления с известным дирекционным углом АВ ставят один из выверяемых приборов, принятый за контрольный; на точках 1, 2, 3 … n — остальные выверяемые приборы.
На буссольных шкалах контрольного прибора устанавливают отсчет, равный дирекционному углу АВ, и при этом отсчете наводят монокуляр в точку В. Ориентировав таким путем прибор, последовательно отмечаются им по точкам 1, 2, 3 … n. Изменив полученные отметки на 30-00, получают дирекционные углы направлений с точек 1, 2, 3 … n на точку А.
В
то же время на всех точках 1, 2, 3 … n
ориентируют приборы по магнитной
стрелке и по команде (сигналу) организующего
выверку одновременно начинают измерение
буссоли направления на точку А. Измерение
буссоли повторяется не менее 4—5 раз, и
каждый раз приборы ориентируются
заново. Среднее значение докладывают
организующему выверку.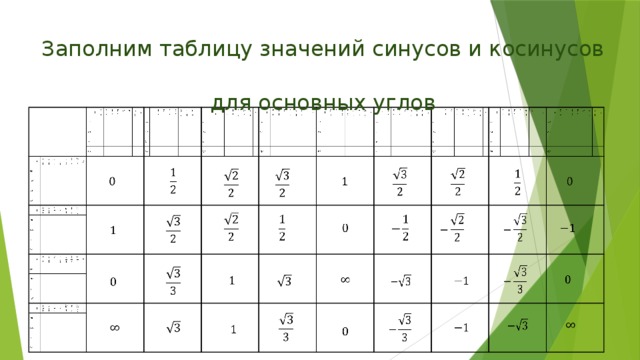
Контрольным прибором измеряют одновременно буссоль направления на ориентирную точку В. Для повышения точности и, главное, для обнаружения возможных грубых промахов производится повторное измерение буссоли.
По приказанию организующего выверку снимают приборы с точек 1, 2, 3 … n (треноги остаются на месте) и перемещают их с точки 1 на точку 2, с точки 2 на точку 3 и т. д. По команде (сигналу) измеряют буссоли направлений на точку А (4—5 независимых измерений). Среднее значение буссоли докладывают организующему выверку.
Организующий выверку отмечает по часам начало первого измерения и конец второго измерения буссоли; полученные средние значения буссоли записывают в журнале и для каждого измерения вычисляют поправки буссолей всех приборов по формуле
m =m – α,
где m — поправка буссоли;
m-буссоль направления на точку А (среднее значение), для контрольного прибора — на точку В;
α-дирекционный
угол направления на точку А (для
контрольного прибора — на точку В).
Вычисленные значения сводят в таблицы.
Значения поправок буссолей с указанием времени и места их определения записывают на бирках, вкладываемых в футляр каждого прибора.
Перестановка буссольных шкал приборов для приведения поправки буссоли к нулю или к величине поправки буссоли другого прибора категорически запрещается.
Найденные значения поправок буссолей действительны только на момент их определения и на удалении не более 10 км (в неаномальном районе) от точки, на которой производилось определение поправок буссолей.
При
перемещении в новый район на расстояние
более 10 км поправки буссолей
определяются заново. В этом случае
поправки буссолей определяют не для
всех приборов, выверенных на первоначальной
точке, а лишь для двух из них. Получив
для каждого из этих двух приборов
разность поправок буссолей: «вновь
полученная минус ранее определенная»,
берут среднее и на эту величину, с учетом
ее знака, изменяют поправки буссолей
всех приборов, выверенных на
первоначальной точке.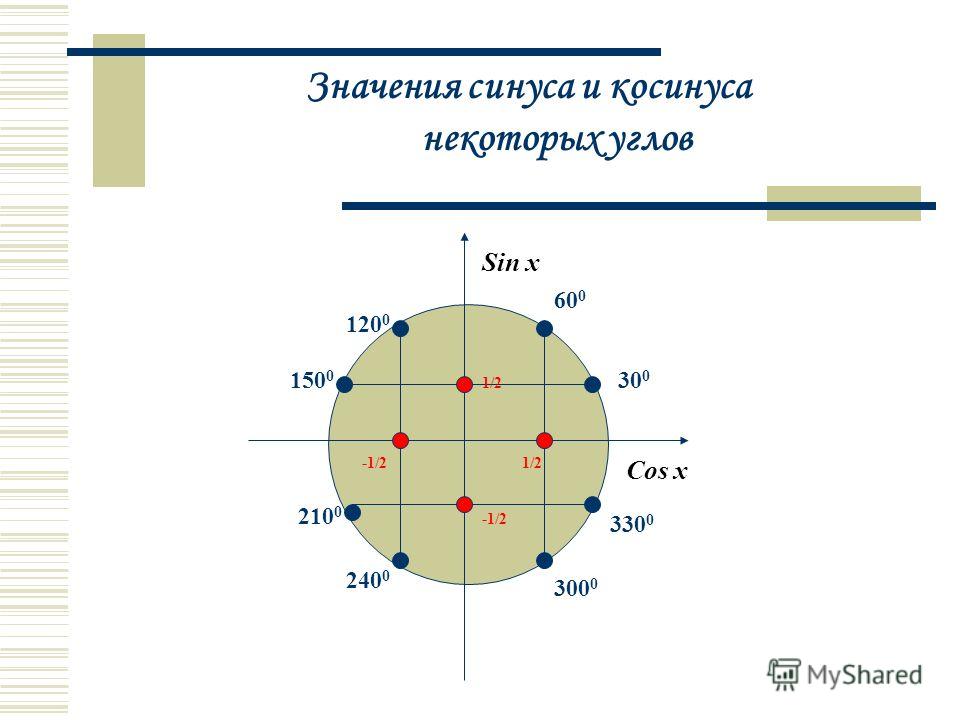
При использовании найденного значения поправки буссоли для ориентирования в дневные часы суток весной, летом и осенью надо учитывать ее суточное изменение. Зимой и ночью суточное изменение не учитывается. Учет суточного изменения поправки буссоли производят путем введения в нее поправки, получаемой по графику. Числа вдоль верхней и нижней рамок графика обозначают поясное декретное время. Вдоль левой и правой рамок снимают отсчеты, соответствующие пересечению вертикальных линий с кривой суточного изменения поправок буссоли. Например, для момента 17 ч 00 мин отсчет равен 0-03,6.
Для получения по графику поправки на момент ориентирования надо из отсчета для этого момента вычесть отсчет для момента определения поправки буссоли. Полученную по графику поправку прибавляют, учитывая ее знак, к поправке буссоли.
Значения синуса, косинуса, тангенса и котангенса углов.
Класс 9 Дата Предмет алгебра Подпись проверяющего — Урок № 56
Тема урока: Глава 3. Значения синуса, косинуса, тангенса и котангенса углов.
Значения синуса, косинуса, тангенса и котангенса углов.
Цели урока:
Оценка: определяют результаты своей работы на уроке Синтез: используют значения тригонометрических функций в решении задач Анализ: изучают значения тригонометрических функций, работают с таблицей Применение: демонстрируют применение значения синуса, косинуса, тангенса и котангенса произвольного угла Понимание: обсуждают значения синуса, косинуса, тангенса и котангенса произвольного угла Знание: рассказывают значения синуса, косинуса, тангенса и котангенса произвольного угла |
Учебно-воспитательные задачи: Образовательная: |
Познакомиться со значениями синуса, косинуса, тангенса и котангенса произвольного угла, обеспечить усвоение новых знаний по данной теме, сформировать навыки применения знаний по данной теме |
Развивающая: развитие способности выражать мысли, познавательных способностей, формирование алгоритмического мышления, расширение кругозора |
Воспитательная: способствовать выявлению, раскрытию способностей учащихся, возбуждать интерес к предмету, побуждать учащихся к применению полученных знаний |
Результаты обучения: Учащиеся знают значения синуса, косинуса, тангенса и котангенса произвольного угла |
Учащиеся умеют: применять значения тригонометрических функций в решении задач, ясно выражать мысли, участвовать в дискуссии, умеют слушать и слышать |
Тип урока: сообщение новых знаний
Форма проведения урока: беседа
Методы обучения:
По источнику получения знаний: словесные, наглядные, практические.
По способу организации познавательной деятельности: объяснительно-иллюстративные, репродуктивные.
Методы воспитания: Организация деятельности, формирование мировоззрения, стимулирование деятельности, осуществление контроля, взаимоконтроля, самоконтроля.
Формы обучения: коллективные, индивидуальные, групповые
Основные понятия темы:
Задание на дом: №368, 372
Оборудование, ресурсы, наглядные пособия: учебник, раздаточный материал
Учитель: Шуринова Е.К.
Ход урока
Этапы урока | Содержание этапа |
Оргмомент. Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению | Приветствие Проверка подготовленности к уроку Организация внимания школьников Ознакомление с планом проведения урока |
Проверка домашнего задания. Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы | Выявление степени усвоения заданного учебного материала Ликвидация обнаруженных недостатков. Проверка выполнения домашнего задания у доски |
Вызов. Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия. | Сообщение темы урока Формулируют цели: сформировать навыки применения знаний по данной теме |
Актуализация знаний и умений Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т. | У доски игра «крестики-нолики» sin 30° cos 45° tg 0° тg 90° sin 60° cos 0° сos 60° tg 180° sin 0° tg π/3 sin π/4 tg π/6 sin π/2 cos π/6 tg π/4 cos π/2 cos π sin π Переведите:60°, 120°, 270°, в радианную меру. Переведите:90°, 135°, 360°, в радианную меру. Переведите: π/2, π/4, 3π/4, в градусную меру. Переведите: π, π/6, 5 π/6, в градусную меру. |
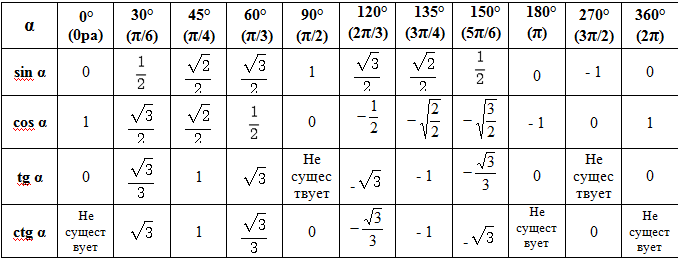
Осмысление Изучение нового материала. Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации | Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов Тригонометрические определения синуса, косинуса, тангенса и котангенсапозволяют указать значения тригонометрических функций для углов 0 и 90градусов: В курсе геометрии из прямоугольных треугольников с углами 30, 60 и 90 градусов, а также 45, 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов: Занесем указанные значения тригонометрических функций для углов 0, 30, 45, 60 и90 градусов (0, π/6, π/4, π/3, π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса. Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120, 135, 150, 180, 210, 225, 240, 270, 300,315, 330 и 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид. Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть |
Закрепления новых знаний и умений. Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения | tg π/4*cos π/6+2sin45° 4cos60°-3sinπ/2+1/2tg45° 6sin π/2-1,5tg180°-√3cos π/6 √2cos π/4+√3tg30°+1,5cosπ |
Проверка новых знаний Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления | Работа с учебником №369-372 Уровень В № 375,376 |
Коррекция знаний. Задачи: скорректировать выявленные проблемы | Организация деятельности учащихся по коррекции выявленных недостатков Индивидуальное задание. Повторное разъяснение учителя. |
Подведение итогов. Рефлексия. Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса | Мобилизация учащихся на рефлексию В занятии для меня было: Самым полезным_________________________________________________ Самым приятным __________________________________________________ самым интересным ______________________________________________ .Выставление оценок. |
Рефлексия учителя о проведенном уроке:
Как высчитать синус угла
Таблица Брадиса.

Она содержит рассчитанные значения синусов, косинусов, тангенсов и котангенсов углов, начиная с 0° до 360°. Воспользовавшись таблицей тригонометрических функций, можно производить расчеты и без инженерного калькулятора. В таблице можно легко найти значение тригонометрических функций от заданного Вам угла.
Таблица синусов.
Как известно, прямоугольный треугольник имеет три угла, два катета и гипотенузу. Отношения сторон выражаются некоторыми числами. Отношение величины противолежащего от острого угла катета к величине гипотенузы называется синусом угла.
sinа = а/с
где а — противолежащий катет;
с — гипотенуза;
а — угол.
Для того, чтобы найти синус заданного угла, достаточно просто воспользоваться таблицей тригонометрических функций. В данной таблице помещены величины синусов всех углов, начиная с 0° до 360°. При решении многих задач требуется найти величину стороны треугольника, если известны противолежащий угол и гипотенуза. Воспользовавшись таблицей, находим синус угла, а потом требуемую сторону. Онлайн калькулятор вам поможет быстро и правильно совершить необходимые расчеты. Для этого вам потребуется лишь внести исходные данные.
Воспользовавшись таблицей, находим синус угла, а потом требуемую сторону. Онлайн калькулятор вам поможет быстро и правильно совершить необходимые расчеты. Для этого вам потребуется лишь внести исходные данные.
Тригонометрические функции: синус угла
Зачем надо знать значение синуса? Представим ситуацию: известен один из углов (А=60⁰), вписанный в прямоугольный треугольник, и длина гипотенузы. Больше нет никакой информации. Надо узнать вычислить дальний к углу (А) катет. Как поступить?
Ситуация очень простая: смотрим таблицы Брадиса, находим значение sin(60⁰)=0,866, подставляем данные в формулу тригонометрической функции и решаем линейное уравнение. Из школьного курса известно, что sin угла – это отношение дальнего к углу, в данном случае А=60⁰, катета к гипотенузе.
Произвести все расчеты проще, если воспользоваться онлайн калькулятором на сайте. Таким образом можно вычислить длину любой из сторон прямоугольного треугольника.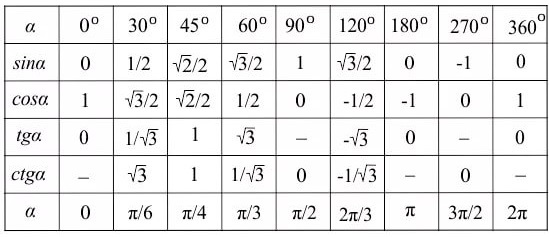 Знаем угол – значит, знаем sin этого угла. И наоборот, знаем sin – найти угол не составит проблемы.
Знаем угол – значит, знаем sin этого угла. И наоборот, знаем sin – найти угол не составит проблемы.
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z – любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов.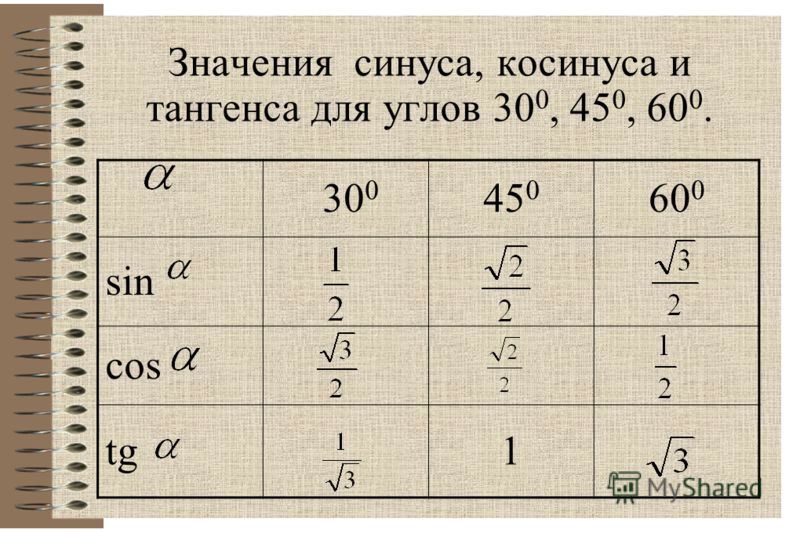 После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( – 52 ° ) ≈ – 0 , 78 и cos ( – 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( – 52 ° ) ≈ – 0 , 78 0 , 62 ≈ – 1 , 26 и c t g ( – 52 ° ) ≈ 0 , 62 – 0 , 78 ≈ – 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 – 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .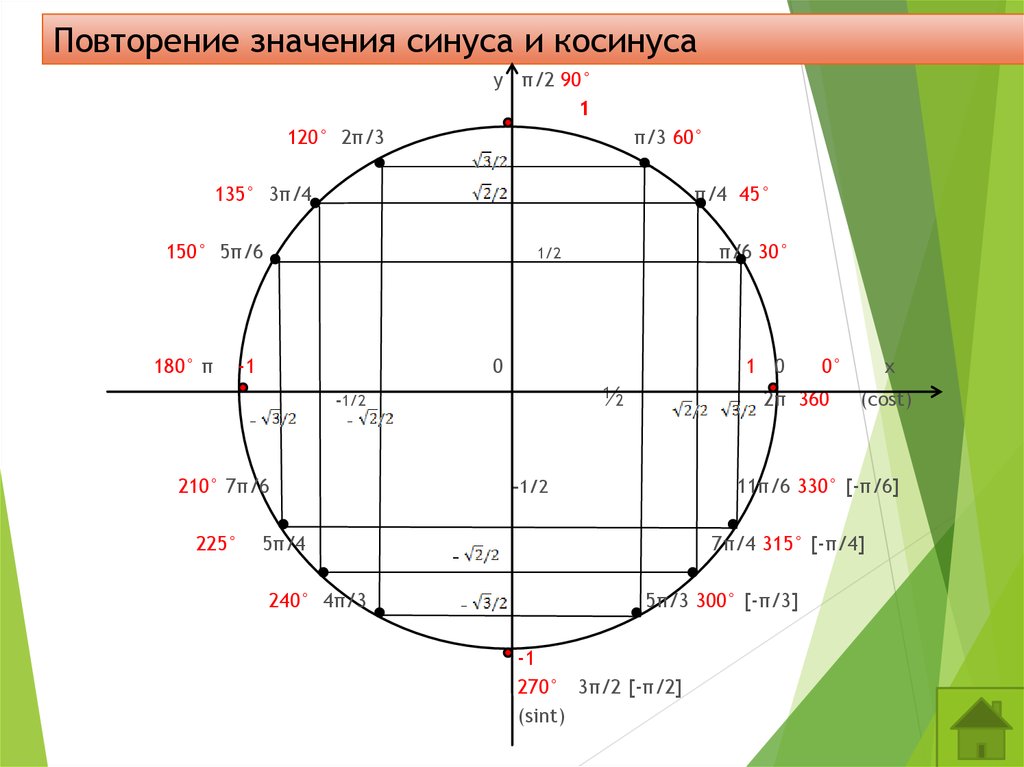
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 – 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 – 1 = 2 + 1 ( 2 – 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 – 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 – 2 2 · ( 2 + 2 ) · ( 2 – 2 ) = = 2 – 2 2 · ( 2 2 – ( 2 ) 2 ) = 2 – 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 – 2 4 = 2 – 2 2 . sin π 8 = 2 – 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = – sin 30 ° = – 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° – 60 ° ) = – cos 60 ° = – 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 – cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 – cos π 4 1 + cos π 4 = 1 – 2 2 1 + 2 2 = 2 – 2 2 + 2 = = ( 2 – 2 ) 2 ( 2 + 2 ) · ( 2 – 2 ) = ( 2 – 2 ) 2 2 2 – ( 2 ) 2 = ( 2 – 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 – 2 ) 2 2 = 2 – 2 2 = 2 – 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Как никогда не путать табличные значения синусов и косинусов Секрет моей классной
Единственный в мире Музей Смайликов | Скачать 259.2 Kb.
|
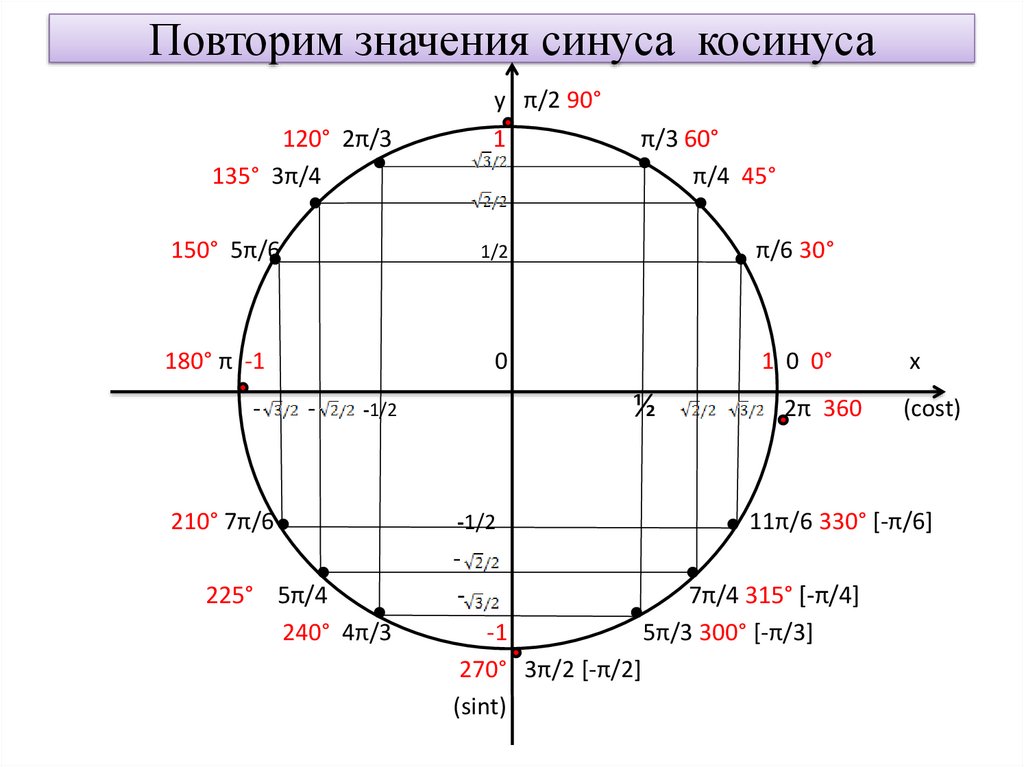
С этим файлом связано 1 файл(ов). Среди них: Проблемы социального обеспечения граждан РФ (доработка).pdf. Показать все связанные файлы Подборка по базе: Урок Поповой Л.В. Табличные модели.pptx, Урок Поповой Л.В. Табличные модели.docx, То, что никогда не понадобится.docx, Не тот велик кто никогда не падал.docx, ЗАДАНИЕ Табличные данные.doc, Сегодня как никогда особую остроту приобретает этическая проблем, 12 причин никогда не сдаваться.pdf Как никогда не путать табличные значения синусов и косинусов? Секрет моей классной… 17 октября 2020 Вчера помогала сыну разобраться с задачей из ОГЭ по математике и поняла, что он «плавает» в табличных значениях тригонометрических функций. Объяснила ему, как их запомнить так, чтобы больше никогда не ошибиться. Для начала рисуем единичную окружность, откладываем нужный угол, получаем точку А при пересечении с окружностью. Вспоминаем, что синус — это ордината точки А (координата по оси OY), а косинус — абсцисса точки А (координата по оси OX). Наша замечательная классная руководительница, которая вела у нас математику, учила нас запоминать так: Противоположности притягиваются. Сиииинус (произносим писклявым голоском) — звучит так мяяягко, а с ним в паре орррдинаааата (басом) — звучит жестко… Кооосинус (басом) — звучит твердо, а с ним в паре абсциииисса (пискляво) — звучит мяяягко. Вот так запомнить — даже во сне уже не перепутаешь. Проверено! Обычно ни у кого нет проблем запомнить, что вся эта таблица синусов-косинусов крутится вокруг трех чисел: Осталось только понять, какое из этих чисел чему соответствует. На всякий случай вспомним, что корень из одного, это все равно, что один, тогда наши волшебные числа имеют вид: Ну и тут уж совсем очевидно, что И теперь, когда нам нужно сообразить, чему, например, равен синус угла в тридцать градусов, мы на полях тетради рисуем маленькую единичную окружность (от руки, разумеется, без всяких линеек и циркулей), откладываем там углы 30, 45, 60. По единичной окружности сразу видно, что синус угла 30 градусов равен синусу угла 150 градусов, потому что ординаты у них одинаковые. А вот косинус 150-ти равен самому большому, но отрицательному числу — минус корень из трех на два… Так, пользуясь притяжением противоположностей и единичной окружностью, Вы никогда не перепутаете табличные значения синусов и косинусов! Осталось вспомнить, что тангенс — синус деленный на косинус, а котангенс — наоборот, косинус на синус. И, вспомнив значения синуса и косинуса, легко вычислить тангенс и котангенс. Так что их тоже не забудете. Поначалу, я помню, что эти единичные окружности я прямо рисовала в тетради на полях постоянно, чтобы наглядно все было. А потом в этом отпала необходимость: картинка у меня просто возникала перед мысленным взором. Надеюсь, этот пост кому-нибудь окажется полезным 🙂 Ставьте лайки, и пишите, если нашли неточности… 22 дня Нас ещё научили, как запомнить, кто из них кто. Располагаем треугольник, чтобы угол альфа лежал слева. И тогда:
20 дней Я запомнил так: cos – косить, косят по горизонтали, sin – значит по вертикали! 21 день Синус противолежащий катет, косинус прилежащий. 17 дней Синус угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Чем это отношение больше, тем больше наклон. Это отношение изменяется от нуля до единицы. Ноль – это горизонтально, единица – вертикально. |
тригонометрия — Как изначально рассчитывались таблицы синусов, косинусов и тангенсов?
$\begingroup$
Насколько я понимаю… гм… вектор (косинус, синус) вычислялся для углов (30 градусов, PI/6), (45 градусов, PI/4) и (60 градусов, PI/3) и так далее, однако я хотел бы знать исходный геометрический процесс вычисления величин для каждого вектора в таблице тригонометрического поиска.
Как люди рассчитывали эти значения до появления калькуляторов? Разве люди просто точно измеряли соседние и противоположные длины?
- тригонометрия
$\endgroup$
7
$\begingroup$
На эту тему можно написать целую книгу, и в Интернете есть несколько ресурсов, которые помогут ответить на этот вопрос. Итак, подытожим несколько вещей. \circ$. Например, Птолемей (2 век нашей эры) по существу создал таблицу значений для каждого угла в полградуса. 92 — 4x (\pi — x)}, \qquad \left(0\leq x\leq\pi\right).
$$
\circ$. Например, Птолемей (2 век нашей эры) по существу создал таблицу значений для каждого угла в полградуса. 92 — 4x (\pi — x)}, \qquad \left(0\leq x\leq\pi\right).
$$
Позже были разработаны более подробные таблицы, содержащие значения с большей точностью.
Логарифмические линейки будут содержать шкалы для вычисления тригонометрических функций. Я не уверен, когда именно логарифмические линейки впервые получили триггер. весы на них, но они определенно были до изобретения карманного калькулятора в 20-м веке.
Таким образом, «простой человек» (ученый) «вычислял» значения тригонометрических функций до калькулятора, в основном, используя таблицы и логарифмические линейки. Некоторые математики тогда участвовали в создании этих таблиц.
Пара ссылок, которые я использовал для вышеизложенного:
- https://en.wikipedia.org/wiki/History_of_trigonometry#European_mathematics
- http://www-history.mcs.st-and.ac.uk/HistTopics/Trigonometric_functions.
 html
html - https://en.wikipedia.org/wiki/Ptolemy%27s_table_of_chords
- https://en.wikipedia.org/wiki/Тригонометрические_таблицы
$\endgroup$
$\begingroup$
Вот один из способов, которым я это сделал, когда мне было 6 долларов, и я почти уверен, что именно так можно было это вычислить, грубо : Начертите 10-сантиметровый круг с центром $O$ и нарисуйте диаметр $\ell$, т.е. для удобства, параллельный любому краю бумаги. Затем возьмите транспортир и отметьте точку $A$, где прямая $\theta=\alpha$ (полярные координаты) пересекает окружность $r=10$. Тогда пусть $n$ — прямая, перпендикулярная $\ell$, проходящая через $A$ и пересекающая $\ell$ в точке $B$. Тогда имеем следующее:
$$\sin\alpha=\frac{AB}{10}\\
\cos\alpha=\frac{OB}{10}\\
\tan\alpha=\frac{AB}{OB}$$
Это дает грубое приближение. Для лучшего приближения берите большие радиусы. Тогда мне было $6$, а сейчас я на $8$ лет старше, так что все это основано на памяти.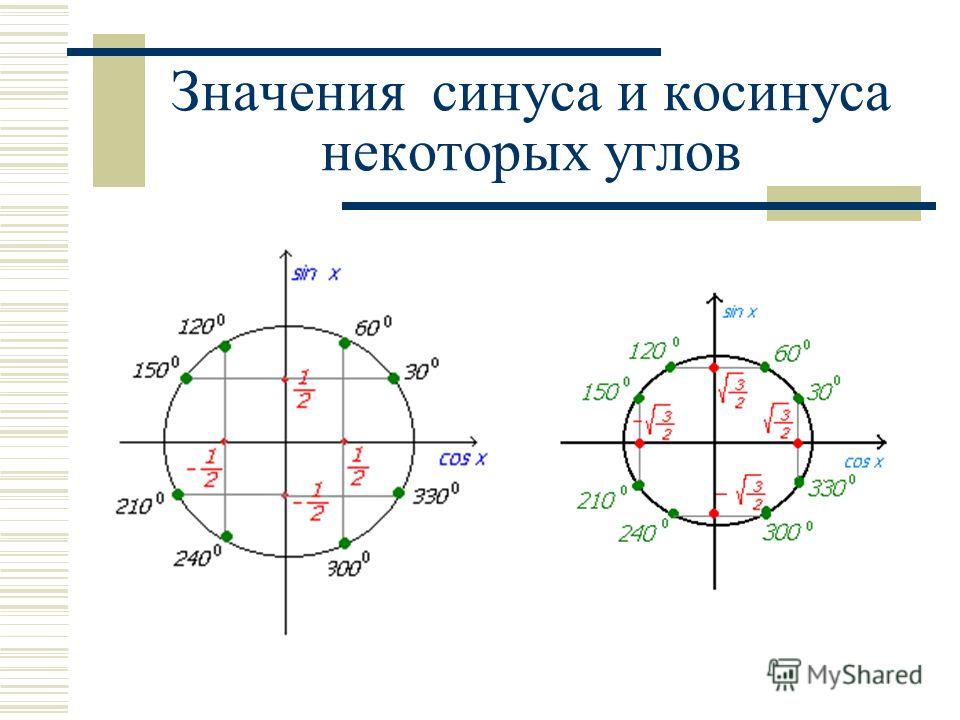 Хотя я почти уверен, что правильно написал. (Поправьте меня, если я ошибаюсь.)
Хотя я почти уверен, что правильно написал. (Поправьте меня, если я ошибаюсь.)
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Чтобы лучше понять некоторые проблемы, связанные с ракетами и движение необходимо использовать некоторые математические идеи из тригонометрия, изучение треугольников. Начнем с некоторых определений и терминологии. который мы будем использовать на этом слайде. Прямоугольный треугольник — это трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов это называется прямой угол , что дало название прямоугольному треугольнику. Мы выбираем один из двух оставшихся углов и обозначаем его c . а третий угол обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , тогда мы знаем, что значение d : 90 + с + г = 180 д = 180 — 90 — в д = 90 — с Определим сторону треугольника, противоположную от прямого угла к
быть гипотенуза . Нас интересуют отношения между сторонами и углами правильный треугольник. Начнем с некоторых определений. Мы позвоним соотношение стороны прямоугольного треугольника, противоположной гипотенузе синус и присвойте ему символ sin . sin = о/ч Отношение прилежащей стороны прямоугольного треугольника к гипотенузе называется косинус и с учетом символа cos . cos = а/ч Наконец, отношение противолежащей стороны к прилежащей стороне называется
касательная и обозначена символом tan . загар = о / а Мы утверждаем, что значение каждого отношения зависит только от значения
угол c образован прилежащим и гипотенузой.
Чтобы продемонстрировать этот факт,
давайте изучим три фигуры в середине страницы.
В этом примере мы имеем
8-футовая лестница, которую мы собираемся прислонить к стене. Стена
8 футов высотой, и мы нарисовали белые линии на стене
и синие линии вдоль земли с интервалом в один фут.
Длина лестницы фиксированная.
Если мы наклоним лестницу так, чтобы ее основание было в 2 футах от стены,
лестница образует с землей угол почти 75,5 градусов.
Лестница, земля и стена образуют прямоугольный треугольник. Соотношение расстояния от
стены (а — примыкающая), к длине лестницы (h — гипотенуза), составляет 2/8 = 0,25.
Это определяется как косинус с = 75,5 градусов. (На
другая страница
мы покажем, что если бы лестница была в два раза длиннее (16 футов),
и наклонен под тем же углом (75,5 градусов), что он будет сидеть в два раза больше, чем
далеко (4 фута) от стены. о = 7,745 Отношение противоположности к гипотенузе равно 0,967 и определяется как синус угла с = 75,5 градусов. Теперь предположим, что мы наклонили 8-футовую лестницу так, чтобы ее основание находилось на расстоянии 4 фута от стены.
Как показано на рисунке, теперь лестница наклонена под меньшим углом, чем на
первый пример. Угол равен 60 градусов, а отношение прилежащего к
гипотенуза теперь 4/8 = 0,5. Уменьшение угла с увеличивает косинус угла, потому что гипотенуза фиксирована
а соседний увеличивается по мере уменьшения угла. Если мы наклоним 8 футов
лестнице так, чтобы ее основание было на расстоянии 6 футов от стены, угол уменьшается до
около 41,4 градуса, и соотношение увеличивается до 6/8, что составляет 0,75. Заметьте также, что по мере увеличения cos(c) sin(c) уменьшается. Если мы наклоним лестницу так, чтобы основание было на расстоянии 6,938 фута от стены, угол c становится равным 30 градусам и отношение прилежащего к гипотенуза равна 0,866. Сравнивая этот результат со вторым примером, мы находим, что: cos(c = 60 градусов) = sin (c = 30 градусов) sin(c = 60 градусов) = cos (c = 30 градусов) Мы можем обобщить это отношение: грех (с) = потому что (90 — с) 90 — c есть величина угла d . грех (с) = потому что (г) Поскольку синус, косинус и тангенс являются функциями угла c , мы можем определить (измерить) коэффициенты один раз и составить таблицы значений синус, косинус и тангенс для различных значений c . Позже, если мы будем знать значение угла в прямоугольном треугольнике, таблицы подскажут нам отношение сторон треугольника. Зная длину любой стороны, мы можем найти длину другой стороны. стороны. Или, если мы знаем отношение любых двух сторон прямоугольного треугольника, мы можем найти величину угла между сторонами. Мы можем использовать таблицы для решения задач. Некоторые примеры задач, связанных с треугольниками и углами, включают силы на модель ракеты во время полет с двигателем, применение крутящие моменты, и резолюция составные части вектора. Вот таблицы синуса, косинуса и тангенса, которые вы можете использовать для решения
проблемы. Экскурсии с гидом
Деятельность: Похожие сайты: |
Видео с вопросами: Использование единичного круга для выражения значений синуса, косинуса и тангенса для 2𝜋 − 𝑥 через их значения для 𝑥, где 𝑥 — любое действительное число
На рисунке точки 𝑀(cos 𝜃, sin 𝜃) и 𝑁 лежат на единичной окружности, и ∠𝐴𝑂𝑁 = 2𝜋 − 𝜃. Выразите значения синуса, косинуса и тангенса 2𝜋 − 𝜃 через их значения для 𝜃. Проверьте, верно ли это для всех значений 𝜃.
Проверьте, верно ли это для всех значений 𝜃.
Стенограмма видео
На рисунке точки 𝑀 cos 𝜃, sin 𝜃 и 𝑁 лежат на единичной окружности, а угол 𝐴𝑂𝑁 равен двум 𝜋 минус 𝜃. Выразите значения sin, cos и тангенс двух 𝜋 минус 𝜃 с точки зрения их значений для 𝜃. Проверьте, верно ли это для всех значения 𝜃.
В вопросе нам говорят, что
точка 𝑀 имеет координаты cos 𝜃, sin 𝜃. И из схемы мы видим, что
угол 𝐴𝑂𝑀 равен 𝜃. Мы знаем, что это справедливо для любого
точка, лежащая на единичной окружности, где 𝜃 измеряется против часовой стрелки
направление от положительной оси 𝑥. Так как угол рефлекса 𝐴𝑂𝑁 равен
равно двум 𝜋 минус 𝜃, точка 𝑁 имеет координаты cos два 𝜋 минус 𝜃, sin два 𝜋
минус 𝜃. Используя тот факт, что существует два
𝜋 радианы в полном круге и мы измеряем отрицательные углы по часовой стрелке
от положительной оси 𝑥, то координаты точки 𝑁 также можно записать в виде
cos отрицательный 𝜃, отрицательный sin 𝜃.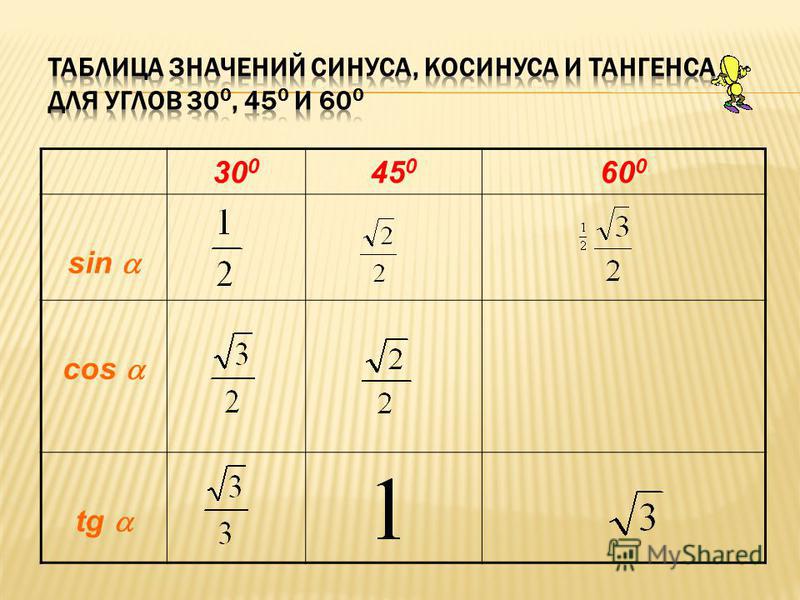
От симметрии агрегата круг, точки 𝑀 и 𝑁 будут иметь одну и ту же 𝑥-координату. Это означает, что cos отрицательного 𝜃 равно cos 𝜃. Это на самом деле стандартный результат что мы можем процитировать продвижение вперед. Поскольку функция косинуса четная, cos отрицательного 𝜃 равен cos 𝜃. А так как кос два 𝜋 минус 𝜃 равно cos отрицательного 𝜃, оно также должно быть равно cos 𝜃.
𝑥-координата точки 𝑁 на
единичный круг также можно записать как cos 𝜃. При работе с
𝑦-координаты точек 𝑀 и 𝑁, мы видим, что 𝑀 находится на одинаковом расстоянии над
𝑥-ось, так как точка 𝑁 находится ниже 𝑥-оси. Это означает, что грех отрицательного
𝜃 равно отрицательному греху 𝜃. Так же, как результат для
потому что отрицательный 𝜃, этот результат верен для всех значений 𝜃, так как синус является нечетным
функция. Грех отрицательного 𝜃 всегда
равно отрицательному греху 𝜃.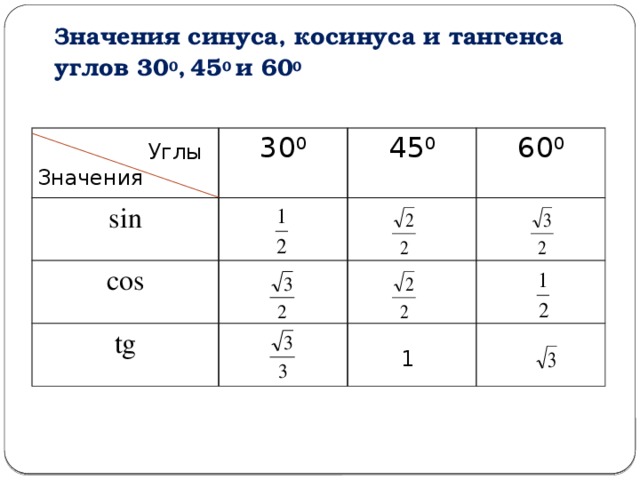 Это означает, что поскольку грех двух 𝜋
минус 𝜃 равен греху отрицательного 𝜃, он также равен отрицательному греху 𝜃. 𝑦-координата точки 𝑁 может
быть записано как отрицательный грех 𝜃.
Это означает, что поскольку грех двух 𝜋
минус 𝜃 равен греху отрицательного 𝜃, он также равен отрицательному греху 𝜃. 𝑦-координата точки 𝑁 может
быть записано как отрицательный грех 𝜃.
Теперь мы выразили значения sin и cos двух 𝜋 минус 𝜃 с точки зрения их значений для 𝜃. грех двух 𝜋 минус 𝜃 равно отрицательный грех 𝜃 и потому что два 𝜋 минус 𝜃 равно cos 𝜃. Теперь мы можем найти выражение для тангенс двух 𝜋 минус 𝜃, используя одно из наших тригонометрических тождеств. Мы знаем, что загар под любым углом 𝛼 равно sin 𝛼, деленному на cos 𝛼. Если разделить первое уравнение на во-вторых, у нас есть грех двух 𝜋 минус 𝜃 над потому что два 𝜋 минус 𝜃 равен к отрицательному греху 𝜃 над потому что 𝜃. Используя приведенное ниже тождество, левая часть упрощается до тангенса двух 𝜋 минус 𝜃, а правая — до негативный загар 𝜃.
Теперь у нас есть три выражения
требуется, значения sin, cos и тангенса двух 𝜋 минус 𝜃 с точки зрения их
значения для 𝜃.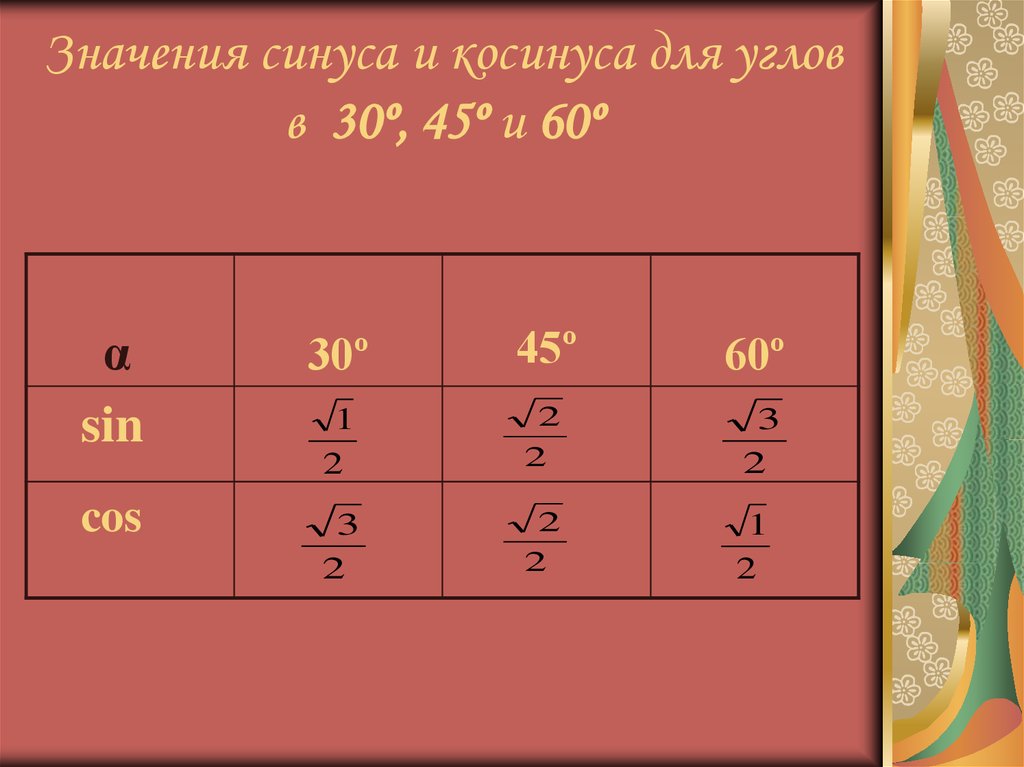 Нас также просят проверить,
это справедливо для всех значений 𝜃. Если мы позволим точке 𝑃 лежать в первом
квадрант, как показано на схеме, где угол 𝐴𝑂𝑃 равен некоторому другому
значение 𝜃, то точка 𝑄, где угол против часовой стрелки 𝐴𝑂𝑄 равен
два 𝜋 минус 𝜃, будут лежать в четвертом квадранте, как показано.
Нас также просят проверить,
это справедливо для всех значений 𝜃. Если мы позволим точке 𝑃 лежать в первом
квадрант, как показано на схеме, где угол 𝐴𝑂𝑃 равен некоторому другому
значение 𝜃, то точка 𝑄, где угол против часовой стрелки 𝐴𝑂𝑄 равен
два 𝜋 минус 𝜃, будут лежать в четвертом квадранте, как показано.
И снова эти точки будут
одна и та же 𝑥-координата, тогда как 𝑦-координаты будут аддитивными, обратными
друг друга. Если точка 𝑃 имеет координаты 𝑥,
𝑦, то точка 𝑄 будет иметь координаты 𝑥, минус 𝑦. И поэтому мы можем сделать вывод, что
выражения для sin, cos и tan двух 𝜋 минус 𝜃 с точки зрения их
значения 𝜃 верны для всех значений 𝜃 в единичном круге. Грех двух 𝜋 минус 𝜃 равно
к отрицательному греху 𝜃. Кос двух 𝜋 минус 𝜃 равно
к потому что 𝜃. И загар двух 𝜋 минус 𝜃 это
равен отрицательному загару 𝜃.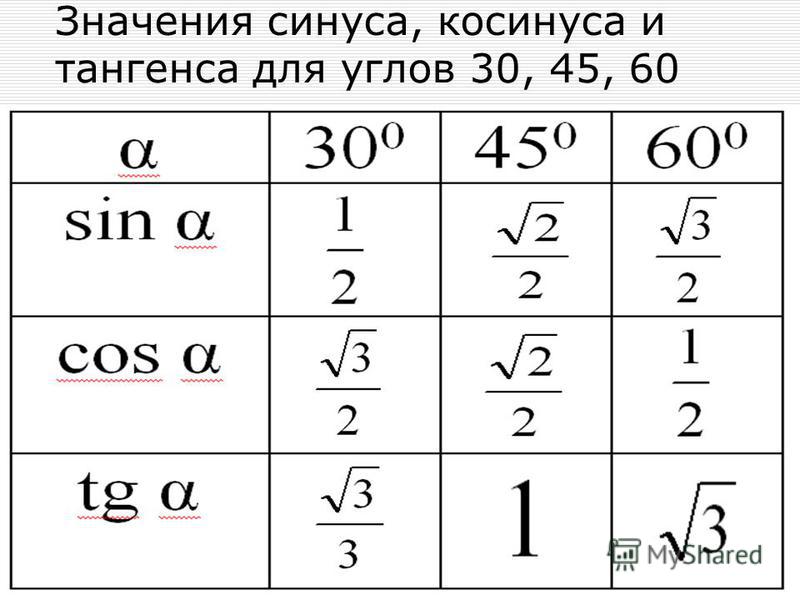 Обратите внимание, что во всех трех случаях
два 𝜋 радиана можно заменить на 360 градусов.
Обратите внимание, что во всех трех случаях
два 𝜋 радиана можно заменить на 360 градусов.
Анимированные синус и косинус
Анимированные синус и косинусАнимированные синус и косинус
Элементарные определения: синус, cosine
Таблица запуска: синус и косинус
Подробная информация о: синус, косинус
Unit Circle: вводная страница
- Синус и косинус
Эта страница содержит более подробное описание поведение синуса (вертикальная составляющая угла или отношение противоположного катета к гипотенузе) и косинус (горизонтальная составляющая угла или отношение прилежащего катета к гипотенузе). Для более широкого обзора триггерных функций см. страницу Unit Circle.
- При нуле градусов, ноль радианов
Как только вы избавитесь от того факта, что вы работать с треугольником, имеющим угол 0° и длину стороны 0, легко.

Вертикальный катет равен 0, поэтому синус равен 0.
Горизонтальный катет равен радиусу, который равен 1. Следовательно, косинус равен 1.
Далее рассмотрим другой способ сказать то же самое, но описав сам угол и единичный круг, а не только треугольник. Вертикальная составляющая угла отсутствует: Вертикальная составляющая угла равна 0, поэтому синус 0° равен 0.
Горизонтальная составляющая угла настолько велика, насколько это возможно. Радиус равен 1, поэтому горизонтальная составляющая равна 1: косинус 0° равен 1.
- В первом квадранте
При увеличении угла от 0° до 90° синус увеличивается от 0 до 1.
При увеличении угла от 0° до 90°, косинус уменьшается от 1 до 0.
- На 90 градусов, /2 радиана
Опять у вас есть угол 0° и сторона длиной 0.

На этот раз вертикальный катет равен 1, как и радиус, поэтому синус равен 1.
Горизонтальный катет равен 0, так как горизонтальной составляющей треугольника нет, поэтому косинус равен 0,
Рассмотрим сам угол и единичную окружность. отсутствует горизонтальная составляющая угол: горизонтальная составляющая угла равна 0, поэтому косинус 90° равен 0.
Вертикальная составляющая угла настолько велика, насколько это возможно. Радиус равен 1, поэтому вертикальная составляющая равна 1: синус 90° равен 1,
- Во втором квадранте
По мере увеличения угла от 90° до 180° синус уменьшается от своего максимальное значение от 1 до значения 0,
По мере увеличения угла от 90° до 180° косинус увеличивается по величине, но теперь отрицательное значение. Косинус идет от 0 до -1.
- На 180 градусов, Радиан
Опять угол 0° и сторона с длиной 0.
 Значения указаны выше.
Значения указаны выше.Снова рассмотрим сам центральный угол и единичную окружность. нет вертикальной составляющей угла: вертикальная составляющая угла равна 0, поэтому синус 180 ° равен 0.
Горизонтальная составляющая угла настолько велика, насколько это возможно, но она также отрицательна. Горизонтальная составляющая равна -1: косинус 180° равен -1.
- В третьем квадранте
Координаты x и y в третьем квадранте отрицательны.
Поскольку гипотенуза равна +1, и синус, и косинус должны быть отрицательными.
При увеличении угла от 180° до 270° синус увеличивается в величина, но теперь отрицательная, поэтому синус уменьшается от 0 до -1.
При увеличении угла от 180° до 270° косинус уменьшается в величина, но теперь отрицательная, поэтому косинус увеличивается с минимума -1 до значения 0,
- На 270 градусов, 3/2 радиана
Опять у вас есть угол 0° и сторона с длиной 0.
 Значения указаны выше.
Значения указаны выше.Рассмотрим сам центральный угол и единичную окружность. Горизонтальная составляющая отсутствует. угла: горизонтальная составляющая угла равна 0, поэтому косинус 270° равен 0.
Вертикальная составляющая угла равна радиусу, но также имеет отрицательное значение. Вертикальная составляющая равна -1: синус 270° равен -1.
- В четвертом квадранте
При увеличении угла с 270° до 360° синус увеличивается с -1 до 0.
При увеличении угла с 270° до 360° косинус увеличивается с от 0 до +1.
© 2006, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/330/unitsin.htm |
Исследование синусоиды
Исследование синусоиды
по
Чад Крамли
Это исследование функции y =
a sin b(x — h) + k , где a, b,
h и k — разные значения.
В частности, как эти значения преобразуют график y= sin x . Прежде чем мы начнем, вот как выглядят эти графики
где a, b равны 1, а h, k равны 0.
Константа a
Поскольку a положительны и возрастают, что происходит с графиком? ( a = 1 красный, a = 2 фиолетовый, a = 3 Aqua, A = 3,5 желтого, A = 5 синий, A = 5,8 зеленый)
Таким образом, A . График растянут по вертикали (как в положительную, так и в отрицательную сторону) к значению a . Например, максимальное и минимальное значения, достигнутые синим графиком (когда a = 5), равны 5. Начиная с исходной точки, положительный значение a заставляет график идти вверх первым.
Что происходит, когда a является положительным и уменьшается? ( A = 1 — красным, A = 0,8 Зеленый, A = 0,7 Aqua, A = 0,6 Желтый, A = 0,6, A = 0,6
 a = 0,2 синий)
a = 0,2 синий)
Те же результаты, что и выше, за исключением того, что значение a уменьшается, а график не растягивается наружу но вдавливается внутрь.
Когда и отрицательные? ( A = 1 -красным, A = -1 Фиолетовый, A = -2 Aqua, A = -0,5 Желтый)
Абсолютное значение a называется амплитудой .
графика.
Константы h, k
Для этого исследования a и b будут равны 1. Кроме того, k будет равно 0, так что мы можем сосредоточиться на h . Чтобы упростить некоторые вычисления, ч будет равно некоторой константе, умноженной на число Пи.
Кроме того, k будет равно 0, так что мы можем сосредоточиться на h . Чтобы упростить некоторые вычисления, ч будет равно некоторой константе, умноженной на число Пи.
При увеличении ч что происходит с график? ( h = 0 красный, h = 0,5 фиолетовый, h = 1 синий)
По мере уменьшения h? ( H = 0 в красном, H = -0,25 фиолетового цвета, H = -0,75 Blue)
Выводы: Графики, по -видимому, переводятся правые с правой . перевести влево с меньшим ч .
Теперь пусть ч = 0 и пусть исследовать k .
Вот графики с a =1, b =1, и h = 0. k = 0 выделено красным, k = 1 фиолетовым, k = -0,5 синим.
Выводы: Графики сдвигаются вверх с положительным значением для k и вниз с отрицательным значением k . Наряду с переходом y-перехваты для
кривые к значений.
Наряду с переходом y-перехваты для
кривые к значений.
Константа б
Для этого исследования и будут равны 1 и
h, k будут равны 0.
При увеличении b что происходит с график? ( b = 1 красный, b = 2 фиолетовый, b = 3 синий)
Сравнение графиков с исходным графиком (как будто какая-то сила давит на пружину). Кроме того, фиолетовый график завершает 2 полные циклы от 0 до 2 пи, а синий график завершает 3 цикла. Сравнение период графиков, период красного графика 2 пи, период фиолетовый график равен пи, а период синего графика равен 2 пи / 3,
А б уменьшается? ( b = 1 красный, b = 0,5 фиолетовый, b = 0,25 синий)
вытягивается наружу (как перетянутая пружина). Фиолетовый график завершает один
цикл от 0 до 12 pi, что в два раза длиннее родителя. Синий график
завершает один цикл от 0 до 8 pi, что в 4 раза дольше родительского
график.
Синий график
завершает один цикл от 0 до 8 pi, что в 4 раза дольше родительского
график.
b остается положительным или график отражать по оси x из-за теоремы противоположностей: sin (-x) = -sin (х) .
Сводка
Абсолютное значение и представляет собой амплитуду (вертикальное растяжение).
Период представляет собой 2 пи / (абсолютное значение b ).
ч представляет
сдвиг по горизонтали (или фазовый сдвиг). Терминология фазового сдвига представляет
насколько график сдвинут вправо или влево от исходного положения. 9\circ.$
Ссылка
- Д. С. Айлес, Треугольники и тригонометрия , Учитель математики 64 (1971) 562
- Р. Вакил, Математическая мозаика , Издательство Брендана Келли, 2008 г. (расширенное издание)
Тригонометрия
- Что такое тригонометрия?
- Формулы сложения и вычитания для синуса и косинуса
- Синус формулы суммы
- Формулы сложения и вычитания для синуса и косинуса II
- Формулы сложения и вычитания для синуса и косинуса III
- Формулы сложения и вычитания для синуса и косинуса IV
- Формулы сложения и вычитания
- Закон косинусов (правило косинусов)
- Косинус 36 градусов
- Тангенс 22,5 o — Доказательство без слов
- Синус и косинус угла 15 градусов
- Синус, косинус и теорема Птолемея
- арктангенс(1) + арктангенс(2) + арктангенс(3) = π
- Тригонометрия по наблюдению
- арктангенс (1/2) + арктангенс (1/3) = арктангенс (1)
- Чудо Морли
- Теорема Наполеона
- Тригонометрическое решение сложной задачи сангаку
- Тригонометрическая форма комплексных чисел
- Производные синуса и косинуса
- ΔABC верно тогда и только тогда, когда sin²A + sin²B + sin²C = 2
- Расширенные удостоверения
- Охотничьи прямые углы
- Точка на биссектрисе прямого угла
- Тригонометрические тождества с арктангенсами
- Совпадение высот в треугольнике — тригонометрическое доказательство
- Тригонометрия бабочки
- Формула Бине с косинусами
- Другое лицо и доказательство тригонометрической идентичности
- неравенство cos/sin
- На пересечении kx и |sin(x)|
- Севианы и полукруги
- Формулы двойного и половинного угла
- Хорошая формула триггера
- Еще одно золотое сечение в полукруге
- Тригонометрическая лемма Лео Джуджука
- Другое свойство точек на вписанной окружности
- Многое из малого
- Закон косинусов и закон синусов эквивалентны
- Замечательная тригонометрия в равностороннем треугольнике
- Тригонометрическое наблюдение в прямоугольном треугольнике
- Быстрое доказательство cos(pi/7)cos(2.



 д.
д. 
 Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
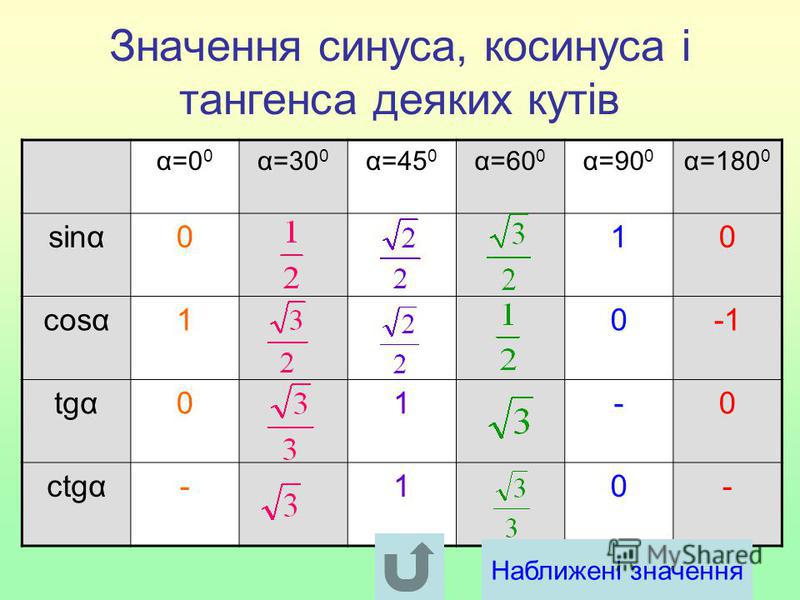 docx
docx
 Видим, что ордината (басом) у угла 30 градусов самая маленькая, значит, синус (пискляво) равен самой маленькой из этих трех величин — одной второй. А абсцисса (пискляво) у этого угла сама большая, значит, косинус (басом) равен самой большой величине — корню из трех на два (простите, что числа пишу словами, в Дзен сложно вставлять формулы в текст).
Видим, что ордината (басом) у угла 30 градусов самая маленькая, значит, синус (пискляво) равен самой маленькой из этих трех величин — одной второй. А абсцисса (пискляво) у этого угла сама большая, значит, косинус (басом) равен самой большой величине — корню из трех на два (простите, что числа пишу словами, в Дзен сложно вставлять формулы в текст).
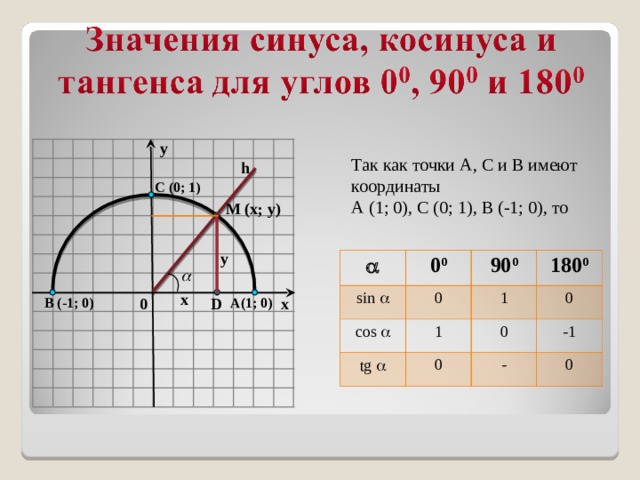
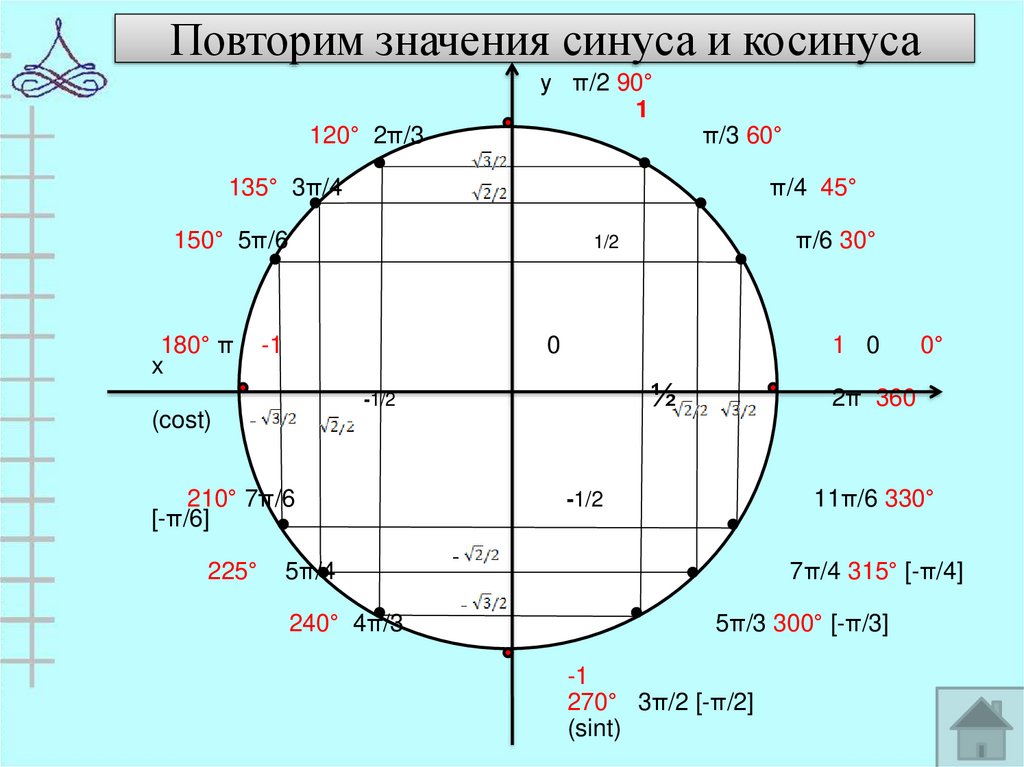 html
html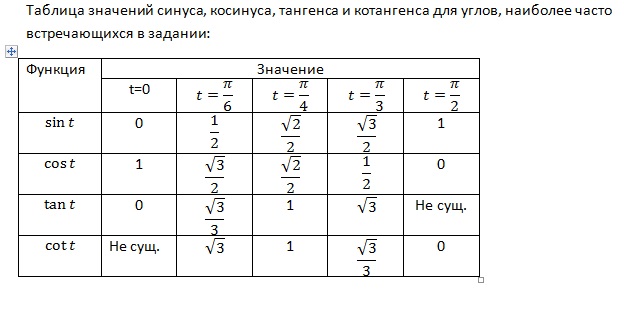 Это самая длинная сторона из трех сторон
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов
что означает «растягиваться», так как это самая длинная сторона. Обозначим гипотенузу символом ч .
Против угла c находится сторона, которую мы обозначили как o .
для «наоборот». Оставшуюся сторону обозначим цифрой 9.0094 и для «соседнего».
Угол c образован пересечением гипотенузы h и соседняя сторона a .
Это самая длинная сторона из трех сторон
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов
что означает «растягиваться», так как это самая длинная сторона. Обозначим гипотенузу символом ч .
Против угла c находится сторона, которую мы обозначили как o .
для «наоборот». Оставшуюся сторону обозначим цифрой 9.0094 и для «соседнего».
Угол c образован пересечением гипотенузы h и соседняя сторона a .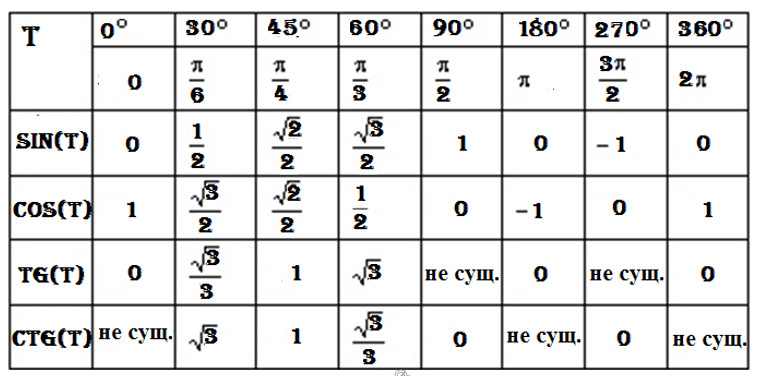
 Отношение остается неизменным для любого прямоугольного треугольника.
с углом 75,5 градусов.)
Если мы измерим место на стене, где лестница соприкасается (o — напротив), расстояние равно
7,745 футов. Вы можете проверить это расстояние с помощью
Теорема Пифагора
которая связывает стороны прямоугольного треугольника:
92 = 64 — 4 = 60
Отношение остается неизменным для любого прямоугольного треугольника.
с углом 75,5 градусов.)
Если мы измерим место на стене, где лестница соприкасается (o — напротив), расстояние равно
7,745 футов. Вы можете проверить это расстояние с помощью
Теорема Пифагора
которая связывает стороны прямоугольного треугольника:
92 = 64 — 4 = 60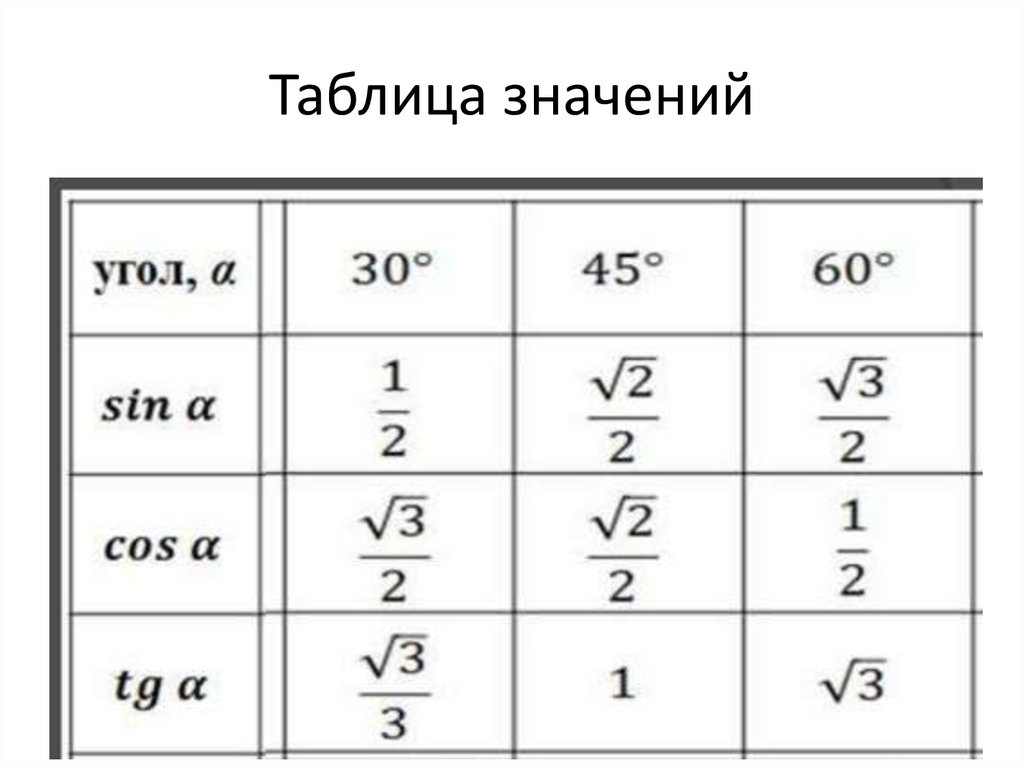 Как видите, для каждого угла
на земле есть уникальная точка, которой касается 8-футовая лестница,
и это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом.
Математики называют эту ситуацию
функция.
Соотношение соседних
сторона гипотенузы есть функция угла c , поэтому мы можем написать
символ как cos(c) = значение .
Как видите, для каждого угла
на земле есть уникальная точка, которой касается 8-футовая лестница,
и это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом.
Математики называют эту ситуацию
функция.
Соотношение соседних
сторона гипотенузы есть функция угла c , поэтому мы можем написать
символ как cos(c) = значение .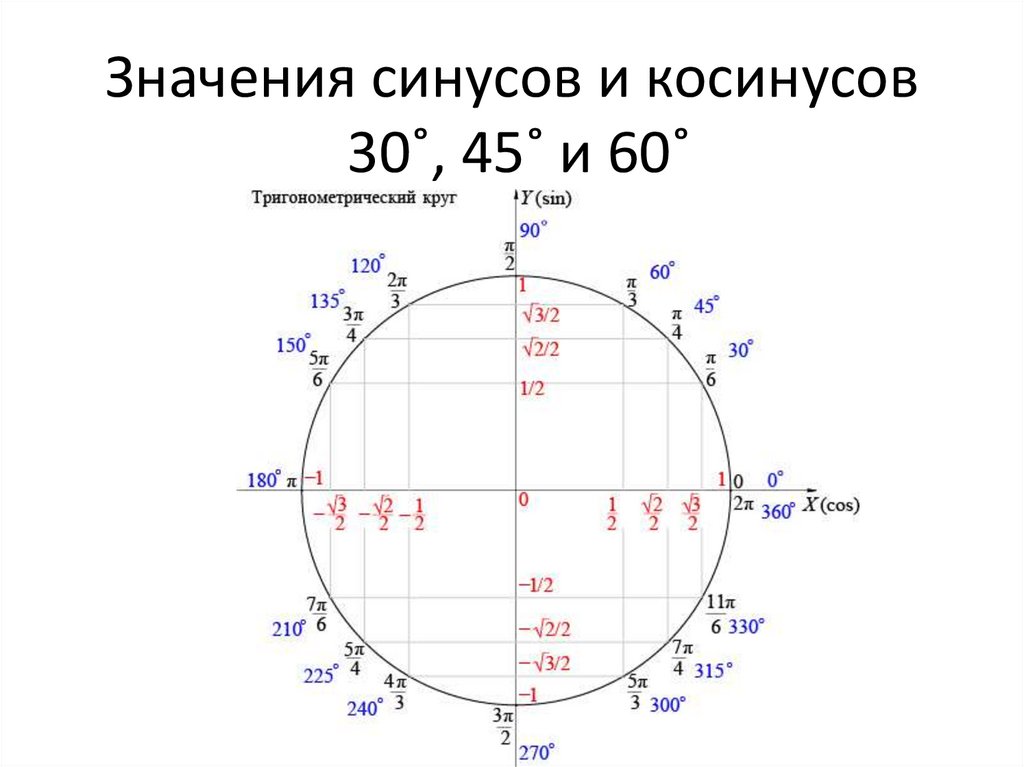 Вот почему мы
отношение прилежащего к гипотенузе называют косинусом угла.
Вот почему мы
отношение прилежащего к гипотенузе называют косинусом угла.


 Значения указаны выше.
Значения указаны выше. Значения указаны выше.
Значения указаны выше.