Знак соотношения: Соотношения

Соотношение и Пропорция

Основой математических исследований является возможность получить знание об определённых величинах, сравнивая их с другими величинами, которые либо равны, либо больше или меньше, чем те которые являются предметом исследования. Это обычно производится с помощью ряда уравнений и пропорций. Когда мы используем уравнения, то мы определяем искомую величину, находя её равенство с какой-то другой уже знакомой величиной или величинами.

Однако, часто бывает, что мы сравниваем неизвестную величину с другими, которые не равны ей, а больше или меньше её. Здесь нужен другой подход к обработке данных. Нам может понадобиться узнать, например, на сколько одна величина больше чем другая, или сколько раз одна содержит другую. Для нахождения ответа на эти вопросы мы узнаем что такое соотношение двух величин. Одно соотношение называется арифметическим, а другое геометрическим.

Хоть и стоит заметить, что оба эти термина не были приняты случайно или только в целях отличия. Как арифметическое, так и геометрическое соотношения применимы как к арифметике, так и к геометрии.

Являясь компонентом обширного и важного предмета, пропорция зависит от соотношений, поэтому необходимо чёткое и полное понимание этих понятий.

338. Арифметическое соотношение это разница между двумя величинами или рядом величин. Сами по себе величины называются членами соотношения, то есть члены, между которыми есть соотношение. Таким образом 2 это арифметическое соотношение 5 и 3. Это выражается помещая знак минус между двумя величинами, то есть 5 — 3. Конечно термин арифметического соотношения и его расписывание по пунктам практически бесполезно, так как происходит лишь замещение слова разница на знак минус в выражении.

339. Если оба члена арифметического соотношения умножить или разделить на одну и ту же величину, то

соотношение, в конечном итоге, будет умножено или разделено на эту величину.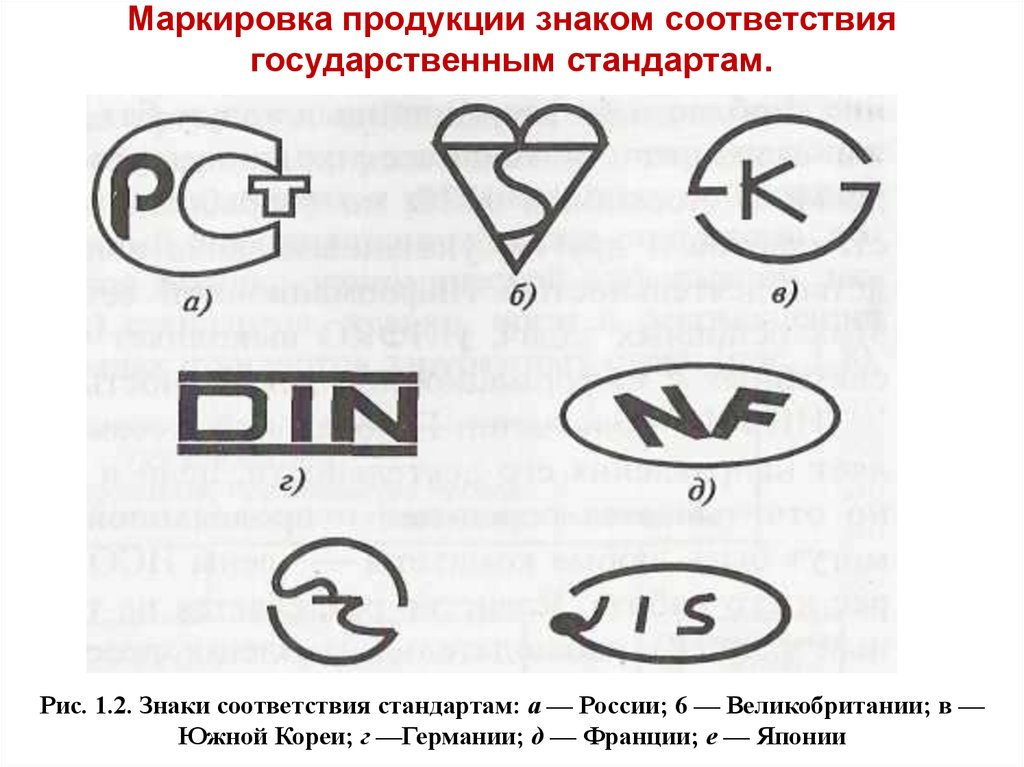
Таким образом, если имеем      a — b = r
Тогда перемножим обе стороны на h , (Акс. 3.) ha — hb = hr
И разделив на h, (Акс. 4.) $\frac{a}{h}-\frac{b}{h}=\frac{r}{h}$

340. Если члены арифметического соотношения добавляют или отнимают от соответствующих членов другого, то соотношение суммы или разности будет равно сумме или разности двух соотношений.
Если a — b
И d — h,
являются двумя соотношениями,
Тогда (a + d) — (b + h) = (a — b) + (d — h). Что в каждом случае = a + d — b — h.
И (a — d) — (b — h) = (a — b) — (d — h). Что в каждом случае = a — d — b + h.
      Таким образом арифметическое отношение 11 — 4 равно 7
      И арифметическое отношение 5 — 2 равно 3
Отношение суммы членов 16 — 6 это 10, — сумма соотношений.

Отношение разности членов 6 — 2 это 4, — разность соотношений.

341. Геометрическое соотношение — это отношение между величинами, которое выражается ЧАСТНЫМ, если одну величину делят на другую.
Таким образом соотношение 8 к 4, можно записать как 8/4 или 2. То есть частное деления 8 на 4. Другими словами, оно показывает сколько раз 4 содержится в 8.

Тем же самым способом, соотношение любой величины к другой может быть определено, разделив первую на вторую или, что, в принципе, одно и то же, сделав первую числителем дроби, а вторую — знаменателем.
            Так соотношение a к b это $\frac{a}{b}$
            Соотношение d + h к b + c это $\frac{d+h}{b+c}$.

342. Геометрическое соотношение также записывается, размещая две точки одну над другой между сравниваемыми величинами.

Таким образом a:b это запись соотношения a к b, а 12:4 — соотношения 12 к 4. Две величины вместе формируют пару, в которой первый член называется антецедентом, а последний — консеквентом.

343. Эта запись с помощью точек и другая, в форме дроби, являются взаимозаменяемыми по мере необходимости, при этом антецедент становится числителем дроби, а консеквент — знаменателем.
Таким образом 10:5 это то же, что и $\frac{10}{5}$ а b:d, то же, что и $\frac{b}{d}$.

344. Если из этих трёх значений: антецедента, консеквента и соотношения даны любые два, то третье можно найти.

Пусть a= антецедент, c= консеквент, r= соотношение.
По определению $r=\frac{a}{c}$, то есть, соотношение равно антецеденту разделённому на консеквент.
Умножая на c, a = cr, то есть, антецедент равен консеквенту умноженному на соотношение.
Разделим на r, $c=\frac{a}{r}$, то есть, консеквент равен антецеденту делёному на соотношение.

Соотв. 1. Если у двух пар антецеденты и консеквенты равны, то их соотношения тоже равны.

Соотв. 2. Если у двух пар соотношения и антеценденты равны, то и консеквенты равны и если соотношения и консеквенты равны, то и антецеденты равны.

345. Если две сравниваемые величины равны, то их соотношение равно единице или соотношению равенства. Соотношение 3*6:18 равно единице, так как частное любой величины разделённой на саму себя равно 1.

Если антецедент пары больше, чем консеквент, то соотношение больше единицы. Так как делимое больше, чем делитель, то частное больше единицы. Так соотношение 18:6 равно 3. Это называется соотношение большего неравенства.

С другой стороны, если антецедент меньше, чем консеквент, то соотношение меньше единциы и это называется соотношением меньшего неравенства. Так соотношение 2:3 меньше единицы, потому что делимое меньше делителя.

346. Обратное соотношение — это соотношение двух обратных величин.
Так соотношение обратное 6 к 3 это ⅙ к ⅓, то есть ⅙:⅓.
Прямое соотношение a к b это $\frac{a}{b}$, то есть антецедент разделённый на консеквент.
Обратное соотношение это $\frac{1}{a}$:$\frac{1}{b}$ или $\frac{1}{a}.\frac{b}{1}=\frac{b}{a}$.
то есть косеквент b разделённый на антецедент a.

Отсюда обратное соотношение выражается путём инвертирования дроби, которая отображает прямое соотношение, либо, когда запись ведётся с помощью точек, инвертируя порядок записи членов.
Таким образом a относится к b обратно тому, как b к a.

347. Сложное соотношение это соотношение произведений соответствующих членов с двумя и более простыми соотношениями.
            Так соотношение          6:3, равно 2
            И соотношение           12:4, равно 3
Составленное из них соотношение           72:12 = 6.

Здесь сложное соотношение получается, умножая между собой два антецедента и также два консеквента простых соотношений.
Так соотношение составленное
      Из соотношения         a:b
      И соотношения            c:d
      и соотношения             h:y

      Это соотношение         $ach:bdy=\frac{ach}{bdy}$.
Сложное соотношение не отличается по своей природе от любого другого соотношения. Этот термин используется, чтобы в определённых случаях показать происхождение соотношения.

Соотв. Сложное соотношение равно произведению простых соотношений.
      Соотношение        a:b, равно $\frac{a}{b}$
      Соотношение         c:d, равно $\frac{c}{d}$
      Соотношение         h:y, равно $\frac{h}{y}$
И соотношение сложенное из этих трёх будет ach/bdy, что является произведением дробей, которые выражают простые соотношения.

348. Если в последовательности соотношений в каждой предыдущей паре консеквент является антецедентом в последующей, то соотношение первого антецедента и последнего консеквента равны тому, которое получено из промежуточных соотношений.

Так в ряде соотношений
            a:b
            b:c
            c:d
            d:h
соотношение a:h равно соотношению, сложенному из соотношений a:b, и b:c, и c:d, и d:h. Так сложное соотношение в последней статье равно $\frac{abcd}{bcdh}=\frac{a}{h}$, или a:h.

Таким же образом все величины, которые являются и антецедентами и консеквентами исчезнут, когда произведение дробей будет упрощено до своих младших членов и в остатке сложное соотношение будет выражаться первым антецедентом и последним консеквентом.

349. Особый класс сложных соотношений получается при умножении простого соотношения на самого себя или на другое равное соотношение. Эти соотношения называются двойными, тройными, четверными, и так далее, в соответствии с количеством операций умножения.

Соотношение, составленное из двух равных соотношений, то есть, квадрата простого соотношения, называют двойным соотношением.

Составленное из трёх, то есть, куб простого соотношения, называют тройным, и так далее.

Аналогично соотношение квадратных корней двух величин, называется соотношением квадратного корня, а соотношение кубических корней — соотношением кубического корня, и так далее.
      Таким образом простое соотношение a к b, равно a:b
      Двойное соотношение a к b, равно a²:b²
      Тройное соотношение a к b, равно a³:b³
      Соотношение квадратного корня a к b, равно √a:√b
      Соотношение кубического корня a к b, равно ³√a:³√b, и так далее.
      Термины двойной, тройной, и так далее не нужно смешивать с удвоенным, утроенным, и так далее.

Соотношение 6 к 2 равно      6:2 = 3
Удвоим это соотношение, то есть, соотношение дважды, то получим   12:2 = 6
Утроим это соотношение, то есть это соотношение трижды, то получим  18:2 = 9
А двойное соотношение, то есть квадрат соотношения, равен 6²:2² = 9
И тройное соотношение, то есть куб соотношения, равен 6³:2³ = 27

350. Для того, чтобы величины можно соотнести друг с другом, они должны быть одинакового рода, так, чтобы можно было с уверенностью утверждать равны ли они между собой, или одна из них больше или меньше. Фут относится к дюйму, как 12 к 1: он в 12 раз больше, чем дюйм. Но нельзя, например, сказать, что час длиннее или короче, чем палка, или акр больше или меньше, чем градус. Однако, если эти величины выражены в числах, то может существовать соотношение между этими числами. То есть может существовать соотношение между количеством минут в часе и количеством шагов в миле.

351. Обратившись к природе соотношений, следующим шагом нам нужно учесть способ, каким образом скажется на самом соотношении изменение одного или двух членов, которые сравнивают между собой. Вспомним, что прямое соотношение выражается в виде дроби, где антецедет пары всегда это числитель, а консеквент — знаменатель. Тогда будет легко из свойства дробей получить, что изменения в соотношении происходят путём варьирования сравниваемых величин. Соотношение двух величин такое же как и значение дробей, каждая из которых представляет частное: числитель делённый на знаменатель. (Статья. 341.) Теперь было показано, что умножать числитель дроби на любую величину, это то же, что и умножать значение на эту же величину и что деленить числитель, это то же, что и деленить значения дроби. Поэтому,

352. Умножать антецедент пары на любую величину, значит умножать соотношения на эту величину, а делить антецедент — деленить это соотношение.
            Таким образом соотношение      6:2 равное 3
            И соотношение      24:2 равное 12.
Здесь антецедент и соотношение в последней паре в 4 раза больше, чем в первой.
Отношение a:b равно      $\frac{a}{b}$
И отношение na:b равно $\frac{na}{b}$.

Соотв. При известном консеквенте, чем больше антецедент, тем больше соотношение, и, наоборот, чем больше соотношение, тем больше антецедент.

353. Умножая консеквент пары на любую величину, в результате получаем деление соотношения на эту величину, а деля консеквент — умножаем соотношение. Умножая знаменатель дроби, делим значение, а деля знаменатель — значение умножается..
      Так соотношение 12:2 равно 6
      И соотношение 12:4 равно 3.
Здесь консеквент второй пары в два раза больше, а соотношение в два раза меньше, чем первое.
            Соотношение a:b равно $\frac{a}{b}$
      И соотношение a:nb равно $\frac{a}{nb}$.

Соотв. При данном антецеденте, чем больше консеквент, тем меньше соотношение. И наоборот, чем больше соотношение, тем меньше консеквент.

354. Из двух последних статей следует, что умножение антецедента пары на любую величину окажет такой же эффект на соотношение, как деление консеквента на эту величину, а деление антецедента, окажет такой же эффект, как умножение консеквента.
      Поэтому соотношение         8:4, равно 2
      Умножая антецедент на 2, соотношение 16:4 равно 4
      Разделив антецедент на 2, соотношение 8:2 равно 4.

Соотв. Любой множитель или делитель может быть перенесён от антецедента пары к консеквенту или от консеквента к антецеденту без изменения соотношения.

Стоит заметить, что когда множитель таким образом переносится от одного члена к другому, то он становится делителем, а переносимый делитель становится множителем.
      Так соотношение      3.6:9 = 2
Перенеся множитель 3,      $6:\frac{9}{3}=2$
то же самое соотношение.

Соотношение      $\frac{ma}{y}:b=\frac{ma}{by}$
Перенеся y      $ma:by=\frac{ma}{by}$
Перенеся m,      a:$a:\frac{m}{by}=\frac{ma}{by}$.

355. Как очевидно из Статей. 352 и 353, если антецедент и консеквент оба умножить или разделить на одну и ту же величину, то соотношение не меняется.

Соотв. 1. Соотношение двух дробей, у которых есть общий знаменатель, такое же как отношение их числителей.
Таким образом соотношение a/n:b/n, то же самое, что и a:b.

Соотв. 2. Прямое соотношение двух дробей, у которых есть общий числитель, равно обратному соотношению их знаменателей.

356. Из статьи легко определить соотношение любых двух дробей. Если каждый член умножить на два знаменателя, то соотношение будет задано интегральными выражениями. Таким образом умножая члены пары a/b:c/d на bd, получаем $\frac{abd}{b}$:$\frac{bcd}{d}$, что становится ad:bc, путём сокращения общих величин из числителей и знаменателей.

356. b. Соотношение большего неравенства, сложенное с другим соотношением, увеличивает его
Пусть соотношение большего неравенства будет задано как      1+n:1
И любое соотношение как          a:b     
Сложное соотношение будет (Статья. 347,)     a + na:b
Что больше, чем соотношение a:b (Статья. 351. соотв.)
Но соотношение меньшего неравенства, сложенное с другим соотношением, уменьшает его.
Пусть соотношение меньшей разности      1-n:1
Любой заданное соотношение          a:b     
Сложное соотношение        a — na:b
Что меньше, чем a:b.

357. Если к или от членов любой пары прибавить или отнять две другие величины, которые находятся в таком же соотношении, то суммы или остатки будут иметь такое же соотношение.
      Пусть соотношение      a:b
      Будет такое же, как и       c:d
Тогда соотношение суммы антецедентов к сумме консеквентов, а именно, a + c to b + d, тоже одинаковое.
То есть $\frac{a+c}{b+d}$ = $\frac{c}{d}$ = $\frac{a}{b}$.

Доказательство.

1. Согласно предположению,         $\frac{a}{b}$ = $\frac{c}{d}$
2. Умножаем на b и на d,         ad = bc
3. Добавляем cd к обеим сторонам,         ad + cd = bc + cd
4. Делим на d,          $a+c=\frac{bc+cd}{d}$
5. Делим на b + d,            $\frac{a+c}{b+d}$ = $\frac{c}{d}$ = $\frac{a}{b}$.

Соотношение разницы антецедентов к разнице консеквентов также одинаковое.

358. Если в нескольких парах соотношения равны, то сумма всех антецедентоа относится к сумме всех консеквентов, как любой антецедент к своему консеквенту.
Таким образом соотношение
            |12:6 = 2
            |10:5 = 2
            |8:4 = 2
            |6:3 = 2
Таким образом соотношение (12 + 10 + 8 + 6):(6 + 5 + 4 + 3) = 2. 2-ab+ax)}{a(a+x)}$.

Так как последний числитель больше, чем другой, то соотношение больше.
        Если вместо добавления ту же самую величину отнять от двух членов, то очевидно, что эффект на соотношение будет обратным.

Примеры.

1. Что больше: соотношение 11:9, или соотношение 44:35?

2. Что больше: соотношение $(a+3):\frac{a}{6}$, или соотношение $(2a+7):\frac{a}{3}$?

3. Если антецедент пары равен 65, а соотношение равно 13, то какой консеквент?

4. Если консеквент пары равен 7, и соотношение равно 18, то какой антецедент?

5. Как выглядит сложное соотношение составленное из 8:7, и 2a:5b, а также (7x+1):(3y-2)?

6. Как выглядит сложное соотношение составленное из (x+y):b, и (x-y):(a + b), а также (a+b):h?         Отв. (x² — y²):bh.

7. Если соотношения (5x+7):(2x-3), и $(x+2):\left(\frac{x}{2}+3\right)$ образуют сложное соотношение, то какое соотношение получится: большее или меньшее неравенство?      Отв. 2}{a}$?         Отв. Соотношение равенства.

9. Каково соотношение сложенное из 7:5, и удвоенного соотношения 4:9, и утроенного соотношения 3:2?
              Отв. 14:15.

10. Каково соотношение составленное из 3:7, и утроенного соотношения x:y, и извлечения корня из соотношения 49:9?
              Отв. x³:y³.

Знак соответствия РСТ, знак соответствия продукции

Таблицы кодов

Общероссийский классификатор продукции (ОКП)

Товарная номенклатура внешнеэкономической деятельности (ТН ВЭД)

Полезная информация

Применение знаков соответствия даёт массу преимуществ, главным среди которых является доверие к выпускаемой продукции со стороны покупателей

Для обеспечения защиты потребителей от некачественных услуг, товаров или продукции в России разработаны и действуют специализированные системы сертификации, которые являются совокупностью и комплексом мероприятий, направленных на всестороннюю оценку свойств и характеристик продукции и установления или подтверждения её соответствия принятым стандартам и нормативам качества. Итоговым результатом сертификации считается выдача и дальнейшая регистрация соответствующих разрешительных документов.

Наряду с существованием в РФ систем обязательной сертификации в стране также действуют более двухсот добровольных, практически каждая из которых имеет собственный знак соответствия, зарегистрированный согласно установленным порядкам.

Знак соответствия является своеобразной эмблемой, которая подтверждает соответствие характеристик и свойств продукции требованиям и правилам конкретной системы сертификации, сертификационной организации или установленному стандарту. Данным знаком маркируется товар, упаковочный материал или товарный ярлык.

---

Основная цель маркировки заключается в следующем:

• возможность наглядного предоставления потребителям информации о соответствии выбранной ими продукции установленным качественным требованиям и наличии сертификационной разрешительной документации на конкретный вид товара;
• определение организации проводившей сертификацию продукции;
• обозначение выбранной системы сертификации;
• использование знака в рекламных целях для увеличения спроса на товар, поскольку именно продукция, прошедшая все этапы сертификации, пользуется большим доверием у покупателей.

Наибольшую известность и популярность среди потребителей и производителей продукции получил знак соответствия РСТ, который устанавливает и подтверждает факт проведения сертификации в национальной системе ГОСТ. Не следует также путать используемый знак РСТ со знаком обращения на рынке, поскольку это два совершенно разных, как по смысловому назначению, так и по виду символа.

Знак РСТ является графическим изображением, которое свидетельствует о прохождении продукции сертификации и соответствии её установленным российским стандартам качества. Знак РСТ наносится непосредственно на саму продукцию или её упаковку, ярлык, этикетку, а также сопроводительную техническую документацию.

Выделяется всего несколько знаков соответствия, правила нанесения и обозначение которых зависит от формы и области применения сертификации, в которой осуществлялась оценка безопасности и качества продукции:

• знак соответствия при проведении обязательной сертификации – ставится на продукцию, для которой проводилась обязательная сертификация с выдачей сертификата соответствия. Отличительная особенность знака заключается в размещении под эмблемой из сочетания трёх букв «РСТ», цифрового и буквенного обозначения кода сертификационного органа, который наделил производителя продукции правом применения подобного знака;
• знак соответствия при осуществлении добровольной сертификации – данным знаком маркируется продукция, прошедшая процедуру добровольной сертификации и получившая сертификат соответствия. Представляет собой знак РСТ, однако, без указания под графическим изображением информации об органе сертификации, оформившего документ и нанесением по контуру круговой надписи «Добровольная сертификация». Маркировка продукции подобным знаком не является обязательным требованием;
• знак соответствия, подтверждающий декларирование товаров – наносится на оборудование или продукцию, которые подлежат декларированию и получили зарегистрированную декларацию о соответствии. В таком случае код сертификационного органа не указывается под графическим знаком РСТ. Нанесение такого знака является обязательным условием при осуществлении маркировки товаров, отражённых в номенклатуре декларируемой продукции;
• знак соответствия ТР (техническому регламенту) – используется для нанесения на продукцию или товар, с успехом прошедшие испытание на соответствие установленным и действующим техническим регламентам РФ и получившие сертификат соответствия ТР. Наносимый знак представляет собой комбинацию букв «Р» и «Т» с обозначенной сверху точкой, вписанные в букву «С», стилизованную под измерительную скобу. Для обеспечения правильной идентификации наносимое изображение обязательно должно контрастировать с общей поверхностью покрытия;
• знак соответствия (обращения) продукции на рынке ТС – используется для обозначения товарной продукции, прошедшей проверку качества утверждённым и действующим техрегламентам ТС. Знак является сочетанием букв «Е», «А» и «С» с чёткими прописанными параметрами и размерами, наносимыми на контрастном или светлом фоне.

Знак соответствия может размещаться на упаковке, продукции, а также документации, прилагаемой к изделиям. К основным правилам нанесения знаков соответствия относят:

• знак РСТ наносится на продукцию полностью;
• не допускается использование отдельных его составных частей или упущения какого-либо обозначения. При невозможности нанесения знака непосредственно на товар (жидкие или сыпучие продукты и др.), то маркировка ставится на упаковочном материале;
• пропорциональные соотношения знака соответствия устанавливаются ГОСТом. При маркировке масштаб и размер знака определяется предприятием, получившего право его использования. При этом организация должна гарантировать различимость элементов и точность изображения маркировки невооружённым глазом;
• маркировка выполняется чёрным цветом на светлом или белом фоне;
• по завершению сроков действия сертификатов знак соответствия наносить нельзя;
• запрещено применять знак РСТ по истечению срока годности, обнаружения брака или повреждении упаковки;
• при использовании продукции не по прямому назначению, маркировка не производится, а уже нанесённые знаки должны быть сняты.

Запрещается также наносить знаки на символы, флаги и транспортные средства.

В качестве технологических приёмов нанесения используют тиснение, печать или клеймение. В некоторых случаях знак соответствия может располагаться на съёмных бирках, которые прикрепляются к промышленному оборудованию или другой продукции.

Изготовитель имеет право размещать знак соответствия на папках, пакетах, визитках и сайтах своей организации в качестве рекламы.

Применение знаков соответствия даёт распространителям, реализаторам и производителям массу преимуществ, главным среди которых является доверие к выпускаемой продукции со стороны покупателей. Не взирая на определённые вложения, сертификация в целях получения права на использование знаков соответствия всегда будет целиком оправданным шагом.

Импортеру

Раздел посвещен процессу импорта товара и получения на ввозимый товар соответсвующих правовых и разрешительных документов

Импортеру о сертификации

Оформить заявку

Вопрос / ответ

• Зачем нужна сертификация продукции?
• Сколько времени необходимо для получения сертификата?
• Какой вид сертификации мне нужен?
• Подлежит ли мой товар обязательной сертификации?
• Сергификат ГОСТ-Р или сертификат ЕАС?
• Что такое декларирование товара?

Расчитать стоимость

Форма для расчета стоимости сертификации

Расчитать стоимость

Производителю

В данном разделе приведен порядок провдения сертификации отечественной продукци, описаны шаги получения сертификата

Сертификация продукции отечественного производства

Отношение и пропорция – основы, определения, примеры

Отношение используется для сравнения двух величин одного и того же вида. Формула соотношения для двух чисел, a и b, выражается как a : b или a/b. Когда два или более отношения равны, говорят, что они пропорциональны. Понятие соотношения и пропорции основано на дробях. Соотношение и пропорция являются ключевыми основами для различных других понятий в математике. Соотношение и пропорция находят свое применение в решении многих повседневных задач, например, когда мы сравниваем рост, вес, расстояние или время, или при добавлении ингредиентов при приготовлении пищи и так далее.

1.	Что такое отношение и пропорция?
2.	Определение коэффициента
3.	Определение доли
4.	Формула соотношения и пропорции
5.	Разница между отношением и долей
6.	Часто задаваемые вопросы о соотношении и пропорции

Что такое соотношение и пропорция?

Сравнение двух величин путем деления называется отношением, а равенство двух отношений называется пропорцией. Соотношение может быть записано в различных формах, таких как x : y или x/y, и обычно читается как x к y.

С другой стороны, пропорция — это уравнение, в котором говорится, что два отношения эквивалентны. Пропорция записывается как x : y : : z : w и читается как x к y, как z к w. Здесь x/y = z/w, где w и y не равны 0,

Определение коэффициента

Отношение – это сравнение двух величин, которое получается путем деления первой величины на другую. Если a и b — две величины одного и того же вида и с одинаковыми единицами измерения, такие, что b не равно 0, то частное a/b называется отношением между a и b. Соотношения выражаются с помощью символа двоеточия (:). Это означает, что отношение a/b не имеет единиц измерения и может быть записано как a : b

.

Определение пропорции

Пропорция означает равенство двух соотношений. Два эквивалентных отношения всегда пропорциональны. Пропорции обозначаются символом (::) и помогают нам решать неизвестные величины. Другими словами, пропорция — это уравнение или утверждение, которое используется для изображения того, что два соотношения или дроби эквивалентны. Четыре ненулевых величины a, b, c, d называются пропорциональными, если a : b = c : d. Теперь рассмотрим два соотношения — 3 : 5 и 15 : 25. Здесь 3 : 5 можно выразить как 3:5 = 3/5 = 0,6, а 15:25 можно выразить как 15:25 = 15/25. = 3/5 = 0,6. Поскольку оба отношения равны, мы можем сказать, что они пропорциональны.

Есть два типа пропорций.

• Прямая пропорция
• Обратная пропорция

Прямая пропорция

Прямая пропорция описывает прямую зависимость между двумя величинами. Если увеличивается одна величина, то увеличивается и другая величина, и наоборот. Таким образом, прямая пропорция записывается как y ∝ x. Например, если скорость автомобиля увеличивается, то он преодолевает большее расстояние за фиксированный период времени.

Обратная пропорция

Обратная пропорция описывает соотношение между двумя величинами, при котором увеличение одной величины приводит к уменьшению другой величины, и наоборот. Таким образом, обратная пропорция записывается как y ∝ 1/x. Например, если скорость автомобиля увеличивается, он будет преодолевать фиксированное расстояние за меньшее время.

Формула соотношения и пропорции

Формула отношения выражается как a : b ⇒ a/b, где

• a = первый член или предшественник.
• b = второй член или следствие.

Например, соотношение 2 : 7 также представляется как 2/7, где 2 — антецедент, а 7 — консеквент.

Теперь, чтобы выразить пропорцию двух отношений, a : b и c : d, запишем ее как \(a: b:: c: d \longrightarrow \frac{a}{b}= \frac{c}{d}\)

• Два термина b и c называются средними терминами.
• Два термина a и d известны как крайние термины.
• В a: b = c : d величины a и b должны быть одного вида в одних и тех же единицах, тогда как c и d могут быть одного вида и в одних и тех же единицах по отдельности. Например, 5 кг : 15 кг = рупий. 75 : рупий. 225
• Формула пропорции может быть выражена как a/b = c/d или a : b : : c : d.
• В пропорции произведение средних = произведение крайностей. Следовательно, в формуле пропорции a:b::c:d получаем b×c=a×d. Например, в 5 : 15 :: 75 : 225 мы получим 15 × 75 = 5 × 225

Разница между соотношением и пропорцией

Разницу между соотношением и пропорцией можно увидеть в следующей таблице.

Соотношение	Пропорция
Используется для сравнения размера двух величин с одной и той же единицей измерения.	Используется для выражения отношения двух соотношений.
Символы, используемые для выражения отношения — двоеточие (:), косая черта (/)	Символ, используемый для выражения пропорции — двойное двоеточие (::)
Называется выражением.	Это называется уравнением.

Важные примечания по соотношению и пропорции

• Можно сравнивать любые две величины с одинаковыми единицами измерения.
• Два отношения называются пропорциональными, только если они равны.
• Чтобы проверить, равны ли два отношения и пропорциональны ли они, мы также можем использовать метод перекрестного произведения.
• Если мы умножим и разделим каждый член соотношения на одно и то же число, отношение останется прежним.
• Для любых трех величин, если отношение между первой и второй равно отношению между второй и третьей, то говорят, что они находятся в непрерывной пропорции.
• Аналогично, в случае любых четырех величин в непрерывной пропорции отношение между первой и второй равно отношению между третьей и четвертой.

☛ Связанные статьи

• Формула анализа соотношения
• Калькулятор пропорций
• Калькулятор процентных пропорций
• Что означает эквивалентность двух отношений?

 

Примеры соотношения и пропорции

1. Пример 1: Выясните, пропорциональны ли соотношения 6:8 и 24:32.

   Решение:

   Указанные соотношения: 6:8 и 24:32. 6:8 = 3/4 = 0,75 и 24:32 = 3/4 = 0,75. Здесь оба соотношения равны. Следовательно, 6:8 и 24:32 пропорциональны.

2. Пример 2: В классе 30 учеников. Количество студентов, которым нравится математика, и тех, кто любит естествознание, выражается в соотношении 2:3. Найдите количество учеников, которым нравится математика, и тех, кто любит естественные науки.

   Решение:

   Общее количество учеников = 30. Пусть количество учеников, которым нравится математика, умножается на 2, а количество учеников, которым нравятся естествознание, умножается на 3. Мы можем сказать, что 2x + 3x = 30 ⇒ 5x = 30 ⇒ x = 6. Подставив значение x = 6, мы получим количество учеников, которым нравится математика = 2x = 2 × 6 = 12, а количество учеников, которым нравятся естественные науки = 3x = 3 × 6 = 18.

   Следовательно, 12 учащихся любят математику, а 18 — естественные науки.

3. Пример 3: Укажите, верно или неверно:

   а.) Говорят, что два отношения пропорциональны, только если они эквивалентны.

   b.) В отношении 6 : 8 6 является консеквентом, а 8 — антецедентом.

   Решение:

   а.) Верно, что два отношения называются пропорциональными, только если они эквивалентны.

   б.) Неверно, в отношении 6 : 8 6 — антецедент, 8 — консеквент.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.

Записаться на бесплатный пробный урок

Практические вопросы по соотношению и пропорции

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о соотношении и пропорции

Что такое соотношение и пропорция?

Соотношение – это сравнение величин в одной и той же единице измерения. Получается делением первой величины на другую. Если a и b — две величины одного и того же вида и с одинаковыми единицами измерения, такие, что b не равно 0, то частное a/b называется отношением между a и b. С другой стороны, пропорция определяется как сравнительное отношение между двумя отношениями.

Что такое Формула соотношения и пропорции?

Формула соотношения для любых двух величин выражается как a : b ⇒ a/b. С другой стороны, формула пропорции выражается как \(a : b : : c : d \longrightarrow \frac{a}{b}=\frac{c}{d}\).

В чем разница между соотношением и пропорцией?

Соотношение изображает сравнение двух величин, тогда как пропорция изображает равенство двух отношений.

Как соотношение и пропорция используются в реальной жизни?

Соотношение и пропорция используются в нашей повседневной жизни. Например, пища, которую мы едим, имеет фиксированное соотношение ингредиентов. Дом или здание, в котором мы живем, имеет фиксированное соотношение и пропорцию цемента и песка.

Как отношение и пропорция связаны друг с другом?

Соотношение и пропорция связаны друг с другом. Отношение используется для сравнения двух величин одного и того же вида. Когда два или более таких отношения равны, говорят, что они пропорциональны.

Как дробь связана с соотношением и пропорцией?

Отношение также может быть выражено дробью. Например, 1:3 можно записать и как 1/3. Когда соотношение записывается в виде дроби, дробь необходимо упростить. Например, если дробь 13/39 записать в виде отношения, то получится 1:3. Если это неправильная дробь, мы не преобразовываем ее в смешанную дробь и оставляем как неправильную дробь, потому что отношение всегда сравнивает две величины.

Какие две части пропорции?

В пропорции четыре части, но в зависимости от их расположения в пропорции они разделены на две группы: средние и крайние. Внешние термины называются крайностями, а внутренние термины называются средними. Например, в пропорции 3:4:24:32 числа 6 и 32 — крайние, а 8 и 24 — средние.

В чем разница между прямой и обратной пропорцией?

В прямой зависимости увеличение одной величины приводит к увеличению другой или наоборот, тогда как в обратной зависимости увеличение одной величины приводит к уменьшению другой.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по отношениям и пропорциям

Двоеточие как символ отношения и деления

Двоеточие как символ отношения и деления

Скачать PDF

Ваша статья скачана

Слайдер с тремя статьями на слайде. Используйте кнопки «Назад» и «Далее» для перемещения по слайдам или кнопки контроллера слайдов в конце для перемещения по каждому слайду.

Скачать PDF

• Опубликовано: 31 декабря 1914 г.

• ФЛОРИАН КАЙОРИ ¹  

Природа том 94 , страница 477 (1914)Цитировать эту статью

• 4283 Доступы

• 1 Цитаты

• Детали показателей

Abstract

В 1902 г. профессор В. В. Беман из Мичиганского университета указал («L’Interm diaire des math maticiens», T.9, Paris, стр. 229, вопрос 2424), что двоеточие (:) появляется как обозначение геометрического отношения в конце тригонометрических и логарифмических таблиц, опубликованных вместе с «Тригонометрией» Уильяма Отреда 1657 года. Беман спрашивает, имеет ли этот символ для геометрического отношения еще более раннюю дату.

Информация об авторе

Авторы и организации

1. Лондон

   FLORIAN CAJORI

Авторы

1. FLORIAN 90 0 публикаций 3 публикации 0 CAJORI 90 02 Вы также можете искать этого автора в PubMed Google Scholar

Права и разрешения

Перепечатка и разрешения

Об этой статье

Эта статья цитируется

• Комментарий к книге Сильвио Белли «О соотношении и пропорции»

  • Стивен Р.

    No related posts.