Знаки синуса, косинуса, тангенса и котангенса
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
17.05.2022
Поворот точки
вокруг
начала
Устный счет
координат
Учитель математики МБОУ СОШ № 25 г. Крымска Е.В. Малая
Назовите числа t, соответствующее точкам
числовой окружности:
y
2
М3 3
?
В 2
?
М2 3
?
5
М4 6
?
Числовая окружность разделена
точками на 12 равных частей
0 t 2
6
М
1
0
А ?
С ?
0
x
11
М8 6
?
7
М5 6
?
4
М6 3
?
3
D
2
?
5
М7 3
?
Обход окружности совершается
в положительном направлении
Назовите числа t, соответствующее точкам
числовой окружности:
y
2
В ?
3
М2 4
?
С ?
Числовая окружность разделена
точками на 8 равных частей
М1 ?4
0 t 2
А ?0
0
М3 5
4
?
x
М4 7?
D 3?
2
4Обход
окружности совершается
в положительном направлении
Устная разминка:
cos90°
01
sin90°
12
3
√2/2
sin(π/4)
4
cos180°
-1
5
sin270°
-1
6 3)
sin(π/
√3/2
7
√3/2
cos(π/6)
cos360°
18
9
ctg(π/6)
√3
10
-1 2)
sin(3π/
11
cos(2π)
1
12
cos(‒π)
-1
13
tg(π/4)
1
0 2)
14
cos(-π/
15
1/2
cos(π/3)
☺
I
II
III
Поворот точки
Математический
вокруг начала
диктант
координат
1 вариант
2 вариант
cos 00 + 3· sin 900
cos 1800 + 5· sin 900
sin 2700–2· cos1800 sin 1800 – 3· cos00
1+ctg 2700–5 tg3600 sin 600 + cos 300
sin 300 + cos 600
tg3600–2ctg 2700+3
sin 450 + cos 450
tg450+ctg 300
Ответы:
1 вариант
2 вариант
4
4
1
–3
1
√3
1
3
√2
1+√3
17.
 05.2022
05.2022Тема урока:
Учитель математики МБОУ СОШ № 25 г. Крымска Е.В. Малая
Знаки синуса и косинуса по четвертям
sin α = у
II
y>0
I
+ +
— III
y<0
IV
Знаки синуса и косинуса по четвертям
cos α = x
I
II
x<0
III
— +
— +
x>0
IV
Знаки синуса и косинуса по четвертям
sin α > 0
sin α > 0
cos α > 0
cos α < 0
tg α 0
сtg α 0
sin α < 0
cos α < 0
tg α > 0
сtg α > 0
III
tg α > 0
I
сtg α > 0
sin α < 0
IV
cos α > 0
tg α 0
сtg α 0
Знаки тригонометрических функций
sin a
1
y
cos a
+
+
–
–
–1
–
+
x
–
+
1
–1
tg a
ctg a
– +
+
–
–
+
+ –
English Русский Правила
Обучающая карточка по теме «Знаки синуса, косинуса,тангенса и котангенса»
Обучающая карточка по теме «Знаки синуса, косинуса,тангенса и котангенса»| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Методические разработки
▪Фрагменты уроков
Материал опубликовала
18
#10 класс #Алгебра #ФГОС #Методические разработки #Учитель-предметник #Школьное образование #Фрагмент урока #УМК Ш. А. Алимова
Обучающая карточка
Тема: «Знаки синуса, косинуса и тангенса»,параграф 24
Класс: 10
«Алгебра и начала математического анализа 10-11» авт. Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачёва
Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачёва
Цель: научить учащихся определять знаки тригонометрических функций.
Карточка
DOCX / 2.39 Мб
Опубликовано в группе «Математическая мозаика»
Елена Владимировна, 29.07.19 в 19:57 2ОтветитьПожаловаться
Спасибо, Светлана Николаевна, за новую работу в методкопилку!
Белянина Светлана Николаевна, 30.07.19 в 08:41 2ОтветитьПожаловаться
Готовлюсь к новому учебному году.Перебираю,редактирую,исправляю.Благодарю за внимание!
Медведева Татьяна Петровна, 30.07.19 в 07:55 2ОтветитьПожаловаться
Светлана Николаевна, спасибо за качественный ресурс.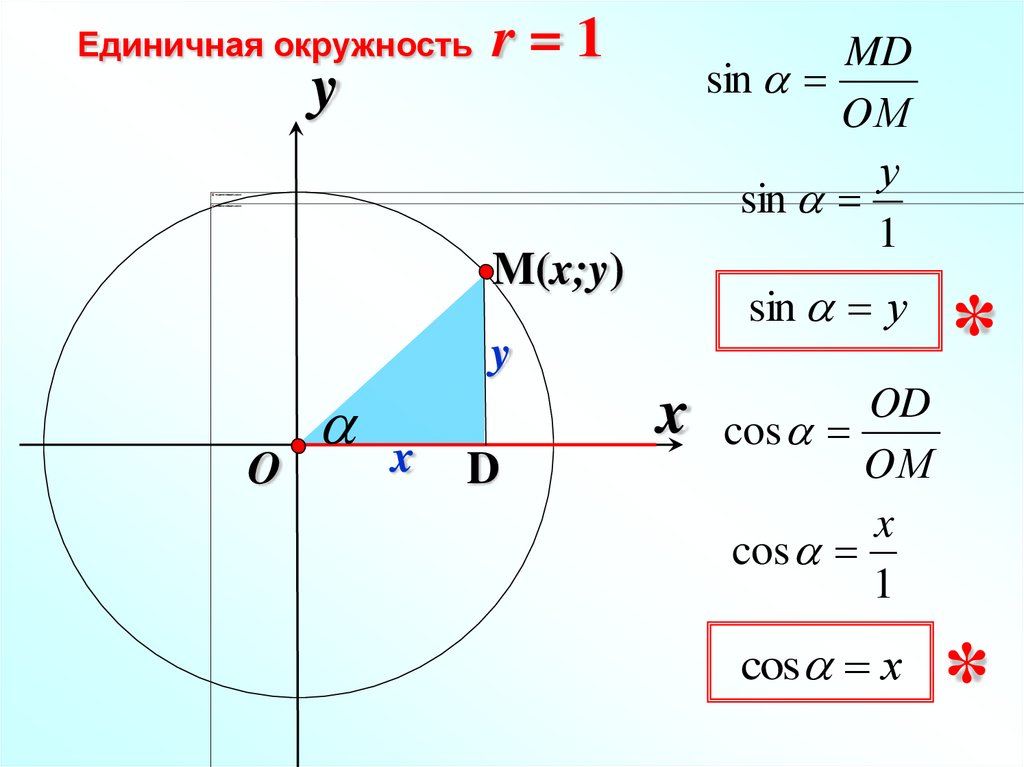
Белянина Светлана Николаевна, 30.07.19 в 08:42 1ОтветитьПожаловаться
Очень рада Вашему отзыву,Татьяна Петровна!
Янова Татьяна Викторовна, 03.08.19 в 21:03 0ОтветитьПожаловаться
Спасибо, Светлана Николаевна, за материал!
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
Знаки тригонометрических функций
Тригонометрические функции синуса, косинуса, тангенса, котангенса основаны на знаках координат y и x в соответствующих четырех квадрантах.
| θ lies in which Quadrant | I | II | III | IV |
| Trigonometric functions | ||||
| Sin θ | +ve | +ve | -ve | -ve |
| Cos θ | +ve | -ve | -ve | +ve |
| Tan θ | +ve | -ve | +ve | -ve |
| Cot θ | +ve | -ve | +ve | -ve |
| Cosec θ | +ve | +ve | -ve | -ve |
| Sec θ | +ve | -ve | -ve | +VE |
Из вышеупомянутого,
Ккадем дуги из I квадранта являются положительными, так как положительные координаты данных точек – P, S₁ и S₂, которые определяют их конкретные значения.
Квадрант II: Из точек 2-го квадранта для дуг P и S₂ обе состоят из отрицательных абсцисс (на рисунке выше), поэтому котангенс и косинус существуют как отрицательные. Ордината конечной точки P равна + ve, поэтому синус равен + ve, а ордината точки S₁ равна — ve и, следовательно, касательная отрицательна.
(
Квадрант III: Поскольку абсциссы плюс конечные точки P, ординаты дуг из 3-го квадранта (см. рисунок выше) равны -ve. Отсюда следует, что функции синуса и косинуса заданных дуг равны — ve. Ординаты точки S1 плюс абсцисса точки S2, принадлежащей дуге из III квадранта, равны + ve. Следовательно, котангенс и касательная данных дуг равны + ve.
Квадрант IV: Функции, включающие тангенс, синус и котангенс заданных дуг из IV квадранта, равны -ve, аналогично точкам S₁, S₂ и координатам P, которые принадлежат только им. Только функции арккосинуса из IV квадранта + ve являются абсциссами точки P, которая принадлежит им, как вы можете видеть на рисунке выше.
| Квадрант | Значения дуги | Sin x | Cos x | Tan x | Cot x |
| I | From 0 to 90º | + | + | + | + |
| II | From 90º to 180º | + | – | – | |
| III | From 180º to 270º | – | – | + | + |
| IV | From 270º to 360º | — | + | — | — |
Пример
. 0013
0013
Решение: Синус 146º = Sin (90º + 56º) = Поскольку синус лежит от 0º до 90º, следовательно, Знак будет положительным.
Вопрос 2: Cos 455º
Решение: Cos (360 º + 95º) = Cos (90º + 5º) = Cos 5º
Из приведенного выше решения ясно, что знак положительный.
Вопрос 3: Тан 573º
Решение: Тан (360 º + 213 º ) = Тан (180 º + 33 3 0 9)0012 º
Следовательно, Tan 573º положительный
Пожалуйста, поделитесь
Свернуть
Содержание
Теорема Пифагора
Определение правила CAST
Оценка алгебраического представления правила CAST
Правило CAST — это специальное правило, часто используемое в качестве аббревиатуры для запоминания в тригонометрии. По сути, «CAST» означает КОСИНУС-ВСЕ-СИНУС, ТАНГЕНТ. Начиная с четвертого квадранта и двигаясь против часовой стрелки, правило CAST покажет нам, какие тригонометрические отношения (косинус, синус и тангенс) всегда положительны в указанных квадрантах.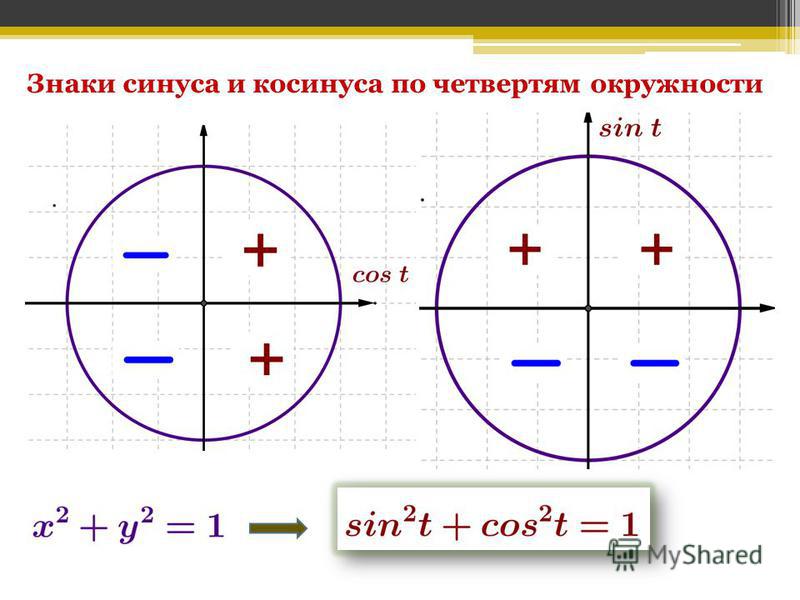 92 \end{equation}
92 \end{equation}
Где c — гипотенуза (или самая длинная сторона прямоугольного треугольника), а a и b — произвольно две другие стороны.
Геометрически следующая диаграмма иллюстрирует теорему Пифагора:
Где площадь c-квадрата равна площади a-квадрата плюс b-квадрат для любого прямоугольного треугольника.
Тем не менее, это свойство будет важно, когда мы будем определять правило CAST.
Помните, что при определении единичной окружности мы вписали прямоугольные треугольники, определяемые частью оси x и некоторым лучом, S и перпендикулярной линией от окончания S к оси x? Создание нами этой перпендикулярной линии от конца луча S к оси x означает, что мы, по существу, сформировали прямоугольные треугольники. Следовательно, мы можем эффективно использовать теорему Пифагора для определения правила CAST. Давайте сначала посмотрим на треугольники, которые мы сделали в квадранте 1:9.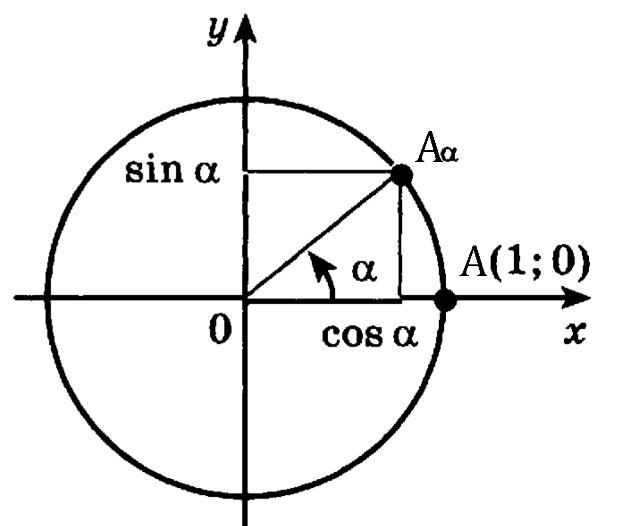 0005
0005
Мы замечаем, что в квадранте 1 наши значения x ограничены от 0 до ∞, в то время как наши значения y также ограничены от 0 до ∞. Точнее, значения x нашего единичного круга ограничены от 0 до 1, в то время как наши значения y также ограничены от 0 до 1.
Таким образом, для квадранта 1 мы говорим, что:
(2)
\begin{align} 0 < x_{Q1} < 1 \quad , \quad 0 < y_{Q1} < 1 \end{align}
Но мы знаем, что:
(3)
\begin{align} x = cos(\theta) \quad , \quad y = sin(\theta) \end{align}
Таким образом, мы можем получить неравенство:
(4)
\begin{align} 0 < cos(\theta)_{Q1} < 1 \quad , \quad 0 < sin(\theta)_{Q1} < 1 \end{align}
По сути, мы знаем что в квадранте 1 cos Θ и sin Θ положительны в квадрантах 1, поскольку их значения должны быть между 0 и 1, когда мы строим вписанный треугольник в квадранте 1.
Однако мы знаем, что:
(5)
\begin{align} tan(\theta) = \frac{sin(\theta)}{cos(\theta)} \end{align}
Но так как cosΘ и sinΘ оба положительны в квадранте 1, то tanΘ также должен быть положительным, поскольку tanΘ можно выразить через cosΘ и sinΘ, таким образом, мы получаем:
(6)
\begin{align} 0 < tan(\theta)_{Q1} < 1 \end{align}
Теперь рассмотрим треугольники, построенные в квадранте 2:
Заметим, что угол, вписанный в квадрант 2, значения x ограничены между -∞ и 0, а значения y ограничены между 0 и ∞. Точнее, для нашего единичного круга значения x ограничены от -1 до 0, а значения y ограничены от 0 до ∞. Отсюда получаем:
Точнее, для нашего единичного круга значения x ограничены от -1 до 0, а значения y ограничены от 0 до ∞. Отсюда получаем:
(7)
\begin{align} -1 < x_{Q2} < 0 \quad , \quad 0 < y_{Q2} < 1 \end{align}
(8)
\begin{align} -1 < cos(\theta)_{Q2} < 0 \quad , \quad 0 < sin(\theta)_{Q2} < 1 \end{align}
Или точнее cosΘ будет отрицательным, а sinΘ будет положительным в квадранте 2. Однако мы знаем, что tanΘ представлен в терминах cosΘ и sinΘ. С точки зрения только положительных/отрицательных знаков мы получаем:
(9)
\begin{align} tan(\theta) = \frac{sin(\theta)}{cos(\theta)} \end{align}
(10)
\begin{align} tan(\theta) = \frac{+}{-} \end{align}
Или, точнее, tanΘ всегда будет отрицательным в квадранте 2.
Теперь давайте посмотрим на квадрант 3 на следующей диаграмме ниже:
Мы знаем, что когда построенный треугольник находится в квадранте 3, то значения x ограничены от -∞ до 0, а значения y ограничены от -∞ до 0.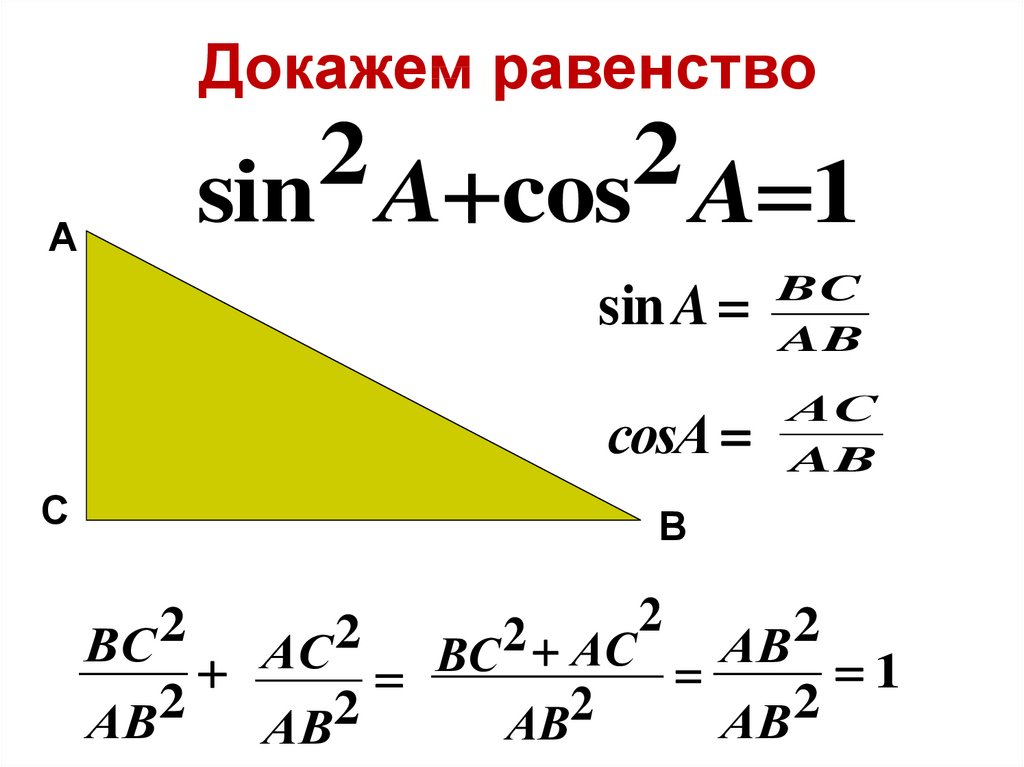 Точнее, для нашего единичного круга значения x ограничены от -1 до 0, а значения y ограничены от -1 до 0. Таким образом, мы получаем:
Точнее, для нашего единичного круга значения x ограничены от -1 до 0, а значения y ограничены от -1 до 0. Таким образом, мы получаем:
(11)
\begin{align} -1 < x_{Q3} < 0 \quad , \quad -1 < y_{Q3} < 0 \end{align}
(12)
\begin{align} -1 < cos(\theta)_{Q3} < 0 \quad , \quad -1 < sin(\theta)_{Q3} < 0 \end{align}
(13)
\begin{align} tan(\theta) = \frac{-}{-} \end{align}
Таким образом, мы получаем, что cosΘ и sinΘ всегда будут отрицательными при построении в квадранте 3, а tanΘ всегда будет положительный, потому что отрицательное, деленное на отрицательное, является положительным.
Мы не будем проходить через квадрант 4, однако процедура аналогична процедуре для квадрантов 1, 2 и 3, которую мы вывели выше. В таблице ниже приведены знаки (положительные или отрицательные) для косинуса, синуса и тангенса:
| Кос Θ | Грех | ТанΘ | |
|---|---|---|---|
| Квадрант 1 | Положительный | Положительный | Положительный |
| Квадрант 2 | Отрицательный | Положительный | Отрицательный |
| Квадрант 3 | Отрицательный | Негативы | Положительный |
| Квадрант 4 | Положительный | Негативы | Отрицательный |
Из этой диаграммы мы можем определить, что cosΘ положителен в квадрантах 1 и 4, sinΘ положителен в квадрантах 1 и 2, а tanΘ положителен в квадрантах 1 и 3.

 РФ
РФ