Числовые ряды. Знакоположительные ряды | Математика, которая мне нравится
Определение. Пусть — последовательность вещественных чисел. Числовым рядом называется
Сумма называется частной суммой ряда.
Определение. Если последовательность чисел сходится к конечному пределу , то говорят, что ряд сходится и его сумма равна
Если же последовательность расходится, то говорят, что ряд расходится.
Числа называются членами ряда. Всякая конечная сумма называется отрезком ряда.
Если все числа положительны (неположительны, неотрицательны, отрицательны), ряд называется знакоположительным (знаконеположительным, знаконеотрицательным, знакоотрицательным).
Пример. Рассмотрим ряд
где — некоторое фиксированное число. Частные суммы этого ряда
Если , то .
При ряд расходится, так как неограниченно возрастает.
При . Следовательно, ряд расходится.
При Следовательно, не имеет предела, и ряд расходится.
Значит, ряд сходится при , а при расходится.
Теорема (критерий Коши для ряда). Ряд
сходится тогда и только тогда, когда
В частности, если ряд сходится, то для любого . Таким образом, у сходящегося ряда — необходимое условие сходимости. Однако оно не является достаточным.
Для знаконеотрицательных рядов из ограниченности последовательности частичных сумм следует сходимость ряда.
Теорема (признак сравнения). Если знаконеотрицательный ряд сходится и существуют и : , то тогда и ряд сходится.
Доказательство. Пусть , . Тогда при
Последовательность возрастает и ограничена сверху, следовательно, она имеет предел.
Пример. Если для неотрицательного ряда
где и , то ряд сходится.
Теорема (признак Даламбера). Если для знакоположительного ряда
выполняется неравенство
то ряд сходится.
Если
то ряд расходится.
Доказательство. Если , то существует : начиная с некоторого номера , выполняется неравенство
Отсюда
и по признаку сравнения ряд сходится.
С именем Даламбера связан один забавный случай. Рассказывают, что, обучая математике очень тупого и очень знатного ученика и не добившись понимания доказательства, Даламбер в отчаянии воскликнул: “Ну, честное слово, сударь, эта теорема верна!” На что ученик отвечал: “Сударь, почему вы сразу так мне не сказали? Вы — дворянин, и я — дворянин; Вашего слова для меня вполне достаточно”.
Пример. Ряд
сходится, поскольку
Теорема (признак Коши). Если для знакоположительного ряда
выполняется неравенство
то ряд сходится.
Если же
то ряд расходится.
Доказательство. Если , то существует : . Следовательно, , и по признаку сравнения ряд сходится.
Если же , то существует : . Значит, члены ряда не стремятся к нулю, и ряд расходится.
Пример. Ряд
сходится, так как
Пример. Гармонический ряд (каждый член этого ряда, начиная со второго, — среднее гармоническое двух соседних его членов: ) расходится.
Доказательство.
Частная сумма гармонического ряда может быть сделана больше чего угодно.
Лекция 11 Знакоположительные ряды.
⇐ ПредыдущаяСтр 7 из 10Следующая ⇒Числовой ряд называется знакоположительным, если все его члены – положительные (неотрицательные) числа.
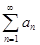
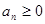
Основная и довольно приятная особенность знакоположительных рядов в том, что частичные суммы ряда представляют собой неубывающую последовательность.
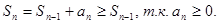
Поэтому достаточно проверить, что последовательность частичных сумм ограничена сверху, чтобы по теореме Вейерштрасса утверждать, что последовательность частичных сумм имеет конечный предел, т.е. ряд сходится.
На этом основаны, практически, все признаки сходимости рядов.
Ряд может сравниваться с несобственным интегралом (интегральный признак Коши), с другими рядами (признаки сравнения рядов), в частности, со сходящейся геометрической прогрессией (признак Даламбера, радикальный признак Коши).
Каждый признак можно сравнить с увеличительным стеклом. У каждого признака есть своя область применения, более широкая или более узкая (как поле зрения линзы) и своя сила. Одни признаки сильнее, позволяют различать слабо сходящиеся или слабо расходящиеся ряды, но имеют узкую область применения (например, интегральный признак Коши). Другие, наоборот, имеют широкую область применения, но довольно слабы, ряды, близкие к границе сходимости, с их помощью не различишь (например, признаки Даламбера и Коши (радикальный)).
Пока в библиотеке рядов, которые мы можем использовать для сравнения, всего два ряда: сходящийся ряд — бесконечно убывающая геометрическая прогрессия, известная еще из школы, и расходящийся гармонический ряд, полученный по критерию Коши.
Заметим, что критерий Коши (как критерий сходимости), вообще, самый сильный инструмент при исследовании сходимости ряда, но его область применимости узка.
Интегральный признак Коши, основанный на сравнении с несобственным интегралом – очень сильный признак. В самом деле, если аппроксимировать непрерывную подинтегральную функцию кусочно-постоянной, то площадь под графиком функции (интеграл) и площадь под графиком кусочно-постоянной функции будут различаться на конечное число.
Интегральный признак Коши.
Доказательство. 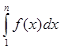 — это площадь под графиком функции
— это площадь под графиком функции 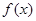 при
при 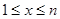 .
.
Так как 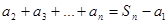 (сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а
(сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а 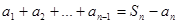
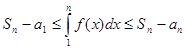 .
.
. Достаточность. Если интеграл сходится, то 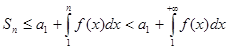 , поэтому последовательность
, поэтому последовательность 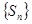 ограничена сверху. Так как эта последовательность не убывает, то по теореме Вейерштрасса
ограничена сверху. Так как эта последовательность не убывает, то по теореме Вейерштрасса 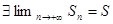 . Поэтому ряд
. Поэтому ряд 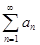 сходится.
сходится.
Необходимость. Если ряд 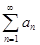 сходится, то
сходится, то 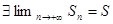 , а по необходимому признаку сходимости ряда
, а по необходимому признаку сходимости ряда 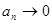
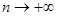 . Поэтому последовательность
. Поэтому последовательность 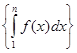 (неубывающая, так как
(неубывающая, так как 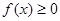 ) ограничена сверху. Следовательно, по теореме Вейерштрасса
) ограничена сверху. Следовательно, по теореме Вейерштрасса 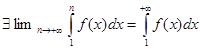 , т.е. несобственный интеграл сходится.
, т.е. несобственный интеграл сходится.
Если ряд расходится, то и интеграл расходится и наоборот. Это легко доказывается от противного.
Поэтому говорят, что несобственный интеграл и ряд сходятся или расходятся «одновременно», т.е. один из них сходится, то и другой сходится, если один расходится, то и другой расходится. Это понятие часто употребляют при сравнении рядов.
Пример. Применим интегральный признак к гармоническому ряду.
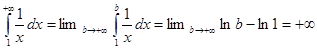 — интеграл расходится, поэтому и гармонический ряд расходится.
— интеграл расходится, поэтому и гармонический ряд расходится.
Пример. Рассмотрим «ряды Дирихле» 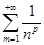 . Название взято в кавычки, так неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы.
. Название взято в кавычки, так неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы.
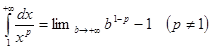 . Ясно, что интеграл сходится при p>1 и расходится при P<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод
. Ясно, что интеграл сходится при p>1 и расходится при P<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод
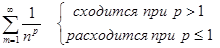 .
.
Интересно, что ряд 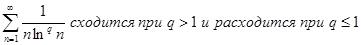
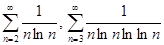 расходятся (проверьте по интегральному признаку).
расходятся (проверьте по интегральному признаку).
Теперь становится яснее, где пролегает граница между сходящимися и расходящимися рядами. Заодно накоплена библиотека сходящихся и расходящихся рядов, которые можно использовать как эталонные при сравнении рядов. Сравнивать ряды можно с помощью признаков сравнения.
Признаки сравнения рядов.
Сходимость знакоположительных рядов — Викиверситет
Определение. Числовой ряд ∑ k = 1 ∞ x k {\displaystyle \sum _{k=1}^{\infty }x_{k}} называется знакоположительным, если x k ≥ 0 {\displaystyle x_{k}\geq 0} для любого k {\displaystyle k} .Ограниченность частных сумм[править]
Теорема.
Знакоположительный числовой ряд сходится тогда и только тогда, когда последовательность S n {\displaystyle S_{n}} ограничена.
Доказательство.
Если ряд сходится, то последовательность ограничена как сходящаяся подпоследовательность. Обратно, S n + 1 − S n = x n + 1 ≥ 0 {\displaystyle S_{n+1}-S_{n}=x_{n+1}\geq 0} , поэтому последовательность S n {\displaystyle S_{n}} не убывает. Тогда ее сходимость следует из ограниченности по теореме Вейерштрасса.
Оценочный признак[править]
Теорема (второй признак сравнения). Даны числовые ряды ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} , ∑ n = 1 ∞ b n {\displaystyle \sum _{n=1}^{\infty }b_{n}} , a n ≥ 0 , b n > 0 , ∀ n {\displaystyle a_{n}\geq 0,b_{n}>0,\forall n}Пусть ∃ lim n → ∞ a n b n = L > 0 {\displaystyle \exists \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}=L>0} , тогда ряды сходятся или расходятся одновременно.
Признак Даламбера[править]
Теорема (признак Даламбера). Дан ряд ∑ n = 1 ∞ a n , a n > 0 ∀ n {\displaystyle \sum _{n=1}^{\infty }a_{n},a_{n}>0\forall n} . Пусть ∃ lim n → ∞ a n + 1 a n = λ {\displaystyle \exists \lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}=\lambda } , тогда- Если λ < 1 {\displaystyle \lambda <1} — ряд сходится
- Если λ > 1 {\displaystyle \lambda >1} — ряд расходится
1. Пусть 0 ≤ λ < 1 {\displaystyle 0\leq \lambda <1} , тогда ∃ q : λ < q < 1 {\displaystyle \exists q:\lambda <q<1}
∃ lim a n + 1 a n = λ ⇒ {\displaystyle \exists \lim {\frac {a_{n+1}}{a_{n}}}=\lambda \Rightarrow } для ε = q − λ > 0 {\displaystyle \varepsilon =q-\lambda >0} ∃ N : ∀ n > N | a n + 1 a n − λ | < ε ⇒ {\displaystyle \exists N:\forall n>N\quad |{\frac {a_{n+1}}{a_{n}}}-\lambda |<\varepsilon \Rightarrow }
⇒ − ( q − λ ) < a n + 1 a n − λ < q − λ {\displaystyle \Rightarrow -(q-\lambda )<{\frac {a_{n+1}}{a_{n}}}-\lambda <q-\lambda } ; a n + 1 a n < q ∀ n > N ⇒ {\displaystyle {\frac {a_{n+1}}{a_{n}}}<q\forall n>N\Rightarrow }
⇒ a n + 1 < q a n , ∀ n > N ⇒ a N + 2 < q a N + 1 , a N + 3 < q a N + 2 < q 2 a N + 1 . . . . {\displaystyle \Rightarrow a_{n+1}<qa_{n},\forall n>N\Rightarrow a_{N+2}<qa_{N+1},a_{N+3}<qa_{N+2}<q^{2}a_{N+1}….}
a n + k < q k − 1 a N + 1 ∀ k ≥ 2 {\displaystyle a_{n+k}<q^{k-1}a_{N+1}\quad \forall k\geq 2}
Ряд ∑ k = 1 ∞ q k − 1 {\displaystyle \sum _{k=1}^{\infty }q^{k-1}} — сходится, так как | q | < 1 ⇒ {\displaystyle |q|<1\Rightarrow } ряд ∑ k = 2 ∞ q k − 1 {\displaystyle \sum _{k=2}^{\infty }q^{k-1}} — сходится ⇒ {\displaystyle \Rightarrow } по I признаку сравнения ряд ∑ k = 2 ∞ a N + k {\displaystyle \sum _{k=2}^{\infty }a_{N+k}} — сходится ⇒ {\displaystyle \Rightarrow } ряд ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} — сходится.
2. Пусть λ > 1 {\displaystyle \lambda >1} . Пусть ε > 0 : λ − ε > 1 {\displaystyle \varepsilon >0:\lambda -\varepsilon >1}
∃ lim n → ∞ a n + 1 a n = λ ⇒ {\displaystyle \exists \lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}=\lambda \Rightarrow } для ε > 0 N : ∀ n > N | a n + 1 a n − λ | < ε {\displaystyle \varepsilon >0\quad N:\forall n>N\quad |{\frac {a_{n+1}}{a_{n}}}-\lambda |<\varepsilon }
λ − ε < a n + 1 a n < λ + ε ∀ n > N {\displaystyle \lambda -\varepsilon <{\frac {a_{n+1}}{a_{n}}}<\lambda +\varepsilon \forall n>N} ; a n + 1 a n > λ − ε > 1 , ∀ n > N {\displaystyle {\frac {a_{n+1}}{a_{n}}}>\lambda -\varepsilon >1,\forall n>N}
⇒ a n + 1 > a n ∀ n > N {\displaystyle \Rightarrow a_{n+1}>a_{n}\forall n>N} ; 0 < a N + 1 < a N + 2 < . . . {\displaystyle 0<a_{N+1}<a_{N+2}<…}
⇒ a n > a N = 1 > 0 , ∀ n ≥ N + 2 ⇒ {\displaystyle \Rightarrow a_{n}>a_{N=1}>0,\forall n\geq N+2\Rightarrow } lim n → ∞ a n ≥ a N + 1 > 0 ⇒ lim n → ∞ a n ≠ 0 ⇒ {\displaystyle \lim _{n\to \infty }a_{n}\geq a_{N+1}>0\Rightarrow \lim _{n\to \infty }a_{n}\neq 0\Rightarrow } не выполнен необходимый признак сходимости ⇒ {\displaystyle \Rightarrow } ряд ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} расходится.
Интегральный признак[править]
Знакоположительные ряды — Студопедия
Знакоположительным рядом называется ряд вида
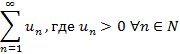
Теорема 1 – Признак сравнения: Пусть для знакоположительных рядов 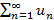 и
и 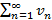 выполняется
выполняется 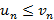 , тогда справедливо следующее: из сходимости большего следует сходимость меньшего или из расходимости меньшего следует расходимость большего.
, тогда справедливо следующее: из сходимости большего следует сходимость меньшего или из расходимости меньшего следует расходимость большего.
Теорема 2 — Предельный признак: Если для знакоположительных рядов 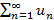 и
и 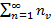 существует конечный предел вида
существует конечный предел вида 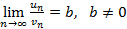 , тогда ряды ведут себя одинаково: оба сходятся или оба расходятся.
, тогда ряды ведут себя одинаково: оба сходятся или оба расходятся.
Теорема 3 – Признак Даламбера:Пусть для знакоположительного ряда 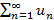 выполняется
выполняется 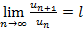 , тогда если
, тогда если 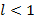 – ряд сходится,
– ряд сходится, 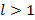 – ряд расходится,
– ряд расходится, 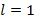 – признак не работает.
– признак не работает.
Теорема 4 – Признак Коши: Пусть для знакоположительного ряда 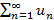 существует предел вида
существует предел вида 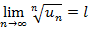 , тогда если
, тогда если 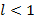 – ряд сходится,
– ряд сходится, 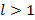 – ряд расходится,
– ряд расходится, 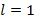 – признак не работает.
– признак не работает.
Теорема 5 – Интегральный признак Коши: Пусть для знакоположительного ряда 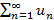 найдена функция
найдена функция 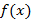 , определенная на отрезке
, определенная на отрезке 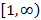 со свойствами:
со свойствами: 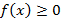 ,
, 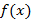 монотонно убывает,
монотонно убывает, 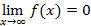 ,
, 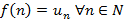 . Тогда ряд и несобственный интеграл
. Тогда ряд и несобственный интеграл 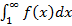 ведут себя одинаково: оба сходятся или оба расходятся.
ведут себя одинаково: оба сходятся или оба расходятся.
Знакопеременные и знакочередующиеся ряды
Ряд 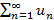 , у которого присутствуют и положительные и отрицательные слагаемые называется знакопеременным.
, у которого присутствуют и положительные и отрицательные слагаемые называется знакопеременным.
Ряды вида 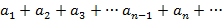 , где
, где 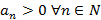 называется знакочередующимся.
называется знакочередующимся.
Теорема – Признак Лейбница: Если для модулей членов знакочередующегося ряда выполняются следующие условия: 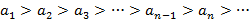 и
и 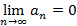 , тогда ряд сходится и его сумма по модулю оценивается как
, тогда ряд сходится и его сумма по модулю оценивается как 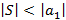 .
.
Если у знакопеременного ряда сходится ряд из модулей, тогда сам исходный ряд также сходится (обратное высказывание неверно). Если у сходящегося знакопеременного ряда ряд из модулей сходится, тогда исходный ряд называется абсолютно сходящимся. Если ряд из модулей расходится – условно сходящимся.
Если ряд сходится абсолютно, тогда перестановка бесконечного числа слагаемых не влияет на сумму. Перестановка слагаемых у условно сходящегося ряда может привести к любому значению суммы или привести к расходимости ряда.
Функциональные ряды
Бесконечная сумма вида 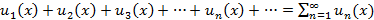 называется функциональным рядом. Если у функционального ряда зафиксировать точку
называется функциональным рядом. Если у функционального ряда зафиксировать точку 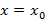 , тогда ряд станет числовым.
, тогда ряд станет числовым.
Множество всех значений x, при которых функциональный ряд сходится называется областью сходимости ряда. Аналогично числовым рядам можно ввести частичные суммы следующего вида
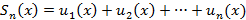
Если x принадлежит области сходимости, тогда сумма ряда 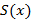 определена на области сходимости ряда
определена на области сходимости ряда
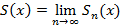
Степенные ряды
Функциональный ряд называется степенным, если элементы ряда определены степенной функцией
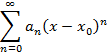
Частный случай при 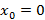 , тогда степенной ряд примет вид
, тогда степенной ряд примет вид
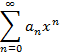
У степенного ряда вида 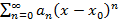 всегда существует число R со следующим свойством: ряд сходится на интервале
всегда существует число R со следующим свойством: ряд сходится на интервале 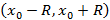 и расходится на лучах
и расходится на лучах 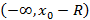 и
и 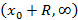 . Число R называется радиусом сходимости, а интервал
. Число R называется радиусом сходимости, а интервал 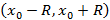 – радиусом сходимости. Радиус сходимости можно найти из следующих соотношений
– радиусом сходимости. Радиус сходимости можно найти из следующих соотношений
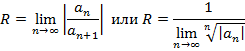
На концах интервала сходимости ряд может быть сходящимся, так и расходящимся.
Если степенной ряд сходится на своем интервале сходимости к функции суммы ряда 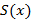 , тогда справедливы следующие высказывания:
, тогда справедливы следующие высказывания:
1. 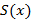 непрерывна на интервале сходимости;
непрерывна на интервале сходимости;
2. Ряд можно почленно дифференцировать
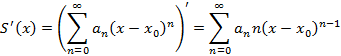
3. Ряд можно почленно интегрировать
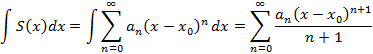
Полученные ряды также имеют интервал сходимости.
Знакоположительные ряды. Теоремы сравнения.

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Лекция 5
Тема: Числовой ряд. Ряд из членов геометрической прогрессии. Необходимый признак сходимости ряда. Действие над рядами. Законоположительные ряды. Признаки сравнения.
Определение ряда. Определение сходимости ряда. Примеры.
Определение 1. Выражение вида 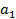 +
+ 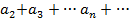
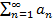 называется рядом,
называется рядом, 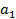 ,
, 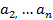 …- члены ряда,
…- члены ряда, 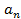 — общий член ряда.
— общий член ряда.
Вначале будем изучать ряды, членами которых являются действительные числа.
Приведем примеры рядов:
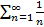 – гармонический ряд,
– гармонический ряд,
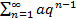 =
= 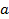 +
+ 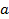 q+
q+ 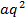 +…
+… 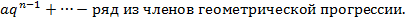 а — первый член прогрессии, q — знаменатель прогрессии.
а — первый член прогрессии, q — знаменатель прогрессии.
Определение 2. Ряд 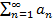 называется сходящимся, если существует предел его частных сумм, т.е.
называется сходящимся, если существует предел его частных сумм, т.е. 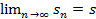 , где
, где 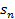 — сумма первых n членов ряда. Если
— сумма первых n членов ряда. Если 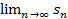 не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.
Пример 1. Исследовать на сходимость гармонический ряд 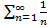
Решение: Рассмотрим группу слагаемых 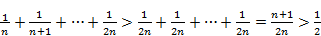
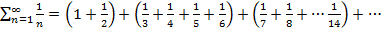 , где каждая их скобок больше
, где каждая их скобок больше  .
.
Отсюда следует, что 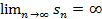 , т.е. предел не существует, т.к. при n
, т.е. предел не существует, т.к. при n 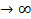 число скобок в
число скобок в 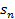 тоже стремиться к
тоже стремиться к 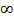 . Гармонический ряд расходится.
. Гармонический ряд расходится.
Пример 2. Исследовать на сходимость ряд из членов геометрической прогрессии 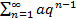 , a
, a 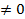 , q
, q 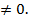
Решение: Рассмотрим частичную сумму данного ряда.
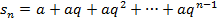
q 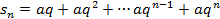
(1-q) 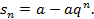
Если q 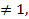 то
то 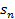 =
= 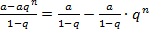 .
.
Рассмотрим предел частичных сумм:
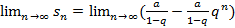 =
= 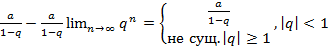
Остается рассмотреть случай, когда q=1. В этом случае имеем ряд а+а+а….,
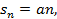
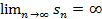 , т.к. а
, т.к. а 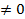 .
.
Итак, ряд из членов геометрической прогрессии при 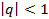 сходится и его сумма s=
сходится и его сумма s= 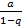 , а при
, а при 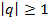 расходится.
расходится.
Пример 3. Найти сумму ряда 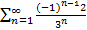 .
.
Решение. Данный ряд 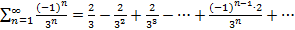 является рядом из членов геометрической прогрессии, где а=2, q=
является рядом из членов геометрической прогрессии, где а=2, q= 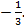 Так как
Так как 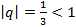 , то данный ряд сходится и s=
, то данный ряд сходится и s= 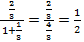
Пример 4. Исследовать на сходимость ряд 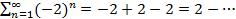 . Является рядом из членов геометрической прогрессии, где a=-2, q= -1. Так как
. Является рядом из членов геометрической прогрессии, где a=-2, q= -1. Так как 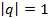 , то данный ряд расходится.
, то данный ряд расходится.
Необходимый признак сходимости.
Теорема 1. Если ряд 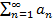 сходится, то предел его общего члена равен 0,
сходится, то предел его общего члена равен 0,
т.е. 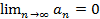 .
.
Доказательство. По условию данный ряд сходится. Это означает, что
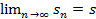 ,
, 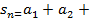 …
… 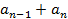 =
= 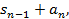
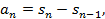
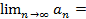 lim(
lim( 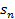 —
— 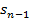 )=
)= 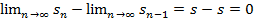 .
.
Следствие. Если общий член ряда к нулю не стремится, то ряд расходится.
Действие над рядами.
1) Сложение рядов.
Пусть даны два ряда 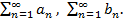 Суммой двух рядов называется ряд
Суммой двух рядов называется ряд
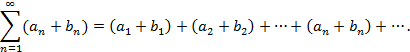
Теорема 2.Если ряды 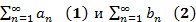 сходятся соответственно к
сходятся соответственно к 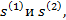 то ряд
то ряд 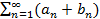 сходится к
сходится к 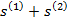 .
.
Доказательство. По условию ряды 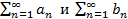 сходятся, то
сходятся, то 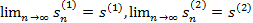 и
и 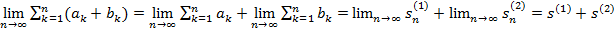
2) Умножение ряда на число.
Произведение ряда 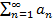 на число
на число 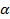 или числа
или числа 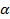 на ряд
на ряд 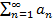 называется ряд
называется ряд 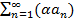 (3)
(3)
Теорема 3. Если ряд 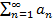 сходится и его сумма равна s, то ряд
сходится и его сумма равна s, то ряд 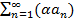 тоже сходится и его сумма равна
тоже сходится и его сумма равна 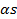 .
.
Если 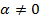 то оба ряда
то оба ряда 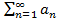 и
и 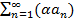 либо одновременно сходятся или одновременно расходятся.
либо одновременно сходятся или одновременно расходятся.
Доказательство. Справедливость теоремы вытекает из равенства: 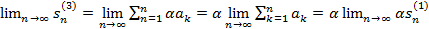
Теорема 4. Сходимость ряда не измениться если отбросить или прибавить конечное число первых членов ряда.
Доказательство. Рассмотрим два ряда:
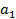 +
+ 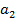 +….+
+….+ 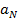 +
+ 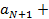 …+
…+ 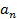 +… (4)
+… (4)
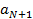 +
+ 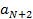 +…+
+…+ 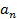 +… (5)
+… (5)
Справедливость теоремы вытекает из равенства:
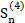 =
= 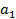 +
+ 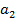 +….+
+….+ 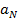 +
+ 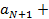 …+
…+ 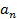 =
= 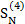 +
+ 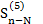 ,где
,где 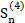 является константой, не зависящей от n.
является константой, не зависящей от n.
Знакоположительные ряды. Теоремы сравнения.
Ряд 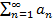 называется знакоположительным, если
называется знакоположительным, если 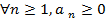 .
.
Теоремы, которые справедливы для знакоположительных рядов, справедливы для знакоотрицательных рядов, так, как умножение ряда на (-1), сходимость ряда не изменяет.
Теорема 5:
Для того, чтобы знакоположительный ряд сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.
Доказательство. Дан знакоположительный ряд
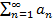 ,
, 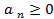 ,
, 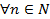 ,
, 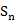 =
= 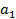 +
+ 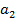 +
+ 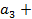 …+
…+ 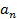 .
.
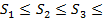 …..
….. 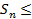 ….
….
Последовательность частичных сумм 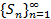 , неубывающая. Для того, чтобы неубывающая последовательность имела предел, необходимо и достаточно, чтобы она была ограничена сверху.
, неубывающая. Для того, чтобы неубывающая последовательность имела предел, необходимо и достаточно, чтобы она была ограничена сверху.
Теорема 6:
Пусть даны два знакоположительных ряда 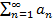 (1) ,
(1) , 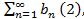 для которых выполняются неравенства
для которых выполняются неравенства 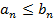

Тогда если ряд (2) сходится, то ряд (1) тоже сходится. Если же ряд (1) расходится, то ряд (2) тоже расходится.
Доказательство. Справедливость теоремы вытекает из неравенства 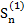 =
= 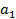 +
+ 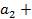 …+
…+ 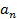
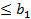 +
+ 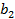 +…
+…  =
= 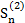 и теоремы 4. В самом деле, если ряд (2) сходится, то последовательность {
и теоремы 4. В самом деле, если ряд (2) сходится, то последовательность { 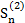 } ограничена сверху, тогда {
} ограничена сверху, тогда { 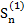 } ограничена сверху и ряд (1) сходится. Если ряд (1) расходится, то {
} ограничена сверху и ряд (1) сходится. Если ряд (1) расходится, то { 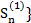 не ограничена сверху и тем более
не ограничена сверху и тем более 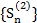 не ограничена сверху. Следовательно, ряд (2) расходится.
не ограничена сверху. Следовательно, ряд (2) расходится.
Замечание 1. Учитывая теорему 3, можно утверждать, что теорема 5 справедлива при выполнении неравенств 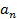
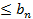 ,
, 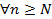 .
.
Чтобы применять теорему 5 при исследовании сходимости рядов, нужно иметь набор сходящихся и расходящихся рядов. Примером сходящихся рядов могут служить знакоположительные ряды из членов геометрической прогрессии при q 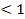 , а примерами расходящихся рядов могут быть знакоположительные ряды из членов геометрической прогрессии, при 1
, а примерами расходящихся рядов могут быть знакоположительные ряды из членов геометрической прогрессии, при 1 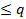 .
.
Примером расходящегося ряда может служить гармонический ряд 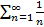 .
.
Ряды Дирихле: 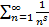
Ряды Дирихле мы исследуем позже с помощью интегрального признака Коши.
А сейчас отметим, что ряды Дирихле при 1<S сходятся, а при S 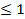 расходятся.
расходятся.
Ряд Дирихле при S=1 является гармоническим рядом.
Пример 5:Исследовать на сходимость ряд 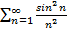 .
.
Решение: 0 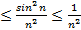 ,
, 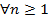 . Так как ряд Дирихле
. Так как ряд Дирихле 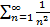 сходится, то по теореме сравнения данный ряд тоже сходится.
сходится, то по теореме сравнения данный ряд тоже сходится.
Пример 6:Исследовать на сходимость ряд 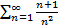
Решение:  <
< 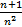
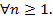 Так как гармонический ряд расходится, то данный ряд тоже расходится.
Так как гармонический ряд расходится, то данный ряд тоже расходится.
Теорема 7:
Пусть даны два знакоположительных ряда 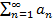 (1) ;
(1) ; 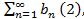 для которых существует предел
для которых существует предел 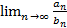 = c
= c 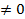 , то ряды (1) и (2) либо одновременно сходятся, либо одновременно расходятся.
, то ряды (1) и (2) либо одновременно сходятся, либо одновременно расходятся.
Пример 7:Исследовать на сходимость ряд 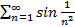
Решение: так как Sinx 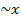 при x
при x 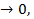 то данный ряд надо сравнить с рядом Дирихле
то данный ряд надо сравнить с рядом Дирихле 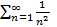 , который сходится.
, который сходится.
Рассмотрим предел 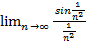 = 1
= 1 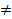 0 в силу первого замечательного предела.
0 в силу первого замечательного предела.
Следовательно, данный ряд сходится.
Дистанционный курс высшей математики НИЯУ МИФИ
Рассмотрим ряд, все члены которого неотрицательны: : ∀ n ⇒ un ≥ 0. Такой ряд называется знакоположительным. Аналогично можно рассмотреть знакоотрицательный ряд, все члены которого неположительны. Оба типа рядов носят название знакопостоянных (знакоопределенных). Для таких рядов можно сформулировать особые признаки сходимости. Поскольку конечное число членов ряда не влияет на его сходимость, то логично считать ряд знакопостоянным, если его члены становятся неотрицательными (неположительными) хотя бы начиная с некоторого конечного номера N0. Далее будем рассматривать только знакоположительные ряды (знакоотрицательные сводятся к ним путем умножения на −1).
Для знакоположительных рядов имеется аналог теоремы о монотонных последовательностях.
Теорема
Ряд с неотрицательными членами сходится ⇔ последовательность его частичных сумм ограничена сверху
(т. е. ∃ M > 0: ∀ n ⇒ Sn ≤ M).
Доказательство
|⇒| Пусть сходится ⇒ ∃ конечный ограничена.
|⇐| Поскольку члены ряда неотрицательны, то ∀ n ⇒ Sn+1 = Sn + un+1 ≥ Sn ⇒ не убывает и, по условию, ограничена сверху ⇒ ∃ конечный сходится.
Замечание
Очевидно, что расходящийся знакоположительный числовой ряд всегда имеет сумму S, и S = +∞.
11/28
24.Знакоположительные числовые ряды. Ряд геометрической прогрессии.
Числовые
ряды – рассмотрим числовую последовательность: 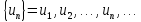 un –
числа.
un –
числа.
Составим
суммы: 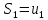 ;
;
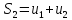 ;
;
…………………..
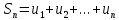 ;
;
Выражение: 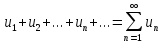 – называется числовым рядом (1)
– называется числовым рядом (1)
Числа 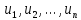 — называются
членами ряда. Если они положительны, то
ряд называется знакоположительным.
— называются
членами ряда. Если они положительны, то
ряд называется знакоположительным.
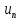 —
называется n-ый
член ряда или общий член ряда.
—
называется n-ый
член ряда или общий член ряда.
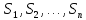 —
частичные суммы.
—
частичные суммы.
Числовой
ряд (1) называется сходящимся,
если последовательность частичных сумм
сходится к некоторому числу S,
которое называется суммой ряда, т.е. ряд
сходится если существует предел: 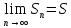 .
Если предел не существует или равен
бесконечности, то ряд называетсярасходящимся.
Ряд может быть задан перечислением
нескольких членов или в виде формулы
общего члена ряда.
.
Если предел не существует или равен
бесконечности, то ряд называетсярасходящимся.
Ряд может быть задан перечислением
нескольких членов или в виде формулы
общего члена ряда.
Ряд
геометрической прогрессии – Исследуем на сходимость ряд: 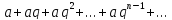 Этот ряд называетсярядом (2)
Этот ряд называетсярядом (2)
геометрической
прогрессии.
Сумму первых n-членов
ряда геометрической прогрессии находим
по формуле: 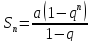 ,
,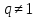
Найдем 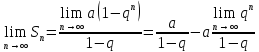
Рассмотрим следующие случаи:
1) ,
тогда
,
тогда 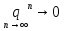 ,
поэтому
,
поэтому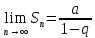 –
ряд сходится;
–
ряд сходится;
2)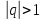 ,
тогда
,
тогда 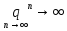 ,
и
,
и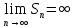 —
ряд расходится;
—
ряд расходится;
3)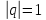 ,
тогда ряд (2) имеет вид:
,
тогда ряд (2) имеет вид: 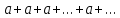 ,
его сумма
,
его сумма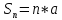 ,
,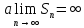 — ряд расходится;
— ряд расходится;
Вывод: ряд геометрической прогрессии (2)
сходится, при 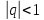 и
и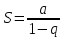 его и расходится, при
его и расходится, при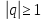 .
.
25.Свойства числовых рядов. Необходимые условия сходимости ряда.
Простейшие свойства числовых рядов:
1.Суммой
двух рядов 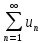 и
и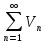 называется ряд
называется ряд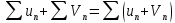 ;
;
2.Произведением
ряда на действительное число α называется ряд: 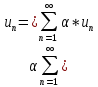 ;
;
3.Сходимость ряда не нарушается, если произвольно изменить (переставить, добавить или отбросить) конечное число членов. Сумма может измениться;
4.Сходящийся
ряд можно почленно умножать на любой
множитель α,
и если сумма ряда равна 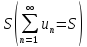 ,
то сумма
,
то сумма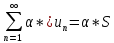 ;
;
5.Сходящиеся
ряды можно почленно складывать и
вычитать: 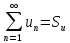 ;
; 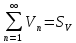 ,то
,то 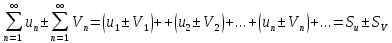 ;
;
Необходимое условие сходимости ряда:
Теорема: Если
ряд 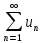 сходится, то его общий член
сходится, то его общий член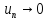 ,
т.е.
,
т.е.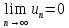 (1)
(1)
Доказательство: Если ряд 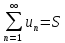 ,
, 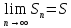 .Запишем:
.Запишем: 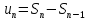 и
найдем его предел
и
найдем его предел 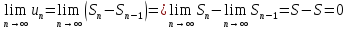 ч.т.д.
ч.т.д.
Если
условие (1) не выполняется, то ряд
расходится. Условие (1) не является
достаточным условием сходимости ряда,
т.е. из выполнения равенства 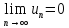 не обязательно вытекает сходимость
ряда.
не обязательно вытекает сходимость
ряда.
26.Достаточные признаки сходимости: признак Даламбера, радикальный признак Коши.
Необходимый признак сходимости не дает, вообще говоря, о том сходится ряд или нет. Сходимость и расходимость ряда можно установить с помощью достаточных признаков.
Признак
Даламбера – пусть дан ряд 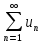 знакоположительный и существует предел
отношения последнего члена ряда к
предыдущему, т.е.:
знакоположительный и существует предел
отношения последнего члена ряда к
предыдущему, т.е.: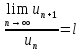 ,
тогда, если
,
тогда, если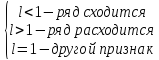 .
.
Радикальный
признак Коши – дан знакоположительный ряд 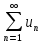 ,
если существует предел
,
если существует предел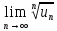 ,
тогда если
,
тогда если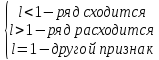 .
.
27.Достаточный признак сходимости: интегральный признак Коши. Сходимость обобщённого гармонического ряда.
Необходимый признак сходимости не дает, вообще говоря, о том сходится ряд или нет. Сходимость и расходимость ряда можно установить с помощью достаточных признаков.
Интегральный
признак Коши – дан знакоположительный ряд 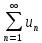 ,
пусть его члены могут быть представлены
как числовые значения некоторой функцииf(x),
которая убывает на промежутке [1;+∞),
т.е.:
,
пусть его члены могут быть представлены
как числовые значения некоторой функцииf(x),
которая убывает на промежутке [1;+∞),
т.е.: 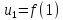 ;
;
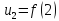 ;
;
…………..
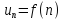 ;
;
тогда: 1.Если
несобственный интеграл: 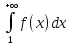 сходится, то и ряд сходится;
сходится, то и ряд сходится;
2.Если
несобственный интеграл: 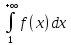 расходится, то и ряд расходится;
расходится, то и ряд расходится;
Замечание
(о сходимости несобственного интеграла): 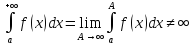 интеграл сходится, еслиlim = ∞,
или не существует, интеграл расходится.
интеграл сходится, еслиlim = ∞,
или не существует, интеграл расходится.
Обобщенный гармонический ряд:
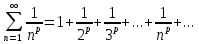 ,
где p>0 – действительное число (1)
,
где p>0 – действительное число (1)
Ряд
(1) называется рядом Дирихле. Исследуем
ряд на сходимость по интегральному
признаку. Рассмотрим функцию 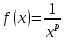 ,
, 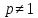 это
функция убывает на интервале (1;
это
функция убывает на интервале (1; 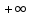 ).
).
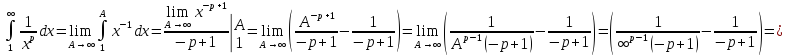
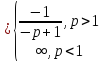
Вывод: ряд Дирихле 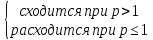
при 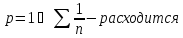
Этот ряд удобно использовать в признаках сравнения.
python 3.x — Как выбрать строки только с положительными или отрицательными значениями в Pandas
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Выбрать верхние (или нижние) n строк (по значению) — top_n • dplyr
top_n () заменено на slice_min () / slice_max () .
Хотя в ближайшем будущем он не будет прекращен, выход на пенсию означает
что мы будем исправлять только критические ошибки, поэтому мы рекомендуем перейти на
новые альтернативы.
top_n () было заменено, потому что имя фундаментально сбивало с толку, так как
он вернул то, что вы могли бы разумно считать нижним ряды.Кроме того, переменная wt имела непонятное имя и странное название.
по умолчанию (последний столбец во фрейме данных). К сожалению, мы не смогли
увидеть простой способ исправить существующую функцию top_n () без нарушения
существующий код, поэтому мы создали новую альтернативу.
top_n (x, n, вес) top_frac (x, n, вес)
Аргументы
| х | Фрейм данных. |
|---|---|
| н. | Число строк, возвращаемых для |
| вес | (необязательно). Переменная, используемая для заказа. Если не указана, по умолчанию используется последняя переменная в таблице. |
Примеры
df <- data.frame (x = c (6, 4, 1, 10, 3, 1, 1)) df%>% top_n (2) # самые высокие значения.#> Выбор по x
#> x #> 1 6 #> 2 10
df%>% top_n (-2) # самые низкие значения
#> Выбор по x
#> x #> 1 1 #> 2 1 #> 3 1
#> x #> 1 10 #> 2 6
#> x #> 1 1 #> 2 1 #> 3 1
# top_frac () -> аргумент prop для slice_min () / slice_max () df%>% top_frac (.5)
#> Выбор по x
#> x #> 1 6 #> 2 4 #> 3 10
#> x #> 1 10 #> 2 6 #> 3 4
python — подсчитать положительные значения в столбце pandas
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
Интерпретация результатов тестов | Понимание надежности
Скачать PDF-версию Что такое PDF?
Наука тестирования
Женщине необходимо знать, есть ли у нее беременная. С распространением домашних тестов на беременность и многие другие виды медицинского обследования, полезно рассмотреть как правильно интерпретировать данный результат теста. Хотя это — сложная тема, выходящая за рамки этого обзора, базовые концепции могут быть освоены с относительной легкостью.
После изучения и понимания читатели будут лучше ответить на такие вопросы, как:
Мой домашний тест на беременность положительный. Какова вероятность того, что я действительно беременна?
Мой домашний тест на беременность отрицательный. Какова вероятность того, что я действительно не беременна?
Моя любимая марка домашних тестов на беременность утверждает, что чувствительность составляет 98%. Что это значит? Теряет ли тест точность, если его выполняет непрофессионал, а не лаборант?
Каковы подводные камни проведения универсальных скрининговых тестов на такие заболевания, как ВИЧ?
Отборочные испытания
 Идеальный скрининговый тест — низкая стоимость,
прост в применении и интерпретации, неинвазивен и
широко доступный.Не менее важно идеальное скрининг
тест дает положительный результат для всех без исключения
с исследуемым состоянием (чувствительность = 100%)
и отрицательный результат для всех без исключения
без исследуемого состояния (специфичность 100%).
Однако ни один тест не является идеальным, и важно понимать
ограничения данного теста и данного результата теста.
Идеальный скрининговый тест — низкая стоимость,
прост в применении и интерпретации, неинвазивен и
широко доступный.Не менее важно идеальное скрининг
тест дает положительный результат для всех без исключения
с исследуемым состоянием (чувствительность = 100%)
и отрицательный результат для всех без исключения
без исследуемого состояния (специфичность 100%).
Однако ни один тест не является идеальным, и важно понимать
ограничения данного теста и данного результата теста.
 Это
Следует отметить, что скрининговые тесты чаще всего
используется для выявления болезненных состояний, но на самом деле может использоваться
для обнаружения любого условия или состояния.Отборочный тест
может стремиться идентифицировать людей с IQ, превышающим
160 или беременным или детям с
рыжие волосы. IQ гения или беременность
или рыжие волосы не имеют ничего общего с болезнью
заявляет, но принципы скрининга этих состояний
применяются тем не менее.
Это
Следует отметить, что скрининговые тесты чаще всего
используется для выявления болезненных состояний, но на самом деле может использоваться
для обнаружения любого условия или состояния.Отборочный тест
может стремиться идентифицировать людей с IQ, превышающим
160 или беременным или детям с
рыжие волосы. IQ гения или беременность
или рыжие волосы не имеют ничего общего с болезнью
заявляет, но принципы скрининга этих состояний
применяются тем не менее.
Давайте начнем с некоторых определений, а затем с нескольких примеров.
В следующей таблице люди сгруппированы в одну четырех категорий.Две колонки делят людей на группы в зависимости от того, имеют ли они или нет условие учиться. Две строки разделяют людей в зависимости от того, иметь положительный или отрицательный результат скринингового теста.
| Скрининг Результаты тестов: | Действительно есть состояние? | Всего | |
|---|---|---|---|
| Да (столбец 1) | № (графа 2) | ||
| Положительный (строка 1) | a | б | а + б |
| Отрицательный (строка 2) | c | d | к + д |
| Всего | а + с | б + д | а + б + в + г |
Пусть a = количество людей с изучаемым заболеванием и с положительным результатом скринингового теста
Пусть b = количество людей без изучаемого заболевания и с положительным результатом скринингового теста
Пусть c = количество людей с изучаемым заболеванием и с отрицательным результатом скринингового теста
Пусть d = количество людей без изучаемого заболевания и с отрицательным результатом скринингового теста
Чувствительность = [a / (a + c) × 100%] =
процент людей с изучаемым заболеванием с положительным тестом, деленный на общее количество людей с этим заболеванием
Специфичность = [d / (b + d) × 100%] =
процент людей без изучаемого состояния с отрицательным тестом, деленный на общее количество людей без состояния
Чувствительность — это мера, используемая для определения эффективности теста для выявления людей с заболеванием.Чем выше чувствительность, тем лучше.
Специфичность — это мера, используемая для определения эффективности теста для выявления людей без заболевания. Чем выше специфичность, тем лучше.
Реальные вопросы, на которые необходимо ответить, следующие:
Если у человека положительный тест, какова вероятность заболевания?
Если у человека отрицательный результат теста, какова вероятность не заболеть?
Вопросы, подобные этим, относятся к так называемой «положительной прогнозируемой ценности» и «отрицательной прогнозной ценности».
Используя переменные в таблице выше, мы можем определить эти количества следующим образом:
Положительное прогнозное значение (PPV) = [a / (a + b)] × 100%]
Отрицательное прогнозное значение (ЧПС) = [d / (c + d)] × 100%]
Последняя важная переменная при оценке тестов а результаты анализов — это распространенность рассматриваемого заболевания. Распространенность определяется как процент людей в исследуемая популяция, имеющая заболевание.(Это отличается от заболеваемости, которая относится к тому, сколько новых людей приобретают болезнь в данный период времени.)
Распространенность = число заболевших / общая популяция
 Давайте попробуем разобраться в этих концепциях на нескольких примерах:
Давайте попробуем разобраться в этих концепциях на нескольких примерах:
Проблема A
Дано: Мы используем новый скрининговый тест, предназначенный для выявления астмы у 100 000 человек.
Дано: Десять процентов этого населения страдает астмой.
Дано: Этот новый скрининговый тест на астму имеет чувствительность 98% и специфичность 90%.
Теперь у нас достаточно информации, чтобы оценить полезность этого нового теста.
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | a | б | а + б |
| отрицательный | c | d | к + д |
| Всего | a + c Общее количество заболевших | б + д Всего без болезней | a + b + c + d Всего |
Наша первая задача — вставить числа в девять полей ниже из информации выше.Общая численность населения составляет 100 000 человек. Это по определению общее количество людей, которое указывается в правом нижнем поле.
Поскольку распространенность астмы составляет 10%, мы можем легко заключить, что 10 × 100 000 = 10 000 человек страдают астмой, а 90 000 — нет. Эти значения предполагают итоги первого и второго столбцов соответственно.
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | a | б | а + б |
| отрицательный | c | d | к + д |
| Всего | 10 000 Всего заболевших | Всего не заболевших | 100000 Всего |

Теперь мы используем указанные значения чувствительности и специфичности.
Учитывая чувствительность 98% или 0,98, мы можем с уверенностью заключить, что 98% людей с этим заболеванием будут иметь положительный результат скринингового теста, так что a = 0,98 × 10 000 = 9800. Это потому, что по определению чувствительность = a / (a + c), поэтому 0,98 = a / 10,000 a = 9800
Если a = 9800, c должно быть равно 200, потому что a + c = 10 000 c = 10 000 — 9800 = 200
Точно так же, учитывая специфичность 90% или 0,90, мы можем с уверенностью заключить, что 90 процентов людей без заболевания будут иметь отрицательный результат теста, поэтому d =.90 × 90 000 = 81 000. Это потому, что по определению специфичность = d / (b + d), поэтому 0,90 = d / 90 000 d = 0,90 × 90 000 = 81 000
.Если d = 81000, b должно быть равно 9000, потому что b + d =
d = — 81000 = 9000
Мы можем заполнить эту дополнительную информацию, как показано ниже.
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | 9 800 | 9 000 | а + б |
| отрицательный | 200 | 81 000 | к + д |
| Всего | 10 000 Всего заболевших | Всего не заболевших | 100000 Всего |
Последние два поля вычисляются с простым сложением, чтобы окончательно заполнить таблицу:
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | 9 800 | 9 000 | 18 800 |
| отрицательный | 200 | 81 000 | 81 200 |
| Всего | 10 000 Всего заболевших | Всего не заболевших | 100000 Всего |
В качестве внутренней проверки нашей работы обратите внимание:
18 800 плюс 81 200, как и следовало ожидать, составляет 100 000.
Теперь у нас есть четыре группы людей с разными характеристиками:
9800 человек страдают астмой и имеют положительный результат теста. Им поставили правильный диагноз — астма. Они называются «Истинные положительные результаты (TP)».
200 человек страдают астмой, но имеют отрицательный результат теста. Им был поставлен неправильный диагноз: они не страдают астмой. Они называются «Ложноотрицательные (ЛО)».
Есть 9000 человек без астмы, но с положительным тестом.У них неправильно диагностировали астму. Они называются «ложными срабатываниями (FP)».
81 000 человек не страдают астмой и имеют отрицательный результат теста. Им был поставлен правильный диагноз: они не страдают астмой. Они называются «Истинно-отрицательные (TN)».
Распространенность = 10%, Чувствительность = 98, Специфичность = 90%
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | 9,800 TP (истинно положительные результаты) | 9000 FP (ложные срабатывания) | 18 800 |
| отрицательный | 200 FN (ложноотрицательные) | 81000 TN (True Negatives) | 81 200 |
| Всего | 10 000 Всего заболевших | Всего не заболевших | 100000 Всего |
В-третьих, у нас есть две группы людей с серьезными проблемами.200 человек в столбце 1 страдают астмой, но результат теста отрицательный. Кроме того, у 9000 человек есть положительный тест на астму, но на самом деле астма не наблюдается.
Теперь давайте определим положительные и отрицательные прогнозные значения. (PPV и NPV)
PPV = [a / (a + b)] × 100%], поэтому 9 800/18 800 × 100% = 52,1%
NPV = [d / (d + c)] × 100%], поэтому 81 000/81 200 × 100% = 99,75%
Что все это значит?
 Прогнозируемое положительное значение 52.1% означает, что только 52,1% людей с положительным результатом теста действительно болеют. Другими словами, вероятность заболевания астмой у людей с положительным тестом составляет 52,1%. Хотя этот тест правильно определил большинство (9800 из 10 000) людей, страдающих астмой, в процессе он неправильно определил подозрение на астму почти равному количеству (9000) людей. Это очень проблематично.
Прогнозируемое положительное значение 52.1% означает, что только 52,1% людей с положительным результатом теста действительно болеют. Другими словами, вероятность заболевания астмой у людей с положительным тестом составляет 52,1%. Хотя этот тест правильно определил большинство (9800 из 10 000) людей, страдающих астмой, в процессе он неправильно определил подозрение на астму почти равному количеству (9000) людей. Это очень проблематично.
Отрицательная прогностическая ценность 99,75% означает, что 99,75% людей с отрицательным результатом теста действительно не страдают астмой.Другими словами, люди с отрицательным результатом теста имеют 99,75% шанс избавиться от астмы. Это дает полезную и надежную информацию. У небольшого числа (200 из 100 000 протестированных) людей с ложноотрицательными тестами возникнет ложное чувство безопасности.
Этот тест является точной оценкой почти для всех тех, кто дал отрицательный результат. Для тех, кто дал положительный результат, тест почти не имеет смысла, так как люди почти не страдают астмой, как и страдают астмой.
Если бы это был недорогой, неинвазивный, широко доступный тест, его основная ценность заключалась бы в выявлении людей, не страдающих астмой.Тем, у кого тест положительный, потребуется дополнительное, более дорогое тестирование, чтобы ответить на вопрос.
Теперь давайте посмотрим на тот же тест, но давайте изменим распространенность болезни на 2% и 25% и посмотрим, что произойдет.
Распространенность = 2%, Чувствительность = 98, Специфичность = 90%
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | 1 960 | 9 800 | 11 760 |
| отрицательный | 40 | 88 200 | 88 240 |
| Всего | 2000 Общее количество заболевших | 98000 Всего без болезней | 100000 Всего |
PPV = 1960/11760 = 16.67% NPV = 88,200 / 88,240 = 99,95%
Распространенность = 25%, чувствительность = 98, специфичность = 90%
| Результатов тестов: | Болеете? | Всего | |
|---|---|---|---|
| Есть | Нет | ||
| Положительный | 24 500 | 7 500 | 32 000 |
| отрицательный | 500 | 67 500 | 68 000 |
| Всего | 25000 Всего заболевших | 75000 Всего не заболевших | 100000 Всего |
PPV = 24 500/32 000 = 76.56% NPV = 67 500/68 000 = 99,26%
Сводка данных с различной распространенностью
| Распространенность (%) | PPV (%) | ЧПС (%) |
|---|---|---|
| 2 | 16,67 | 99.95 |
| 10 | 52,1 | 99.75 |
| 25 | 76,56 | 99,26 |
При использовании этого теста чем ниже распространенность заболевания, тем ниже PPV и выше NPV.
Этот пример подчеркивает проблемы, возникающие при проведении массовых обследований среди населения с низкой распространенностью заболевания. Каждый человек с положительным результатом теста, но на самом деле не болеющий, должен пройти дополнительное ненужное, часто дорогостоящее, а иногда и болезненное обследование, а также пережить тревогу из-за того, что ему поставили диагноз потенциально серьезного заболевания.Эти скрининговые тесты позволяют выявлять здоровых людей с высокой степенью надежности. Лица с положительным результатом теста требуют дальнейшего тестирования. По мере того, как распространенность заболевания падает, положительная прогностическая ценность падает.
Интерпретация домашних тестов на беременность
 Для правильной интерпретации домашних тестов на беременность важно знать чувствительность, специфичность, а также положительные и отрицательные прогностические значения для теста, когда он проводится людьми, не имеющими медицинской или лабораторной подготовки.Большинство производителей домашних тестов на беременность имеют эти данные и предоставляют их по запросу. Даже знание этих фактов и максимально тщательное выполнение этих тестов не гарантирует достоверности результатов каждого отдельного теста.
Для правильной интерпретации домашних тестов на беременность важно знать чувствительность, специфичность, а также положительные и отрицательные прогностические значения для теста, когда он проводится людьми, не имеющими медицинской или лабораторной подготовки.Большинство производителей домашних тестов на беременность имеют эти данные и предоставляют их по запросу. Даже знание этих фактов и максимально тщательное выполнение этих тестов не гарантирует достоверности результатов каждого отдельного теста.
Если вы подозреваете беременность, обратитесь к соответствующему врачу, чтобы он ответил на этот жизненно важный вопрос.

Беременны или нет? Это вопрос
С точки зрения здоровья, для женщины «благороднее» (не говоря уже о жизненно важном) знать, беременна ли она.Если вы беременны, обратитесь к соответствующему врачу для тестирования на беременность и убедитесь, что ваш врач осведомлен обо всех симптомах, которые могут у вас возникнуть. Любая боль в животе, кровотечение, спазмы, головокружение, обморок или множество других симптомов могут указывать на наличие внематочной беременности, которая может быть опасной для жизни, если ее не обнаружить и не лечить на ранней стадии. Внематочная беременность возникает, когда эмбрион на ранней стадии имплантируется не во внутреннюю оболочку матки, а в другом месте. В этих случаях у эмбриона нет шансов на выживание, но его присутствие может вызвать у женщины сильное внутреннее кровотечение, которое может привести к геморрагическому шоку и смерти.Большинство внематочных беременностей происходит в фаллопиевых или маточных трубах. Редко имплантация может происходить в брюшной полости. Каждый случай подозрения на внематочную беременность следует рассматривать как неотложную медицинскую помощь, и все беременные женщины должны быть обследованы соответствующим врачом, чтобы убедиться, что внематочная беременность отсутствует.
Женщины с историей повреждения фаллопиевых труб, например, вызванного воспалительным заболеванием тазовых органов (из-за хламидиоза или гонореи), перенесенными операциями на брюшной полости или внематочной беременностью или перевязкой маточных труб (хирургическая процедура, направленная на окончательное отключение фаллопиевых труб с целью предотвращения беременности) имеют значительно более высокий риск внематочной беременности.Фактически, предполагается, что женщина, ранее перенесшая операцию по перевязке маточных труб и имеющая положительный результат теста на беременность, имела внематочную беременность, пока не будет доказано обратное. Риск также увеличивается при использовании определенных видов контрацепции и с возрастом. 1 Однако внематочная беременность может наступить и происходит у женщин без каких-либо известных факторов риска, и возможность ее наличия необходимо учитывать при каждой беременности.
Есть и другие важные причины для скорейшего установления беременности.Ранняя диагностика позволяет получить максимальную пользу от пренатальных витаминов и дородового ухода и позволяет женщине избегать небезопасных лекарств, алкоголя, табака и всех других потенциально вредных воздействий.
1 Cunningham, et al., William’s Obstetrics, 21st Edition (New York: McGraw-Hill, 2001), 884-885.
.