Знаменатель прогрессии это: Геометрическая прогрессия — урок. Алгебра, 9 класс.

Члены геометрической прогрессии | Онлайн калькулятор

Все калькуляторы

/

Учеба и наука

/

Математика

/   Члены геометрической прогрессии

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Члены геометрической прогрессии представляют собой числа, выстроенные строго по порядковым номерам, где непосредственно порядковый номер определяет значение члена последовательности. Первый член геометрической прогрессии может быть любым числом, кроме нуля (b≠0). Для того чтобы найти n член геометрической прогрессии необходимо первый член умножить на знаменатель прогрессии нужное количество раз.

Знаменателем прогрессии является заданное число, которое неизменно на протяжении всего числового ряда. Для того чтобы увидеть суть последовательности, рассмотрим числовой ряд, где выписаны b_n— это первые несколько членов прогрессии с порядковым номером n, а q — это знаменатель прогрессии.
b₁
b₂=b₁ q
b₃=b₂ q=b₁ qq=b₁ q^{2
b₄=b₃ q=b₁ q2 q=b₁ q3
…}

Отсюда наглядно видно, что знаменатель геометрической прогрессии собирается в степень, показателем которой является число на одну единицу меньше порядкового номера члена прогрессии, который нужно найти, и все члены зависят от первого. Общая формула членов геометрической прогрессии будет выглядеть так: b_n=b₁ q^(n-1)

Исходя из этого, зная первый член геометрической прогрессии, можно

найти первые три, четыре члена прогрессии, умножая на знаменатель в нужной степени. Подобный онлайн калькулятор рассчитывает и в обратную сторону, то есть, зная любой из членов последовательности, можно найти первый. Чтобы проделать подобную операцию, калькулятор переворачивает формулу, в которой первый член геометрической прогрессии будет равен отношению заданного по условиям задачи члена к знаменателю, возведенному в степень n-1, где n — это порядковый номер известного члена.

Другой способ найти первый член геометрической прогрессии заложен в определении суммы первых нескольких членов прогрессии. Сама сумма равна произведению первого члена прогрессии на разность знаменателя в степени порядкового номера последнего участвующего члена и единицы, затем полученный результат необходимо разделить на еще одну разность знаменателя, в этот раз без степени, и единицы:

Порядок уменьшаемого и вычитаемого в скобках может меняться, это не будет влиять на результат до тех пор, пока это происходит синхронно:

Тогда при перераспределении параметров в формуле выходит, что первый член прогрессии равен произведению суммы с разностью единицы и знаменателя, деленной на разность единицы и знаменателя в степени н:

×

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Скачать калькулятор

Select rating12345

Рейтинг: 2. 6 (Голосов 33)

Сообщить об ошибке

Смотрите также

Алгебра

Алгебра

Гельфанд И. М., Шень А. X. Алгебра. — М.: ФАЗИС, 1998. — 192 с. Эта книга — про алгебру. Алгебра — наука древняя, и от повседневного употребления её сокровища поблекли. Авторы старались вернуть им первоначальный блеск. Основную часть книги составляют задачи, большинство которых приводится с решениями. Начав с элементарной арифметики, читатель постепенно знакомится с основными темами школьного курса алгебры, а также с некоторыми вопросами, выходящими за рамки школьной программы, так что школьники разных классов (6 — 11) могут найти в книге темы для размышлений. Оглавление 1. 2 + bх + c = 0 53. Бще одна формула корней квадратного уравнения 54. Квадратное уравнение становится линейным 55. График квадратного трехчлена 56. Квадратные неравенства 57. Максимум и минимум квадратного трехчлена 58. Биквадратные уравнения 59. Возвратные уравнения 60. Как завалить на экзамене. Советы экзаменатору 61. Корни 62. Степень с дробным показателем 63. Доказательства числовых неравенств 64. Среднее арифметическое и среднее геометрическое 65. Среднее геометрическое не больше среднего арифметического 66. Задачи на максимум и минимум 67. Геометрические иллюстрации 68. Средние многих чисел 69. Среднее квадратическое 70. Среднее гармоническое 71. Книги для дальнейшего чтения

Как найти формулу общего члена последовательности — Криста Кинг Математика

Каков общий член последовательности?

Общий член последовательности ???a_n??? является термином, который может представлять любой другой термин в последовательности.

Он связывает каждый член последовательности с его местом в последовательности.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Например, дана последовательность

???\{-1,-2,-3,-4,-5,\ …\}???

нам нужно понять, что

первый член последовательности равен ???-1???

второй член последовательности равен ???-2???

третий член последовательности ???-3???

четвертый член последовательности ???-4???

пятый член последовательности ???-5???

Другими словами

, когда ???n=1???, значение последовательности равно ???-1???

когда ???n=2???, значение последовательности равно ???-2???

когда ???n=3???, значение последовательности равно ???-3???

когда ???n=4???, значение последовательности равно ???-4???

когда ???n=5???, значение последовательности равно ???-5???

Основываясь на этой информации, значение последовательности всегда ???-n???, поэтому формула для общего члена последовательности:

???a_n=-n???

Это был простой пример, но мы всегда будем следовать этому же процессу, чтобы найти общий член любой последовательности. мы будем

Сопоставьте члены последовательности с их местом в последовательности ???n???

Найдите закономерность, связывающую каждый термин с соответствующим ему значением ???n???

Мы всегда должны обращать особое внимание на знаки терминов в последовательности.

Если все члены последовательности положительны, ???a_n??? будет положительным.

Если все члены последовательности отрицательные, ???a_n??? будет отрицательным (???-a_n???).

Если знаки членов чередуются, и 9{n+1}???

Как найти общий термин для последовательности, связав образец в терминах с соответствующим значением n

Пройти курс

Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого. 🙂

Узнать больше

Разделение числителя и знаменателя отдельно для нахождения общего члена

Пример

Найдите формулу для общего термина ???a_n??? последовательности. n???. 93???.

Общий термин последовательности a_n — это термин, который может представлять любой другой термин в последовательности.

Он связывает каждый член последовательности с его местом в последовательности.

Теперь давайте посмотрим на знаменатель каждого члена в нашей последовательности. Взяв только знаменатель, мы видим, что

Знаменатель каждого термина всегда равен ???3??? выше соответствующего значения ???n???, что означает, что знаменатель каждого члена в нашей последовательности может быть представлен как ???n+3???, поэтому знаменатель общего члена ???a_n ??? будет ???n+3???. 93}{п+3}???

Текст

Получить доступ к полному курсу Calculus 2

Начать

Изучайте математикуКриста Кинг 4 февраля 2021 математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 2, исчисление ii, исчисление 2, исчисление ii, исчисление с одной переменной, вычисление с одной переменной, последовательности и ряды, последовательности, ряды, формулы для общего члена, общего члена, общего члена последовательности

0 лайков Видео с вопросами

: нахождение общего отношения и общего члена геометрической последовательности

В геометрической последовательности отношение между любыми двумя последовательными членами является фиксированным отношением 𝑟.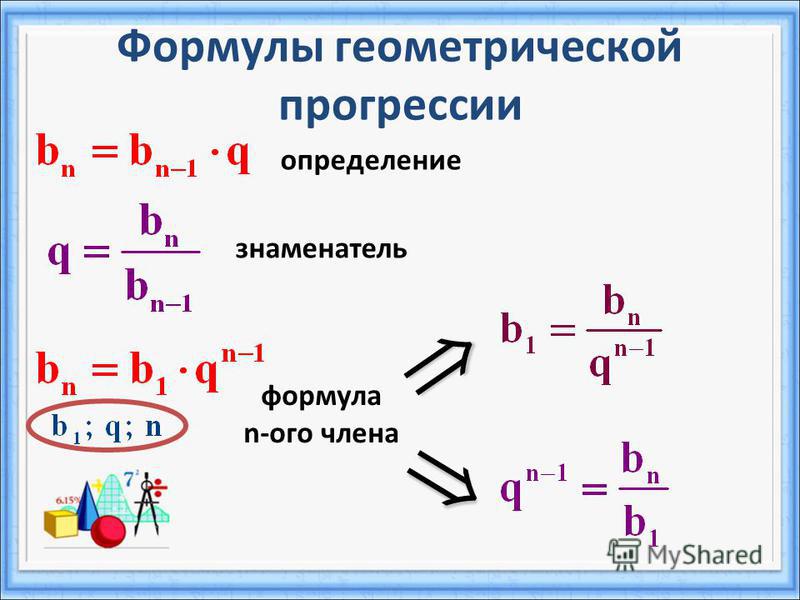

Рассмотрим последовательность 1/2, 1/4, 1/8, 1/16, ⋯. Является ли эта последовательность геометрической? Рассмотрим последовательность 1/2, 1/4, 1/8, 1/16, ⋯. Какова ценность 𝑟? Рассмотрим последовательность 1/2, 1/4, 1/8, 1/16, ⋯. Каков общий член этой последовательности?

Стенограмма видео

В геометрической последовательности отношение между любыми двумя последовательными членами является фиксированным отношением 𝑟. Рассмотрим последовательность наполовину, одна четверть, одна восьмая, одна шестнадцатая и так далее. Является ли эта последовательность геометрической? Рассмотрим последовательность наполовину, одна четверть, одна восьмая, одна шестнадцатая и так далее. Какова ценность 𝑟? Рассмотрим последовательность наполовину, одна четверть, одна восьмая, одна шестнадцатая и так далее. Что такое общий срок эта последовательность?

В этом вопросе нам дается напоминание о том, что такое геометрическая прогрессия. Это тот, который имеет фиксированный отношение или обыкновенное отношение между любыми двумя последовательными терминами. В каждой из трех частей этот вопрос, мы рассматриваем ту же последовательность. И в первой части этого вопрос, нас спрашивают, является ли данная последовательность геометрической. Итак, давайте запишем это последовательность. Если он геометрический, то будет обыкновенным отношением 𝑟 между любыми двумя последовательными или последовательными терминами. Итак, давайте посмотрим, сможем ли мы найти отношение между первыми двумя членами, половина и одна четверть. Чтобы найти отношение, возьмем второй член одной четверти и разделить его пополам.

Когда мы делим дроби, записываем первую дробь и умножаем ее на обратную вторую доля. Мы можем вынести общий множитель двух из числителя и знаменателя. А затем умножить числители дают нам единицу, а умножение знаменателей дает нам два. Это означает, что отношение между первым и вторым членом составляет половину. Далее найдем отношение между вторым и третьим членом одной четверти и одной восьмой, поэтому мы будем вычислить одну восьмую, деленную на одну четверть. Умножение на обратное из дроби одна четвертая, мы вычисляем одну восьмую, умноженную на четыре по один. И так, в очередной раз получаем отношение половинное.

Похоже, да имеют общее соотношение, но всегда стоит проверить все условия, чтобы убедиться что есть общее отношение на всех из них. И когда мы вычисляем один шестнадцатую делим на одну восьмую, тоже получаем отношение половины. Поэтому мы установили что эта последовательность имеет фиксированное или обычное отношение, и поэтому она должна быть геометрический. И мы можем сказать да, поскольку ответ на первую часть этого вопроса. Во второй части этого вопрос, нас просят найти значение 𝑟 для той же последовательности. Помните, что 𝑟 является фиксированным соотношение, и это красиво и просто. Мы только что разобрались с этим быть наполовину, что является ответом на вторую часть этого вопроса.

В последней части этого вопрос, нас просят найти общий член этой последовательности. И мы можем помнить, что общий термин — это еще один способ задать 𝑛-й термин. Если бы мы начали с первого термин, записанный как 𝑎 sub один, равный половине, тогда второй термин будет 𝑎 меньше двух, и это будет одна четверть. Третий и четвертый члены могут быть записано как 𝑎 под три и 𝑎 под четыре. Поэтому, когда мы находим общий термин, мы действительно ищем правило, которое позволило бы нам выработать 𝑛-й член или 𝑎 под 𝑛.

Мы помним, что есть общая формула, позволяющая нам вычислить 𝑛-й член любого геометрического последовательность. 𝑎 sub 𝑛 равно 𝑎 умножается на 𝑟 в степени 𝑛 минус один, где 𝑎 — первый член, а 𝑟 является обычным соотношением. Значения, которые нам нужно подключить в формулу будет 𝑎 равно половине, так как это был первый член, и 𝑟 мы работали вдвоем. Следовательно, 𝑛-й член эту последовательность можно представить как половину, умноженную на половину в степени 𝑛 минус один. Когда мы даем свой ответ, это важно, чтобы мы указали значения 𝑛. Когда мы находим 𝑛-й член или общий термин, мы начали с 𝑛 равно единице. Итак, ответ на третий часть вопроса в том, что общий член последовательности равен половине умножается на половину в степени 𝑛 минус один для значений 𝑛 больше больше или равно единице.