Значащие и верные цифры. Правило округления
Определение численных методов. Погрешности.
Прикладная математика – математическая наука, целью которой является решение прикладных задач: изучение явлений природы, получение их математического описания (математической модели) и его исследование.
Примеры мат.моделей: модель абсолютно твердого тела, модель звездного неба, модель человеческого организма, модели экономических, химических задач и т. д.
Каждая математическая модель содержит некоторые допущения (чем-то пренебрегают).
Основные требования, предъявляемые математическим моделям: 1) адекватность рассматриваемому явлению, 2) сравнительная простота и доступность, 3) необходимость правильной оценки области применения.
Определение. Создание математической модели процесса или явления называется математическим моделированием.
Для решения математических задач используются группы методов: аналитические, графические, численные.
1) Аналитические методы.
Особенность методов состоит в использовании детерминированной информации, строгой алгоритмизации действий и однозначности установленной функциональной зависимости. Для решения задач используются символьные вычисления — это преобразования и работа с математическими равенствами и формулами как с последовательностью символов. Разработкой и реализацией аналитических методов решения математических задач на компьютере занимается компьютерная алгебра, в которой предполагается, что исходные данные, как и результаты решения, сформулированы в аналитическом (символьном) виде. Аналитические решения чаще удаётся получить для наиболее грубых (простых) моделей, реже — для более точных. Аналитические методы основываются на фундаментальной теории математического анализа, функционального анализа, интегральных и дифференциальных исчислений, разработанной группой выдающихся отечественных ученых — А.Н. Колмогоровым, С.В. Фоминым, Л.В. Канторовичем и др.
Недостаток – не всегда можно получить точное решение: многие решения не всегда выражаются в известных функциях или точных методов нахождения решений попросту не существует.
2) Графические методы.
Графические методы считаются весьма важным и эффективным орудием современной науки, они надежно вошли в методику научных исследований.
Недостаток – невысокая точность полученного решения, невозможность построить графики.
3) Численные методы.
Численные методы – раздел прикладной математики.
Определение. Численные (вычислительные) методы — методы решения математических задач в численном виде, иначе, это методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, при этом результат также получается в виде числовых значений.
Численные методы появились в связи с тем, что искомые решения не всегда выражаются в привычных для нас элементарных или других известных функциях, то есть аналитическим и численным методами отыскать их невозможно. С появлением численных методов появилось решение, но его отыскание было затруднено громоздкими арифметическими операциями над числами, что привело к созданию ЭВМ.
За математическими выражениями в численных методах стоят приближённые численные значения, так как исходные данные в задаче, так и её решения представляются в виде числа или набора чисел. Результат вычислений — также приближенное число. Существуют методы, при помощи которых можно получить и точное решение, например, метод Гаусса для решения систем линейных алгебраических уравнений.
Определение. Численный метод называется сходящимся, если получаемое численное решение задачи очень близко к истинному решению.
Существует достаточно большое количество численных методов, обладающих своими достоинствами и недостатками, которые зависят, прежде всего, от свойств функций, значение которых ищется. Одним из сравнительных показателей качества метода является количество значений функции, которое нужно вычислить для решения задачи с заданной погрешностью. Чем это число меньше, тем при прочих равных условиях эффективнее метод.
Численные методы позволяют получить частные численные решения многих задач, даже сложных математических моделей. К тому же при решении большинства практических задач точное решение не всегда является необходимым.
Как было сказано выше – результатом вычислений с помощью численных методов является приближенные числа.
Определение. Математические действия над приближенными числами называются приближенными вычислениями.
Поэтому главным вопросом является вопрос о погрешности вычислений.
Определение.Погрешность – отклонение точного значения от приближенного.
Источники погрешности – 1)несоответствие математической модели изучаемому явлению, 2) погрешность исходных данных, 3) погрешность метода решения, 4) ошибки округления исходных данных.
Классификация погрешностей – а) неустранимая (источники 1 и 2), b) погрешность метода (источник 3), c) погрешность округления (источник 4)
Пусть а – точное неизвестное числовое значение величины, а* известное приближенное числовое значение этой величины (приближенное число).
Определение. Число называется абсолютной погрешностью округления.
Абсолютная погрешность не полностью характеризует точность измерения. Качество измерения более характеризуется относительной погрешностью.
Определение. Относительной погрешностью называется .
Относительная погрешность безразмерна, часто выражается в процентах.
Любое приближенное число а* может быть представлено в виде:
, где m – величина разряда или разряд, а — цифра числа. Например, 38, 57 =
Определяющим точность вычисления является не число десятичных знаков, а число значащих цифр результата.
Определение. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.
Например, 25, 047 – 5 значащих цифр, 0,00250 – 3 значащие цифры.
Определение. Значащая цифра приближенного числа а* называется верной в широком смысле, если абсолютная погрешность не превосходит единицы десятичного разряда, в котором стоит : , и верной в узком смысле, если .
Пример. Сколько верных цифр содержит число ?
Решение. m = 1, так как
В широком смысле:
, с другой стороны , отсюда 2 – n = -2, то есть n = 4. Верные в широком смысле цифры – 8, 5, 2, 6.
В узком смысле:
, с другой стороны , отсюда 2 – n = -1, то есть n = 3. Верные в широком смысле цифры – 8, 5, 2.
Числа 23,56 и 23,5600 как приближенные различны.
Если число записано без указания его абсолютной погрешности, то выписаны только верные цифры.
Употребляя запись надо помнить правило: выписывать с одной или двумя значащими цифрами, а младший разряд в а* должен соответствовать младшему разряду в .
— правильно, и — неправильно.
Определение. Число цифр после запятой от первой цифры до последней верной цифры называется числом верных цифр после запятой.
В основе процессов округления числа лежит идея минимальной разности числа а и его округленного значения а*.
Правило округления (правило четной цифры): если в старшем из отбрасываемых разрядов стоит цифра меньше 5, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется 1 с тем же знаком, что и у самого числа. При этом, если первая слева из отброшенных цифр равна 5, и за ней не следуют отличные от нуля цифры, то последняя оставшаяся цифра усиливается, если она нечетная, и остается без изменений, если она четная.
, , , , .
Абсолютная погрешность округления не превосходит половины единицы разряда, определяемого последней оставленной значащей цифрой.
Похожие статьи:
poznayka.org
1.3. Запись приближенных значений величин. Верные знаки
Приближенные значения величин обычно записывают в виде десятичных дробей с конечным числом цифр.
Значащими цифрами в записи десятичной дроби называются все цифры, начиная с первой ненулевой слева. Например, в дроби 0,00102030004 значащими цифрами (подчеркнуты) являются все цифры, начиная с третьей после запятой.
Цифра в записи
приближенного значения 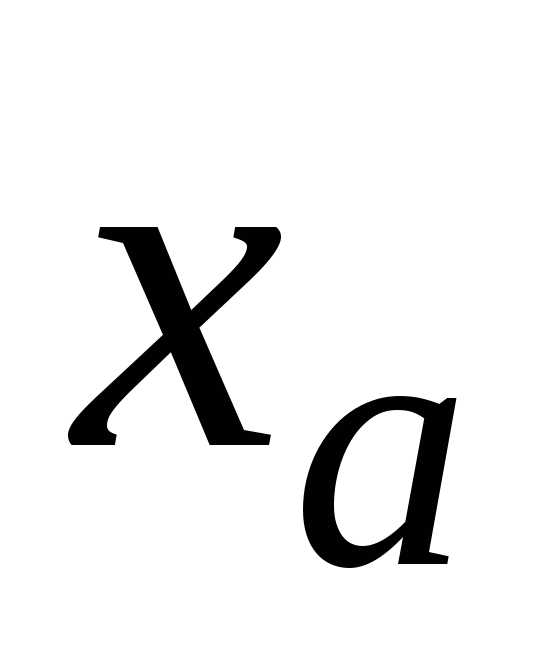 числовой величиныx называется верной в широком (строгом)
смысле слова,
если абсолютная погрешность
числовой величиныx называется верной в широком (строгом)
смысле слова,
если абсолютная погрешность 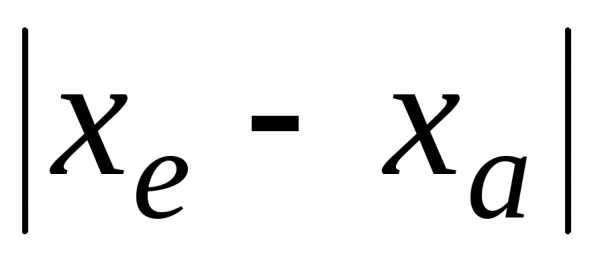 приближенного значения
приближенного значения 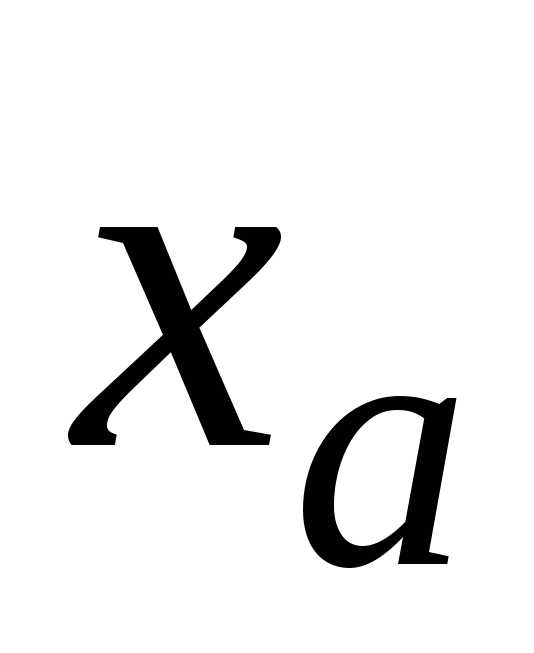 не превышает
единицы (половины единицы) разряда, в
котором стоит эта цифра.
не превышает
единицы (половины единицы) разряда, в
котором стоит эта цифра.
Все цифры верные в строгом смысле слова, очевидно, будут верными и в широком смысле. Рассмотрим несколько примеров.
Пример 1
Пусть
,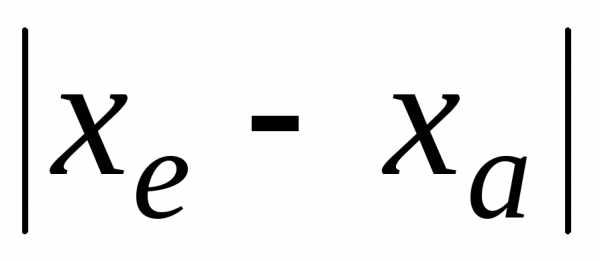 = 0,000007899.Требуется найти верные цифры в
записи
= 0,000007899.Требуется найти верные цифры в
записи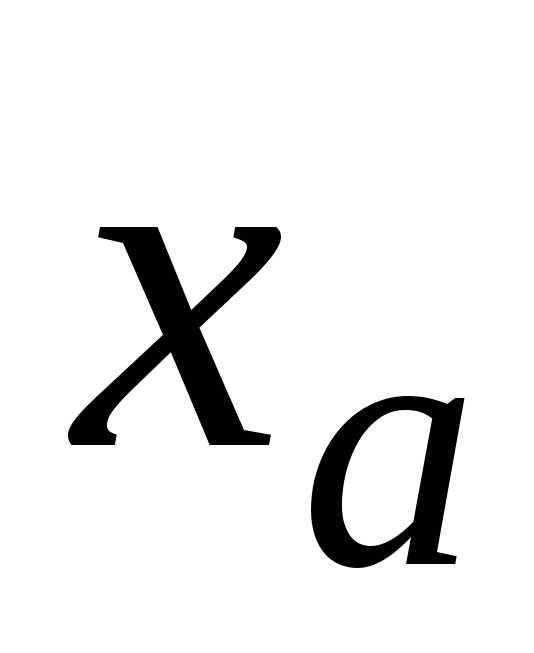 в широком и строгом смысле слова и
подчеркнуть их одинарной и двойной
линией соответственно. Проверяя для
каждой цифры в записи
в широком и строгом смысле слова и
подчеркнуть их одинарной и двойной
линией соответственно. Проверяя для
каждой цифры в записи требование, сформулированное в определении
верных цифр, получим, что цифры 0, 1, 2, 3 и
4 будут верными в широком и строгом
смысле слова одновременно. Цифра 5 будет
верной в широком смысле слова, но не
будет верной в строгом смысле слова:.
требование, сформулированное в определении
верных цифр, получим, что цифры 0, 1, 2, 3 и
4 будут верными в широком и строгом
смысле слова одновременно. Цифра 5 будет
верной в широком смысле слова, но не
будет верной в строгом смысле слова:.
Отметим, что в разрядах, в которых в записи
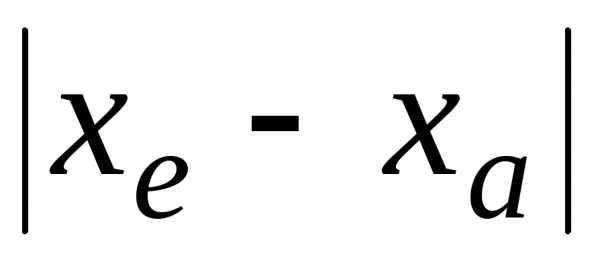 стоят незначащие нули, в записи
стоят незначащие нули, в записи 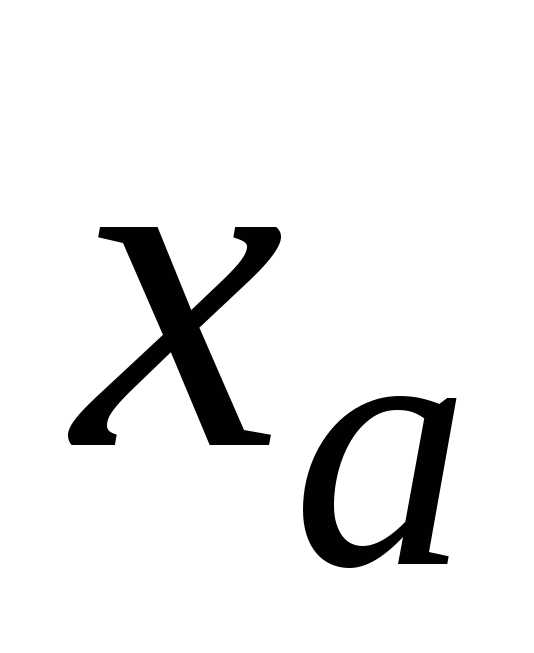 стоят верные цифры в широком смысле
слова.
стоят верные цифры в широком смысле
слова.Пример 2
Пусть теперь
,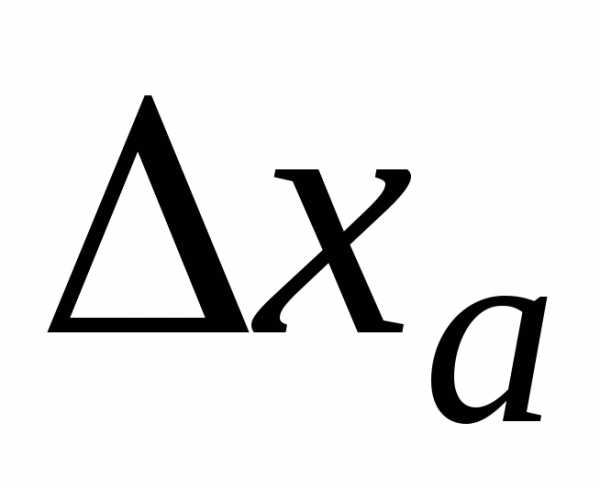 =0,000007899. Требуется найти верные цифры в
записи
=0,000007899. Требуется найти верные цифры в
записи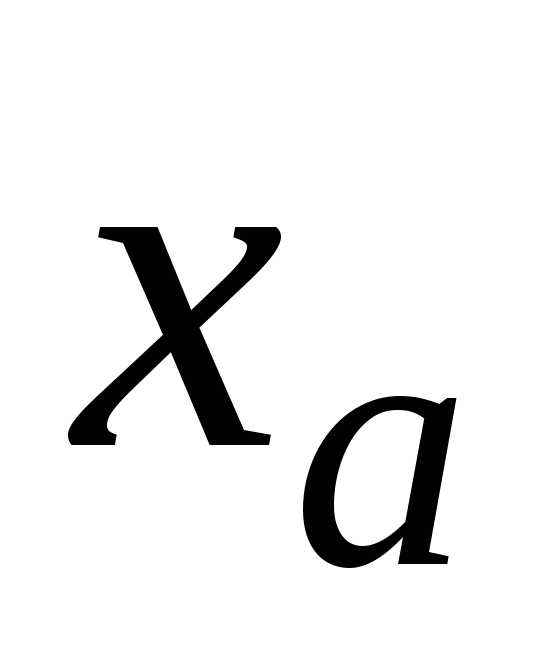 в широком и строгом смысле слова.
в широком и строгом смысле слова.
Абсолютная
погрешность 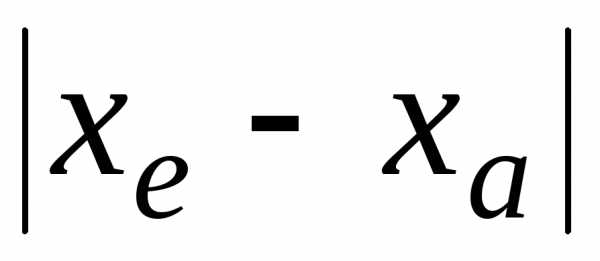 нам неизвестна, а известна лишь ее оценка
нам неизвестна, а известна лишь ее оценка  .
Если оценка абсолютной погрешности
.
Если оценка абсолютной погрешности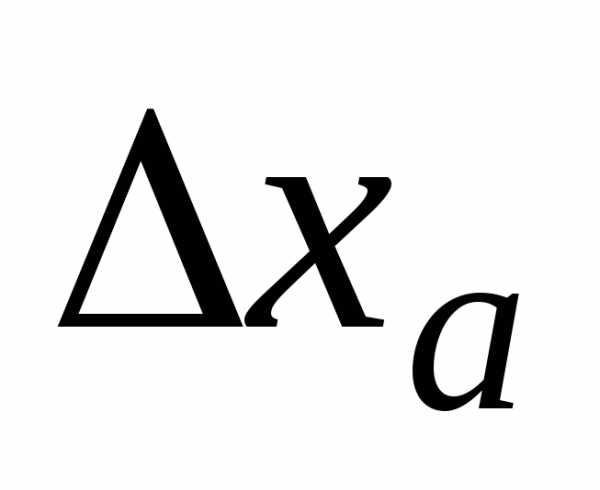 приближенного значения
приближенного значения 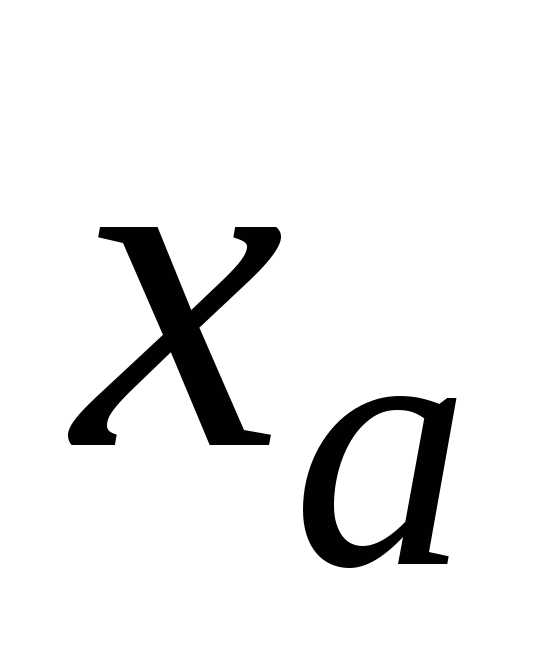 не превышает
единицы (половины единицы) разряда, в
котором стоит цифра (в записи
не превышает
единицы (половины единицы) разряда, в
котором стоит цифра (в записи 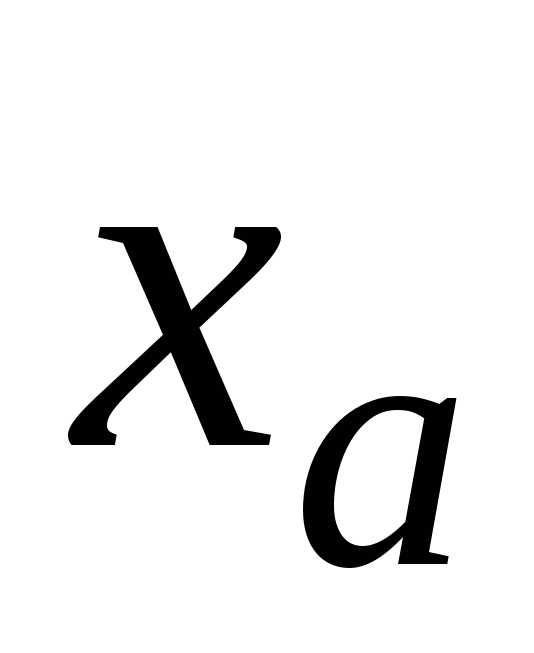 ),
то эта цифра, очевидно, также будет
верной в широком (строгом) смысле слова
.
Проверяя для каждой цифры в записи
),
то эта цифра, очевидно, также будет
верной в широком (строгом) смысле слова
.
Проверяя для каждой цифры в записи 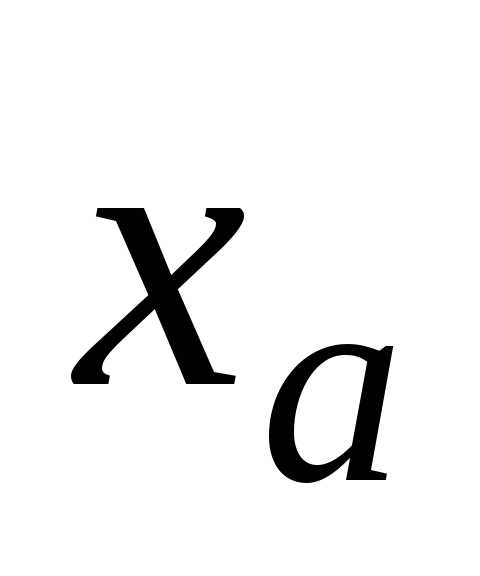 это требование,
получим часть верных цифр:
.
Но, поскольку мы проверяем заведомо
более жесткое требование, чемэто,
среди неподчеркнутых цифр также могут
оказаться верные, если погрешность
это требование,
получим часть верных цифр:
.
Но, поскольку мы проверяем заведомо
более жесткое требование, чемэто,
среди неподчеркнутых цифр также могут
оказаться верные, если погрешность 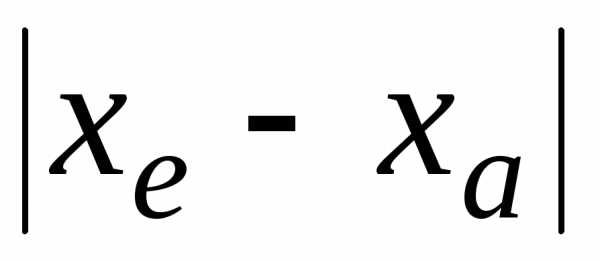 окажется намного меньше своей оценки
окажется намного меньше своей оценки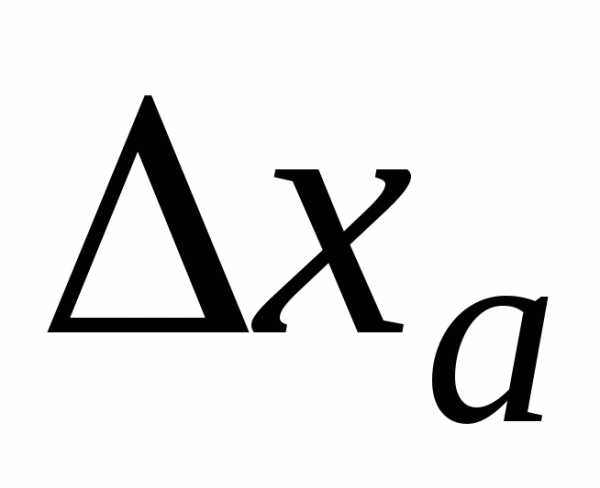 .
.
Отметим, что в тех
разрядах, в которых в записи 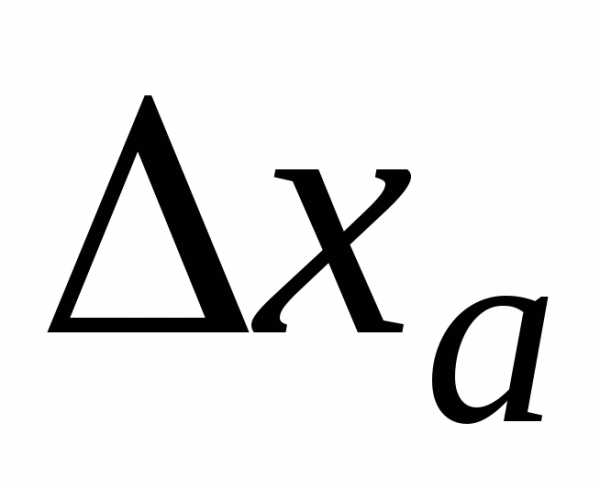 стоят незначащие нули, в записи
стоят незначащие нули, в записи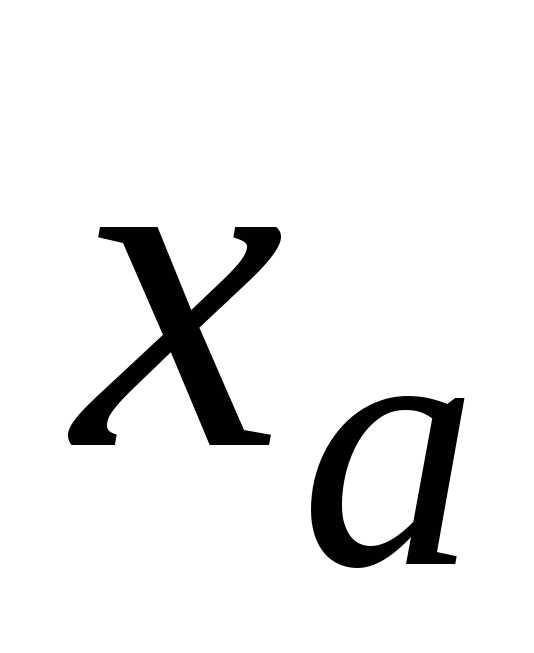 стоят верные цифры в широком смысле
слова.
стоят верные цифры в широком смысле
слова.
Пример 3
Пусть,  =0,123456789,
=0,123456789, 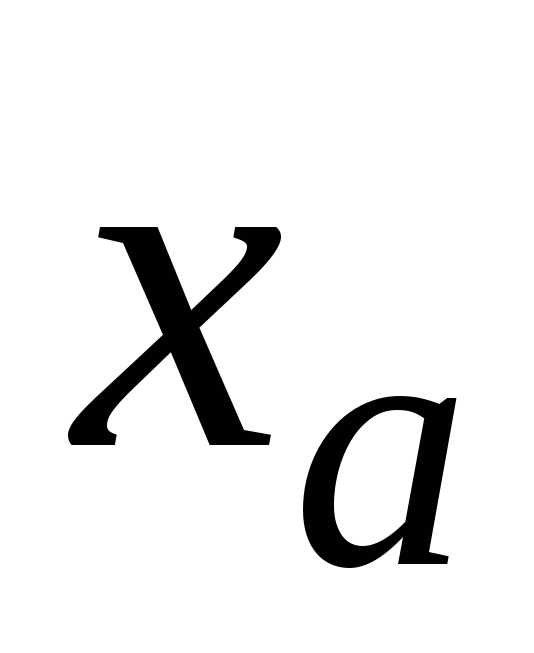 =0,123457899.
В записи точного и приближенного значений
подчеркнуты совпадающие цифры.
Непосредственная проверка для каждой
цифры в записи
=0,123457899.
В записи точного и приближенного значений
подчеркнуты совпадающие цифры.
Непосредственная проверка для каждой
цифры в записи 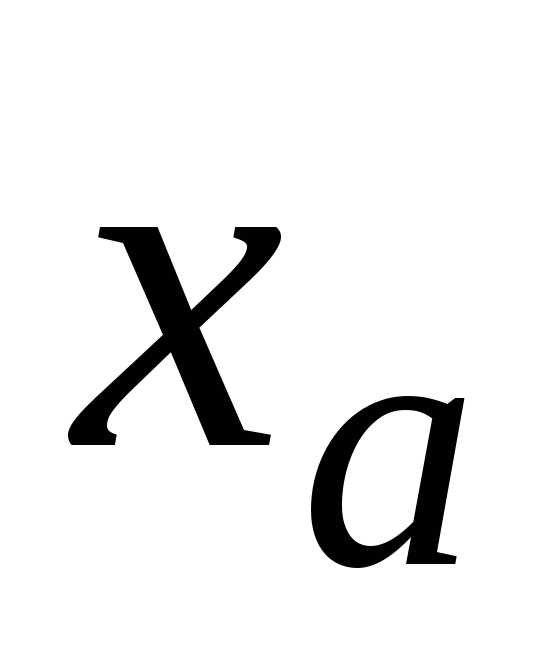 требования, сформулированного в
определении верных цифр, показывает,
что все подчеркнутые (совпадающие) цифры
являются верными в широком смысле слова,
а неподчеркнутые – неверными.
требования, сформулированного в
определении верных цифр, показывает,
что все подчеркнутые (совпадающие) цифры
являются верными в широком смысле слова,
а неподчеркнутые – неверными.
Но такое совпадение
верных цифр (в широком смысле слова) в
записи 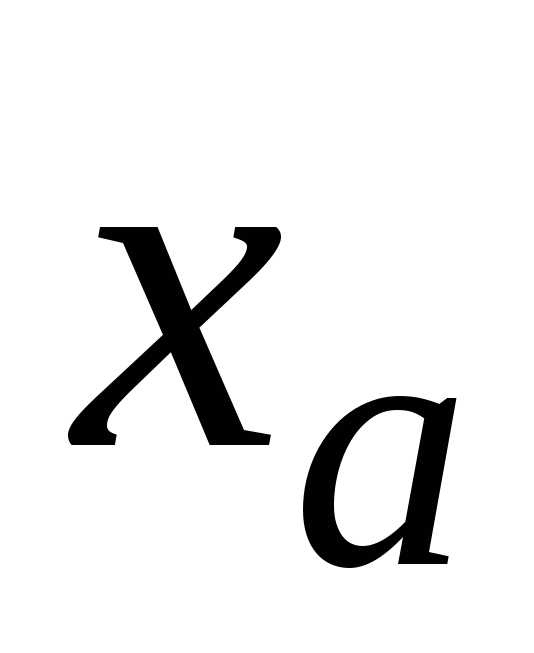 с соответствующими цифрами в записи
с соответствующими цифрами в записи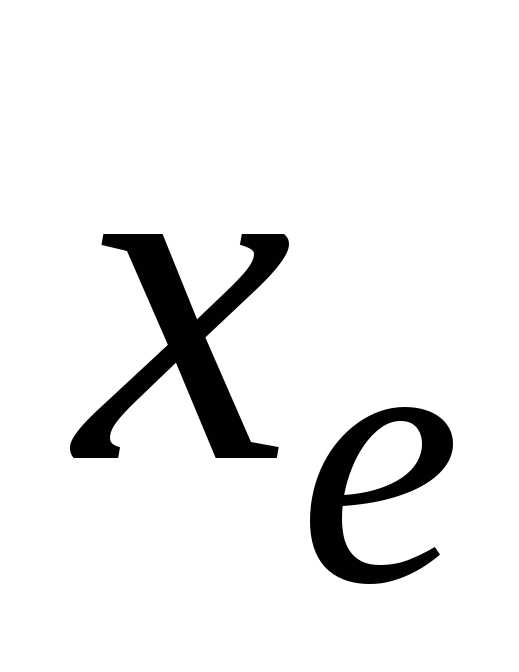 иногда нарушается. Это связано с тем,
что некоторые вещественные числа могут
записываться в десятичной системе двумя
различными способами, например
1=1,0000…=0,9999… .
иногда нарушается. Это связано с тем,
что некоторые вещественные числа могут
записываться в десятичной системе двумя
различными способами, например
1=1,0000…=0,9999… .
Пример 4
Пусть 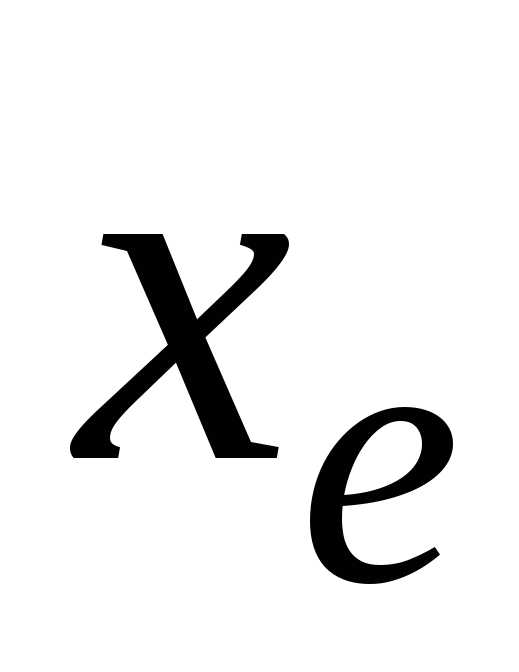 =1,0000…,
=1,0000…,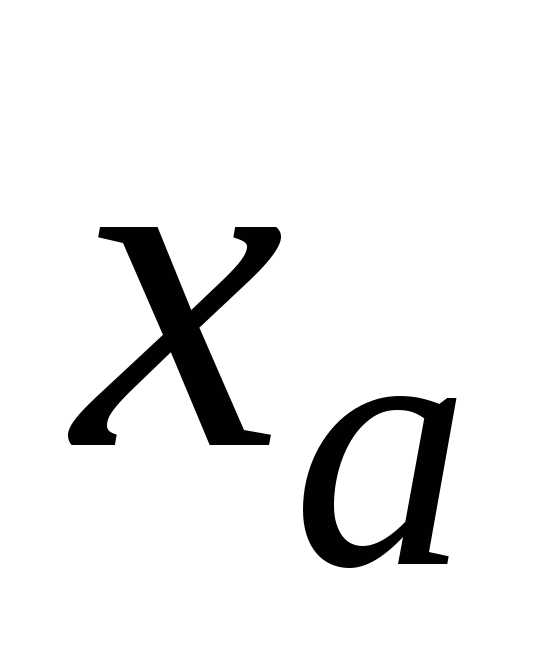 =0,9999.
В записи точного и приближенного значений
нет ни одной совпадающей цифры.
Непосредственная проверка для каждой
цифры в записи
=0,9999.
В записи точного и приближенного значений
нет ни одной совпадающей цифры.
Непосредственная проверка для каждой
цифры в записи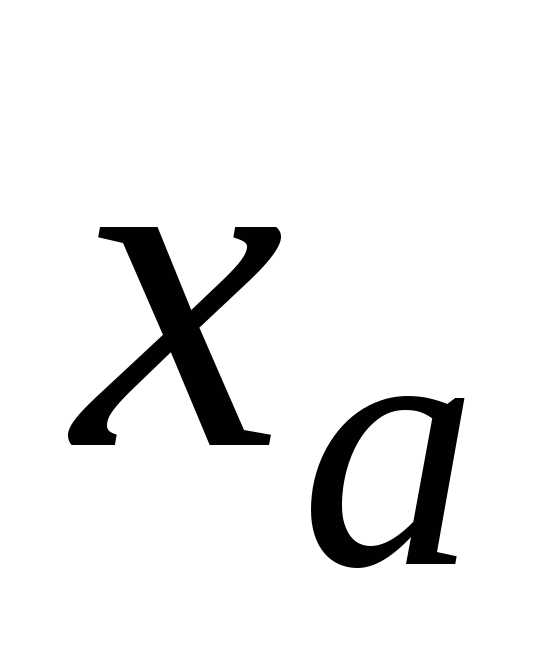 требования, сформулированного в
определении верных цифр, показывает,
что цифры в записи
требования, сформулированного в
определении верных цифр, показывает,
что цифры в записи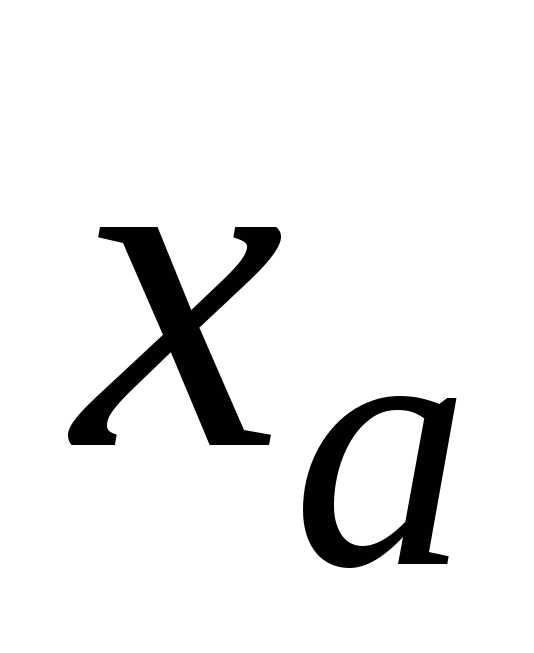 являются верными в широком смысле слова.
В то же время если записать
являются верными в широком смысле слова.
В то же время если записать другим способом
другим способом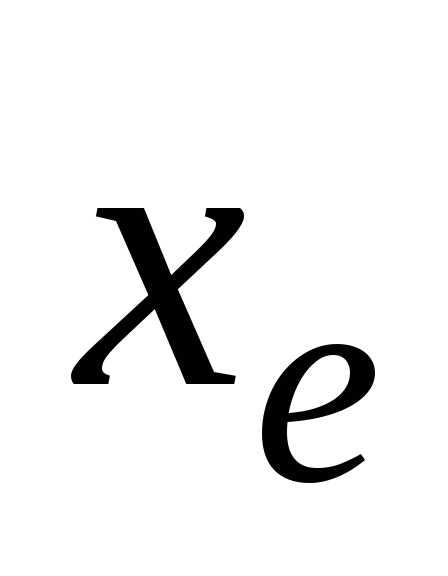 =0,9999…,
то все верные цифры в записи
=0,9999…,
то все верные цифры в записи будут совпадать с соответствующими
цифрами в записи точного значения
будут совпадать с соответствующими
цифрами в записи точного значения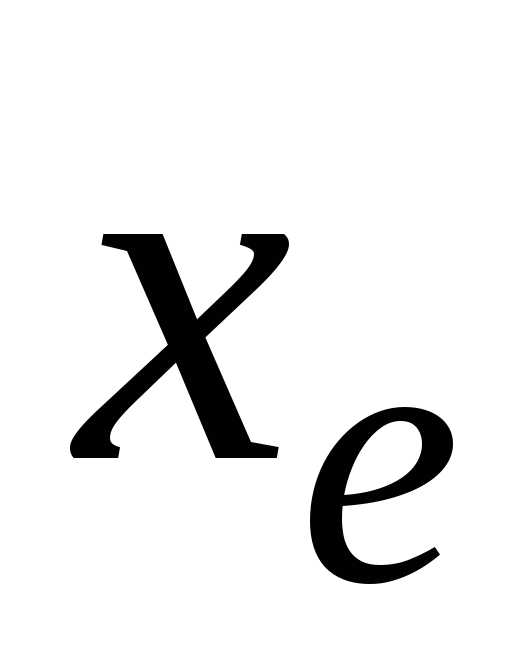 .
.
Рассмотренные примеры позволяют сформулировать некоторые свойства верных цифр.
Свойства верных цифр:
В тех десятичных разрядах, где в записи
 (или
(или )
стоят незначащие нули, в записи
)
стоят незначащие нули, в записи должны стоять верные цифры в широком
смысле слова (докажите это самостоятельно).
должны стоять верные цифры в широком
смысле слова (докажите это самостоятельно).Верные цифры в записи приближенного значения
 всегда совпадают с соответствующими
цифрами в записи точного значения
всегда совпадают с соответствующими
цифрами в записи точного значения ,
если выбрать необходимую форму его
записи в виде десятичной дроби
,
если выбрать необходимую форму его
записи в виде десятичной дроби
Установим теперь
связь между величинами абсолютной и
относительной погрешностей приближенного
значения и количеством верных цифр в
его записи. Пусть абсолютная погрешность
приближенного значения  равна.
Определим количество верных цифр в
широком смысле слова в записи
равна.
Определим количество верных цифр в
широком смысле слова в записи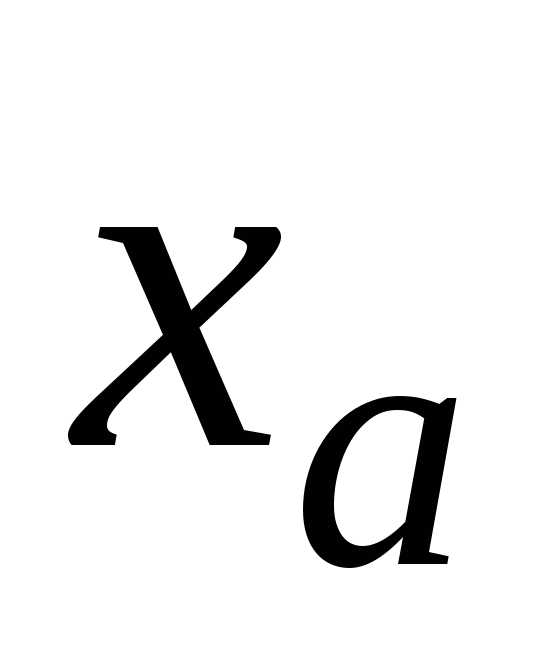 после запятой. Запишем
после запятой. Запишем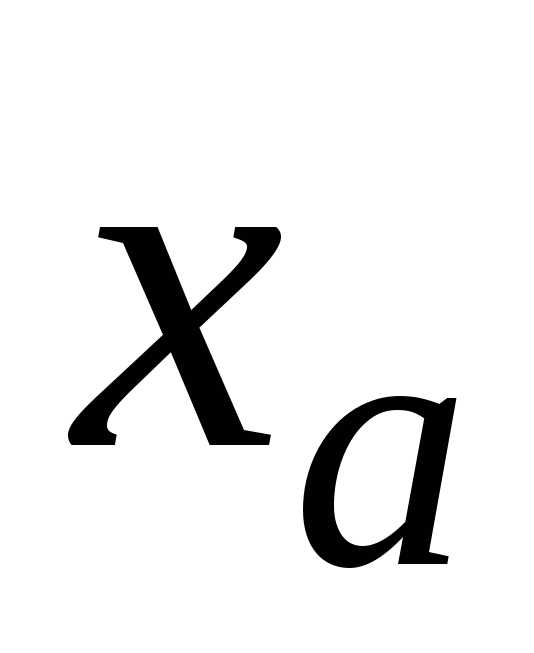 в общем виде, указывая только разряды
и не указывая конкретных цифр, и подчеркнем
разряды, в которых будут располагаться
верные цифры в широком смысле слова:
в общем виде, указывая только разряды
и не указывая конкретных цифр, и подчеркнем
разряды, в которых будут располагаться
верные цифры в широком смысле слова:
.
Итак, если
абсолютная погрешность приближенного
значения
равна ,
то после
десятичной запятой в записи 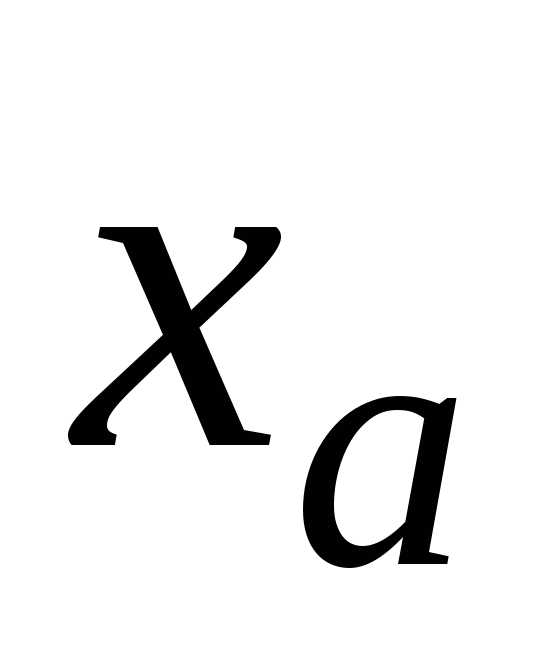 будетn верных
знаков.
будетn верных
знаков.
Пусть теперь
относительная погрешность приближенного
значения 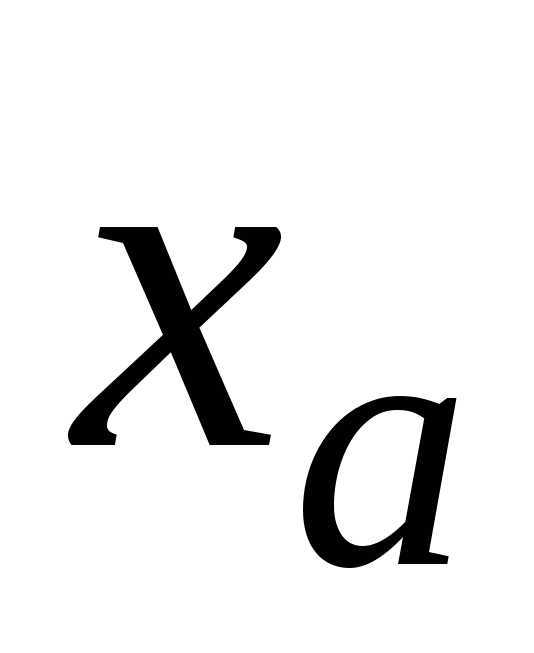 равна.
Установим общее количество верных
знаков в записи
равна.
Установим общее количество верных
знаков в записи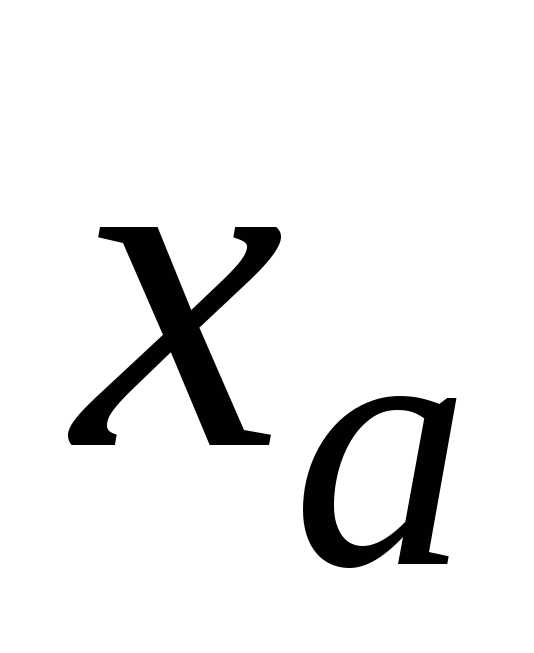 .
Для этого представим
.
Для этого представим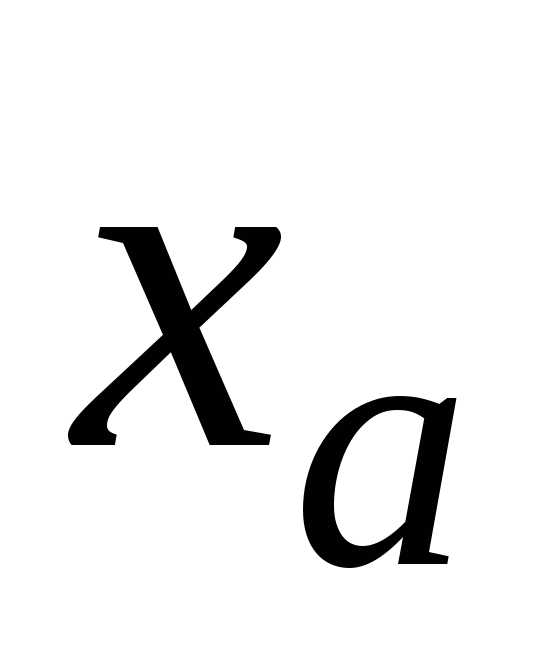 в показательной форме:.
Здесь
в показательной форме:.
Здесь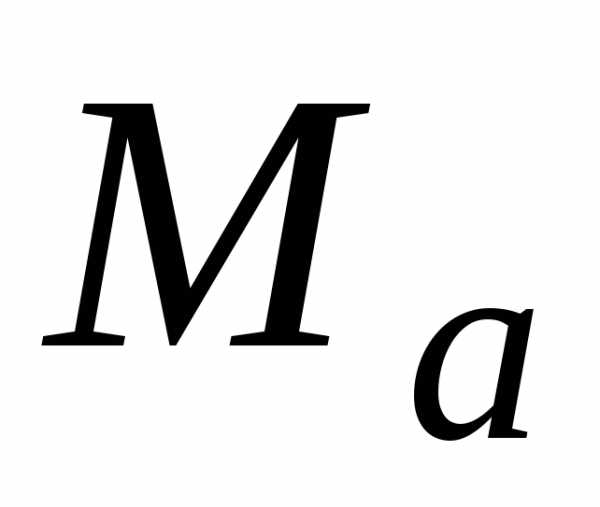 –
вещественное число, называемое мантиссой,
ар – целое число, называемое порядком
–
вещественное число, называемое мантиссой,
ар – целое число, называемое порядком 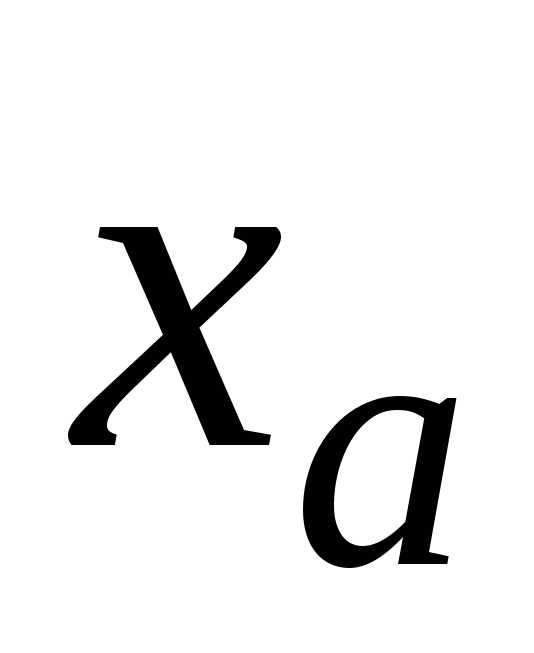 .
А для того, чтобы такое представление
дроби было однозначным потребуем, чтобы
.
А для того, чтобы такое представление
дроби было однозначным потребуем, чтобы
. (1.3.1)
Точное значение
величины 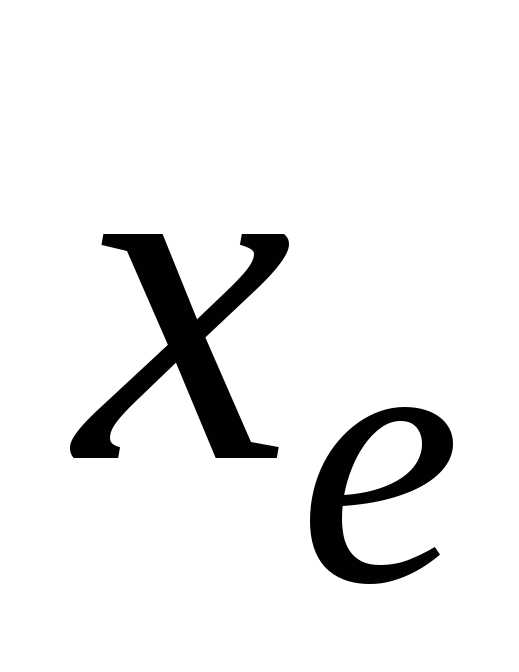 также запишем в показательной форме,
причем с тем же порядкомp:
.
Для мантиссы точного значения
также запишем в показательной форме,
причем с тем же порядкомp:
.
Для мантиссы точного значения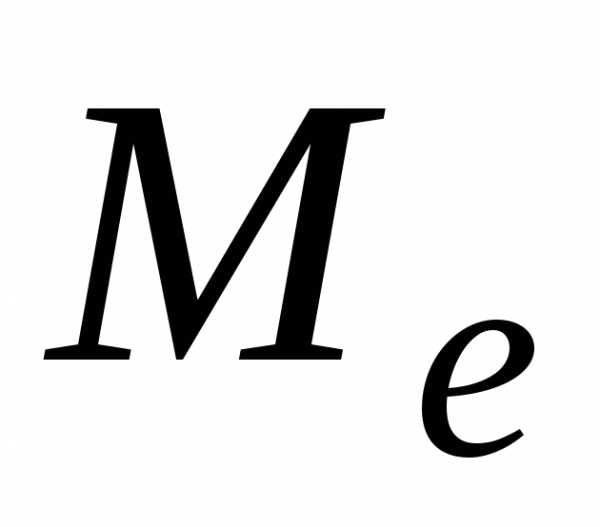 не будет выполняться условие (1.3.1).
Значения
не будет выполняться условие (1.3.1).
Значения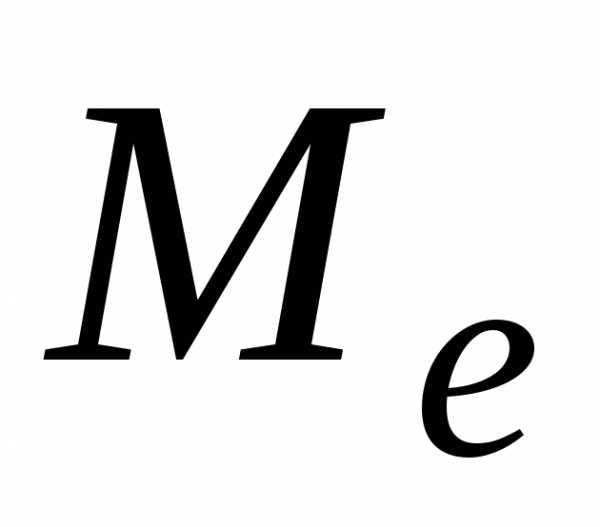 и
и естественно считать точным и приближенным
значениями мантиссы величиныx.
Тогда
естественно считать точным и приближенным
значениями мантиссы величиныx.
Тогда 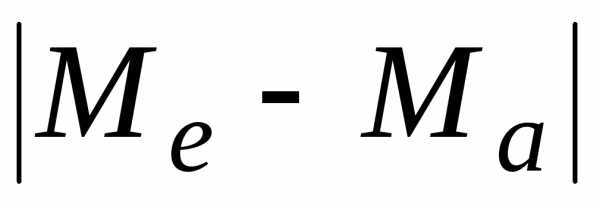 и
и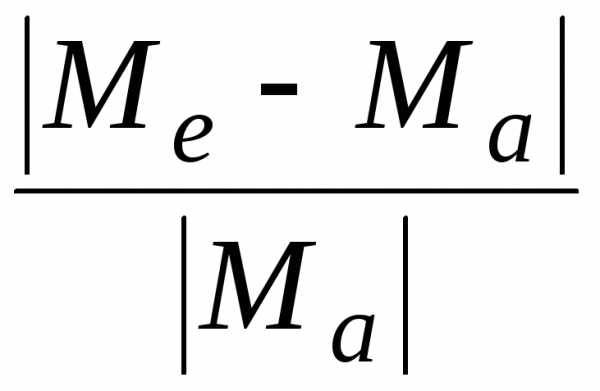 представляют собой абсолютную и
относительную погрешности приближенного
значения мантиссы
представляют собой абсолютную и
относительную погрешности приближенного
значения мантиссы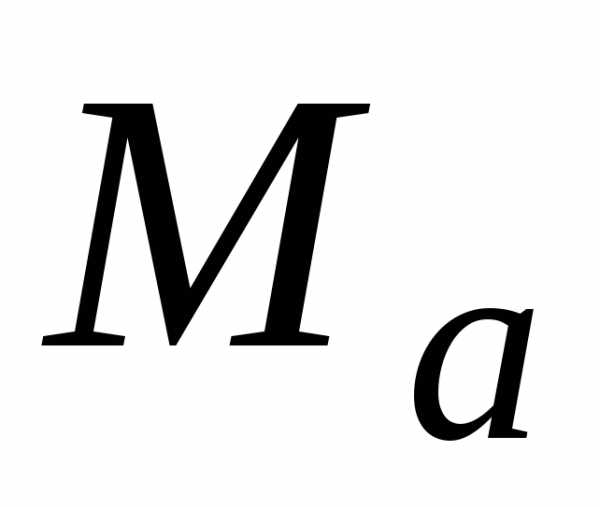 .
Соответствующие цифры в записи
.
Соответствующие цифры в записи и
и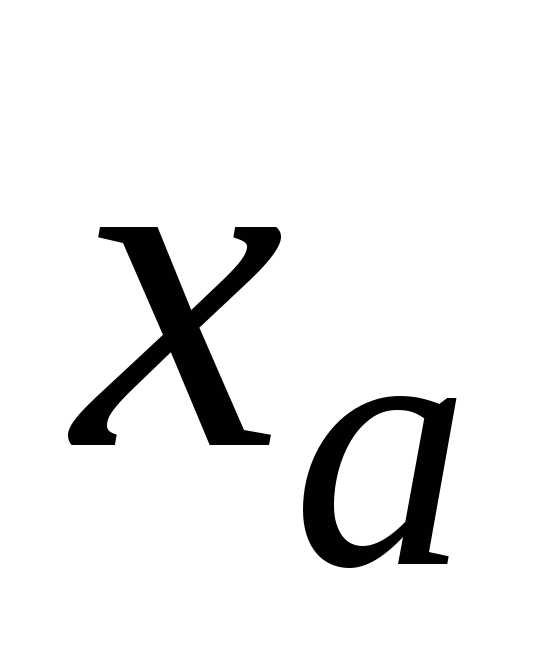 должны совпадать попарно.Поэтому
и количество верных цифр в записи
должны совпадать попарно.Поэтому
и количество верных цифр в записи 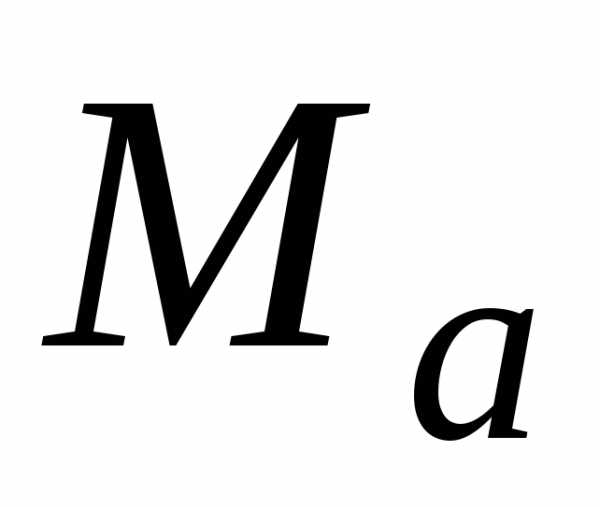 и
и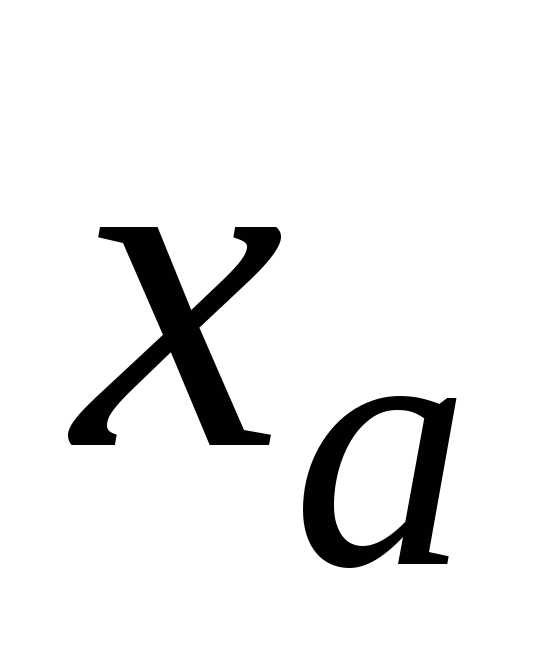 будет одинаковым. Далее определяем
количество верных цифр в записи
будет одинаковым. Далее определяем
количество верных цифр в записи .
Запишем относительную погрешность
.
Запишем относительную погрешность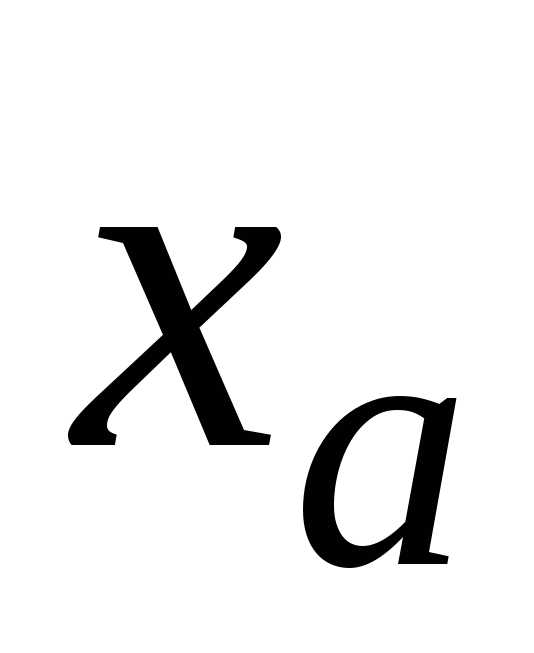
.
Отсюда
,
и, согласно формуле
(1.3.1), для абсолютной погрешности 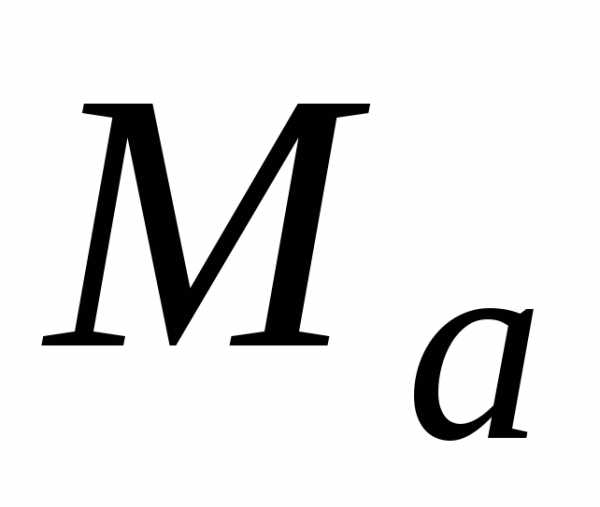 получается оценка
получается оценка
(1.3.2)
Запишем 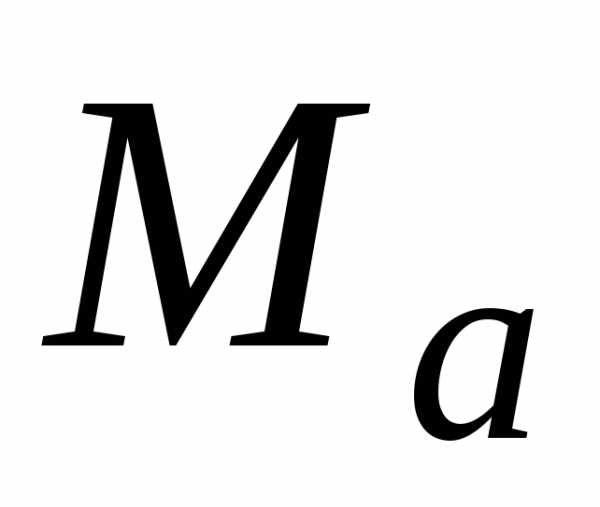 в общем виде
в общем виде
.
Из формулы (1.3.1)
следует, что первая цифра после десятичной
запятой в записи 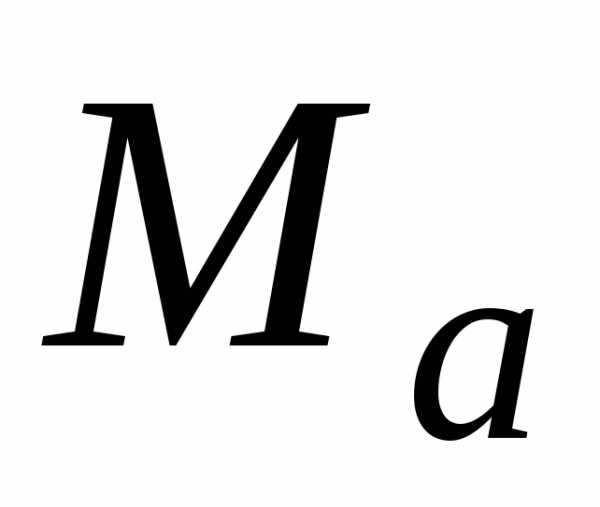 должна быть отлична от нуля. Поэтому
все цифры в записи
должна быть отлична от нуля. Поэтому
все цифры в записи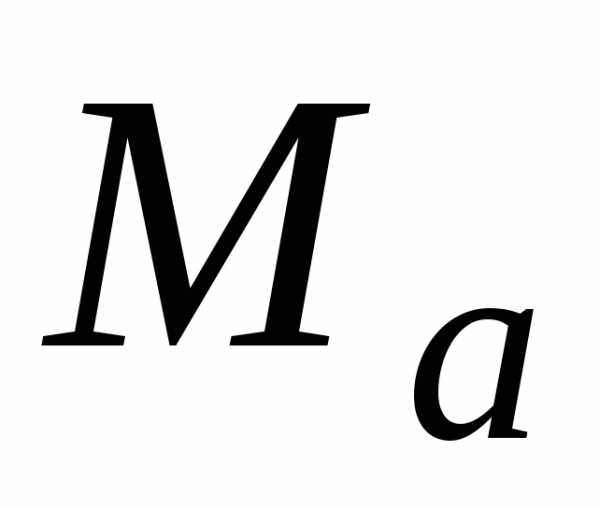 после запятой являются значащими. Из
формулы (1.3.2) следует, что в записи
мантиссы должно быть не меньшеn и не больше (n+1)
верной цифры после десятичной запятой,
причем все они являются значащими. Итак,
в мантиссе имеется или n или (n+1)
верная значащая цифра. Поэтому общее
количество верных значащих цифр в записи
после запятой являются значащими. Из
формулы (1.3.2) следует, что в записи
мантиссы должно быть не меньшеn и не больше (n+1)
верной цифры после десятичной запятой,
причем все они являются значащими. Итак,
в мантиссе имеется или n или (n+1)
верная значащая цифра. Поэтому общее
количество верных значащих цифр в записи 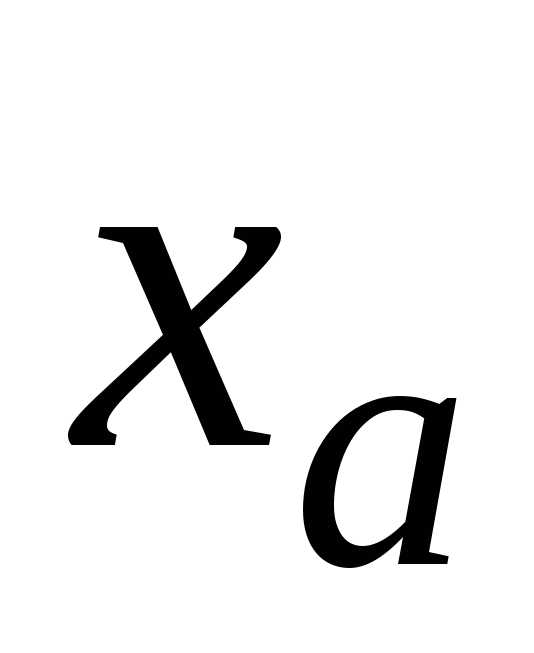 также будет равно либоn, либо (n+1).
также будет равно либоn, либо (n+1).
Таким образом, мы
показали, что если
относительная погрешность приближенного
значения 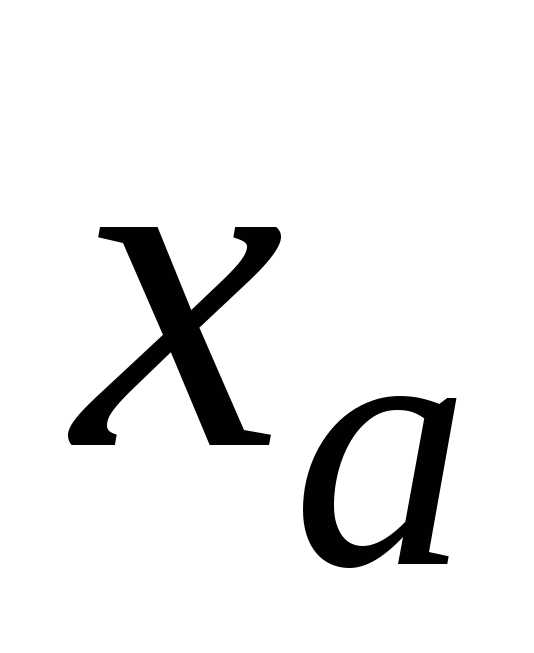 равна
,
то общее количество верных значащих
цифр в записи
равна
,
то общее количество верных значащих
цифр в записи 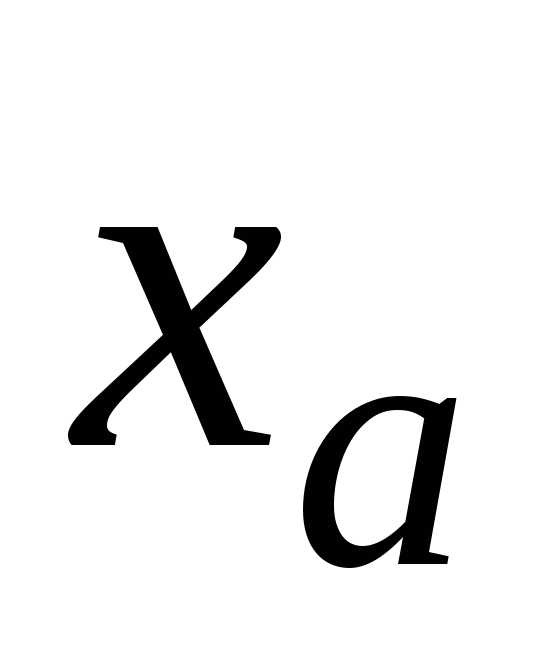 равно либо n, либо (n+1).
равно либо n, либо (n+1).
studfiles.net
|
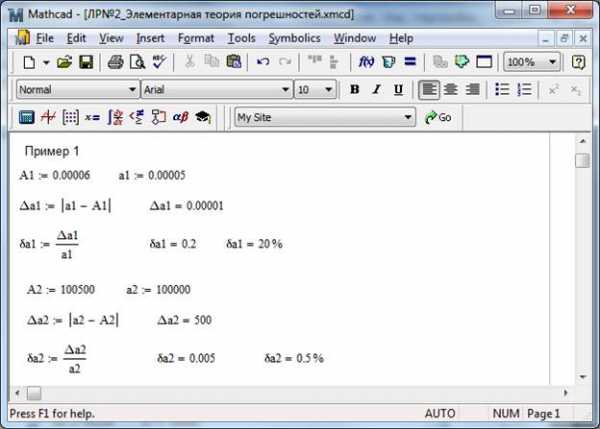
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ Теоретические сведения Абсолютная и относительная погрешности. Знак равенства в приближенных вычислениях имеет не тот смысл, как в алгебре. Равенство означает не совпадение значений, а лишь близость значений. Точность приближенного равенства, т.е. степень близости точного значения и приближенного , характеризует абсолютная погрешность, . На практике вместо абсолютной погрешности, которая обычно неизвестна, используют предельную абсолютную погрешность, причем слово предельная для краткости опускают. Если интересует точность уже проведенного расчета, то за берут число, которое возможно ближе к “истинной” погрешности. Называют это оценкой погрешности. Оценка погрешности может быть грубой или более точной. Погрешность может быть задана заранее, тогда вычисление проводится так, чтобы это неравенство выполнялось. Для того чтобы записать, что является приближенным значением с абсолютной погрешностью , пишут: Относительной погрешностью, часто выражаемой в процентах, называют величину такую, что Относительная погрешность более полно характеризует степень точности приближенного числа, поскольку можно сравнивать точность задания величин, как существенно различающихся по порядку, так и выраженных в разных единицах измерения. Верные и сомнительные цифры. Значащую цифру называют верной в узком смысле, если абсолютная погрешность числа не превышает 1/2 единицы разряда, соответствующего этой цифре. Например, ; ; . Имеем ; также . Следовательно, верные цифры в узком смысле 9 и 3. Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превышает единицы разряда, соответствующего этой цифре (В примере 9, 3 и 4). Цифры, стоящие в более младших разрядах, называют сомнительными. Последовательность выполнения работы Пример 1. Заданы точное и приближенное значения числа. Найти абсолютную и относительную погрешности (решение приведено на рис. 2.1) ; ;
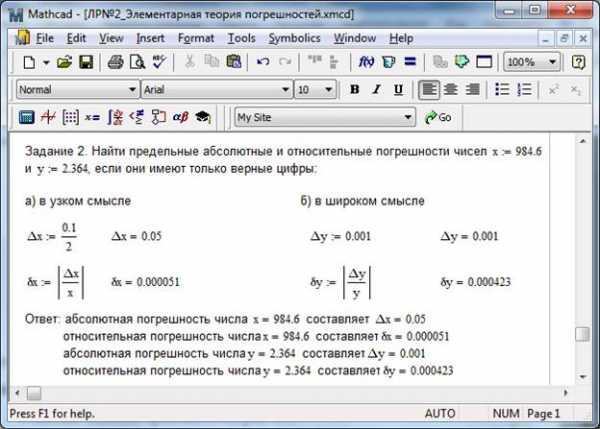
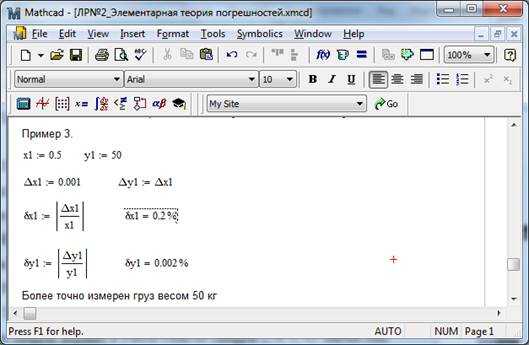
Рис. 2.1 – Решение примера 1 Пример 2. Найти предельные абсолютные и относительные погрешности чисел и , если они имеют только верные цифры: а) в узком смысле, б) в широком смысле. Решение задания приведено на рис. 2.2 Рис. 2.2 – Решение примера 2 Пример 3. Задано число и относительная погрешность . Определить количество верных цифр числа по его относительной погрешности. Решение: так как и , то число имеет, по крайней мере, две цифры, верных в узком смысле. Определим абсолютную погрешность: Значит, в узком смысле верными являются цифры 2 и 3. Пример 4. Пусть , . Определить количество верных цифр в числе . Решение: так как и , то число имеет, по крайней мере, одну цифру, верную в узком смысле (цифра 9). Проверим этот результат, используя определение цифры, верной в узком смысле. Для этого определим абсолютную погрешность: Полученная абсолютная погрешность не превышает половину единицы разряда сотен. Следовательно, цифра 9 верна в узком смысле, как по относительной погрешности, так и по абсолютной. Пример 5. Пусть , . Определить все верные цифры числа. Решение: так как , то число имеет, по крайней мере, четыре цифры, верных в узком смысле (цифры 2, 4, 3, 0). Вычислим Пример 6. При взвешивании двух грузов получили следующие значения их масс кг и кг. Считая абсолютную погрешность взвешивания равной 1 г, определить относительную погрешность измерения масс тел . Какое из тел взвешено более точно? Решение примера на рис. 2.3.
Рис. 2.3 – Решение примера 6 Пример 7. Определить, какое равенство точнее или Решение: найдем значения данных выражений с бóльшим числом десятичных знаков: , . Вычислим предельные абсолютные погрешности, округляя их с избытком: Предельные относительные погрешности составляют: Так как , то равенство является более точным. Пример 8.Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле ; б) в широком смысле . Определить абсолютную погрешность результата. Решение: а) пусть . Согласно условию, погрешность ; это означает, что в числе верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдём приближенное значение числа, сохранив десятые доли: Полученная погрешность больше 0,05; значит, нужно уменьшить число цифр в приближенном числе до двух: Поэтому обе оставшиеся цифры верны в узком смысле. б) ; тогда . В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры: Значит, и в округлённом числе все три цифры верны в широком смысле. Пример 9. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле ; б) в широком смысле Решение: а) так как все четыре цифры верны в узком смысле, то абсолютная погрешность , а относительная погрешность б) так как все пять цифр числа верны в широком смысле, то: ; da=1/(1∙104)=0,0001= 0,01%. Пример 10. Вычислить и определить погрешности результата. где Решение. Находим Далее имеем откуда 4. Контрольные вопросы: 1. Что такое абсолютная и относительная погрешности? 2. Что значит цифра, верная в широком и узком смыслах? 3. Как определить количество верных цифр по относительной погрешности приближенного числа? 4. Как определяются абсолютная и относительная погрешности в арифметических действиях? Варианты заданий к лабораторной работе 2 Задание 1 1) Определить, какое равенство точнее. 2) Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата. 3) Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле. Варианты заданий приведены в табл. 1.1.
Задание 2 Задание. Вычислить и определить погрешности результата. Варианты заданий приведены в табл. 1.2
Рекомендуемые страницы: Воспользуйтесь поиском по сайту: ©2015- 2019 megalektsii.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
megalektsii.ru
Верные и значащие цифры. Запись приближенных значений — Студопедия.Нет
Цифра числа называется верной (в широком смысле), если ее абсолютная погрешность не превосходит единицы разряда, вкотором стоит эта цифра.
Пример. Х=6,328 Х=0,0007 X<0,001 следовательно цифра 8-верная
Пример: А). Пусть 0 = 2,91385, В числе а верны в широком смысле цифры 2, 9, 1.
Б) Возьмем в качестве приближения к числу = 3,141592… число = 3,142. Тогда (рис.) откуда следует, что в приближенном значении = 3,142 все цифры являются верными.
В) Вычислим на 8-разрядном МК частное точных чисел 3,2 и 2,3, получим ответ: 1,3913043. Ответ содержит ошибку, поскольку
Рис. 1. Приближение числа
разрядная сетка МК не вместила всех цифр результата и все разряды начиная с восьмого были опущены. (В том, что ответ неточен, легко убедиться, проверив деление умножением: 1,3913043 2,3 = 3,9999998.) Не зная истинного значения допущенной ошибки, вычислитель в подобной ситуации всегда может быть уверен, что ее величина не превышает единицы самого младшего из изображенных на индикаторе разряда результата. Следовательно, в полученном результате все цифры верны.
Первая отброшенная (неверная) цифра часто называется сомнительной.
Говорят, что приближенное данное записано правильно, если в его записи все цифры верные. Если число записано правильно, то по одной только его записи в виде десятичной дроби можно судить о точности этого числа. Пусть, например, записано приближенное число а = 16,784, в котором все цифры верны. Из того, что верна последняя цифра 4, которая стоит в разряде тысячных, следует, что абсолютная погрешность значения а не превышает 0,001. Это значит, что можно принять т.е. а = 16,784±0,001.
Очевидно, что правильная запись приближенных данных не только допускает, но и обязывает выписывать нули в последних разрядах, если эти нули являются выражением верных цифр. Например, в записи = 109,070 нуль в конце означает, что цифра в разряде тысячных верна и она равна нулю. Предельной абсолютной погрешностью значения , как следует из записи, можно считать Для сравнения можно заметить, что значение с = 109,07 является менее точным, так как из его записи приходится принять, что
Значащими цифрами в записи числа называются все цифры в его десятичном изображении, отличные от нуля, и нули, если они расположены между значащими цифрами или стоят в конце для выражения верных знаков.
Пример а) 0,2409 — четыре значащие цифры; б) 24,09 — четыре значащие цифры; в) 100,700 — шесть значащих цифр.
Выдача числовых значений в ЭВМ, как правило, устроена таким образом, что нули в конце записи числа, даже если они верные, не сообщаются. Это означает, что если, например, ЭВМ показывает результат 247,064 и в то же время известно, что в этом результате верными должны быть восемь значащих цифр, то полученный ответ следует дополнить нулями: 247,06400.
В процессе вычислений часто происходит округление чисел, т.е. замена чисел их значениями с меньшим количеством значащих цифр. При округлении возникает погрешность, называемая погрешностью округления. Пусть х -данное число, а х1 — результат округления. Погрешность округления определяется как модуль разности прежнего и нового значений числа:
(5)
В отдельных случаях вместо ∆окр приходится использовать его верхнюю оценку.
Задание 1.Округляя точные числа до трех значащих цифр, определить абсолютную и относительную погрешности полученных приближенных чисел.
Дано:
Найти:
Решение:
— приближенное значение числа A
Абсолютная погрешность:
Относительная погрешность:
Ответ: ;
Задание 2.Определить абсолютную погрешность приближенных чисел aпо их относительной погрешностиd.
Дано: a = 4,872; d = 5%.
Найти:
Решение:
Абсолютная погрешность:
Ответ:
Задание 3. Решить задачу.
При измерении длины с точностью до 5 м получено км, а при определении другой длины с точностью до 0.5 см, получено метров. Какое измерение по своему качеству лучше?
Дано: Км, М, М, См
Сравнить: и
Решение: Итак, по 1-му измерению, результат Км = М с точностью до М
( — абсолютная погрешность величины ).
Тогда относительная погрешность: %
По 2-му измерению, результат Км с точностью до См = М ( — абсолютная погрешность величины ).
Тогда относительная погрешность: %
Так как , то измерение можно считать по качеству лучше, чем .
Ответ: измерение по качеству лучше, чем .
Задание 4. а) Определить количество верных знаков в числе , если известна его предельная абсолютная погрешность
Дано:
Найти:
Решение:
По определению, n первые значащие цифры являются верными в узком смысле, если абсолютная погрешность этого числа не превышает половины единицы разряда младшей цифры, считая слева направо.
Абсолютная погрешность: , поэтому значащие цифры 8 и 4 числа 0,00842 верны в узком смысле.
Ответ: число X имеет две верных цифры в узком смысле (8 и 4), то есть
б) Определить количество верных знаков в числе , если известна его предельная относительная погрешность .
Дано: %
Найти:
Решение:
Предельная абсолютная погрешность:
Только первая значащая цифра 1 числа A верна в узком смысле.
Ответ: число A имеет одну верную цифру в узком смысле (1), то есть
Дано: %
Найти:
Решение:
Предельная абсолютная погрешность:
Только первая значащая цифра 1 числа A верна в узком смысле.
Ответ: число A имеет одну верную цифру в узком смысле (1), то есть
Задание 5.Найти предельные относительные погрешности, допускаемые при взятии вместо чисел 3.1, 3.14, 3.1416:
а) считая, что у них все записанные знаки являются верными;
б) зная, что
Провести сравнения погрешностей и сделать необходимые выводы.
Дано: , ,
Найти:
Решение:
А) :
Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:
Предельная абсолютная погрешность:
Тогда предельная относительная погрешность:
%
:
Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:
Предельная абсолютная погрешность:
Тогда предельная относительная погрешность:
:
Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:
Предельная абсолютная погрешность:
Тогда предельная относительная погрешность:
%
б) Пусть (прервем запись числа на 7-м знаке после запятой и считаем полученное число точным значением числа ).
Тогда абсолютная погрешность первого представления числа : .
Относительная погрешность: %
Абсолютная погрешность второго представления числа : .
Относительная погрешность: %
Абсолютная погрешность третьего представления числа : %.
Относительная погрешность: %
Выводы:
1) Можно заметить, что , то есть ;
, то есть ;
, то есть
Иными словами, для трех чисел их «истинная» относительная погрешность ограничена предельной относительной погрешностью, определенной из условия верности знаков чисел. Причем, для каждого числа две оценки отличаются меньше, чем на порядок. Значит, предположение о верности всех знаков чисел Обосновано.
2) Сравнение относительных погрешностей чисел :
показывает,
Что числа Перечислены
В порядке увеличения точности представления числа ,
То есть точнее , точнее .
Ответ: а)
б)
Задание 6.Найти сумму приближенных чисел , , считая в них все знаки верными, т. е. что абсолютная погрешность каждого слагаемого не превосходит половины единицы младшего разряда этого слагаемого. Определить абсолютную и относительную погрешности суммы.
Дано: , ,
Найти:
Решение:
1) Считаем, что в числах , , все знаки верны в узком смысле, то есть
Число с наибольшей абсолютной погрешностью .
2) Остальные числа округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым :
, абсолютная погрешность округления
, абсолютная погрешность округления
3) Сложим все эти числа, учитывая все сохраненные знаки:
4) Полученный результат округлим на один знак (формально):
, абсолютная погрешность округления
5) Полную абсолютную погрешность суммы будем складывать из трех компонентов:
A) суммы предельных абсолютных погрешностей исходных чисел;
B) абсолютной величины суммы ошибок округления слагаемых;
C) заключительной погрешности округления результата.
— абсолютная погрешность суммы.
% — относительная погрешность суммы.
Ответ: ; %.
Задание 7.Найти предельную абсолютную и относительную погрешности при вычислении объема прямого кругового цилиндра, если значения его высоты и радиуса основания имеют все верные знаки.
Дано: ,
Найти:
Решение:
,
Примем
1) Так как в числах и все числа верны, то их абсолютные погрешности:
Число с наибольшей абсолютной погрешностью .
Число R округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым :
, абсолютная погрешность округления (округления не требуется)
2) перемножим числа, учитывая все сохраненные знаки:
3) Полученный результат округляем, сохраняя столько значащих цифр, сколько верных цифр имеется в числе H, то есть 2 значащих цифры:
;
Абсолютная погрешность округления
4) Полную абсолютную погрешность произведения будем складывать из двух слагаемых:
A) предельной абсолютной погрешности произведения до его округления;
B) заключительной погрешности округления произведения.
Абсолютную погрешность произведения до округления вычислим на основе предварительно найденной относительной погрешности произведения округленных сомножителей:
%.
Полная абсолютная погрешность
Теперь перейдем к искомому объему.
(Здесь полученный результат округляем до трех значащих цифр).
— предельная абсолютная погрешность объема.
% — предельная относительная погрешность объема.
Ответ: , , %
Задание 8.Привести пример потери точности при вычитании двух близких чисел.
Решение:
Пусть и — два близких числа; примем, что у них одинаковое число знаков после запятой.
Считаем, что все знаки в числах и верны в узком смысле. Тогда абсолютные погрешности:
Относительные погрешности:
%
%
Так как , то
Абсолютная погрешность результата:
Относительная погрешность результата: %
При вычитании двух близких чисел и относительная погрешность возросла на 3 порядка!
studopedia.net
A1. Элементы теории погрешностей — Мегаобучалка
Задание из Таблицы №1:
а) Определить какое равенство точнее.
б) Округлить сомнительные цифра числа, оставив верные знаки: 1) в узком смысле; 2) в широком смысле. Определить предельные абсолютную и относительную погрешности результата.
в) Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: 1) в узком смысле; 2) в широком смысле.
Таблица № 1
Образец выполнения задания А1.
A1. a) Какое равенство точнее .
Обозначим , ; , .
Тогда , ,
, .
Так как , то равенство определено точнее.
Ответ: Равенство определено точнее.
б)Округлить сомнительные цифра числа, оставив верные знаки: 1) в узком смысле; 2) в широком смысле. Определить предельные абсолютную и относительную погрешности результата.
1) Дано приближенное число , где .
Определим число верных знаков в узком смысле используя следующее выражение
.
Так как , и верно неравенство , то получим , . Округлим до трех верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равен .
Определим число верных знаков приближенного числа .
, , . Округлим до двух верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равен .
Определим число верных знаков приближенного числа .
, , . Так как , то приближенное число имеет только верные знаки.
Определим предельную относительную погрешность приближенного числа . Для этого используем определение предельной погрешности: , .
Тогда получим .
Ответ: , .
2) Дано приближенное число , где . Определим число верных знаков в широком смысле используя следующее выражение .
Так как , и верно неравенство , то получим , . Округлим до трех верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равна .
Определим число верных знаков приближенного числа . , , . Округлим до двух верных знаков и получим с погрешностью округления . При этом погрешность полученного приближенного числа равна .
Определим число верных знаков приближенного числа .
Из условия , получим , . Так как , то приближенное число имеет только верные знаки.
Определим предельную относительную погрешность приближенного числа . Для этого используем определение предельной погрешности: , .
Тогда получим .
Ответ: , .
в) Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: 1) в узком смысле; 2) в широком смысле.
1) Дано приближенное число .
Так как это число имеет только верные цифры в узком смысле, то . Определим предельную абсолютную погрешность числа из выражения . Тогда .
Следовательно, для предельной абсолютной погрешности имеем . Для определения предельной относительной погрешности числа можно использовать выражение .
Так как , то .
Ответ: .
2) Дано приближенное число .
Так как это число имеет только верные цифры в широком смысле, то . Определим предельную абсолютную погрешность числа из выражения . Тогда .
Следовательно, для предельной абсолютной погрешности имеем . Для определения предельной относительной погрешности числа можно использовать выражение .
Тогда, получим .
Ответ: .
A2. Элементы теории погрешностей.
а) Вычислить и определить предельные абсолютную и относительную погрешности результата.
б) Вычислить и определить предельные абсолютную и относительную погрешности результата.
в) Вычислить и определить предельные абсолютную и относительную погрешности результата пользуясь общей формулой погрешности: 1) в узком смысле; 2) в широком смысле.
Задание из Таблицы 2 определяется по следующей схеме:
Если , то номер задания равен номеру варианта ( ), а исходные данные из Кол.1;
Если , то номер задания равен ( ) , а исходные данные из Кол.2;
Если , то номер задания равен ( ) , а исходные данные из Кол.3;
Если , то номер задания равен ( ) , а исходные данные из Кол.4.
Таблица 2
megaobuchalka.ru
ПРАВИЛЬНАЯ ЗАПИСЬ И ОКРУГЛЕНИЕ ЧИСЕЛ — МегаЛекции
Цифра числа называется верной (в широком смысле), если абсолютная погрешность этого числа не превосходит единицы разряда, в котором стоит эта цифра.
Пример 3. а).Пусть а = 2,91385, ?a = 0,0097.
?a?1 2
?a?0,1 9
?a?0,01 1
?a?0,001 3
В числе а верны в широком смысле цифры 2, 9, 1.
б).Возьмем в качестве приближения к числу ?= 3,141592… число ?’ = 3,142. Тогда /?-?’/ < 0,001 = ??’, откуда следует, что в приближенном значении ?’ = 3,142 все цифры являются верными.
в).Вычислим на 8-разрядном МК частное точных чисел 3,2 и 2,3, получим ответ: 1,3913043. Ответ содержит ошибку, поскольку разрядная сетка МК не вместила всех цифр результата и все разряды, начиная с восьмого, были опущены. Не зная истинного значения допущенной ошибки, вычислитель, однако, может быть уверен, что оно не превышает единицы самого младшего из изображенных на индикаторе разряда результата. Следовательно, в полученном результате все цифры верны.
Отметим, что первая отброшенная (неверная) цифра часто называетсясомнительной.
Говорят, что приближенное данное записано правильно, если в его записи все цифры верные.
Если число записано правильно, то по одной только его записи в виде десятичной дроби можно судить о точности этого числа. Пусть, к примеру, записано приближенное число а = 16,784, в котором все цифры верны. Из того, что верна последняя цифра 4, которая стоит в разряде тысячных, следует, что абсолютная погрешность значения а не превышает 0,001. Это значит, что можно принять ?а = 0,001, т.е. а=16,784±0,001.
Значащими цифрами в записи числа называются все цифры в его десятичном изображении, отличные от нуля, и нули, если они расположены между значащими цифрами или стоят в конце для выражения верных знаков.
Можно сказать короче: значащими цифрами числа являются все цифры в его правильной записи, начиная с первой ненулевой слева.
Пример 4.0,2409 — четыре значащие цифры; 24,09 — четыре значащие цифры; 100,700 — шесть значащих цифр.
В процессе вычислений часто происходит округление чисел, т. е. замена чисел их значениями с меньшим количеством значащих цифр.
При округлении возникает погрешность, называемая погрешностью округления. Пусть x– данное число, а x1 – результат округления. Погрешность округления определяется как модуль разности прежнего и нового значений числа:
Например, если выполнить на 8-разрядном МК действие 1:6. На индикаторе высветится число 0,1666666. Произошло автоматическое округление бесконечной десятичной дроби 0,1(6) до количества разрядов, вмещающихся в регистре МК. При этом можно принять ?окр = 0,7 *10-7.
Рассмотренный случай «принудительного» округления называютокруглением методом отбрасывания. Очевидно, что сам по себе метод отбрасывания оставляет все сохраняемые цифры округленного числа верными.
Если вычисления ведутся с точностью меньшей, чем машинная точность, целесообразнее пользоваться способом симметрического округления, который приводит к меньшей величине округления, чем способ отбрасывания. Симметрическое округление выполняется по следующим правилам:
если первая слева из отбрасываемых цифр меньше 5, то сохраняемые десятичные знаки остаются без изменения;
если первая слева из отбрасываемых цифр больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу.
Из правил симметрического округления следует, что его погрешность не превышает половины единицы последнего сохраняемого разряда. Это обстоятельство позволяет вести счет с точностью большей, чем единица последнего сохраняемого разряда. По этой причине наряду с понятием «верная цифра в широком смысле», соответствующем методике округления путем отбрасывания, используется понятие «цифра, верная в строгом смысле», применяемое в вычислениях с симметрическим округлением.
Отметим, что погрешности принято записывать с одной значащей цифрой (редко — с двумя). Кроме того, при округлении погрешности обычные правила округления неприменимы: погрешности, по понятной причине, всегда округляют с завышением (как это и делается в данной книге).
Цифра числа называется верной в строгом смысле, если абсолютная погрешность этого числа не превосходит половины единицы разряда, в котором стоит эта цифра.
Абсолютная погрешность числа x1, получаемого в результате округления приближенного значения х, складывается из абсолютной погрешности первоначального числа х (являющегося приближением точного значения X)и погрешности округления. Если в результате округления приближенного числа xполучено значение х1, то предельной абсолютной погрешностью числа х1можно считать сумму предельной абсолютной погрешности числа х и погрешности округления.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Тема 1.1. Погрешности приближенных значений чис..
№2. Раздел 1. Элементы вычислительной математики.
Тема 1.1. Погрешности приближенных значений чисел. (2 часа, лекция).
План: 1) Абсолютная погрешность приближенного значения числа.
2) Граница абсолютной погрешности.
3) Верная цифра числа.
4) Запись приближенного значения числа.
5) Округление приближенных значений чисел.
6) Относительная погрешность приближенного значения числа.
В практической деятельности человеку приходится измерять различные величины, производить различные вычисления. Числа, полученные в результате измерения, лишь приблизительно, с некоторой точностью, характеризуют искомые величины. Точные измерения невозможны ввиду неточности измерительных приборов.
Пусть результат измерения величины x с некоторой точностью равен a. Тогда a называют приближенным значением величины x.
Разность между точным и приближенным значениями величины называется погрешностью приближения,( x-a).
Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближения, т.е.
∝=x-a, где ∝-абсолютная погрешность, x- точное значение,
а- приближенное.
Пример: Известно, что — 0,333 является приближенным значением числа — 13. Найти абсолютную погрешность этого приближения.
Решение: x=-13; a =- 0,333;
∝=x-a=-13+0,333=-13+3331000=-13000=13000;
Абсолютная погрешность приближения не характеризует качества измерений. Действительно, если мы измеряем с точностью до 1см. какую- либо длину, то в том случае, когда речь идет об определении длины карандаша, это будет плохая точность. Если же с точностью до 1см. определить длину или ширину волейбольной площадки, то это будет высокая точность. Для характеристики качества измерения вводится понятие относительной погрешности.
Относительной погрешностью δ приближенного значения а числа x называется отношение абсолютной погрешности ∝ этого приближения к числу a:
δ=∝a ; Чем меньше относительная погрешность, тем выше качество измерений и вычислений. Относительную погрешность часто выражают в % . На практике результаты измерений и вычислений обычно выражаются в виде конечных десятичных дробей. Операция округления десятичной дроби состоит в отбрасывании единиц младших разрядов начиная с некоторого. Полученное число принимается за приближенное значение этой дроби.
Абсолютная погрешность , допускаемая при округлении, называется погрешностью округления.
Существует три способа округления положительных десятичных дробей:
Округление с недостатком:
54,376 ≈ 54 ( до единиц),
54,376 ≈ 54,3 (до десятых),
54,376 ≈ 54,37 (до сотых),
Погрешности округления: 0,376; 0,076; 0,006.
Округление с избытком:
54,376 ≈ 55 ( до единиц),
54,376 ≈ 54,4 (до десятых),
54,376 ≈ 54,38 (до сотых),
Погрешности округления: 0,624; 0,024; 0,004.
Самым распространенным округлением является округление с наименьшей погрешностью.
Правило:
единицы младших разрядов отбрасываются или заменяются нулями;
число единиц данного разряда не меняется, если следующая цифра данной дроби меньше 5, и увеличивается на единицу, если следующая цифра больше или равна 5.
Пример: 54,376 ≈ 54 погрешности: 0,376
54,376 ≈ 54,4 0,024
54,376 ≈ 54,38 0,004.
Граница абсолютной погрешности.
Любое положительное число ∆а, удовлетворяющее неравенству х-а≤∆а,
называется границей абсолютной погрешности.
Существует бесконечное множество чисел ∆а, удовлетворяющих неравенству
∝≤∆а; поэтому на практике стараются подобрать, возможно, меньшее и простое по записи число ∆а.По известной
filesclub.net

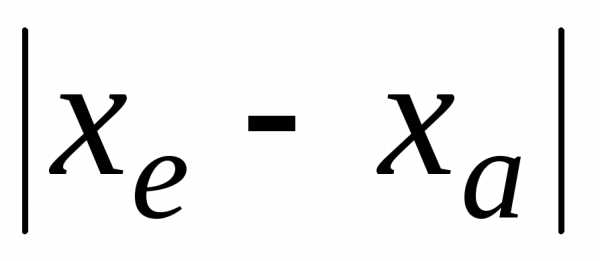 (или
(или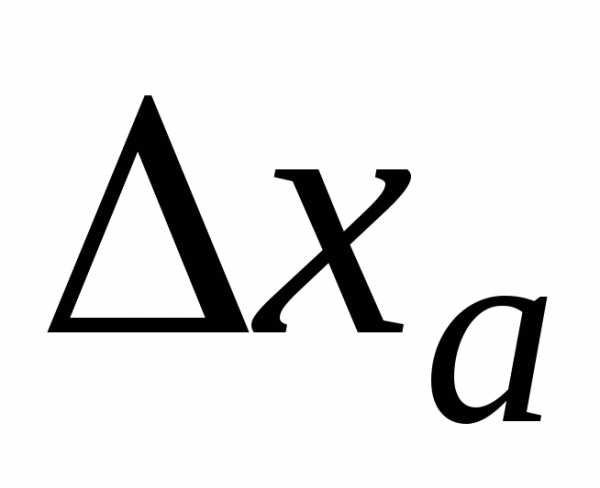 )
стоят незначащие нули, в записи
)
стоят незначащие нули, в записи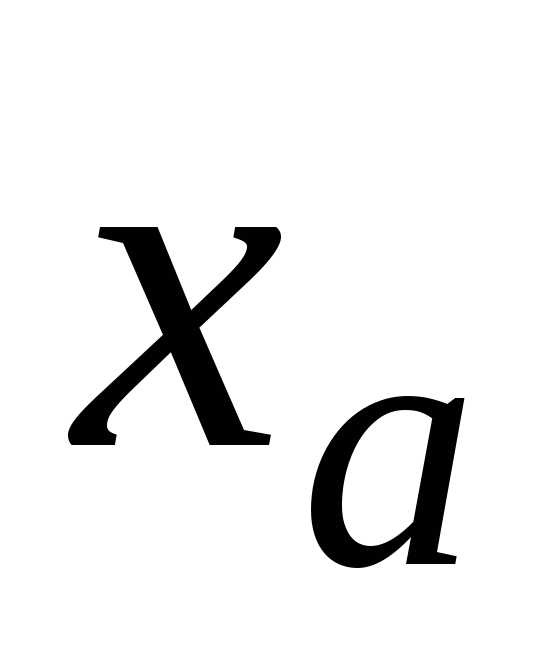 должны стоять верные цифры в широком
смысле слова (докажите это самостоятельно).
должны стоять верные цифры в широком
смысле слова (докажите это самостоятельно).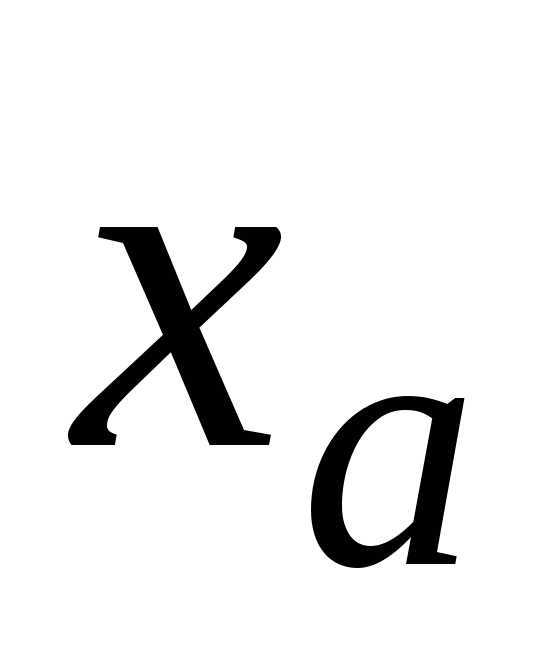 всегда совпадают с соответствующими
цифрами в записи точного значения
всегда совпадают с соответствующими
цифрами в записи точного значения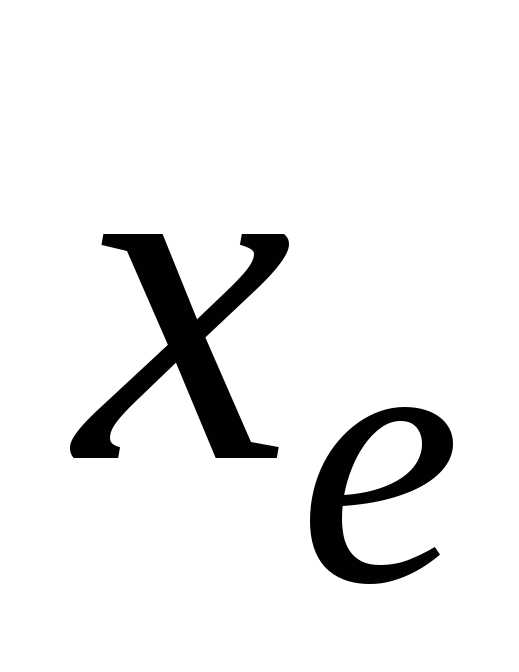 ,
если выбрать необходимую форму его
записи в виде десятичной дроби
,
если выбрать необходимую форму его
записи в виде десятичной дроби