Действия с числами в степени – .

Возведение в степень | Математика

6. Подобно тому, как сложение одинаковых чисел привело к новому действию – к умножению, так точно умножение одинаковых чисел может привести к мысли о необходимости создания нового действия. Это новое действие, заменяющее собой умножение одинаковых чисел, называется возведением в степень.

Вместо a ∙ a ∙ a ∙ a пишут a⁴,

что читают: «возвести число a в четвертую степень». Также точно:

17² = 17 ∙ 17 = 289; 6³ = 6 ∙ 6 ∙ 6 = 216; 3⁵ = 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 243;
; и т. п.

Для возведения в степень задаются 2 числа: одно выражает каждый множитель, – и оно называется основанием степени, другое показывает число одинаковых множителей, – оно называется показателем степени; в результате возведения в степень получается новое число, выражающее произведение одинаковых множителей – оно называется степенью. Вот пример, где указано значение этих названий:

Если показатель степени = 2, то вместо «возвести во вторую степень» говорят «возвести в квадрат», а вместо слова «степень» употребляют название «квадрат». Также точно вместо «третьей степени» употребляют название «куб» («возвести в куб»).

Читают:
     a². . . . . квадрат числа a
     b³. . . . . куб числа b
     x⁴. . . . . четвертая степень числа x
     cⁿ. . . . . n-ая степень числа c и т. д.

Вот более сложные формулы:
     a² + b² . . . . сумма квадратов чисел a и b
     (a + b)² . . . . квадрат суммы чисел a и b
     (a + b + c)³ . . куб суммы трех чисел
     . . . частное от деления разности квадратов двух чисел на сумму квадратов тех же чисел
     a + a² + a³ + a⁴ . . . сумма первой, второй, третьей и четвертой степеней числа a и т. д.

Возведение в степень не обладает переместительным законом, т. е. a^b не равно b

a. Это видно из простейших примеров:

3² = 3 ∙ 3 = 9, но 2³ = 2 ∙ 2 ∙ 2 = 8.

maths-public.ru

Что такое степень числа Возведение в степень отрицательного числа Порядок действий в примерах со степенями — Арифметика

Обращаем ваше внимание, что в данном разделе разбирается понятиестепени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 4⁶ и произносят «четыре в шестой степени».

4 • 4 • 4 • 4 • 4 • 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:

• 4 — основание степени;
• 6 — показатель степени .

В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:

 

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

Запись aⁿ читается так: «а в степени n» или «n-ая степень числа a».

Исключение составляют записи:

• a² — её можно произносить как «а в квадрате»;
• a³ — её можно произносить как «а в кубе».

Конечно, выражения выше можно читать и по определению степени:

• a² — «а во второй степени»;
• a³ — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).

 

Степенью числа «а» с показателем n = 1 является само это число:

a¹ = a

Любое число в нулевой степени равно единице.

a⁰ = 1

Ноль в любой натуральной степени равен нулю.

0ⁿ = 0

Единица в любой степени равна 1.

1ⁿ = 1

Выражение 0⁰ (ноль в нулевой степени) считают лишённым смыслом.

• (-32)⁰ = 1
• 0²⁵³ = 0
• 1⁴ = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

Пример. Возвести в степень.

• 5³ = 5 • 5 • 5 = 125
• 2.5² = 2.5 • 2.5 = 6.25
• ( )⁴ =   •   •   •   = 

  3 • 3 • 3 • 3

  4 • 4 • 4 • 4

   = 

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

 

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

 

Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётнуюстепень, — число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:

a² ≥ 0 при любом a.

• 2 • (- 3)² = 2 • (- 3) • (- 3) = 2 • 9 = 18
• — 5 • (- 2)³ = — 5 • (- 8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)⁴ и -5⁴ это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (- 5)⁴ означает найти значение четвёртой степени отрицательного числа.

(- 5)⁴ = (- 5) • (- 5) • (- 5) • (- 5) = 625

В то время как найти -5⁴ означает, что пример нужно решать в 2 действия:

1. Возвести в четвёртую степень положительное число 5. 
   5⁴ = 5 • 5 • 5 • 5 = 625
2. Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание). 
   -5⁴ = — 625

Пример. Вычислить: — 6² — (- 1)⁴

— 6

2 — (- 1)⁴ = — 37

1. 6² = 6 • 6 = 36
2. -6² = — 36
3. (- 1)⁴ = (- 1) • (- 1) • (- 1) • (- 1) = 1
4. — (- 1)⁴ = — 1
5. — 36 — 1 = — 37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

 

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

Для облегчения решения примеров полезно знать и пользоватьсятаблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

intellect.icu

Основные арифметические действия

Сложение

Сложение – одна из основных операций, позволяющая объединить два слагаемых.

Запись сложения: 8 + 3 = 11

8 и 3 – слагаемые

11 – сумма

Вычитание

Вычитание – действие, обратное сложению.

Запись: 15–7 = 8

15 – уменьшаемое

7 – вычитаемое

8 – разность

Если разность 8, сложить с вычитаемым 7, это даст уменьшаемое 15. Операция сложения 8 + 7 = 15 является контрольной проверкой вычитания 15 – 7 = 8.

Умножение

Умножение – арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

Запись: 12 × 5 = 60 или 12 • 5 = 60

12 – множимое

5 – множитель

60 – произведение

12 × 5 = 12 + 12 + 12 + 12 + 12

В случае если множимое и множитель поменять ролями, произведение остается одним и тем же. Например:

2 × 5 = 2 + 2 + 2 + 2 + 2 = 10

5 × 2 = 5 + 5 = 10

Поэтому и множитель, и множимое называются «сомножителями».

Деление

Деление – арифметическое действие обратное умножению.

Запись:

48 : 6 = 8 или 48 / 6 = 8

48 – делимое

6 – делитель

8 – частное

В данном случае произведение делителя 6 и частного 8, в качестве проверки, дает делимое 48

Если в результате операции деления, частное является не целым числом, то его можно представить дробью 3 / 5. Если частное является целым числом, в таком случае говорят, что первое из озвученных чисел нацело делится или, проще говоря, делится на второе.

Например, число 35 полностью делится на 5, ибо частное это целое число 7. Второе число в данном случае называется делителем первого, первое же – кратным второго.

Пример 1

Число 5 является делителем чисел 25, 60, 80 и не действует в качестве делителя для чисел

4, 13, 42, 61.

Пример 2

Число 60 кратное чисел 15, 20, 30 и не является кратным для чисел 17, 40, 90.

В случае, когда делимое не делится полностью, иногда применяют так называемое деление с остатком. Деление с остатком, это отыскание наибольшего подходящего целого числа, которое в произведении с делителем дает нужное число, не превышающее делимое.

Такое искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком, которое всегда меньше делителя.

Возведение в степень

Возведение степень – операция умножения числа на самого себя несколько (n) раз.

Основание степени называется число, которое повторяется сомножителем определённое количество раз.

Показателем степени называется число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, получаемое в результате взаимодействия основания и показателя степени.

Запись: 34 = 81

3 – основание степени

4 – показатель степени

81 – степень

34 = 3 × 3 × 3 × 3

Вторая степень называется иначе квадратом, третья степень – кубом. Первой степенью числа называют само это число.

Извлечение корня

Извлечение корня – арифметическое действие, обратное возведению в степень.

Запись:4√81 = 3

81 – подкоренное число

4 – показатель корня

3 – корень

З4 = 81 – возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня)

2√16 = 4 – корень второй степени называется – квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4

3√8 = 2 – корень третьей степени называется – кубичным.

Сложение и вычитание, умножение и деление, а так же возведение в степень и извлечение корня попарно представляют собой обратными действиями.

Правила первых четырех действий регулирующие взаимодействия с целыми числами предполагаются известными. Возведение в степень выполняется повторным умножением.

simple-math.ru

Действия, обратные возведению в степень

7. В виду последней особенности действий возведения в степень для него можно составить 2 обратных задачи. Напр.:

1) Я задумал число, возвел его в третью степень (или: в куб), получилось 64; какое число я задумал?

Эту задачу можно записать в виде

(?)³ = 64

2) Я взял число 3, возвел его в некоторую степень, – получилось 81. В какую степень было возведено число 3.

Эту задачу можно записать в виде:

3^? = 81

Теперь уже, так как возведение в степень не обладает переместительным законом, эти две задачи следует считать совершенно различными.

Сначала решать их можно подбором: попробуем число 1, 1³ = 1, а не 64, след., 1 не годится; 2³ = 8, а не 64, след., 2 не годится, 3³ = 27, а не 64, след., 3 не годится; 4³ = 64, след., в 1 задаче было задумано число 4. Также выясним, что во второй задаче число 3 было возведено в 4-ую степень.

Так как таких задач можно составить очень много, то для их решения необходимо изобрести новые действия. Эти действия обратны возведению в степень. Итак, для возведения в степень существуют два обратных действия: первое из них называется извлечением корня и служит для решения вопросов, подобных первой из наших задач; второе называется нахождением логарифма и служит для решения вопросов, подобных второй задаче.

Если мы обратим внимание на то, что в первой задаче нам даны степень 64 и показатель степени 3, то мы установим определение:

Извлечением корня называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному показателю находят основание степени.

Также точно: во второй задаче даны степень (81) и основание степени (3), а надо найти показателя степени. Поэтому

нахождением логарифма называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному основанию находится показатель степени.

maths-public.ru

Возведение в степень чисел | Математика

Возьмем сначала какое-либо положительное число, напр., +3, и станем его возводить в разные степени:

(+3)² = (+3) ∙ (+3) = +9;    (+3)³ = (+3) ∙ (+3) ∙ (+3) = +27;    (+3)⁴ = (+3) ∙ (+3) ∙ (+3) ∙ (+3) = +81 и т.д.

Из этих примеров уже становится совершенно ясным, что при возведении в любую степень положительного числа результат всегда получается положительным.

Возьмем затем отрицательное число, напр., –3, и станем его возводить в разные степени:

(–3)² = (–3) ∙ (–3) = +9;    (–3)³ = (–3) ∙ (–3) ∙ (–3) = –27;    (–3)⁴ = (–3) ∙ (–3) ∙ (–3) ∙ (–3) = +81;    (–3)⁵ = (–3) ∙ (–3) ∙ (–3) ∙ (–3) ∙ (–3) = –243 и т. д.

Рассматривая эти примеры, придем к общему заключению, что при возведении отрицательного числа в четную степень (во 2-ую, в 4-ую, в 6-ую и т. д.) результат получается положительный, а при возведении его в нечетную степень (в 3-ю, в 5-ую, в 7-ую и т. д.) результат получается отрицательным.

Вот еще примеры:

Выполним два примера на вычисление, где помимо, возведения в степень, входят и другие действия.

Сначала надо выполнить действия внутри каждых скобок, причем внутри квадратных скобок пришлось бы сначала выполнить умножение , но второй множитель еще не вычислен – надо, поэтому, предварительно вычислить его. Итак,

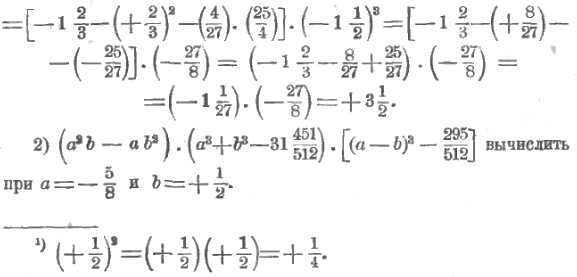
Будем вычислять по множителям. Первый множитель есть a²b – ab². Здесь написана разность между произведением квадрата числа a на число b и произведением числа a на квадрат числа b. Согласно этому, и следует вести вычисления: сначала число a возвести в квадрат, полученный результат умножить на число b, – получим уменьшаемое; затем число b возвести в квадрат, умножить число a на полученный результат, – получим вычитаемое, после чего надо выполнить вычитание:

Действия, обратные возведению в степень, будут разучиваться в дальнейшем курсе.

maths-public.ru