Десятичный логарифм — Википедия. Что такое Десятичный логарифм
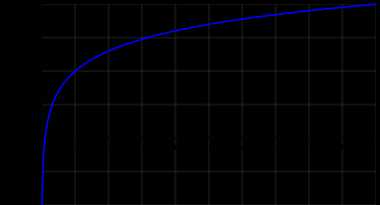График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b{\displaystyle b} есть решение уравнения 10x=b.{\displaystyle 10^{x}=b.}
Вещественный десятичный логарифм числа b{\displaystyle b} существует, если b>0{\displaystyle b>0} (комплексный десятичный логарифм существует для всех b≠0{\displaystyle b\neq 0}). Принято (спецификация ISO 31-11) обозначать его lgb{\displaystyle \lg \,b}. Примеры:
- lg1=0;lg10=1;lg100=2{\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2}
- lg1000000=6;lg0,1=−1;lg0,001=−3{\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log,Log,Log10{\displaystyle \operatorname {log} ,\operatorname {Log} ,\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны[1]:
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
- lg|xy|=lg(|x|)+lg(|y|),{\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}
- lg|xy|=lg(|x|)−lg(|y|),{\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
- lg(x1x2…xn)=lg(x1)+lg(x2)+⋯+lg(xn){\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел x,y{\displaystyle x,y}.
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения x⋅y{\displaystyle x\cdot y}.
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
- lnx≈2,30259 lgx;lgx≈0,43429 lnx{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
- lg0,012=lg(10−2×1,2)=−2+lg1,2≈−2+0,079181=−1,920819{\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
- lg0,012≈−2+0,079181=2¯,079181{\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y=lgx.{\displaystyle y=\lg \,x.} Она определена при всех x>0.{\displaystyle x>0.} Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
- ddxlgx=lgex{\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}
Ось ординат (x=0){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:
- limx→0+0lgx=−∞{\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }
Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x{\displaystyle x} (характеристику логарифма) [lgx]{\displaystyle [\lg x]} легко определить.
- Если x⩾1{\displaystyle x\geqslant 1}, то [lgx]{\displaystyle [\lg x]} на 1 меньше числа цифр в целой части числа x{\displaystyle x}. Например, сразу очевидно, что lg345{\displaystyle \lg 345} находится в промежутке (2,3){\displaystyle (2,3)}.
- Если 0<x<1{\displaystyle 0<x<1}, то ближайшее к lgx{\displaystyle \lg x} целое в меньшую сторону равно общему числу нулей в x{\displaystyle x} перед первой ненулевой цифрой (включая ноль перед запятой), взятому со знаком минус. Например, lg0,0014{\displaystyle \lg 0{,}0014} находится в интервале (−3,−2){\displaystyle (-3,-2)}.
Кроме того, при переносе десятичной запятой в числе на n{\displaystyle n} разрядов значение десятичного логарифма этого числа изменяется на n.{\displaystyle n.} Например:
- lg8314,63=lg8,31463+3{\displaystyle \lg 8314{,}63=\lg 8{,}31463+3}
Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от 1{\displaystyle 1} до 10{\displaystyle 10}[4]. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным
| Число | логарифм | характеристика | мантисса | запись |
|---|---|---|---|---|
| n | lg(n) | C = floor(lg(n) ) | M = (lg(n) − характеристика) | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Обратите внимание, что у всех приведенных в таблице чисел одна и та же мантисса.[прояснить]
История
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker)[6].
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[7]. В СССР выпускались несколько сборников таблиц логарифмов[8]
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Литература
- Теория логарифмов
- История логарифмов
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.
Ссылки
Примечания
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187..
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Элементарная математика, 1976, с. 94—100.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406..
- ↑ История математики, том II, 1970, с. 62..
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4.
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
wiki.sc
Десятичный логарифм Википедия
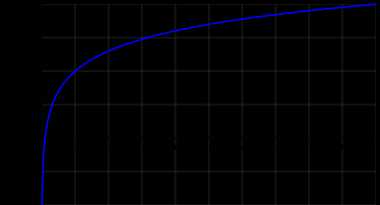График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b{\displaystyle b} есть решение уравнения 10x=b.{\displaystyle 10^{x}=b.}
Вещественный десятичный логарифм числа b{\displaystyle b} существует, если b>0{\displaystyle b>0} (комплексный десятичный логарифм существует для всех b≠0{\displaystyle b\neq 0}). Принято (спецификация ISO 31-11) обозначать его lgb{\displaystyle \lg \,b}. Примеры:
- lg1=0;lg10=1;lg100=2{\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2}
- lg1000000=6;lg0,1=−1;lg0,001=−3{\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log,Log,Log10{\displaystyle \operatorname {log} ,\operatorname {Log} ,\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны[1]:
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
- lg|xy|=lg(|x|)+lg(|y|),{\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}
- lg|xy|=lg(|x|)−lg(|y|),{\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
- lg(x1x2…xn)=lg(x1)+lg(x2)+⋯+lg(xn){\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x,y{\displaystyle x,y} с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел x,y{\displaystyle x,y}.
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения x⋅y{\displaystyle x\cdot y}.
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
- lnx≈2,30259 lgx;lgx≈0,43429 lnx{\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
- lg0,012=lg(10−2×1,2)=−2+lg1,2≈−2+0,079181=−1,920819{\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
- lg0,012≈−2+0,079181=2¯,079181{\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y=lgx.{\displaystyle y=\lg \,x.} Она определена при всех x>0.{\displaystyle x>0.} Область значений: E(y)=(−∞;+∞){\displaystyle E(y)=(-\infty ;+\infty )}. График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
- ddxlgx=lgex{\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}
Ось ординат (x=0){\displaystyle (x=0)} является вертикальной асимптотой, поскольку:
- limx→0+0lgx=−∞{\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }
Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x{\displaystyle x} (характеристику логарифма) [lgx]{\displaystyle [\lg x]} легко определить.
- Если x⩾1{\displaystyle x\geqslant 1}, то [lgx]{\displaystyle [\lg x]} на 1 меньше числа цифр в целой части числа x{\displaystyle x}. Например, сразу очевидно, что lg345{\displaystyle \lg 345} находится в промежутке (2,3){\displaystyle (2,3)}.
- Если 0<x<1{\displaystyle 0<x<1}, то ближайшее к lgx{\displaystyle \lg x} целое в меньшую сторону равно общему числу нулей в x{\displaystyle x} перед первой ненулевой цифрой (включая ноль перед запятой), взятому со знаком минус. Например, lg0,0014{\displaystyle \lg 0{,}0014} находится в интервале (−3,−2){\displaystyle (-3,-2)}.
Кроме того, при переносе десятичной запятой в числе на n{\displaystyle n} разрядов значение десятичного логарифма этого числа изменяется на n.{\displaystyle n.} Например:
- lg8314,63=lg8,31463+3{\displaystyle \lg 8314{,}63=\lg 8{,}31463+3}
Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от 1{\displaystyle 1} до 10{\displaystyle 10}[4]. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным[5]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
| Число | Логарифм | Характеристика | Мантисса | Запись |
|---|---|---|---|---|
| n | lg(n) | C | M = lg(n) − C | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Обратите внимание, что у всех приведенных в таблице чисел n{\displaystyle n} одна и та же мантисса M{\displaystyle M}, поскольку:
- lg(n)=lg(x×10C)=lg(x)+lg(10C)=lg(x)+C{\displaystyle \lg(n)=\lg \left(x\times 10^{C}\right)=\lg(x)+\lg \left(10^{C}\right)=\lg(x)+C},
где 1<x<10{\displaystyle 1<x<10} — значащая часть числа n{\displaystyle n}.
История
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker)[6].
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[7]. В СССР выпускались несколько сборников таблиц логарифмов[8]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Литература
- Теория логарифмов
- История логарифмов
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.
Ссылки
Примечания
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187..
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Элементарная математика, 1976, с. 94—100.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406..
- ↑ История математики, том II, 1970, с. 62..
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4.
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
wikiredia.ru
Десятичный логарифм Википедия
График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b{\displaystyle b} есть решение уравнения 10x=b.{\displaystyle 10^{x}=b.}
Вещественный десятичный логарифм числа b{\displaystyle b} существует, если b>0{\displaystyle b>0} (комплексный десятичный логарифм существует для всех b≠0{\displaystyle b\neq 0}). Принято (спецификация ISO 31-11) обозначать его lgb{\displaystyle \lg \,b}. Примеры:
- lg1=0;lg10=1;lg100=2{\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2}
- lg1000000=6;lg0,1=−1;lg0,001=−3{\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log,Log,Log10{\displaystyle \operatorname {log} ,\operatorname {Log} ,\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства[ | ]
В нижеследующей таблице предполагается, что все значения положительны[1]:
| Формула | Пример | |
|---|---|---|
| Произведение | lg(xy)=lg(x)+lg(y){\displaystyle \lg(xy)=\lg(x)+\lg(y)} |
ru-wiki.ru
Десятичный логарифм Википедия
График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b{\displaystyle b} есть решение уравнения 10x=b.{\displaystyle 10^{x}=b.}
Вещественный десятичный логарифм числа b{\displaystyle b} существует, если b>0{\displaystyle b>0} (комплексный десятичный логарифм существует для всех b≠0{\displaystyle b\neq 0}). Принято (спецификация ISO 31-11) обозначать его lgb{\displaystyle \lg \,b}. Примеры:
- lg1=0;lg10=1;lg100=2{\displaystyle \lg \,1=0;\,\lg \,10=1;\,\lg \,100=2}
- lg1000000=6;lg0,1=−1;lg0,001=−3{\displaystyle \lg \,1000000=6;\,\lg \,0{,}1=-1;\,\lg \,0{,}001=-3}
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log,Log,Log10{\displaystyle \operatorname {log} ,\operatorname {Log} ,\operatorname {Log10} }, причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
ruwikiorg.ru
Десятичный логарифм — это… Что такое Десятичный логарифм?
График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа есть решение уравнения
Десятичный логарифм числа существует, если Принято (спецификация ISO 31-11) обозначать его . Примеры:
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: , причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны[1]:
Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел .
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: . Она определена при всех . Область значений: . График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
Ось ординат является левой вертикальной асимптотой, поскольку:
Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа (характеристику логарифма) легко определить.
Кроме того, при переносе десятичной запятой в числе на разрядов значение десятичного логарифма этого числа изменяется на Например:
Отсюда следует, что достаточно составить таблицу мантисс (дробных частей) десятичных логарифмов для чисел в диапазоне от 1 до 10. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным[4]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
| Число | логарифм | характеристика | мантисса | запись |
|---|---|---|---|---|
| n | lg(n) | C = floor(lg(n) ) | M = (lg(n) − характеристика) | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Обратите внимание, что у всех приведенных в таблице чисел одна и та же мантисса.
Десятичная логарифмическая шкала на логарифмической линейкеИстория
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker)[5].
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[6]. В СССР выпускались несколько сборников таблиц логарифмов[7]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Литература
- Теория логарифмов
- История логарифмов
Ссылки
Примечания
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189.
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406.
- ↑ История математики, том II, 1970, с. 62.
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
veter.academic.ru
Десятичный логарифм — Википедия
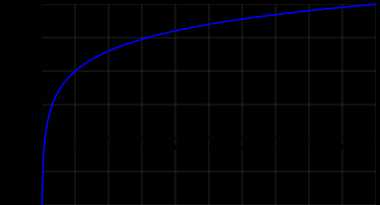График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа есть решение уравнения
Десятичный логарифм числа существует, если Принято (спецификация ISO 31-11) обозначать его . Примеры:
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: , причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства[править]
В нижеследующей таблице предполагается, что все значения положительны[1]:
Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел .
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма[править]
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: Она определена при всех Область значений: . График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
Ось ординат является левой вертикальной асимптотой, поскольку:
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа (
Кроме того, при переносе десятичной запятой в числе на разрядов значение десятичного логарифма этого числа изменяется на Например:
Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от до [4]. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным[5]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
| Число | логарифм | характеристика | мантисса | запись |
|---|---|---|---|---|
| n | lg(n) | C = floor(lg(n) ) | M = (lg(n) − характеристика) | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker)[6].
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[7]. В СССР выпускались несколько сборников таблиц логарифмов[8]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
- Теория логарифмов
- История логарифмов
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189.
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Ошибка цитирования Неверный тег
<ref>; для сносокZAY94не указан текст - ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406.
- ↑ История математики, том II, 1970, с. 62.
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4.
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
www.wikiznanie.ru
Десятичный логарифм — это… Что такое Десятичный логарифм?
График десятичного логарифмаДесятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа есть решение уравнения
Десятичный логарифм числа существует, если Принято (спецификация ISO 31-11) обозначать его . Примеры:
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: , причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны[1]:
Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
- Найти в таблицах логарифмы чисел .
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: . Она определена при всех . Область значений: . График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
Ось ординат является левой вертикальной асимптотой, поскольку:
Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа (характеристику логарифма) легко определить.
Кроме того, при переносе десятичной запятой в числе на разрядов значение десятичного логарифма этого числа изменяется на Например:
Отсюда следует, что достаточно составить таблицу мантисс (дробных частей) десятичных логарифмов для чисел в диапазоне от 1 до 10. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным[4]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
| Число | логарифм | характеристика | мантисса | запись |
|---|---|---|---|---|
| n | lg(n) | C = floor(lg(n) ) | M = (lg(n) − характеристика) | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Обратите внимание, что у всех приведенных в таблице чисел одна и та же мантисса.
Десятичная логарифмическая шкала на логарифмической линейкеИстория
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1857 году в Берлине (таблицы Бремикера, Carl Bremiker)[5].
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[6]. В СССР выпускались несколько сборников таблиц логарифмов[7]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Литература
- Теория логарифмов
- История логарифмов
Ссылки
Примечания
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189.
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406.
- ↑ История математики, том II, 1970, с. 62.
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
dis.academic.ru