Дискретная случайная величина х задана законом распределения – 1. | — Pandia.ru

Найти закон распределения — 25 Октября 2012 — Примеры решений задач

Задача. Дискретная случайная величина Х задана законом распределения: Найти: Р2; функцию распределения F(х) и построить ее график; математическое ожидание; дисперсию и среднеквадратическое отклонение случайной величины Х. Найти закон распределения случайной величины Y, где Y = 2X, Y = X2. РЕШЕНИЕ 1) Определим Р2. Так как сумма всех вероятностей, указанных в таблице, должна быть равна единице (то есть Р1 + Р2 + Р3 = 1), то Р2 найдем из формулы: Р2 = 1 — Р1 — Р3 Р2 = 1 – 0,4 – 0,1 = 0,5. 2) Построим функцию распределения а) Рассмотрим первый интервал х <= 2: б) Рассмотрим второй интервал 2 < х <= 5: в) Рассмотрим третий интервал 5 < х <= 8: г) Рассмотрим четвертый интервал х > 8: Запишем закон распределения: 3) Построим график функции распределения: 4) Определим математическое ожидание данной случайной величины Х (математическое ожидание характеризует среднее значение случайной величины при большом числе испытаний): М(Х) = 2 ? 0,4 + 5 ? 0,5 + 8 ? 0,1 = 4,1. 5) Определим дисперсию для данной случайной величины по формуле (дисперсия характеризует средний квадрат отклонения случайной величины от среднего): Д(Х) = М(Х2) – М2(Х) М(Х2) = 22 ? 0,4 + 52 ? 0,5 + 82 ? 0,1 = 20,5. Д(Х) = 20,5 – 4,12 = 3,69. 6) Определим среднеквадратическое отклонение, которое характеризует среднее отклонение случайной величины от среднего, по формуле: 7) Составим закон распределения для функций Y = 2X и Y = X2 X 2 5 8 Y=2X 4 10 16 Y=X2 4 25 64 P 0,4 P2 0,1

www.reshim.su

Функция распределения вероятностей дискретной величины

Рассмотрим пространство элементарных событий, в котором каждому элементарному событию в соответствие ставится число или вектор , т.е. на множестве есть определенная функция , которая для каждого элементарного события находит элемент одномерного пространства или — мерного пространства .

Эту функцию называют случайной величиной. В случае, когда отражает множество на одномерное пространство случайную величину называют одномерной. Если отображение осуществляется на , то случайную величину называют n- мерной (системой n случайных величин или n — мерным случайным вектором).

Величина называется случайной, если в результате проведения опыта под влиянием случайных факторов она приобретает то или другое возможное числовое значение с определенной вероятностью.

Если множество возможных значений случайной величины является счетно, то ее называют дискретной. В противном случае ее называют непрерывной.

Случайные величины для удобства обозначают прописными буквами латинского алфавита , а их возможные значения — строчными .

Для установления случайной величины необходимо знать не только множество возможных ее значений, но и указать, с какими вероятностями она приобретает то или иное возможное значение.

С этой целью вводят понятие закона распределения вероятностей – зависимость, которая устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины часто задают в табличной форме, функцией, или графически с помощью вероятностного многоугольника.

При табличной формы записи закона указывается множество возможных значений случайной величины находится в порядке их возрастания в первой строке, и соответствующих им вероятностей в следующей:

Случайные события должны быть попарно несовместимы и образовывать полную группу, то есть удовлетворять условие:

Приведенную зависимость называют условием нормировки для дискретной случайной величины , а таблицу распределения – рядом распределения.

Функция распределения вероятностей и ее свойства

Закон распределения вероятностей можно представить в виде функции распределения вероятностей случайной величины , которая может использоваться как для дискретных, так и для непрерывных случайных величин.

Функцию аргумента , устанавливающую вероятность случайного события называют функцией распределения вероятностей:

Ее следует понимать как функцию, которая устанавливает вероятность случайной величины, которая может принимать значения, меньше .

Функция распределения обладает следующими свойствами:

1. Она всегда положительная со значениями в пределах от нуля до единицы

2. Функция является монотонно возрастающей, а именно , если .

С этого свойства получают приведенные выводы:

a) Вероятность вступления случайной величиной возможных значений из промежутка равна прироста ее интегральной функции на этом промежутке:

б) Вероятность, что непрерывная случайная величина примет конкретное возможное значение, всегда равна нулю

Для непрерывной случайной величины выполняются такие равенства:

3. На крайних точках непрерывная случайная величина принимает значение 0 и 1.

Из этих границ следует, что для дискретной случайной величины с возможными значениями из ограниченного промежутка имеем

для

для

—————————-

Приведем решения задач на отыскание функции распределения.

Пример 1. Закон распределения дискретной случайной величины задан таблицей:

Построить функцию распределения и ее график.

Решение. Согласно свойствами функции получим приведенные дальше значение.
1)
2)
3)
4)
5)
6)

Компактно функция распределения иметь запись

График функции распределения изображен на рисунке ниже

—————————-

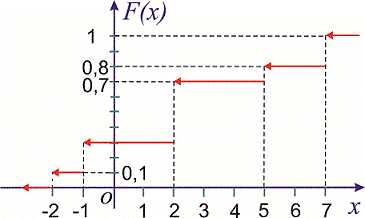
Пример 2. Есть три коробки с шарами. В первой содержится 6 желтых и 4 синие шарики, во втором — 7 желтых и 3 синие, а в третьем — 2 желтых и 8 синих. Из каждой коробки наугад берут по одному шарику. Построить закон распределения вероятностей дискретной случайной величины – появления числа синих шариков среди трех наугад взятых, определить закон распределения и построить график этой функции.

Решение. Среди трех наугад взятых шариков число синих может быть 0, 1, 2, 3.
В табличной форме закон распределения дискретной случайной величины имеет вид:

Вычислим вероятности . С этой целью обозначим — случайное событие, заключающееся соответственно в появлении желтого шарики и – появление синего с первой коробки. Подобным образом для остальных коробок . Вероятности этих событий такие:

Поскольку случайные события независимы, то вероятности находим по формулам:

Вычисление достаточно просты и сделаны обозначения полностью все объясняют. Проверим выполнение условия нормировки

Всегда выполняйте проверку данного условия: это достаточно просто сделать и позволяет быстро проверить правильность вычислений вероятности. В случаях, когда условие нормировки не выполняется нужно отыскать ошибку и исправить ее.

У нас же все вычисления правильны, потому записываем закон распределения вероятностей в табличной форме:

Вычисляем значение интегральной функции
1)
2)
3)
4)
5)

В случае ошибок при нахождении вероятностей последнее соотношение дает отличный от единицы результат, поэтому можете проверять и по этому значению. Упрощенно функция распределения будет иметь вид

а ее график следующий

—————————-

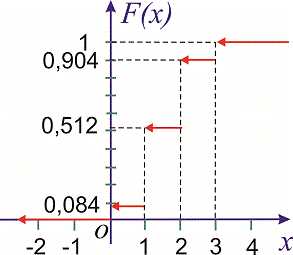
Пример 3. Закон распределения случайной величины задан функцией распределения вероятностей

Построить график функции распределения и вычислить вероятность, что случайная величина принадлежит промежутку .

Решение. Функция распределения будет иметь вид.

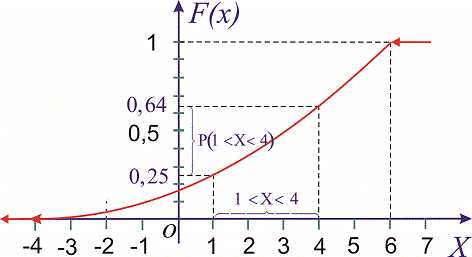
Используя определение, вычислим

Таким образом вероятность, что случайная величина принадлежит промежутку [1,4] равна 0,36.

—————————-

Внимательно разберитесь с приведенными примерами нахождения функции распределения, это Вам пригодится на практических занятиях. Старайтесь проверять условие нормирования, чтобы избежать дальнейших ошибок и правильно определяйте вероятности.

———————————————-

yukhym.com

Примеры решения задач на тему «Случайные величины»

Примеры решения задач на тему «Случайные величины».

  

   Задача 1. В лотерее выпущено 100 билетов. Разыгрывался один выигрыш в 50 у.е. и десять выигрышей по 10 у.е. Найти закон распределения величины X – стоимости возможного выигрыша.

Решение. Возможные значения величины X: x₁ = 0; x₂ = 10 и x₃ = 50. Так как «пустых» билетов – 89, то p₁ = 0,89, вероятность выигрыша 10 у.е. (10 билетов) – p₂ = 0,10 и для выигрыша 50 у.е. – p₃ = 0,01. Таким образом:

X	0	10	50
P	0,89	0,10	0,01

Легко проконтролировать:.

 

   Задача 2. Вероятность того, что покупатель ознакомился заранее с рекламой товара равна 0,6 (р=0,6). Осуществляется выборочный контроль качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее. Составить ряд распределения количества опрошенных покупателей.

Решение.  Согласно условию задачи р = 0,6. Откуда: q=1-p = 0,4. Подставив данные значения, получим:  и построим ряд распределения:

 

Х	1	2	…	m	…
pi	0,6	0,24	…		…

 

   Задача 3. Компьютер состоит из трех независимо работающих элементов: системного блока, монитора и клавиатуры. При однократном резком повышении напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения Бернулли составить закон распределения числа отказавших элементов при скачке напряжения в сети.

Решение. Рассмотрим распределение Бернулли (или биномиальное): вероятность того, что в n  испытаниях событие А появится ровно k раз: , или:

X	0	1	…		…	n
P	qn		…		…	pn

Вернёмся к задаче.

Возможные значения величины X (число отказов):

x₀ =0 – ни один из элементов не отказал;

x₁ =1 – отказ одного элемента;

x₂ =2 – отказ двух элементов;

x₃ =3 – отказ всех элементов.

Так как, по условию, p = 0,1, то q = 1 – p = 0,9. Используя формулу Бернулли, получим

, ,

, .

Контроль: .

Следовательно, искомый закон распределения:

 

X	0	1	2	3
p	0,729	0,243	0,027	0,001

 

   Задача 4. Произведено 5000 патронов. Вероятность того, что один патрон бракованный . Какова вероятность того, что во всей партии будет ровно 3 бракованных патрона?

Решение. Применим распределение Пуассона: это распределение используется для определения вероятности того, что при очень большом

 

количестве испытаний (массовые испытания), в каждом из которых вероятность события A очень мала, событие A наступит  k раз: , где .

Здесь n = 5000, p = 0,0002, k = 3. Находим  , тогда искомая вероятность: .

 

   Задача 5. При стрельбе до первого попадания с вероятностью попадания p = 0,6 при выстреле надо найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. Применим геометрическое распределение: пусть производятся независимые испытания, в каждом из которых событие A имеет вероятность появления p (и непоявления q = 1 – p). Испытания заканчиваются, как только произойдет событие A.

При таких условиях вероятность того, что событие A произойдет на k-ом испытании, определяется по формуле: . Здесь p = 0,6; q = 1 – 0,6 = 0,4;  k = 3. Следовательно, .

 

   Задача 6. Пусть задан закон распределения случайной величины X:

Найти математическое ожидание.

Решение. .

Заметим, что вероятностный смысл математического ожидания – это среднее значение случайной величины.

 

   Задача 7. Найти дисперсию случайной величины X со следующим законом распределения:

Решение. Здесь .

Закон распределения квадрата величины X

2:

.

Искомая дисперсия: .

Дисперсия характеризует меру отклонения (рассеяния) случайной величины от её математического ожидания.

 

   Задача 8. Пусть случайная величина задается распределением:

X	2м	3м	10м
P	0,1	0,4	0,5

Найти её числовые характеристики.   

Решение: м, м²,

м²,   м.

Про случайную величину X можно сказать либо – ее математическое ожидание 6,4 м с дисперсией 13,04 м

2, либо – ее математическое ожидание 6,4 м с отклонением  м. Вторая формулировка, очевидно, нагляднее.

   Задача 9. Случайная величина X задана функцией распределения: .

Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале .

Решение. Вероятность того, что X примет значение из заданного интервала, равно приращению интегральной функции в этом интервале, т.е. . В нашем случае  и , поэтому

.

 

   Задача 10. Дискретная случайная величина X задана законом распределения:

Найти функцию распределения F(x) и построить ее график.

Решение. Так как функция распределения,

 для , то

при  ;

при  ;

при  ;

при  ;

Соответствующий график:

 

   Задача 11. Непрерывная случайная величина X задана дифференциальной функцией распределения: .

Найти вероятность попадания X в интервал

.

Решение. Заметим, что это частный случай показательного закона распределения.

Воспользуемся формулой: .

.

 

   Задача 12. Найти числовые характеристики дискретной случайной величины X, заданной законом распределения:

X	–5	2	3	4
p	0,4	0,3	0,1	0,2

Решение. Математическое ожидание:

.

Запишем закон распределения X²:

X2	25	4	9	16
p	0,4	0,3	0,1	0,2

Математическое ожидание:

.

Находим дисперсию:

, .

 

   Задача 13. Непрерывная случайная величина задана на интервале  плотностью распределения , а вне этого интервала . Найти ее числовые характеристики.

Решение. Математическое ожидание:

.

Дисперсия: .

Среднее квадратическое отклонение: .

   

   Задача 14. Найти числовые характеристики случайной величины X, равномерно распределенной на интервале .

Решение. Для случайной величины, равномерно распределеной на интервале , плотность распределения: ,

поэтому: ; ;   .  

 

   Задача 15. Математическое ожидание нормально распределенной случайной величины  , а среднее квадратическое отклонение — . Найти вероятность того, что в результате испытания X примет значение из интервала  и записать закон распределения.

Решение. Запишем вначале закон распределения. Общая формула имеет вид: .

Подставляя  и , получим: .

Вероятность того, что X примет значение из интервала  имеет вид:

, где – функция Лапласа.

Значения этой функции находятся с помощью таблицы.

В нашем случае: .

По таблице находим: , следовательно:

.

 

war-math.narod.ru

Найти математическое ожидание дискретной случайной величины, заданной законом распределения

A. 0,535;

B. 1,36;

C. 1;

D. 0,453.

Сравните величины σ для двух кривых НРС B

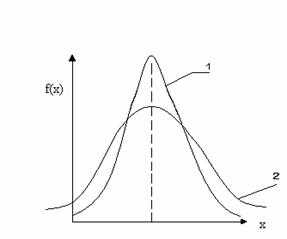A.

Непрерывная случайная величина Х задана плотностью распределения вероятностей . Тогда математическое ожидание этой нормально распределенной случайной величины равно

C. 4.

Для стандартизованного нормального распределения величина σ равна:

A. 1;

B. 2;

C.

Непрерывная случайная величина, возможные значения которой лежат в некоторых конечных пределах, распределена по закону равномерной плотности, если:

A. плотность вероятности постоянна;

B. все значения случайной величины имеют одинаковую вероятность;

C. плотность вероятности будет неотрицательной величиной и интеграл от плотности по отрезку, в котором заключены все значения случайной величины, равен единице.

Укажите условие нормировки непрерывной случайной величины:

A.

B.

C.

D.

Вероятность появления какого-либо события из нескольких несовместных событий…

A. больше вероятности каждого отдельного события;

B. меньше вероятности каждого отдельного события;

C. равна вероятности каждого отдельного события;

D. равна вероятности наиболее вероятного события;

E. равна вероятности наименее вероятного события.

Укажите формулу для определения математического ожидания дискретной случайной величины:

A.

B.

C.

D.

Укажите формулу для определения математического ожидания непрерывной случайной величины:

A.

B.

C.

D.

Укажите формулу для определения дисперсии дискретной случайной величины:

A.

B.

C.

D.

Функция распределения дискретной случайной величины…

A. показывает вероятность того, что случайная величина примет значения меньше величины , т.е

B. показывает вероятность того, что случайная величина примет значения больше величины , т.е.

C. равна вероятность того, что случайная величина примет значения , т.е.

D. показывает вероятность того, что случайная величина примет значения меньше либо равно величины , т.е.

Функция распределения дискретной случайной величины может быть представлена следующим образом:

A.

B.

C.

D.

Укажите формулу для определения среднего квадратического отклонения случайной величины:

A.

B.

C.

D.

Укажите правильные высказывания:

A. Относительной частотой случайного события А называется величина, равная пределу, к которому стремится отношение числа случаев, в которых реализуется событие А, к общему числу испытаний при неограниченном увеличении числа испытаний.

B. Относительной частотой случайного события А называется величина, равная отношению числа испытаний, в которых реализуется событие А, к общему числу испытаний.

C. Вероятность появления какого-либо события из нескольких несовместных событий больше вероятности каждого отдельного события.

D. Вероятность появления какого-либо события из нескольких несовместных событий равна произведению их вероятностей.

Укажите правильные высказывания:

A. Функция распределения непрерывной случайной величины указывает вероятность нахождения случайной величины в некотором интервале, отнесенную к ширине этого интервала.

B. Вероятность появления какого-либо события из нескольких несовместных событий меньше вероятности каждого отдельного события.

C. Плотность вероятности непрерывной случайной величины указывает вероятность того, что случайная величина принимает значения не больше х.

D. Функция распределения непрерывной случайной величины указывает вероятность того, что случайная величина принимает значения меньшие х.

Укажите правильные высказывания:

A. Плотность вероятности непрерывной случайной величины указывает вероятность нахождения случайной величины в некотором интервале, отнесенную к ширине этого интервала.

B. Площадь фигуры, ограниченной графиком функции плотности вероятности нормального закона распределения и осью абсцисс, равна 0,5.

C. Площадь фигуры, ограниченной графиком функции плотности вероятности нормального закона распределения и осью абсцисс, равна 1.

D. Математическое ожидание характеризует среднее значение случайной величины.

E. Дисперсия характеризует среднее значение случайной величины.

Укажите правильные высказывания:

A. Среднее квадратическое отклонение характеризует среднее значение случайной величины.

B. Математическое ожидание характеризует среднее значение случайной величины.

C. Дисперсия характеризует рассеяние случайной величины относительно ее математического ожидания.

D. Случайная величина называется непрерывной, если она принимает любые значения внутри некоторого интервала.

E. Случайная величина называется дискретной, если она принимает любое из значений в некотором интервале.

Укажите формулу плотности вероятности нормально распределенной непрерывной случайной – формулу Гаусса:

A.

B.

C

Случайная величина Х распределена нормально m=1,σ=3 , Укажите функцию плотности распределения величины Х:

A.

B.

C.

D.

cyberpedia.su

No related posts.