Метод математической индукции
Описание метода
Метод математической индукции является одним из наиболее часто встречающихся методов в математике. Допустим требуется доказать некоторое утверждение  , которое содержит целочисленный (индукционный) параметр , где . Наиболее часто в качестве параметра используются натуральные числа. Непосредственная проверка утверждения
, которое содержит целочисленный (индукционный) параметр , где . Наиболее часто в качестве параметра используются натуральные числа. Непосредственная проверка утверждения  для каждого конкретного значения невозможна, поскольку множество натуральных чисел бесконечно.
для каждого конкретного значения невозможна, поскольку множество натуральных чисел бесконечно.
Метод математической индукции выполняется в три этапа.
На первом этапе необходимо убедиться в справедливости утверждения  для начального значения параметра , т.е. необходимо убедиться в справедливости утверждения . Данный этап метода называется базой (базисом) индукции.
для начального значения параметра , т.е. необходимо убедиться в справедливости утверждения . Данный этап метода называется базой (базисом) индукции.
На втором этапе предполагается, что утверждение  справедливо при условии, что . Этот этап метода называется индукционным предположением.
справедливо при условии, что . Этот этап метода называется индукционным предположением.
Если на третьем этапе будет доказано утверждение  , то справедливость утверждения
, то справедливость утверждения  будет иметь место для произвольного значения
будет иметь место для произвольного значения  . Отметим, что выполнение третьего этапа метода обычно является наиболее трудоемкой частью метода.
. Отметим, что выполнение третьего этапа метода обычно является наиболее трудоемкой частью метода.
Ниже предлагаются примеры задач, решение которых осуществляется методом математической индукции.
Примеры решения задач
Пример 1. Доказать, что
, (1)
где  .
.
Доказательство. Обозначим .
Пусть  , тогда
, тогда  и из формулы (1) следует
и из формулы (1) следует  .
.
Предположим, что
 . (2)
. (2)
Теперь требуется убедиться в том, что формула (1) выполняется и при , т.е. надо показать, что
. (3)
Из формул (1) и (2) получаем
, или .
Отсюда следует формула (3). Следовательно, утверждение (1) доказано.
Пример 2. Доказать, что
, (4)
где  .
.
Доказательство. Обозначим .
Пусть , тогда и .
Пусть  и справедлива формула
и справедлива формула
. (5)
Пусть . Докажем, что или
. (6)
Так как , то с учетом индукционного предположения (5) получаем
.
Следовательно, формула (6) является доказанной, а рассматриваемое равенство (4) справедливо для произвольных значений  .
.
Пример 3. Доказать, что
, (7)
где  .
.
Доказательство. Обозначим .
Если , то  и
и  .
.
Предположим, что
Докажем, что .
Из формул (7) и (8) следует, что
.
Отсюда вытекает справедливость формулы (7) для произвольных значений  .
.
Пример 4. Если числовая последовательность является геометрической прогрессией, знаменатель которой равен  , то
, то
(9)
Доказательство. Обозначим .
Если  , то
, то 
Пусть  Необходимо показать, что
Необходимо показать, что 
Так как и  , то с учетом индукционного предположения имеем
, то с учетом индукционного предположения имеем
,
или 
Отсюда следует справедливость формулы (9).
Пример 5. Доказать, что
, (10)
где  .
.
Доказательство. Обозначим левую часть равенства (10) как 
Если  , то и .
, то и .
Пусть  . Покажем, что .
. Покажем, что .
Из определения  и равенства
и равенства  следует, что
следует, что
. (11)
Если воспользоваться известной формулой ,
то из равенства (11) получим ,
или .
Отсюда, согласно принципу математической индукции, следует справедливость формулы (10).
Пример 6. Доказать, что
, (12)
где  .
.
Доказательство. Обозначим .
Пусть  . Тогда
. Тогда  и
и  .
.
Предположим, что  , и покажем, что .
, и покажем, что .
Поскольку  , то ,
, то ,
 или .
или .
Формула (12) доказана.
Пример 7. Доказать неравенство
, (13)
где  .
.
Доказательство. Обозначим .
Если  , то
, то  , т.е. неравенство (13) выполняется.
, т.е. неравенство (13) выполняется.
Предположим, что . Покажем, что .
Так как  и , то .
и , то .
Очевидно, что для решения задачи требуется доказать неравенство
, (14)
которое выполняется для произвольных натуральных  .
.
Доказательство неравенства (14) будем вести методом от противного. Допустим, что существуют такие значения  , при которых выполняется противоположное неравенство, т.е. имеет место неравенство
, при которых выполняется противоположное неравенство, т.е. имеет место неравенство
. (15)
Преобразуем неравенство (15) следующим образом:
, или .
Поскольку получили числовое противоречие , то неравенство (14) верно. Тем самым доказано, что и неравенство (13) выполняется для любых значений  , где
, где 
Примечание. Проведя аналогичные рассуждения, можно доказать: если , то .
Пример 8. Доказать, что выражение кратно  (делится на число
(делится на число  без остатка), где
без остатка), где  .
.
Доказательство. Если  , то . Очевидно, что в данном случае требуемое утверждение выполняется.
, то . Очевидно, что в данном случае требуемое утверждение выполняется.
Пусть кратно  . Покажем, что выражение
. Покажем, что выражение  также будет делиться на число
также будет делиться на число  без остатка.
без остатка.
Так как , то
, или . (16)
Согласно индукционному предположению, выражение кратно  , поэтому из формулы (16) следует, что таковым будет и выражение
, поэтому из формулы (16) следует, что таковым будет и выражение  .
.
В этой связи утверждение задачи доказано.
Пример 9. Доказать, что для любого натурального  выражение кратно
выражение кратно  .
.
Доказательство. Если  , то
, то  и кратно
и кратно  . Предположим, что
. Предположим, что  кратно
кратно  . Убедимся в том, что
. Убедимся в том, что  также будет кратно
также будет кратно  .
.
Так как , то , или . (17)
Поскольку  натуральное число, то выражение
натуральное число, то выражение  всегда принимает только четные значения. В этой связи выражение кратно
всегда принимает только четные значения. В этой связи выражение кратно  . Согласно индукционному предположению
. Согласно индукционному предположению  кратно
кратно  и поэтому из формулы (17) следует, что
и поэтому из формулы (17) следует, что  делится на число
делится на число  без остатка.
без остатка.
Утверждение задачи доказано.
blog.tutoronline.ru
Примеры — Математическая индукция
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
Решение.
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
Учитывая равенство 1 + 2 + … + n = n(n + 1)/2, получаем
13 + 23 + … + n3 + (n + 1)3 = (1 + 2 + … + n + (n + 1))2,
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
| g) формула бинома Ньютона: |
www.sites.google.com
Во многих разделах математики приходится доказывать истинность утверждения, зависящего от , т. е. истинность высказывания P(N) Для «NÎN (для любого NÎN P(N) Верно).
Часто это удается доказать Методом математической индукции.
В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение P(N) считается истинным для всех натуральных значений переменной, если выполнены два условия:
1. Предложение P(N) истинно для N = 1.
2. Из предложения, что P(N) истинно для N = K (K — Произвольное натуральное число) следует, что оно истинно для N = K + 1.
Под методом математической индукции понимают следующий способ доказательства
1. Проверяют истинность утверждения для N = 1 – база индукции.
2. Предполагают, что утверждение верно для N = K – Индуктивное предположение.
3. Доказывают, что тогда оно верно и для N = K + 1 индуктивный переход.
Иногда предложение P(N) оказывается верным не для всех натуральных N, а начиная с некоторого для N = N0. В этом случае в базе индукции проверяется истинность P(N) при N = N0.
Пример 1. Пусть . Доказать, что
1. База индукции: при N = 1 по определению S1 = 1 и по формуле получаем один результат. Утверждение верно.
2. Индуктивное предположение. Пусть N = k и .
3. Индуктивный переход. Пусть N = k + 1. Докажем, что .
Действительно, в силу индуктивного предположения
Преобразуем это выражение
Индуктивный переход доказан.
Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!
Пример 2. Доказать
.
1. База индукции. При N = 1, утверждение, очевидно, верно.
2. Индуктивное предположение. Пусть N = K и
3. Индуктивный переход. Пусть N = K + 1. Докажем:
Действительно, возведем правую сторону в квадрат как сумму двух чисел:
Используя индуктивное предположение и формулу суммы арифметической прогрессии: , получим
Пример 3. Доказать неравенство
для .
1. Базой индукции в этом случае является проверка истинности утверждения для , т. е. необходимо проверить неравенство . Для этого достаточно возвести неравенство в квадрат: или 63 < 64 – неравенство верно.
2. Пусть неравенство верно для , т. е.
.
3. Пусть , докажем:
.
Используем предположение индукции
Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть
Остается установить, что лишний множитель не превосходит единицы. Действительно,
.
Пример 4. Доказать, что при любом натуральном число оканчивается цифрой .
1. Наименьшее натуральное , с которого справедливо утверждение, равно . .
2. Пусть при число оканчивается на . Это означает, что это число можно записать в виде , где – какое-то натуральное число. Тогда .
3. Пусть . Докажем, что оканчивается на . Используя полученное представление, получим
Последнее число имеет ровно единиц.
Задачи.
1. Доказать, что при каждом верны равенства
1) .
2) .
3) .
4) .
5) .
6) .
7) .
8) .
9) .
10).
2. Доказать, что при любом .
1) кратно .
2) кратно .
3) кратно .
4) кратно .
5) кратно .
6) кратно 19.
3. Доказать справедливость следующих неравенств для всех натуральных .
1) .
2) .
3) .
4) .
5) .
4. Доказать, что при любом натуральном верно неравенство
1) . 2) .
5. Доказать равенство для любого
1) ,
(в левой части содержится корней).
2) .
6. Пусть – произвольные неотрицательные числа, причем
.
Доказать, что .
7. Доказать неравенство Бернулли
,
8.Пусть – произвольные положительные числа, причем
. Доказать, что .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Метод математической индукции
Брянский Городской Лицей №1
Исследовательская работа на тему:
Метод Математической Индукции
Выполнил
М елешко К онстантин
ученик 10 физико-математического
Брянского Городского Лицея №1
Проверил
Т юкачева О льга И вановна
-2003-
Содержание исследовательской работы
Содержание_ _ _ _ _ _ _ _ _ _ _ _ _ _ 2
Введение_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 3
Основная часть
Полная и неполная индукция_ _ _ _ _ _ _ _ _3-4
Принцип математической индукции_ _ _ _ _4-5
Метод математической индукции_ _ _ _ _ _ 6
Решение Методом Математической Индукции
К задачам на суммирование_ _ _ _ _ _ _ _ _ 7
К задачам на доказательство неравенств_ _8
К задачам на делимость _ _ _ _ _ _ _ _ _ _ _11
К задачам на доказательство тождеств _ _ _12
К другим задачам _ _ _ _ _ _ _ _ _ _ _ _ _ _ 13
Заключение_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 16
Список использованной литературы _ _ _ _17
Введение
Слово индукция по-русски означает наведение, а индуктивными называют выводы, сделанные на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.
Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. И хотя теоретическая механика основывается на трех законах движения Ньютона, сами эти законы явились результатом глубокого продумывания опытных данных, в частности законов Кеплера движения планет, выведенных им при обработке многолетних наблюдений датского астронома Тихо Браге. Наблюдение, индукция оказываются полезными и в дальнейшем для уточнения сделанных предположений. После опытов Майкельсона по измерению скорости света в движущейся среде оказалось необходимым уточнить законы физики, создать теорию относительности.
В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство
.Лежащее в основе арифметики понятие «следовать за» тоже появилось при наблюдениях за строем солдат, кораблей и другими упорядоченными множествами.
Не следует, однако, думать, что этим исчерпывается роль индукции в математике. Разумеется, мы не должны экспериментально проверять теоремы, логически выведенные из аксиом: если при выводе не было сделано логических ошибок, то они постольку верны, поскольку истинны принятые нами аксиомы. Но из данной системы аксиом можно вывести очень много утверждений. И отбор тех утверждений, которые надо доказывать, вновь подсказывается индукцией. Именно она позволяет отделить полезные теоремы от бесполезных, указывает, какие теоремы могут оказаться верными, и даже помогает наметить путь доказательства.
Суть Математической Индукции
Покажем на примере использование М етода М атематической И ндукции и в конце сделаем обобщающий вывод.
Пусть требуется установить, что каждое натуральное чётное число nв пределах 44=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;
14=7+7; 16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.
Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).
Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.
Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:
1+3+5+…+(2n-1)=n2
т.е. сумма n первых последовательных нечётных чисел равна n2
Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости при-
ведённой формулы.
Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии. Неполная же индукция часто приводит к ошибочным результатам.
Во многих случаях выход из такого рода затруднений заключается в обращении к особому методу рассуждений, называемому методом математической индукции. Он заключается в следующем.
Пусть нужно доказать справедливость некоторого утверждения для любого натурального числаn(например нужно доказать, что сумма первых n нечётных чисел равна n2 ). Непосредственная проверка этого утверждения для каждого значения nневозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n=1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n=k вытекает его справедливость и при n=k+1.
Тогда утверждение считается доказанным для всех n. В самом деле, утверждение справедливо при n=1. Но тогда оно справедливо и для следующего числа n=1+1=2. Из справедливости утверждения для n=2 вытекает его справедливость для n=2+
+1=3. Отсюда следует справедливость утверждения для n=4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.
Обобщая сказанное, сформулируем следующий общий принцип.
Принцип математической индукции.
Если предложение А( n ), зависящее от натурального числа n , истинно для n =1 и из того, что оно истинно для n = k (где k -любое натуральное число), следует, что оно истинно и для следующего числа n = k +1, то предположение А( n ) истинно для любого натурального числа n .
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n> p, где p-фиксированное натуральное число. В этом случае принципматематической индукции формулируется следующим образом.
Если предложение А( n ) истинно при n = p и если А( k ) Þ А( k +1) для любого k > p , то предложение А( n ) истинно для любого n > p .Доказательство по методу математической индукции проводиться следующим образом. Сначала доказываемое утверждение проверяется для n=1, т.е. устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным шагом. В этой части доказывают справедливость утверждения для n=k+1 в предположении справедливости утверждения для n=k (предположение индукции), т.е. доказывают, что А(k)ÞA(k+1).
Применение метода математической индукции в задачах на суммирование
Применение метода математической индукции в задачах на суммирование
Пример:
Доказать, что
1+x2 +x3 +x4 +….+xn =
, где x1Решение.
, следовательно, при n=1 формула верна.Пусть k- любое натуральное число и пусть формула верна при n=k, т.е.
Докажем тогда
В самом деле ,
.
Значит, по принципу математической индукции формула верна для любого натурального n.
Примеры применения метода математической индукции к доказательству неравенств.
Доказать, что при любом натуральном n>1
.Решение.
Обозначим левую часть неравенства через
. , следовательно, при n=2 неравенство справедливо.Пусть
при некотором k. Докажем, что тогда и . Имеем , .mirznanii.com
Метод математической индукции (ММИ) | Математика, которая мне нравится
Рассмотрим на примере, как работает метод.
Задача. Доказать, что для всех натуральных справедливо равенство
Решение. Обозначим через левую часть равенства, а через — его правую часть.
1) Докажем сначала, что .
Доказательство.
2) Дано: . Нужно доказать: .
Доказательство.

Тем самым, утверждение доказано для любого , поскольку из его истинности для следует, что оно истинно для , из его истинности при следует его истинность для и т.д.
Предположим, что нам нужно доказать последовательность утверждений
Для того чтобы доказать все эти утверждения, достаточно доказать две теоремы:
1. — верное утверждение.
2. Если для какого-либо натурального верно утверждение , то верно и утверждение .
Такой способ доказательства последовательности утверждений называется методом математической индукции. Первая часть метода называется базой индукции, вторая — индукционным переходом.
Теорема. Если последовательности и таковы, что , и для любого натурального
то для всех натуральных выполняется равенство .
С помощью метода математической индукции можно также доказывать неравенства.
Теорема. Если последовательности и таковы, что , и для любого натурального
то для всех натуральных выполняется неравенство .
Пример. Доказать, что для всех натуральных
Доказательство.
1.
Действительно,
2.
Теорема. Если последовательности и с положительными членами таковы, что , и для любого натурального
то для всех натуральных выполняется неравенство .
Задачи. Доказать
1. .
2. .
3. при .
4. при .
5. Доказать, что сумма всевозможных произведений квадратов натуральных чисел, взятых по два (от 1 до ), равна
6. Доказать, что для всех натуральных
(четверок — ).
7. Доказать, что для всех натуральных
8. Доказать, что для всех натуральных
9. Доказать, что для всех натуральных
10. Доказать, что сторона правильного вписанного в окружность -угольника выражается формулой
где — радиус этой окружности (двоек — ).
11. Доказать, что прямых, пересекающихся в одной точке и лежащих в одной плоскости, делят эту плоскость на частей.
12. Доказать, что различных прямых, лежащих в одной плоскости, разбивают эту плоскость на области, которые могут быть закрашены красной и синей краской так, что все смежные области (т.е. области, имеющие общий отрезок прямой) будут закрашены разными красками.
13. Доказать, что если — суммы членов геометрических прогрессий, у которых первые члены , а знаменатели соответственно равны , то
14. Доказать, что сумма всех членов каждой горизонтальной строки таблицы
равна квадрату нечетного числа.
15. Доказать, что произведение
состоящее из сомножителей, равно
16. Доказать, что сумма всевозможных парных произведений натуральных чисел равна
17. Доказать, что для любого натурального
hijos.ru
Лекция 06. Метод математической индукции
Лекция 6. Метод математической индукции.
Новые знания в науке и жизни добываются разными способами, но все они (если не углубляться в детали) делятся на два вида – переход от общего к частному и от частного к общему. Первый – это дедукция, второй – индукция. Дедуктивные рассуждения – это то, что в математике обычно называют логическими рассуждениями, и в математической науке дедукция является единственным законным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные (с такими «псевдологическими» рассуждениями мы часто встречаемся в СМИ).
Индукция (induction – по-латыни наведение) наглядно иллюстрируется известной легендой о том, как Исаак Ньютон сформулировал закон всемирного тяготения после того, как ему на голову упало яблоко. Ещё пример из физики: в таком явлении, как электромагнитная индукция, электрическое поле создает, «наводит» магнитное поле. «Ньютоново яблоко» – типичный пример ситуации, когда один или несколько частных случаев, то есть наблюдения, «наводят» на общее утверждение, общий вывод делается на основании частных случаев. Индуктивный метод является основным для получения общих закономерностей и в естественных, и в гуманитарных науках. Но он имеет весьма существенный недостаток: на основании частных примеров может быть сделан неверный вывод. Гипотезы, возникающие при частных наблюдениях, не всегда являются правильными. Рассмотрим пример, принадлежащий Эйлеру.
Будем вычислять значение трехчлена при некоторых первых значенияхn:
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
43 | 47 | 53 | 61 | 71 | 83 | 97 | 113 |
Заметим, что получаемые в результате вычислений числа являются простыми. И непосредственно можно убедиться, что для каждого n от 1 до 39 значение многочлена является простым числом. Однако приn=40 получаем число 1681=412, которое не является простым. Таким образом, гипотеза, которая здесь могла возникнуть, то есть гипотеза о том, что при каждом n число является простым, оказывается неверной.
Лейбниц в 17 веке
доказал, что при всяком целом положительном n число  делится на 3, числоделится на 5 и т.д. На основании этого он
предположил, что при всяком нечётномk и любом натуральном n число
делится на 3, числоделится на 5 и т.д. На основании этого он
предположил, что при всяком нечётномk и любом натуральном n число 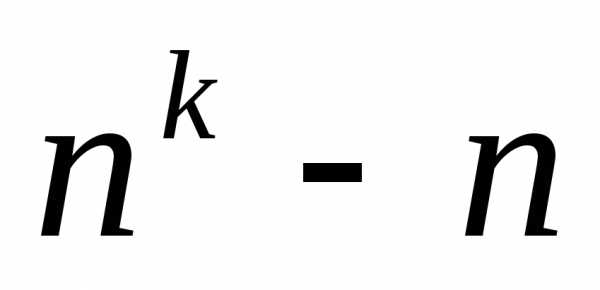 делится наk,
но скоро сам заметил, что
не делится на 9.
делится наk,
но скоро сам заметил, что
не делится на 9.
Рассмотренные примеры позволяют сделать важный вывод: утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще. Вопрос о справедливости утверждения в общем случае удается решить посредством применения особого метода рассуждений, называемого методом математической индукции (полной индукции, совершенной индукции).
6.1. Принцип математической индукции.
♦ В основе метода математической индукции лежит принцип математической индукции, заключающийся в следующем:
1) проверяется справедливость этого утверждения для n=1 (базис индукции),
2) предполагается справедливость этого утверждения для n=k, где k – произвольное натуральное число 1 (предположение индукции), и с учётом этого предположения устанавливается справедливость его для n=k+1.
Доказательство. Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального n. Тогда существует такое натуральное m, что:
1) утверждение для n=m несправедливо,
2) для всякого n, меньшего m, утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо).
Очевидно, что m>1,
т.к. для n=1
утверждение справедливо (условие 1).
Следовательно,  – натуральное число. Выходит, что для
натурального числа
– натуральное число. Выходит, что для
натурального числа утверждение справедливо, а для следующего
натурального числаm оно несправедливо. Это противоречит
условию 2. ■
утверждение справедливо, а для следующего
натурального числаm оно несправедливо. Это противоречит
условию 2. ■
Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.
Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции.
Пример 6.1. Доказать, что при любом натуральном n число делится на 3.
Решение. Воспользуемся методом полной математической индукции.
1) При n=1 , поэтому a1 делится на 3 и утверждение справедливо при n=1.
2) Предположим, что
утверждение справедливо при n=k, 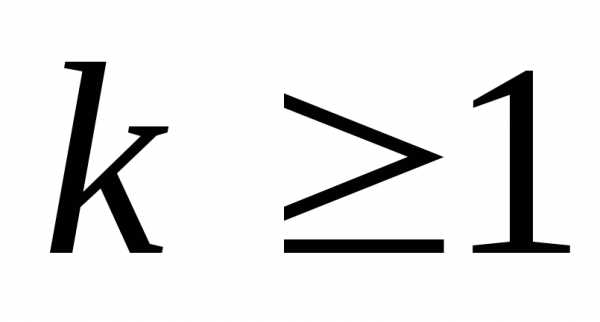 ,
то есть что число делится на 3, и установим, что при n=k+1
число
делится на 3.
,
то есть что число делится на 3, и установим, что при n=k+1
число
делится на 3.
В самом деле,
.
Т.к. каждое слагаемое делится на 3, то их сумма также делится на 3. ■
Пример 6.2. Доказать, что сумма первых n натуральных нечётных чисел равна квадрату их числа, то есть .
Решение. Воспользуемся методом полной математической индукции.
1) Проверяем справедливость данного утверждения при n=1: 1=12 – это верно.
2) Предположим, что
сумма первых k (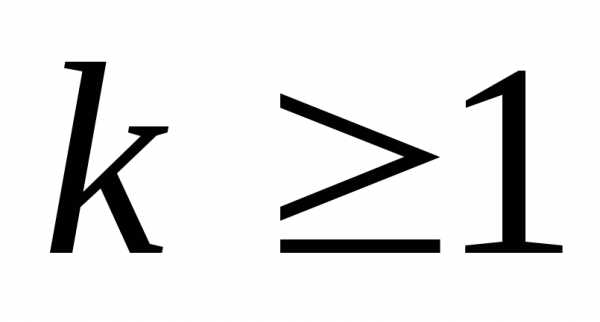 )
нечётных чисел равна квадрату числа
этих чисел, то есть
.
Исходя из этого равенства, установим,
что сумма первых k+1
нечётных чисел равна
)
нечётных чисел равна квадрату числа
этих чисел, то есть
.
Исходя из этого равенства, установим,
что сумма первых k+1
нечётных чисел равна  ,
то есть
.
,
то есть
.
Пользуемся нашим предположением и получаем
. ■
Метод полной математической индукции применяется для доказательства некоторых неравенств. Докажем неравенство Бернулли.
Пример 6.3. Доказать, что при 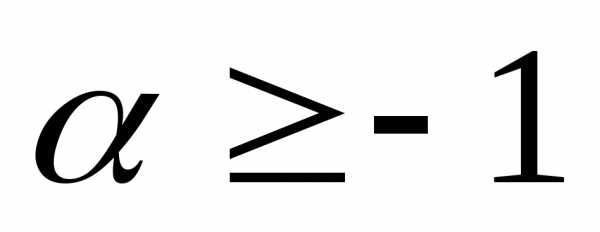 и любом натуральномn справедливо неравенство (неравенство
Бернулли).
и любом натуральномn справедливо неравенство (неравенство
Бернулли).
Решение. 1) При n=1 получаем , что верно.
2) Предполагаем,
что при n=k имеет место неравенство
(*). Используя это предположение, докажем,
что.
Отметим, что при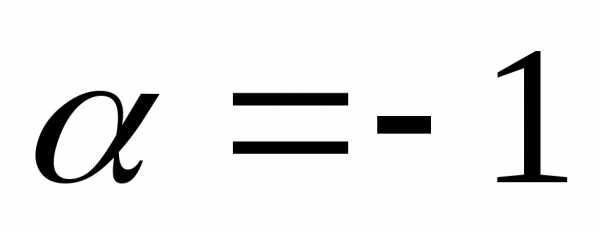 это неравенство выполняется и поэтому
достаточно рассмотреть случай
это неравенство выполняется и поэтому
достаточно рассмотреть случай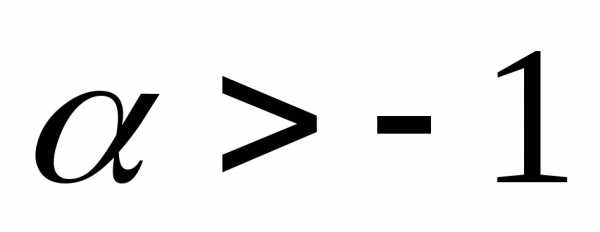 .
.
Умножим обе части
неравенства (*) на число 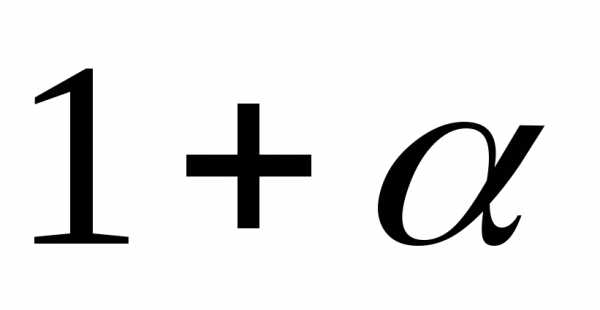 и получим:
и получим:
, то есть (1+.■
Доказательство
методом неполной
математической индукции некоторого утверждения, зависящего от n,
где 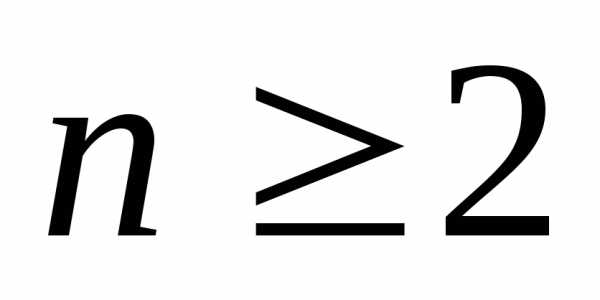 проводится аналогичным образом, но в
начале устанавливается справедливость
для наименьшего значенияn.
проводится аналогичным образом, но в
начале устанавливается справедливость
для наименьшего значенияn.
В некоторых задачах явно не сформулировано утверждение, которое можно доказать методом математической индукции. В таких случаях надо самим установить закономерность и высказать гипотезу о справедливости этой закономерности, а затем методом математической индукции проверить предполагаемую гипотезу.
Пример 6.4. Найти сумму .
Решение. Найдём
суммы S1, S2, S3.
Имеем  ,,.
Высказываем гипотезу, что при любом
натуральномn справедлива формула
,,.
Высказываем гипотезу, что при любом
натуральномn справедлива формула  .
Для проверки этой гипотезы воспользуемся
методом полной математической индукции.
.
Для проверки этой гипотезы воспользуемся
методом полной математической индукции.
1) При n=1
гипотеза верна, т.к. 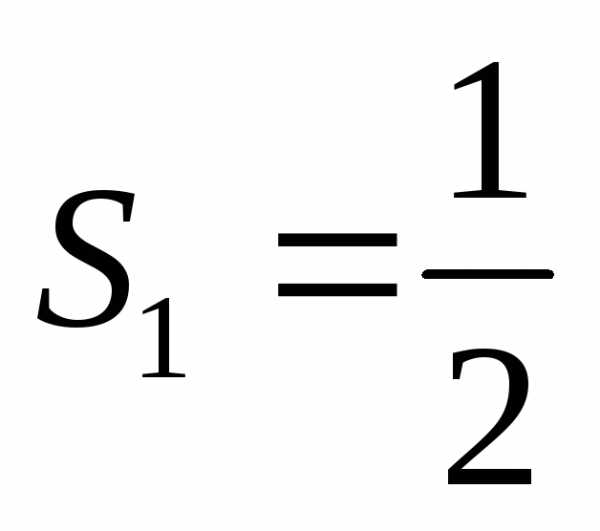 .
.
2) Предположим, что
гипотеза верна при n=k, 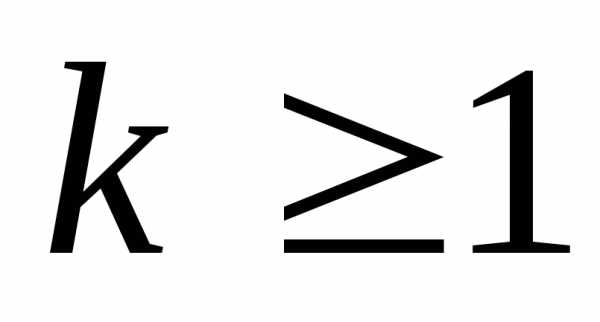 ,
то есть
,
то есть  .
Используя эту формулу, установим, что
гипотеза верна и приn=k+1,
то есть
.
Используя эту формулу, установим, что
гипотеза верна и приn=k+1,
то есть
.
В самом деле,
.
Итак, исходя из
предположения, что гипотеза верна при n=k, 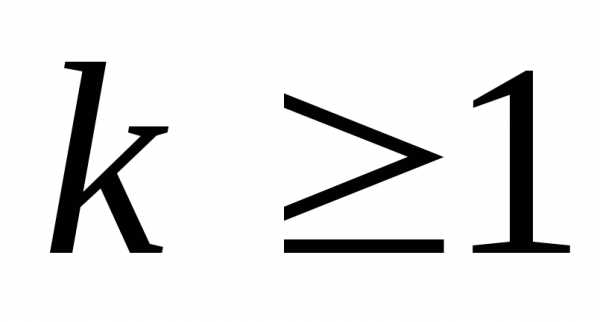 ,
доказано, что она верна и при n=k+1,
и на основании принципа математической
индукции делаем вывод, что формула
справедлива при любом натуральном n.
■
,
доказано, что она верна и при n=k+1,
и на основании принципа математической
индукции делаем вывод, что формула
справедлива при любом натуральном n.
■
Пример 6.5. В математике доказывается, что сумма
двух равномерно непрерывных функций
является равномерно непрерывной
функцией. Опираясь на это утверждение,
нужно доказать, что сумма любого числа  равномерно непрерывных функций является
равномерно непрерывной функцией. Но
поскольку мы ещё не ввели понятие
«равномерно непрерывная функция»,
поставим задачу более абстрактно: пусть
известно, что сумма двух функций,
обладающих некоторым свойством S,
сама обладает свойством S.
Докажем, что сумма любого числа функций
обладает свойством S.
равномерно непрерывных функций является
равномерно непрерывной функцией. Но
поскольку мы ещё не ввели понятие
«равномерно непрерывная функция»,
поставим задачу более абстрактно: пусть
известно, что сумма двух функций,
обладающих некоторым свойством S,
сама обладает свойством S.
Докажем, что сумма любого числа функций
обладает свойством S.
Решение. Базис индукции здесь содержится в самой
формулировке задачи. Сделав предположение
индукции, рассмотрим  функций f1, f2,
…, fn, fn+1,
обладающих свойством S.
Тогда
.
В правой части первое слагаемое обладает
свойствомS по предположению индукции, второе
слагаемое обладает свойством S по условию. Следовательно, их сумма
обладает свойством S – для двух слагаемых «работает» базис
индукции.
функций f1, f2,
…, fn, fn+1,
обладающих свойством S.
Тогда
.
В правой части первое слагаемое обладает
свойствомS по предположению индукции, второе
слагаемое обладает свойством S по условию. Следовательно, их сумма
обладает свойством S – для двух слагаемых «работает» базис
индукции.
Тем самым утверждение доказано и будем использовать его далее. ■
Пример 6.6. Найти все натуральные n, для которых справедливо неравенство
 .
.
Решение. Рассмотрим n=1,
2, 3, 4, 5, 6. Имеем: 21>12,
22=22,
23<32,
24=42,
25>52,
26>62.
Таким образом, можно высказать гипотезу:
неравенство 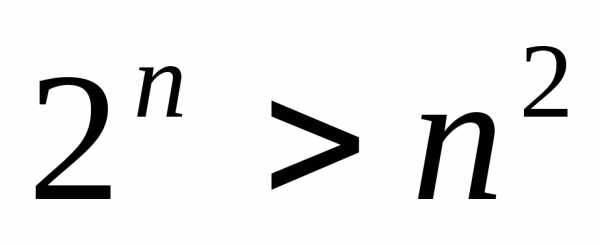 имеет место для каждого
имеет место для каждого  .
Для доказательства истинности этой
гипотезы воспользуемся принципом
неполной математической индукции.
.
Для доказательства истинности этой
гипотезы воспользуемся принципом
неполной математической индукции.
1) Как было установлено выше, данная гипотеза истинна при n=5.
2) Предположим, что
она истинна для n=k,  ,
то есть справедливо неравенство
,
то есть справедливо неравенство  .
Используя это предположение, докажем,
что справедливо неравенство.
.
Используя это предположение, докажем,
что справедливо неравенство.
Т. к.
и при 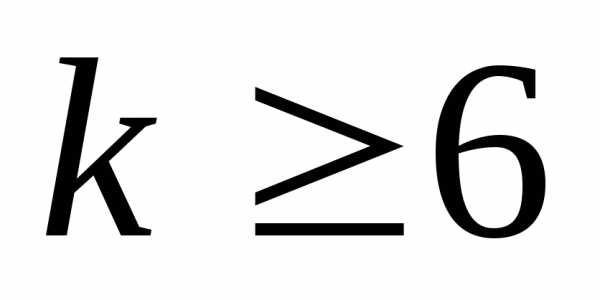 имеет место неравенство
имеет место неравенство
при  ,
,
то получаем, что
.
Итак, истинность гипотезы приn=k+1
следует из предположения, что она верна
при n=k, 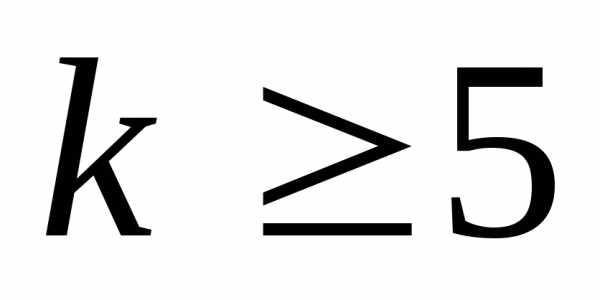 .
.
Из пп. 1 и 2 на
основании принципа неполной математической
индукции следует, что неравенство 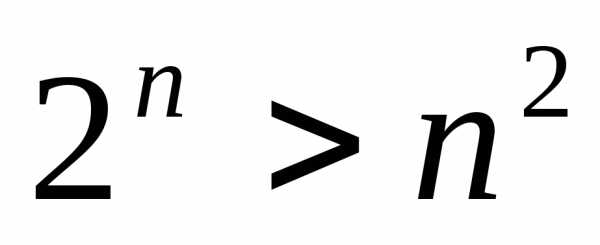 верно при каждом натуральном
верно при каждом натуральном 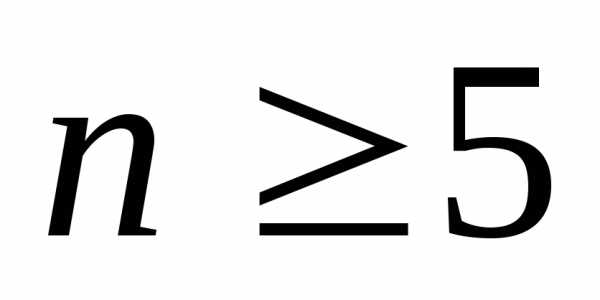 .
■
.
■
Пример 6.7. Доказать, что для любого натурального числа n справедлива формула дифференцирования .
Решение. При n=1
данная формула имеет вид 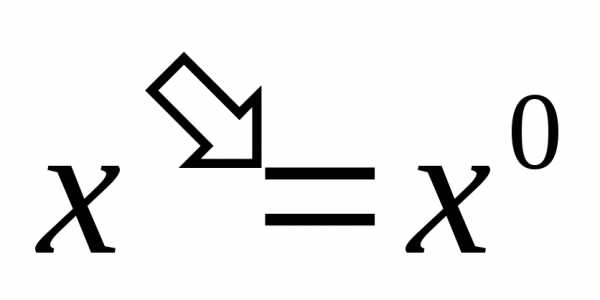 ,
или 1=1, то есть она верна. Сделав
предположение индукции, будем иметь:
,
или 1=1, то есть она верна. Сделав
предположение индукции, будем иметь:
,
что и требовалось доказать. ■
Пример 6.8. Доказать,
что множество, состоящее из n элементов, имеет  подмножеств.
подмножеств.
Решение. Множество, состоящее из одного элемента а, имеет два подмножества. Это верно, поскольку все его подмножества – пустое множество и само это множество, и 21=2.
Предположим, что
всякое множество из n элементов имеет  подмножеств. Если множество А состоит
изn+1
элементов, то фиксируем в нём один
элемент – обозначим его d,
и разобьём все подмножества на два
класса – не содержащие d и содержащие d.
Все подмножества из первого класса
являются подмножествами множества В,
получающегося из А выбрасыванием
элемента d.
подмножеств. Если множество А состоит
изn+1
элементов, то фиксируем в нём один
элемент – обозначим его d,
и разобьём все подмножества на два
класса – не содержащие d и содержащие d.
Все подмножества из первого класса
являются подмножествами множества В,
получающегося из А выбрасыванием
элемента d.
Множество В состоит
из n элементов, и поэтому, по предположению
индукции, у него 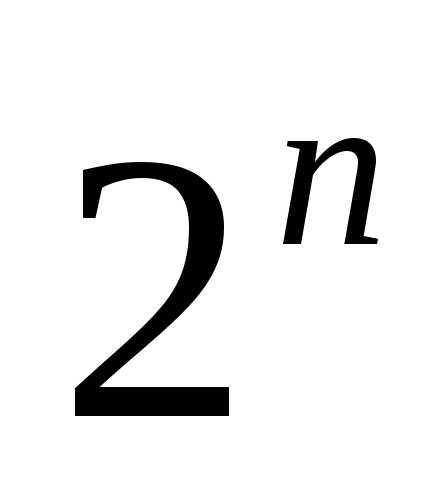 подмножеств, так что в первом классе
подмножеств, так что в первом классе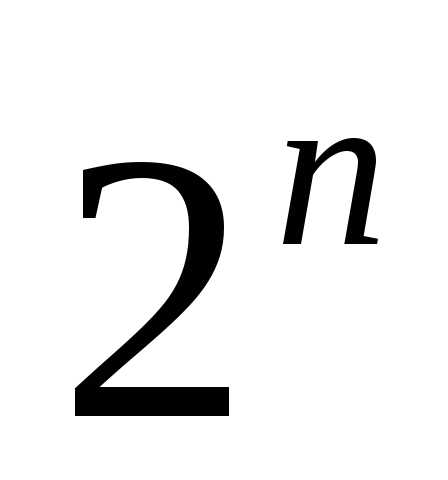 подмножеств.
подмножеств.
Но во втором классе подмножеств столько же: каждое из них получается ровно из одного подмножества первого класса добавлением элемента d. Следовательно, всего у множества А подмножеств.
Тем самым утверждение доказано. Отметим, что оно справедливо и для множества, состоящего из 0 элементов – пустого множества: оно имеет единственное подмножество – самого себя, и 20=1. ■
29
studfiles.net
Метод математической индукции
Во
многих разделах математики приходится
доказывать истинность утверждения,
зависящего от  ,
т.е. истинность высказыванияp(n) для nN
(для любого nN p(n) верно).
,
т.е. истинность высказыванияp(n) для nN
(для любого nN p(n) верно).
Часто это удается доказать методом математической индукции.
В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены два условия:
1. Предложение p(n) истинно для n = 1.
2. Из предложения, что p(n) истинно для n = k (k — произвольное натуральное число) следует, что оно истинно для n = k + 1.
Под методом математической индукции понимают следующий способ доказательства
1. Проверяют истинность утверждения для n = 1 – база индукции.
2. Предполагают, что утверждение верно для n = k – индуктивное предположение.
3. Доказывают, что тогда оно верно и для n = k + 1 индуктивный переход.
Иногда предложение p(n) оказывается верным не для всех натуральных n, а начиная с некоторого для n = n0. В этом случае в базе индукции проверяется истинность p(n) при n = n0.
Пример 1. Пусть . Доказать, что
1.
База индукции: при n = 1 по определению S1 = 1 и по формуле  получаем один результат. Утверждение
верно.
получаем один результат. Утверждение
верно.
2. Индуктивное предположение. Пусть n = k и .
3. Индуктивный переход. Пусть n = k + 1. Докажем, что .
Действительно, в силу индуктивного предположения
Преобразуем это выражение
Индуктивный переход доказан.
Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!
Пример 2. Доказать
.
1. База индукции. При n = 1, утверждение, очевидно, верно.
2. Индуктивное предположение. Пусть n = k и
3. Индуктивный переход. Пусть n = k + 1. Докажем:
Действительно, возведем правую сторону в квадрат как сумму двух чисел:
Используя индуктивное предположение и формулу суммы арифметической прогрессии: , получим
Пример 3. Доказать неравенство
для  .
.
1.
Базой индукции в этом случае является
проверка истинности утверждения для  ,
т.е. необходимо проверить неравенство
,
т.е. необходимо проверить неравенство .
Для этого достаточно возвести неравенство
в квадрат:
.
Для этого достаточно возвести неравенство
в квадрат: или 63 < 64 – неравенство верно.
или 63 < 64 – неравенство верно.
2.
Пусть неравенство верно для  ,
т.е.
,
т.е.
.
3. Пусть , докажем:
.
Используем предположение индукции
Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть
Остается
установить, что лишний множитель 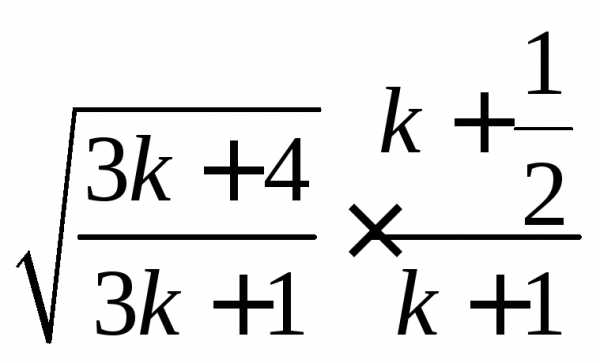 не превосходит единицы. Действительно,
не превосходит единицы. Действительно,
.
Пример
4. Доказать,
что при любом натуральном  число
число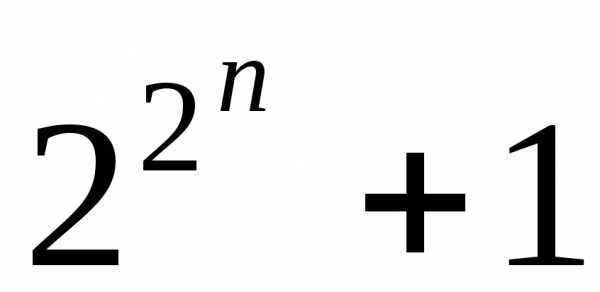 оканчивается цифрой
оканчивается цифрой .
.
1.
Наименьшее натуральное 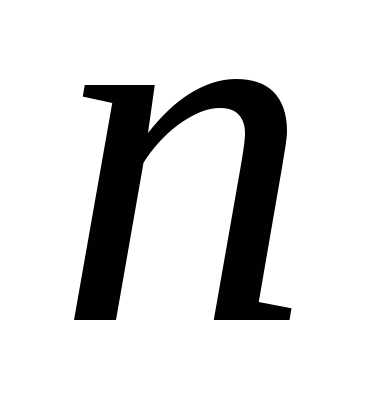 ,
с которого справедливо утверждение,
равно
,
с которого справедливо утверждение,
равно ..
..
2.
Пусть при 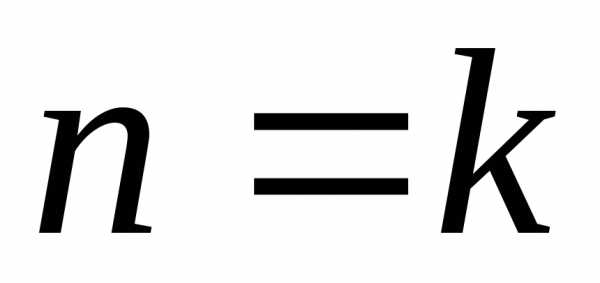 число
число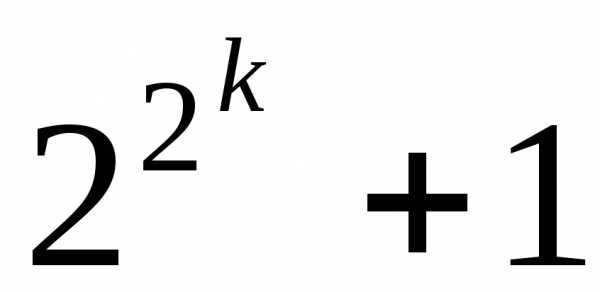 оканчивается на
оканчивается на .
Это означает, что это число можно записать
в виде,
где
.
Это означает, что это число можно записать
в виде,
где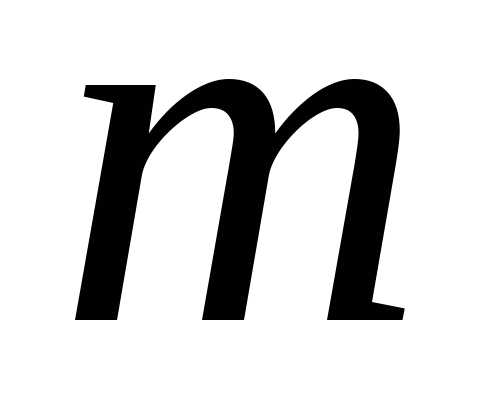 – какое-то натуральное число. Тогда.
– какое-то натуральное число. Тогда.
3.
Пусть
.
Докажем, что оканчивается на
оканчивается на .
Используя полученное представление,
получим
.
Используя полученное представление,
получим
Последнее
число имеет ровно  единиц.
единиц.
Задачи.
1.
Доказать, что при каждом  верны равенства
верны равенства
.
.
.
.
.
.
.
8) .
9) .
10).
2.
Доказать, что при любом  .
.
кратно
 .
. кратно
кратно  .
. кратно
кратно  .
.кратно
 .
.кратно
 .
.кратно 19.
3.
Доказать справедливость следующих
неравенств для всех натуральных 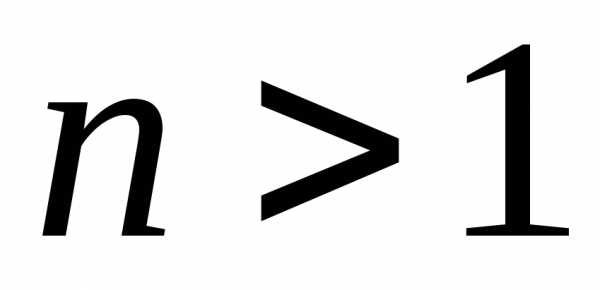 .
.
.
.
.
 .
..
4.
Доказать, что при любом натуральном  верно неравенство
верно неравенство
1) . 2).
5.
Доказать равенство для любого 
,
(в
левой части содержится  корней).
корней).
.
6.
Пусть 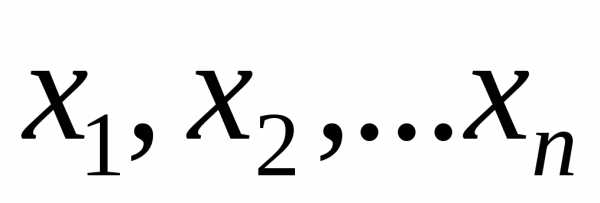 – произвольные неотрицательные числа,
причем
– произвольные неотрицательные числа,
причем
.
Доказать, что .
7. Доказать неравенство Бернулли
,
8.Пусть  – произвольные положительные числа,
причем
– произвольные положительные числа,
причем
. Доказать, что .
studfiles.net

 .
. кратно
кратно  .
. кратно
кратно  .
. .
. .
. .
.