Производные гиперболических функций — КиберПедия
Гиперболические функции встречаются в механике, электротехнике и других технических дисциплинах. Многие формулы для гиперболических функций похожи на формулы для тригонометрических функций, кроме свойства ограниченности.
Формулы для гиперболических функций
1. .
Доказательство. Рассмотрим искомую разность
. Соединяя начало и конец, получим доказываемое равенство: .
2. .
Доказательство. Рассмотрим произведение
. Соединяя начало и конец, получим доказываемое равенство: .
3. .
Доказательство. Рассмотрим произведение
.
Рассмотрим произведение .
Сложим два произведения и приведем подобные:
. Соединяя начало и конец, получим доказываемое равенство: .
Ещё много других свойств гиперболических функций похожих на свойства тригонометрических функций, которые доказываются аналогично.
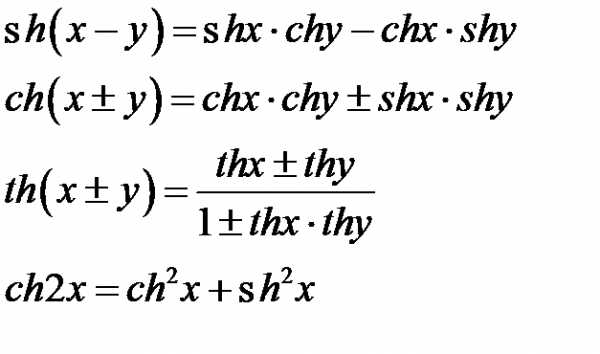
Докажем формулы для производных гиперболических функций.
1. Рассмотрим гиперболический синус .
При нахождении производной константу выносим за знак производной. Далее применяем свойство о производной разности двух функций и . Находим производную функции по таблице производных: . Производную функции ищем как производную сложной функции .
Поэтому, производная .
Соединяя начало и конец, получим доказываемое равенство: .
2. Рассмотрим гиперболический косинус .
Полностью применяем предыдущий алгоритм, только вместо свойства о производной разности двух функций и применяем свойство о производной суммы двух этих функций. .
Соединяя начало и конец, получим доказываемое равенство: .
3. Рассмотрим гиперболический тангенс .
Находим производную по правилу отыскания производной дроби.
.
4. Производную гиперболического котангенса
можно найти как производную сложной функции .
Соединяя начало и конец, получим доказываемое равенство: .
Дифференциал функции
Пусть функция – дифференцируема в точке , тогда её приращение этой функции в точке , соответствующее приращению аргумента , может быть представлено в виде
, (8.1)
где – некоторое число, не зависящее от , а – функция аргумента , которая является бесконечно малой при .
Таким образом, приращение функции представляет собой сумму двух бесконечно малых слагаемых и . Было показано, что второе слагаемое является бесконечно малой функцией более высокого порядка, чем т.е. (см. 8.1). Поэтому первое слагаемое является главной линейной частью приращения функции . В замечании 8.1. получена другая формула (8.1.1) для приращения функции , а именно: . (8.1.1)
Определение 8.3.Дифференциаломфункции в точке называется главная линейная частью её приращения, равная произведению производной в этой точке на произвольное приращение аргумента , и обозначается (или ):
(8.4)
Дифференциал функции называют также дифференциалом первого порядка.
Под дифференциалом независимой переменной понимается любое, независящее от , число. Чаще всего, в качестве этого числа берётся приращение переменной , т.е. . Это согласуется с правилом(8.4) нахождения дифференциала функции
Рассмотрим функцию и найдем её дифференциал.
, т.к. производная . Таким образом, получили: и дифференциал функции можно находить по формуле
. (8.4.1)
Замечание 8.7.Из формулу (8.4.1) следует, что.
Таким образом, запись можно понимать не только как обозначение для производной , но и как отношение дифференциалов зависимого и независимого переменных.
8.7. Геометрический смысл дифференциала функции
Пусть к графику функции проведена (см. рис. 8.1) касательная . Точка находится на графике функции и имеет абсциссу – . Даем произвольное приращение , такое, чтобы точка не вышла из области определения функции .
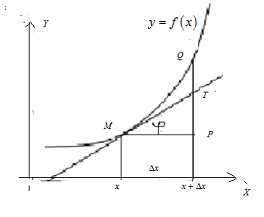
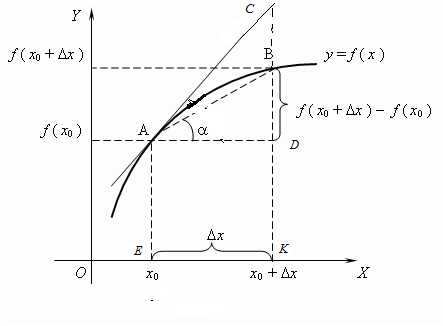
Рисунок 8.1 Изображение графика функции
Точка имеет координаты . Отрезок . Точка лежит на касательной к графику функции и имеет абсциссу – . Из прямоугольного следует, что , где угол – угол между положительным направлением оси и касательной, проведенной к графику функции в точке . По определению дифференциала функции и геометрического смысла производной функции в точке , делаем вывод, что . Таким образом, геометрический смысл дифференциала функции заключается в том, что дифференциал представляет собойприращение ординаты касательной к графику функции в точке .
Замечание 8.8.
На рисунке 8.1точка лежит на графике функции и имеет координаты . Отрезок .
На рисунке 8.1 выполнено неравенство , т.е. . Но возможны случаи, когда справедливо противоположное неравенство . Это выполняется для линейной функции и для выпуклой вверх функции.
cyberpedia.su
Найти производную y’ = f'(x) = sinh(sinh(sinh(x))) (гиперболический синус от (гиперболический синус от (гиперболический синус от (х))))
Решение
$$\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )}$$
Первая производная[LaTeX]
cosh(x)*cosh(sinh(x))*cosh(sinh(sinh(x)))
$$\cosh{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )}$$
Вторая производная[LaTeX]
2 2 2 cosh (x)*cosh (sinh(x))*sinh(sinh(sinh(x))) + cosh (x)*cosh(sinh(sinh(x)))*sinh(sinh(x)) + cosh(sinh(x))*cosh(sinh(sinh(x)))*sinh(x)
$$\sinh{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + \sinh{\left (\sinh{\left (x \right )} \right )} \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh^{2}{\left (\sinh{\left (x \right )} \right )}$$
Третья производная[LaTeX]
/ 2 3 2 2 2 \ \cosh(sinh(x))*cosh(sinh(sinh(x))) + cosh (x)*cosh (sinh(x))*cosh(sinh(sinh(x))) + cosh (x)*cosh(sinh(x))*cosh(sinh(sinh(x))) + 3*cosh (sinh(x))*sinh(x)*sinh(sinh(sinh(x))) + 3*cosh(sinh(sinh(x)))*sinh(x)*sinh(sinh(x)) + 3*cosh (x)*cosh(sinh(x))*sinh(sinh(x))*sinh(sinh(sinh(x)))/*cosh(x)
$$\left(3 \sinh{\left (x \right )} \sinh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + 3 \sinh{\left (x \right )} \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh^{2}{\left (\sinh{\left (x \right )} \right )} + 3 \sinh{\left (\sinh{\left (x \right )} \right )} \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} + \cosh^{2}{\left (x \right )} \cosh^{3}{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )}\right) \cosh{\left (x \right )}$$
www.kontrolnaya-rabota.ru
Найти производную y’ = f'(x) = sinh(sinh(sinh(sinh(x)))) (гиперболический синус от (гиперболический синус от (гиперболический синус от (гиперболический синус от (х)))))
Решение
sinh(sinh(sinh(sinh(x))))
$$\sinh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )}$$
Первая производная[LaTeX]
cosh(x)*cosh(sinh(x))*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x))))
$$\cosh{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )}$$
Вторая производная[LaTeX]
2 2 2 2 2 2 cosh (x)*cosh (sinh(x))*cosh (sinh(sinh(x)))*sinh(sinh(sinh(sinh(x)))) + cosh (x)*cosh (sinh(x))*cosh(sinh(sinh(sinh(x))))*sinh(sinh(sinh(x))) + cosh (x)*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x))))*sinh(sinh(x)) + cosh(sinh(x))*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x))))*sinh(x)
$$\sinh{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + \sinh{\left (\sinh{\left (x \right )} \right )} \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh^{2}{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + \sinh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh^{2}{\left (\sinh{\left (x \right )} \right )} \cosh^{2}{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )}$$
Третья производная[LaTeX]
/ 2 3 3 2 3 2 2 2 2 2 3 2 2 2 \ \cosh(sinh(x))*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x)))) + cosh (x)*cosh (sinh(x))*cosh (sinh(sinh(x)))*cosh(sinh(sinh(sinh(x)))) + cosh (x)*cosh (sinh(x))*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x)))) + cosh (x)*cosh(sinh(x))*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x)))) + 3*cosh (sinh(x))*cosh (sinh(sinh(x)))*sinh(x)*sinh(sinh(sinh(sinh(x)))) + 3*cosh (sinh(x))*cosh(sinh(sinh(sinh(x))))*sinh(x)*sinh(sinh(sinh(x))) + 3*cosh(sinh(sinh(x)))*cosh(sinh(sinh(sinh(x))))*sinh(x)*sinh(sinh(x)) + 3*cosh (x)*cosh (sinh(x))*cosh(sinh(sinh(x)))*sinh(sinh(sinh(x)))*sinh(sinh(sinh(sinh(x)))) + 3*cosh (x)*cosh (sinh(sinh(x)))*cosh(sinh(x))*sinh(sinh(x))*sinh(sinh(sinh(sinh(x)))) + 3*cosh (x)*cosh(sinh(x))*cosh(sinh(sinh(sinh(x))))*sinh(sinh(x))*sinh(sinh(sinh(x)))/*cosh(x)
$$\left(3 \sinh{\left (x \right )} \sinh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + 3 \sinh{\left (x \right )} \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh^{2}{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + 3 \sinh{\left (x \right )} \sinh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} \cosh^{2}{\left (\sinh{\left (x \right )} \right )} \cosh^{2}{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + 3 \sinh{\left (\sinh{\left (x \right )} \right )} \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + 3 \sinh{\left (\sinh{\left (x \right )} \right )} \sinh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh^{2}{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + 3 \sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \sinh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} \cosh^{2}{\left (x \right )} \cosh^{3}{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} + \cosh^{2}{\left (x \right )} \cosh^{3}{\left (\sinh{\left (x \right )} \right )} \cosh^{3}{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + \cosh^{2}{\left (x \right )} \cosh^{3}{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + \cosh^{2}{\left (x \right )} \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )} + \cosh{\left (\sinh{\left (x \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \cosh{\left (\sinh{\left (\sinh{\left (\sinh{\left (x \right )} \right )} \right )} \right )}\right) \cosh{\left (x \right )}$$
www.kontrolnaya-rabota.ru
Таблица первообразных
Таблица первообразных («интегралов»). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
Таблица первообразных («интегралов»). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). | |
Интеграл степенной функции. | Интеграл степенной функции. |
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
|
Интеграл экспоненциальной функции. | Интеграл экспоненты, где a-постоянное число. |
Интеграл сложной экспоненциальной функции. | Интеграл экспоненциальной функции. |
|
|
Интеграл, равняющийся натуральному логорифму. |
Интеграл : «Длинный логарифм». |
|
Интеграл : «Длинный логарифм». |
Интеграл : «Высокий логарифм». | Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму. |
Интеграл : «Высокий логарифм». |
|
|
|
Интеграл косинуса. | Интеграл синуса. |
Интеграл, равный тангенсу. | Интеграл, равный котангенсу. |
|
|
Интеграл, равный как арксинусу, так и арккосинусу | Интеграл, равный как арктангенсу, так и арккотангенсу. |
Интеграл, равный как арксинусу, так и арккосинусу. | Интеграл, равный как арктангенсу, так и арккотангенсу. |
| |
Интеграл равный косекансу. |
Интеграл, равный секансу. |
Интеграл, равный арксекансу. | Интеграл, равный арккосекансу. |
Интеграл, равный арксекансу. | Интеграл, равный арксекансу. |
|
|
Интеграл, равный гиперболическому синусу. | Интеграл, равный гиперболическому косинусу. |
Интеграл, равный гиперболическому тангенсу. | Интеграл, равный гиперболическому котангенсу. |
Интеграл, равный гиперболическому синусу, где sinhx — гиперболический синус в ангийской версии. | Интеграл, равный гиперболическому косинусу, где sinhx — гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому тангенсу. | Интеграл, равный гиперболическому котангенсу. |
Интеграл, равный гиперболическому секансу. | Интеграл, равный гиперболическому косекансу. |
Формулы интегрирования по частям. Правила интегрирования.
Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования. | |
Интегрирование произведения (функции) на постоянную: | |
Интегрирование суммы функций: | |
Формула интегрирования по частям неопределенные интегралы: |
|
Формула интегрирования по частям определенные интегралы: |
|
Формула Ньютона-Лейбница определенные интегралы: | Где F(a),F(b)-значения первообразных в точках b и a соответственно. |
Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
Если x — независимая переменная, то:
Таблица производных. Табличные производные.»таблица производный»-да, к сожалению, именно так их и ищут в интернете | |
Производная степенной функции | Производная степенной функции |
| |
Производная экспоненциальной функции | Производная экспоненты |
Производная сложной экспоненциальной функции | Производная экспоненциальной функции |
| |
Производная логарифмической функции | Производная натурального логарифма |
| Производная натурального логарифма функции |
| |
Производная синуса | Производная косинуса |
Производная косеканса | Производная секанса |
Производная арксинуса | Производная арккосинуса |
Производная арксинуса |
Производная арккосинуса |
Производная тангенса | Производная котангенса |
Производная арктангенса | Производная арккотангенса |
Производная арктангенса | Производная арккотангенса |
Производная арксеканса | Производная арккосеканса |
Производная арксеканса | Производная арккосеканса |
| |
Производная гиперболического синуса Производная гиперболического синуса в английской версии | Производная гиперболического косинуса Производная гиперболического косинуса в английской версии |
Производная гиперболического тангенса | Производная гиперболического котангенса |
Производная гиперболического секанса | Производная гиперболического косеканса |
Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции. | |
Производная произведения (функции) на постоянную: | |
Производная суммы (функций): | |
Производная произведения (функций): | |
Производная частного (функций): |
|
Производная сложной функции: |
|
Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
Основное логарифмическое тождество | |
Покажем как можно любую функцию вида a b сделать экспоненциальной. Поскольку функция вида ех называется экспоненциальной, то | |
Любая функция вида a b может быть представлена в виде степени десяти |
Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045… ) ln(e)=1; ln(1)=0
При | логарифм числа (1+х) разлагается в ряд: | |
Например, | ||
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1), где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена( =Макларена, Тейлора в окрестностях точки 0)
Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
studfiles.net
Онлайн калькулятор: Обратные гиперболические функции
Гиперболические функции уже есть, теперь для общности и обратные гиперболические функции. А там, глядишь, и до решения кубических уравнений дойдем.
Итак, калькулятор ниже, описание обратных гиперболических функций — под ним.
Знаков после запятой: 2
Сохранить share extension
Обратный гиперболический синус, гиперболический арксинус, ареасинус:
Функция нечетная, строго возрастает. Определена для всей числовой оси. Область значений — вся числовая ось.
Обратный гиперболический косинус, гиперболический арккосинус, ареакосинус
Функция строго возрастает. Определена для интервала от единицы включительно до плюс бесконечности. Область значений — от нуля до плюс бесконечности.
Обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс:
Функция нечетная, строго возрастает. Определена для интервала от минус единицы до плюс единицы исключительно. Область значений — вся числовая ось.
Обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс:
Функция нечетная, строго убывает на интервалах от минус бесконечности до минус единицы исключительно и от единицы исключительно до плюс бесконечности.
Обратный гиперболический секанс, гиперболический арксеканс, ареасеканс:
Функция строго убывает на интервале от нуля до единицы включительно. Функция многозначная, то есть каждому аргументу соответствует два результата — положительный и отрицательный.
Обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс:
Функция нечетная, строго убывает на интервалах от минус бесконечности до нуля и от нуля до плюс бесконечности.
planetcalc.ru
