Координатная плоскость | Matemsha
В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.
Координаты могут обозначаться самыми разными наборами цифр или букв.
Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.
Координаты— это набор данных, по которому определяется положение того или иного объекта.
Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.
Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.
Декартова система координат
Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.
Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.
- На плоскости такими ориентирами будут служить две числовые оси. На чертеже обычно первую ось рисуют горизонтально, её называют осью АБСЦИССи обозначают буквой «X», записывают ось «Ox». Положительное направление на оси абсцисс выбираютслева направои показывают стрелкой.
- Вторую ось проводят вертикально, её называютосью ОРДИНАТи обозначают буквой «Y», записывают ось «Oy». Положительное направление на оси ординат выбираютснизу вверхи показывают стрелкой.
Оси взаимно перпендикулярны (т.е. угол между ними равен 90°) и пересекаются в точке, которую обозначают «O». Точка «O» является началом отсчёта для каждой из осей.

Запомните
Система координат— это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс«Ox» — горизонтальная ось.
Ось ординат«Oy» — вертикальная ось.
Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как «x0y».
Обращаем ваше внимание на выбор длины единичных отрезков по осям.
Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси «Oy». Цифры на оси «Ox», как правило, пишут внизу под осью.
Обычно единичный отрезок на оси «0y» равен единичному отрезку на оси «0x». Но бывают случаи, когда они не равны друг другу.
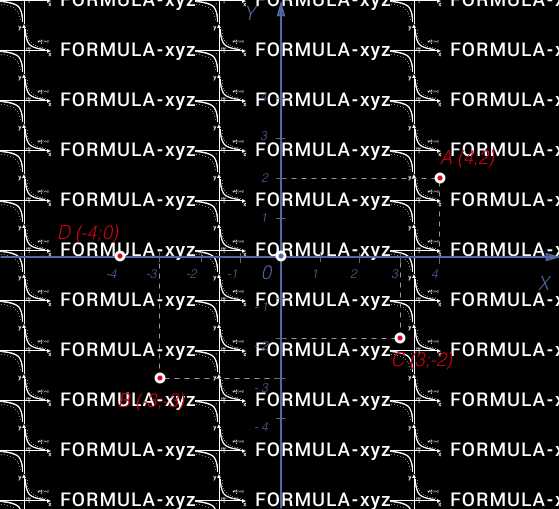
Оси координат делят плоскость на 4угла, которые называют координатными четвертями. Четверть, образованная положительными полуосями (правый верхний угол), считают первой I.
Отсчитываем четверти (или координатные углы) против часовой стрелки.

matemsha.ru
Координатные четверти | Алгебра
Выясним, как в тригонометрии координатные четверти связаны с градусной и радианной мерой углов.
Тригонометрические углы получают в результате поворота луча OP0 вокруг точки O. Поэтому точка P0 соответствует углу 0°.
При положительном направлении обхода поворот луча происходит по часовой стрелке. Градусная мера всей окружности равна 360°. Каждая из четвертей занимает угол в 90°.
Таким образом,
I координатной четверти соответствуют углы от 0° до 90°,
II — от 90° до 180°,
III — от 180° до 270°,
IV — от 270° до 360°.
Переводя градусную меру в радианную, получим аналогичное разбиение окружности по координатным четвертям в радианах:
Углы 0°, 90°, 180°,270°, 360° не принадлежат ни одной из координатных четвертей.
Отрицательные значения углов получают поворотом луча против часовой стрелки. Соответственно, иллюстрация разбиения по координатным четвертям в этом случае выглядит так:
Примеры.
Определить, углом какой четверти является угол:
а) 47°; -24°; 300°; 185°; -203°;1200°;
Решение:
а) 47° — угол I координатной четверти, так как 0°<47°<90°;
-24° — угол IV координатной четверти, так как -90°<-24°<0°;
300° — угол IV координатной четверти, так как 270°<300°<360°;
185° лежит в III координатной четверти, так как 180°<185°<270°;
-203° лежит во II координатной четверти, так как
-180°<-203°<-270°;
1200°=120°+360°·3.
120° — угол II координатной четверти, поскольку 90°<120°<180°. Значит, 1200° также является углом II четверти.
b) π/5 — угол I координатной четверти, так как
7π/6 — угол II координатной четверти, так как
Сравнение радианной меры угла с 0, π/2, π, 3π/2 и 2π иногда вызывает затруднения. В этом случае можно перевести радианную меру в градусную.
Другой способ: если дробь неправильная, можно найти ближайшее к коэффициенту перед π в числителе число, которое делится нацело на знаменатель, и представить числитель как сумму (или разность) этого целого числа и остатка.
Очевидно, что 7π/6>π. Поскольку π/6 — острый угол, то π/6<π/2. Следовательно, 7π/6<3π/2.
откуда 13π/8 — угол IV координатной четверти.
значит — 9 π/5 — угол I четверти.
Следовательно, 19π/4 — угол II четверти.
www.algebraclass.ru
№ урока 142-143 Дата: 09.03.2017 | Класс: 6 | Предмет: математика | Учитель: Олейник Т.А. | |
Тема | Координатная плоскость. Прямоугольная система координат. Построение точки по ее координатам | |||
Общие цели | Обучающие- контроль и оценка знаний, умений и навыков, связанных с координатной плоскостью, прямоугольной системой координат, построением точки по ее координатам. Развивающие – развивать внимание, зрительную память, логическое мышление, математическую речь, смекалку, умение самооценивать и анализировать свои ошибки; | |||
Результаты обучения: | Ученики будут знать: -прямоугольную систему координат; -координатную плоскость; -абциссу и ординату. Ученики должны уметь: -найти абциссу и ординату точки; -записать точку с ее абциссой и ординатой; -построить точку с заданной абциссой и ординатой. | |||
Источники, оснащение и оборудование | Учебник «Математика» 6 класс, Алматы «Атамура» 2015 | |||
Модули | Модули критического мышления, лидерства и управления, ИКТ, формативное и суммативное оценивание. | |||
Ход урока | Деятельность учителя | Деятельность учащихся | ||
Организационный момент | Подготовка учащихся к работе на уроке. | Подготовка к уроку. | ||
Определение темы, цели и задач урока | Постановка целей и задач урока. | Слушают учителя. | ||
Проверка домашнего задания | Установление правильности и осознанности выполнения домашнего задания всеми учащимися, выявление пробелов и их коррекция. | Вопросы по выполнению задания. | ||
Актуализация знаний Мозговой штурм | Какие прямые являются пересекающимися? Сколько общих точек имеют пересекающиеся прямые? Какие прямые являются перпендикулярными ? Чему равно расстояние от заданной точки до прямой ? | Учащиеся отвечают на вопросы. | ||
Изучение новой темы | Состоит из двух перпендикулярных координатных осей, пересекающихся в Ось абсцисс — горизонтальная ось, обозначается OX или X. Ось ординат — вертикальная ось OY или Y. Координатная плоскость — плоскость, на которой построена система координат. Координатная четверть (квадрант) — каждая из четырех частей, на которые оси OX и OY делят координатную плоскость.
Координаты точки М — пара чисел (x, y). Первое число x — координата основания перпендикуляра, опущенного из точки M на ось OX; второе число y — на ось OY.
Записывают M (x;y). Где x — абсцисса точки M, y — ордината точки M.
| Записывают примеры с доски. | ||
Физ. минутка | Ну-ка делайте со мною | Выполняют упражнения под стихи. | ||
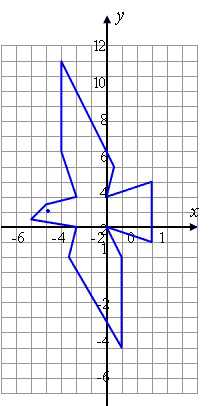
Закрепление пройденного материала | Диагностика усвоения знаний и умений учащихся А теперь перейдем к построению фигуры с помощью точек на координатной плоскости.Даны координаты точек. Построить фигуру, соединяя, по мере построения, соседние точки друг с другом. 1) (-3; 10),2) (-3; 5), 3) (-2; 2), 4) (-4; 1,5), 5) (-5; 0,5), 6) (-2; 0), 7) (-2,5; -2), 8) (1; -8), 9) (1; -2), 10) (0; 0), 11) (3; -1), 12) (3; 3), 13) (0; 2), 14) (0,5; 4), 15) (-3; 10). Глаз: (-4;1) |
| ||
infourok.ru
Урок по математике «Координатная плоскость»
Технологическая карта урока математики
Тема: Координатная плоскость
Дидактическая цель: создать условия для обобщения и систематизации материала по теме «Координатная плоскость»
Тип урока: урок обобщения и систематизации знаний учащихся
Цели по содержанию урока:
Образовательные:
Обобщить и систематизировать знания учащихся по теме «Координатная плоскость»
Проверить умения и навыки учащихся по теме «Координатная плоскость»
Развивающие:
Развивать мышление, внимание, память учащихся,
Развивать навыки работать в группе и самостоятельно
Развивать навыки работы на компьютере
Воспитательные:
Прививать интерес к предмету через применение информационно-коммуникационных технологий
Воспитывать бережное отношение к учебе
Формы организации познавательной деятельности: фронтальная, парная, индивидуальная
Методы урока: частично-поисковый, практический
Средства обучения: рабочая тетрадь, презентация для интерактивной доски, тесты
Оборудование: проектор, интерактивная доска, ноутбуки
Этап урока
Деятельность учителя
Деятельность ученика1. Организационный момент
Проверка готовности к уроку, приветственное слово.
Тренинг «Улыбка друг другу», пожелание успехов в работе.
Объяснение работы в тетради, оценивания
Проверяют готовность к работе.
Участвуют в тренинге, желают успехов работе.
Слушают и запоминают.
2. Актуализация знаний
Вопросы:
1. Внимательно рассмотрите объекты на экране. Скажите, что объединяет эти объекты?
2. Назовите математика, изображенного на экране?
3. Чем знаменит этот математика?
4. Сформулируйте тему нашего урока.
5. Скажите, чем на уроке мы будем заниматься?
Рассматривают, отвечают на вопросы.
Координаты, координатная плоскость
Рене Декарт
Автор понятия «координатная плоскость», иначе «декартова система координат»
«Координатная плоскость»
Решать задачи по теме «Координатная плоскость»
3. Закрепление
Задание на закрепление и проверку знаний.
Задание 1. «Элементы координатной плоскости». Вставьте пропущенные слова.
Задание 2. «Алгоритм определения координат точек». Определите координаты точек.
Задание 3. «Расположение точек по четвертям (координатным углам)». Распределение точек по координатным углам
Самостоятельная работа. Самопроверка
Самостоятельно в рабочих тетрадях, 2 ученика у доски. Самопроверка и фронтальная проверка.
Самостоятельно в рабочих тетрадях, 2 ученика у доски. Самопроверка и фронтальная проверка.
4. Применение знаний
Организация работы на компьютере.
Тренажёр «Рисуем по координатам»
Работа в парах, каждой группе индивидуальный рисунок. Самооценка работы в группе.
5. Физминутка
Организация проведения физминуток.
Физминутка для глаз (стенд)
Физминутка динамическая («елочка»)
Выполнение упражнений.
6. Контроль
Тест «Координатная плоскость)
Выполнение теста, взаимопроверка, оценивание
Итог урока
10 – 12 баллов — оценка «5»
7 – 9 баллов — оценка «4»
5-6 баллов – оценка «3»
0-4 баллов — «Старайся, лучше!»
Подсчитывание итога в баллах, и выставление оценки
Домашнее задание
Задание дифференцированное:
Нарисовать рисунок на координатной плоскости, используя:
10 точек
15 точек
20 точек
Выбор оптимального задания, фиксирование в дневник.
Рефлексия
Задание:
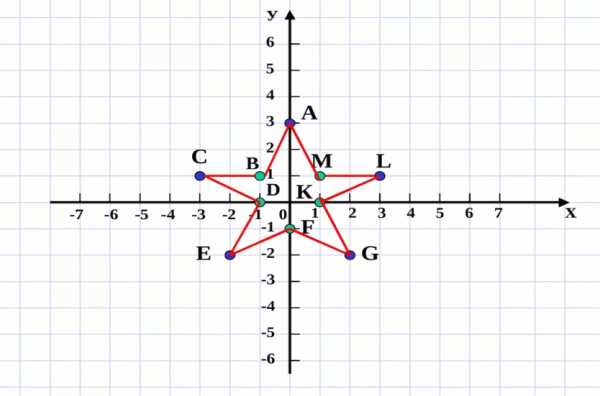
Расположите свою звезду в соответствующую четверть:
I – «У меня все получилось»
II – «Получилось, но не все»
III – «Я не старался и не хотел работать»
IV – «Я старался, но результат средний»
Самооценка своей работы на уроке, расположение звезд на плоскости на доске.
infourok.ru
Координатная плоскость, 6 класс
Координатная плоскость.
Цели урока:
I.Развивающая:
-развитие навыков работы с системой координат,
-развитие графической культуры учащихся, математической речи учащихся
-развитие смекалки, творческих способностей
-расширение кругозора.
II.Воспитывающая:
-воспитание познавательной активности, аккуратности, обдуманности;
-формирование навыков самоконтроля и взаимоконтроля
-повышение интереса к предмету
III.Обучающая:
-ознакомление с прямоугольной системой координат на плоскости
-активизация мыслительной деятельности;
-свободное оперирование координатами точек
Ход урока
Организация начала занятия.
Проверка дом. задания.
Новая тема.
— В речи взрослых вы могли слышать такую фразу: «Оставьте мне ваши координаты». Это выражение означает, что ваш собеседник должен оставить свой адрес или номер телефона, которые и считаются координатами человека. Главное здесь в том, что по этим данным человека можно найти.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило по которому определяется положение того или иного объекта.
— Системы координат пронизывают всю практическую жизнь человека.
Зрительный зал.
Шахматы
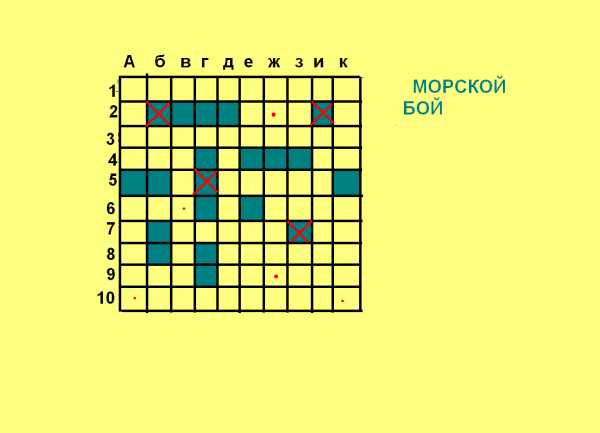
Игра «Морской бой».

Географические координаты.
Тема урока «Координатная плоскость».
(записываем в тетрадях дату, тему)
Цель нашего урока: научиться отмечать точки на плоскости по их координатам и по данным точкам на плоскости определять их координаты.
Итак, мы отправляемся в путь. Но сначала проверим, готовы ли вы к испытаниям.
1. На пути нам встретилась речка, через которую перекинут мост. Но перейти по нему можно лишь в том случае, если на дорожном указателе все записи верны. Ребята, как вы думаете, сможем перейти через мост?
-Какие прямые называют параллельными?
-Какие прямые называются перпендикулярными?
—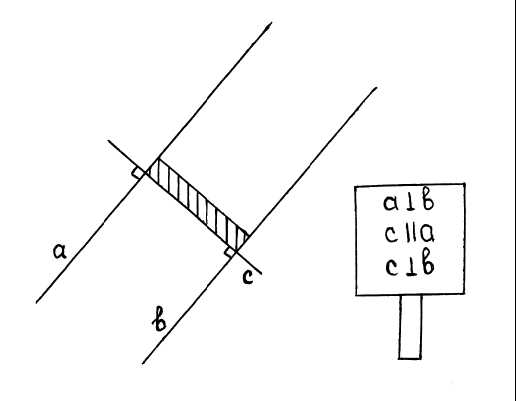
С помощью каких чертежных инструментов строят перпендикулярные прямые?
(исправляют записи и записывают на доске)
2. –Что такое координатная прямая?
-Что называют координатами точки на прямой?
-Какими числами являются координаты точек на горизонтальной прямой, расположенных справа от начала координат, слева от начала координат?
Какими числами обозначают координаты точек на вертикальной прямой, расположенных выше начала координат, ниже начала координат?
-Какую координату имеет эта точка?
(указкой показываю на точки, расположенные на координатной прямой, дети говорят координату этой точки)
Молодцы! Теперь мы с вами можем идти дальше.
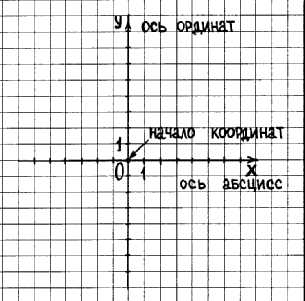
3. Проведем две перпендикулярные координатные прямые х и у с равными единичными отрезками, которые пересекаются в начале отсчета- точке О.
(проектирую, рассказываю детям, хором читаем название осей. Предлагаю построить систему координат у себя в тетради, я в это время записываю на доске: ось Ох- ось абсцисс, ось Оу — ось ординат)
Ось абсцисс и ось ординат вместе образуют систему координат на плоскости.
Точка О — начало координат.
Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Построенная нами система координат называется прямоугольной или декартовой системой координат.
В XIV веке французский математик Никола Оресм ввел по аналогии с географическими координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широту и долготу ординатой и абсциссой. Это нововведение оказалось чрезвычайно удачным. На его основе возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании этого метода принадлежит великому французскому математику Рене Декарту (1596-1650). В его честь такая система координат называется декартовой.
-Какие еще способы указания места, основанные на этой системе, вы знаете?
(На этой системе основаны многие способы указания места. Например, билет в театре — ряд и место, шахматы — буква и число; игра «Морской бой» — буква и число и др. )
П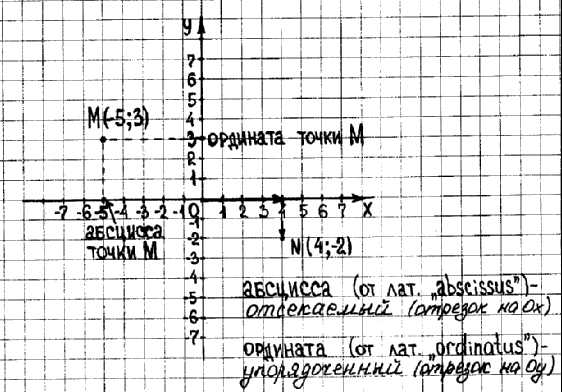
оложение точки М определяется парой чисел (-5;3)
Эту пару чисел называют координатами точки М
Число –5 называют абсциссой,
Число 3-ординатой точки М.
При записи координат точки необходимо соблюдать следующий порядок:
абсцисса всегда пишется на первом месте, а ордината – на втором.
(Абсцисса — от лат. «abscissus» — отсекаемый (отрезок на оси х).
Ордината — от лат. «ordinatus» — упорядоченный (отрезок на оси у). )
Запись М(-5;3) можно прочитать так: точка эм с абсциссой –5 и ординатой 3.
Откройте учебник на стр.245, прочитаем другие варианты чтения этой записи.
-На сколько частей разбивают плоскость оси координат?
Полученные части называют координатными четвертями.
(на доске ставим знаки координат точек, расположенных в каждой из четвертей)
(Рассмотрим координатную плоскость на окружающей местности).
-Где еще могут лежать точки?
-Как вы думаете, чему равна ордината точки, лежащей на оси абсцисс (точка В)?
—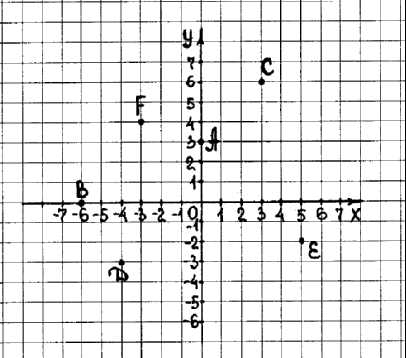
Как вы думаете, чему равна абсцисса точки, лежащей на оси ординат (точка А)?
IV. Закрепление нового материала.
А) Игра math (строим точки на плоскости по координатам, при проверке получается «рыба»)
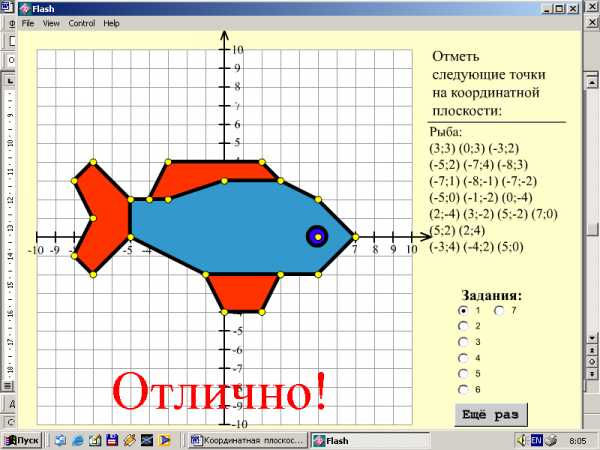
Б) Программа «Координатная плоскость»
V. Подведение итогов урока.
VI. Домашнее задание: изучить п.45; решить №1417, №1418, №1421(а).
infourok.ru
Координатная плоскость
В повседневной жизни вы могли слышать такую фразу: «Оставьте мне ваши координаты!».
Как вы понимаете эту фразу?
Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, т.е. данные, по которым его можно найти.
Определение
Числа, с помощью которых указывают, где находится некоторый объект, называют его координатами.
С координатами вы уже не раз встречались и в математике. Вы умеете выполнять две операции: отмечать на координатной прямой точку с заданной координатой и, наоборот, определять координату заданной точки. Для этого на прямой выбирают начало отсчёта, положительное направление и единичный отрезок. После этого любая точка прямой получает свою собственную координату.
Координата точки указывает, таким образом, её место на координатной прямой.
Возникает вопрос: а можно ли определить местоположение точки на плоскости?
Наверняка, хоть раз в жизни вы играли в такую игру как «Морской бой».
Поле этой игры состоит из квадрата размерами 10 на 10 клеточек. В этом поле изображаются корабли: 1 четырёхклеточный, 2 трёхклеточных, 3 двухклеточных и 4 одноклеточных. При этом между любыми двумя соседними кораблями должен оставаться промежуток не меньше одной клетки.
На экране изображён один из вариантов расположения кораблей. Каждая клеточка квадрата обозначается парой: (буква –число), указанных вдоль нижней и левой сторон квадрата. Например, корабль расположен в клетке (Ж; 4). Суть этой игры найти все корабли соперника первым. При обозначении положения клетки первой указывают её горизонтальную координату, а второй – вертикальную.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.
Системы координат встречаются в нашей жизни постоянно.
Вы знакомы с системой координат в зрительном зале кинотеатра (номер ряда и номер места), в поезде (номер вагона и номер места), с системой географических координат (долгота и широта).
Что нужно знать для того, чтобы найти своё место в кинотеатре? Места в зрительном зале кинотеатра задают двумя числами: первым числом обозначают номер ряда, а вторым – номер кресла в этом ряду. Значит, чтобы правильно занять своё место в зрительном зале необходимо знать две координаты: ряд и место.
Например, в билете указаны: 3 ряд 2 место. Посмотрите где это место расположено.
Обратите внимание, что при определении местоположения нам необходимо знать две характеристики или два значения.
Подобным образом можно обозначить и положение точки на плоскости.
Рене Декарт – французский математик ввёл в 1637 году систему координат, которая используется во всем мире и известна каждому школьнику. Её называют также «Декартова система координат».
Чтобы задать декартову прямоугольную систему координат на плоскости проводят две взаимно перпендикулярные координатные прямые х и у, называемые координатными осями.
Точка пересечения осей – «O» называется началом координат.
На каждой оси ОX и ОY задаётся положительное направление и выбирается единичный отрезок.
Каждая из координатных осей имеет своё название: горизонтальную ось называют осью абсцисс (или осью х), вертикальную ось называют осью ординат (или осью у). Эти прямые составляют систему координат на плоскости.
Определение
Плоскость, на которой задана система координат, называется координатной плоскостью.
Оси разбивают координатную плоскость на четыре части, которые называют координатными четвертями. Их нумеруют римскими цифрами и против часовой стрелки.
Говорят: первая четверть, вторая четверть, третья четверть и четвертая четверть.
Каждая точка такой плоскости имеет две координаты.
Рассмотрим, как определяется положение точки на координатной плоскости.
Например, у нас есть точка М. И нужно определить её координаты. Для этого проведём перпендикуляр из этой точки на горизонтальную ось или ось абсцисс.
Точка пересечения с осью х называется абсциссой точки М.
В нашем случае, абсцисса точки М 3.
Далее, из этой же точки проведём перпендикуляр до пересечения с вертикальной осью, или осью ординат.
Точка пересечения с осью у называется ординатой точки М.
В нашем случае, ордината точки М 5.
Абсцисса и ордината точки М называются координатами этой точки. Их принято записывать рядом с буквой, обозначающей точку, в круглых скобках. Причем, на первом месте всегда пишется абсцисса, а на втором – ордината.
Читают эту запись так: «точка М с абсциссой 3 и ординатой 5», или «точка М с координатами 3 и 5». Обратите внимание, если переставить координаты местами, то получится совсем другая точка. Например, точка N (5; 3).
Определение
Координаты точки (х;у) на плоскости – это пара чисел, в которой на первом месте стоит абсцисса (х), а на втором – ордината (у) этой точки.
Сделаем вывод: координаты можно указать для любой точки координатной плоскости: для этого надо из точки провести перпендикуляры на координатные оси и определить, какому числу координатной оси соответствует основание перпендикуляра.
Точки любой прямой, перпендикулярной оси абсцисс, имеют одну и ту же абсциссу.
Например, все точки прямой а имеют абсциссу 4. Все точки оси ординат имеют абсциссу 0, т.е. координаты любой точки оси ординат имеют вид (0; у).
Точки любой прямой, перпендикулярной оси ординат, имеют одну и ту же ординату.
Например, все точки прямой b имеют ординату -3. Все точки оси абсцисс имеют ординату 0, т.е. координаты любой точки оси абсцисс имеют вид (х; 0).
Начало координат – точка О – лежит и на оси абсцисс, и на оси ординат. Значит, её координаты (0; 0).
Построить точку по её координатам можно несколькими способами.
Например, построим точку А (-5; 7).
Первый способ: на оси х находим абсциссу точки А. Она у нас равна -5. Проводим перпендикуляр из этой точки относительно оси ОХ. Далее, на оси у, найдём ординату точки. Она равна 7. Проводим перпендикуляр из этой точки относительно оси ОУ. Точка, где пересеклись оба перпендикуляра, и есть искомая точка А.
Второй способ построения точки по заданным координатам. Можно сместиться по оси ОХ влево на 5 единиц, т.к. абсцисса точки – отрицательное число. А затем, параллельно оси ОX вверх на 7 единиц, т.к. ордината точки положительное число. Точка, где пересеклись оба перпендикуляра, и есть искомая точка А.
Сделаем ещё один очень важный вывод:
Каждой точке на координатной плоскости соответствует пара чисел: её абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Задание
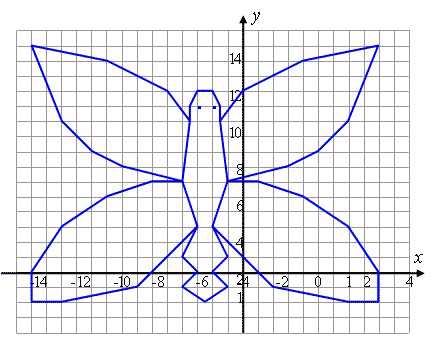
Построите на координатной плоскости точки, а затем последовательно соедините их отрезками.
Какая фигура у нас получилась в итоге? Правильно! Это котик!!!
videouroki.net
Координатная плоскость
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (2,1 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок закрепления и применения знаний, умений, навыков
Цели:
повторить основные понятия
и определения по теме; обобщить и
систематизировать знания учащихся по теме
“Координатная плоскость”; вырабатывать умения
и навыки в построении и нахождении точек на
координатной плоскости по заданным координатам;
проверить ЗУН учащихся в ходе выполнения
самостоятельной работы.
Задачи: обобщить и систематизировать сведения и прямоугольной системе координат; отрабатывать умение определять координаты точки, строить точки по заданным координатам; воспитывать самостоятельность, аккуратность, точность выполнения заданий; чувство коллективизма; развивать логическое мышление, память, внимание, культуру речи
Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят ученики в ходе урока: закрепят и актуализируют знания, умения и навыки в построении координатных осей, в нахождении точки по заданным координатам, в построении точки по заданным координатам.
Оборудование: компьютер, проектор, интерактивная доска (если есть) презентация PowerPoint, карточки с заданиями для самостоятельной работы, карточки с изображением смайликов для рефлексии.
Мотивация: презентация, в урок включены игровые моменты.
Важно: в данной презентации используется макроса DragAndDrop. Чтобы он работал, нужно его включить. Для этого делаем следующее: режим показа слайдов/выскакивает окно: Оповещение системы безопасности – макрос/щелкаем мышкой на Включить содержимое и щелкаем ОК. Макрос включен.
План:
- Организационный момент.
- Устная работа
- Решение задач
- Физкультминутка
- Решение задач (продолжение)
- Самостоятельная работа
- Итог урока
- Домашнее задание
- Рефлексия
Ход урока
1. Организационный момент
Здравствуйте, ребята! Сегодня у нас завершающий урок по теме “Координатная плоскость” и на этом уроке с помощью различных игр мы еще раз вспомним все основные понятия по данной теме, а так же повторим и закрепим построение и нахождение точек на координатной плоскости. Откройте тетради, запишите число, классная работа и тему урока.
(Слайд 1)
Для начала поработаем устно.
2. Устная работа
Разгадайте кроссворд (слайд 4)
Чтобы вспомнить все основные понятия разгадаем кроссворд.
- Как располагаются координатные прямые Х и У на плоскости? (перпендикулярно)
- Координатную прямую Х называют ось….(абсцисс)
- Координатную прямую У называют ось….(ординат)
- На сколько четвертей делят координатные прямые Х и У плоскость? (четыре)
- Под каким углом пересекаются координатные прямые? (прямым)
- Как называется точка пересечения координатных прямых? (началом)
- Как называют пару чисел, определяющих положение точки на плоскости? (координаты)
- Сколько чисел нужно указать, чтобы задать положение точки на координатной плоскости? (две)
(Кроссворд анимированный, сделан с помощью автофигур, поэтому чтобы он работал нужно нажать на любую из цифр, в произвольном порядке – появиться вопрос, после прочтения вопроса еще раз нажать на эту же цифру – в сетке кроссворда появиться ответ).
Игра “Кукарямба” (слайд 6)
Давайте поиграем в игру “Кукарямба”. Правила игры: на координатной плоскости отмечены точки, я показываю на точку, вы называете ее координату. Если коо
xn--i1abbnckbmcl9fb.xn--p1ai