Лекция 4. Матрицы и определители
Матрицы и определители. Лекция 4.
Матрицы.
Основные понятия.
Матрицей называется прямоугольная таблица чисел.
Пример 13. , ,,.
В общем случае матрица может содержать строк истолбцов
.
Числа называютсяэлементами матрицы, где — указывает номер строки,— указывает номер столбца.
Элементы образуютглавную диагональ матрицы. Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров называетсяматрицей – го порядка.
Матрицы называются равными, если у них равны элементы, стоящие на соответствующих местах, т. е. тогда и только тогда, когда, для всех,.
Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной.
Пример 14. .
Если все элементы матрицы равны нулю, то матрица называется нулевой.
Пример 15. .
Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной.
Пример 16. , .
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю.
Пример 17. ,.
Матрица, содержащая одну строку (столбец), называется вектором (вектор-строкой, вектор-столбцом).
Пример 18. ,.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной .
Пример 19. ;
Очевидно, что .
Действия над матрицами.
Матрицы одинаковых размерностей можно складывать и вычитать. Если
, , то, причем
, для всех .
Пример 20. ,
.
Умножение матрицы на число.
Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.
Пример 21. Пусть , тогда. Матрицаназываетсяпротивоположной к матрице.
Умножение матриц.
Умножение матриц можно только в том случае, когда число столбцов матрицыравно числу строк матрицыВ этом случае справедливо соотношение, причем элементы матрицыравны,,. Другими словами строки матрицыумножаются на столбцы матрицы
Пример 22. Пусть ,. Тогда
,
.
Видим, что в общем случае . Если же выполняется условие, то матрицыиназываютсяперестановочными друг с другом.
Матрица называется ступенчатой, если для её элементов выполняются условия:
под первым не нулевым элементом каждой строки находится 0;
первый ненулевой элемент любой строки находится правее первого не нулевого элемента любой строки, расположенной выше.
Пример 23. Следующая матрица является ступенчатой.
.
Элементарные преобразования матриц.
Элементарными преобразованиями матриц являются:
Перестановка местами двух любых её строк (столбцов).
Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число.
Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Две матрицы называютсяэквивалентными, если одна из них получается из другой с помощью элементарных преобразований
Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
Определители.
Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.
Пример 24. Если , то. Так.
Если , то.
Так .
Если , то
. Так
.
С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.
Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.
Вычисление определителей более высоких порядков осуществляется путем использования их свойств.
Свойства определителей.
Пусть дана квадратная матрица
Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы и обозначается
Минором некоторого элемента определителя называют определитель, который получается вычеркиванием из негостроки истолбца. Например
, .
Алгебраическим дополнением элемента определителя называют число. Например
, .
Свойства определителей.
1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. е. .
2. Определитель меняет знак при перестановке любых двух его строк (столбцов).
3. Определитель, имеющий две равные строки (столбца), равен 0.
4. Общий множитель строки (столбца) можно выносить за знак определителя, например
.
5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например
6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.
(I=I+II).
7. Определитель треугольной матрицы равен произведению её диагональных элементов.
8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например
.
Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов.
9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.
22
studfiles.netОпределитель матрицы | umath.ru
Рассмотрим набор натуральных чисел от до : . Перестановкой этих чисел называется их запись в некотором порядке без повторений. Например, последовательность является перестановкой множества .
Обозначим перестановки этих чисел как . Из комбинаторики известно, что число всех таких различных перестановок равно .
Определение. Говорят, что числа и перестановки образуют инверсию (или беспорядок), если при верно неравенство . Число всех инверсий в перестановке обозначим .
Например, , так как перед числом стоит число , а перед числом стоят числа , большие единицы.
Пусть дана квадратная матрица
Определение. Определителем (или детерминантом) квадратной матрицы размера называется число
где сумма берётся по всевозможным перестановкам номеров столбцов матрицы .
Определитель матрицы принято обозначать следующим образом:
Свойства определителей
- Определитель единичной матрицы равен единице:
- При транспонировании матрицы её определитель не изменяется:
- При перестановке двух столбцов или строк матрицы знак её определителя меняется на противоположный.
- Определитель матрицы, содержащей два одинаковых столбца (строки), равен нулю.
- При вычислении определителя матрицы из столбца (строки) можно выносить общий множитель.
- При добавлении к некоторому столбцу (строке) матрицы линейной комбинации остальных столбцов определитель матрицы не изменяется.
Линейной комбинацией столбцов называется сумма этих столбцов, умноженных на некоторые коэффициенты.
- Определитель обратной матрицы (в случае, если она существует) равен
- Определитель произведения матриц размера равен произведению их определителей:
umath.ru
Определитель матрицы
Определителем
квадратной матрицы  называется число, которое обозначается
как
называется число, которое обозначается
как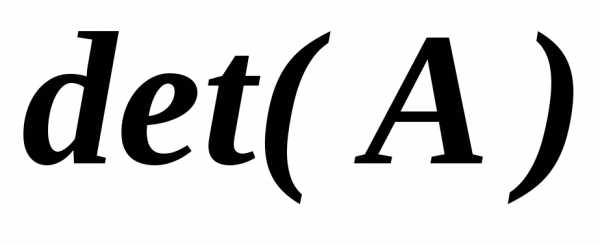 или
или и вычисляется при помощи следующих трех
правил.
и вычисляется при помощи следующих трех
правил.
Правило 1. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.
Замечание: Определитель одноэлементной матрицы равен самому элементу.
Правило 2. Общий множитель элементов любой строки или столбца матрицы можно вынести за знак определителя.
 .
.Правило 3. Определитель матрицы не изменится, если к одной из строк (столбцов) матрицы прибавить другую строку (столбец) этой матрицы.
Свойства определителя матрицы.
1. Определитель не меняется при транспонировании.
2. Если в определителе переставить две строки, определитель поменяет знак.
3. Определитель, содержащий две одинаковые строки, равен нулю.
4. Определитель, содержащий две пропорциональные строки, равен нулю.
5. Если
все элементы  строки определителя представлены в
виде суммы двух слагаемых,
то определитель равен сумме определителей,
у которых все строки, кроме
строки определителя представлены в
виде суммы двух слагаемых,
то определитель равен сумме определителей,
у которых все строки, кроме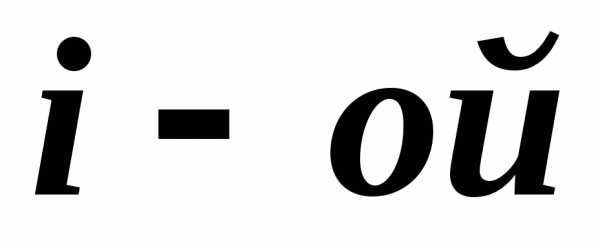
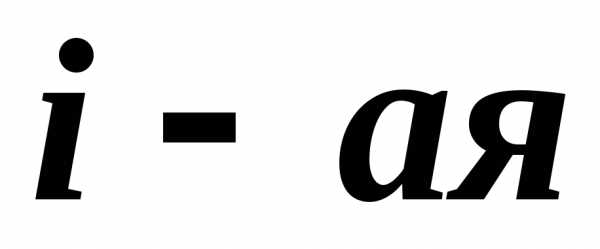 строка в одном из слагаемых состоит из
элементов
строка в одном из слагаемых состоит из
элементов ,
в другом — из элементов
,
в другом — из элементов .
.Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Миноры и алгебраические дополнения
Обозначим
через  матрицу, которая остается при вычеркивании
из матрицы
матрицу, которая остается при вычеркивании
из матрицы
 строки и
строки и столбца. Тогда
столбца. Тогда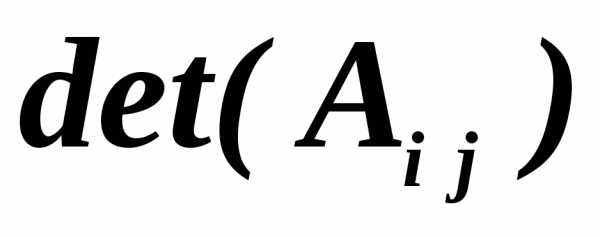 называется минором элемента
называется минором элемента .
Величинаназывается алгебраическим дополнением
элемента
.
Величинаназывается алгебраическим дополнением
элемента
Разложение определителя матрицы по элементам строки или столбца.
Теорема.
Определитель каждой матрицы равен сумме
произведений элементов любой ее строки
(столбца) на их алгебраические дополнения,
т. е. при разложении по элементам  строки
строки
Для вычисления значений определителей матриц второго порядка пользуются формулой:
Для вычисления значений определителей матриц третьего порядка можно воспользоваться формулой разложения определителя по первой строке:
Пример
7. Не
вычисляя определителя 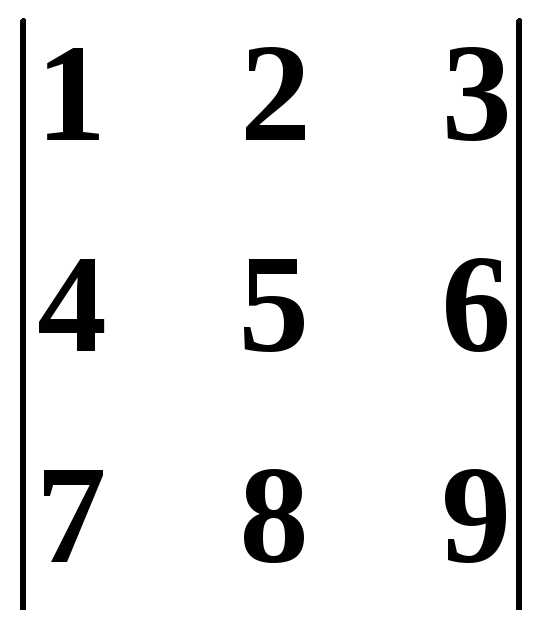 ,
показать, что он равен нулю.
,
показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель
 ,
равный исходному. Если из третьей
строки также вычесть первую, то получится
определитель
,
равный исходному. Если из третьей
строки также вычесть первую, то получится
определитель 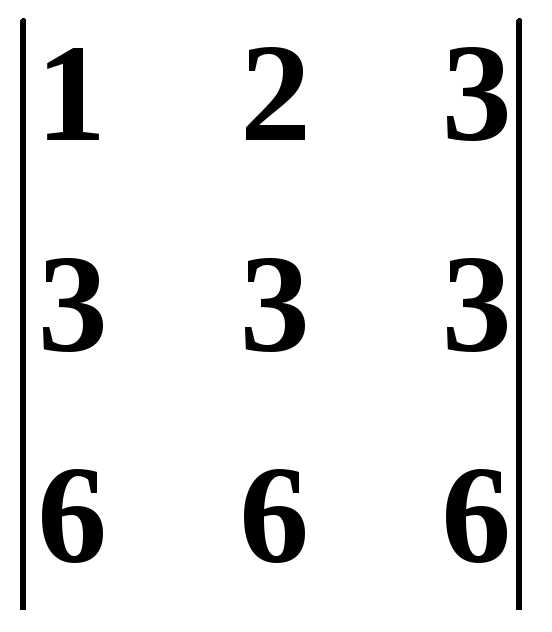 ,
в котором две строки пропорциональны.
Такой определитель равен нулю.
,
в котором две строки пропорциональны.
Такой определитель равен нулю.
Пример
8. Вычислить
определитель 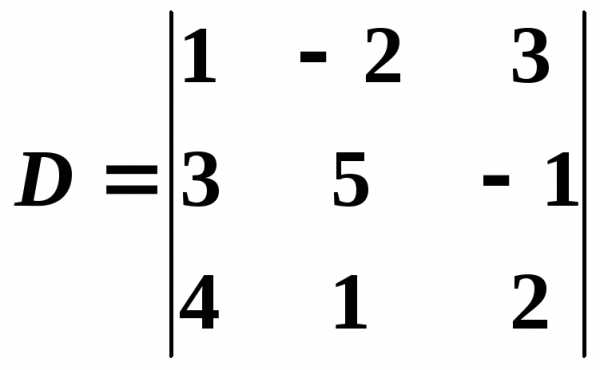 ,
разложив его по элементам второго
столбца.
,
разложив его по элементам второго
столбца.
Решение. Разложим определитель по элементам второго столбца:
4. Ранг матрицы
Рассмотрим
прямоугольную матрицу  .
Если в этой матрице выделить произвольно
.
Если в этой матрице выделить произвольно строк и
строк и столбцов, то элементы, стоящие на
пересечении выделенных строк и столбцов,
образуют квадратную матрицу
столбцов, то элементы, стоящие на
пересечении выделенных строк и столбцов,
образуют квадратную матрицу порядка. Определитель этой матрицы
называетсяминором
k-го порядка матрицы
порядка. Определитель этой матрицы
называетсяминором
k-го порядка матрицы  .
Очевидно, что матрица
.
Очевидно, что матрица обладает минорами любого порядка от
обладает минорами любого порядка от до наименьшего из чисели
до наименьшего из чисели .
Некоторые среди них будут равны нулю.
Среди всех отличных от нуля миноров
матрицы
.
Некоторые среди них будут равны нулю.
Среди всех отличных от нуля миноров
матрицы найдется, по крайней мере, один минор,
порядок которого будет наибольшим.
Наибольший из порядков миноров данной
матрицы, отличных от нуля, называется рангом матрицы. Если ранг
матрицы
найдется, по крайней мере, один минор,
порядок которого будет наибольшим.
Наибольший из порядков миноров данной
матрицы, отличных от нуля, называется рангом матрицы. Если ранг
матрицы  равен
равен ,
то это означает, что в матрице
,
то это означает, что в матрице имеется отличный от нуля минор порядка
имеется отличный от нуля минор порядка ,
но всякий минор порядка, большего чем
,
но всякий минор порядка, большего чем ,
равен нулю. Ранг матрицы
,
равен нулю. Ранг матрицы обозначается через
обозначается через .
Очевидно, что выполняется соотношение
.
Очевидно, что выполняется соотношение
Ранг
матрицы находится либо методом окаймления
миноров, либо методом элементарных
преобразований. При вычислении ранга
матрицы первым способом следует
переходить от миноров низших порядков
к минорам более высокого порядка. Если
уже найден минор 
 порядка матрицы
порядка матрицы ,
отличный от нуля, то требуют вычисления
лишь минорыпорядка, окаймляющие минор
,
отличный от нуля, то требуют вычисления
лишь минорыпорядка, окаймляющие минор ,
т.е. содержащие его в качестве минора.
Если все они равны нулю, то ранг матрицы
равен
,
т.е. содержащие его в качестве минора.
Если все они равны нулю, то ранг матрицы
равен .
.
Элементарными называются следующие преобразования матрицы:
перестановка двух любых строк (или столбцов),
умножение строки (или столбца) на отличное от нуля число,
прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные
матрицы не являются, вообще говоря,
равными, но их ранги равны. Если матрицы  и
и  эквивалентны, то это записывается так:
эквивалентны, то это записывается так: 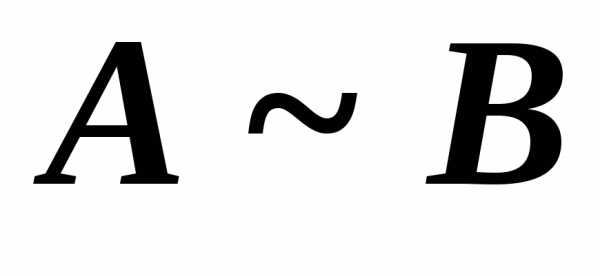 .
.
Каноническойматрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,
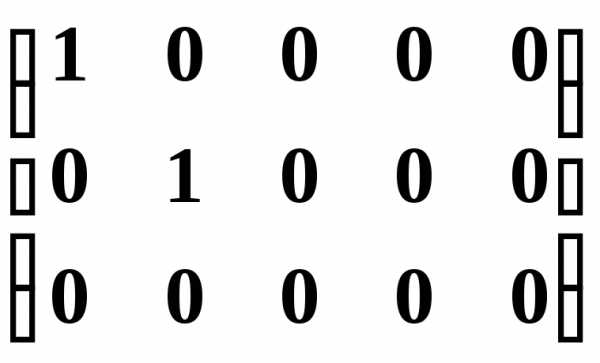 .
.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример 11. Найти методом окаймления миноров ранг матрицы

Решение. Начинаем
с миноров 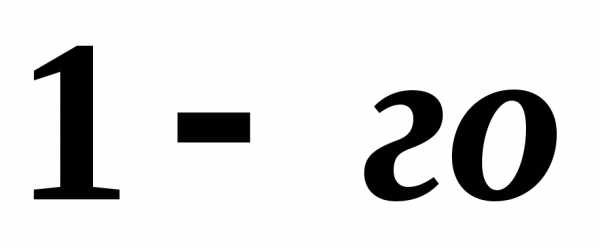 порядка, (т.е. с элементов матрицы
порядка, (т.е. с элементов матрицы ).
Выберем, например, минор (элемент)
).
Выберем, например, минор (элемент)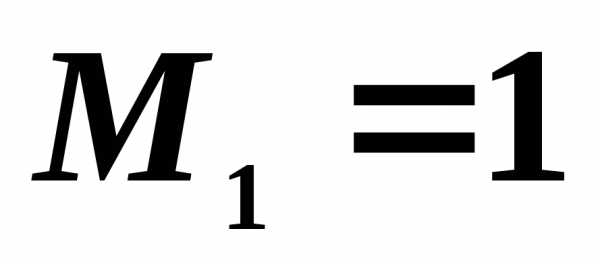 ,
расположенный в первой строке и первом
столбце. Окаймляя при помощи второй
строки и третьего столбца, получаем
минор
,
расположенный в первой строке и первом
столбце. Окаймляя при помощи второй
строки и третьего столбца, получаем
минор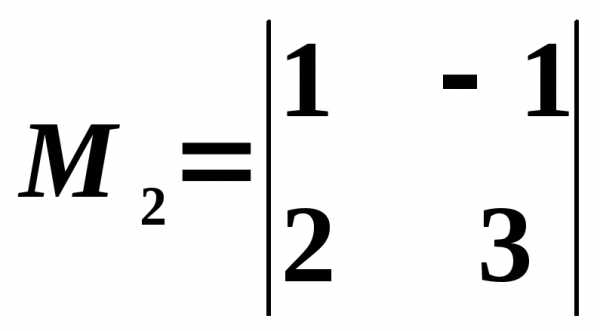 ,
отличный от нуля. Переходим теперь к
минорам
,
отличный от нуля. Переходим теперь к
минорам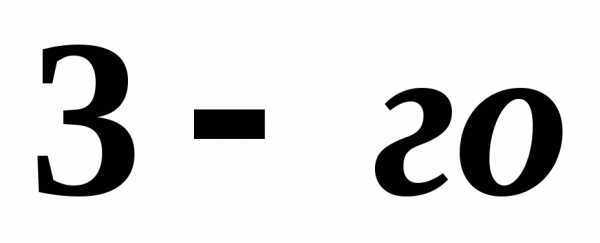 порядка, окаймляющим
порядка, окаймляющим .
Их всего два (можно добавить второй
столбец или четвертый). Вычисляем их:
.
Их всего два (можно добавить второй
столбец или четвертый). Вычисляем их:
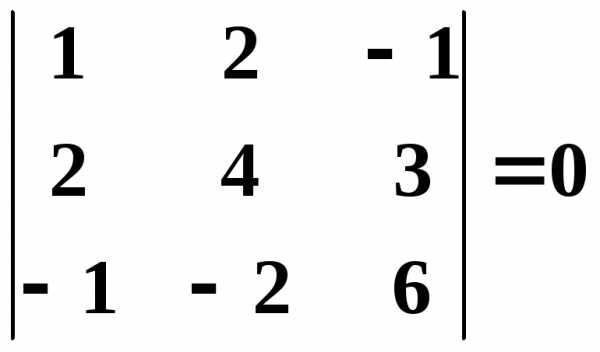 ,
,  .
.
Таким
образом, все окаймляющие миноры третьего
порядка оказались равными нулю. Ранг
матрицы  равен двум.
равен двум.
Пример 12. Найти ранг матрицы

и привести ее к каноническому виду.
Решение. Из второй строки вычтем первую и переставим эти строки:
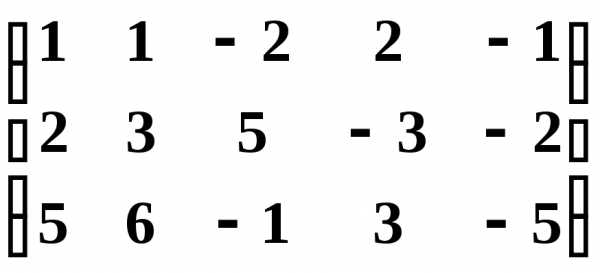 .
.
Теперь из второй и третьей
строк вычтем первую, умноженную
соответственно на  и
и :
:
 ;
;
из третьей строки вычтем вторую, при этом получим матрицу
 ,
,
которая эквивалентна матрице  ,
так как получена из нее с помощью
конечного множества элементарных
преобразований. Очевидно, что ранг
матрицы
,
так как получена из нее с помощью
конечного множества элементарных
преобразований. Очевидно, что ранг
матрицы равен
равен ,
а следовательно, и
,
а следовательно, и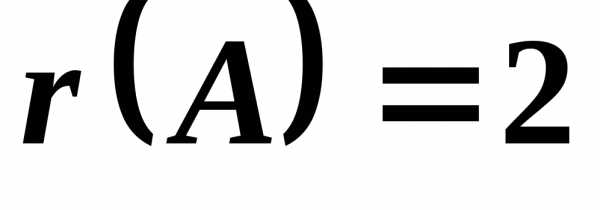 .
.
Матрицу  легко привести к канонической.
легко привести к канонической.
Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются.

Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
. 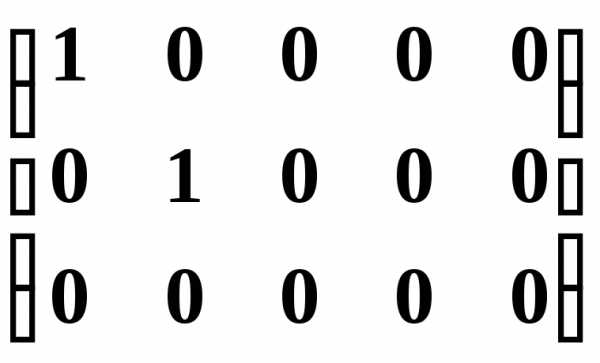
studfiles.net
Определитель матрицы и его свойства
Основной числовой характеристикой квадратной матрицы является ее определитель. Рассмотрим квадратную матрицу второго порядка
.
Определителем или детерминантом второго порядка называется число, вычисленное по следующему правилу
Например,
Рассмотрим теперь квадратную матрицу третьего порядка
.
Определителем третьего порядка называется число, вычисленное по следующему правилу
.
В целях запоминания сочетания слагаемых, входящих в выражения для определения определителя третьего порядка обычно используют правило Саррюса: первое из трех слагаемых , входящих в правую часть со знаком плюс есть произведение элементов, стоящих на главной диагонали матрицы , а каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла матрицы.
Последние три слагаемые, входящие со знаком минус определяются аналогичным образом, только относительно побочной диагонали.
Пример:
Основные свойства определителей матрицы
1. Величина определителя не изменяется при транспонировании матрицы.
2. При перестановки местами строк или столбцов матрицы, определитель меняет лишь знак, сохраняя абсолютную величину.
3. Определитель, содержащий пропорциональные строки или столбцы равен нулю.
4. Общий множитель элементов некоторой строки или столбца можно выносить за знак определителя.
5. Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
6. Если к элементам отдельной строки или столбца определителя прибавить элементы другой строки или столбца, умноженные на произвольный невырожденный множитель , то величина определителя не изменится.
Минором матрицы называется определитель, полученный вычеркиванием из квадратной матрицы одинакового числа столбцов и строк.
Если все миноры порядка выше , которые можно составить из матрицы, равны нулю, а среди миноров порядка хотя бы один отличен от нуля, то число называется рангом этой матрицы.
Алгебраическим дополнением элемента определителя порядка будем называть его минор порядка, получаемый вычеркиванием соответствующей строки и столбца, на пересечении которых, стоит элемент , взятый со знаком плюс, если сумма индексов равна четному числу и со знаком минус в противном случае.
Таким образом
,
где соответствующий минор порядка.
Вычисление определителя матрицы путем разложения по элементам строки или столбца
Определитель матрицы равен сумме произведений элементов какой- либо строки (какого- либо столбца) матрицы на соответствующие алгебраические дополнения элементов этой строки (этого столбца). При вычислении определителя матрицы таким способом следует руководствоваться следующим правилом: выбирать строку или столбец с наибольшим числом нулевых элементов. Этот прием позволяет значительно сократить объем вычислений.
Пример: .
При вычислении данного определителя, воспользовались приемом разложения его по элементам первого столбца. Как видно из приведенной формулы нет необходимости вычислять последний из определителей второго порядка, т.к. он умножается на ноль.
Вычисление обратной матрицы
При решении матричных уравнений широко используют обратную матрицу. Она в известной степени заменяет операцию деления, которая в явном виде в алгебре матриц отсутствует.
Квадратные матрицы одинакового порядка, произведение которых дает единичную матрицу , называются взаимообратными или обратными. Обозначается обратная матрица и для нее справедливо
.
Вычислить обратную матрицу можно только для такой матрицы , для которой .
Классический алгоритм вычисления обратной матрицы
1. Записывают матрицу , транспонированную к матрице .
2. Заменяют каждый элемент матрицы определителем, полученным в результате вычеркивания строки и столбца, на пересечении которых расположен данный элемент.
3. Этот определитель сопровождают знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае.
4. Делят полученную матрицу на определитель матрицы .
Пример. Требуется вычислить обратную матрицу
.
Матрица будет иметь вид
.
Заменим каждый элемент определителем, полученным при вычеркивании соответствующей строки и столбца:
.
Поменяем знаки у элементов с нечетной суммой индексов:
Разделим все элементы матрицы на . В результате получаем обратную матрицу
.
Если теперь умножить полученную обратную матрицу на матрицу , то в результате получим единичную матрицу.
infopedia.su
Матрицы и определители | Математика, которая мне нравится
1. След матрицы
Определение. Следом матрицы называется сумма элементов, стоящих по главной диагонали.
Обозначение: .
Свойства следа:
1. .
2. .
3. .
Задача. Доказать, что матричное уравнение , где — квадратная матрица , — единичная матрица, решений не имеет.
Решение. След матрицы, стоящей в левой части уравнения, равен , а в правой части — .
2. Вычисление некоторых определителей
2.1. Циклический определитель (циркулянт)
В строках циклически передвигаются .
Прибавим к последней строке все предшествующие. Получим
Теперь получим нули в последней строке, вычитая из каждого столбца предыдущий:
Вычтем первую строчку из всех последующих, и полученный определитель разложим по последнему столбцу:
2.2. Определитель Вандермонда
Вычтем последовательно из -го, -го, , второго столбца предыдущий, домноженный на :
разложим по первой строке, и вынесем общие множители элементов строк получившегося определителя -го порядка:
Определитель имеет тот же вид, что и исходный, но на единицу меньший порядок. Его можно преобразовать аналогично:
Продолжая процесс далее, приходим к окончательному ответу
2.3. Циклический определитель (циркулянт) еще раз
А теперь рассмотрим циркулянт общего вида
Рассмотрим полином . Домножим циркулянт на определитель Вандермонда, составленный по ( — корень степени из ) и воспользуемся равенством . Получим
откуда
поскольку определитель Вандермонда здесь отличен от нуля.
2.4. Ганкелев определитель
Ганкелевой матрицей называется симметричная матрица следущего вида:
Элементы — образующие ганкелевой матрицы.
Теорема. Если при , то
Доказательство. Матрицу можно представить в виде произведения:
На основании теоремы Бинe — Коши, равен тогда произведению двух определителей Вандермонда:
2.5. Определитель Коши
Вычтем из второго, третьего и т.д., -го столбца первый:
и вынесем общие множители из числителей и знаменателей строк и столбцов:
Вычтем первую строку полученного определителя из второй, третьей и т.д., -й:
разложим по первому столбцу и вынесем общие множители из числителей и знаменателей строк и столбцов:
В результате получили определитель той же структуры, что и исходный, но на единицу меньшего порядка. Продолжая процесс по аналогии, получим окончательно:
2.6. Определитель матрицы Гильберта
Если при , то определитель матрицы Гильберта
равен
Он получается из определителя Коши, если положить , .
2.7. Ленточный определитель
Определитель Якоби:
после разложения по общей формуле разложения определителя будет представлять из себя полином по , линейный по каждой переменной. Если разложить по последней строке, то получим:
Теорема. Значение равно сумме главного члена и всевозможных произведений, получающихся из него заменой одной или нескольких пар соседних множителей на .
Частный случай определителя Якоби — континуант:
Его величина совпадает с континуантой.
Исследуем еще один частный случай определителя Якоби (при
одинаковых элементах на диагоналях):
В этом случае уравнение получим
Таким образом, для нахождения определителя нужно решить линейное рекуррентное соотношение второго порядка. Начальные данные находим, вычислив определители и :
Упражнение. Вычислить определитель
Задачи.
1. Пусть матрица , , и — минор элемента . Пусть — матрица, составленная из элементов , и . Докажите, что .
2. Пусть
Для каких уравнение имеет кратные корни по ?
3. Пусть — матрица с элементами . Найдите .
4. Пусть — единичная матрица ,
Докажите, что наибольший общий делитель элементов матрицы стремится к бесконечности при .
5. Пусть — матрица, диагональные элементы ее все равны и , если четно и , если нечетно. Найдите
6. Вычислите
7. Найдите определитель -го порядка
8. Пусть и — вещественные не равные матрицы , такие, что и . можно ли выбрать матрицы и так, чтобы матрица была обратима?
9. Пусть — конечная группа, состоящая из вещественных матриц с операцией матричного умножения. Сумма следов всех элементов равна нулю. Докажите, что сумма всех элементов — нулевая матрица.
10. Пусть и — матрицы с целыми элементами. Пусть матрицы и имеют обратные с целыми элементами. Докажите, что и матрица тоже имеет обратную с целыми элементами.
11. Доказать, что определитель вещественной кососимметрической матрицы не может быть отрицательным числом.
12. Пусть
Существует ли матрица такая, что ?
13. Даны две матрицы и размерами и соответственно, причем известно, что
Найдите .
14. Пусть — матрица: при и . Докажите, что число ненулевых элементов в разложении равно .
Больше о матрицах и определителях (и не только): http://pmpu.ru/vf4/
hijos.ru
