Формула ho – Formula Browser

alexxlab / / Школьная жизнь

Mathway | Популярные задачи

1 Найти число нейтронов H
2 Найти массу одного моля H_2O
3 Определить кислотность pH 0.76M(HCl)(solution)
4 Найти массу одного моля H_2O
5 Баланс H_2(SO_4)+K(OH)→K_2(SO_4)+H(OH)
6 Найти массу одного моля H
7 Найти число нейтронов Fe
8		 Найти число нейтронов Tc
9 Найти конфигурацию электронов H
10 Найти число нейтронов Ca
11 Баланс CH_4+O_2→H_2O+CO_2
12 Найти число нейтронов C
13 Найти число протонов H
14 Найти число нейтронов O
15 Найти массу одного моля
CO_2
16 Баланс (a+b/c)(d-e)=f
17 Баланс CH_4+O_2→H_2O+CO_2
18 Баланс C_8H_18+O_2→CO_2+H_2O
19 Найти атомную массу H
20 Определить, растворима ли смесь в воде H_2O
21 Найти конфигурацию электронов Na
22 Найти массу одного атома H
23 Найти число нейтронов Nb
24 Найти число нейтронов Au
25 Найти число нейтронов Mn
26 Найти число нейтронов Ru
27 Найти конфигурацию электронов O
28 Найти массовую долю H_2O
29 Упростить корень пятой степени 243
30 Определить, растворима ли смесь в воде NaCl
31 Найти эмпирическую/простейшую формулу H_2O
32 Найти степень окисления H_2O
33 Найти конфигурацию электронов K
34 Найти конфигурацию электронов Mg
35 Найти конфигурацию электронов Ca
36 Найти число нейтронов Rh
37		 Найти число нейтронов Na
38 Найти число нейтронов Pt
39 Найти число нейтронов Be Be
40 Найти число нейтронов Cr
41 Найти массу одного моля H_2SO_4
42 Найти массу одного моля HCl
43 Найти массу одного моля Fe
44 Найти массу одного моля C
45 Найти число нейтронов Cu
46 Найти число нейтронов S
47 Найти степень окисления H
48 Баланс CH_4+O_2→CO_2+H_2O
49 Найти атомную массу O
50 Найти атомное число H
51 Найти число нейтронов Mo
52 Найти число нейтронов Os
53 Найти массу одного моля NaOH
54 Найти массу одного моля O
55 Найти конфигурацию электронов H
56 Найти конфигурацию электронов Fe
57 Найти конфигурацию электронов C
58 Найти массовую долю NaCl
59
Найти массу одного моля		 K
60 Найти массу одного атома Na
61 Найти число нейтронов N
62 Найти число нейтронов Li
63 Найти число нейтронов V
64 Найти число протонов N
65 Вычислить 2+2
66 Упростить H^2O
67 Упростить h*2o
68 Определить, растворима ли смесь в воде H
69 Найти плотность при стандартной температуре и давлении H_2O
70 Найти степень окисления NaCl
71 Найти степень окисления H_2O
72 Найти атомную массу He He
73 Найти атомную массу Mg
74 Вычислить (1.0*10^-15)/(4.2*10^-7)
75 Найти число электронов H
76 Найти число электронов O
77 Найти число электронов S
78 Найти число нейтронов Pd
79 Найти число нейтронов Hg
80 Найти число нейтронов B
81 Найти массу одного атома Li
82 Найти массу одного моля H_2O
83 Найти эмпирическую формулу H=12% , C=54% , N=20 , ,
84 Найти число протонов Be Be
85 Найти массу одного моля Na
86 Найти конфигурацию электронов Co
87 Найти конфигурацию электронов S
88 Баланс C_2H_6+O_2→CO_2+H_2O
89 Баланс H_2+O_2→H_2O
90 Баланс C_2H_6+O_2→CO_2+H_2O
91 Найти конфигурацию электронов P
92 Найти конфигурацию электронов Pb
93 Найти конфигурацию электронов Al
94 Найти конфигурацию электронов Ar
95 Найти массу одного моля O_2
96 Найти массу одного моля H_2
97 Баланс CH_4+O_2→CO_2+H_2O
98 Найти число нейтронов K
99 Найти число нейтронов P
100 Найти число нейтронов Mg

www.mathway.com

Список неорганических соединений по элементам

HoBr3бромид гольмия
Ho23оксалат гольмия
HoCl3хлорид гольмия
HoF3фторид гольмия
HoI3иодид гольмия
Ho3нитрат гольмия
Ho2O3оксид гольмия
Ho3гидроксид гольмия
Ho23сульфат гольмия
NO3нитрат дисеребра иода
IBrмонобромид иода
Csхлоробромоиодат цезия
Csдибромоиодат цезия
Kдибромоиодат калия
IClмонохлорид иода
I2Cl6гексахлорид дииода
Csдихлороиодат цезия
Csтетрахлороиодат цезия
Hтетрахлороиодат водорода
Kдихлороиодат калия
Kтетрахлороиодат калия
IFмонофторид иода
IF3трифторид иода
IF5пентафторид иода
IF7гептафторид иода
Csдииодоиодат цезия
Kдииодоиодат калия
NH4дииодоиодат аммония
Rbдииодоиодат рубидия
I3Nнитрид трииода
I3тринитрат иода
I2O5пентаоксид дииода
IF3трифторид-оксид иода
IF5пентафторид-оксид иода
IO2Fфторид-диоксид иода
IO2F3трифторид-диоксид иода
IO3Fфторид-триоксид иода
Hтетрафтородиоксоиодат водорода
IO3иодат оксоиода
IO4метапериодат диоксоиода
HIиодоводород
HIO3йодноватая кислота
HIO4метаиодная кислота
H4I2O9нонаоксодииодат водорода
H5IO6ортоиодная кислота

4108.ru

Таблица Менделеева online — Ho

Относительная электроотрицательность (по Полингу):
Температура плавления: 1474°C
Температура кипения: 2700°C
Теплопроводность: 22
Плотность: 8,8 г/см3
Открыт: И. Сорет
Цвет в твёрдом состоянии: Серебристо-белый
Тип: Редкоземельный
Орбитали: 1s22s22p63s23p63d104s24p64d104f115s25p65d05f06s2
Электронная формула: Ho — 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 4f11 6s2
Ho — [Xe] 4f11 6s2
Валентность: +3
Степени окисления: 0, + III
Сверхпроводящее состояние при температуре: 0 К
Потенциалы ионизации: 11,805 В
22,843 В
Электропроводность в тв. фазе: 1,11*106 при 273K
Ковалентный радиус: 1,58 Å
Атомный объем: 18,4 см3/моль
Атомный радиус: 2,45 Å
Теплота распада: 19,9 Кдж/моль
Теплота парообразования: 261 Кдж/моль
Кристаллическая структура: Гексагональная. Радиус описанной вокруг основания окружности не равен высоте фигуры. Боковая сторона перпендикулярна основанию

table-mendeleev.ru

Определение и свойства геометрической прогрессии, формула n-го члена

Тема: Геометрическая прогрессия

Урок: Определение и свойства геометрической прогрессии, формула n–го члена

На уроке дается определение геометрической прогрессии, выводится формула общего члена, решаются типовые задачи.

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют геометрической прогрессией. При этом число q называют знаменателем прогрессии.

Математическая запись.

геометрическая прогрессия, ее члены , при этом:

Иная запись:, т.е. .

Рассмотрим примеры геометрических прогрессий:

 здесь каждый следующий член получается из предыдущего умножением на 2; полученная последовательность при этом возрастает (

2.  здесь каждый следующий член получается из предыдущего умножением на ; полученная последовательность при этом убывает (

Теперь выведем формулу n–го члена геометрической прогрессии.

Рассмотрим геометрическую прогрессию , при этом

.

Тогда,

. . . . . . . . . . .

n=1,2,3,…

Докажем полученную формулу методом полной математической индукции.

Дано:геометрическая прогрессия,

.

Доказать:.

Доказательство.

1. Проверим справедливость формулы дляn =1:

2. Предположим, что формула справедлива для n=k:

3. Докажем, что из справедливости формулы для n=k следует справедливость формулы для n=k+1:

Вывод:  формула верна для всех

Рассмотрим геометрическую прогрессию как функцию натурального аргумента и построим ее график.

Обозначим, тогда

,  это показательная функция натурального аргумента.

Рассмотрим примеры.

1.  

.

Перейдя к функции, имеем

Составим таблицу значений функции.

n

1

2

3

4

    

  1  

  2  

  4  

  8  

И построим ее график.
 

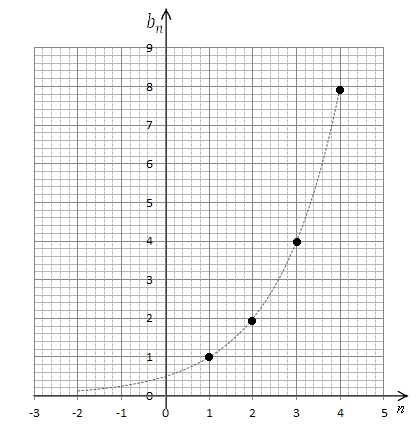
Рис. 1.

, поэтому график – это только отдельные точки, которые лежат на показательной кривой.

2.  ;

.

Перейдя к функции, имеем

Составим таблицу значений функции.

n

1

2

3

4

    

  1  

    

    

    

И построим ее график.
 

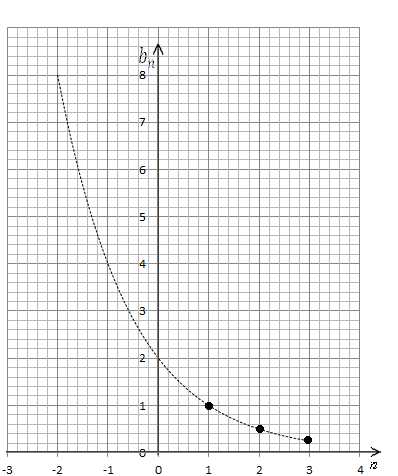
Рис. 2

Снова график – это отдельные точки, лежащие на показательной кривой.

Из графиков видно, что если геометрическая прогрессия возрастает, то возрастает очень быстро, а если убывает, то убывает тоже быстро (как показательная функция).

Далее рассмотрим типовые задачи, для решения которых понадобится формула общего члена геометрической прогрессии:

1. Дано:геометрическая прогрессия, . Найти: . Решение: Ответ:

2. Дано:геометрическая прогрессия,. Проверить, является ли число 1536 членом этой прогрессии, если да, найти его номер. Решение: Ответ:

3. Дано:геометрическая прогрессия, .  Найти: Решение: Ответ:

4. Дано:геометрическая прогрессия, .  Найти: Решение: Ответ:

Если известны два члена геометрической прогрессии то справедлива формула:

.

Действительно, Рассмотрим еще одну задачу.

5. Дано:геометрическая прогрессия, .  Найти: Решение: Ответ:

 

Методические замечания:

1. В видео уроке на доске график на рисунке 2 подписан  вместо

2. Не рассмотрена очень полезная для решения задач формула , которая была добавлена в конце конспекта и на использование формулы приведен соответствующий пример.

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Рекомендованные ссылки на  ресурсы интернет

1. Открытая математика (Источник).

2. Задачи (Источник).

3. РЕШУ ЕГЭ (Источник).

 

Рекомендованное домашнее задание

Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений /А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.

№№ 485, 486, 488, 490, 497.

interneturok.ru

Определение и свойства арифметической прогрессии, формула ее n-го члена

Тема: Прогрессии

Урок: Определение и свойства арифметической прогрессии, формула n-го члена

Вспомним, что числовая последовательность – частный случай функции, функции, определенной на множестве натуральных чисел. Арифметическая прогрессия – частный случай числовой последовательности.

Рассмотрим примеры, дающие представление об арифметической прогрессии.

1. Задана последовательность чисел:

Закономерность образования данной последовательности: каждый последующий член больше предыдущего на 4 (обозначим это число буквой d), т.е.  Данную последовательность можно задать рекуррентно: . Заметим, что эта последовательность является возрастающей  () .

2. Задана последовательность чисел:  В этой последовательности все числа равны между собой, .

3. Задана последовательность чисел:

Закономерность образования данной последовательности: каждый последующий член меньше предыдущего на 2. Чтобы получить последующий член надо к предыдущему прибавить число (-2), т.е.  Данную последовательность можно задать рекуррентно: . Заметим, что эта последовательность является убывающей () .

Дадим определение  арифметической прогрессии.

Числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называется арифметической прогрессией, число d называется ее разностью. 

Арифметическая прогрессия обозначается следующим образом:.

Арифметическая прогрессия может быть задана рекуррентно:  

Непосредственно из определения арифметической прогрессии следуют такие свойства:

— если , то арифметическая прогрессия — возрастающая;

— если , то арифметическая прогрессия — убывающая.

Из определения арифметической прогрессии следует истинность равенств: . Тогда

  и т.д. Значит,

Т.е., зная первый член и разность арифметической прогрессии, можно найти любой ее член.

Арифметическую прогрессию считают заданной, если известен ее первый член и разность.

Формулу  называют формулой n-го члена арифметической прогрессии.

Формулу n-го члена арифметической прогрессии можно доказать с помощью метода математической индукции.

Дано: , .

Доказать:  (1)

Доказательство.

Формула (1) верна при n=1. Действительно, .

Предположим, что формула (1) верна при n=k, т.е. .

Докажем, что формула (1) верна и при n=k+1, т.е. .

Из условия  и предположения  получаем:

.

Согласно принципу математической индукции формула (1) верна для любого натурального числа.

Из формулы n-го члена арифметической прогрессии следует, что

. Это означает, что арифметическая прогрессия зависит от n, т.е. является функцией натурального аргумента.

Вывод: арифметическая прогрессия – это линейная функция натурального аргумента , где .

Если , то линейная функция возрастает и арифметическая прогрессия — возрастающая;

если , то линейная функция убывает и  арифметическая прогрессия — убывающая.

Пример 1.

Дано: =.

Найти: формулу n-го члена арифметической прогрессии .

Доказать: — возрастающая.

Дать: геометрическую иллюстрацию.

Решение.

.Тогда , т.е. .

Поскольку , заданная арифметическая прогрессия – возрастающая.

Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции  и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).

Рис. 1. График функции

Пример 2.

Дано: =.

Найти: формулу n-го члена арифметической прогрессии .

Дать: геометрическую иллюстрацию.

Решение.

.

Тогда  для любого натурального числа.

Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции  и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис.  2).

Рис. 2. График функции

Пример 3.

Дано: =.

Найти: формулу n-го члена арифметической прогрессии .

Доказать: — убывающая.

Дать: геометрическую иллюстрацию.

Решение.

.

Тогда , т.е. .

Поскольку , заданная арифметическая прогрессия – убывающая.

Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции  и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 3).

Рис. 3. График функции

Пример 4.

Дано: , .

Найти: ; наименьший положительный член.

Решение.

Формула n-го члена арифметической прогрессии:

interneturok.ru

Формула • ru.knowledgr.com

В науке формула — краткий способ выразить информацию символически как в математической или химической формуле. Неофициальное использование термина формула в науке относится к общей конструкции отношений между данными количествами. Множественное число формулы может быть записано или как формулы или как формулы (с оригинальной латыни).

В математике формула — построенное использование предприятия символов и правил формирования данного логического языка. Например, определение объема сферы требует существенного количества интегрального исчисления или его геометрического аналога, метода истощения; но, сделав это однажды с точки зрения некоторого параметра (радиус, например), математики произвели формулу, чтобы описать объем: Эта особая формула:

Получив этот результат и знание радиуса любой рассматриваемой сферы, мы можем быстро и легко определить ее объем. Обратите внимание на то, что том V и радиус r выражены как единственные письма вместо слов или фраз. Это соглашение, в то время как менее важный в относительно простой формуле, означает, что математики могут более быстро управлять большими и более сложными формулами. Математические формулы часто — алгебраическая, закрытая форма, и/или аналитичный.

В современной химии химическая формула — способ выразить информацию о пропорциях атомов, которые составляют особое химическое соединение, используя единственную линию символов химического элемента, чисел, и иногда других символов, таких как круглые скобки, скобки, и плюс (+) и минус (−) знаки. Например, HO — химическая формула для воды, определяя, что каждая молекула состоит из двух водорода (H) атомы и один кислород (O) атом. Точно так же O обозначает молекулу озона, состоящую из трех атомов кислорода и имеющую чистый отрицательный заряд.

В общем контексте формулы применены, чтобы предоставить математическое решение для проблем реального мира. Некоторые могут быть общими: который является одним выражением второго закона Ньютона, применимо к широкому диапазону физических ситуаций. Другие формулы могут быть особенно созданы, чтобы решить особую проблему; например, использование уравнения синуса изгибается, чтобы смоделировать движение потоков в заливе. Во всех случаях, однако, формулы формируют основание для вычислений.

Выражения отличны от формул, в которых они не могут содержать, равняется знаку (=). Принимая во внимание, что формулы сопоставимы с предложениями, выражения больше походят на фразы.

Химические формулы

Химическая формула определяет каждый учредительный элемент своим химическим символом и указывает на пропорциональное число атомов каждого элемента. В эмпирических формулах эти пропорции начинаются с основного элемента и затем назначают числа атомов других элементов в составе как отношения к основному элементу. Для молекулярных составов эти числа отношения могут все быть выражены как целые числа. Например, эмпирическая формула этанола может быть написана CHO, потому что молекулы этанола все содержат два атома углерода, шесть водородных атомов и один атом кислорода. Некоторые типы ионных составов, однако, не могут быть написаны с полностью целым числом эмпирические формулы. Пример — карбид бора, чья формула CB — переменное отношение нецелого числа с n, располагающимся из-за 4 к больше чем 6,5.

Когда химическое соединение формулы состоит из простых молекул, химические формулы часто используют способы предложить структуру молекулы. Эти типы формул по-разному известны как молекулярные формулы и сжатые формулы. Молекулярная формула перечисляет число атомов, чтобы отразить тех в молекуле, так, чтобы молекулярная формула для глюкозы была CHO, а не глюкозой эмпирическая формула, которая является CHO. За исключением очень простых веществ, молекулярное химическое отсутствие формул нуждалось в структурной информации и неоднозначно.

В вычислении

В вычислении формула, как правило, описывает вычисление, такое как дополнение, чтобы быть выполненной на одной или более переменных. Формула часто неявно обеспечивается в форме компьютерной инструкции такой как.

: Градусы Цельсия = (5/9) * (Градусы по Фаренгейту — 32)

В компьютерном программном обеспечении электронной таблицы формула, указывающая, как вычислить ценность клетки скажем A3, написана, такие как

:

=A1+A2

где A1 и A2 относятся к другим клеткам (колонка A, ряд 1 или 2) в рамках электронной таблицы. Это — короткий путь для «бумажной» формы A3 = A1+A2, где A3, в соответствии с соглашением, опущенным, потому что результат всегда хранится в самой клетке и заявлении, что ее имя было бы избыточно.

Формулы с предписанными единицами

Физическое количество может быть выражено как продукт числа и физической единицы. Формула выражает отношения между физическими количествами. Необходимое условие для формулы, чтобы быть действительным состоит в том, что у всех условий есть то же самое измерение, означая, что каждый термин в формуле мог быть потенциально преобразован, чтобы содержать идентичную единицу (или продукт идентичных единиц).

В примере выше, для объема сферы, мы можем хотеть вычислить с r = 2,0 см, который приводит

к

:

Есть обширное образовательное обучение о сдерживающих единицах в вычислениях и единицах преобразования к желательной форме, такой как в преобразовании единиц этикеткой фактора.

Подавляющее большинство вычислений с измерениями сделано в компьютерных программах без средства для сохранения символического вычисления единиц. Только числовое количество используется в вычислении. Это требует, чтобы универсальная формула была преобразована в формулу, которая предназначена, чтобы использоваться только с предписанными единицами, означая, что числовое количество, как неявно предполагается, умножает особую единицу. Требования о предписанных единицах должны быть даны пользователям входа и продукции формулы.

Например, предположите, что формула должна потребовать, чтобы, то, где ст. л. — американская столовая ложка (как замечено в преобразовании единиц) и VOL, было названием числа, используемого компьютером. Точно так же формула должна потребовать

. Происхождение формулы продолжается как:

:

Учитывая, что,

формула с предписанными единицами —

:

Формула не полна без слов, таких как:

«VOL — объем в ст. л., и RAD — радиус в cm».

Другие возможные слова — «VOL, отношение к ст. л., и RAD — отношение к cm».

Формула с предписанными единицами могла также появиться с простыми символами,

возможно, даже идентичные символы как в оригинальной размерной формуле:

:

и сопровождающие слова могли быть: «где V объем (ст. л.), и r — радиус (cm)».

Если физическая формула не размерностно гомогенная, и поэтому ошибочная,

неправда становится очевидной в невозможности

получить формулу с предписанными единицами. Это не было бы возможно к

получите формулу, состоящую только из чисел и безразмерных отношений.

В науке

Формулы, используемые в науке почти всегда, требуют выбора единиц. Формулы используются, чтобы выразить отношения между различными количествами, такими как температура, масса или обвинение в физике; поставка, прибыль или требование в экономике; или широкий диапазон других количеств в других дисциплинах.

Примером формулы, используемой в науке, является формула энтропии Больцманна. В статистической термодинамике это — уравнение вероятности, связывающее энтропию S идеального газа к количеству W, который является числом микрогосударств, соответствующих данному макрогосударству:

: (1) S = k ln W

где k — константа Больцманна, равная 1.38062 x, 10 joule/kelvin и W — число микрогосударств, совместимых с данным макрогосударством.

См. также

  • Редактор формулы
  • Формула (математическая логика)
  • Единица формулы
  • Математическое примечание
  • Символ (химический элемент)

Внешние ссылки

  • fxSolver: база данных формулы Онлайн и изображающий в виде графика калькулятор для математики, естествознания и разработки.
  • vCalc: интернет-страница с модифицируемым пользователем уравнением и библиотекой формулы.

ru.knowledgr.com

Гликоген формула ho — Здоровая печень

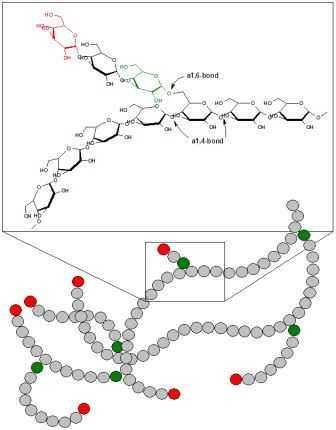Гликоген представляет собой многоразветвленный полисахарид глюкозы, который служит в качестве формы хранения энергии у людей, животных, грибов и бактерий. Полисахаридная структура представляет собой основную форму хранения глюкозы в организме. У людей, гликоген производится и хранится, в основном, в клетках печени и мышцах, гидратированных тремя или четырьмя частями воды. 1) Гликоген функционирует как вторичное долговременное хранилище энергии, причем первичные запасы энергии являются жирами, содержащимися в жировой ткани. Мышечный гликоген превращается в глюкозу мышечными клетками, а гликоген печени превращается в глюкозу для использования по всему телу, включая центральную нервную систему. Гликоген является аналогом крахмала, глюкозного полимера, который функционирует как хранилище энергии в растениях. Он имеет структуру, похожую на амилопектин (компонент крахмала), но более интенсивно разветвленную и компактную, чем крахмал. Оба являются белыми порошками в сухом состоянии. Гликоген встречается в виде гранул в цитозоле / цитоплазме во многих типах клеток и играет важную роль в цикле глюкозы. Гликоген образует запас энергии, который можно быстро мобилизовать для удовлетворения внезапной потребности в глюкозе, но менее компактен, чем энергетические запасы триглицеридов (липидов). В печени, гликоген может составлять от 5 до 6% от массы тела (100-120 г у взрослого человека). Только гликоген, хранящийся в печени, может быть доступен другим органам. В мышцах, гликоген находится в низкой концентрации (1-2% от массы мышц). Количество гликогена, хранящегося в организме, особенно в мышцах, печени и красных кровяных клетках 2), в основном, зависит от тренировок, базового метаболизма и привычек в еде. Небольшое количество гликогена находится в почках и даже меньшее количество – в некоторых глиальных клетках мозга и лейкоцитов. Матка также хранит гликоген во время беременности, чтобы питать эмбрион.

Структура

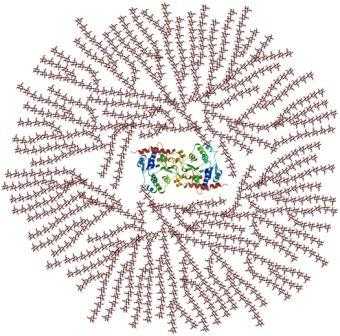Гликоген представляет собой разветвленный биополимер, состоящий из линейных цепей глюкозных остатков с дальнейшими цепями, разветвляющимися каждые 8-12 глюкоз или около того. Глюкозы связаны линейно с помощью α (1 → 4) гликозидных связей от одной глюкозы к следующей. Ветви связаны с цепями, от которых они отделяются гликозидными связями α (1 → 6) между первой глюкозой новой ветви и глюкозой в цепочке стволовых клеток 3). Из-за того, как синтезируется гликоген, каждая гликогенная гранула имеет в своем составе гликогениновый белок. Гликоген в мышцах, печени и жировых клетках хранится в гидратированной форме, состоящей из трех или четырех частей воды на часть гликогена, связанной с 0,45 миллимолями калия на грамм гликогена.

Функции

Печень

Поскольку еда, содержащая углеводы или белок, съедается и переваривается, уровень глюкозы в крови повышается, а поджелудочная железа выделяет инсулин. Кровь глюкозы из воротной вены поступает в клетки печени (гепатоциты). Инсулин воздействует на гепатоциты, чтобы стимулировать действие нескольких ферментов, включая гликогенсинтазу. Молекулы глюкозы добавляются к цепям гликогена до тех пор, пока как инсулин, так и глюкоза остаются обильными. В этом постпрандиальном или «сытом» состоянии печень берет больше глюкозы из крови, чем высвобождает. После того, как еда была переварена и уровень глюкозы начинает падать, секреция инсулина снижается, и синтез гликогена прекращается. Когда это необходимо для энергии, гликоген разрушается и снова превращается в глюкозу. Гликогенфосфорилаза является основным ферментом распада гликогена. В течение следующих 8-12 часов, глюкоза, полученная из гликогена печени, является основным источником глюкозы в крови, используемой остальной частью организма для получения топлива. Глюкагон, еще один гормон, вырабатываемый поджелудочной железой, во многом служит противодействующим сигналом к инсулину. В ответ на уровень инсулина ниже нормы (когда уровень глюкозы в крови начинает падать ниже нормального диапазона), глюкагон секретируется в возрастающих количествах и стимулирует как гликогенолиз (распад гликогена), так и глюконеогенез (производство глюкозы из других источников).

Мышцы

Гликоген мышечной клетки, по-видимому, функционирует как непосредственный резервный источник доступной глюкозы для мышечных клеток. Другие ячейки, которые содержат небольшие количества, также используют его локально. Поскольку мышечным клеткам не хватает глюкозо-6-фосфатазы, которая требуется для приема глюкозы в кровь, гликоген, который они хранят, доступен исключительно для внутреннего использования и не распространяется на другие клетки. Это контрастирует с клетками печени, которые по требованию легко разрушают свой сохраненный гликоген в глюкозу и отправляют его через кровоток в качестве топлива для других органов.

История

Гликоген был обнаружен Клодом Бернардом. Его эксперименты показали, что в печени содержится вещество, которое может привести к восстановлению сахара под действием «фермента» в печени. К 1857 году он описал выделение вещества, которое он назвал «la matière glycogène», или «сахарообразующее вещество». Вскоре после открытия гликогена в печени, А. Сансон обнаружил, что мышечная ткань также содержит гликоген. Эмпирическая формула для гликогена (C6h20О5)n был установлен Кекуле в 1858 году. 4)

Метаболизм

Синтез

Синтез гликогена, в отличие от его разрушения, является эндергоническим – он требует ввода энергии. Энергия для синтеза гликогена приходит из уридин трифосфата (УТФ), который реагирует с глюкозо-1-фосфатом, образуя УДФ-глюкозу, в реакции, катализируемой УТФ-глюкозо-1-фосфатной уридилтрансферазой. Гликоген синтезируется из мономеров УДФ-глюкозы изначально белком гликогенином, который имеет два тирозиновых анкера для восстанавливающего конца гликогена, поскольку гликогенин является гомодимером. После того, как к тирозиновому остатку добавляется около восьми молекул глюкозы, фермент гликогенсинтаза постепенно удлиняет гликогенную цепь с использованием УДФ-глюкозы, добавляя α (1 → 4) -связанную глюкозу. Фермент гликогена катализирует перенос концевого фрагмента из шести или семи остатков глюкозы из нередуцирующего конца в гидроксильную группу С-6 глюкозного остатка глубже во внутреннюю часть молекулы гликогена. Разветвляющийся фермент может действовать только на ветку, имеющую, по меньшей мере, 11 остатков, и фермент может переноситься в одну и ту же цепь глюкозы или соседние цепи глюкозы.

Гликогенолиз

Гликоген расщепляется от нередуцирующих концов цепи ферментом гликогенфосфорилазы с получением мономеров глюкозо-1-фосфата. In vivo, фосфорилиз протекает в направлении распада гликогена, поскольку соотношение фосфата и глюкозо-1-фосфата обычно больше 100. 5) Затем глюкозо-1-фосфат превращается в 6-фосфат глюкозы (G6P) фосфоглюкомтазой. Для удаления α (1-6) ветвей в разветвленном гликоге необходим специальный ферментационный фермент, преобразующий цепочку в линейный полимер. Полученные мономеры G6P имеют три возможных судьбы: G6P может продолжаться по пути гликолиза и использоваться в качестве топлива. G6P может проникать через пентозофосфатный путь через фермент глюкозо-6-фосфатдегидрогеназу для получения НАДФН и 5-углеродных сахаров. В печени и почках, G6P можно дефосфорилировать обратно в глюкозу ферментом глюкозо-6-фосфатазой. Это последний шаг в пути глюконеогенеза.

Клиническая значимость

Нарушения метаболизма гликогена

Наиболее распространенным заболеванием, при котором метаболизм гликогена становится ненормальным, является диабет, при котором из-за аномальных количеств инсулина гликоген печени может аномально накапливаться или истощаться. Восстановление нормального метаболизма глюкозы обычно нормализует метаболизм гликогена. При гипогликемии, вызванной чрезмерным уровнем инсулина, количества гликогена в печени высоки, но высокие уровни инсулина предотвращают гликогенолиз, необходимый для поддержания нормального уровня сахара в крови. Глюкагон является распространенным методом лечения этого типа гипогликемии. Различные врожденные ошибки метаболизма вызваны недостатками ферментов, необходимых для синтеза или расщепления гликогена. Они также называются заболеваниями, связанными с хранением гликогена.

Эффект истощения гликогена и выносливость

Спортсмены, бегающие на длинные дистанции, такие как марафонские бегуны, лыжники и велосипедисты, часто испытывают истощение гликогена, когда почти все запасы гликогена в организме спортсмена истощаются после длительных нагрузок без достаточного потребления углеводов. Истощение гликогена может быть предотвращено тремя возможными способами. Во-первых, во время упражнения углеводы с максимально возможной скоростью преобразования в глюкозу крови (высокий гликемический индекс) поступают непрерывно. Наилучший результат этой стратегии заменяет около 35% глюкозы, потребляемой при сердечных ритмах, выше примерно 80% от максимума. Во-вторых, благодаря адаптационным тренировкам на выносливость и специализированным схемам (например, тренировки с низкой степенью выносливости плюс диета), организм может определять мышечные волокна типа I для улучшения эффективности использования топлива и рабочей нагрузки для увеличения процента жирных кислот, используемых в качестве топлива, 6) чтобы сберечь углеводы. В-третьих, при потреблении больших количеств углеводов после истощения запасов гликогена в результате физических упражнений или диеты, организм может увеличить емкость хранилищ внутримышечных гликогенов. Этот процесс известен как «углеводная нагрузка». В общем, гликемический индекс источника углеводов не имеет значения, поскольку чувствительность мышечного инсулина в результате временного истощения гликогена увеличивается. 7) При недостатке гликогена, спортсмены часто испытывают сильную усталость, до такой степени, что им может быть трудно просто ходить. Что интересно, самые лучшие профессиональные велосипедисты в мире, как правило, заканчивают 4-5-ступенчатую гонку прямо на пределе истощения гликогена с использованием первых трех стратегий. Когда спортсмены употребляют углевод и кофеин после истощающих упражнений, их запасы гликогена, как правило, пополняются быстрее 8), однако минимальная доза кофеина, при которой наблюдается клинически значимое влияние на насыщение гликогена, не установлена.

:Tags

Список использованной литературы:
1) Kreitzman SN, Coxon AY, Szaz KF (1992). «Glycogen storage: illusions of easy weight loss, excessive weight regain, and distortions in estimates of body composition» (PDF). The American Journal of Clinical Nutrition. 56 (1 Suppl): 292s–293s. PMID 1615908 2) Miwa I, Suzuki S (November 2002). «An improved quantitative assay of glycogen in erythrocytes». Annals of Clinical Biochemistry. 39 (Pt 6): 612–3. PMID 12564847. doi:10.1258/000456302760413432 3) Berg, Tymoczko & Stryer (2012). Biochemistry (7th, International ed.). W. H. Freeman. p. 338. ISBN 1429203145. 4) F. G. Young (1957). «Claude Bernard and the Discovery of Glycogen». British Medical Journal. 1 (5033 (Jun. 22, 1957)): 1431–7. JSTOR 25382898. doi:10.1136/bmj.1.5033.1431 5) Stryer, L. (1988) Biochemistry, 3rd ed., Freeman (p. 451) 7) McDonald, Lyle. The Ultimate Diet 2.0. Lyle McDonald, 2003 8) Beelen M, Burke LM, Gibala MJ, van Loon L JC (December 2010). «Nutritional strategies to promote postexercise recovery». International Journal of Sport Nutrition and Exercise Metabolism. 20 (6): 515–532. PMID 21116024. doi:10.1123/ijsnem.20.6.515

гликоген.txt · Последние изменения: 2017/08/23 10:02 — nataly



Source: lifebio.wiki

Мы в соц.сетях:

Больше информации:

  • лфк при мкб При мочекаменной болезни широко применяются различные комплексы лечебной […]
  • узи печени с нагрузкой УЗИ желчного пузыря с определением функции – достаточно информативная […]
  • диета при холестерине повышенном у женщин Содержание статьи: Наличие холестерина в организме жизненно необходимо. Именно он […]
  • препараты от холецистита панкреатита Холецистит представляет собой патологический процесс в желчном пузыре. Почти во всех […]
  • карсил показания цена Карсил — гепатопротекторный препарат, в состав которого входит […]
  • какова функция желчи выделяемой печенью Желчь — секрет, вырабатываемый печенью. Она является важнейшим элементом, участвующим в […]
  • мирамистин гепатит Здравствуйте.Препарат: раствор хлоргексидина биглюконата 0,05% убивает грамположительные […]
  • сколько можно пить воды с одной почкой Часто люди, имеющие одну почку, живут много лет не болея, и только случайно узнают, что […]
  • гиперазотемия продукционная […]
  • как удалить коралловидный камень в почке Коралловидный камень в почке, увы, вряд ли можно считать редкостью, так как данный […]
Опубликовано в Без рубрики
Комментариев нет »

gepasoft.su

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *