Площади плоских фигур
Площадь простой фигуры – это положительная величина, численное значение которой обладает следующими свойствами:
- равные фигуры имеют равные площади;
- если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей;
- площадь квадрата со стороной, равной единице измерения, равна единице.
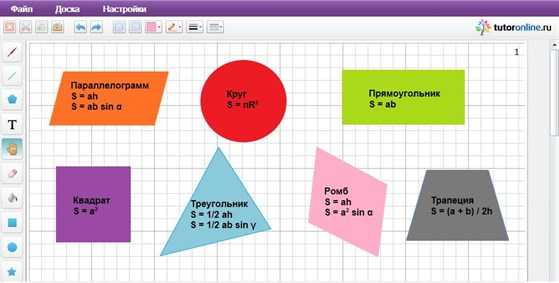 Площадь прямоугольника можно найти следующим образом:
Площадь прямоугольника можно найти следующим образом:
S = ab,
Где a и b – стороны прямоугольника.
Квадрат – это прямоугольник, у которого стороны равны, а, значит, площадь квадрата со стороной a равна a2, то есть
S = a2,
где а – его сторона.
Площадь квадрата можно также вычислить по формуле
S = d2/2,
где d – диагональ квадрата.
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне, то есть вычисляется по формуле
S = ah,
где а – его сторона, h – высота, проведённая к этой стороне.
Площадь параллелограмма можно вычислить и по формуле
S = ab sin α,
где а и b – стороны, α – угол параллелограмма.
Ромб – «частный случай» параллелограмма, значит, его площадь можно находить так же, как и площадь параллелограмма. Кроме того, имеются и другие формулы площади ромба:
S = a2 sin α,
где а – сторона ромба, α – угол ромба;
S = 1/2 d1 d2,
где d1и d2 – диагонали ромба.
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне, то есть её можно найти по формуле
S = 1/2 ah.
Есть и другие формулы для нахождения площади треугольника:
S = 1/2 ab sin γ,
где а и b – стороны, γ – угол между этими сторонами.
При необходимости для нахождения площади треугольника можно использовать формулу Герона, древнегреческого учёного, который жил в Александрии в I веке нашей эры:
,
где а, b, с – стороны треугольника, p – его полупериметр p = (а + b + с)/2 .
Площадь трапеции равна произведению полусуммы её оснований на высоту:
S = (а + b) / 2 · h,
где а и b – основания трапеции, h – высота.
Также советуем вам посмотреть наш новый видеоурок по теме нахождения площади плоских фигур:
Данные формулы позволяют нам решать многие геометрические задачи, рассмотрим некоторые из них.
Задача 1.
В параллелограмме ABCD сторона AB = 12 см и диагональ AC = 16 см. Вершина D удалена от диагонали AC на 4 см. Найдите расстояние от точки D до прямой AB.
Решение.
S ABCD = 2S ADC = AC · DM = 64 см2,
а так как S ABCD = AB · DK,
то DK = 64/12,
то есть DK = около 5,33 см.
Ответ. ≈ 5,33 см.
Задача 2.
Через центр О квадрата ABCD со стороной а проведена прямая k, пересекающая сторону AB, но не проходящая через точки A и B. Выразить сумму расстояния от вершин B и C до прямой k через a и b, если b – длина отрезка прямой k, заключённого внутри квадрата.
Решение.
Обозначим искомую сумму через с, тогда в силу центральной симметрии фигуры с = 2 (h1 + h2).
S AOB = 0,25a2, S AOB = 0,25 b (h1 + h2),
откуда 0,25a2, S AOB = 0,25 b (h1 + h2) и с = 2a2/b.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Все формулы площади плоских фигур
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
Формула площади равнобедренной трапеции через стороны и угол
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
R
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
zdesformula.ru
Формулы площадей плоских фигур
Формулы площадей плоских фигур
Формулы площади треугольника
Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

Формула площади треугольника по трем сторонам
Формула Герона
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,
— полупериметр треугольника.
Формулы площади квадрата
Формула площади квадрата по длине стороныПлощадь квадрата равна квадрату длины его стороны.

Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
a — длины сторон квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторонгде S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма
Формула площади параллелограмма по длине стороны и высотеПлощадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — высота параллелограмма,
γ — угол между диагоналями параллелограмма,
α — угол между сторонами параллелограмма,
d1, d2 — длины диагоналей параллелограмма.
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
a – длина стороны ромба,
h — высота ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей ромба.
Формулы площади трапеции
Формула Герона для трапеции
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — площадь трапеции,
a, b — длины оснований трапеции,
c, d — длины боковых сторон трапеции,
h — высота трапеции,
— полупериметр трапеции.
Формулы площади выпуклого четырехугольника
Формула площади четырехугольника по длине диагоналей и углу между нимиПлощадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.

Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
Формула площади четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
— полусумма двух противоположных углов четырехугольника,
— полупериметр четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность
Формулы площади круга
Формула площади круга через радиусПлощадь круга равна произведению квадрата радиуса на число пи.

Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
infourok.ru
Все формулы площади плоских фигур
Все формулы площади плоских фигур
Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
R- радиус вписанной окружности
D- диаметр вписанной окружности
O- центр вписанной окружности
H- высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d- диагональ трапеции
α,β- углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c- боковая сторона
m- средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
Площадь треугольника по стороне и двум углам, формула.
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Площадь правильного многоугольника, (S):
Формула (Герона) площади треугольника через полупериметр (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h – высота
Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h – высота
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
p = (a+d+c)/2
Формула радиуса описанной окружности трапеции, (R)
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
.Доказать, что площадь вписанного четырёхугольника равна
\/(р — а)(р — b) (р — с) (р — d),
где р — полупериметр и а, b, с и d — стороны четырёхугольника.
Доказать, что площадь вписанного в круг четырёхугольника равна
1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.
S = √[ a • ƀ • c • d] • sin ½ (α + β). — Читайте подробнее на FB.ru:
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:
где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты
а описанного (рис. 1.14, б) () – по формуле
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
Формула Пика
Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, — число клеток, которые целиком лежат внутри многоугольника, и — число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку .
Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
.
studfiles.net
1. Вычисление площадей плоских фигур.
Если плоская фигура ограничена прямыми и кривыми, причем,, то её площадь вычисляется по формуле
 .
.
В
отдельных случаях левая граница 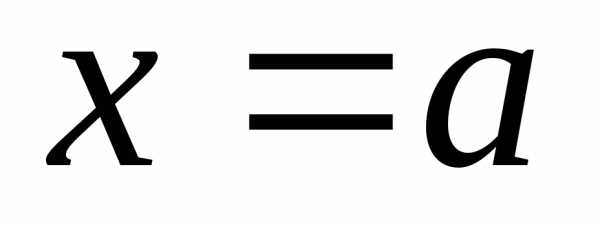 (или
правая граница
(или
правая граница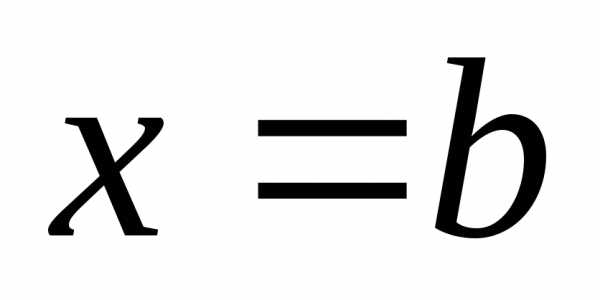 )
может выродиться в точку пересечения
кривых
)
может выродиться в точку пересечения
кривых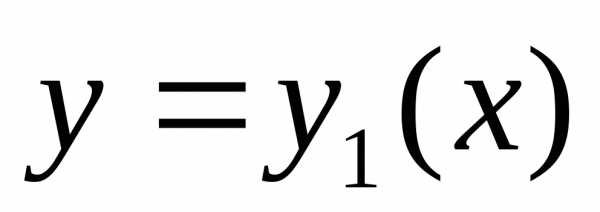 и
и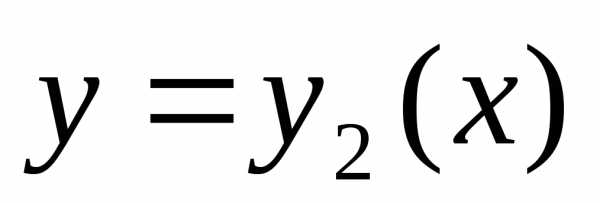 .
В этих случаях величины
.
В этих случаях величины и
и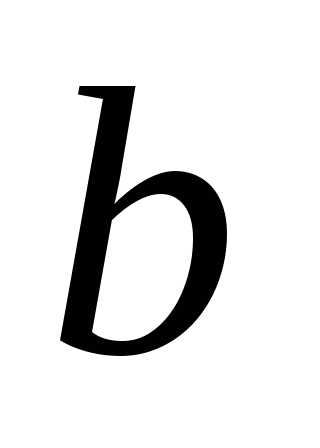 отыскиваются
как абсциссы точек пересечения указанных
кривых (см.рис.4.1.)
отыскиваются
как абсциссы точек пересечения указанных
кривых (см.рис.4.1.)
Если граница фигуры задана параметрическими уравнениями, то площадь фигуры вычисляется по одной из трёх формул:
,
где  и
и 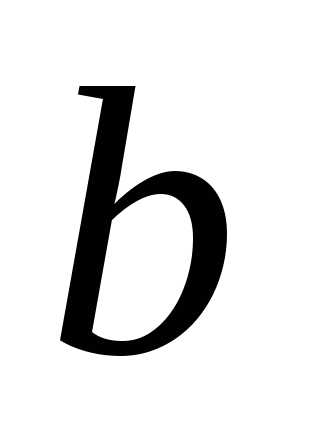 —
значения параметра
—
значения параметра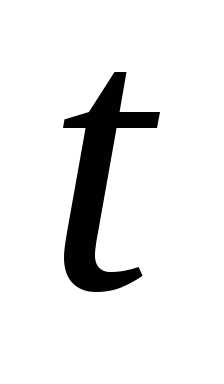 ,соответствующие
началу и концу обхода контура в
положительном направлении (при котором
фигура остается слева).
,соответствующие
началу и концу обхода контура в
положительном направлении (при котором
фигура остается слева).
В
полярных координатах площадь сектора,
ограниченного дугой кривой
и
лучами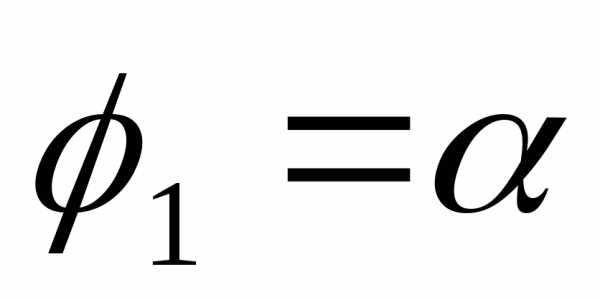 и
и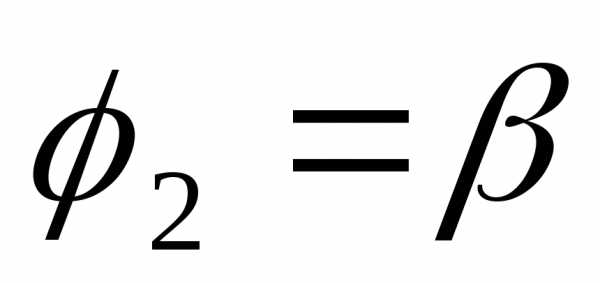 , выражается
формулой
, выражается
формулой
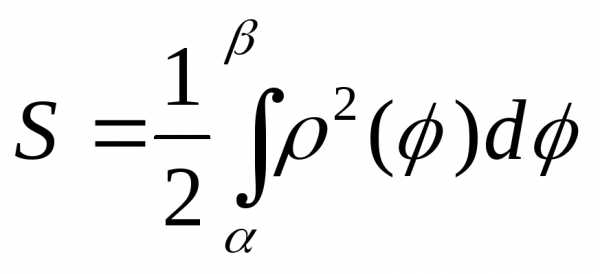 .
.
Пример.
Вычислить
площадь фигуры, ограниченной прямыми 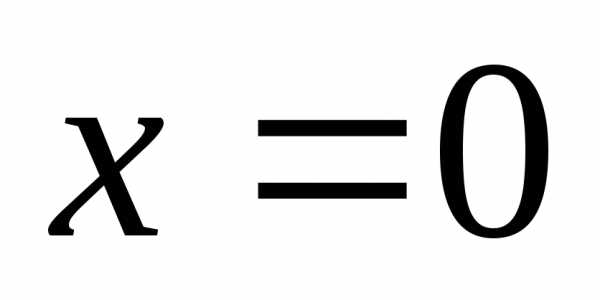 ,
,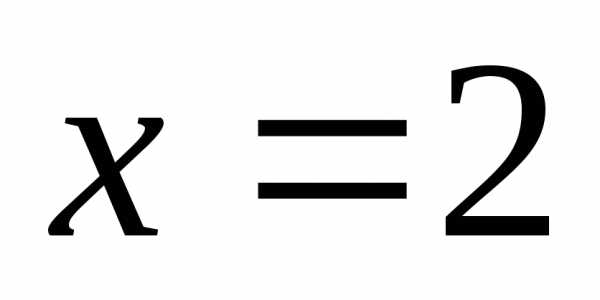 и кривыми
и кривыми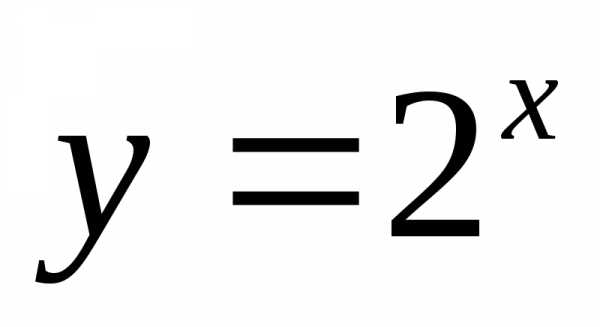 ,.
,.
Решение.
Так
как максимум функции достигается
в точке 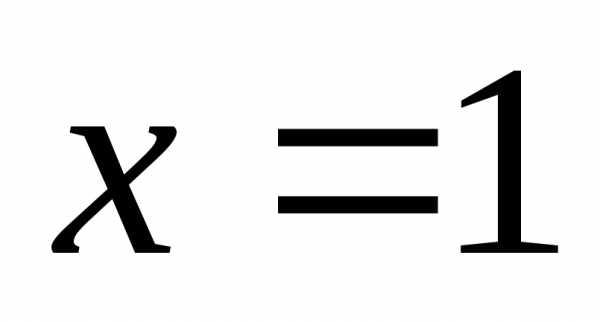 и равен 1, а функцияна отрезке
и равен 1, а функцияна отрезке ,
то (см. рис. 4.2.)
,
то (см. рис. 4.2.)
.
Пример.
Вычислить
площадь фигуры, ограниченной параболами 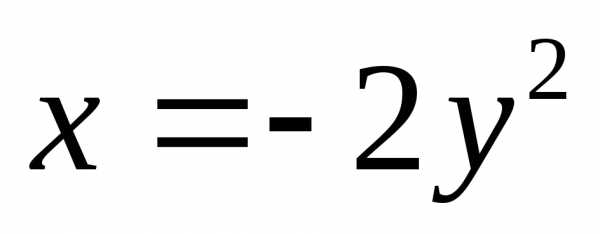 ,
,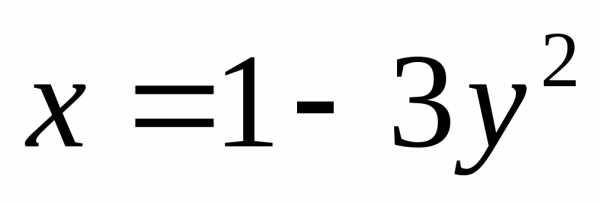 .
.
Решение.
Решая систему уравнений
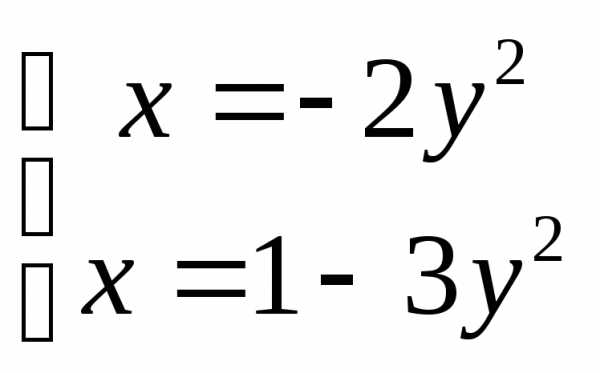
найдем
ординаты точек пересечения кривых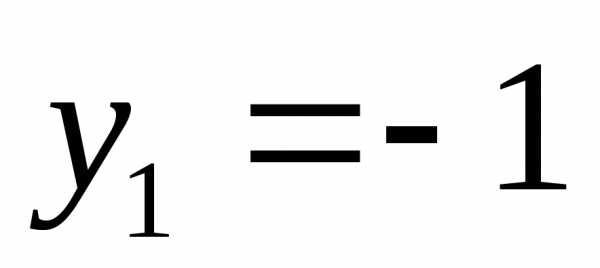 ,
,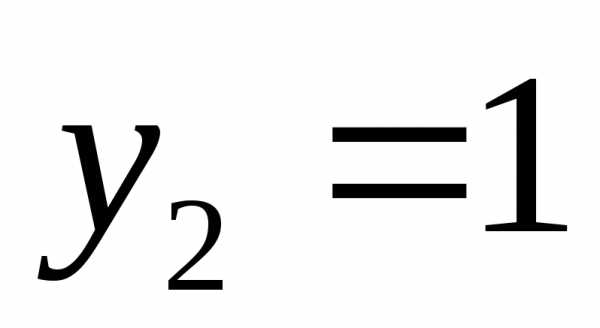 .
.
Так как при,то
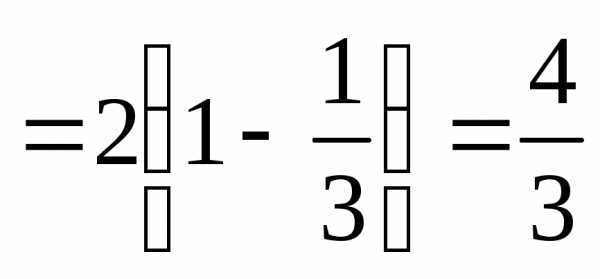 .
.
Пример.
Вычислить площадь фигуры, ограниченной эллипсом
Решение.
Здесь удобно вычислить сначала
.
Отсюда
.
Пример.
Найти площадь фигуры, ограниченной одним лепестком кривой (лемниската).
Решение.
Правая
часть уравнения кривой неотрицательна
при значениях  , для которых.
, для которых.
Поэтому первый лепесток лежит в угловом секторе, в котором
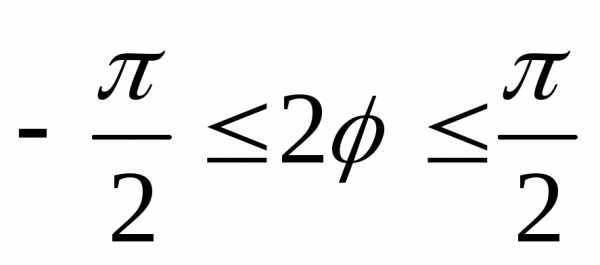 ,т.е.
,т.е. 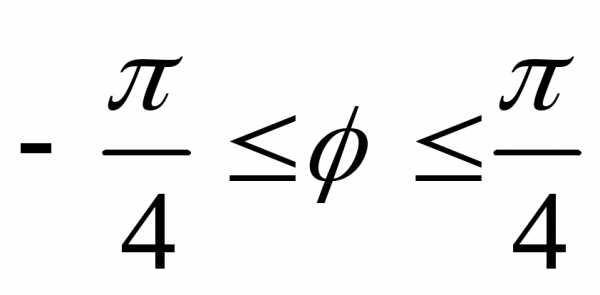 .
.
Следовательно,
.
2. Вычисление длин дуг плоских кривых
Если
плоская кривая задана уравнением в
декартовых координатах 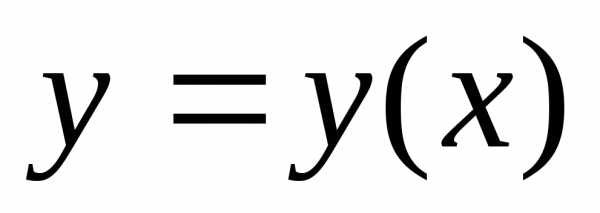 и производная
и производная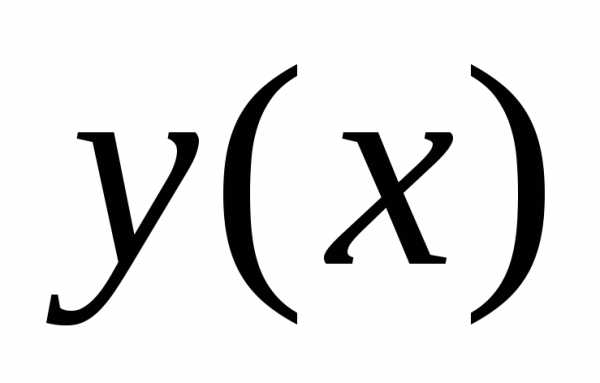 непрерывна,
то длина дуги этой кривой вычисляется
по формуле
непрерывна,
то длина дуги этой кривой вычисляется
по формуле
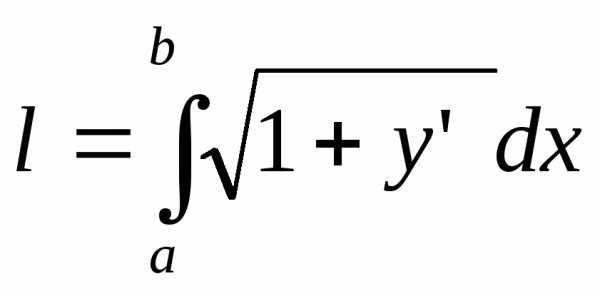 ,
,
где  и
и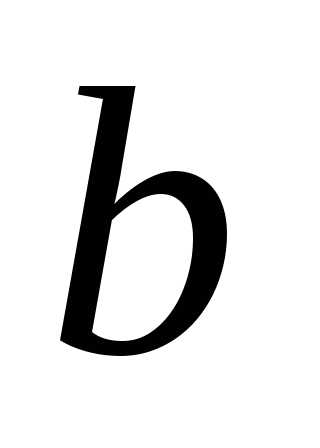 -абсциссы
концов данной дуги.
-абсциссы
концов данной дуги.
Если
кривая задана уравнениями в параметрической
форме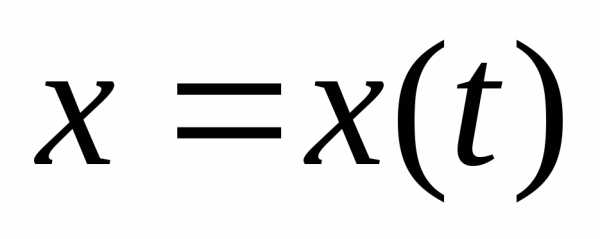 ,
,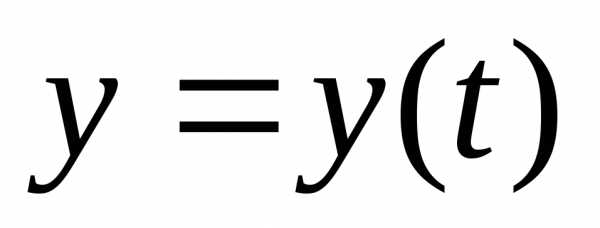 и производные
и производные 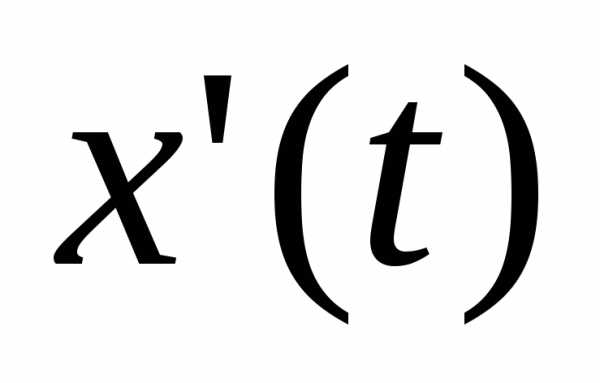 и
и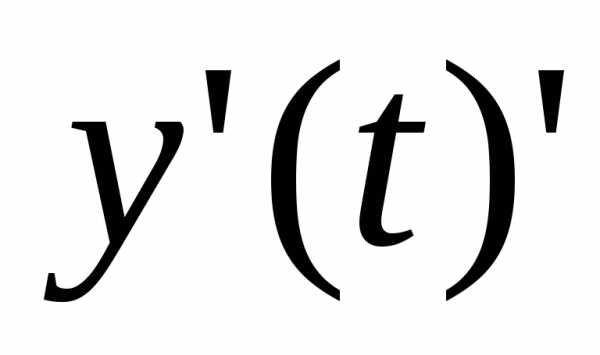 непрерывны
на отрезке
непрерывны
на отрезке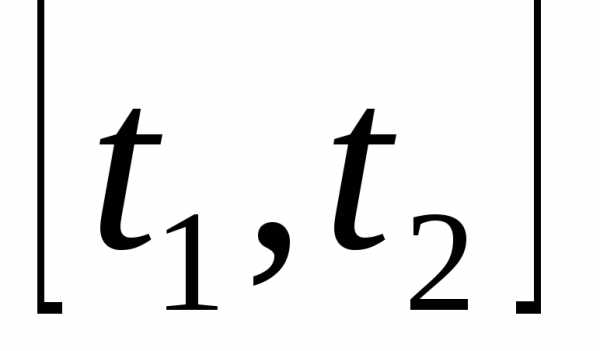 , то длина
дуги кривой выражается формулой
, то длина
дуги кривой выражается формулой
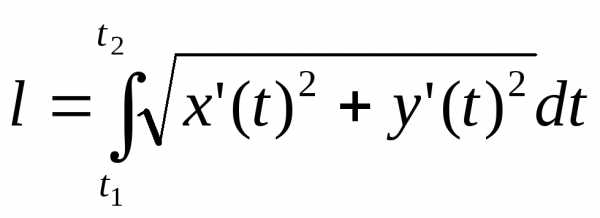 ,
,
где  и
и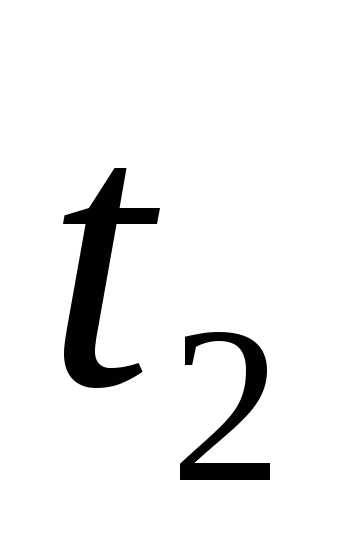 — значения параметра
— значения параметра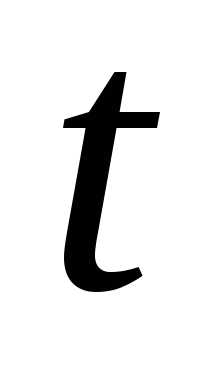 , соответствующие
концам дуги
, соответствующие
концам дуги  .
.
Если
кривая задана уравнением
в
полярных координатах, то длина дуги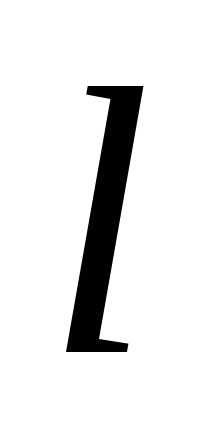 кривой выражается интегралом
кривой выражается интегралом
,
где  и
и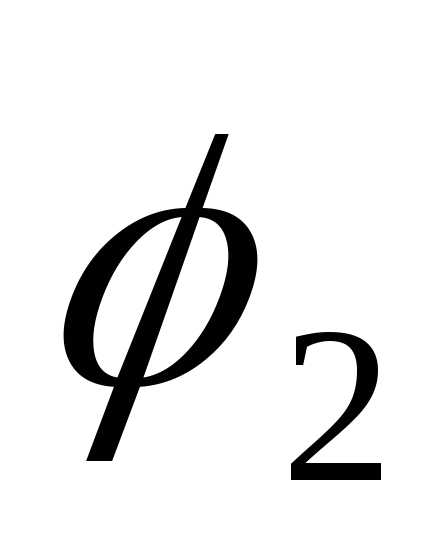 — значения полярного угла
— значения полярного угла в
концах дуги
в
концах дуги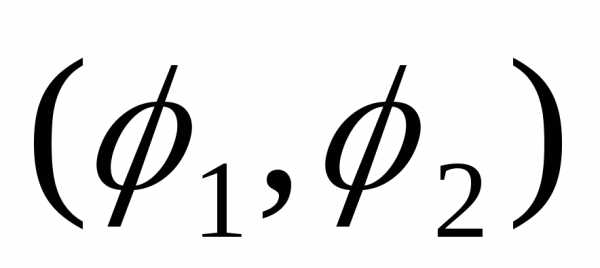 .
.
Пример.
Вычислить
длину дуги полукубической параболы  , заключенной
между точками
, заключенной
между точками 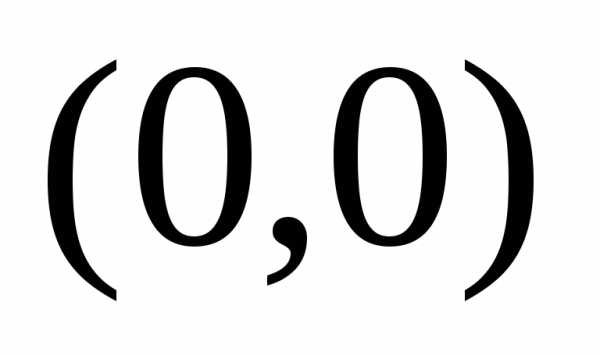 и
и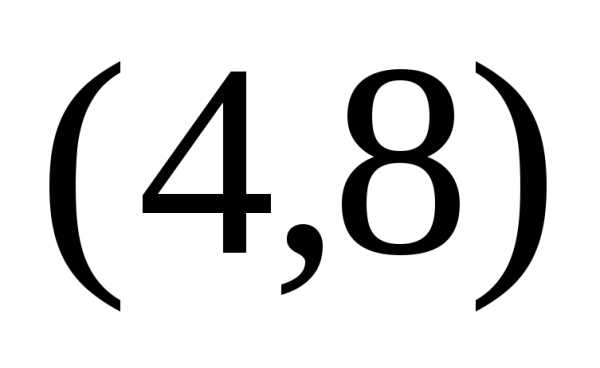 .
.
Решение.
Функция 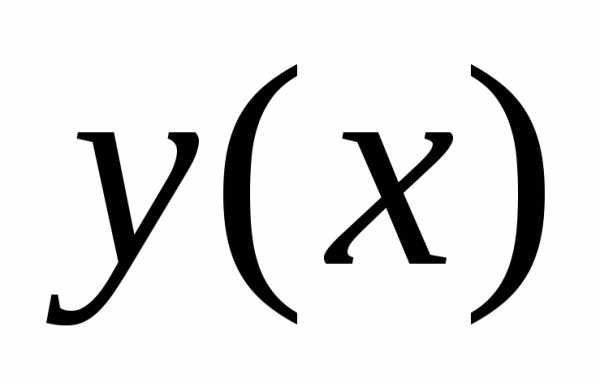 определена
при
определена
при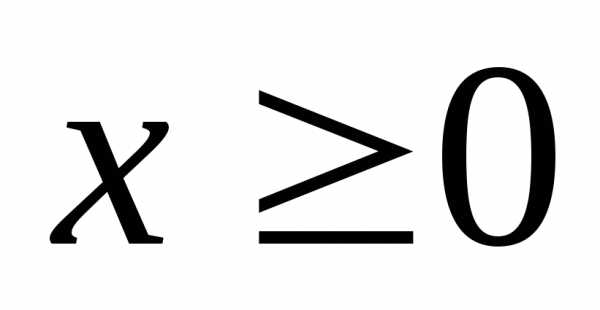 .
Поскольку данные точки
.
Поскольку данные точки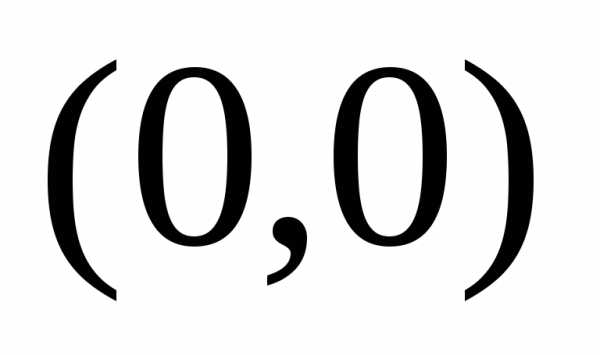 и
и 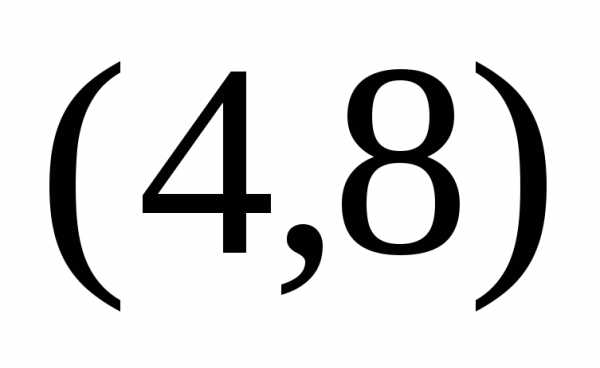 лежат в первой четверти, то
лежат в первой четверти, то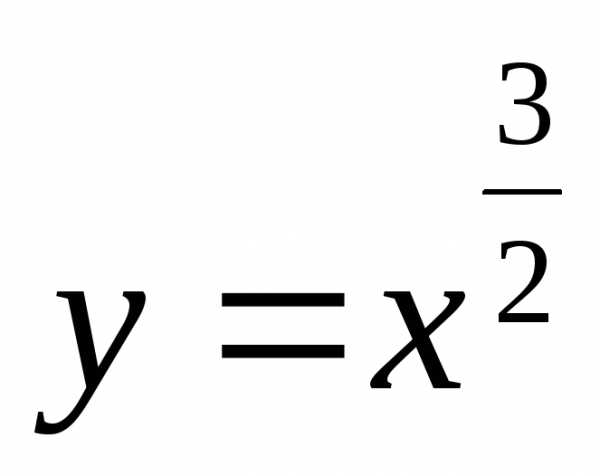 .
.
Отсюда
,
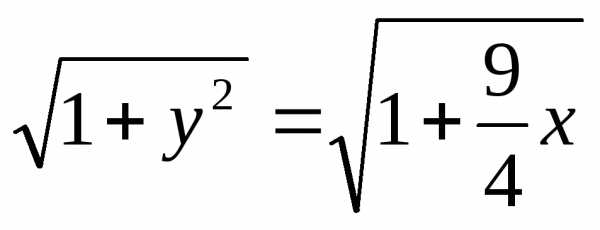 .
.
Следовательно,
.
Пример.
Вычислить длину дуги развертки круга
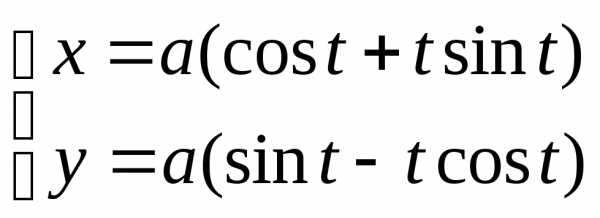 от
от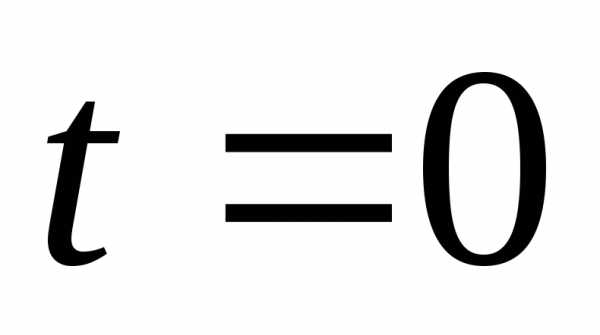 до
до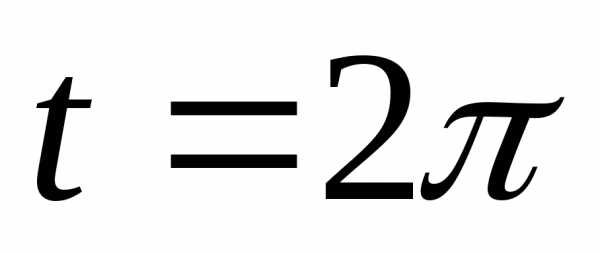 .
.
Решение.
Дифференцируя
по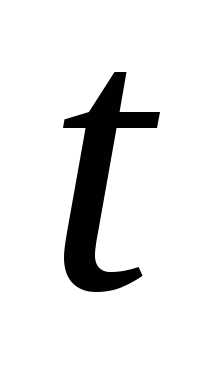 , получим
, получим
,
откуда .
Следовательно,
.
Пример.
Найти длину первого витка архимедовой спирали.
Решение.
Первый
виток архимедовой спирали образуется
при изменении полярного угла от 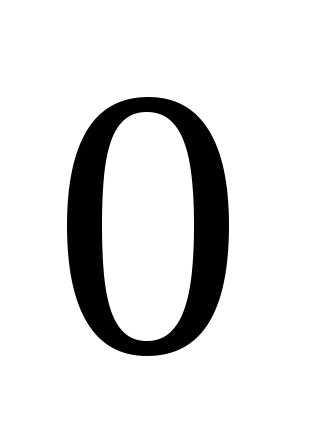 до
до .
Поэтому
.
Поэтому
.
Вычислим
первообразную для функции 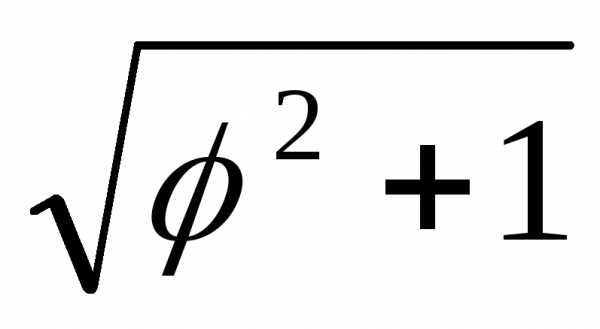 методом интегрирования по частям:
методом интегрирования по частям:
.
Откуда
,
,
и, следовательно,
.
3. Вычисление объемов тел
Объем тела выражается интегралом
 ,
,
где 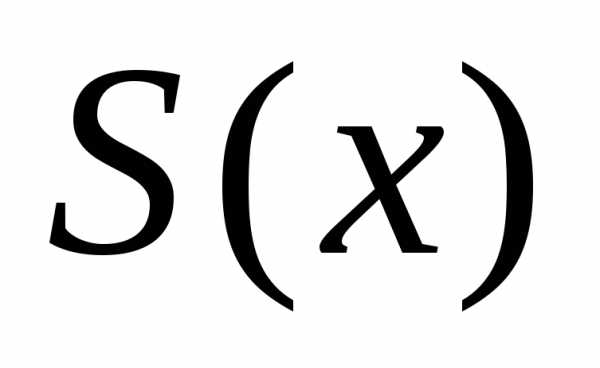 —
площадь сечения тела плоскостью,
перпендикулярной к оси
—
площадь сечения тела плоскостью,
перпендикулярной к оси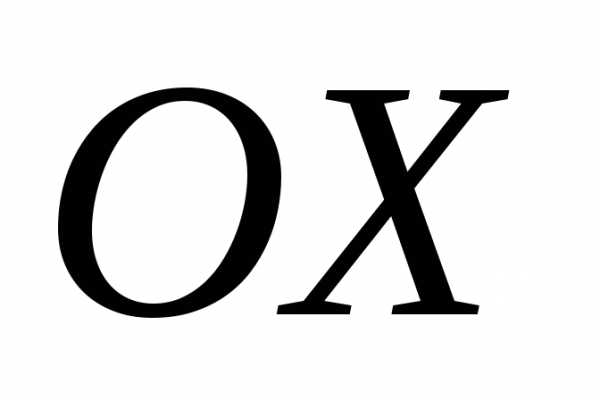 в точке с абсциссой
в точке с абсциссой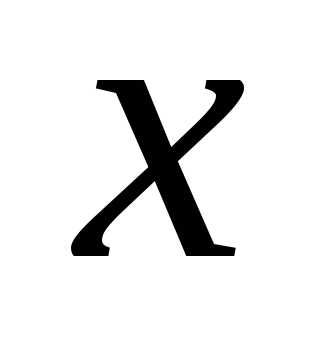 .
. и
и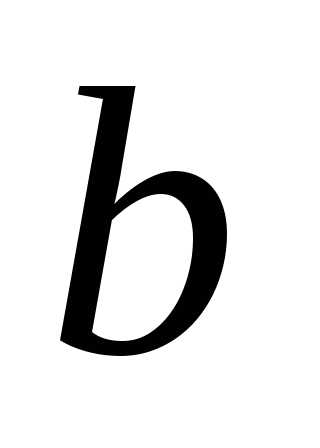 — левая и правая границы изменения
— левая и правая границы изменения ,
, непрерывна
при
непрерывна
при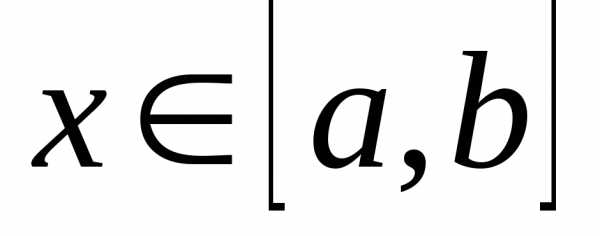 .
.
Объем
тела, образованного вращением вокруг
оси 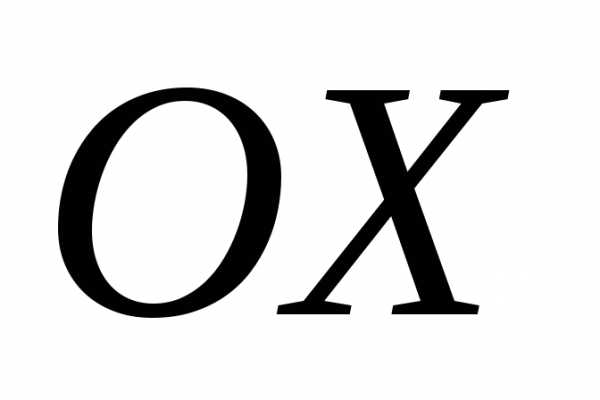 криволинейной трапеции, ограниченной
кривой,
осью абсцисс и прямыми,
криволинейной трапеции, ограниченной
кривой,
осью абсцисс и прямыми,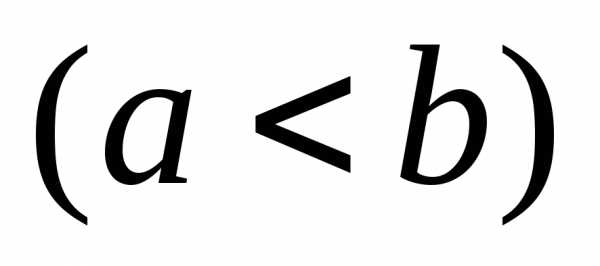 , выражается
интегралом
, выражается
интегралом
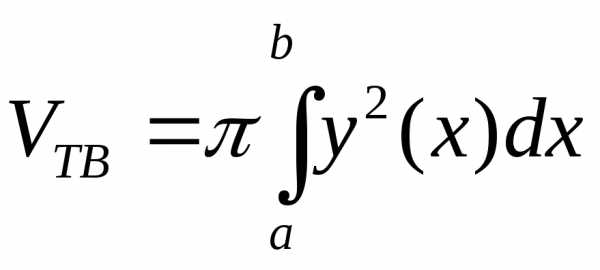 .
.
Объем
тела, образованного вращением вокруг
оси 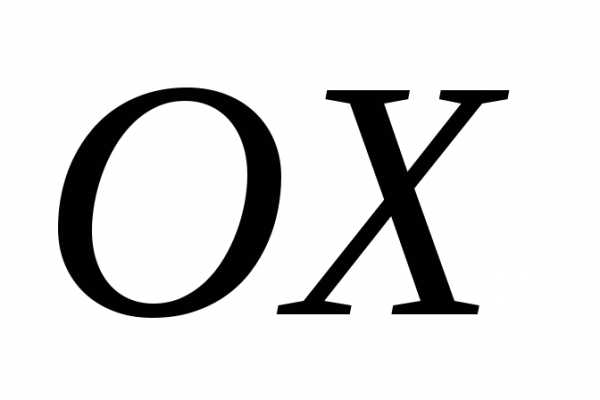 фигуры,
ограниченной кривыми
фигуры,
ограниченной кривыми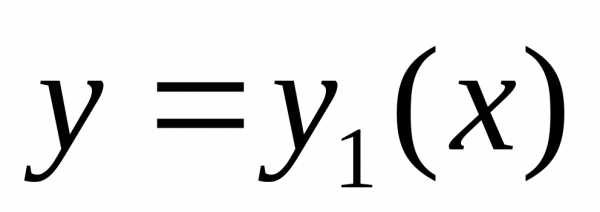 ии прямыми
ии прямыми и
и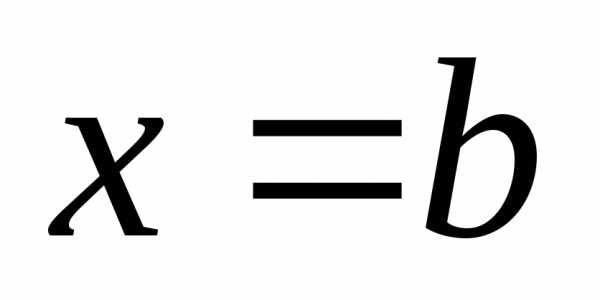 ,
выражается формулой
,
выражается формулой
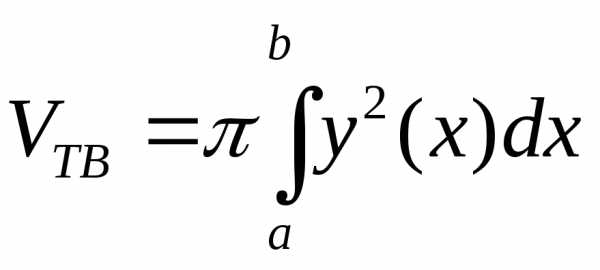 .
.
Если кривая задана параметрически или в полярных координатах, то следует сделать соответствующую замену переменной в указанных формулах.
Пример.
Найти объем эллипсоида
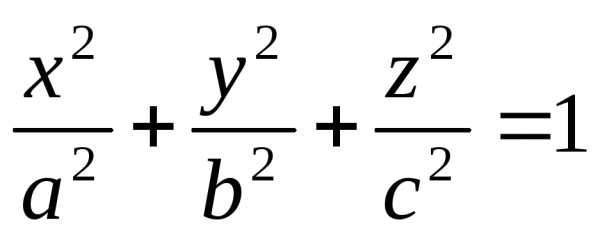 .
.
Решение.
Сечение эллипсоида плоскостью есть эллипс

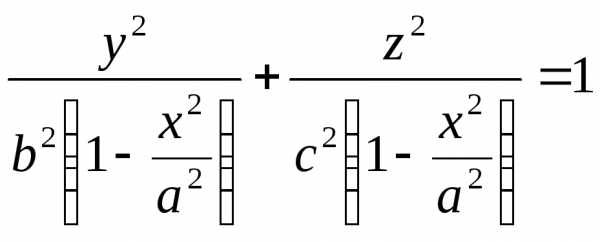
с
полуосями  и
и .
.
Следовательно площадь сечения
Поэтому объем эллипсоида
.
Положив, в частности,,получим объем шара
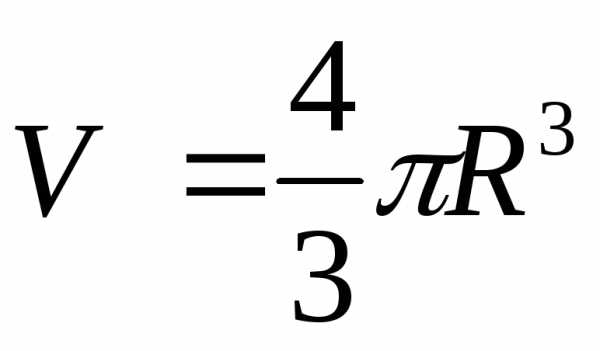 .
.
Пример.
Вычислить вокруг оси абсцисс объем тела, которое образуется при вращении одной арки циклоиды
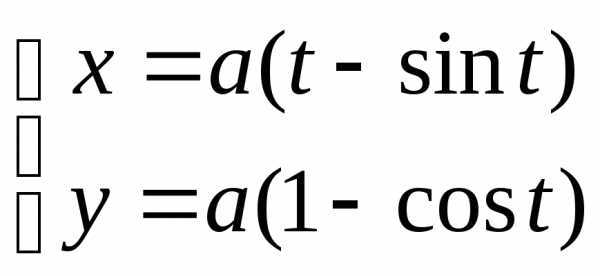
вокруг оси абсцисс.
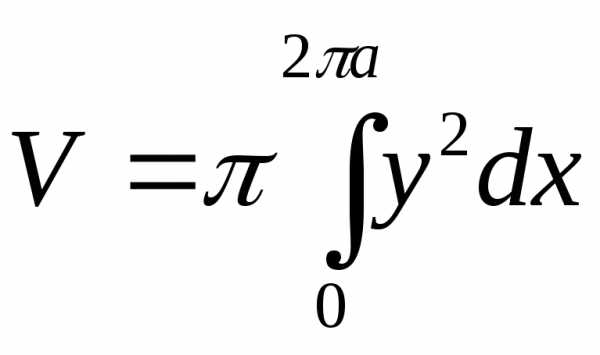
делаем замену переменной, полагая
.
.
Контрольная работа №4 по теме
studfiles.net
Площади фигур | Формулы с примерами
Площади фигур формулыПлощадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь ромба
Площадь треугольника

Площадь правильного треугольника
Площадь полупериметра
Площадь трапеции
Площадь описанного n угольника
Площадь произвольного четырехугольника
Площадь окружности
Площадь круга
formula-xyz.ru
Площадь плоской фигуры — Циклопедия
Видеоурок по математике «Вычисление площади фигуры» // Математика от alwebra.com.ua [4:30] Лекция 19.Вычисление площади плоской фигуры // NWTU [7:58]Площадь плоской фигуры — это действительное число, характеризующее плоскую фигуру в единицах измерения площади.
[править] Прямоугольная система координат
Площадь плоской фигуры, заданной неравенством f(x, y)≤0, считается по формулам:
- [math]S_\text{фиг}=\iint\limits_{f(x,y) \ge 0}1dxdy \Leftrightarrow S_\text{фиг}=\int\limits_{x_1}^{x_2}dx\int\limits_{y_1(x)}^{y_2(x)}1dy \Leftrightarrow[/math]
- [math]\Leftrightarrow S_\text{фиг}=\int\limits_{x_1}^{x_2}\left.y\right|_{y_1(x)}^{y_2(x)}dx \Leftrightarrow S_\text{фиг}=\int\limits_{x_1}^{x_2} \left[y_2(x)-y_1(x)\right]dx \Leftrightarrow[/math]
- [math]\Leftrightarrow S_\text{фиг}=\int\limits_{y_1}^{y_2}dy\int\limits_{x_1(y)}^{x_2(y)}1dx \Leftrightarrow S_\text{фиг}=\int\limits_{y_1}^{y_2}x\left.\right|_{x_1(y)}^{x_2(y)}dy \Leftrightarrow[/math]
- [math]\Leftrightarrow S_\text{фиг}=\int\limits_{y_1}^{y_2} \left[x_2(y)-x_1(y)\right]dy[/math]
[править] Полярная система координат
Площадь плоской фигуры, заданной неравенством f(rcosφ,rsinφ)≤0, считается по формулам:
- [math]S_\text{фиг}=\iint\limits_{f(r\cos\varphi,r\sin\varphi) \le 0} drd\varphi \Leftrightarrow S_\text{фиг}=\int\limits_{\varphi_1}^{\varphi_2}d\varphi\int\limits_{r_1(\varphi)}^{r_2(\varphi)}rdr \Leftrightarrow [/math]
- [math]\Leftrightarrow S_\text{фиг}=\frac{1}{2}\int\limits_{\varphi_1}^{\varphi_2}\left.r^2\right|_{r_1(\varphi)}^{r_2(\varphi)}d\varphi \Leftrightarrow S_\text{фиг}=\frac{1}{2}\int\limits_{\varphi_1}^{\varphi_2} \left[r_2^2(\varphi)-r_1^2(\varphi)\right]d\varphi[/math]
[править] Параметрически заданная фигура
Площадь плоской фигуры, заданной неравенством f(x(t), y(t))≤0 или системой неравенств, считается по формулам:
- [math]S_\text{фиг}=\int\limits_{f(x(t),y(t)) \le 0}y(t)x’_t(t)dt \Leftrightarrow S_\text{фиг}=\int\limits_{t_1}^{t_2}y(t)x’_t(t)dt \Leftrightarrow[/math]
- [math]S_\text{фиг}=\int\limits_{f(x(t),y(t)) \le 0}x(t)y’_t(t)dt \Leftrightarrow S_\text{фиг}=\int\limits_{t_1}^{t_2}x(t)y’_t(t)dt[/math]
[править] Площади плоских фигур:
[править] Другие формулы
- Бронштейн М. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.428.
cyclowiki.org
