Уравнения и неравенства с модулем 8 класс
Профильная практика
Обобщающая лекция по теме «Уравнения и неравенства с модулем» 8 класс
Вспомним определение модуля числа
Решить простейшие уравнения с модулем с помощью определения:
- | x | = 2
- | x-2 | = 0
- | 3x-5 | = -2
- | 3 – 4x | = 3
- Геометрический смысл модуля
| a | – расстояние от точки А (а) координатной прямой до начала отсчета.
1) | x | = 3 2) | x | ≥ 3 3) | x | ≤ 3
X X X
-3 0 3 -3 0 3 -3 0 3
Ответ: -3;3
Ответ: Ответ: [ — 3; 3]
Решить неравенства, используя геометрический смысл модуля:
4) | 1+x | ≤ 0,3 5) | 3-2x | >
6) | x-2 | ≤ a 7) | 3 – 2x | ≥ a
- Решение уравнений с модулем
Решить уравнение несколькими способами: | x – 1 | = | x – 2 |
1 способ:
2 способ: подмодульные корни x = 1 , x = 2
– + + x-1
– 1 – 2 + x-2
- a) x < 1 б) 1 ≤ x < 2 в) x ≥ 2
1 – x = 2 – x x – 1 = 2 – x x – 1 = x – 2
0x = 1 2x = 3 0x = –1
x = 1,5
Решить самостоятельно а) | x + 3 | = | x – 5 |
б) | x + 6 | + 4x =5
в)
- Где еще мы встречались с модулем?
– тождество
Решить уравнение
так как , то
| x – 7 | = x – 7 , значит
x – 7 ≥ 0 по определению модуля
x ≥ 7
Ответ: [ 7 ; ∞ )
Упростить выражение
1)
2) y
Построить график функции
0 1 x
Построить график функции
- y = | x2 – 5x + 6|
б) y = x2 – 5| x | – 6
в) y =
- Решить неравенство с модулем
x x
0 2 0 6
Ответ: ( 2 ; ∞)
Ответ: (– 6 ; – 2) U (2 ; 6) y
- | x2 + 4x + 3 | > | x + 3 |
решим графическим способом
y = | x2 + 4x +3 |
x2 + 4x +3 = 0
x1 = –1, x2 = –3 – нули функции
, yв = –1
y = | x + 3 |
x
Ответ: (–∞ ; –3 ) U ( –3 ; –2 ) U ( 0 ; ∞ ) –3 –2 –1 0
Решить неравенства самостоятельно:
- | 2x + 3 | > | 4x – 3 |
- | x2 – x + 1 | ≤ | x2 – 3x + 4 |
Обобщающая лекция по теме
«Уравнения и неравенства с параметром»
8 класс
- Для каждого значения а решите уравнение
(5a – 1)x = 2a + 3
если
0x = 3,4
если
- Для каждого b решите уравнение
(b2
– 9)x = b + 3b2 – 9 = 0
b = ± 3
если b = 3, то 0x = 6,
если b = -3, то 0x = 0, x Î R
если b ≠ ± 3, то
- При каком значении а уравнение не имеет решений?
(3x – a)2 +(4x + 1)2 = (5x – 1)2
9x2 – 6ax + a2 + 16x2 +8x + 1 = 25x2 – 10x + 1
10x – 6ax + 8x = – a2
6(3 – a)x = – a2
если а = 3, 0х = – 9,
если а ≠ 3,
Ответ: при а = 3 уравнение не имеет решений.
- Для каких значений b уравнение x2 – bx + 2b – 3 = 0 имеет один корень?
D = 0, D = b2 – 4(2b – 3) = b2 – 8b + 12
b2 – 8b + 12 = 0
D = 64 – 48 = 16
b1 = 6, b2 = 2
Ответ: при b = 6 и b = 2 уравнение имеет один корень
- При каких а уравнение имеет два различных корня?
x2(a – 2) + ax + 1 = 0
квадратное уравнение имеет два различных корня, если D > 0
D = a2 – 4(a – 2) = a2 – 4a + 8
a2 – 4a + 8 >0 Если а = 2, то уравнение будет линейным
y = a2 – 4a + 8 0 + 2x + 1 = 0
D = 16 – 32 < 0 x = — 0,5 1 корень
Ответ: при а ≠ 2 уравнение имеет два
различных корня
a
x Î R
Решите самостоятельно
- Для каждого значения m решите уравнение
Ответ: при m = 4 один корень x = –1 ,
при m = -1 один корень x = 4,
при m ≠ 4, m ≠ –1 два корня x = 4, x = – 1
- Для каждого значения а найдите число различных корней уравнения
(3x – 1)(ax2 + 3x – 2) = 0
Ответ: при один корень
при , а = 0, а = 9 два различных корня
при три различных корня
Автор публикации
не в сети 2 часа
admin
3 Комментарии: 8Публикации: 464Регистрация: 30-11—0001pedagogru.ru
Урок для 8 класса «Уравнения и неравенства с модулем»
Приложение №5
Профильная практика
Урок для 8 класса «Уравнения и неравенства с модулем»
Вспомним определение модуля числа
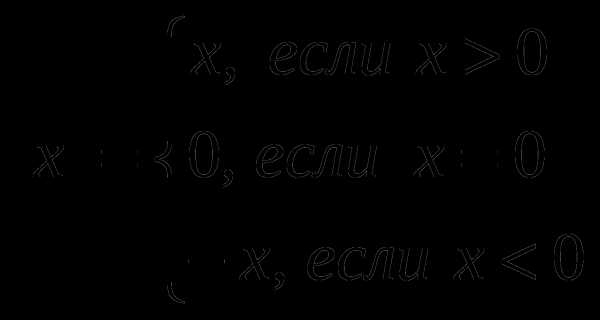
Решить простейшие уравнения с модулем с помощью определения:
| x | = 2
| x-2 | = 0
| 3x-5 | = -2
| 3 – 4x | = 3
Геометрический смысл модуля
| a | – расстояние от точки А (а) координатной прямой до начала отсчета.
1) | x | = 3 2) | x | ≥ 3 3) | x | ≤ 3
X X X
-3 0 3 -3 0 3 -3 0 3
Ответ: -3;3 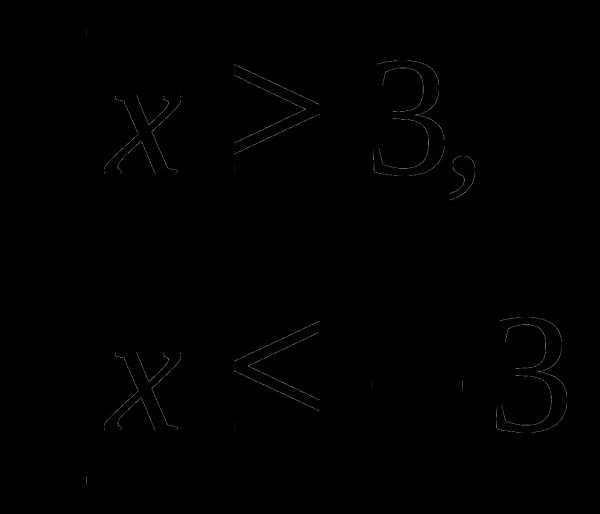
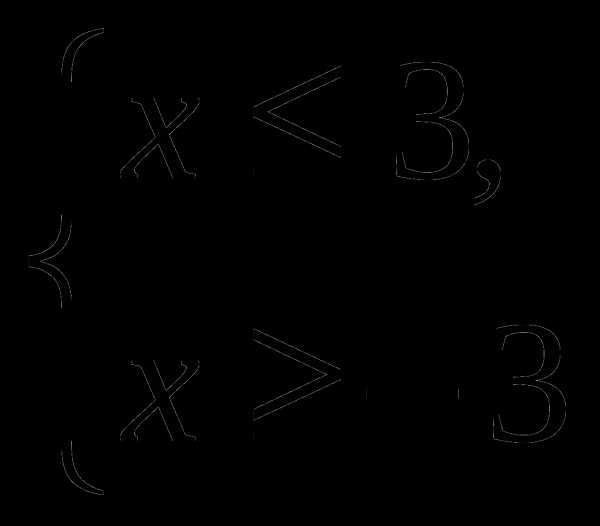
Ответ: Ответ: [ — 3; 3]
Решить неравенства, используя геометрический смысл модуля:
4) | 1+x | ≤ 0,3 5) | 3-2x | > 
6) | x-2 | ≤ a 7) | 3 – 2x | ≥ a
Решение уравнений с модулем
Решить уравнение несколькими способами: | x – 1 | = | x – 2 |
1 способ:
2 способ: подмодульные корни x = 1 , x = 2
– + + x-1
– 1 – 2 + x-2
a) x x x ≥ 2
1 – x = 2 – x x – 1 = 2 – x x – 1 = x – 2
0x = 1 2x = 3 0x = –1
 x = 1,5
x = 1,5 
Решить самостоятельно а) | x + 3 | = | x – 5 |
б) | x + 6 | + 4x =5
в) 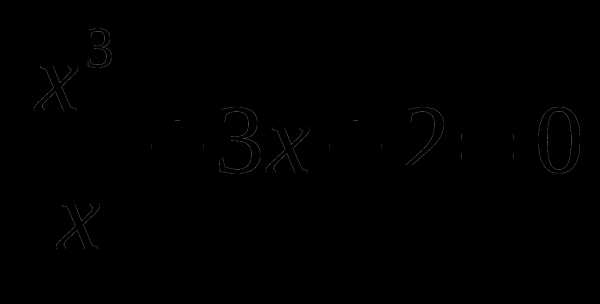
Где еще мы встречались с модулем?
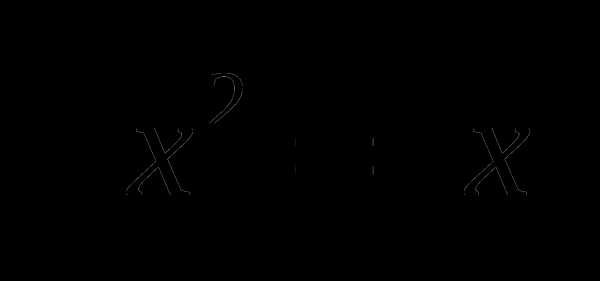
– тождество
Решить уравнение
так как , то
| x – 7 | = x – 7 , значит
x – 7 ≥ 0 по определению модуля
x ≥ 7
Ответ: [ 7 ; ∞ )
Упростить выражение
1)
2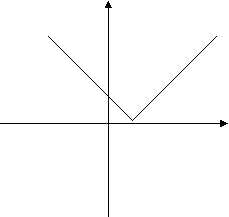 ) y
) y
Построить график функции
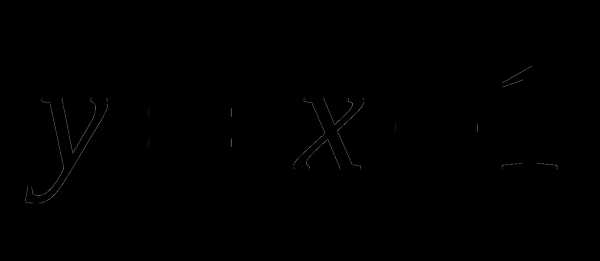 0 1 x
0 1 x
Построить график функции
y = | x2 – 5x + 6|
б) y = x2 – 5| x | – 6
в) y =
Решить неравенство с модулем
| x | > 6 – 2x
 x x
x x
0 2 0 6
Ответ: ( 2 ; ∞)
2

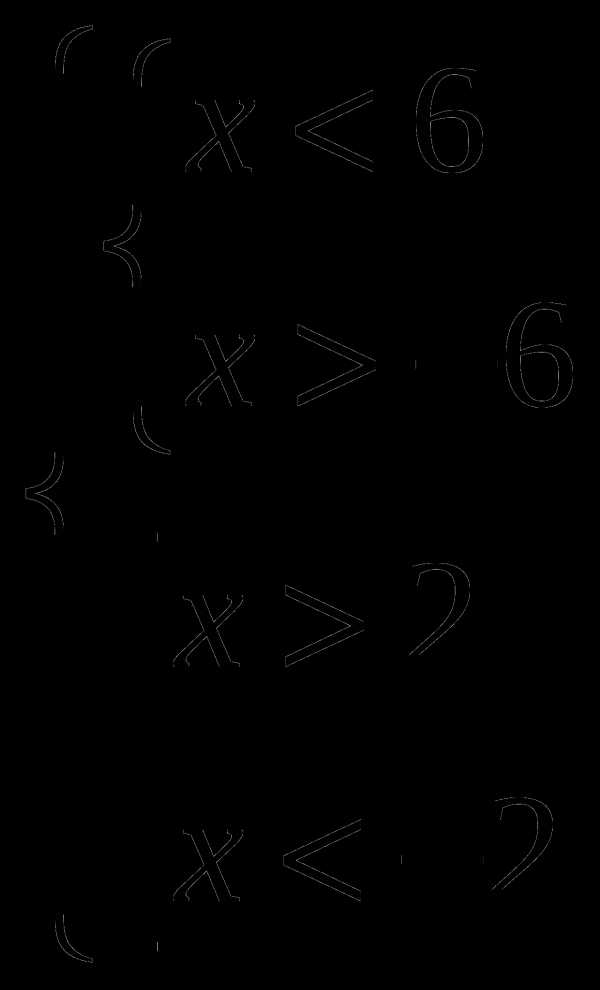
О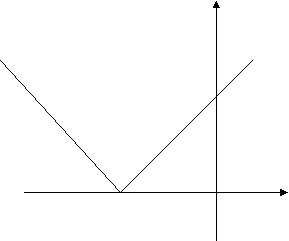 твет: (– 6 ; – 2) U (2 ; 6) y
твет: (– 6 ; – 2) U (2 ; 6) y
| x2 + 4x + 3 | > | x + 3 |
решим графическим способом
y = | x2 + 4x +3 |
x2 + 4x +3 = 0
x1 = –1, x2 = –3 – нули функции
 , yв = –1
, yв = –1
y = | x + 3 |
x
Ответ: (–∞ ; –3 ) U ( –3 ; –2 ) U ( 0 ; ∞ ) –3 –2 –1 0
Решить неравенства самостоятельно:
| 2x + 3 | > | 4x – 3 |
| x2 – x + 1 | ≤ | x2 – 3x + 4 |
Обобщающая лекция по теме
«Уравнения и неравенства с параметром»
8 класс
Для каждого значения а решите уравнение
(5a – 1)x = 2a + 3
если
0x = 3,4

если
Для каждого b решите уравнение
(b2 – 9)x = b + 3
b2 – 9 = 0
b = ± 3
если b = 3, то 0x = 6, 
если b = -3, то 0x = 0, x R
если b ≠ ± 3, то
При каком значении а уравнение не имеет решений?
(3x – a)2 +(4x + 1)2 = (5x – 1)2
9x2 – 6ax + a2 + 16x2 +8x + 1 = 25x2 – 10x + 1
10x – 6ax + 8x = – a2
6(3 – a)x = – a2
если а = 3, 0х = – 9, 
если а ≠ 3, 
Ответ: при а = 3 уравнение не имеет решений.
Для каких значений b уравнение x2 – bx + 2b – 3 = 0 имеет один корень?
D = 0, D = b2 – 4(2b – 3) = b2 – 8b + 12
b2 – 8b + 12 = 0
D = 64 – 48 = 16
b1 = 6, b2 = 2
Ответ: при b = 6 и b = 2 уравнение имеет один корень
При каких а уравнение имеет два различных корня?
x2(a – 2) + ax + 1 = 0
квадратное уравнение имеет два различных корня, если D > 0
D = a2 – 4(a – 2) = a2 – 4a + 8
a2 – 4a + 8 >0 Если а = 2, то уравнение будет линейным
y = a2 – 4a + 8 0 + 2x + 1 = 0
D = 16 – 32 корень
Ответ: при а ≠ 2 уравнение имеет два
различных корня
a
x R
Решите самостоятельно
Для каждого значения m решите уравнение
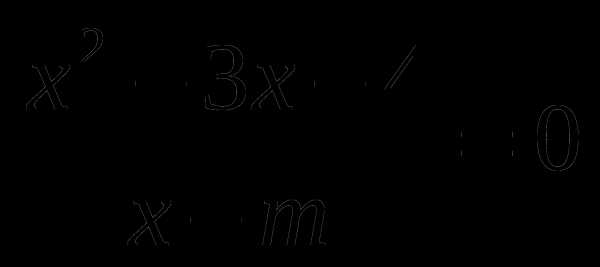
Ответ: при m = 4 один корень x = –1 ,
при m = -1 один корень x = 4,
при m ≠ 4, m ≠ –1 два корня x = 4, x = – 1
Для каждого значения а найдите число различных корней уравнения
(3x – 1)(ax2 + 3x – 2) = 0
Ответ: при  один корень
один корень
при  , а = 0, а = 9 два различных корня
, а = 0, а = 9 два различных корня
при три различных корня
doc4web.ru
8 класс неравенства с модулем
Вы искали 8 класс неравенства с модулем? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгоритм решения неравенств с модулем, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «8 класс неравенства с модулем».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 8 класс неравенства с модулем,алгоритм решения неравенств с модулем,дробные неравенства с модулем,дробные неравенства с модулем как решать,как раскрывается модуль в неравенствах,как раскрывать модуль в неравенствах,как раскрыть модуль в неравенстве,как решать дробные неравенства с модулем,как решать модульные неравенства,как решать неравенства с двумя модулями,как решать неравенства с модулем,как решать неравенства с модулем 10 класс,как решать неравенства с модулем 8 класс,как решать неравенства с модулем 9 класс,как решать неравенства с модулем дробные,как решать неравенства с модулями,как решать неравенство с двумя модулями,как решаются неравенства с модулем,как решить неравенства с модулем,как решить неравенство с модулем,как решить неравенство с модулем 9 класс,как решить систему неравенств с модулем,калькулятор неравенств с модулем,квадратное неравенство с модулем,квадратные неравенства с модулем,квадратные неравенства с модулем примеры решения,линейные неравенства с модулем,линейные неравенства с модулем примеры решения,методы решения неравенств с модулем,модули неравенства,модуль больше модуля,модуль в неравенствах,модуль неравенства,модульное неравенство,модульные неравенства,модульные неравенства как решать,модульные неравенства решение,неравенств с модулем,неравенства дробные с модулем,неравенства модули,неравенства модуль,неравенства онлайн с модулем,неравенства с двумя модулями как решать,неравенства с двумя модулями решение,неравенства с модулем,неравенства с модулем 10 класс,неравенства с модулем 10 класс как решать,неравенства с модулем 10 класс примеры,неравенства с модулем 8 класс примеры решения,неравенства с модулем 9 класс,неравенства с модулем 9 класс как решать,неравенства с модулем 9 класс примеры решения,неравенства с модулем дробные,неравенства с модулем как решать,неравенства с модулем как решать 8 класс,неравенства с модулем как решать 9 класс,неравенства с модулем квадратные,неравенства с модулем онлайн,неравенства с модулем онлайн решение,неравенства с модулем примеры,неравенства с модулем примеры 10 класс,неравенства с модулем примеры решения,неравенства с модулем примеры решения 10 класс,неравенства с модулем примеры решения 8 класс,неравенства с модулем примеры решения 9 класс,неравенства с модулем решение,неравенства с модулем решение онлайн,неравенства с модулем сложные,неравенства с модулем теория,неравенства с модулями,неравенства с модулями как решать,неравенства с модулями онлайн,неравенства с модулями примеры,неравенства содержащие модуль,неравенство с двумя модулями,неравенство с двумя модулями как решать,неравенство с модулем,неравенство с модулем квадратное,неравенство с модулем примеры,неравенство с модулем решение,неравенство с модулем решение онлайн,неравенство с модулем решить онлайн,онлайн неравенства с модулем,онлайн решение неравенств с модулем,онлайн решение неравенств с модулями,онлайн решение неравенства с модулем,примеры неравенств с модулем,примеры неравенства с модулем,примеры неравенства с модулями,примеры решение неравенств с модулем,примеры с модулем неравенства,простейшие неравенства с модулем,раскрытие модуля в неравенствах,решение квадратных неравенств с модулем,решение модулей неравенства,решение модульных неравенств,решение неравенств методом интервалов с модулем,решение неравенств онлайн с модулем,решение неравенств онлайн с модулями,решение неравенств с двумя модулями,решение неравенств с модулем,решение неравенств с модулем 10 класс примеры,решение неравенств с модулем калькулятор онлайн,решение неравенств с модулем методом интервалов,решение неравенств с модулем онлайн,решение неравенств с модулем онлайн с подробным решением,решение неравенств с модулем примеры,решение неравенств с модулем примеры 10 класс,решение неравенств с модулем решение онлайн,решение неравенств с модулем с подробным решением,решение неравенств с модулями,решение неравенств с модулями 10 класс,решение неравенств с модулями онлайн,решение неравенств содержащих модуль,решение неравенства модулей,решение неравенства онлайн с модулем,решение неравенства с двумя модулями,решение неравенства с модулем,решение неравенства с модулем онлайн,решение неравенство с модулем онлайн,решение онлайн модульных неравенств,решение онлайн неравенства с модулем,решения неравенств с модулем,решите неравенство с модулем,решить неравенства с модулем онлайн с решением,решить неравенство онлайн с модулем,решить неравенство онлайн с модулем с подробным решением,решить неравенство онлайн с подробным решением с модулем,решить неравенство с модулем,решить неравенство с модулем онлайн с подробным решением,решить неравенство с модулем онлайн с решением,решить онлайн неравенство с модулем,системы неравенств с модулем,сложные неравенства с модулем,способы решения неравенств с модулем,способы решения неравенств с модулями,теория неравенства с модулем,уравнения и неравенства с модулем 8 класс,уравнения и неравенства с модулем примеры с решением. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 8 класс неравенства с модулем. Просто введите задачу в окошко и нажмите «решить» здесь (например, дробные неравенства с модулем).
Где можно решить любую задачу по математике, а так же 8 класс неравенства с модулем Онлайн?
Решить задачу 8 класс неравенства с модулем вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
www.pocketteacher.ru
Классный час по алгебре (8 класс) на тему: Конспект урока в 8 классе по теме «Линейные неравенства с модулем»
Урок математики на тему: «Решение неравенств с модулем»
Разделы: Преподавание математики
Тема:«Решение неравенств с модулем»
Тип урока: закрепление и расширение знаний.
Класс: 8
Цели урока:
- Повторить теоретические знания учащихся по изученной теме;
- Отработать навыки решения линейных неравенств с модулем;
- Расширить знания учащихся по решению более сложных неравенств с модулем;
- Через дидактические игры (подбор упражнений по теме) расширить кругозор учащихся по истории и биологии;
- Прививать навыки самостоятельной работы, оценивания своей работы.
Оборудование: раздаточный материал для каждого ученика (задания устной работы, карточки с заданиями самостоятельной работы).
Ход урока
1. Организационный момент.
2. Устная работа по актуализации знаний.
Решите уравнения:
3. Решите неравенства:
Используя полученные ответы и данные в таблицах, заполните пропуски в тексте, записывая слова в нужных падежах.
4. Упражнения по закреплению знаний.
4.1 Учитель читает задание:
«Знаменитые итальянские мастера: Страдивари, Амати, Гварнери свои музыкальные инструменты – скрипки и виолончели – всегда делали из дерева одной породы.
Найдите область определения функции . Используя полученный ответ и данные таблицы, узнайте, как называется это дерево?
Итальянская | Морёный дуб | Ель | Красное дерево |
4.2
Решить двойные неравенства:
4.3
Решить неравенства:
4.4
Устно:
- Что является решением системы неравенств?
- Найти решение системы неравенств:
Что является решением совокупности неравенств?
- Найти решение совокупности неравенств:
4.5
Вспомним основные тождества для арифметического квадратного корня.
4.6 Решение более сложных неравенств с модулем.
- Для решения первого неравенства «сильный» ученик вызывается к доске.
— самостоятельно с проверкой
- Найдите область определения функции: для нахождения функции, записанной под А) ученик вызывается к доске.
5. Проверка знаний учащихся.
Мини — самостоятельная работа.
6. Оценка знаний учащихся.
Каждый ученик записывает ответ в виде среднего арифметического чисел, являющихся ответами на задания самостоятельной работы. (Ответ: ). Это и есть оценка его знаний по теме, если ученик её усвоил хорошо.
Учитель комментирует домашнее задание.
nsportal.ru
Урок алгебры в 8-м классе. Тема «Неравенства, содержащие модуль». Повторение
Разделы: Математика
Цель урока: повторить различные способы решения неравенств с одной переменной и рассмотреть применение неравенств к решению задач и упражнений.
Ход урока
- Организационный момент. Постановка цели.
- Индивидуальная работа по карточкам (во время фронтального опроса).
1 карточка.
Решить неравенства:
1. 6x+2>9-x;
2. 2(x+3)-(x-8)<4.
2 карточка.
Решить неравенства:
1. ;
2. 5x+4>12-(x-3).
3 карточка.
Решить неравенства:
- ;
4 карточка.
Решить неравенства:
1. x-4>12
2.
- Фронтальный опрос (используются слайды презентации учителя).
1.Что называется модулем числа а?
2.Решить неравенства
а)
б)
в)
г)
д)
3. на координатной плоскости изображены графики двух линейных функций. При каких x значения обеих функций одновременно положительны? Отрицательны?
Cм. Презентацию, слайды 3–5.
4.Самостоятельная работа (по вариантам)
Cм. Презентацию, слайд 6.
5. Актуализация опорных знаний.
Учитель. Очень часто при решении неравенств со знаком модуля возникает необходимость перейти либо к системе неравенств, либо к совокупности.
Вопросы?
- Когда неравенство равносильно системе неравенств?
- Когда число а является решением совокупности неравенств?
Экспресс-опрос (шесть человек работают у доски по карточкам, а в то же время остальные учащиеся работают со слайдом, на котором видно задание каждого ребенка, который стоит у доски).
Задание представлено в виде теста. По окончании решения необходимо выбрать правильный ответ, а букву, соответствующую этому варианту ответа, занести в соответствующую клетку кроссворда.
1 вариант.
2 вариант.
3 вариант.
4 вариант.
5 вариант.
6 вариант.
Итак, мы прочли Гарриот, это имя. Историческую справку о Гарриоте подготовил ученик.
Томас Гарриот (1560-1621)- английский математик. Родился в Оксфорде. Образование получил в Оксфордском университете. Переписывался с Галиллеем и Кеплером. Развивал алгебраическую символику, в частности, ввел знаки > и < , которые сразу были приняты. Гарриот пользовался для обозначений чисел строчными буквами алфавита, записывал уравнения в форме, близкой к современной. В этом отношении он шел дальше своего друга Франсуа Виета. Гарриот первый заметил, что число корней уравнения определяется его степенью и что левая часть уравнения должна разлагаться на такое же число линейных множителей. Гарриот строил уравнения по их корням.
Вопрос: какие существуют способы решения неравенств с одной переменной?
6. Решение задач и упражнений.
1.Задача. При каких значениях х точки графика функции лежат выше точек графика функции ?
Задача решается графическим способом.
2.Решить неравенство
Используется аналитический способ решения.
3.Найти допустимые значения переменной
7. Домашнее задание. Его необходимо выполнить в виде творческой работы:
- Составить и решить по 2 неравенства со знаком модуля, решениями которых будут в одном случае система, а в другом- совокупность неравенств;
- Придумать задачу, где применяется неравенство, а затем рассмотреть графический и аналитический способы решения этой задачи.
8. Сообщение учащегося из дополнительной литературы.
Учитель: Неравенства занимают важное место в курсе алгебры не только 8 класса, они встретятся нам и в 9 классе, и далее. Но уже сегодня, используя свойства известных нам неравенств, можно решать и более сложные задачи.
Ученик: напомним, что для любых двух действительных чисел а и b справедливо неравенство
(*)
Причем знак равенства достигается в том и только случае, когда
Решим задачу. Найти наименьшее значение функции
В силу неравенства (*)
Таким образом , причем знак равенства достигается только в том случае, когда х=0. Отсюда наименьшее значение функции равно 1 при х=0.
9. Итог урока. Оценки.
Учитель. Наш великий соотечественник Давидов Август Юльевич сказал: “Алгебра учит рассуждать о величинах. При этом она изображает их буквами и означает особыми знаками зависимость между ними”.
Вот этим сегодня мы и занимались на уроке.
18.03.2009
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Конспект урока с презентацией по математике на тему «Неравенства, содержащие модуль» (8 класс)
ПЛАН-КОНСПЕКТ УРОКА | Беляева Людмила Зиатдиновна | |||
Место работы | МБОУ «средняя общеобразовательная школа № 60» г.Набережные Челны | |||
Должность | Учитель математики | |||
Предмет | математика | |||
Класс | 8 | |||
Тема и номер урока в теме | Решение неравенств содержащих переменную под знаком модуля | |||
Базовый учебник | Алгебра. 8 класс: учебник для общеобразовательных учреждений /Ю.Н. Макарычев,Н.Г.Миндюк и др. – 9 – е изд., стереотипное. – М. : Мнемозина, 2011г.. | |||
Цель урока: Cформировать умения решения неравенств, содержащих переменную под знаком модуля, выработать навыки решения неравенств.
Педагогические задачи:
— Предметные: формирование способности учащихся к новому способу действия, закрепить навыки решения уравнений, сформировать понятии неравенств с модулями и их решение на начальном этапе.
—Метапредметные:
1) Регулятивные: самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы.
2) Коммуникативные: формирование навыков сотрудничества с учителем и сверстниками; планировать общие способы работы; обмениваться знаниями для принятия эффективных совместных решений.
3) Познавательные: произвольно и осознанно владеть общим приемом решения неравенств.
Тип урока: урок открытия нового знания.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Необходимое техническое оборудование: ПК, интерактивная доска, презентация, VOTUM-тренажер.
Структура и ход урока.
Этап урока
Деятельность учителя
Деятельность учащегося
УУД
Организационный блок
Приветствие
Настрой на урок
Мотивационный блок
Учитель предлагает вспомнить определение модуля числа и выполнить самостоятельную работу с целью проверить знания, умение решения уравнений с модулем и постановки проблем (проверка ответов проводиться с помощью VOTUM-тренажера). Ответы:
1. Ответ:7 ;1
2. Ответ: -11;11
3. Ответ: -1;2;3;6.
4. Ответ: -2 ; 10.
5. Ответ: 3
2.Учитель оценивает данный этап работы.
Ученики отвечают на вопросы учителя.
Анализируют,решают, приводимые уравнения, извлекают необходимую информацию для подведения под новое понятие.
1. Решить уравнения:
1. |х-4|=3
2. ||х|-5|=6
3. |х2— 5х|=6
4. |х-2|=|2х+8|
Найти наименьшее целое решение неравенства:
5. |x+3|<2x+1
Формулирование проблемы.
Сообщение темы урока,определение цели .
Учитель организует формирование темы урока обучающимися, постановку учебной задачи.
Вопрос.1) Входе работы где у вас возникли трудности? Что для этого нужно сделать?
2) Какие знания могли бы применить для решения этой проблемы?
3)Учитель предлагает начать с простейшего неравенства
|х|<6
Построение логической цепи рассуждений и выдвижение гипотез и их обоснование.
1) Предполагаемый ответ: при решении пятого задания. Нужно научиться решать неравенства содержащие модуль.
2) Нужно применить определение и геометрический смысл модуля. Ученики проговаривают определение модуля, его геометрический смысл.
Ученики формулируют тему и цель урока .
3) Предлагают решение -6<х <6 ,поясняют , проверяют и записывают в тетрадь. (слайд 4)
Постановка учебной цели и задачи урока.
Информационный блок
(Открытие нового знания , способа действия)
Предлагается обсудить и решить неравенства и сделать вывод (работают в паре):
| х-2|<4
|x-2|<-4 .
Учитель фронтально проверяет правильность рассуждения, затем рассматривают слайд 5,6 и записывают вывод.
Учитель просит оценить работу и внести отметку в оценочный лист.
Выражают свои мысли с достаточной полнотой и точностью аргументируют свое мнение.
Выходят на необходимость формулирования вывода .Решают неравенства ,проговаривают партнеру, проверяют решения и вывод ,делают запись в тетрадь(слайд5,6).
1. -4<x-2<4
-2<x<6
2.решения нет
Вывод: если |£(х)|<d ,то решение –d<£ (x)<d,
если |£(х)|<-d то –неравенство решение не имеет.
Договариваться и приходить к общему решению в совместной деятельности.
1. Предлагается самостоятельно ответить на вопрос задачи :
Найти наибольшее целое решение неравенства |x-2|<x.(Проверка проводится по образцу(слайд7),самооценка.)
2. Предлагается решить неравенство (самостоятельно, проверка учителем) .
2.Решить неравенство 7.
Учащиеся решают, затем проверяют и оценивают свое решение сравнивая его с решением на доске и делают вывод и самооценка. Участвуют в диалоге и делают вывод
В ситуации затруднения регулируют свою деятельность.
Вывод: |f(x)|<g(x) то
— g(x) < f(x)|< g(x)
Проявлять познавательную инициативу в учебном процессе.
Делают выводы.
Переходим к другому виду неравенств.
1. |x|>8.
Какое множество является решением данного неравенства ?
2.|x|>-8
Отвечают на задаваемые вопросы в процессе обсуждения, сотрудничают в поиске и выборе информации .
Предполагаемый ответ:
1.Решением данного неравенства
являются совокупность неравенств х<-8 и x>8.
2.
Вывод проговаривается и записывается(слайд11).
Владеют диалоговой речью.
Аналитический блок
(Включение нового знания в активное использование).
Учитель предлагает решить неравенства
1.|.5х+1|> 5х+1 с последующей проверкой и оценкой (слайд12)
Решить (самостоятельно-работу проверяет учитель) вспомнить основное свойство неравенств.
2. |x+5|>|x-6|
1.Выполняют работу в паре. Работают в парах с учениками и учатся сотрудничать с учителем во время фронтальной работы класса. Контроль за работой своей и партнера, оценка и коррекция деятельности (слайд12).
2.Предполагаемый ответ: при решение неравенства нужно применить свойство ,если а>в, то а2> в2.
Оценивает правильность выполнения действий.
Рефлексия .
Организуется обсуждение: Какую цель и задачу ставили? Что нового узнали? Что вызвало затруднение? т.д.
Отвечают на вопросы.
Проводят рефлексию и оценку своей работы.
Оценка-выделение и осознание того что им уже освоено, и что еще нужно усвоить.
Оценочный блок:
Учитель просит оценить работу учащихся в паре на уроке и оценивает сам .
Оценивают свою работу и вносят в оценочный лист .Тетради и оценочный лист сдают учителю.
Домашнее
Задание
Обсуждение домашнего задания. Пункт42 разобрать примеры 1;2;3.
Решить № 1048(а,б) №1053(а).
Записывают задание. По необходимости задают вопросы.
Приложение
Диагностическая карта группы № _____
Самооценка№ 1
Самооценка
№ 2
Оценил партнер
№ 1
Оценил партнер
№ 2
Оценил учитель
№1
Оценил учитель
№2
Оценил учитель
№3
итог
1
2
infourok.ru
Самостоятельная работа по математике (неравенства с модулем) для 8-го класса от Сообщества математиков в 2017 году
Ответы
Ответы к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 413 | 80 | Загрузок |
|---|---|---|---|
| Добавил | Yagubova | 24.08.2018 | Дата |
| День | Пятница | 16:40 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: Учительская для математиков
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Справочные материалы
Загрузка формул…
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
yagubov.ru
