Формулы разложения – Формулы сокращённого умножения

Formuly_sokrashchennogo_umnozhenija_shpargalka

Формулы сокращенного умножения

Разность квадратов:;

Квадрат суммы:;

Квадрат разности:;

Сумма кубов: ;

Разность кубов:;

Куб суммы:;

Куб разности:;

Квадрат трехчлена:.

Замечание: Формулы в прямом прочтении дают сокращенное умножение многочленов или возведение их в степень. В обратном прочтении – разложение многочлена на множители.

Формула разложения квадратного трехчлена на множители

Следует помнить, что квадратный многочлен можно разложить на множители, если у него есть действительные корни, т. е. . При этом надо обратить особое внимание, что если

, то формула будет иметь вид:

,

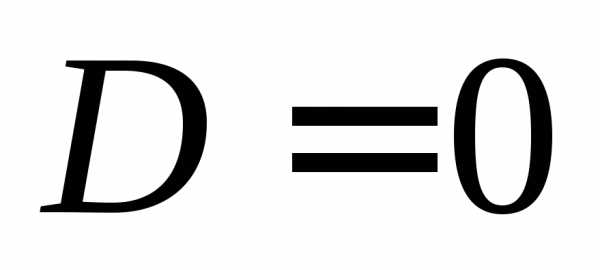
и Вы скорее всего не заметили формулу полного квадрата двучлена (квадрат суммы или квадрат разности).

Стоит так же помнить, что если , то квадратный трехчлен на множители не раскладывается. Так, например, не стоит пытаться разложить на множители неполный квадрат суммы или разности (второй множитель формул суммы и разности кубов):.

Формулы корней квадратного уравнения

Общий вид квадратного уравнения:.

Дискриминант квадратного уравнения: .

Если 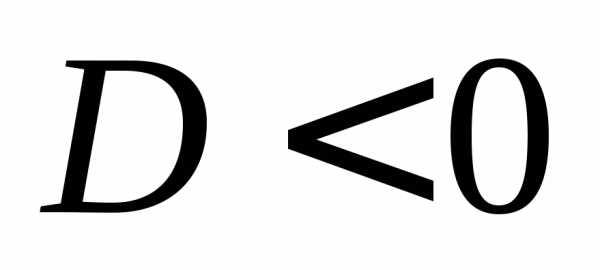, то квадратное уравнение действительных корней не имеет.

Если , то квадратное уравнение имеет одни действительный корень кратности два, который находится по формуле:

.

Если , то квадратное уравнение имеет два действительных корня, которые находятся по формулам:.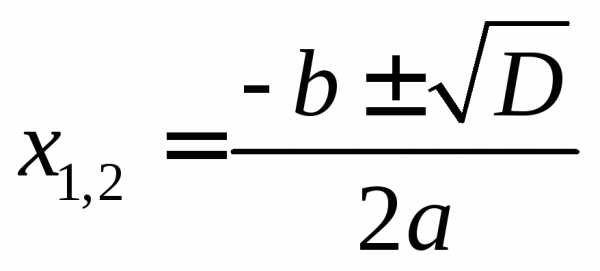

Формулы корней квадратного уравнения с четным вторым коэффициентом.

Общий вид уравнения:.

Дискриминант:.

Условия существования корней прежние, т. е..

Корни:.

Теорема Виета.

Квадратное уравнение называется приведенным, если его старший коэффициент равен 1. Любое квадратное уравнение можно привести, разделив обе его части на старший коэффициент.

Общий вид приведенного квадратного уравнения: .

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.

Верна и обратная теорема.

studfiles.net

Разложение многочлена на множители. Часть 1

Разложение многочлена на множители. Часть 1

Разложение на множители — это универсальный прием, помогающий решить сложные уравнения и неравенства. Первая мысль, которая должна прийти в голову при решении уравнений и неравенств, в которых в правой части стоит ноль — попробовать  разложить левую часть на множители.

Перечислим основные  способы разложения многочлена на множители:

• вынесение общего множителя за скобку
• использование формул сокращенного умножения
• по формуле разложения на множители квадратного трехчлена
• способ группировки
• деление многочлена на двучлен
• метод неопределенных коэффициентов

В этой статье мы остановимся подробно на первых трех способах, остальные рассмотрим в следующих статьях.

1. Вынесение общего множителя за скобку.

Чтобы вынести за скобку общий множитель надо сначала его найти. Коэффициент общего множителя равен наибольшему общему делителю всех коэффициентов.

Буквенная часть общего множителя равна произведению выражений, входящих в состав каждого слагаемого с наименьшим показателем степени.

Схема вынесения общего множителя выглядит так:

Внимание!
Количество членов в скобках равно количеству слагаемых в исходном выражении. Если одно из слагаемых совпадает с общим множителем, то при его делении на общий множитель, получаем единицу.

Пример 1.

Разложить на множители многочлен:  

Вынесем за скобки общий множитель. Для этого сначала его найдем.

1.Находим наибольший общий делитель всех коэффициентов многочлена, т.е. чисел 20, 35 и 15. Он равен 5.

2. Устанавливаем, что переменная  содержится во всех слагаемых, причем наименьший из её показателей степени равен 2. Переменная  содержится во всех слагаемых, и наименьший из её показателей степени равен 3.

Переменная  содержится только во втором слагаемом, поэтому она не входит в состав общего множителя.

Итак, общий множитель равен 

3. Выносим за скобки множитель  пользуясь схемой, приведенной выше:

 

Пример 2. Решить уравнение: 

Решение. Разложим левую часть уравнения на множители. Вынесем за скобки множитель :

Итак, получили уравнение 

Приравняем каждый множитель к нулю:

или 

Получаем  —   корень первого уравнения.

Корни квадратного уравнения  :

или 

Ответ: -1, 2, 4

 

2. Разложение на множители с помощью формул сокращенного умножения.

Если  количество слагаемых в многочлене, который мы собираемся разложить на множители меньше или равно трех, то мы пытаемся применить формулы сокращенного умножения.

1. Если многочлен представляет собой разность двух слагаемых, то пытаемся применить формулу разности квадратов:

   

или формулу разности кубов:

   

Здесь буквы и обозначают  число или алгебраическое выражение.

2. Если многочлен представляет собой сумму двух слагаемых, то, возможно, его можно разложить на множители с помощью формулы суммы кубов:

   

3. Если многочлен состоит из трех слагаемых, то пытаемся применить формулу квадрата суммы:

   

или формулу квадрата разности:

 

   

 

Или пытаемся разложить на множители по

формуле разложения на множители квадратного трехчлена:

Здесь  и  — корни квадратного уравнения 

Пример 3.  Разложить на множители выражение:

Решение. Перед нами сумма двух слагаемых. Попытаемся применить формулу суммы кубов. Для этого нужно сначала каждое слагаемое представить в виде куба какого-то выражения, а затем применить формулу для суммы кубов:

Пример 4. Разложить на множители выражение:  Рещение. Перед нами разность квадратов  двух выражений. Первое выражение: , второе выражение: 

Применим формулу для разности квадратов:

Раскроем скобки и приведем подобные члены, получим:

Пример 5. Разложить на множители выражение:  Решение. Перед нами  многочлен, состоящий из трех слагаемых. Заметим, что ; ;

 Так как перед удвоенным произведением стоит знак «минус», воспользуемся формулой для квадрата разности:

Внимание!  Коэффициенты обоих членов трехчлена, которые являются квадратами одночленов, положительны.

Пример 6. Разложить на множители квадратный трехчлен 

Приготовим для разложения квадратного трехчлена готовую форму:

Впишем значения корней в готовую форму:

Внесем множитель 3 во вторую скобку:

Итак:

ege-ok.ru

Многочлены. Разложение многочлена на множители: способы, примеры :: SYL.ru

Понятия «многочлен» и «разложение многочлена на множители» по алгебре встречаются очень часто, ведь их необходимо знать, чтобы с легкостью производить вычисления c большими многозначными числами. В этой статье будет описано несколько способов разложения. Все они достаточно просты в применении, стоит лишь правильно подобрать нужный в каждом конкретном случае.

Понятие многочлена

Многочлен является суммой одночленов, то есть выражений, содержащих только операцию умножения.

Например, 2 * x * y – это одночлен, а вот 2 * x * y + 25 — многочлен, который состоит из 2 одночленов: 2 * x * y и 25. Такие многочлены называет двучленами.

Иногда для удобства решения примеров с многозначными значениями выражение необходимо преобразовать, например, разложить на некоторое количество множителей, то есть чисел или выражений, между которыми производится действие умножения. Есть ряд способов разложения многочлена на множители. Стоит рассмотреть их начиная с самого примитивного, который применяют еще в начальных классах.

Группировка (запись в общем виде)

Формула разложения многочлена на множители способом группировки в общем виде выглядит таким образом:

ac + bd + bc + ad = (ac + bc) + (ad + bd)

Необходимо сгруппировать одночлены так, чтобы в каждой группе появился общий множитель. В первой скобке это множитель с, а во второй – d. Это нужно сделать для того, чтобы затем вынести его за скобку, тем самым упростив вычисления.

Алгоритм разложения на конкретном примере

Простейший пример разложения многочлена на множители способом группировки приведен ниже:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b)

В первую скобку нужно взять слагаемые с множителем а, который и будет общим, а во вторую – со множителем b. Обратите внимание на знаки + и – в готовом выражении. Мы ставим перед одночленом тот знак, который был в начальном выражении. То есть нужно работать не с выражением 25а, а с выражением -25. Знак минус как бы «приклеить» к стоящему за ним выражению и всегда учитывать его при вычислениях.

На следующем шаге нужно вынести множитель, который является общим, за скобку. Именно для этого и делается группировка. Вынести за скобку – значит выписать перед скобкой (опуская знак умножения) все те множители, которые с точностью повторяются во всех слагаемых, которые находятся в скобке. Если в скобке не 2, а 3 слагаемых и больше, общий множитель должен содержаться в каждом из них, иначе его нельзя вынести за скобку.

В нашем случае — только по 2 слагаемых в скобках. Общий множитель сразу виден. В первой скобке – это а, во второй – b. Здесь нужно обратить внимание на цифровые коэффициенты. В первой скобке оба коэффициента (10 и 25) кратны 5. Это значит, что можно вынести за скобку не только а, но и 5а. Перед скобкой выписать 5а, а затем каждое из слагаемых в скобках поделить на общий множитель, который был вынесен, и также записать частное в скобках, не забывая о знаках + и — Со второй скобкой поступить также, вынести 7b, так как и 14 и 35 кратно 7.

Итак:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b) = 5а(2c — 5) + 7b(2c – 5).

Получилось 2 слагаемых: 5а(2c — 5) и 7b(2c – 5). Каждое из них содержит общий множитель (все выражение в скобках здесь совпадает, значит, является общим множителем): 2с – 5. Его тоже нужно вынести за скобку, то есть во второй скобке остаются слагаемые 5а и 7b:

5а(2c — 5) + 7b(2c – 5) = (2c – 5)*(5а + 7b).

Итак, полное выражение:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b) = 5а(2c — 5) + 7b(2c – 5) = (2c – 5)*(5а + 7b).

Таким образом, многочлен 10ас + 14bc – 25a — 35b раскладываается на 2 множителя: (2c – 5) и (5а + 7b). Знак умножения между ними при записи можно опускать

Иногда встречаются выражения такого типа: 5а² + 50а³ , здесь можно вынести за скобку не только а или 5а, а даже 5а². Всегда нужно стараться вынести максимально большой общий множитель за скобку. В нашем случае, если разделить каждое слагаемое на общий множитель, то получается:

5а² / 5а² = 1; 50а³ / 5а² = 10а (при вычислении частного нескольких степеней с равными основаниями основание сохраняется, а показатель степени вычитается). Таким образом, в скобке остается единица (ни в коем случае не забывайте писать единицу, если выносите за скобку целиком одно из слагаемых) и частное от деления: 10а. Получается, что:

5а² + 50а³ = 5а² (1 + 10а)

Формулы квадратов

Для удобства вычислений были выведены несколько формул. Они называются формулами сокращенного умножения и используются довольно часто. Эти формулы помогают разложить на множители многочлены, содержащие степени. Это еще один действенный способ разложения на множители. Итак, вот они:

• a² + 2ab + b² = (a + b)² — формула, получившая название «квадрат суммы», так как в результате разложения в квадрат берется сумма чисел, заключенная в скобки, то есть значение этой суммы умножается само на себя 2 раза, а значит, является множителем.
• a² + 2ab — b² = (a — b)^{2 —} формула квадрата разности, она аналогична предыдущей. В результате получается разность, заключенная в скобки, содержащаяся в квадратной степени.
• a² — b² = (a + b)(а — b) — это формула разности квадратов, так как изначально многочлен состоит из 2 квадратов чисел или выражений, между которыми производится вычитание. Пожалуй, из трех названных она используется чаще всего.

Примеры на вычисления по формулам квадратов

Вычисления по ним производятся достаточно просто. Например:

1. 25x² + 20xy + 4y² — используем формулу «квадрат суммы».
2. 25x² являетсяквадратом выражения 5х. 20ху — удвоенное произведение 2*(5х*2у), а 4y² — это квадрат 2у.
3. Таким образом, 25x² + 20xy + 4y² = (5x+ 2у)² = (5x+ 2у)(5x+ 2у). Данный многочлен раскладывается на 2 множителя (множители одинаковые, поэтому записывается в виде выражения с квадратной степенью).

Действия по формуле квадрата разности производятся аналогично этим. Остается формула разность квадратов. Примеры на эту формулу очень легко определить и найти среди других выражений. Например:

• 25а² — 400 = (5а — 20)(5а + 20). Так как 25а² = (5а)², а 400 = 20²
• 36х² — 25у² = (6х — 5у) (6х + 5у). Так как 36х² = (6х)², а 25у² = (5у²)
• с² — 169b² = (с — 13b)(c + 13b). Так как 169b² = (13b)²

Важно, чтобы каждое из слагаемых являлось квадратом какого-либо выражения. Тогда этот многочлен подлежит разложению на множители по формуле разности квадратов. Для этого не обязательно, чтобы над числом стояла именно вторая степень. Встречаются многочлены, содежащие большие степени, но все равно подходящие к этим формулам.

a⁸+10a⁴+25 = (a⁴)² + 2*a⁴*5 + 5² = (a⁴+5)²

В данном примере а⁸можно представить как (a⁴)², то есть квадрат некого выражения. 25 — это 5², а 10а⁴ — это удвоенное произведение слагаемых 2*a⁴*5. То есть данное выражение, несмотря на наличие степеней с большими показателями, можно разложить на 2 множителя, чтобы в последствии работать с ними.

Формулы кубов

Такие же формулы существуют для разложения на множители многочленов, содержащих кубы. Они немного посложнее тех, что с квадратами:

• a³ + b³ = (а + b)(a² — ab + b²) — эту формулу называют суммой кубов, так как в начальном виде многочлен представляет собой сумму двух выражений или чисел, заключенных в куб.
• a³ — b³ = (а — b)(a² + ab + b²) — формула, идентичная предыдущей, обозначена как разность кубов.
• a³ + 3a²b + 3ab²+ b³ = (a + b)^{3 —} куб суммы, в результате вычислений получается сумма чисел или выражений, заключенная в скобки и умноженная сама на себя 3 раза, то есть находящаяся в кубе
• a³ — 3a²b + 3ab² — b³ = (a — b)³ — формула, составленная по аналогии предыдущей с изменением лишь некоторых знаков математических операций (плюс и минус), имеет название «куб разности».

Последние две формулы практически не испольуются с целью разложения многочлена на множители, так как они сложны, и достаточно редко встречаются многочлены, полностью соответствующие именно такому строению, чтобы их можно было разложить по этим формулам. Но их все равно нужно знать, так как они потребуются при действиях в обратном направлении — при раскрытии скобок.

Примеры на формулы кубов

Рассмотрим пример: 64a³ − 8b³ = (4a)³ − (2b)³ = (4a − 2b)((4a)² + 4a*2b + (2b)²) = (4a−2b)(16a² + 8ab + 4b²).

Здесь взяты достаточно простые числа, поэтому сразу можно увидеть, что 64а³ — это (4а)³, а 8b³ — это (2b)³. Таким образом, этот многочлен раскладывается по формуле разность кубов на 2 множителя. Действия по формуле суммы кубов производятся по аналогии.

Важно понимать, что далеко не все многочлены подлежат разложению хотя бы одним из способов. Но есть такие выражения, которые содержат большие степени, чем квадрат или куб, но их также можно разложить по формуам сокращенного умножения. Например: x¹² + 125y³=(x⁴)³+(5y)³=(x⁴+5y)*((x⁴)² − x⁴*5y+(5y)²)=(x⁴ + 5y)(x⁸ − 5x⁴y + 25y²).

В этом примере содержится аж 12 степень. Но даже его возможно разложить на множители по формуле суммы кубов. Для этого нужно представить х¹² как (x⁴)³ , то есть как куб какого-либо выражения. Теперь в формулу вместо а нужно подставлять именно его. Ну а выражение 125у³ — это куб 5у. Далее следует составить произведение по формуле и произвести вычисления.

На первых порах или в случае возникших сомнений, вы всегда можете произвести проверку обратным умножением. Вам нужно лишь раскрыть скобки в получившемся выражении и выполнить действия с подобными слагаемыми. Этот метод относится ко всем перечисленным способам сокращения: как к работе с общим множителем и группировке, так и к действиям по формулам кубов и квадратных степеней.

www.syl.ru

«ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ»

Тема консультации: «ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ.

РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ»

Дидактическая основа

Дидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивают личностные и метапредметные результаты образования, соответствующие ФГОС.

Содержание консультации

В соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 7 класса в феврале продолжается работа с четвертой главой «Введение в теорию многочленов». Изучаются три пункта второго параграфа:
4.3.2. Разность квадратов;
4.3.3. Куб суммы и разности;
4.3.4. Сумма и разность кубов.
После чего начинается работа с четвертым параграфом «Разложение многочленов на множители», из которого изучаются пункты:
4.4.1. Вынесение общего множителя за скобки;
4.4.2. Способ группировки;
4.4.3. Формулы сокращенного умножения и разложение многочленов.

Основные содержательные цели

• сформировать умение представлять разность квадратов, сумму и разность кубов в виде произведения и наоборот преобразовывать произведения многочленов определенного вида в разность квадратов, сумму и разность кубов с помощью соответствующих формул сокращенного умножения;
• сформировать умение представлять куб суммы и разности в виде многочлена стандартного вида и наоборот преобразовывать многочлен определенного вида в куб суммы или разности с помощью соответствующей формулы сокращенного умножения;
• сформировать умение применять формулы сокращенного умножения для алгебраических преобразований, связанных с умножением, и рационализации вычислений;
• сформировать умение раскладывать многочлены на множители следующими способами: вынесением за скобки общего множителя, способом группировки, с помощью формул сокращенного умножения;
• сформировать умение применять при разложении многочленов на множители различные вспомогательные приемы, такие как, перестановка слагаемых; представление члена многочлена в виде суммы или разности подобных ему членов; прибавление и вычитание одного и того же слагаемого, выделение полного квадрата;
• сформировать умение применять разложение на множители для алгебраических преобразований, решений уравнений и рационализации вычислений.

Тематическое планирование

В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по данному учебнику возможно в условиях различных учебных планов образовательных учреждений. Поэтому тематическое планирование по изучению данного курса разработано в двух вариантах на 102 ч и на 136 ч. Вариант планирования, разработанный для 3 часов в неделю, обеспечивает выполнение государственного стандарта знаний, усвоение учебного содержания курса (по темам, обязательным для рассмотрения) и продвижение учащихся в развитии мышления, речи, познавательных интересов. При 4 часах в неделю содержание курса существенно расширяется.

Мы предлагаем Вам скачать тематическое планирование на 3 четверть (3 ч в неделю).

(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)

Центр системно – деятельностной педагогики «Школа 2000…» рекомендует для работы по учебнику математики для 7 класса средней школы Л.Г. Петерсон, Д.Л. Абрарова, Е.В. Чутковой использовать по возможности 4 часа в неделю.

Мы предлагаем Вам скачать тематическое планирование на 3 четверть (4 ч в неделю).

(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)

Методические рекомендации к организации учебного процесса

Глава 4. Введение в теорию многочленов

§ 3. Формулы сокращенного умножения

П. 2. Разность квадратов

1) В данном пункте учащиеся знакомятся с двумя формулами сокращенного умножения – формулой произведения суммы и разности двух выражений и формулой разности квадратов, которые, по сути, являются одинаковыми равенствами, в которых поменяли местами правую и левую части. Традиционно эта формула рассматривалась как одна – формула разности квадратов, что приводило к трудностям, возникающим у учащихся при умножении разности двух выражений на их сумму. Поэтому, чаще всего учителю приходилось регулярно использовать на уроках такой прием, как чтение данной формулы «в обратную сторону». Чтобы раз и навсегда показать учащимся, что любая из формул сокращенного умножения «работает» как справа налево, так и слева направо можно использовать материал данного пункта и специально обратить внимание учащихся на это. Можно пояснить учащимся, что для других «обратных» формул не используют отдельного названия, т.к. звучат их названия менее благозвучно, чем у формулы произведения разности и суммы двух выражений.
2) В качестве мотивации к выводу новых формул можно предложить учащимся вычислить

 за 30 секунд. После того как они не справятся с этим заданием за указанное время, пояснить, что с помощью формулы сокращенного умножения, открытой сегодня им это легко удастся.
3) Для открытия данных формул учащимся предлагается записать произведение суммы и разности а и b как многочлен стандартного вида. После этого учащимся предлагается обобщить полученное равенство для всех произведений подобного вида и сформулировать правило умножения суммы двух выражений на их разность. Опираясь на полученную формулу, учащиеся формулируют, как можно найти разность квадратов двух выражений (№ 318). Эту работу они могут выполнять самостоятельно в группах или в парах.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 2, а также понятия «сумма» и «разность». Для этого можно использовать задания №№ 316–317.
5) Чтобы показать геометрический смысл данной формулы можно использовать предметные геометрические модели прямоугольника и квадрата, предложенные в учебнике. Необходимо вырезать, прикладывать и перемещать предметные модели либо использовать возможности анимации современной техники. Это поможет учащимся с образным мышлением запомнить данные формулы.
6) Важно показать учащимся применение формул для рационализации вычислений (№№ 322, 337).
7) При 4-часовом планировании рекомендуется отвести больше времени на выполнение заданий более высокого уровня сложности (№№ 340–347).
8) Учащиеся применяют новые формулы для сокращения алгебраических дробей (№ 333), решения уравнений (№ 327, № 336), доказательства утверждений и тождеств (№№ 329, 334, 335). Для формирования умения применять формулы сокращенного умножения в учебнике и другие задания, которые предполагают решение задач с помощью уравнения (№ 339), сравнение значений выражений (№№ 342 – 343) и пр. Учитель выбирает из этих заданий те, которые считает целесообразным выполнить с учащимися.
9) При выполнении заданий на нахождение наибольшего и наименьшего значения выражений (№№ 345 – 346) следует вспомнить с учащимися необходимые свойства. Рекомендуется, после применения формулы произведения суммы выражений на их разность актуализировать, как изменяется разность при изменении ее компонентов. Свойство разности «Если значение уменьшаемого увеличить, то значение разности увеличится» и подобные ему свойства известны учащимся с начальной школы. Кроме того, рекомендуется спросить, какое наименьшее значение может принимать квадрат любого выражения (нуля).

П. 3. Куб суммы и разности

1) В данном пункте учащиеся знакомятся с двумя формулами сокращенного умножения – формулой куба суммы и куба разности.
2) Для проблематизации можно предложить учащимся записать выражение

как многочлен стандартного вида, не используя правило умножения многочленов
3) Для открытия формулы куба суммы (разности) учащимся предлагается использовать задание № 377, в котором проедложены шаги по построению новой формулы. Рекомендуется сначала дать возможность учащимся составить план открытия нового знания самостоятельно. Имея опыт, построения формулы квадрата суммы и разности данная задача является для семиклассников посильной задачей.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 3, а также понятия «куб суммы» и «куб разности». Для этого можно использовать задания №№ 374–376.
5) Важно показать учащимся применение формул для рационализации вычислений (№№ 381 – 382).
6) Для формирования умения применять формулы куба суммы и разности в учебнике предлагается целый перечень заданий, которые предполагают доказательство тождеств, нахождение значений выражений, составление и решение уравнений. Учитель выбирает из них те задания, которые считает целесообразным выполнить со своими учениками.
7) После знакомства с формулами куба суммы и куба разности с учащимися следует обобщить, что теперь им известно как возводить двучлен во 2-ю и 3-ю степени и сообщить, что существуют формулы, позволяющие возводить двучлен в более высокую степень. Можно попросить одного из «сильных» учащихся сформулировать идею вывода подобных формул. При 4-часовом планировании (либо в более подготовленных классах) рекомендуется познакомить учащихся с алгоритмом возведения двучлена в n–ю степень (№№ 399 – 400).

П.4. Сумма и разность кубов

1) В данном пункте учащиеся знакомятся с формулами суммы и разности кубов.
2) Для проблематизации можно предложить учащимся записать многочлены:

в виде произведения двух многочленов.
3) В связи с особенностями этих формул учащимся вряд ли удастся самостоятельно составить план открытия нового знания, поэтому учащимся предлагается использовать задание № 434, в котором даны шаги по построению новых формул.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 3, а также понятия «сумма кубов» и «разность кубов». Для этого можно использовать задания №№ 432–433.
5) Важно показать учащимся применение формул для рационализации вычислений (№№ 439).
6) Для формирования умения применять формулы суммы и разности кубов в учебнике также как и в других пунктах третьего параграфа предлагается перечень заданий, которые предполагают доказательство тождеств, нахождение значений выражений, составление и решение уравнений с использованием данных формул. Учитель выбирает из них те задания, которые считает целесообразным выполнить со своими учениками.
7) При 4-часовом планировании рекомендуется уделить больше времени на выполнение заданий более высокого уровня сложности (№№ 453–460).
8) При выполнении задания № 459 рекомендуется сначала проанализировать данные равенства, задать, например, следующие вопросы:

• Что записано в левой части равенства? (Произведение многочленов.)
• Что записано в правой части равенства? (Многочлены.)
• Как перейти от произведения многочленов к многочлену? (Перемножить данные многочлены.)
• Как можно рационализировать умножение алгебраических выражений? (Формулы сокращенного умножения помогают при таких преобразованиях.)
• Какие формулы вы здесь сразу видите, подчеркните соответствующие выражения.

После устного разбора учащиеся самостоятельно выполняют данные преобразования и проверяют себя по образцу (естественно образец должен демонстрировать не только самый рациональный способ, но и все возможные способы, которые могли использовать семиклассники). Можно подготовить образец заранее либо вызвать на закрытую доску сильного ученика.
Полезным будет показать рациональные способы выполнения данных преобразований, для этого можно воспользоваться заранее заготовленными образцами. Если по какой-либо причине подготовить образцы не удастся можно вызывать к доске не одного, а нескольких учащихся, которые бы параллельно доказывали тождество. После выполнения задания разобрать другие способы, которыми пользовались ученики. Кроме того, можно после того как основная часть класса закончит доказательство, следует поинтересоваться, кто нашел другой, более рациональный способ доказательства. Эти способы демонстрируются с помощью специального технического оборудования либо идея преобразования проговаривается вслух.
Целесообразно на примере а) сравнить два способа доказательства тождеств:
1) приведение левой части к правой, при котором придется применить формулу произведения суммы выражений на их разность и в полученном произведении «увидеть» формулу разности кубов;
2) приведение правой части к левой, при котором в разности шестых степеней можно «увидеть» разность кубов и разложить эту разность на произведение двучлена на трехчлен, а полученный двучлен разложить на сумму и разность по формуле разности квадратов.
Второй способ рекомендуется показать после применения первого. На данном этапе он рассматривается с целью опережающей подготовки учащихся к изучению темы «Разложение на множители с помощью формул сокращенного умножения».

§ 4. Разложение многочлена на множители

П.1 Вынесение общего множителя за скобки

1) В данном пункте учащиеся учатся выносить общий множитель за скобки, они уже имеют опыт простейших преобразований такого рода. Так, для первичного формирования умения приводить подобные слагаемые учащиеся выносили общий множитель за скобки на основании распределительного закона умножения.
2) В данном пункте у учащихся формируется понятие разложения многочлена на множители. Нужно отметить, что под разложением на множители понимается разложение на буквенные множители. Так, вынесение за скобки числового множителя не является операцией разложения на множители. Например, представление многочлена 2a + 2ac в виде произведения 2(а + ас) не является разложением на множители, а в виде 2а (1 + с) является. Этот «нюанс» можно обговорить с учащимися при выполнении № 489.
3) Здесь же формируется умение раскладывать на множители путем вынесения общего множителя за скобки. Теперь учащиеся выполняют это преобразование на основании четко сформулированного правила: чтобы вынести за скобки общий множитель с можно в скобках записать многочлен, каждый член которого получен в результате его деления на с. Можно использовать предложенный в учебнике алгоритм вынесения за скобки общего множителя (в более подготовленном классе учащиеся могут построить его самостоятельно – № 493).
4) В связи с тем, что учащиеся уже знакомы с вынесением за скобки общего множителя, для проблематизации можно предложить учащимся сформулировать, что такое «разложение многочлена на буквенные множители».
5) Для построения логики открытия при подготовке к уроку учитель может воспользоваться заданием № 488.
6) Чтобы подготовить учащихся к открытию следует актуализировать с ними распределительное свойство умножения, использование этого свойства для рационализации вычислений. Для этой целей рекомендуется использовать задания №№ 485 – 488.
7) Задание № 497 готовит учащихся к следующему пункту. Часто у учащихся возникает сложность с вынесением за скобки общего множителя, который является многочленом. Чтобы преодолеть это возможное затруднение рекомендуется выполнить это задание с подчеркиванием общего множителя.
8) Задание № 498 показывает применение нового преобразования для решения уравнений. Особо следует подчеркнуть, что без разложения на множители уравнения данного вида учащиеся пока решить не могут.
9) Важно показать учащимся применение правила вынесения общего множителя для рационализации вычислений (№№ 496, 502).

П.2 Способ группировки

1) В данном пункте учащиеся учатся применять еще один способ разложения на множители – способ группировки.
2) Для проблематизации можно предложить учащимся разложить на множители многочлен:

Причиной возникшего затруднения будет то, что данные одночлены не имеют общего множителя. Чтобы преодолеть свое затруднения учащиеся должны будут открыть новый способ разложения на множители.
3) Чтобы подготовить учащихся к открытию рекомендуется выполнить задание № 533, в котором учащимся придется переставлять слагаемые местами и группировать произведения, имеющие одинаковые множители, а также № 535. Позже эти идеи помогут семиклассникам построить новый способ самостоятельно.
4) Алгоритм способа группировки, построенный учащимися, может иметь вид:
1) Объединить члены многочлена в группы таким образом, чтобы в каждой группе были общие множители.
2) Найти общий множитель в каждой группе и вынести его.
3) Найти общий множитель в новом многочлене и вынести его.
5) Подготовка, проведенная в предыдущем пункте, дает возможность наряду с простейшими ситуациями использования способа группировки рассмотреть и случаи, которые требуют специальных приемов:

• перестановка слагаемых;
• представление члена многочлена в виде суммы или разности подобных ему членов;
• прибавление и вычитание одного и того же слагаемого.

Последним двум приемам рекомендуется посвятить отдельный урок открытия нового знания. Эти приемы будут использоваться учащимися в дальнейшем и для других способов разложения на множители.
6) Для проблематизации можно предложить учащимся разложить на множители с использованием способа группировки многочлены:
7) Для организации открытия можно воспользоваться учебником. Учащиеся самостоятельно отбирают и рассматривают примеры 2, 3 и 4 из текста. После работы с текстом учащимся предлагается выполнить задания на пробное действие.
8) Задания №№ 546, 554 показывают применение нового преобразования для решения уравнений. Причем, если раньше указание разложить на множители давалось в задании, то теперь такого указания в тексте задания нет. Анализируя вид уравнения, учащиеся должны понимать, что нужно преобразовать левую часть уравнения в произведение многочленов. Особо следует подчеркнуть, что без разложения на множители уравнения данного вида учащиеся пока решить не могут.

П.3 Формулы сокращенного умножения и разложение многочленов на множители

1) В данном пункте учащиеся учатся раскладывать на множители многочлены с использованием формул сокращенного умножения. Умение использовать формулы, в которых та или иная формула представлена в явном виде, должно быть уже сформировано в предыдущем параграфе. Теперь с учащимися разбираются случаи, когда для применения формулы сокращенного умножения необходимо выполнить предварительное преобразование исходного многочлена.
2) Учащиеся учатся видеть в степенях «квадраты» и «кубы», группировать слагаемые для получения нужной формулы, пользуются уже известными приемами: перестановка слагаемых и прибавление и вычитание одного и того же слагаемого.
3) Для этапа актуализации рекомендуется использовать задания №№ 583 – 585, при выполнении которых учащиеся повторят те понятия и способы действий, которые понадобятся им на уроке.
4) № 586 можно использовать для проблематизации. Затруднение, возникшее при выполнении этого задания, потребует новых приемов для применения разложения на множители (либо отбора уже известных приемов для применения в новой ситуации).
5) При изучении данного пункта учащиеся знакомятся с таким приемом, как выделение полного квадрата, который дает возможность применить формулы сокращенного умножения (№ 588 (л–н), № 595(д), № 600 готовят учащихся к этому способу, № 601 требует применения способа). Естественно требовать от каждого ученика умения применять данный способ нельзя. Однако более способные учащиеся должны получить возможность познакомиться с приемом выделения полного квадрата. В восьмом классе этот прием даст возможность вывести формулу для решения квадратных уравнений.

Эталоны

В результате изучения данных пунктов учащиеся знают следующие формулы сокращенного умножения: формулу произведения суммы двух выражений на их разность, формулу разности квадратов; формулы куба суммы и куба разности; формулы суммы и разности кубов и умеют их применять. Учащиеся имеют возможность познакомиться с треугольником Паскаля и соответствующим алгоритмом для возведения двучлена в n–ю степень. Учащиеся знают, что значит разложить многочлен на множители и следующие способы разложения на множители: вынесением за скобки общего множителя, способом группировки, с помощью формул сокращенного умножения и умеют их применять. Учащиеся имеют возможность познакомиться с различными вспомогательными приемами, которые помогают применять вышеперечисленные способы разложения на множители.

Методические рекомендации по планированию уроков

При организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствии с зоной ближайшего развития более подготовленных учащихся. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.
Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000…». В отличие от уроков, опубликованных нами в предыдущих консультациях, этот урок является примером урока рефлексивного типа. Подробнее с методикой подготовки и проведения уроков такого типа в 7-9 классах основной школы вы можете познакомиться в разделе Модификация технологии деятельности метода обучения на уроках разной целевой направленности в 7–9 классах основной школы нашей вводной консультации.

Урок 60

Тип урока: Р
Тема урока: «Формулы сокращённого умножения»
Автор: Л.А Грушевская
Основные содержательные цели:
1) организовать самоконтроль умения применять формулы сокращённого умножения при выполнении заданий различного характера;
2) тренировать умение решать задачи на движение.

Мы предлагаем Вам cкачать сценарий урока

(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)

Уважаемые коллеги! Предлагаем вам скачать решение некоторых задач на смекалку, которые входят в данные параграфы.

(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)

Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.

www.sch2000.ru

Разложения некоторых элементарных функций по формуле Маклорена — ПриМат

Если и существует , то формула Тейлора принимает вид:

(1)

.

Формулу (1) называют формулой Маклорена.

Замечание 1. Пусть функция бесконечно дифференцируема на интервале Если эта функция является четной, то её производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция.
Пусть — четная функция, тогда:
, .
Дифференцируя это тождество, получаем
.
Это означает, что — нечетная функция. Аналогично рассматривается случай, когда — нечетная функция.
Отсюда следует, что для нечетной функции выполняютcя условия , , а для четной функции — условия , , так как любая непрерывная нечетная функция принимает при значение нуль.
Поэтому формулу (1) для бесконечно дифференцируемой четной функции можно записать в виде:

(2)

,

а для нечетной функции — в виде:

(3)

.

а) Показательная функция. Если , то и при любом . Поэтому формула (1) для функции записывается в виде

(4)

,

или

.

б) Гиперболические функции. Так как — нечетная функция, , при , то по формуле (3) получаем

(5)

,

или

.

Аналогично по формуле (2) находим

(6)

,

или

.

Замечание 2. Так как , , то формулы (5) и (6) можно получить, используя равенство (4) и равенство .

в) Тригонометрические функции. Функция является нечетной,

,

откуда

.

Поэтому по формуле (3) находим

(7)

,

или

.

Аналогично, — четная функция, , и по формуле (2) получаем

(8)

,

или

.

Замечание 3.Используя формулу (7)

Для 2 членов разложения:
Для 3 членов разложения:
Для 4 членов разложения:

Как видно по графику, для достижения точности, достаточной для решения большинства практических задач, можно ограничиться 4-5 членами ряда.

г) Степенная функция. Пусть , где . Тогда , откуда получаем . Тогда по формуле (1) получим

(9)

.

Отметим важные частные случаи формулы (9).

1. (10)

   ,

   или

   .

2. (11)

   ,

   или

   .

д) Логарифмическая функция. Если , то , , , и по формуле (1) находим

(12)

,

или

.

Заменяя в формуле (12) на , получаем

(13)

,

или

.

1. Разложить по формуле Тейлора в окрестности точки до функцию , если
   

   Спойлер

   . Применяя формулу (9) при , получаем:

   Обозначим , тогда:

   [свернуть]

2. Разложить по формуле Тейлора в окрестности точки до функцию , если
   

   Спойлер

   Используя равенство

   и формулу (13), находим:

   =

   [свернуть]

3. Разложить по формуле Маклорена до функцию , если
   

   Спойлер

   Используя равенство , получаем:

   ,

   откуда по формуле (8) находим:

   =

   [свернуть]

Разложения некоторых элементарных функций по формуле Маклорена

Лимит времени: 0

Информация

Тесты для самоконтроля

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 4

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Рубрики

1. Математический анализ 0%

Ваш результат был записан в таблицу лидеров

1. С ответом
2. С отметкой о просмотре

ib.mazurok.com

Формула разложения

Количество просмотров публикации Формула разложения — 93

В результате совместного решения системы операторных уравнений получают выражение для искомой функции в операторной форме, ᴛ.ᴇ. ее операторное изображе­ниеF(p). Переход от операторного изображения функ­ции к ее оригиналу, ᴛ.ᴇ. к функ­ции времениf(t), является наиболее трудо­емкой частью операторного метода расчета. На практике для этой цели применяются два способа.

Первый способ – по таблице соответствия. В этом случае оператор­ное выраже­ние искомой функции F(p)преобразуется к одному из табличных видов и по таблице соответствия определяется оригинал функции f(t). Сле­дует заметить, что такое преобразо­вание удается осуществить только для простых выражений, что существенно ограничи­вает возможности этого способа.

Второй способ – по формуле разложения — является более универ­сальным, по­этому находит применение в большинстве практических слу­чаев. Сущность этого спо­соба изложена ниже.

При решении системы операторных уравнений для искомой функ­ции получают операторное выражение F(p) в виде дроби, в числителœе и знаменателœе которой стоят степенные полиномы:

.

Из курса математики известно, что при выполнении условий: а) m>n иб)уравнение не содержит кратных корней, выражение = должна быть представлена в виде суммы простых дробей:

,

где ,,- постоянные коэффициенты, — корни уравнения .

Для определœения коэффициента умножим обе части уравнения на множитель и найдем предел выражения F(p) при . Оче­видно, что в правой части уравнения получим , а в левой – неопределœен­ность, так как . Раскроем эту неопределœенность по правилу Лопи­таля:

.

Следовательно, формула для произвольного коэффициента: .

Тогда выражение искомой функции получает вид:

По таблице соответствия находим, что операторному изображению соответствует оригинал , следовательно, оригинал искомой функ­ции получает вид:

=Û

Это уравнение получило название формулы разложения и исполь­зуется для перехода от операторного изображения функции к ее ори­гиналу, ᴛ.ᴇ. функции вре­мени . Порядок применения формулы разло­жения:

1) Операторное изображение искомой функции преобразуют к виду дроби =, чтобы в числителœе и знаменателœе ее стояли сте­пенные полиномы.

2) Приравнивают к нулю знаменатель дроби и находят корни этого урав­нения .

3) Находят выражение производной знаменателя дроби.

4) Определяют коэффициенты путем поочередной под­становки зна­чений каждого из корней в это выражение.

5) Записывают решение для искомой функции времени в виде суммы от­дельных слагаемых-экспонент, при крайне важно сти упрощают по­лученное выражение: .

Последовательность выполнения отдельных этапов расчета переход­ных процессов операторным методом показано ниже в виде диаграммы.

Примечание. Составление системы операторных уравнений может вы­полняться по одному из двух вариантов: А — путем непосредственного пре­образования дифференциальных уравнений Кирхгофа в операторные в и B —путем составления системы уравнений по одному из методов расчета для опера­торной схемы замеще­ния.

Замечания к формуле разложения.

1) В случае если в исходной схеме имеются источники постоянных ЭДС Е, то уравнение может иметь один корень, равный нулю (). Под­становка этого корня в формулу разложения дает постоянную величину , которая соответ­ст­вует установившейся составляющей искомой функции.

2) В случае если в исходной схеме имеются источники синусоидальных ЭДС , то уравнение будет иметь два чисто мнимых и сопряжен­ных корня и . Подстановка этих корней в формулу разложения в сумме дает синусоидальную функцию времени, кото­рая соответствует установившейся состав­ляющей искомой функции:

3) В случае если уравнение имеет два комплексно сопряженных корня и , то подстановка этих корней в фор­мулу раз­ложения в сумме дает синусоидальную функцию с затухающей амплиту­дой:

4) В случае если уравнение имеет кратные корни (), то фор­мула разложения неприменима. Случай кратных корней может встретиться в практике крайне редко. Чтобы применить формулу разложения в данном случае достаточно несущественно изме­нить параметры одного из элементов схемы.

Пример.Важно заметить, что для схемы рис. 138 с заданными параметрами элементов (Е=100 В, R=50 Ом, R1=20 Ом, R2=30 Ом, С=83,5 мкФ) определить ток после коммутации.

1) Определяется независимое начальное условие из расчета схемы рис. 138 в состоя­нии до коммутации:

B

2) Составляется операторная схема цепи после коммутации (рис. 139):

3) Составляется система контурных уравнений для схемы рис. 139 в операторной форме:

4) Производится решение операторных уравнений относительно ис­комой функции I₁(p):

,

где ; ;

5) Корни уравнения :

;

6) Коэффициенты для отдельных корней p_k:

;

7) Окончательное решение для искомой функции времени:

A

14. Анализ переходных процессов в цепи R, L

Исследуем, как изменяется ток в цепи с резистором R и катушкой L в пере­ходном режиме. В качестве примера рассмотрим переходной процесс при включении цепи R, L к источнику а) постоянной ЭДС =const и б) переменной ЭДС (рис. 140).

Расчет переходного процесса выполним классическим методом.

а) Включение цепи R, L к источнику постоянной ЭДС .

Общий вид решения для тока:

Установившаяся составляющая тока: .

Характеристическое уравнение и его корни:

.

Независимое начальное условие: .

Постоянная интегрирования: .

Окончательное решение для искомой функции:

,

где − постоянная времени, численно равная времени, за ĸᴏᴛᴏᴩᴏᴇ ам­плитуда сво­бодной составляющей затухает в раза. Чем больше , тем медленнее затухает переходной процесс. Теоретически затуха­ние свободной составляющей про­должается до бесконечности. Техническое время переходного процесса определя­ется из условия, что за это время свободная составляющая уменьшается до 0,01 от ее первоначального значения:

, откуда .

На рис. 141 представлена графическая диаграмма искомой функции

Для приближенного построения графической диаграммы свободной составляю­щей можно воспользоваться таблицей значений этой функции в интервале времени :

t		0,5	1,0	1,5
		0,61	0,37	0,22	0,14	0,05	0,02

Постоянная времени должна быть определœена из графической диа­граммы функции как отрезок времени , по краям которого от­ношение значений функции равно раза (рис. 141).

б) Включение цепи R, L к источнику синусоидальной ЭДС

Общий вид решения для тока:

Характеристическое уравнение и его корни:

Установившаяся составляющая тока:

, откуда следует

,

где , , .

Независимое начальное условие:

Постоянная интегрирования:

, откуда

Окончательное решение для искомой функции:

Из анализа решения видно, что амплитуда свободной составляющей А зависит от начальной фазы источника ЭДС. При эта ам­плитуда имеет макси­мальное значение , при этом переходной процесс протекает с максималь­ной интенсивностью. При ампли­туда свободной составляющей равна нулю, и переходной процесс в цепи вообще отсутствует. На рис. 142 представлена графическая диаграмма иско­мой функции при , .

16. Анализ переходных процессов в цепи R, C

Исследуем характер переходных процессов в цепи R, C при включе­нии ее к источнику а)постоянной ЭДС , б)переменной ЭДС (рис. 143).

а) Включение цепи R, C к источнику постоянной ЭДС

Общий вид решения для напряжения :

.

Установившаяся составляющая напряжения: :

Характеристическое уравнение и его корни:

, где — постоянная вре­мени.

Независимое начальное условие:.

Постоянная интегрирования: .

Окончательное решение для искомой функции:

,

.

Подсчитаем баланс энергий при зарядке конденсатора.

Энергия источника ЭДС:

Энергия, выделяемая в резисторе R в виде тепла:

.

Энергия электрического поля конденсатора:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, энергия электрического поля конденсатора составляет ровно поло­вину энергии источника и не зависит от величины сопротивления зарядного резистора R (закон половины).

Графические диаграммы функций и показаны на рис. 144.

б) Включение цепи R, C к источнику синусоидальной ЭДС .

Общий вид решения для напряжения :

Характеристическое уравнение и его корень:

Установившаяся составляющая напряжения:

, откуда

,

где , , .

Независимое начальное условие: .

Определœение постоянной интегрирования:

; откуда .

Как следует из полученного уравнения, амплитуда свободной составляю­щей за­ви­сит от начальной фазы источника ЭДС. При эта амплитуда имеет максимальное значение , при этом переходной процесс протекает с макси­мальной ин­тенсивностью. При амплитуда свободной составляющей равна нулю и переходной процесс в цепи отсутствует.

17. Анализ переходных процессов в цепи R, L, C

Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом ис­точника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес пред­ставляют свободные составляющие, так как харак­тер свободного процесса ока­зывается существенно различным исходя из того, явля­ются ли корни ха­рактеристического уравнения вещественными или комплексными сопря­жен­ными.

Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 145).

Общий вид решения для тока: .

Установившаяся составляющая: .

Характеристическое уравнение и его корни: , откуда:

; .

Дифференциальное уравнение: .

Независимые начальные условия: ; .

Зависимое начальное условие: ; откуда .

Постоянные интегрирования определяется из совместного решения сис­темы уравнений:

, откуда .

Окончательное решение для тока:

.

Исследуем вид функции при различных значениях корней характе­ристиче­ского уравнения.

а) Корни характеристического уравнения вещественные, не равны друг другу. Это имеет место при условии или , тогда , , причем , .

При изменении t от 0 до ∞ отдельные функции и убывают по экспоненци­альному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность . Из этого следует вывод, что искомая функция тока в крайних точках при t = 0 и при t = ∞ равна нулю, а в проме­жутке времени 0 < t < ∞ — всœегда положительна, дос­тигая при некотором зна­чении времени своего максимального значения . Найдем данный момент времени:

, или , откуда .

Графическая диаграмма функции для случая вещественных корней характери­стического уравнения показана на рис. 146.

Продолжительность переходного процесса в данном случае определяется меньшим по модулю корнем: .

Характер переходного процесса при вещественных корнях характеристи­ческого уравнения получил название затухающего или апериодического.

б) Корни характеристического уравнения комплексно сопряженные. Это имеет ме­сто при соотношении параметров или , тогда

,

где — коэффициент затухания, — угловая частота собст­венных ко­лебаний.

Решение для исконной функции должна быть преобразовано к другому виду:

.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в случае комплексно сопряженных корней характеристи­ческого уравнения искомая функция изменяется во времени по гармониче­скому закону с затухающей амплитудой . Графическая диаграмма функции показана на рис. 147.

Период колебаний , продолжительность переходного процесса определя­ется коэффициентом затухания:.

Характер переходного процесса при комплексно сопряженных корнях ха­рактери­сти­ческого уравнения получил название колебательного или периодиче­ского.

В случае комплексно сопряженных корней для определœения свободной составляю­щей применяют частную форму:

или ,

где коэффициенты и или и являются новыми постоянными ин­тегри­рова­ния, ко­торые определяются через начальные условия для искомой функции.

в) Корни характеристического уравнения вещественные и равны друг другу. Это имеет место при условии или , тогда .

Полученное ранее решение для искомой функции в данном случае ста­новится не­определœенным, так как числитель и знаменатель дроби превращаются в нуль. Раскроем эту неопределœенность по правилу Лопиталя, считая , а , которая стре­мится к . Тогда получим:

.

Характер переходного процесса при равных корнях характеристического уравнения получил название критического. Критический характер переходного процесса является гра­ничным между затухающим и колебательным и по форме ничем не отличается от затухаю­щего. Продолжительность переходного про­цесса . При изменении только сопро­тивления резистора затухающий характер переходного процесса соответст­вует об­ласти значений , колебательный характер — также области значе­ний , а критический характер – одной точке . По­этому на практике случай равных корней характеристического уравнения встречается крайне редко.

В случае равных корней для определœения свободной составляющей при­меняют ча­ст­ную форму:

,

где коэффициенты и являются новыми постоянными ин­тегрирования, ко­торые опре­деляются через начальные условия для искомой функции.

Критический режим переходного процесса характерен тем, что его про­должитель­ность имеет минимальное значение . Указанное свойство находит при­менение в электротехнике.

referatwork.ru

Формула разложения — Энциклопедия по машиностроению XXL

Если K=(p(A i), т. е. Х = Х-л… = ==Хп = 0, то формула разложения в ряд Тейлора следует из геометрических соображений, так как производная представляет собой тангенс угла наклона касательной к кривой.  [c.22]

Равенство (9.1) представляет собой формулу разложения силы на составляющие по осям координат.  [c.24]

Ограничиваясь в формуле разложения  [c.317]

Отсюда получаем формулы разложения векторов скорости  [c.147]

Введем спектральное разложение самой пульсирующей скорости v(r) ио обычным формулам разложения Фурье  [c.204]

Отсюда, вспомнив формулу разложения (11) 61 вектора и, получим  [c.288]

Формула разложения вектора т (р) по координатным осям х, у VI г будет иметь вид  [c.161]

Отсюда получаем формулу разложения вектора относительной скорости точки М по подвижным осям  [c.312]

Сравнивая эти выражения с формулами разложения функций в ряд Фурье по косинусам, найдем  [c.291]

Применим к этой функции формулу разложения в биноминальный ряд  [c.185]

К этой же форме для ф придем, воспользовавшись формулой разложения функции в ряд Тейлора.  [c.188]

Пусть 21 2 и, следовательно, р р , применяя формулу разложения натурального логарифма  [c.29]

Так как вектор V выражается формулой (10), то здесь достаточно подставить это выражение во второй член формулы (12 ) и воспользоваться разложением двойного векторного произведения (26) гл. I, чтобы получить соотношение (12). В самом деле, по формуле разложения  [c.167]

Для компактности дальнейшего изложения введем обозначения X = (х , Хд,…, х ) — вектор X без компоненты х,-, т.е. X = (Х , х,-). Будем также условно обозначать х,- = 1 через 1,-, -а х,- = О — через Oj. В этих обозначениях формула разложения логической функции по аргументу х,- примет вид ф (X) = х, ф fX,, 1,)V Зс ф (Х О,). В случае с мостиковой схемой (см. рис. 4.12) получим при разложении относительно диагонального элемента Ф (X) = Хд ф (Х , Ц) V Хд Ф (Х , О3), где  [c.194]

В таком случае из формулы разложения имеем [17]  [c.158]

Имеют место следующие важные формулы разложения определителя по г-й строке н по /-му столбцу  [c.114]

В частности формула разложения по элементам первой строки имеет вид  [c.114]

Интерполяция. Первая формула Ньютона. Формула разложения по факториальным функциям  [c.256]

Используя формулы разложения / (д ) и 9 (д ) в ряд Фурье, получим  [c.225]

Используя формулы разложения f х) и [c.225]

Запишем это разложение, используя формулу разложения (гл. 3), а именно  [c.190]

Оригиналы изображений (4-3-5) и (4-3-8) найдем посредством обобщенной формулы разложения. После выполнения необходимых преобразований искомое решение нашей задачи запишется в следующем ваде  [c.140]

Используя формулу разложения YI + a= 1 + подсчитаем длину элемента  [c.106]

Пусть замкнутая цилиндрическая оболочка, которую мы хотим рассчитывать при помощи уравнений безмоментной теории, ограничена поперечными краями 1=0, I = Иг, где I — длина оболочки. Тогда о точности безмоментной теории можно судить по погрешности, с которой на интервале (0 I) аппроксимируются потенциальные функции (24.9.1а) и (24.9.2а) выражениями вида (24.9.3). Обозначим через k любой из малых корней характеристического уравнения и выпишем известную формулу разложения экспоненциальной функции  [c.360]

Следует отметить, что при повышении порядка производной ухудшается сходимость рядов. Для увеличения точности вычислений полезно добавить в формулах один-два следующих члена разложения, что легко сделать на основании формулы разложения (IV.35а). При этом необходимо увеличить точность разло- jy  [c.373]

Подставив в эту формулу разложение  [c.228]

Такой ансамбль представляет собой совокупность бесконечно большого количества систем, имеющих последовательно возрастающее до бесконечности число молекул N, причем каждая система описывается канонической статистической суммой (110). Подставляя (115) в (116), делая перестановку операций суммирования и умножения и учитывая формулу разложения в ряд экспоненты, Курт получил  [c.57]

Подставляя в эти формулы разложения функций А и С по полиномам Сонина —Лагерра (14,14), получаем )  [c.66]

Вспомним формулу разложения Тейлора  [c.183]

Это равенство представляет собой очень важную формулу разложения вектора Р по координатным осям. Напомним еще «раз, что в формуле разложения вектора по координатным осям скалярные  [c.56]

Пример 8. Вектор Р, модуль которого Р — 10, лежит в плоскости Оху и образует с осью х угол а = 150° (отсчитываемый от положительного направления этой оси против часовой стрелки). Написать формулу разложения этого вектора по координатным осям.  [c.57]

Пример 9. Формула разложения данного вектора по координатным осям имеет следующий вид  [c.57]

Из равенств (11) и (12) следует также, что формула разложения равнодействующей Д по координатным осям имеет следующий вид  [c.59]

Воспользуемся известной формулой разложения экспоненциаль-  [c.126]

Формула разложения двойного векторногэ произведения (23) находит очень часто применение в приложениях векторного исчисления. Из этой формулы вытекает, между прочим, что свойством сочетательности векторное произведение не обладает, т. е. двойные произведения [V и [[г) ] 2]> Бообш е, не равнь.  [c.41]

ПО обыкновенной (формуле разложения показательной фз нкции в ряд. [c.111]

Для параксиальных лучей условия отображения без искажений соблюдены с большой точностью, однако не абсолютно. Другими словами, параксиальное приближение описывает параксиальные лучи приближенно, хотя и с большой точностью. Поэтому полученная в параксиальном приближении идеальная картина изображений в действительности не осуществляется на практике.Отклонения фактически получаемого изображения от идеального называются аберрациями. Для параксиальных лучей аберрации малы и ими пренебрегают. Если же лучи не параксиальны, то аберрации становятся значительными и сильно искажают изображение. Поэтому первый источник аберраций состоит в том, что линзы, ограниченные сферическими поверхностями, преломляют лучи не совсем так, как это принимается в параксиальном приближении. Например, фокусы для лучей, падающих на линзу на разных расстояниях от оси линзы, различны и т. д. Такие аберрации наг ывают геометрическими. Их можно классифицировать по определенным признакам, например, параксиальное приближение основывается на том, что точнь1е формулы разложения синуса в ряд (22.1) обрываются на первом члене, пропорциональном а. Не учтенный в параксиальном приближении член а -приводит к аберрациям третьего порядка.  [c.134]

Уравнение Френеля. Аналогичные заключения могуг быть сделаны и-относите 1ьно волн, распространяющихся в направлении осей А» и У. Для того чтобы изучить поведение волн распространяющихся в произвольном направлении, необходимо вместо уравнений (40.3 а, б), которые являются частным случаем уравнений (40.2 а б), проанализировать общий случай. Подставляя выражение для Н из (40.26) в уравнение (40.2а) и пользуясь формулой разложения двойного векторного произведения, находим  [c.265]

Кроме того, (/ )пт = (/тп) Отсюда для веш ественных физических величин получим пт = тп такая матрица называется эрмитовой. Диагональный элемент пп не зависит от времени, веш ественнен и представляет собой среднее значение величины / в состоянии С помош ью формулы разложения  [c.469]

---

mash-xxl.info