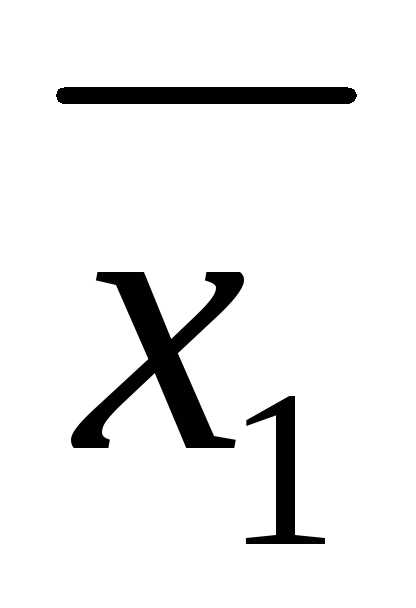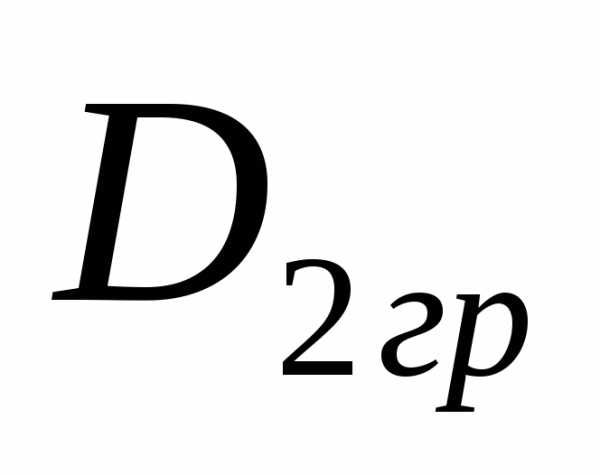29. Генеральная и выборочная дисперсия. Исправленная дисперсия. Стандарт.
Генеральная дисперсия.Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.
Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения. Если все значения признака генеральной совокупности объема N различны, то
Dг= ()/N.
Если же значения признака имеют соответственно частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то
Dг= ()/N.
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.
Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: Ϭг = √Dг.
Выборочная дисперсия.Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику- выборочную дисперсию.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
Если все значения признака выборки различны, то ^Dв= ()/n;
если же все значения имеют частоты n1, n2,…,nk, то ^Dв= ()/n.
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой — средним квадратическим отклонением.
Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии: ^Ϭв = √^Dв.
Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:
D=‾x^2 – [‾x]^2.
Замечание: если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.
30. Интервальные статистические оценки параметров. Надёжность, доверительный интервал.
Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d , то чем меньше d , тем оценка точнее.
Таким образом, положительное число d характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки называют вероятность g, с которой осуществляется неравенство |Q—Q* | <d .
Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что, |Q- Q*| <d равна g: P(|Q- Q*| <d)= g.
Заменив неравенство равносильным ему двойным неравенством получим: Р [Q* —d< Q < Q* +d] = g
Это соотношение следует понимать так: вероятность того, что интервал Q* — d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.
Интервал (Q* — d Q* +d) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью g.
studfiles.net
Лекция 5. Генеральная дисперсия. Выборочная дисперсия. Формула для вычисления дисперсии.
Задача скачана с сайта www.matburo.ru МатБюро — Решение задач по высшей математике
Тема: Статистика Задача скачана с сайта MatBuroru ЗАДАНИЕ Имеются данные 6%-ного механического отбора магазинов торговой фирмы по стоимости основных фондов (млрд руб): 4,,9 3,1 3,9 1,7,8 1,8,9 7,1,5 4,7
ПодробнееЛекция 5. Показатели вариации
Лекция 5. Показатели вариации Основные показатели вариации Вариация значений признака представляет наибольший интерес при исследовании социально-экономических явлений и процессов. Вариация колеблемость,
Подробнее5. ОЦЕНКА ГЕНЕРАЛЬНЫХ ПАРАМЕТРОВ
Оценка параметров 30 5. ОЦЕНКА ГЕНЕРАЛЬНЫХ ПАРАМЕТРОВ 5.. Введение Материал, содержащийся в предыдущих главах, можно рассматривать как минимальный набор сведений, необходимых для использования основных
Интервальные оценки.
Лекция 1. Интервальные оценки. Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается
Подробнее6.7. Статистические испытания
Лекция.33. Статистические испытания. Доверительный интервал. Доверительная вероятность. Выборки. Гистограмма и эмпирическая 6.7. Статистические испытания Рассмотрим следующую общую задачу. Имеется случайная
ПодробнееМатематическая статистика.
Лекция. Математическая статистика. Основной задачей математической статистики является разработка методов получения научно обоснованных выводов о массовых явлениях и процессах из данных наблюдений и экспериментов.
ПодробнееЛекция 9. Тема Введение в теорию оценок.
Лекция 9 Тема Введение в теорию оценок. Содержание темы Предмет, цель и метод задачи оценивания Точечные выборочные оценки, свойства оценок Теоремы об оценках Интервальные оценки и интеграл Лапласа Основные
ПодробнееЛекция 1. Выборочное пространство
Лекция 1. Выборочное пространство Грауэр Л.В., Архипова О.А. CS center Санкт-Петербург, 2014 Грауэр Л.В., Архипова О.А. (CSC) Лекция 1. Выборочное пространство Санкт-Петербург, 2014 1 / 29 Cодержание Содержание
Подробнее4 Проверка параметрических гипотез
4 Проверка параметрических гипотез Статистическая гипотеза Параметрическая гипотеза 3 Критерии проверки статистических гипотез Статистической называют гипотезу о виде неизвестного распределения или о параметрах
ПодробнееПРИМЕР РЕШЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ 6 (МПМ, 2 курс, 3 семестр) Тема «Математическая статистика»
Задача 1. ПРИМЕР РЕШЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ 6 (МПМ, 2 курс, 3 семестр) Тема «Математическая статистика» В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0,
ПодробнееКраткая теория погрешностей
I. Измерение физических величин. Краткая теория погрешностей измерения прямые измерения, которые представляют собой косвенные измерения, которые представляют собой сравнение значения физической вычисление
ПодробнееЭлементы математической статистики
Элементы математической статистики Математическая статистика является частью общей прикладной математической дисциплины «Теория вероятностей и математическая статистика», однако задачи, решаемые ею, носят
ПодробнееАННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ
ПодробнееВ. Сидоренко МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1 Министерство образования и науки Республики Казахстан ВОСТОЧНО-КАЗАХСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Д.Серикбаева В. Сидоренко МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Методические указания по выполнению
Иррациональные уравнения и неравенства 1
Иррациональные уравнения и неравенства Оглавление Свойства корней й степени Свойства корней Свойства степеней с рациональным показателем Примеры 5 Свойства корней -й степени Арифметическим корнем й степени
ПодробнееМАТЕМАТИЧЕСКАЯ СТАТИСТИКА
АЛМАТИНСКИЙ ФИЛИАЛ НЕГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ ПРОФСОЮЗОВ» С.Ж. КАРАТАБАНОВА, Л.А. ХАРАСАХАЛ МАТЕМАТИЧЕСКАЯ
Подробнее1. ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
1. ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ 1.1. Цели освоения дисциплины: научить студентов языку теории вероятностей и статистики; быть поставщиком понятий и результатов, необходимых в других математических
ПодробнееПлан лекций 1 семестр
План лекций 1 семестр 1. Введение. 1.1. Предмет, метод и задачи статистики; источники статистической информации. 1.2. Кратка история развития статистики. Структура статистических органов на современном
ПодробнееЛекция 7. Выборочные наблюдения
Лекция 7. Выборочные наблюдения Выборочным называется такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием
ПодробнееЗадачи по статистике
Задачи по статистике Задача 1. Статистические группировки. Произвести группировку 25-ти предприятий по стоимости основных фондов, выделив, пять групп с равными интервалами. : Интервал находили по формуле
ПодробнееУЧЕБНАЯ ПРОГРАММА ПО ДИСЦИПЛИНЕ
Учреждение образования «Белорусский государственный педагогический университет имени Максима Танка» Институт повышения квалификации и переподготовки Факультет переподготовки специалистов образования Кафедра
ПодробнееЭлементы теории оценок и проверки гипотез
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Основной принцип проверки ПРОВЕРКА ГИПОТЕЗ О ЧИСЛОВЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ дисперсия известна дисперсия неизвестна t распределение распределение
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа по алгебре составлена на основе федерального компонента государственного образовательного стандарта основного общего образования по математике 004 года, примерной
ПодробнееJohann Carl Friedrich Gauß
ПРИЛОЖЕНИЕ 1 Все вероятности равны 50%. Либо случится, либо нет. Мерфология, Логические предложения Кольварда Типовые распределения При проверке гипотез широкое применение находит ряд теоретических законов
ПодробнееЗадачи по математической статистике
Задачи по математической статистике Задача. По данным распределения возрастного состава участников революционного движения в России 70-х годов 9-го века была построена следующая таблица Возраст 7-3 3-9
Математическая статистика
Математическая статистика 1 Выборка X x, x,, x Опр.1 Пусть одномерная с.в., а 1 значения с.в.,полученные в результате испытания. Будем называть полученные значения выборкой из генеральной совокупности
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа составлена к учебнику «Алгебра 8» авторов Ю.Н.Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой. Цель изучения курса алгебры в 8 классе развить интерес к решению
ПодробнееОТВЕТЫ
МАТЕМАТИКА, 9 класс Ответы и критерии, Март 01 / задание 1 4 5 6 7 8 9 10 ОТВЕТЫ 1 4 5 6 7 8 9 10 1 4-1 1 71 1 0 648 54 1-5 1 1080 54 4-5 11 50 00 1-1 8 1 0 60 — — 4 4 4 64 4-1 4 5 8 1 11 7 0 400 1000-1
Подробнее(a 1)(a + 2) (a + 4)(a 3) = (a 2 + a 2) (a 2 + a 6).
3.. Методы решения рациональных неравенств 3..1. Числовые неравенства Сначала определим, что мы понимаем под утверждением a > b. Определение 3..1. Число a больше числа b, если разность между ними положительна.
ПодробнееТеория статистики. Т. Г. Старостина
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Ульяновский государственный технический университет Т. Г. Старостина Теория статистики
ПодробнееЛабораторная работа 1.
Компьютерные методы моделирования строительства скважин. Лабораторная работа. Построение вариационных рядов. Расчет числовых характеристик Цель работы: овладение способами построения рядов распределения
Подробнееdocplayer.ru
§ 12. Сложение дисперсий
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
Dобщ =Dвнгр + Dмежгр.
Доказательство. Для упрощения доказательства предположим, что вся совокупность значений количественного признака X разбита на две следующие группы:
Группа…………………… | первая | вторая | |
Значение признака……….. | x1 x2 | x1 x2 | |
Частота……………………. | m1 m2 | n1 n2 | |
Объем группы……………. | N1= m1+ m2 | N2= n1+ n2 | |
Групповая средняя………. | | | |
Групповая дисперсия……. |
|
| |
Объем своей совокупности | n=N1+N2 | ||
Далее для удобства записи
вместо знака суммы 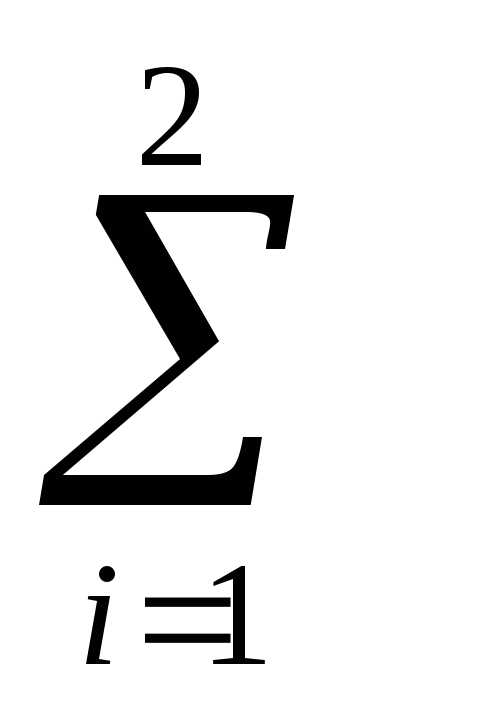 пишется
знак
пишется
знак .
.
Например, .
Следует также иметь в виду, что если под знаком суммы стоит постоянная величина, то ее целесообразно выносить за знак суммы.
Например, .
Найдем общую дисперсию:
Dобщ=. (*)
Преобразуем первое слагаемое
числителя, вычтя и прибавив  :
:
.
Так как
(равенство следует из соотношения ) и в силу § 7
,
тo первое слагаемое принимает вид
. (**)
Аналогично можно представить
второе слагаемое числителя (*) (вычтя и
прибавив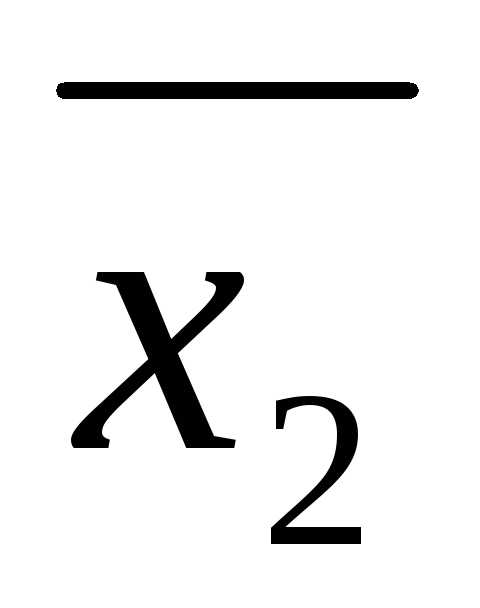 ):
):
. (***)
Подставим (**) и (***) в (*):
.
Итак,
Dобщ =Dвнгр + Dмежгр.
Пример, иллюстрирующий доказанную теорему, приведен в предыдущем параграфе.
Замечание. Теорема имеет не только теоретическое, но и важное практическое значение. Например, если в результате наблюдений получены несколько групп значений признака, то для вычисления общей дисперсии можно группы в единую совокупность не объединять. С другой стороны, если совокупность имеет большой объем, то целесообразно разбить ее на несколько групп. В том и другом случаях непосредственное вычисление общей дисперсии заменяется вычислением дисперсий отдельных групп, что облегчает расчеты.
§ 13. Оценка генеральной дисперсий по исправленной выборочной
Пусть из генеральной совокупности в результате n независимых наблюдений над количественным признаком X извлечена повторная выборка объема n:
значения признака………
x1
x2
…
xk
частоты……………………
n1
n2
…
nk
При этом n1 + n2 + … + nk = п.
Требуется по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию Dг. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия является смещенной оценкой Dг, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
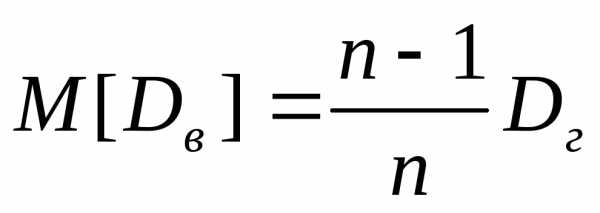 .
.
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить Dв на дробь n/(n-1). Сделав это, получим исправленную дисперсию, которую обычно обозначают через s2:
.
Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии. Действительно,
.
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
.
Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
.
Подчеркнем, что s не является несмещенной оценкой; чтобы отразить этот факт, мы написали и будем писать далее так: «исправленное» среднее квадратическое отклонение.
Замечание. Сравнивая формулы
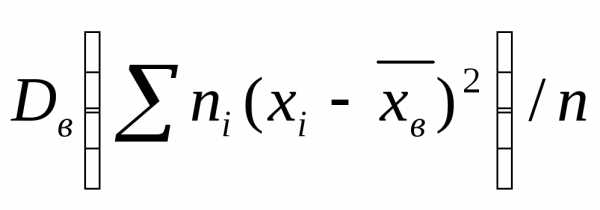 и
.
и
.
видим, что они отличаются лишь знаменателями. Очевидно, при достаточно больших значениях n объема выборки выборочная и исправленная дисперсии различаются мало. На практике пользуются исправленной дисперсией, если примерно n < 30.
studfiles.net
Генеральная дисперсия.
Количество просмотров публикации Генеральная дисперсия. — 150
Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.
Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения.
В случае если все значения признака генеральной совокупности объёма N различны, то
В случае если же значения признака имеют соответственно частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.
Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:
Выборочная дисперсия.
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику — выборочную дисперсию.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
В случае если все значения признака выборки различны, то
если же все значения имеют частоты n1, n2,…,nk, то
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой — средним квадратическим отклонением.
Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:
Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии: .
Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом
Вычисление дисперсии — выборочной или генеральной, можно упростить, используя формулу:
Замечание: если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.
referatwork.ru
§ 9. Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
Пусть генеральная совокупность распределена нормально, причем генеральная дисперсия хотя и неизвестна, но имеются основания предполагать, что она равна гипотетическому (предполагаемому) значению σ20. На практике σ20 устанавливается на основании предшествующего опыта или теоретически.
Пусть из генеральной совокупности извлечена выборка объема n и по ней найдена исправленная выборочная дисперсия S2 с k=n—1 степенями свободы. Требуется по исправленной дисперсии при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральная дисперсия рассматриваемой совокупности равна гипотетическому значению σ20.
Учитывая, что S2 является несмещенной оценкой генеральной дисперсии, нулевую гипотезу можно записать так:
H0:М(S2)= σ20.
Итак, требуется проверить, что математическое ожидание исправленной дисперсии равно гипотетическому значению генеральной дисперсии. Другими словами, требуется установить, значимо или незначимо различаются исправленная выборочная и гипотетическая генеральная дисперсии.
На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и устойчивость технологических процессов. Например, если известна допустимая характеристика рассеяния контролируемого размера деталей, изготавливаемых станком-автоматом, равная σ20, а найденная по выборке окажется значимо больше σ20, то станок требует подналадки.
В качестве критерия проверки нулевой гипотезы примем случайную величину (n—1)S2/ σ20. Эта величина случайная, потому что в разных опытах S2 принимает различные, наперед неизвестные значения. Поскольку можно доказать, что она имеет распределение χ2 с k=n—1 степенями свободы (см. гл. XII, § 13), обозначим ее через χ2.
Итак, критерий проверки нулевой гипотезы
Χ2=(n — 1)S2/ σ20.
Критическая область строится в зависимости от вида конкурирующей гипотезы.
Первый случай. Нулевая гипотеза Н0: σ2 = σ20. Конкурирующая гипотеза Н1: σ2 > σ20.
В этом случае строят правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:
Р[χ2> χ2кр(α,k)]=α.
Критическую точку χ2кр(α,k) находят по таблице критических точек распределения χ2 (см. приложение 5), и тогда правосторонняя критическая область определяется неравенством χ2 > χ2кр, а область принятия нулевой гипотезы — неравенством χ2 < χ2кр.
Обозначим значение критерия, вычисленное по данным наблюдений, через χ2набл и сформулируем правило проверки нулевой гипотезы.
Правило 1. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу Н0: σ2 = σ20 о равенстве неизвестной генеральной дисперсии нормальной совокупности гипотетическому значению при конкурирующей гипотезе Н1: σ2 > σ20, надо вычислить наблюдаемое значение критерия χ2набл=(n — 1)S2/ σ20 и по таблице критических точек распределения χ2, по заданному уровню значимости α и числу степеней свободы k = n—1 найти критическую точку χ2кр(α,k).
Если χ2набл < χ2кр —нет оснований отвергнуть нулевую гипотезу. Если χ2набл > χ2кр —нулевую гипотезу отвергают.
Пример 1. Из нормальной генеральной совокупности извлечена выборка объема n=13 и по ней найдена исправленная выборочная дисперсия s2= 14,6. Требуется при уровне значимости 0,01 проверить нулевую гипотезу Н0: σ2 = σ20 = 12, приняв в качестве конкурирующей гипотезы Н1: σ2 > 12.
Решение. Найдем наблюденное значение критерия:
χ2набл=(n — 1)S2/ σ20 = ((13-1)·14,6)/12=14,6.
По условию, конкурирующая гипотеза имеет вид σ2 > 12, поэтому критическая область правосторонняя.
По таблице приложения 5, по уровню значимости 0,01 и числу степеней свободы k = n— 1 == 13— 1 == 12 находим критическую точку χ2кр (0,01; 12) =26,2.
Так как χ2набл < χ2кр —нет оснований отвергнуть нулевую гипотезу. Другими словами, различие между исправленной дисперсией (14,6) и гипотетической генеральной дисперсией (12) — незначимое.
Второй случай. Нулевая гипотеза Н0: σ2 = σ20. Конкурирующая гипотеза Н1: σ2 ≠ σ20.
В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α.
Критические точки—левую и правую границы критической области—находят, требуя, чтобы вероятность попадания критерия в каждой из двух интервалов критической области была равна α/2:
P[ χ2 < χ2лев.кр(α/2,k) ]=α/2,
P[ χ2 > χ2лев.кр(α/2,k) ]=α/2.
В таблице критических точек распределения χ2 указаны лишь «правые» критические точки, поэтому возникает кажущееся затруднение в отыскании «левой» критической точки. Это затруднение легко преодолеть, если принять во внимание, что события χ2 < χ2лев.кр и χ2 > χ2лев.кр противоположны и, следовательно, сумма их вероятностей равна единице:
Р (χ2 < χ2лев.кр) + Р (χ2 > χ2лев.кр) =1.
Отсюда
Р (χ2 < χ2лев.кр) =1- Р (χ2 > χ2лев.кр) =1-(α/2).
Мы видим, что левую критическую точку можно искать как правую (и значит, ее можно найти по таблице), исходя из требования, чтобы вероятность попадания критерия в интервал, расположенный правее этой точки, была равна 1—(α/2).
Правило 2. Для того чтобы при заданном уровне значимости а проверить нулевую гипотезу о равенстве неизвестной генеральной дисперсии σ2 нормальной совокупности гипотетическому значению σ20 при конкурирующей гипотезе Н1: σ2 ≠ σ20 надо вычислить наблюдаемое значение критерия χ2набл=(n — 1)S2/ σ20 и по таблице найти левую критическую точку χ2кр (1—α/2; k) и правую критическую точку χ2кр (α/2;k).
Если χ2лев.кр < χ2набл < χ2прав.кр — нет оснований отвергнуть нулевую гипотезу.
Если χ2набл < χ2лев.кр или χ2набл > χ2прав.кр — нулевую гипотезу отвергают.
Пример 2. Из нормальной генеральной совокупности извлечена выборка объема n=13 и по ней найдена исправленная выборочная дисперсия s2=10,3. Требуется при уровне значимости 0,02 проверить нулевую гипотезу Н0: σ2 = σ20 = 12, приняв в качестве конкурирующей гипотезы Н1: σ2 ≠ 12.
Решение. Найдем наблюдавшееся значение критерия:
χ2набл=(n — 1)S2/ σ20 = ((13-1)·10,3)/12= 10,3.
Так как конкурирующая гипотеза имеет вид σ2 ≠ 12, то критическая область — двусторонняя.
По таблице приложения 5 находим критические точки: левую — χ2кр (1—α/2; k) = χ2кр (1-0,02/2; 12) = χ2кр (0,99; 12) =3,57 и правую — χ2кр (α/2; k) = χ2кр (0,01; 12)=26,2. Так как наблюдавшееся значение критерия принадлежит области принятия гипотезы (3,57 < 10,3 < 26,2)—нет оснований ее отвергнуть. Другими словами, исправленная выборочная дисперсия (10,3) незначимо отличается от гипотетической генеральной дисперсии (12).
Третий случай. Конкурирующая гипотеза Н1: σ2 < σ20.
Правило 3. При конкурирующей гипотезе Н1: σ2 < σ20 находят критическую точку χ2кр (1—α; k).
Если χ2набл > χ2кр (1—α; k)—нет оснований отвергнуть нулевую гипотезу.
Если χ2набл < χ2кр (1—α; k)—нулевую гипотезу отвергают.
Замечание 1. В случае, если найдена выборочная дисперсия Dв, в качестве критерия принимают случайную величину χ2 =Dв/ σ20, которая имеет распределение χ2 с k=n—1 степенями свободы, либо переходят к s2 = [n/(n— 1)] Dв.
Замечание 2. Если число степеней свободы k > 30, то критическую точку можно найти приближенно по равенству Уилсона – Гилферти
.
где zα определяют, используя функцию Лапласа (см. приложение 2), по равенству Ф(zα)=(1—2α)/2.
studfiles.net
Дисперсия генеральная — Справочник химика 21
Дисперсию генеральной совокупности сг2 нормально распределенной случайной величины можно оценить, если известно распределение ее оценки — выборочной дисперсии . Распределение выборочной дисперсии можно получить при помощи распределения Пирсона или распределения. Если имеется выборка и независимых наблюдений х,, х ,х над нормально распределенной случайной величиной, то можно показать, что сумма [c.47]Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость изучаемой случайной величины. Для этого производится разложение суммарной выборочной дисперсии на составляющие, обусловленные независимыми факторами. Каждая из этих составляющих представляет собой оценку дисперсии генеральной совокупности. Чтобы решить, значимо ли влияние данного фактора, необходимо оценить значимость соответствующей выборочной дисперсии в сравнении с дисперсией воспроизводимости, обусловленной случайными факторами. Проверка значимости оценок дисперсий проводится по критерию Фишера (см. гл. II, 11). Если рассчитанное значение критерия Фишера окажется меньше табличного, то влияние рассматриваемого фактора нет оснований считать значимым. Если же рассчитанное значение критерия Фишера окажется больше табличного, то рассматриваемый фактор влияет на изменчивость средних. В дальнейшем будем полагать, что выполняются следующие допущения 1) случайные ошибки наблюдений имеют нормальное распределение 2) факторы влияют только на изменение средних значений, а дисперсия наблюдений остается постоянной эксперименты равноточны. [c.75]
Воспроизводимость — метрологический параметр, характеризующий случайную погрешность методики анализа. Показателем воспроизводимости служит величина стандартного отклонения воспроизводимости, т. е. корень квадратный из выборочной дисперсии или дисперсии генеральной совокупности, взятый со знаком плюс. [c.39]
Величину называют дисперсией генеральной совокупности. [c.138]
Оценка математического ожидания норд1ально распределенной случайной величины. При отсутствии грубых и систематических ошибок математическое ожидание случайной величины совпадает с истинным результатом наблюдений. Поэтому оценка математического ожидания имеет важное значение при обработке наблюдений. Легче всего оценить математическое ожидание при известной дисперсии генеральной совокупности (см. гл. II. 8). Генеральную дисперсию аг нельзя получить из наблюдений, ее можно только оценить при помощи выборочной дисперсии iP. Ошибка от замены генеральной дисперсии выборочной будет тем меньше, чем больше объем выборки и. На практике эту погрешность не учитьшают при л >50 и в формуле (11.49) для доверительного интервала генеральный параметр заменяют выборочным стандартом. В дальнейшем предполагается, что наблюдаемая случайная величина имеет нормальное распределение. [c.45]
Определение дисперсии по текущим измерениям. Математическое ожидание (среднее) и дисперсия генеральной совокупности оцениваются средним и дисперсией выборки тем точнее, чем больше объем выборки. При этом среднее характеризует результат измерений, а дисперсия — точность этого результата дисперсия воспроизводимости) (см. гл. П, 4). Если проделано т параллельных опытов (опытов, проведенных при неизменном комплексе основных факторов) и получена выборка у,, у , Ут значений измеряемой величины, то дисперсия воспроизводимости равна [c.37]
Определение дисперсии по текущим измерениям. Математическое ожидание (среднее) и дисперсия генеральной совокупности оцениваются средним и дисперсией выборки тем точнее, чем больше объем выборки. При этом среднее характеризует результат измерений, а дисперсия — точность этого результата дисперсия вос [c.32]
Число степеней свободы у общей дисперсии воспроизводимости, определяемой по формулам (11.39) и (11.42), гораздо больше, чем у каждой частной дисперсии в отдельности. Поэтому общая дисперсия воспроизводимости намного точнее оценивает дисперсию генеральной совокупности Сз2, р. [c.39]
Оценка математического ожидания нормально распределенной случайной величины. При отсутствии грубых и систематических ошибок математическое ожидание случайной величины, совпадает с истинным результатом наблюдений. Поэтому оценка математического ожидания имеет важное значение при обработке наблюдений. Легче всего оценить математическое ожидание при известной дисперсии генеральной совокупности (см. гл. П, 8). [c.41]
Пусть требуется сравнить две различные по величине оценки стандартных отклонений 1 и 2 со степенями свободы Д и /г. Надо решить, лежит ли различие между 1 и 2 в границах возможных случайных колебаний (см. разд. 5.3), т.е. можно ли оба значения и 2 рассматривать как оценку одной и той же дисперсии генеральной совокупности с нормальным распределением. Проверяемая (параметрическая) гипотеза, следовательно, такова (т = (Т2 =. Если данное предположение выполняется, то отношение следует -распределению (см. [c.116]
При статистической обработке материалов наблюдений (анализов) для характеристики распределения (рассеивания) случайной величины от ее среднего обычно используется понятие дисперсия , представляющее собой средний квадрат отклонения частных значений показателя от его среднего арифметического значения. Дисперсия генеральной совокупности называется общей дисперсией и вычисляется по формуле [c.218]
Полученное значение Fэк n сравнивают с табличным (табл. 2.5) при числе степеней свободы /1- Заметим, что в таблицах число степеней свободы большей дисперсии приводится в горизонтальном ряду, мёньшей — в вертикальном и что /2) Ф Р /2, /). Если при выбранном уровне значимости (обычно р = 0,05 или р = 0,01), то расхождение между дисперсиями значимо и рассматриваемые выборочные совокупности отличаются по воспроизводимости. Если приближенными оценкам одной и той же общей для обеих выборок дисперсии генеральной совокупности. [c.52]
Полученное значение / эксп- сравнивают с табличными Чабл (табл. 2.7) при выбранной доверительной вероятности и числе степеней свободы/ = 1 — I п/2= 2- 1- В таблицах число степеней свободы большей дисперсии приводится в горизонтальном ряду, меньшей — в вертикальном ряду. Если > Р Р,при выбранной
www.chem21.info
Генеральная дисперсия определяет
1. меру рассеяния значений количественного признака Х генеральной совокупности около генеральной средней
2. среднее арифметическое квадратов отклонений величин хi генеральной совокупности от их среднего арифметического или m*
3. значение количественного признака Х генеральной совокупности
Генеральная дисперсия может быть представлена выражением
1. *
2.
3.
Выборочная дисперсия может быть представлена выражением
1.
2.
3. , где: mi — частота появления признака*
Выборочная средняя является
1. смещенной оценкой оцениваемого параметра генеральной совокупности.
2. несмещенной оценкой аналогичного параметра генеральной совокупности, так как выполняется условие: *
3. оценкой несмещенной аналогичного параметра генеральной совокупности, так как выполняется условие:
Оценка генеральной дисперсии может быть произведена при помощи выражения
1. при условии, что n > 30
2. , при условии, что n < 30*
3. , при условии, что n > 30
25. Для выборки объемом 11 вариант была вычислена выборочная дисперсия, равная 4. Тогда оценка генеральной дисперсии, сделанная по этой выборке будет равна
1. 4
2. 5
3. 4,5
4. 4,4*
26. Для выборки объемом 11 вариант была вычислена выборочная средняя, равная 5. Тогда оценка генеральной средней, сделанная по этой выборке будет равна
1. 4
2. 5*
3. 4,5
4. 4,4
В интервальной оценке устанавливается
1. вероятность того, что непрерывная случайная величина может принять то или иное значение из некоторого доверительного интервала*
2. доверительная вероятность, с которой эта оценка попадает в оцененный интервал
3. интервал, в котором принимают значения все случайные величины, входящие в генеральную совокупность
28. Коэффициент Стьюдента (tp,n) вводится
1. при интервальной оценке некоторого параметра генеральной совокупности для корректировки доверительного интервала, если мощность выборки n > 30
2. при интервальной оценке некоторого параметра генеральной совокупности для корректировки доверительного интервала, если мощность выборки n < 30*
3. при точечной оценке параметра генеральной совокупности для корректировки доверительного интервала, если мощность выборки n < 30
29. Погрешность (ошибка) среднего арифметического равна 0,5. Доверительный интервал при коэффициенте Стьюдента 2 будет равен
1. 1*
2. 2
3. 0,5
Коэффициент Стьюдента зависит
1. как от мощности выборки, так и от выбранной доверительной вероятности*
2. только от мощности выборки
3. от выбранной доверительной вероятности (вероятности, с которой интервальная оценка покроет оцениваемый параметр) и не зависит от мощности выборки
Уровень значимости оценивает
1. вероятность допустимой ошибки*
2. вероятность того, что числовое значение характеристики генеральной совокупности находится вне доверительного интервала
3. вероятность того, что числовое значение характеристики генеральной совокупности находится в пределах доверительного интервала
32. Нулевая гипотеза H0 – статистическая гипотеза, исходящая из предположения
1. что между генеральными параметрами сравниваемых групп разница равна нулю и различия, наблюдаемые между выборочными показателями, носят не систематический, а случайный характер*
2. об отсутствии различия между выборочными параметрами
3. о равенстве нулю разницы между соответствующими генеральными и выборочными параметрами независимо от уровня значимости
33. Конкурирующая (или альтернативная) гипотеза HА – статистическая гипотеза, исходящая из предположения
1. о равенстве нулю разницы между соответствующими генеральными и выборочными параметрами, но только при определенном уровне значимости
2. о равенстве нулю разницы между соответствующими генеральными и выборочными параметрами при любом уровне значимости
3. о наличии разницы между генеральными параметрами, оцениваемыми по выборочным показателям*
Критерий значимости (достоверности) – это показатель, позволяющий судить
1. об ошибочности выводов относительно принятой гипотезы
2. о вероятности выводов относительно принятой гипотезы
3. о надежности выводов относительно принятой гипотезы*
Рекомендуемые страницы:
lektsia.com