Гипербола сопряженная – Сопряжённые гиперболы — это… Что такое Сопряжённые гиперболы?

Гипербола

Гипербола — это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются.
Формула гиперболы y = k/x, при условии, что k не равно 0. То есть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним.

Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.

Основные понятия

1. Гипербола состоит из двух отдельных кривых, которые называют ветвями.
2. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
3. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
4. Середина большой оси называется центром гиперболы.
5. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. Обычно обозначается a.
6. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. Обычно обозначается c.
7. Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
8. Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряженной осью гиперболы.
9. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный к её действительной оси, называется фокальным параметром.
10. Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. Обычно обозначается b.

• Каноническое уравнение гиперболы в декартовых координатах:

x² / a² — y² / b² = 1

• Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

x_ox / a² — y_oy / b² = 1

или

y = y_o + (b²x_o)(x — x_o) / (a²y_o)

• Уравнение нормали к гиперболе имеет вид:

y = y_o — (a²y_o)(x — x_o) / (b²x_o)

Некоторые типы гипербол

Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:

xy = a² / 2,

при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a).

Гиперболы, связанные с треугольником:

1. гипербола Енжабека — кривая, изогонально сопряженная прямой Эйлера.
2. гипербола Киперта — кривая, изогонально сопряженная прямой проходящей через точку Лемуана и центр описанной окружности данного треугольника.

Свойства гиперболы

1. Оптическое свойство: свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
   Иначе говоря, если F1 и F2 фокусы гиперболы, то касательная в любой точки X гиперболы является биссектрисой угла ∠F1XF2.
2. Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
3. Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
4. Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними.

---

Другие заметки по алгебре и геометрии

edu.glavsprav.ru

Сопряженных гипербол

( рис.12.39)

Если построить гиперболу n, сопряжен-ную с гиперболой m и отнесенную к её асимптотам, то их директрисы d¹, d², d³ и d⁴, пересекаясь, определят директрисный пря-моугольник ( 2а х 2b ), выдержанный в «зо-лотой пропорции» ( 2а : 2b =1,236 : 2,0) ,т.е., как 0,618 : 1,0. В такой же пропорции нахо-дятся стороны прямоугольника, одна из ко-торых равна расстоянию между вершинами А и В гиперболы m, а вторая, — расстоянию между фокусами F³ и F

4 гипер-болы n, т.е., длине фокальной хорды гиперболы m.

К числу интересных конст-руктивных особенностей таких сопряженных гипербол относят-ся следующие:

1. Основания К и L дирек-трис d¹ и d²гиперболы m в па-

ре с основаниями M и N ди-ректрис d³иd⁴задают направ-ления касательных к ветвям m¹, m² гиперболы m, точки касания к которым определяют фокаль-ные хорды этих ветвей как поля-ры, отнесенные к точкам K и L как к полюсам;

2. Фокальные хорды F^{3 ,}F⁴ гиперболы n определяются точ-ками касания к

n¹, n² прямых, за-даваемых основаниями М и N их директрис d³ , d⁴, а также точками 1 и 2 на её мнимой оси, удалёнными от центра на расстояния, равные величинам ОС и ОD её действи-тельных полуосей;

3. Касательные к ветвям n¹ и n² гипер-

болы n перпендикулярны к её асимптотам;

4. Диагонали «фокально-вершинного» ромба F¹CF²D находятся в золотой пропор-ции, так как CD : F¹F² = 2 : 2,236;

5. Собственно ветви m¹, m

² и n¹, n² со-пряженных гипербол m и n являются резу-льтатом подерных преобразований окруж-ностей радиусов ОА и ОС относительно со-ответственных фокусов F¹, F² и F³, F⁴, и т.д.

Внимательный анализ системы этих 2-х гипербол раскроет ещё ряд интересных конструктивных особенностей их геометри-ческой структуры, не наблюдаемых у ги-пербол с пропорциями их элементов, отлич-ными от золотой. Это даёт основание наз-вать такие сопряженные гиперболы золоты-ми.

Определение 12.12. Две сопряженные гиперболы, директрисы которых, пересе-каясь, образуют прямоугольник с золотым отношением сторон, называются золо-тыми.

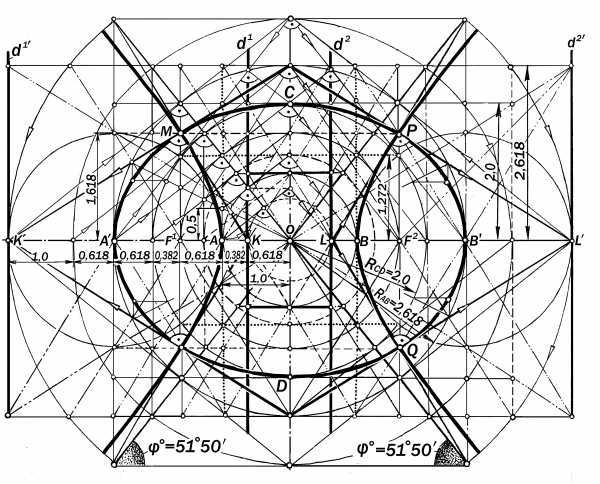
12.4.4. Композиция из золотых

софокусных эллипса и гиперболы

(рис.12.40)

. Если эллипс ( по рис. 12.37) и гипербо-ла ( по рис. 12.38 ) с о ф о к у с н ы, т.е., имеют общие фокусы, то они образуют гар-моничную геометрическую систему с зако-номерной структурой конструктивных свя-зей и отношений между их элементами.

К числу основных изобразительных свойств этой структуры относятся следую-щие:

1. Софокусные эллипс и гипербола «взаимно-перпендикулярны», т.е., ортого-нально сопряжены, так как в точках их пере-сечения M, N, P и Q касательные к одной линии являются нормалями к другой и нао-борот;

2. Ортогональная сопряженность элли-пса и гиперболы определяет ортогональ-ную сопряженность их конструктивных эле-ментов: вершин, фокусов и оснований ди-ректрис. Это значит, что эти точки являются концами тождественно-расположенных на горизонтальной оси K O

L гипотенуз пря-моугольных треугольников, прямые углы ко-торых инцидентны вертикальной оси СОD. В частности:

2.1. Директрисы эллипса и гиперболы соответственны в ортогональном сопряже-нии, так как их основания являются раз-ными полюсами одних и тех же поляр,— об-щих фокальных хорд MN и PQ ;

2.2. Вершинам А и В эллипса ортого-нально сопряжены (соответствуют) фокусы F¹и F² гиперболы и наоборот, вершинам А

и В гиперболы соответствуют фокусы F¹и F²эллипса;

2.3.Точки М, N, P и Q пересечения софокусных гиперболы и эллипса явля-ются вершинами квадрата со сторонами, равными их фокальным хордам;

2.4

. Центральный прямоугольник, длин-ные стороны которого совпадают с дирек-трисами d¹и d²гиперболы, а короткие друг от друга на расстояние между её вершинами А и В, является золо-тым, так как он выдержан в пропор-ции 1,236 : 2 или 0,618 : 1,000;

2.5. Все прямоугольники данной структуры, диагонали которых па-раллельны или соответственно пер-пендикулярны диагоналям центра-льного золотого прямоугольника, яв-ляются золотыми;

2.6. Отношения диагоналей ром-бов, образованных касательными как к гиперболе, так и к эллипсу, являются золотыми, и др.

Эти свойства дают основания назвать всю геометро-графическую композицию из софокусных гипербо-лы и эллипса золотой, так как она приводит в закономерное гармонич-ное расположение различные точки, прямые, прямоугольники, ромбы, ок-ружности, эллипс и гиперболу.

Рис. 12.40. Композиция из софокусных золотых

эллипса и гиперболы

studfiles.net

Равнобочная гипербола — это… Что такое Равнобочная гипербола?

Гипербола и её фокусы

Гипе́рбола — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F₁ и F₂ (называемых фокусами) постоянно, то есть

| | F₁M | − | F₂M | | = C

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.

Термин «гипербола» (греч. ύπερβολή — избыток) был введён Аполлонием Пергским, поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Каноническое уравнение гиперболы

Гипербола, её полуоси и асимптоты

Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением:

Числа и называются соответственно вещественной и мнимой полуосями гиперболы.

Асимптотика

Каждая гипербола имеет пару асимптот:

и .

Связанные определения

Соотношения между элементами гиперболы

Диаметры гиперболы

Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Уравнение гиперболы в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

Равнобочная гипербола

Равнобочная гипербола

Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

xy = a² / 2.

Примером равнобочной гиперболы служит график функции y = 1 / x.

Гиперболы, связанные с треугольником

Оптические свойства гиперболы

Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

См. также

Литература

Wikimedia Foundation. 2010.

dic.academic.ru

Сопряженная гипербола — Большая Энциклопедия Нефти и Газа, статья, страница 2

Сопряженная гипербола

Cтраница 2

Диагонали параллелограмма, вписанного в эллипс, будут сопряженными диаметрами, когда отношение сторон параллелограмма к параллельным им диаметрам одно и то же для обеих сторон; диагонали параллелограмма, вписанного в гиперболу, будут сопряженными диаметрами, если отношение стороны параллелограмма к параллельному ей диаметру, пересекающему гиперболу, равно отношению другой стороны параллелограмма к параллельному ей диаметру, пересекающему сопряженную гиперболу. Точка пересечения прямых, соединяющих середины противоположных сторон параллелограмма, совпадает с точкой пересечения его диагоналей.  [16]

У сопряженных гипербол действительная ось одной является мнимой осью другой, мнимая же ось одной является действительной осью другой. Сопряженные гиперболы имеют одни и те же асимптоты.  [17]

Заметим в заключение, что на одной и той же евклидовой плоскости можно задать бесконечно много различных метрик Минковского. Каждой из них соответствует своя пара сопряженных гипербол в качестве единичной окружности; обратно, любая пара сопряженных гипербол служит единичной окружностью для некоторой ( вполне определенной) метрики Минковского.  [18]

Заметим в заключение, что на одной и той же евклидовой плоскости можно задать бесконечно много различных метрик Минковского. Каждой из них соответствует своя пара сопряженных гипербол в качестве единичной окружности; обратно, любая пара сопряженных гипербол служит единичной окружностью для некоторой ( вполне определенной) метрики Минковского.  [19]

Рассмотрим плоские сечения гиперболического параболоида. На рис. 126 приведен отсек гиперболического параболоида, выделенный секущими плоскостями в предыдущем примере. На горизонтальной проекции эти линии сечений изображаются сопряженными гиперболами с общими асимптотами.  [20]

Кривая расположена в двух вертикальных углах и является геометрическим местом точек, произведение расстояний которых до двух взаимно перпендикулярных прямых постоянно. Эти прямые являются асимптотами кривой. В аффинной формулировке, которая распространяется на все гиперболы, имеем: Совокупность двух сопряженных гипербол является геометрическим местом точек М, для которых параллелограмм с диагональю ОМ и с двумя сторонами, отложенными на асимптотах, имеет постоянную площадь.  [21]

Это и есть уравнение индикатрисы Дюпена. Кривая эта дает геометрически наглядное представление об изменении величины радиуса кривизны при вращении нормального сечения вокруг нормали к поверхности. В эллиптическом случае кривая ( 58) есть эллипс, и в правой части надо брать определенный знак. В гиперболическом случае уравнению ( 58) соответствуют две сопряженные гиперболы.  [22]

Страницы:      1    2

www.ngpedia.ru

Сопряженная гипербола — Большая Энциклопедия Нефти и Газа, статья, страница 1

Сопряженная гипербола

Cтраница 1

Сопряженные гиперболы имеют общие асимптоты ( U U и V V на черт.  [1]

Сопряженные гиперболы имеют общие асимптоты ( U U и VV на черт.  [2]

Радиусы сопряженных гипербол ( 1) и ( 2), имеющие сопряженные направления, называются сопряженными ( ср.  [3]

У сопряженных гипербол действительная ось одной является мнимой осью другой, мнимая же ось одной является действительной осью другой. Сопряженные гиперболы имеют одни и те же асимптоты.  [4]

Доказать, что сопряженные гиперболы имеют одни и те же оси и центр симметрии.  [5]

Очевидно, что сопряженная гипербола имеет те же асимптоты, что и данная.  [6]

Дюпена, которая состоит из двух сопряженных гипербол.  [7]

Здесь рп меняет знак, индикатриса слагается из двух сопряженных гипербол, имеющих в качестве асимптот асимптотические направлений поверхности 5 в точке т; на одной из этих гипербол рп положительно, на другой отрицательно.  [8]

Гиперболы ( 16) и ( 18) называются сопряженными гиперболами.  [9]

Если С0 — пустое множество, если С0 — пара данных прямых, если С0 — две сопряженные гиперболы.  [10]

Две прямолинейные образующие поверхности дают в данном случае направление асимптот индикатрисы Дюпена, которая состоит из двух сопряженных гипербол.  [11]

Во всякой точке минимальной поверхности главные кривизны равны и имеют обратные знаки, индикатриса состоит из двух равнобочных сопряженных гипербол и асимптотические направления взаимно перпендикулярны.  [12]

Для равносторонней гиперболы, один из фокусов которой находится в точке ( — 7) / 2; 0), написать уравнение сопряженной гиперболы.  [13]

Что касается случая испарения, то здесь представляются две возможности в зависимости от знака С ( если выбрать С 0), так как может получиться одна из двух сопряженных гипербол. В случае вырождения свободная поверхность обращается в отрезки двух, прямых.  [14]

Заметим, что приведенные здесь соображения относительно движения особой точки в поле изобар, имеющих форму кривых второго порядка, могут иметь значение и в общем случае, если принять во внимание, что в достаточно малой окрестности особой точки изобары всегда имеют форму эллипса, пары сопряженных гипербол или пары параллельных прямых, как это вытекает из свойств индикатрисы кривизны Дюпена, построенной для поверхности р р ( х, у, t) в данный момент. С такой точки зрения к вопросу о возникновении барических центров подходит Дедебан.  [15]

Страницы:      1    2

www.ngpedia.ru

сопряженные гиперболы — это… Что такое сопряженные гиперболы?



сопряженные гиперболы

мат. conjugate hyperbolas

Большой англо-русский и русско-английский словарь. 2001.

• сопряженные гиперболоиды
• сопряженные глубины

Смотреть что такое «сопряженные гиперболы» в других словарях:

• Гиперболы — Под этим названием известен в аналитической геометрии ряд кривых линий. 1) Г. второго порядка, или так называемая Аполлониева гипербола. Эта кривая линия была известна уже грекам и принадлежит к числу конических сечений, т. е. получается через… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Гипербола (математика) — У этого термина существуют и другие значения, см. Гипербола. Гипербола и её фокусы …   Википедия

• Равнобочная гипербола — Гипербола и её фокусы Гипербола  геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно, то есть | | F1M | − | F2M | | = C… …   Википедия

• Диаметр конического сечения — прямая проходящая через середины двух параллельных хорд. Диаметр гиперболы Диаметры гиперболы Ди …   Википедия

• МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… …   Энциклопедия Кольера

• Джон Мейнард Кейнс — (John Maynard Keynes) Содержание Содержание 1. Биография Кейнса Личная и семейная жизнь Образование Карьера 2. Предмет и метод изучения Кейнса Психологические склонности человека Основной психологический Концепция мультипликатора 3. Дж.М.Кейнс о… …   Энциклопедия инвестора

dic.academic.ru

Сопряженные гиперболы — Энциклопедия по машиностроению XXL

О различных возможных формах инвариантного конуса можно судить по его пересечению со сферой единичного радиуса, описанной около центра вращения О. При рассматривании из точки оси X, находящейся на далеком расстоянии, все эти кривые имеют вид системы подобных эллипсов. При рассматривании из удаленной точки оси Oz они представляются в таком же виде. Если же смотреть на них из удаленной точки средней оси Оу, то они представятся в виде двух семейств сопряженных- гипербол с асимптотами, изображающими те две плоскости, на которые конус распадается при вырождении. Семейство кривых, видимое при рассматривании из удаленной точки оси Оу, представлено на фиг. 42 для случая, когда  [c.116]
Сокращенное умножение 67 Соленоидальное векторное поле 234 Соприкасающаяся окружность 266 Соприкосновение кривых 266 Сопряженные гиперболы 245 Сопряженные диаметры эллипса 243, 244  [c.585]

В этом случае кривая есть гипербола (фиг. 1-26) (которая становится равнобочной, если а = Ь,п переходит в сопряженную гиперболу при замене 1 на—1).  [c.15]

Рассмотрим плоские сечения гиперболического параболоида. На рис. 126 приведен отсек гиперболического параболоида, выделенный секущими плоскостями в предыдущем примере. В сечении горизонтальными плоскостями, расположенными ниже и выше точки О (вершины поверхности), получаются гиперболы 1 и 2 разных семейств, а также две прямые 5. На горизонтальной проекции эти линии сечений изображаются сопряженными гиперболами с общими асимптотами.  [c.93]

Диаметрами гиперболы называют прямые, проходящие через ее центр. Два диаметра гиперболы, каждый из которых делит пополам хорды, параллельные другому диаметру, называют сопряженными. Оси симметрии (действительная и мнимая) гиперболы являются сопряженными и взаимно перпендикулярными диаметрами.  [c.153]

Точка движется под действием отталкивающей силы, пропорциональной расстоянию от неподвижной точки доказать, что ветвь гиперболы есть орбита, и что скорость в любой точке изменяется пропорционально половине сопряженного диаметра.  [c.87]

В работе [191 приведены результаты исследования влияния формы пластины в плане. При скруглении вершины пластины (радиус окружности составлял 0,063 длины) вместо одной области больших напряжений трения и тепловых потоков вблизи средней линии появились две такие узкие области, распространяющиеся от точек сопряжения окружности с прямыми. Однако на пластине с передней острой кромкой в форме гиперболы (радиус кривизны на оси симметрии был равен 0,03 длины пластины) линии растекания и пики теплового потока исчезли. В работе [19] приведены также сведения о вязком слое, т. е. слое малой плотности (внутренняя часть пограничного слоя), толщина которого не превосходит двух толщин двумерного пограничного слоя для пластины и резко уменьшается (до 0,3 толщины двумерного слоя) вблизи средней линии треугольной пластины. На пластине с передней кромкой в форме гиперболы такого резкого изменения толпщны вязкого слоя не наблюдается. Пики теплового потока устраняются также путем отгиба острого конца треугольной пластины, при кото-  [c.283]

Это будет гипербола, проходящая через точку Л. Сопряженная ей гипербола отличается знаком правой части. Переход от системы [х, t) к системе ( , т) соответствует переходу от прямоугольных координат к косоугольным на плоскости Минковского. Это же следует и из преобразования Лоренца, которое можно представить в виде  [c.637]

Очевидно, что параметры v и ц. определяют семейства гипербол и эллипсов, вращающихся вокруг оси симметрии z и фактически являющихся конфокальными гиперболоидами и сопряженными конфокальными эллипсоидами вращения. Выберем зти ортогональные поверхности в качестве координатных. Так как каждое значение v представляет гиперболоид, а каждое значение ц — эллипсоид, наши новые координаты будут просто Л7 и Х.  [c.94]

Как было показано выше, для любого механизма в любом его положении могут быть определены все мгновенные центры вращения в абсолютном и в относительных движениях его звеньев. Следовательно, если имеется механизм, воспроизводящий то или иное движение, то такое же движение звеньев может быть осуществлено механизмом, представляющим собой две сопряженные центроиды. Так, например, передача движения между кривошипами АО и СВ шарнирного антипараллелограмма может быть воспроизведена двумя эллиптическими фрикционными колесами (рис. 211), передача движения между звеньями АВ и СО — двумя гиперболическими фрикционными колесами (рис. 212) с двойными профилями, соответствующими двум ветвям гиперболы. При этом законы движения звеньев остаются такими же, как и для механизма шарнирного антипараллелограмма. Механизмы, в которых передача движения осуществляется центроидами, носят название центроидных механизмов.  [c.116]

Тени конусов, сопряженных с цилиндром (рис. 228). В этом примере хорошо прослеживается органичная взаимосвязь контуров собственных и падающих теней. Точки исчезновения 5 и 7 падающих теней от конуса на цилиндр и от цилиндра на конус построены с помощью обратных лучей. Наклонная лучевая плоскость, проходя щая через теневую образующую 3 4 конуса, пересекает цилиндр по эллипсу. Другая лучевая плоскость, проходящая через образующую 5 6 цилиндра, пересекает конус по гиперболе. Точка 6 является ее вершиной.  [c.170]

Построим еще две хорды, не параллельные хордам АВ и СО и сопряженный им диаметр. Если оба диаметра пересекаются внутри кривой , как в приведенной задаче, то дуга принадлежит эллипсу. Если они пересекаются вне кривой , то задана дуга гиперболы. Когда диаметры взаимно параллельны, то изображена дуга параболы.  [c.23]

В случае, если заданы точки сопряжения А в В, при этом точка А является вершиной гиперболы, построение гиперболы проводится как показано ва рис. 28. Точка О найдена из условия ОА=АС.  [c.194]

Строим касательные к циклоиде в точке В (раздел 1.1.3, рис. 9) и касательную к гиперболе в точке С (раздел 1.1.3, рис. 7). Восстановив к касательным перпендикуляры, находим на них центры дуг радиусов К, и В,. Сопряжение дуг радиусов В, и К, осуществляется дугой радиуса (раздел 1.1.2, рис. Зв).  [c.200]

Точки сопряжения А, В, С, Е. Точка В — вершина гиперболы. Точка А — точка возврата циклоиды.  [c.250]

В, С, В, Е, Р,С, Л — точки сопряжения I — действительная ось гиперболы, А — вершина гиперболы, Ь — точка заострения эвольвенты.  [c.251]

А, В, С, В, Е, Н — точки сопряжения Ь, и -пересекающиеся прямые с точками сопряжения Б и С параболы Ьз и — асимптоты гиперболы.  [c.253]

Пример 4 Некоторая точка пластины, мгновенно вращающейся вокруг оси, лежащей в ее плоскости, внезапно закрепляется. Показать, что если новая мгновенная ось вращения составляет прямой угол с прежней осью, то точка должна располагаться на гиперболе, одна из асимптот которой перпендикулярна к данной оси, а другая является ей сопряженной по отношению к эллипсу инерции, построенному для центра тяжести.  [c.255]

Ин ликатриса Дюпена имеег вид сопряженных гипербол, если касательная плос-косгь в рассма1риваемой точке пересекает поверхность. Такую точку называют гиперболической. Касательная плоскость к линейчатой поверхности проходит через ее производящую прямую линию.  [c.410]

Заметим, что приведенные здесь соображения относительно движения особой точки в поле изобар, имеюгцих форму кривых второго порядка, могут иметь значение и в обгцем случае, если принять во внимание, что в достаточно малой окрестности особой точки изобары всегда имеют форму эллипса, пары сопряженных гипербол или пары параллельных прямых, как это вытекает из свойств индикатрисы кривизны Дюпена, построенной для поверхности р = р х, y,t) в данный момент. С такой точки зрения к вопросу о возникновении барических центров подходит Дедебан.  [c.200]

Для случая формообразования выпукловогнутого локального участка поверхности Д детали выпуклым участком исходной инструментальной поверхности И (рис. 8.6.1) индикатрисы кривизны поверхностей Д и И представляют собой соответственно эллипс Ind (я) и пару сопряженных гипербол Ind (д). Индикатриса конформности в этом слечае имеет две ветви Ind jo f Д /и) (рис. 8.6.2).  [c.452]

Сопряженными натываю гиперболы, имеющие общие асимптоты. Действительная ось каждой И1 них равна мнимой оси дру10Й и наоборот.  [c.410]

Через точки сопряжения очерковых линий проведены граничные, параллели а, Ь (окружности), по которым поверхности касаются друг друга, образуя плавные переходь . После среза заготовки головки двумя фронтальными плоскостями Г и Л передняя и задняя линии среза (их фронтальные проекции совпадают) составляются из дуги /—2—3 окружности (срез на сфере), дуг 1—6 и 3—4 кривой Персея (срез на торе) и дуги 5—6—4 гиперболы (срез на конусе), стыкующихся на соответственных граничных параллелях а и Ь. Промежуточные точки кривых строят с помощью вспомогательных секущих плоскостей, перпендикулярных оси вращения х, как это показано для точек А В, являющихся точками пересечения параллели с с плоскостью Г.  [c.103]

При параллельном проецировании эллипс и окружность проецируются в эллипс (черт. 212) или, в частном случае, в окружность проекция параболы — парабола, а гиперболы — гипербола. Объясняется это тем, что несобственные точки при этом проецируются только в несобственные, например две несобственные точки гипербо лы- проецируются двумя несобственными точками ее проекции, которая вследствие этого должна быть тоже 1ипер6о. 1ой. Пары сопряженных диаметров кривых проецируются парами сопряженных диаметров их проекций.  [c.57]

Они дают парамгтрическое представление траектории. Траектория есть гипербола, отнесенная к двум сопряженным диаметрам. Исключая t, получим уравнение этой ги перболы в виде  [c.163]

При переходе космического аппарата через границу сферы действия приходится переходить от одного центрального поля тяготения к другому. В каждом поле тяготения движение рассматривается, естественно, как кеплерово, т. е. как происходящее по какому-либо из конических сечений — эллипсу, параболе или гиперболе, причем на границе сферы действия траектории по определенным правилам сопрягаются, склеиваются (как это делается, мы увидим в третьей и четвертой частях книги). В этом заключается приближенный метод расчета космических траекторий, который иногда называют методом сопряженных конических сечений.  [c.70]

IV) Если коитур состоит из конфокальных эллипсов и гипербол,то мы можем, воспользоваться сопряженными функциями Е, I), оцределяемыми уравнением  [c.335]

Рассматривая в данном случае вопрос о построении интегральных кривых с постоянной энергии А, проходящих через Ро (см. 252—253), можно сделать вывод, что на дуге РоР гиперболы С нет точек, сопряженных с Р. В то же время для гиперболы С инутренняя или конечная точки дуги РоР сопряжена с Ро. В первом случае хорда I = РоР не проходит, а во втором случае проходит через общий фокус О гипербол С и С.  [c.232]

Линии на поверхности, в каждой точке касающиеся сопряженных диаметров индикатрисы Дюпена, называются сопряженными. Если в качестве сопряженных в каждой точке приняты главные диаметры, то соответствующие сопряженные линии на поверхности называются линиями кривизн или линиями- главных кривизн. Совершенно очевидно, что, так как не всякие ортогональные направления являются сопряженными, не всякая ортогональная сеть является сетью линий главных кривизн.. Линии на поверхности, всюду касающиеся асимптот индикатрисы Дюпена в той области поверхности, где таковой являются гиперболы или параллельные линии, называются асимптотическими (в случае, если индикатрисой Д1рпена являются две параллельные линии, то обе асимптоты сливаются в одну).  [c.32]

Моторно-осевой подшипник тепловозов ТЭЗ имеет бронзовые вкладыши (бронза ОЦС 4-4-17), смазывание осуществляется путем естественной подачи из масляных объемов подшипниковых узлов через маслоподающий пакет. Для повышения надежности работы МОП скольжения на ТЭД ЭД107А и ЭД118А применена польстерная смазочная система. Польстерный пакет собран из трех пластин тонкошерстного каркасного войлока размером 13Х Х157Х190 мм. Вкладыш моторно-осевого подшипника на внутренней поверхности имеет гиперболическую расточку для уменьшения давления в зоне контакта с осью колесной пары при перекосах узла сопряжения от изгиба оси. Начальный диаметральный зазор в моторно-осевом подшипнике по вершине гиперболы составляет 0,5—0,86 мм, а в процессе эксплуатации он возрастает до 1,8 мм (по норме).  [c.27]

---

mash-xxl.info