Градиент функции калькулятор онлайн – Найти градиент функции | Онлайн калькулятор

Содержание

Градиент — 15 Сентября 2015 — Примеры решений задач

Определение. Вектор с координатами называется градиентом функции u=f(x,y,z) и обозначается

С помощью оператора Гамильтона ( или набла-оператора)

можно кратко записать градиент функции:

Градиент функции в данной точке указывает направление наиболее быстрого возрастания функции.

Модуль градиента определяет крутизну наибольшего ската или подъема поверхности u=f(x,y,z).

Пример 1. Найти градиент grad z, модуль градиента |grad z| для функции z=7-5x²-10y² в точке M(-5;7)

Решение. Для функции двух переменных градиент находим по формуле

1) Находим частные производные (см. калькулятор частных производных)

2) Подставляем в формулу, получаем градиент функции в произвольной точке

Найти градиент функции можно также с помощью калькулятора

3) Подставляем координаты точки M(-5;7), получаем

4) Находим модуль градиента в точке M(-5;7) по формуле:

Вывод: Если движение происходит в направлении градиента функции (50;-140), то получаем скорость максимального изменения функции 148,66 в точке M(-5;7).

Если движение будет происходить в других направлениях, то скорость будет меньше. Покажем это на примере.

Пример 2. Найти скорость изменения функции z=7-5x²-10y² в точке M(-5;7) по направлению вектора l(2;-3).

Решение. Пункты 1),2) и 3) совпадают с решением примера 1.

4) Скорость изменения функции z=7-5x²-10y² в точке M(-5;7) по направлению вектора l(2;-3) находим по формуле производной по направлению:

www.reshim.su

градиент калькулятор онлайн

Вы искали градиент калькулятор онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и градиент найти, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «градиент калькулятор онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как градиент калькулятор онлайн,градиент найти,градиент онлайн калькулятор,градиент функции в точке онлайн калькулятор,градиент функции онлайн,калькулятор онлайн градиент,найти градиент,найти градиент функции в точке онлайн,найти градиент функции в точке онлайн калькулятор,онлайн калькулятор градиент. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и градиент калькулятор онлайн. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, градиент онлайн калькулятор).

Где можно решить любую задачу по математике, а так же градиент калькулятор онлайн Онлайн?

Решить задачу градиент калькулятор онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.

www.pocketteacher.ru

Найти градиент функции | Онлайн калькулятор

Основные функции

: x^a

модуль x: abs(x)

: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]

: sin[x] или Sin[x]

: tan[x] или Tan[x]

: cot[x] или Cot[x]

: sec[x] или Sec[x]

: csc[x] или Csc[x]

: ArcCos[x]

: ArcSin[x]

: ArcTan[x]

: ArcCot[x]

: ArcSec[x]

: ArcCsc[x]

: cosh[x] или Cosh[x]

: sinh[x] или Sinh[x]

: tanh[x] или Tanh[x]

: coth[x] или Coth[x]

: sech[x] или Sech[x]

: csch[x] или Csch[е]

: ArcCosh[x]

: ArcSinh[x]

: ArcTanh[x]

: ArcCoth[x]

: ArcSech[x]

: ArcCsch[x]

[19.67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)

mrcalc.ru

Градиент и производная по направлению. Контрольные онлайн

Градиент и производная по направлению

Даны  скалярное поле  точки , . 
   Найти:
   а) градиент поля  в точке ;
   б) производную функции  в точке  по направлению  от точки  к точке .

Решение
   а) Градиент поля в точке вычисляется по формуле .
   Найдем частные производные данной функции и их значения в точке :
,
,
.
   Следовательно, .
   б) Производная скалярного поля по направлению вектора в точке вычисляется по формуле , где , , .
   Для решаемой задачи , , ,
, , , .    Следовательно, .

www.matem96.ru

Производная по направлению, градиент функции: объяснение, примеры

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

1) функции одной переменной;

2) функции трёх переменных в нашем случае.

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x), соответствующее приращению аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения аргументов x, y, z отображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;

2) произвольный вектор l с направляющими косинусами cosα, cosβ, cosγ.

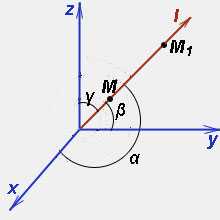
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM1 можно обозначить .

Функция u = f(M) при этом получит приращение

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Пример 1. Найти производную функции в точке M0(1; 2; 3) по направлению вектора .

Решение. Найдём частные производные функции в точке M0:

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Следовательно,

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей

, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке M0(1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M0:

Следовательно, можем найти производную по направлению данной функции по её формуле:

Градиент функции нескольких переменных в точке M0 характеризует направление максимального роста этой функции в точке M0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

Пример 4. Найти градиент функции в точке M0(2; 4;).

Решение. Найдём частные производные функции в точке M0:

Следовательно, можем записать искомый градиент данной функции:

Поделиться с друзьями

Производные

Функции нескольких переменных

function-x.ru

Lection15

Лекция 15. «Дифференцирование функции нескольких переменных»

Градиент функции двух переменных и производная по направлению.

Определение. Градиентом функции

называется вектор

Иначе, этот вектор может быть записан следующим образом:

или

Как видно из определения градиента функции, компонентами вектора градиента являются частные производные функции.

Пример. Вычислить градиент функции

в точке A(2,3).

Решение. Вычислим частные производные функции.

В общем виде градиент функции имеет вид:

Подставим координаты точки A(2,3) в выражения частных производных

В градиент функции в точке A(2,3) имеет вид:

Аналогично можно определить понятие градиента функции трех переменных:

Определение. Градиентом функции от трех переменных

называется вектор

Иначе, этот вектор может быть записан следующим образом:

Определение производной по направлению.

Пусть задана функция двух переменных

и произвольный вектор

Рассмотрим приращение этой функции, взятое вдоль данного вектора

Т.е. вектор коллинеарный по отношению к вектору. Длина приращения аргумента

Производной по некоторому направлению называется предел отношения приращения функции вдоль данного направления на длину приращения аргумента, когда длина приращения аргумента стремиться к 0.

Формула для вычисления производной по направлению.

Исходя из определения градиента, производную функции по направлению, можно посчитать следующим образом.

Пусть

некоторый вектор. Вектор с тем же направлением, но

единичной длины назовем

Координаты этого вектора вычисляются следующим образом:

Из определения производной по направлению , производная по направлениюможет быть вычислена по следующей формуле:

Правая часть этой формулы представляет собой скалярное произведение двух векторов

Поэтому, производную по направлению можно представить в виде следующей формулы:

Из этой формулы следует несколько важных свойств вектора градиента.

Производная в данной точке по направлению вектора S имеет наибольшее значение, если направление вектора S совпадает с направлением градиента; это наибольшее значение производной равно ||.
Производная по направлению вектора, перпендикулярного к вектору равна нулю.

Первое свойство градиента следует из того очевидного факта, что скалярное произведение двух векторов принимает наибольшее значение, когда вектора совпадают по направлению. Второе свойство следует из того, что скалярное произведение перпендикулярных векторов равно нулю. Кроме того, из первого свойства следует геометрический смысл градиента – градиент это вектор, вдоль направления, которого производная по направлению наибольшая. Так как производная по направлению определяет тангенс угла наклона касательной к поверхности функции, то градиент направлен вдоль наибольшего наклона касательной.

Пример 2. Для функции (из примера 1)

Вычислить производную по направлению

в точке A(2,3).

Решение. Для вычисления производной по направлению надо вычислить вектор градиента в указанной точке и единичный вектор направления (т.е. нормализовать вектор).

Вектор градиента был вычислен в примере 1:

Вычисляем единичный вектор направления:

Вычисляем производную по направлению:

#2. Максимум и минимум функции нескольких переменных.

Определение. Функция

Имеет максимум в точке (т. е. прии), если

для всех точек , достаточно близких к точкеи отличных от нее.

Определение. Совершенно аналогично говорят, что функция

Имеет минимум в точке (т. е. прии), если

для всех точек , достаточно близких к точкеи отличных от нее.

Максимум и минимум функции называются экстремумами функции, т. е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.

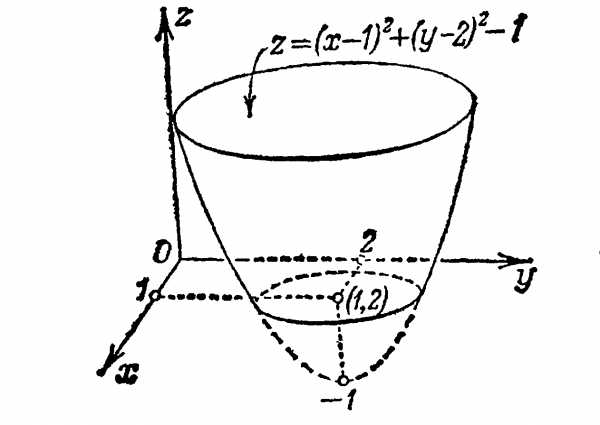
Например, функция

Имеет очевидный минимум z = -1 при x = 1 и y = 2.

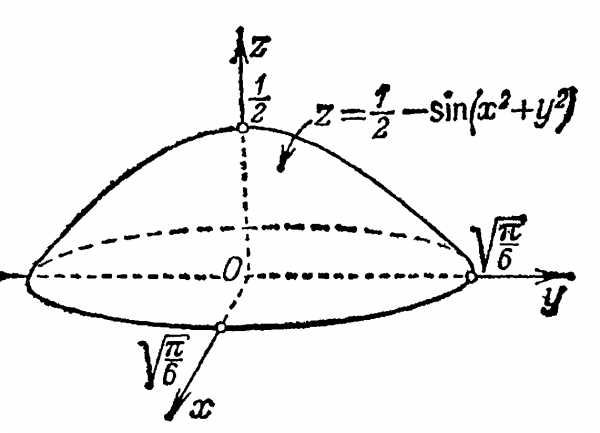
Функция

Имеет максимум в точке приx = 0 и y = 0.

Теорема. (необходимые условия экстремума).

Если функция достигает экстремума при,, то каждая частная производная первого порядка отz или обращается в нуль при этих значениях аргументов, или не существует.

Замечание. Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции. Можно привести примеры функций, которые в некоторых точках имеет нулевые частные производные, но не имеет экстремума в этих точка.

Пример. Функции, которая имеет нулевые частные производные, но не имеет экстремума.

В точке .

В самом деле:

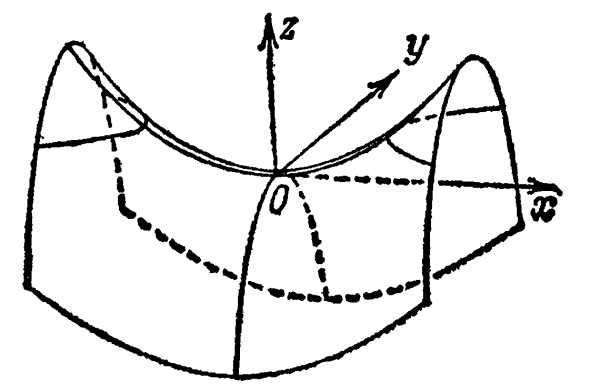
Достаточные условия экстремума.

Теорема. Пусть в некоторой области, содержащей точку , функция имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка является критической точкой функции , т.е.

Тогда при ,

имеет максимум, если

имеет минимум, если

не имеет ни минимума, ни максимума, если

может иметь экстремум, а может и не иметь — требуется дополнительное исследование, если

Пример 3.2. Исследовать на максимум и на минимум функцию

Решение.

Найдем критические точки, т.е. точки, в которых первые частные производные равны нулю или не существуют.

Сначала вычисляем сами частные производные.

Приравниваем частные производные нулю и решаем следующую систему линейных уравнений

= 0

Умножаем второе уравнение на 2 и складываем с первым. Получится уравнение только от y.

Находим и подставляем в первое уравнение

Преобразуем

Находим

Следовательно, точка () является критической.

Вычислим вторые производные второго порядка и подставим в них координаты критической точки.

В нашем случае, подставлять значения критических точек не надо, так как вторые производные являются числами.

В итоге имеем:

Следовательно, найденная критическая точка, является точкой экстремума. Более того, так как

то эта точка минимума.

studfiles.net

Найти градиент, дивергенцию, ротор | UpByte.Net

В области \(V\) задано скалярное поле, если каждой точке \(M\) из \(V\) поставлено в соответствие число \(u\left(M \right)\). Скалярное поле \(u\left(M \right)\) называется дифференцируемым в точке \(M_{0}\) из области \(V\), если приращение поля \(\Delta u\) в этой точке можно представить в виде: \(\Delta u=g\cdot \Delta r+o\left(\rho \right)\), где \(\rho =\rho \left(M_{0},M \right)\) — расстояние между точками \(M_{0}\) и \(M\), \(\Delta u=u\left(M \right)-u\left(M_{0} \right)\). Вектор \(g\left(M_{0} \right)\) называется градиентом дифференцируемого в точке \(M_{0}\) скалярного поля. В декартовой системе координат \[grad u=\frac{\partial u}{\partial x}i+\frac{\partial u}{\partial y}j+\frac{\partial u}{\partial z}k\] Если каждой точке \(M\) из области \(V\) поставлен в соответствие некоторый вектор \(F\left(M \right)\), то говорят, что в \(V\) задано векторное поле. Дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля. Оператор дивергенции, примененный к полю \(F\), обозначается \(divF\) или \(\bigtriangledown \cdot F\). \[div F=\lim_{V\rightarrow 0}\frac{P_{F}}{V}\] где \(P_{F}\)-поток векторного поля \(F\) через сферическую поверхность площадью \(S\), ограничивающую объем \(V\). Ротор — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Обозначается \(rot\) или \(curl\), вычисляется по формуле \(rot F = \bigtriangledown \times F\).

С помощью нашего решебника вы можете вычислить градиент, дивергенцию, ротор векторного поля, выполнить другие операции векторного анализа. Ниже приведены примеры команд. Скопируйте и вставьте в строку решателя или просто наберите ваш пример а затем нажмите кнопку «Решить».

Вычислить градиент функции

grad sin(x^2 y)

del z e^(x^2+y^2)

grad of a scalar field

Вычислить градиент функции в полярных координатах

grad sqrt(r) cos(theta)

Вычислить дивергенцию векторного поля

div (x^2-y^2, 2xy)

div [x^2 sin y, y^2 sin xz, xy sin (cos z)]

divergence calculator

Вычислить ротор векторного поля

curl [-y/(x^2+y^2), -x/(x^2+y^2), z]

rotor operator

Вычислить Лапласиан функции

Laplace e^x sin y

Laplace x^2+y^2+z^2

laplacian calculator

Вычислить выражения

div (grad f)

curl (curl F)

grad (F . G)

upbyte.net