y = 8/x
Дано$$f{\left (x \right )} = \frac{8}{x}$$
График функции
Область определения функции
Точки, в которых функция точно неопределена:
$$x_{1} = 0$$
Точки пересечения с осью координат X
График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$\frac{8}{x} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X
Точки пересечения с осью координат Y
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в 8/x.
$$\frac{8}{0}$$
Результат:
$$f{\left (0 \right )} = tilde{\infty}$$
Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение
$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет
Точки перегибов
Найдем точки перегибов, для этого надо решить уравнение$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет
Вертикальные асимптоты
Есть:
$$x_{1} = 0$$
Горизонтальные асимптоты
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -\infty}\left(\frac{8}{x}\right) = 0$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = 0$$
Наклонные асимптоты
Наклонную асимптоту можно найти, подсчитав предел функции 8/x, делённой на x при x->+oo и x ->-oo$$lim_{x to -\infty}\left(\frac{8}{x^{2}}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева
Чётность и нечётность функции
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$\frac{8}{x} = — \frac{8}{x}$$
— Нет
$$\frac{8}{x} = — \frac{-8}{x}$$
— Да
значит, функция
является
нечётной
uchimatchast.ru
Используя график функции 📝 f(x) найдите : 1)наибольшее
наибольшее значение функции: мы проводим перпендикуляр от самой верхней точки графика на ось у. видим, что единица занимает у нас 2 клетки, то есть каждая клетка вверх прибавляет к значению функции по 0,5. у нас перпендикуляр проведен от верхней точки до седьмой клетки. 0,5*7=3,5.
наименьшее значение функции: проводим перпендикуляр от самой нижней точки графика на ось у. судя по всему функция монотонно (то есть все время и непрерывно) убывает. следовательно фактическое наименьшее значение функции мы найти не можем, но можем указать, какое наименьшее значение она принимает на данном графике: выбираем самую нижнюю точку, ведем перпендикуляр до оси у. это 9 клеток = — 4,5.
промежутки возрастания: это когда функция идет вверх, простыми словами. но перпендикуляры мы уже опускаем на ось х. на нашем графике функция начинается с 6 клетки влево (подняли перпендикуляр от самой нижней точки слева на ось х), видим, что единица по оси х — это 2 клетки, значит, 1 клетка = 1/2 = 0,5.
таким образом, начало функции она берет при х=-0,5*6 = -3
растет она до 2 клетки по оси х. мы знаем, что 2 клетки — это единица. она слева от оси, значит, с минусом. значит, промежуток возрастания = [-3; -1]
промежутки убывания: делаем все то же самое (опускаем перпендикуляр на ось х) только оттуда, где график функции идет вниз.
мы закончили возрастать на точке -1, дальше она начала падать.
следовательно промежуток убывания функции от {-1; 5.5}, 5.5 — последний перпендикуляр данного графика на ось х.
значения х, при котором значения функции меньше либо равны 0:
мы опускаем перпендикуляры на ось х из тех точек, что меньше 0 по оси у. первая точка (самая левая), она ниже оси ох, значит, нам подходит. это как мы знаем 6 клетка на ох, то есть -3. график пересекает ось ох в точке, где х = где-то -2,2. а дальше функция уже становится больше 0.
дальше нам не подходит, следовательно первый промежуток: [-3: -2.2}
а второй промежуток, где график функции опускается ниже оси ох — это {1,75; 5.5] (напомню, перпендикуляры опускаем на ось ох).
yznay.com
График функции
21 января 2014 г. 15:14:10
На взгляд некоторых учёных главное назначение графиков состоит в их значении для эвристической деятельности — иллюстрации к изложению теории и, прежде всего, указание примеров и контрпримеров для доказательства или опровержения связей между различными свойствами функций, т.е. использование вырабатываемой в соответствии с требованиями стандарта «двуязычного» мышления, математического билингвизма.Широкое применение нашла логарифмическая функция в астрономии : Например по ней изменяется величина блеска звезд, если сравнивать характеристики блеска отмеченные глазом и с помощью приборов, то можно составить следующий график: Здесь по вертикальной оси отложим блеск звезд в единицах Гиппарха (распределение звезд по субъективным характеристикам (на глаз) на 6 групп), а на горизонтальной — показания приборов. По графику видно, что объективные и субъективные характеристики не пропорциональны, а прибор регистрирует возрастание блеска не на одну и ту же величину, а в 2,5 раза. Эта зависимость выражается логарифмической функцией.
Рассмотри как же они строятся.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции
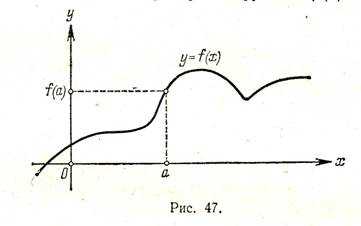
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х < 0 и при х > 2 , отрицательные — при 0 < x < 2; наименьшее значение функция у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у
которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.Таблица выглядит следующим образом:
| x | x 1 | x 2 | x 3 | … | x k |
| y | f(x 1 | f(x 2 ) | f(x 3 ) | … | f(x k ) |
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -1 | 0 | 1 | 2 | 3 |
Соответствующие пять точек показаны на рис. 48.
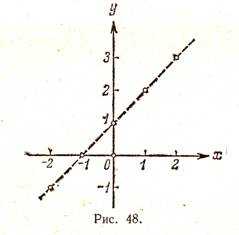
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,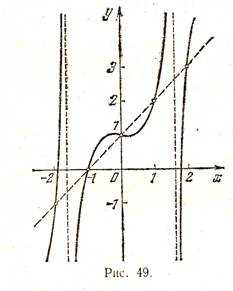 
как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = | f(x) |.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y= | f(x) | можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
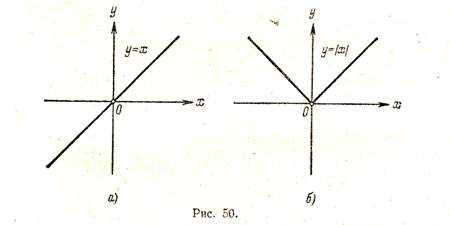
Пример 2. Построить график функции
Решение.
Берем график функции у = х (рис. 50, а) и часть этого графика при х < 0 (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
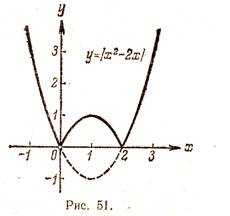Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 —2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0 ), y 2 = g(х 0
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
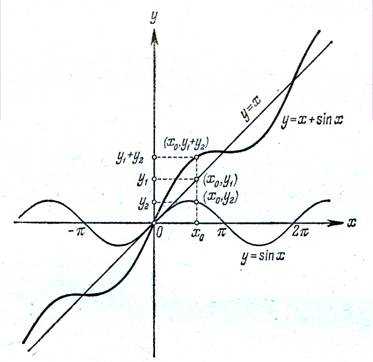
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, — , -0,5 , 0, 0,5 , , 1,5 , 2 . Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
| x | -1,5 | — | -0,5 | 0 | 0,5 | 1,5 | 2 | |
| f(x) = x | -1,5 | — | -0,5 | 0 | 0,5 | 1,5 | 2 | |
| g(x) = sinx | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
| y = x + sinx | 1-1,5 | — | -1-0,5 | 0 | 1+0,5 | 1+1,5 | 2 |
По полученным резултатам построим точки, которые соединим плавной кривой, которая будет эскизом графика функции y = x + sinx .
Графики функций можно строить не только руками по точкам, но и с помощью различных программ(excel, maple), а также программируя на языке Pascal. Изучив язык паскаль, вы одновременно подтяните свои знания по информатике, но и быстро сможете строить разные графики функцицй. примеры функций в Паскале помогут разобраться в синтаксисе языка и построить первые графики самому.
Основные свойства функций.
1) Область определения функции и область значений функции .
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y , которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции .
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции .
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции .
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции .
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x ). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции .
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции .
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими
dz-online.ru
Что такое график функции одной переменной. Функция одной переменной и её характеристики
Если каждому элементу х множ-ва Х (х є Х) ставится в соответствие вполне определённый элемент у множ-ва У (у є У), то говорят, что на множ-ве Х задана функция у = f(x). При этом х назыв. независимой переменной (или аргументом), у – зависимой переменной, а буква f обозначает закон соответсвия. Множ-во Х назыв. областью определения, а множ-во У – областью значений функции.
Способы задания фун-ий.
а)аналитический, если фун-ия задана формулой у = f(x)
б)табличный способ. Состоит в том, что фун-ия задаётся таблицей, содержащей значения аргумента х и соответствующие значения фун-ии f(x).
в)графический. Состоит в изображении графика фун-ии – множества точек (х,у) плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения фун-ии f(x).
г)логический
3 . Односторонний предел. Существование предела в точке.
Число назыв. односторонним пределом слева фун-ии f(x) в точке сгущения x 0, если для ∀ε>0 ∃δ>0, такое, что x∈(x 0 -δ, x 0 ] => f(x)
Число назыв. односторонним пределом справа фун-ии f(x) в точке сгущения х 0 , если если ∀ε>0
∃δ>0, такое, что x∈(x 0 -δ, x 0 ] => f(x)
Число назыв. односторонним пределом справа фун-ии f(x) в точке сгущения х 0 , если если ∀ε>0 ∃δ>0, такое,что х ∈[ x 0, x 0 + δ) =>
Сущ-ие предела в точке. Число А назыв. пределом фун-ии f(x) при х, стремящемся к х 0 (или точке х 0), если для любого, даже сколь угодно малого положительного числа ε>0, найдётся такое положительное число δ>0 (зависящее от ε, δ=δ(ε)), что для всех х, не равных х 0 и удовлетворяющее условию , выполняется неравенство
Обозначается или
2. Предел функции и его свойства.
Предельной точной сгущения множества A называется точка x 0 , если в любой окрестности этой точки найдутся такие множества, отличные от x 0 .
Определение предела по Коши. Функция y=f(x), определенная в A, имеет предел С в точке сгущения x 0 , если ∀ε>0 ∃δ>0, такое, что x∈(x 0 -δ, x 0) ∪(x 0 , x 0 +δ) ⇒ f(x)∈(C-ε, С+ε). Существование предела записывают в виде lim x → x 0 f(x)=C или |x-x 0 |
Определение предела по Гейне. Если для различных последовательностей {x n }, стремящихся к x 0 , последовательность значений функции {f(x n)} сходится к некоторому числу C, то это число называется пределом функции f(x).
Определение Коши используется для обоснования существования предела, а опред-ие Гейна – для обоснования отсутствия предела.
Свойства предела: предел единственен и фун-ия в некоторой окрестности предельной точки ограничена.
1)Предел постоянной величины
Предел постоянной величины равен самой постоянной величине.
Скачать с Depositfiles
ВВЕДЕНИЕ В АНАЛИЗ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Лекция № 13. Тема 1 : Функции
1.1. Определение функции
При изучении определённых процессов реального мира мы встречаемся с характеризующими их величинами, которые меняются во время изучения этих процессов. При этом изменение одной величины сопутствует изменению другой. Например, при прямолинейном равно-мерном движении связь между пройденным путём s , скоростью v и вре-менем t выражается формулой . При заданной скорости v величина пути s зависит от времени t .
В этом случае изменение одной величины (t ) произвольно, а другая (s ) зависит от первой. Тогда говорят, что задана функциональная зависимость. Дадим математическое обоснование этому понятию.
Пусть заданы два множества X и Y .
Определение.
Функцией называется закон или правило, согласно которому каждому элементу
ставится в соответствие единственный элемент
, при этом пишут
или
.
Элемент называется
аргументом функции f , а элемент
значением функции.
Множество X , при котором функция опреде-лена, называется
областью определения функции
, а множество Y
областью изменения функции
. Эти множества соответственно обозначаются
и
.
Примеры функций:
1. Скорость свободного падения тела
. Здесь X и Y
множества действительных неотрицательных чисел.
2. Площадь круга
. Здесь X и Y
множества положитель-ных действительных чисел.
3. Пусть X
множество студентов группы, т.е.
, а
множество оценок на экзамене. Здесь в качестве функции f рассматривается критерий оценки знаний.
В дальнейшем под множествами X и Y будем подразумевать множества чисел и придерживаться обозначения . Для большей наглядности будем использовать геометрическое представление множеств и в
radiobud.ru
как построить? Вычисление значений функции
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f (x ) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у . При этом одно и то же значение у может быть получено при различных х .
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х ), при которых функция определена, т.е. ее значение существует. Обозначается область определения D (y ). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е (у ).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f (x ) называют четной х
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f (x ) называют нечетной , если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х .
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. С
prontapizza.ru
Что называется функцией одной переменной. Определение функции одной переменной
Повторим понятия функции и её свойства, которые нам потребуются для дальнейшего изложения материала.
Определение. Функция F (X ) представляет собой правило, которое позволяет каждому значению хХ поставить в соответствие единственное значение Y = F (X )У, где х — независимая переменная (аргумент), Y — зависимая переменная (значение функции). Говорят, что функция F имеет Область определения D (F )= X и Область значений R (F ) Y .
Определение. Множество пар {(X , F (X )): XD (F )} называется Графиком функции F .
Существует три основных способа задания функции:
при Аналитическом способе задания функции зависимость между переменными определяется формулой;
при Табличном способе задания функции выписываются в определенном порядке значения аргумента и соответствующие значения функции;
при Графическом способе задания функции зависимость между переменными отражается с помощью графика.
Рассмотрим некоторые функциональные зависимости, используемые в экономике:
Функция спроса — зависимость спроса D на некоторый товар от его цены P ;
Функция предложения — зависимость предложения S некоторого товара от его цены P ;
Функция полезности — субъективная числовая оценка данным индивидом полезности И и количества Х товара для него;
Функция издержек — зависимость издержек I на производство Х единиц продукции;
Налоговая ставка — зависимость налоговой ставки N в процентах от величины годового дохода Q .
Все эти функции, кроме последней, весьма трудно выразить аналитически. При необходимости их находят путем кропотливого анализа. Последняя же функция, напротив, обычно довольно хорошо известна всему обществу и законодательно утверждена.
Определение. Функция F ( X ) имеет предел B , когда х стремится к а, если значения F (X ) сколь угодно близко приближаются к числу B , когда значения переменной х сколь угодно близко приближаются к числу а.
Обозначение. .
Следует отметить, что в этом определении рассматриваются значения Х , сколь угодно близкие к числу А , но не совпадающие с А .
Определение. Если функция F (X ) определена в точке а и выполняется равенство , то F (X ) называется непрерывной функцией в точке а.
Определение. Функция, непрерывная в каждой точке своей области определения, называется Непрерывной функцией . В противном случае функцию называют Разрывной .
График непрерывной функции можно начертить без отрыва руки.
Непрерывные функции обладают следующими свойствами:
сумма или произведение непрерывных функций является непрерывной функцией;
отношение двух непрерывных функций является функцией непрерывной во всех точках, в которых знаменатель отношения не обращается в нуль.
Замечание. Метод, эффективный при анализе непрерывных функций, может оказаться неэффективным при исследовании разрывных функций, хотя обратное не исключается .
Определение. Функция F (X ) называется Возрастающей (убывающей) на множестве X , если из того, что X 1 X 2 вытекает, что F (X 1 )F (X 2 ) (F (X 1 )> F (X 2 )). Функция F (X ) называется Неубывающей (невозрастающей) на множестве X , если из того, что X 1 X 2 , X 1 , X 2 X вытекает, что F (X 1 ) F (X 2 ) (F (X 1 ) F (X 2 )).
Теорема. Пусть функция F (X ) дифференцируема на интервале (A , B ). Тогда:
Если первая производная функции Всюду на этом интервале, то функция возрастает на нем;
Если первая производная всюду на этом интервале, то функция убывает;
Первая производная Всюду на этом интервале, то функция постоянна на этом интервале.
Определение. Возрастающие, убывающие, неубывающие, невозрастающие функции называются Монотонными.
Замечание. Монотонная функция не обязательно должна быть непрерывной.
Пример 1. Найти интервалы монотонности функции F (X )=(1- X 2 )3 .
. Находим производную: Решим уравнение . Получим Х1=0, х2=1, х3=-1 . Функция F (X ) определена и непрерывна на всей числовой оси. Поэтому точки Х1, х2, х3 являются критическими точками. Других критических точек нет, так как существует всюду.
Исследуем критические точки, определяя знак слева и справа от каждой этой точки. Для сокращения вычислений и для наглядности это исследование удобно записать в виде табл. 1:
Таблица 1
F (X ) | Возр. | Возр. | Убыв. | Убыв. |
В первой строке помещены все критические точки в порядке расположения их на числовой оси; между ними вставлены промежуточные точки, расположенные слева и справа от критических точек. Во второй строке помещен
radiobud.ru