График функции y = sqrt(x-3)
Решение
$$f{\left (x \right )} = \sqrt{x — 3}$$
График функции[LaTeX]
Точки пересечения с осью координат X[LaTeX]
График функции пересекает ось X при f = 0значит надо решить уравнение:
$$\sqrt{x — 3} = 0$$
Решаем это уравнение
Точки пересечения с осью X:
Аналитическое решение
$$x_{1} = 3$$
Численное решение
$$x_{1} = 3$$
[LaTeX]
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в sqrt(x — 3).
$$\sqrt{-3}$$
Результат:
$$f{\left (0 \right )} = \sqrt{3} i$$
Точка:
(0, i*sqrt(3))Экстремумы функции
[LaTeX]
Для того, чтобы найти экстремумы, нужно решить уравнение(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$\frac{1}{2 \sqrt{x — 3}} = 0$$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет Точки перегибов
[LaTeX]
Найдем точки перегибов, для этого надо решить уравнение$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Вторая производная
$$- \frac{1}{4 \left(x — 3\right)^{\frac{3}{2}}} = 0$$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет Горизонтальные асимптоты
[LaTeX]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo$$\lim_{x \to -\infty} \sqrt{x — 3} = \infty i$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты слева:
$$y = \infty i$$
$$\lim_{x \to \infty} \sqrt{x — 3} = \infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существует Наклонные асимптоты
[LaTeX]
Наклонную асимптоту можно найти, подсчитав предел функции sqrt(x — 3), делённой на x при x->+oo и x ->-oo$$\lim_{x \to -\infty}\left(\frac{1}{x} \sqrt{x — 3}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой справа
$$\lim_{x \to \infty}\left(\frac{1}{x} \sqrt{x — 3}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева Чётность и нечётность функции
[LaTeX]
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$\sqrt{x — 3} = \sqrt{- x — 3}$$
— Нет
$$\sqrt{x — 3} = — \sqrt{- x — 3}$$
— Нет
значит, функция
не является
ни чётной ни нечётной
www.kontrolnaya-rabota.ru
Функция y = √x. Её свойства и график. Решение задач. Видеоурок. Алгебра 8 Класс
Данный урок мы посвятим решению типовых задач на построение графика функции . Вспомним определение квадратного корня.
Определение. Квадратным корнем из неотрицательного числа называется такое неотрицательное число , квадрат которого равен .
.
Изобразим график – это правая ветвь параболы (рис. 1).
Рис. 1.
На графике наглядно виден смысл вычисления квадратного корня. Например, если рассмотреть ординату 16, то ей будет соответствовать абсцисса 4, т. к. . Аналогично, ординате 9 на графике соответствует точка с абсциссой 3, поскольку , ординате 11 соответствует абсцисса , т. к. (квадратный корень из 11 не извлекается в целых числах).
Теперь вспомним график функции (рис. 2).
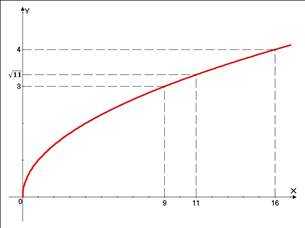
Рис. 2.
На графике для наглядности изображены несколько точек, ординаты которых вычисляются с помощью извлечения квадратного корня: , , .
Пример 1. Постройте и прочтите график функции: а) , б) .
Решение. а) Построение начинается с простейшего вида функции, т. е. в данном случае с графика (пунктиром). Затем для построения искомого графика график функции необходимо сдвинуть влево на 1 (рис. 3). При этом все точки графика сдвинутся на 1 влево, например, точка с координатами (1;1) перейдет в точку с координатами (0;1). В результате получаем искомый график (красная кривая). Проверить такой способ легко при подстановке нескольких значений аргумента.
Рис. 3.
Прочтем график: если аргумент меняется от до , функция возрастает от 0 до . Область определения (ОДЗ) при этом требует, чтобы подкоренное выражение было неотрицательным, т. е. .
б) Для построения графика функции поступим аналогичным образом. Сначала строим график (пунктиром). Затем для построения искомого графика график функции необходимо сдвинуть вправо на 1 (рис. 4). При этом все точки графика сдвинутся на 1 вправо, например, точка с координатами (1;1) прейдет в точку с координатами (2;1). В результате получаем искомый график (красная кривая).
Рис. 4.
Прочтем график: если аргумент меняется от до , функция возрастает от 0 до . Область определения (ОДЗ) аналогична предыдущему случаю: .
Замечание. На указанных примерах несложно сформулировать правило построения функций вида:
.
Пример 2. Постройте и прочтите график функции: а) , б) .
Решение. а) Этот пример также демонстрирует преобразование графиков функций, но только уже другого типа. Начинаем построение с простейшей функции (пунктиром). Затем график построенной функции смещаем на 2 вверх и получаем на рисунке 5 искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;3).
Рис. 5.
Прочтем график: если аргумент меняется от 0 до , функция возрастает от 2 до . Область определения (ОДЗ): .
б) Также начинаем построение с простейшей функции (пунктиром). Затем график построенной функции (рис. 6) смещаем на 1 вниз и получаем искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;0).
Рис. 6.
Прочтем график: если аргумент меняется от 0 до , функция возрастает от до . Область определения (ОДЗ): .
Замечание. С помощью указанных примеров сформулируем правило построения функций вида:
.
Пример 3. Постройте и прочтите график функции .
Решение. Метод построения указанной функции представляет собой комбинацию двух методов, которые мы видели в предыдущих примерах. Сначала строим основную функцию (пунктиром), затем смещаем ее на 1 вправо и на 2 вверх (рис. 7). При этом, например, точка с координатами (1;1) сначала перейдет в точку (2;1), а затем в точку (2;3). Искомая кривая изображена красным цветом.
Рис. 7.
Прочтем график: если аргумент меняется от до , функция возрастает от 2 до . Область определения (ОДЗ) – подкоренное выражение неотрицательно: .
Замечание. Как видно на указанном примере, преобразования графиков функций, которые мы рассмотрели, можно применять последовательно в комплексе.
Пример 4. Постройте и прочтите график функции .
Решение. Для построения данной составной функции изображаем ее части в приведенных диапазонах построения (рис. 8). Для этого сначала изображаем пунктиром всю функцию , затем всю функцию , а затем наводим (красная кривая) только те их области, которые заданы условием задачи. Сливаются два участка кривой в точке с координатами (1;1).
Рис. 8.
Прочтем график: если аргумент меняется от до 1, функция возрастает от 0 до , если аргумент меняется от 1 до , функция убывает от 1 до 0. Область определения (ОДЗ) – подкоренное выражение неотрицательно: .
Пример 5. Графически решить систему уравнений .
Решение. Для решения системы графическим способом необходимо построить графики функций (рис. 9), представляющих собой уравнения системы, и определить координаты их точек пересечения.
Рис. 9.
На графике изображен полезный факт, демонстрирующий, что графики квадратичной функции и квадратного корня симметричны относительно графика функции . По графику видно, что имеем две точки пересечения, т. е. система имеет два решения. Для определения точных значений этих решений подставим стандартные значения аргумента в обе исследуемые функции: 0 и 1. При этом получим: и , т. е. координаты точек пересечения графиков и решения системы: и .
Ответ. (0;0), (1;1).
Пример 6. (С параметром). При каких значениях параметра имеет решение уравнение ?
Решение. Для исследования значений параметра воспользуемся графическим методом и построим график функции . Мы его уже строили на сегодняшнем уроке, поэтому воспользуемся готовым рисунком 10.
Рис. 10.
Прочтем график: если аргумент меняется от до , функция возрастает от 2 до . Из этого следует, что функция принимает значения только , причем при аргументе она принимает свое минимальное значение . Из полученного диапазона изменения можно сделать однозначный вывод, что параметр , который в уравнении приравнивается к рассмотренной функции, может принимать такие же значения . Например, при имеем, что , т. е. у уравнения есть корень и т. д.
Ответ..
На следующем уроке мы рассмотрим свойства квадратных корней.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Математика = это легко! 😉 (Источник).
2. Фестиваль педагогических идей «Открытый урок» (Источник).
3. Квадратный корень из х (Источник).
Домашнее задание
1. №313, 316, 317. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Решите графически уравнение .
3. Постройте график функции .
4. Решите графически уравнение:
interneturok.ru
Функция корень x | Алгебра
Функция квадратный корень из x —
— один из частных случаев степенной функции. Эта функция не имеет своего собственного имени (в отличие от квадратичной функции или кубической функции) и называется просто формулой. График функции y равен корню из x — ветвь параболы.
Для построения графика возьмём несколько точек. Так как под знаком квадратного корня могут стоять только неотрицательные числа, значения аргумента должны бить неотрицательными. Для удобства вычислений берём x, квадратные корни из которых — целые числа:
и т.д. Таким образом, получили точки (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).
Результаты удобнее оформить в виде таблицы:
Эти точки отмечаем на координатной плоскости
и через них проводим график — ветвь параболы:
y=√x
Свойства функции y=√x
1) Область определения — множество неотрицательных чисел:
D: x∈[0;∞).
2) Область значений — множество неотрицательных чисел:
E: y∈[0;∞).
3) Функция имеет один нуль:
y=0 при x=0.
4) Функция возрастает на всей своей области определения:
И наоборот:
www.algebraclass.ru
