Икс в квадрате плюс икс игрек – X квадрате плюс 2 икс игрек плюс игрек в квадрате представить в виде квадрата двучлена квадрат суммы квадрат разности двух выражений

Урок 10. построение графика квадратичной функции — Алгебра — 9 класс

На прошлых уроках мы подробно рассмотрели частные случаи квадратичной функции: игрек равен а икс в квадрате, игрек равен а икс в квадрате плюс эн и игрек равен а умножить на квадрат икс минус эм. При этом последние два получаются параллельным переносом из первого случая. Игрек равен а икс в квадрате плюс эн сдвигом вдоль оси игрек на эн единиц вверх, если эн больше нуля, или на эн единиц вниз, если эн меньше нуля. Функция игрек равен а умножить на квадрат икс минус эм получается с помощью сдвига вдоль оси икс на эм единиц вправо, если эм больше нуля, или на эм единиц влево, если эм меньше нуля.
Так же мы получили график функции игрек равен а умножить на квадрат икс минус эм плюс эн с помощью двух параллельных переносов, который можно производить в любом порядке.
Известно, что графиком любой квадратичной функции является парабола. При изображении графика важно знать координаты вершины параболы.
Мы говорили, что парабола игрек равен а умножить на квадрат икс минус эм плюс эн имеет вершину с координатами эм, эн. Как же определить координаты вершины параболы, которая является графиком квадратичной функции, записанной формулой общего вида?

Так как мы умеем находить вершину параболы игрек равен а умножить на квадрат икс минус эм плюс эн, то попробуем привести квадратичную функцию к данному виду. Запишем правую часть и выделим из неё квадрат двучлена. Вынесем а за скобки. Второе слагаемое в скобках представим в виде удвоенного произведения. Тогда второе выражение равно бэ делённое на два а. Добавим и отнимем квадрат второго выражения. Выделим квадрат суммы. После упрощения получаем выражение.
Мы получили формулу вида а умножить на квадрат икс минус эм плюс эн. Значит можем записать следующие равенства: эм равно минус бэ делённое на два а. Эн равно минус дробь в числителе которой бэ в квадрате минус четыре а цэ, в знаменателе четыре а.
Значит, график квадратичной функции есть парабола, которую можно получить из графика функции игрек равен а икс в квадрате с помощью двух параллельных переносов – сдвига вдоль оси икс и сдвига вдоль оси игрек. Вершина параболы имеет координаты эм, эн. При этом эм равно минус бэ делённое на два а. Эн равно минус дробь в числителе которой бэ в квадрате минус четыре а цэ, в знаменателе четыре а.
Осью симметрии параболы служит прямая икс равен эм, параллельная оси игрек.
Найдём координаты вершины параболы игрек равен минус два икс в квадрате плюс пять икс минус три. Для удобства выпишем коэффициенты квадратного трёхчлена. Вычислим значение эм, подставляя соответствующие значения в формулу минус бэ делённое на два а. Получим эм равно одной целой одной четвёртой. Вычислим эн по формуле. Подставим значения коэффициентов и получим эн равно одной восьмой.
Таким образом, получили координаты вершины параболы: одна целая одна четвёртая, одна восьмая.
Так как прямая икс равен эм является осью симметрии параболы, то ординату вершины параболы можно вычислить без формулы для эн. Подставим значение эм в функцию. Получим, значение игрек равно одной восьмой. Оно совпадает со значением эн.
Значит для того, чтобы найти координаты вершины параболы надо вычислить эм по формуле минус бэ делённое на два а и подставить полученное значение в функцию. Получим значение ординаты вершины.
Запишем алгоритм построения графика квадратичной функции. Первый шаг – определить направление ветвей параболы. Ветви направлены вверх, если коэффициент а положительный. Ветви параболы направлены вниз, если коэффициент а отрицательный. Второй шаг — найти координаты вершины параболы и отметить её на координатной плоскости. Третьим шагом определить ось симметрии икс равен эм. Четвёртый шаг — построить ещё несколько точек, принадлежащих параболе. То есть составить таблицу значений функции с учётом оси симметрии. Последний пятый шаг – соединить полученные точки плавной линией.
Построим график квадратичной функции игрек равен икс в квадрате плюс шесть икс плюс один, придерживаясь полученного алгоритма. Сначала определим направление ветвей параболы. А равно единице, это больше нуля. Значит, ветви параболы направлены вверх. Найдём координаты вершины эм, эн. Вычислим эм по формуле минус бэ делённое на два а. Подставим коэффициенты квадратичной функции. Эм равно мину трём. Вычислим эн, подставив вместо икс в формулу полученное значение эм. Эн равно минус восьми. Отметим на координатной плоскости вершину с координатами минус три, минус восемь. Определим ось симметрии. Это прямая икс равен минус трём. Теперь составим таблицу значений, чтобы получить ещё несколько точек параболы. Возьмём значения икс минус шесть, минус пять, минус четыре, минус два, минус один, нуль. Выбранные значения симметричны относительно оси симметрии. Подставим их в формулу. Получим значения игрек один, минус четыре, минус семь, минус семь, минус четыре и один. Отметим полученные точки на координатной плоскости. Соединим их плавной линией. Получили параболу, которая является графиком функции игрек равен икс в квадрате плюс шесть икс плюс один.

resh.edu.ru

Алгебра Построение графика квадратичной функции

Описание видеоурока

Квадратичная функция имеет вид игрек равно а икс квадрат плюс бэ икс плюс цэ. Запишем эту формулу в виде игрек равно а умноженное на квадрат разности икс и эм плюс эн.

Выделим из трехчлена а икс в квадрате плюс бэ икс плюс це… квадрат двучлена. В итоге получим разность, уменьшаемым которого является произведение а на квадрат суммы икс и бэ деленного на два а, а вычитаемым – дробь, числителем которой является разность между бэ квадрат и четыре а цэ, а знаменателем – четыре а.

Пусть минус бэ деленное на два а будет равно эм; а эн примет значение отрицательного отношения разности бэ квадрат и четыре а це.. к четырем а. Тогда игрек будет равен а умноженному на квадрат разности икс и эм.. плюс эн.

Значит графиком функции игрек равно а икс квадрат плюс бэ икс плюс цэ является парабола, которую можно получить из графика функции игрек равно а икс квадрат с помощью двух параллельных переносов – сдвига вдоль оси икс и сдвига вдоль оси игрек.  Вершиной этого графика является точка с координатами эм, эн, где эм равно минус бэ деленному на два а, эн равно отношению минус бэ квадрат плюс четыре а це к четырем а.

Осью симметрии параболы является прямая икс равная эм, параллельная оси игрек. Если а больше нуля, ветви параболы направлены вверх, если а меньше нуля – вниз.

Для построения графика квадратичной функции необходимо:

• Найти координаты вершины параболы и отметить ее в координатной плоскости;
• Построить несколько точек, принадлежащих параболе;
• Соединить отмеченные точки плавной линией.

Абсциссу эм можно находить по формуле эм равно минус бэ деленное на два а. Ординату эн – подставив найденное значение абсциссы в формулу игрек равно а икс квадрат плюс бэ икс плюс цэ, так как при икс равном эм оно обращается в эн.

Рассмотрим примеры на построение графиков квадратичных функций.

Построим график функции игрек равно ноль целых две десятые икс квадрат плюс четыре икс плюс один.

Его графиком является парабола, ветви которой направлены вверх, так как коэффициент а больше нуля. Найдем координаты вершины параболы…  Координата эм будет равна минус десяти, координата эн – минус девятнадцати. Таким образом, вершиной параболы является точка с координатами минус десять, минус девятнадцать.

Составим таблицу значений функции…, отметим точки на координатной плоскости… и соединим их плавной линией. Получим график функции игрек равно две десятые икс квадрат плюс четыре икс плюс один.

При составлении таблицы и построении графика не забываем, что прямая икс, равная минус десяти, является осью симметрии параболы.

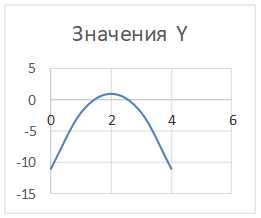
Построим график функции игрек равно минус три икс квадрат плюс двенадцать икс минус одиннадцать.

Графиком функции является парабола, ветви которой направлены вниз, так как коэффициент а меньше нуля. Найдем координаты вершины параболы. Это будет точка два, один.

Вычислим координаты еще нескольких точек с помощью таблицы…., отметим их на координатной плоскости….. и соединим плавной линией.

Получим график функции игрек равно минус три икс квадрат плюс двенадцать икс минус одиннадцать.

Построим график функции игрек равно одна третья икс квадрат плюс два икс плюс три.

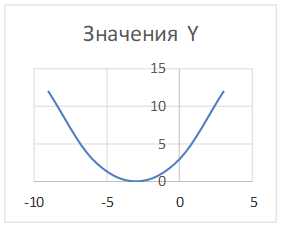
Графиком функции является парабола, ветви которой направлены вверх. Координаты вершины параболы будут равны минус три и нуль… Найдем еще несколько точек с помощью таблицы…., отметим их на координатной плоскости…. и соединим плавной линией. Получим график функции игрек равно одна третья икс квадрат плюс два икс плюс три.

infourok.ru

Урок 9. график функции y = a(x – m)2 — Алгебра — 9 класс

На прошлых уроках мы рассмотрели два частных случая квадратичной функции: игрек равен а икс в квадрате и игрек равен а икс в квадрате плюс эн. Сегодня мы изучим третий частный случай игрек равен а умножить на квадрат икс минус эм.
Для того чтобы установить взаимосвязь между графиками функций игрек равен а икс в квадрате и игрек равен а умножить на квадрат икс минус эм, изобразим в одной координатной плоскости графики следующих функций: игрек равен три икс в квадрате, игрек равен три умножить на квадрат икс плюс два и игрек равен три умножить на квадрат икс минус два. Составим таблицы значений для каждой функции. Возьмём значения аргумента минус два, минус один, нуль, один и два. Чтобы найти значения переменной игрек, подставим каждое значение икс в формулу. Значения функции игрек равен три икс в квадрате соответственно равны двенадцати, трём, нулю, трём и двенадцати. Получаем точки с координатами минус два двенадцать, минус один три, нуль нуль, один три, два двенадцать. Построим параболу три икс в квадрате.

Построим график функции три умножить на квадрат икс плюс два. В этом случае эм равно минус двум. Значения функции найдём для икс равного минус четыре, минус три, минус два, минус один и нуль. При икс равном минус четырём значение функции равно двенадцати. При икс равном минус трём равно трём. При икс равном минус двум равно нулю. При икс равном минус одному равно трём и при икс равном нулю равно двенадцати. Получили точки с координатами минус четыре двенадцать, минус три три, минус два нуль, минус один три и нуль двенадцать. Соединим эти точки и получим график функции три умножить на квадрат икс плюс два.
Изобразим последний график игрек равен три умножить на квадрат икс минус два. Значения этой функции найдём при икс равном нулю, одному, двум, трём и четырём. Соответственно получим значения двенадцать, три, нуль, три и двенадцать. Отметим точки с координатами нуль двенадцать, один три, два нуль, три три, четыре двенадцать. Проведём параболу три умножить на квадрат икс минус два.
Посмотрим внимательно на полученные графики функций.
Заметим, что график функции игрек равен три умножить на квадрат икс плюс два можно получить с помощью параллельного переноса вдоль оси икс графика три икс в квадрате на два единичных отрезка влево и эм равно минус двум. А график функции игрек равен три умножить на квадрат икс минус два с помощью параллельного переноса вдоль оси икс параболы три икс в квадрате на два единичных отрезка вправо, эм равно двум.
Сделаем вывод. График функции игрек равен а умножить на квадрат икс плюс эм является параболой, которую можно получить из графика функции игрек равен а икс в квадрате с помощью параллельного переноса вдоль оси икс на эм единиц вправо, если эм больше нуля, или на минус эм единиц влево, если эм меньше нуля.
Так как выполняется параллельный перенос вправо на эм единиц или влево на минус эм единиц, то вершина параболы а умножить на квадрат икс минус эм будет иметь координаты эм, нуль.
Рассмотрим пример. Используя шаблон параболы игрек равен икс в квадрате, постройте график функции игрек равен икс плюс три всё в квадрате.
Сначала построим шаблон. Составим таблицу значений проведём параболу икс в квадрате. Это мы делали не один раз.
Построим график функции игрек равен икс плюс три всё в квадрате. Так как эм равно минус трём и меньше нуля, то перенесём ключевые точки графика икс в квадрате на три единицы влево. Проведём через полученные точки параболу. Получили график функции игрек равен икс плюс три всё в квадрате с вершиной в точке минус три нуль.
Объединим два частных случая и рассмотрим график функции игрек равен а умножить на квадрат икс минус эм плюс эн. График этой функции является параболой, которую можно получить из графика функции а икс в квадрате с помощью двух параллельных переносов: сдвига вдоль оси икс на эм единиц вправо, если эм больше нуля, или на минус эм единиц влево, если эм меньше нуля, и сдвига вдоль оси игрек на эн единиц вверх, если эн больше нуля, или на минус эн единиц вниз, если эн меньше нуля.
Заметим, что производить параллельные переносы можно в любом порядке: сначала выполнить параллельный перенос вдоль оси икс, а затем вдоль оси игрек или наоборот.
Приведём пример. Используя шаблон параболы игрек равен икс в квадрате, постройте график функции игрек равен разности квадрата икс минус три и двух.
Изобразим параболу игрек равен икс в квадрате. Заметим, что у заданной функции эм равно трём и больше нуля. Значит сдвинем точки шаблона на три единицы вправо. Эн равно минус двум и меньше нуля, значит сдвинем полученный график на две единицы вниз. Получили график функции игрек равен разности квадрата икс минус три и двух. Координаты вершины параболы три, минус два.
Для построения графика функции игрек равен разности квадрата икс минус три и двух мы использовали два вспомогательных графика.
Можно ли обойтись без них?
Заметим, что графиком функции игрек равен разности квадрата икс минус три и двух является та же парабола, что служила графиком функции игрек равен икс в квадрате, только вершина переместилась из начала координат в точку три минус два. Поэтому можно сделать так: перейти к вспомогательной системе координат с началом в точке три минус два. Для этого построим пунктиром прямые икс равен трём и игрек равен минус двум. В этой вспомогательной системе координат построим шаблон парабола игрек равен икс в квадрате, то есть «привяжем» график функции игрек равен икс в квадрате к новой системе координат и в итоге получим требуемый график.
Подведём итог. Сегодня на уроке мы рассмотрели ещё один частный случай квадратичной функции и его график. Это парабола, которую можно получить из из графика функции игрек равен а икс в квадратес помощью параллельного переноса вдоль оси икс на эм единиц вправо, если эм больше нуля, или на минус эм единиц влево, если эм меньше нуля. Вершина будет иметь координаты эм нуль.
Объединив два частных случая, выяснили, что график функции игрек равен а умножить на квадрат икс минус эм плюс эн. является параболой, которую можно получить из графика функции а икс в квадрате с помощью двух параллельных переносов: сдвига вдоль оси икс на эм единиц вправо, если эм больше нуля, или на минус эм единиц влево, если эм меньше нуля, и сдвига вдоль оси игрек на эн единиц вверх, если эн больше нуля, или на минус эн единиц вниз, если эн меньше нуля.
При этом производить параллельные переносы можно в любом порядке.
Так же мы рассмотрели способ построения графика функции с помощью вспомогательной системы координат.

resh.edu.ru

Урок 8. график функции y = ax2 + n — Алгебра — 9 класс

На прошлом уроке мы познакомились с квадратичной функцией и подробно рассмотрели частный случай игрек равен а икс в квадрате. Сегодня на уроке рассмотрим другой частный случай игрек равен а икс в квадрате плюс эн.
Для того чтобы установить взаимосвязь между графиками этих функций, изобразим в одной координатной плоскости графики следующих функций: игрек равен три икс в квадрате, игрек равен три икс в квадрате плюс два и игрек равен три икс в квадрате минус два. Составим таблицы значений для каждой функции. Возьмём значения аргумента минус два, минус один, нуль, один и два. Значения функции игрек равен три икс в квадрате соответственно равны двенадцати, трём, нулю, трём и двенадцати. Отметим полученные точки на координатной плоскости и построим параболу три икс в квадрате.
Составим таблицу значений для функции три икс в квадрате плюс два, взяв те же значения аргумента. Получим значения функции четырнадцать, пять, два, пять и четырнадцать. Отметим полученные точки на координатной плоскости и проведем параболу три икс в квадрате плюс два. Для третьей функции игрек равен три икс в квадрате минус два таблица значений имеет следующий вид. Отметим полученные точки на координатной плоскости и проведём параболу три икс в квадрате минус два.
Посмотрим внимательно на полученные графики функций. Нетрудно заметить, что график функции игрек равен три икс в квадрате плюс два можно получить с помощью параллельного переноса графика три икс в квадрате на два единичных отрезка вверх. А график функции игрек равен три икс в квадрате минус два с помощью параллельного переноса параболы три икс в квадрате на два единичных отрезка вниз.
Сделаем вывод. График функции игрек равен а икс в квадрате плюс эн является параболой, которую можно получить из графика функции игрек равен а икс в квадрате с помощью параллельного переноса вдоль оси игрек на эн единиц вверх, если эн больше нуля, или на минус эн единиц вниз, если эн меньше нуля.
Так как выполняется параллельный перенос вверх на эн единиц или вниз на минус эн единиц, то вершина параболы а икс в квадрате плюс эн будет иметь координаты нуль, эн.
Рассмотрим примеры. Используя шаблон параболы игрек равен икс в квадрате, постройте график функции игрек равен икс в квадрате минус четыре. Составим таблицу значений. Отметим на координатной плоскости точки с координатами минус три девять, минус два четыре, минус один один, нуль нуль, один один, два четыре, три девять. Проведём параболу икс в квадрате.
Построим график функции игрек равен икс в квадрате минус четыре. Так как эн равно минус четырём и меньше нуля, то перенесём ключевые точки графика икс в квадрате на четыре единицы вниз. Проведём через полученные точки параболу. Получили график функции игрек равен икс в квадрате минус четыре с вершиной в точке нуль минус четыре.
Используя этот же шаблон построим график функции игрек равен минус икс в квадрате плюс три. Заметим, что перед икс в квадрате стоит знак минус. На прошлом уроке вы узнали, что график функции игрек равен минус эф от икс симметричен графику функции игрек равен эф от икс относительно оси икс. Поэтому построим точки, симметричные ключевым точкам графика игрек равен икс в квадрате. Получим график функции игрек равен минус икс в квадрате.
График функции игрек равен минус икс в квадрате плюс три получен из графика игрек равен минус икс в квадрате с помощью параллельного переноса на три единицы вверх. Таким образом, получили график функции игрек равен минус икс в квадрате плюс три с вершиной нуль три.
Подведём итог. Сегодня на уроке мы изучили функцию игрек равен а икс в квадрате плюс эн. Выяснили, что график функции можно получить из графика функции игрек равен а икс в квадрате с помощью параллельного переноса вдоль оси игрек на эн единиц вверх, если эн больше нуля, или на минус эн единиц вниз, если эн меньше нуля.

resh.edu.ru