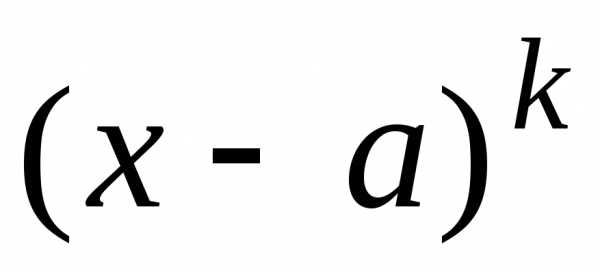Примеры интегрирования рациональных функций (дробей)
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .
Пример 1
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3) меньше степени многочлена числителя (4). Поэтому, вначале необходимо выделить целую часть дроби.
1. Выделим целую часть дроби. Делим x4 на x 3 – 6x 2 + 11x – 6:
Отсюда
.
2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим на x – 1:
Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
3. Разложим дробь на простейшие.
.
Итак, мы нашли:
.
Интегрируем.
Ответ
.
Пример 2
Вычислить интеграл:
.
Решение
Здесь в числителе дроби – многочлен нулевой степени (1 = x 0). В знаменателе – многочлен третьей степени. Поскольку 0 < 3, то дробь правильная. Разложим ее на простейшие дроби.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x). То есть целый корень может быть одним из чисел:
1, 3, –1, –3.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим x 3 + 2x – 3 на x – 1:
Итак,
.
Решаем квадратное уравнение:
x 2 + x + 3 = 0.
Находим дискриминант: D = 1 2 – 4·3 = –11. Поскольку D < 0, то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x – 1)(x 2 + x + 3):
(2.1) .
Подставим x = 1. Тогда x – 1 = 0,
.
Подставим в (2.1) x = 0:
1 = 3A – C;
.
Приравняем в (2.1) коэффициенты при x 2:
;
0 = A + B;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
;
;
.
Вычисляем I2.
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0. Поэтому знак модуля можно опустить.
Поставляем в (2.2):
.
Ответ
.
Пример 3
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли один корень x = –1. Делим на x – (–1) = x + 1:
Итак,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли еще один корень x = –1. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2(x 2 + 2):
(3.1) .
Подставим x = –1. Тогда x + 1 = 0,
.
Продифференцируем (3.1):
;
.
Подставим x = –1 и учтем, что x + 1 = 0:
;
; .
Подставим в (3.1) x = 0:
0 = 2A + 2B + D;
.
Приравняем в (3.1) коэффициенты при x 3:
;
1 = B + C;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
7. Интегрирование дробно-рациональных функций.
Определение 3. Дробно-рациональной функцией (или рациональной дробью) будем называть частное от деления двух многочленов. Общий вид рациональной дроби таков
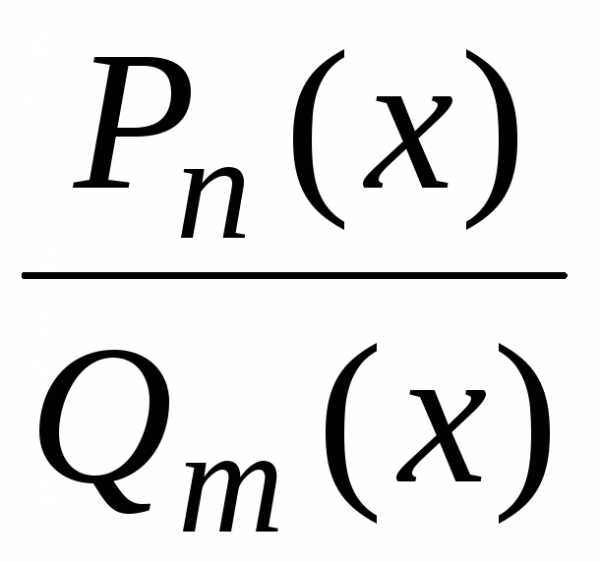 ,
,
где 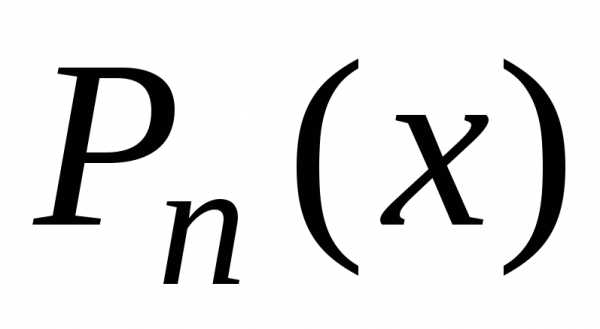 – многочлен степени
– многочлен степени ,
а
,
а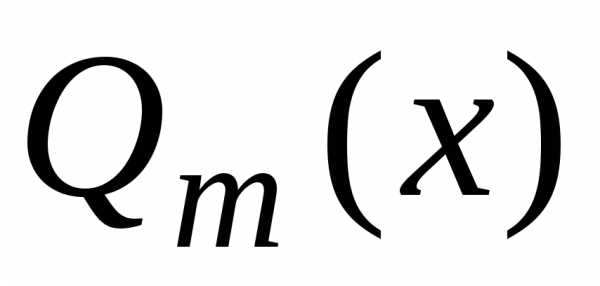 – многочлен степени
– многочлен степени 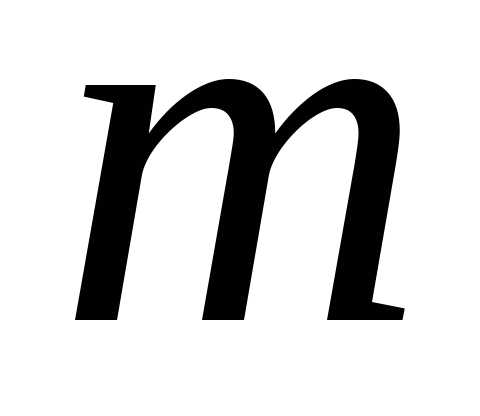 .
.
Если
,
то рациональная дробь называетсяправильной,
если 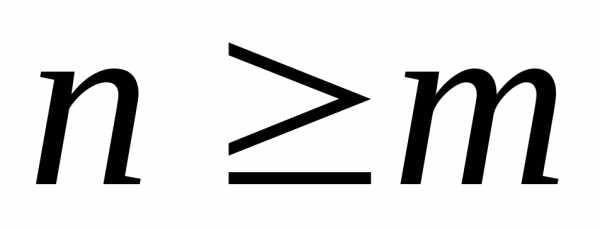 ,
то рациональная дробь называется
,
то рациональная дробь называется
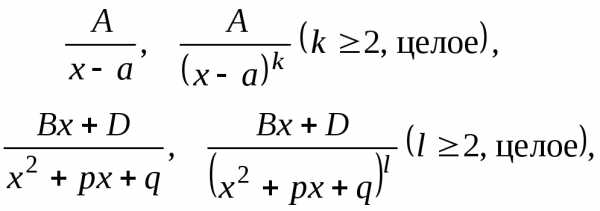
где A, B, D, a, p, q – действительные числа, а трехчлен
не имеет действительных корней (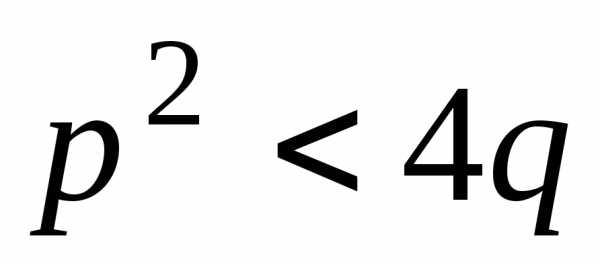 ),
т.е. не раскладывается на множители
первой степени.
),
т.е. не раскладывается на множители
первой степени.
В целом классификацию рациональных дробей можно представить следующим образом.

Интегралы от рациональных дробей всегда являются берущимися. Покажем это, двигаясь по приведённой здесь схеме, поднимаясь с нижнего уровня на верхний уровень.
Интегрирование простейших дробей.Интеграл типа (I) берется с использованием формулы (3.3) таблицы 1 и линейной замены.
.
Интеграл типа (II) берется с использованием формулы (3.2) таблицы 1 и линейной замены.
.
( Здесь 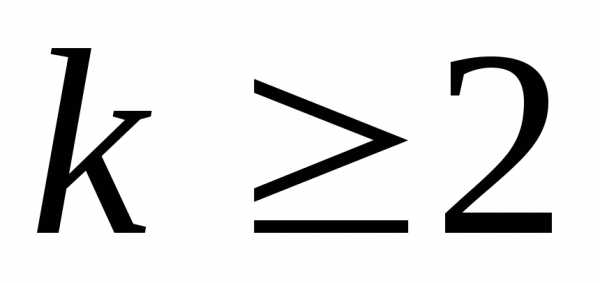 .)
.)
Рассмотрим интеграл типа (III)
 ,
где
,
где .
.
Чтобы вычислить
интеграл 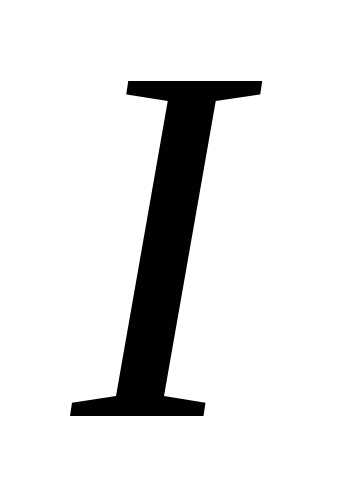 ,
найдём сначала производную знаменателя
подынтегральной функции:
,
найдём сначала производную знаменателя
подынтегральной функции:
.
Далее представим числитель как сумму двух слагаемых:
,
т.е. “выделим” в
числителе производную знаменателя.
Теперь 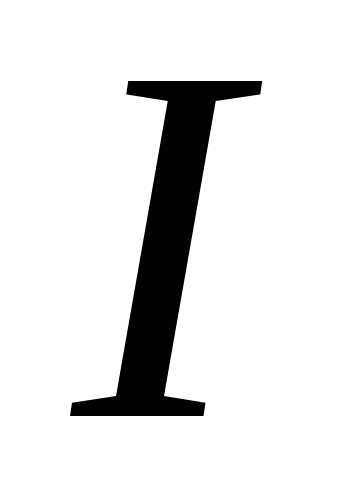 можно представить как сумму двух
слагаемых:
можно представить как сумму двух
слагаемых:
. (7.1)
Вычислим каждый из интегралов, стоящих в правой части (7.1), отдельно:
,
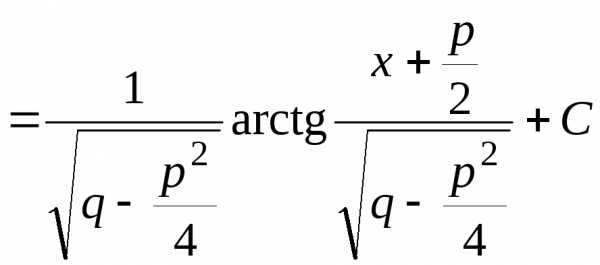 .
.
Таким образом,
. (7.2)
Заметим, что
всегда можно представить как сумму
квадратов в силу того, что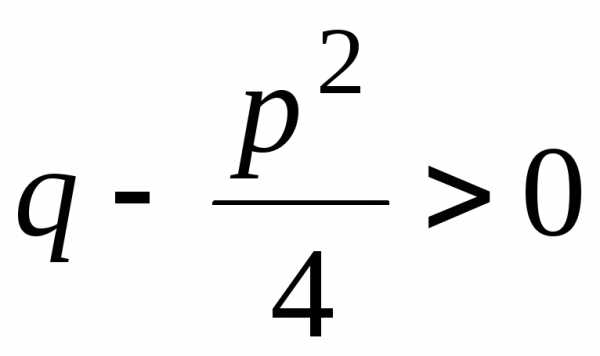 .
.
Формула (7.2) сложна для запоминания. Как правило, ею не пользуются, а непосредственно применяют к конкретному интегралу изложенный здесь метод.
Приведём примеры.
Пример 7.1. .
Пример
7.2. 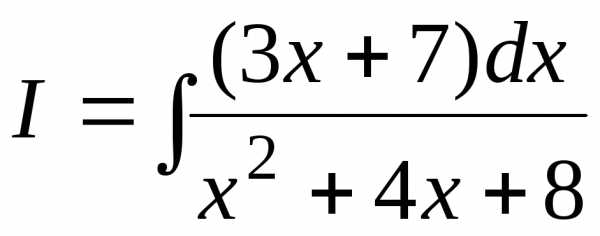 .
Найдем производную знаменателя.
Выделим эту производную в числителе.
Тогда
.
Найдем производную знаменателя.
Выделим эту производную в числителе.
Тогда
.
Пример 7.3. . Воспользуемся формулами
. Тогда
Для интеграла типа (IV) , где
 ,
, ,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.
,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.
Интегрирование правильных дробей общего вида.
Рассмотрим
правильную дробь 
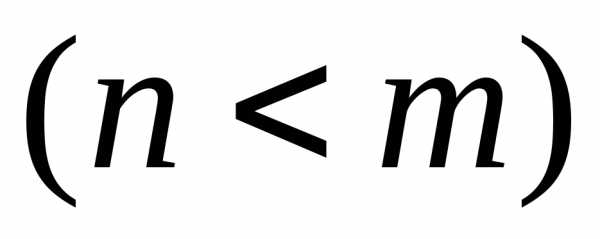 ,
которая не является простейшей дробью.
Чтобы проинтегрировать такую функцию,
её нужно представить в виде суммы
простейших дробей.
,
которая не является простейшей дробью.
Чтобы проинтегрировать такую функцию,
её нужно представить в виде суммы
простейших дробей.Представление правильной дроби в виде суммы простейших дробей осуществляется по следующему правилу.
Знаменатель
 следует разложить на множители вида
следует разложить на множители вида
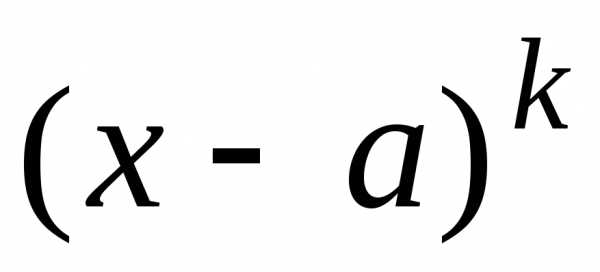 и
,
и
,
где  ,
а
,
а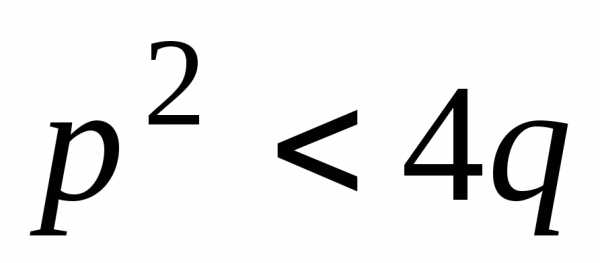 .
Заметим, чтопри условии
.
Заметим, чтопри условии на множители разложить нельзя.
на множители разложить нельзя.
Следует построить “общий вид” представления с неопределёнными пока коэффициентами. При этом каждому множителю
должна соответствовать сумма дробей
, (7.3)
а каждому множителю должна соответствовать сумма дробей
, (7.4)
где коэффициенты 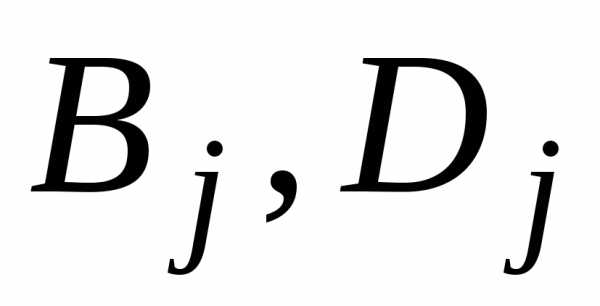 пока неизвестны и представлены буквами.
В суммах (7.3) и (7.4) должны обязательно
присутствовать все перечисленные выше
слагаемые (
пока неизвестны и представлены буквами.
В суммах (7.3) и (7.4) должны обязательно
присутствовать все перечисленные выше
слагаемые ( слагаемых в сумме (7.3) и
слагаемых в (7.4)) . Общий вид представления
содержит в себе все суммы (7.3) и (7.4).
слагаемых в сумме (7.3) и
слагаемых в (7.4)) . Общий вид представления
содержит в себе все суммы (7.3) и (7.4).
Следует определить коэффициенты представления, полученного в пункте 2, исходя из тождественного равенства правильной дроби и суммы простейших дробей, полученной в пункте 2.
Покажем на конкретных примерах, как пользоваться данным правилом.
Пример
7.4. 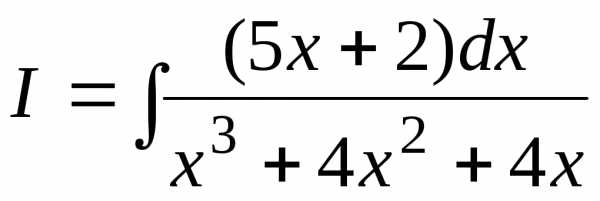 .
.
Применим сформулированное выше правило.
1) Разложим знаменатель дроби, стоящей под знаком интеграла, на множители:
.
2) Построим для дроби, стоящей под знаком интеграла, представление в виде суммы простейших дробей с неизвестными пока коэффициентами
. (7.5)
Множитель  имеет степень 1, и ему соответствует в
сумме одно слагаемое, множитель
имеет степень 1, и ему соответствует в
сумме одно слагаемое, множитель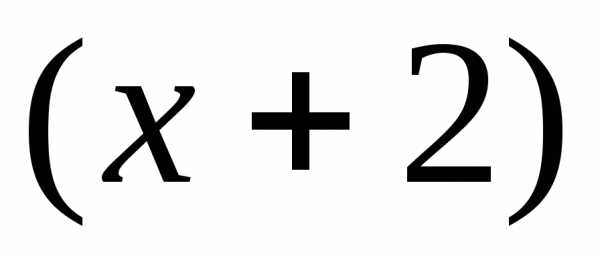 имеет степень 2, и ему в сумме соответствуют
два слагаемых.
имеет степень 2, и ему в сумме соответствуют
два слагаемых.
3) Приведём правую часть равенства (7.5) к общему знаменателю. Получим
. (7.6)
Равенство (7.6)
должно выполняться при всех значениях 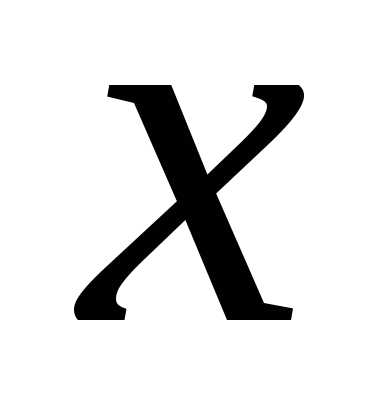 .
Поскольку знаменатели дробей, стоящих
в левой и правой частях (7.6), одинаковы,
числители этих дробей должны быть
тождественно равными. Таким образом,
.
Поскольку знаменатели дробей, стоящих
в левой и правой частях (7.6), одинаковы,
числители этих дробей должны быть
тождественно равными. Таким образом,
(7.7)
при всех значениях 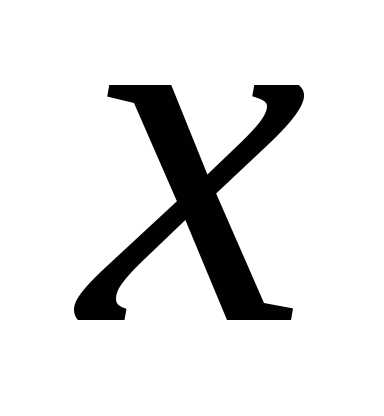 .
Чтобы определить
.
Чтобы определить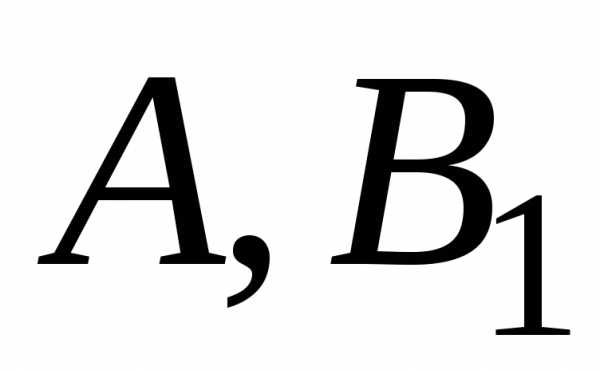 и
и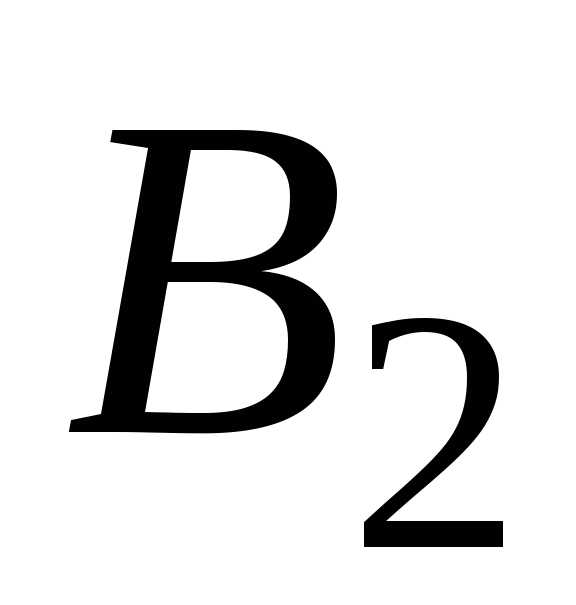 ,
подставим в (7.7) три каких-либо значения
,
подставим в (7.7) три каких-либо значения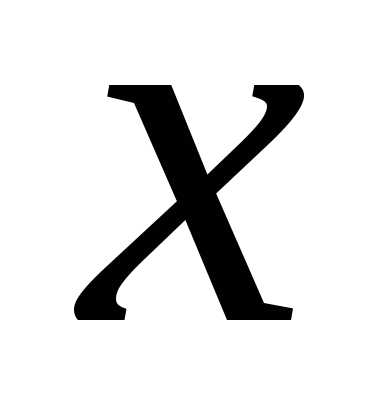 и получим систему трёх уравнений
относительно неизвестных
и получим систему трёх уравнений
относительно неизвестных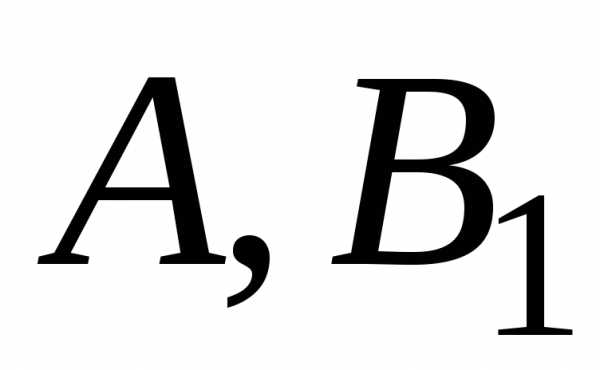 и
и
 обычно выбирают так, чтобы расчеты были
как можно более простыми. В нашем случае
выгодно выбрать
обычно выбирают так, чтобы расчеты были
как можно более простыми. В нашем случае
выгодно выбрать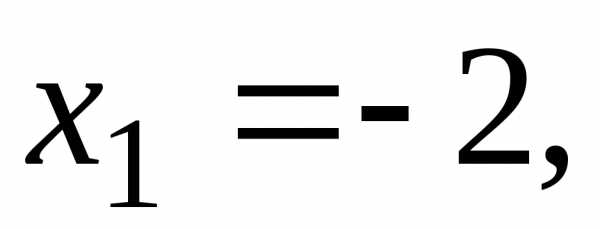
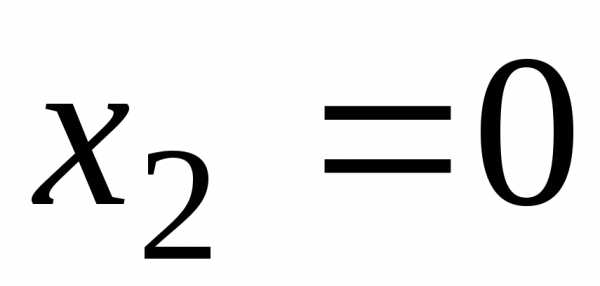 и
и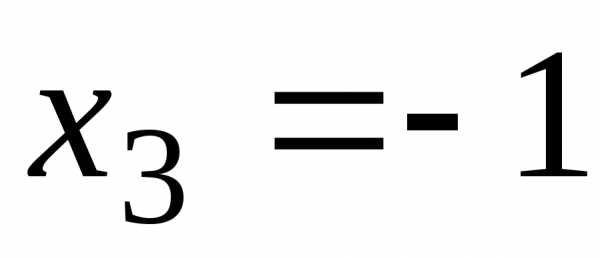 .
Последовательно подставляя эти значения
.
Последовательно подставляя эти значения в тождество (7.7), получим систему
в тождество (7.7), получим систему 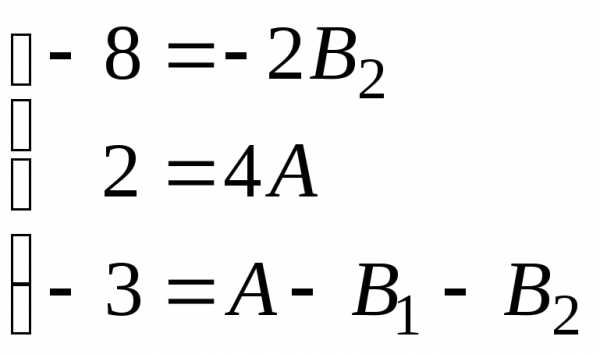 (7.8)
(7.8)
Система (7.8) имеет решение:
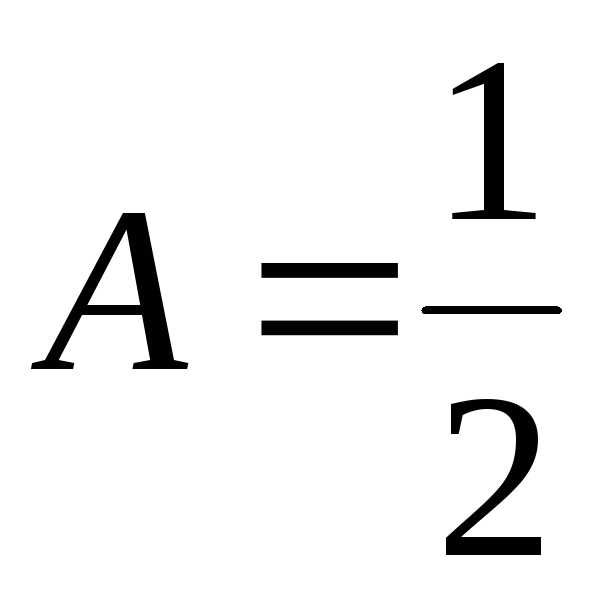 ;
; 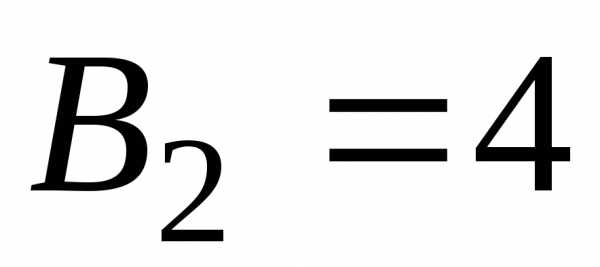
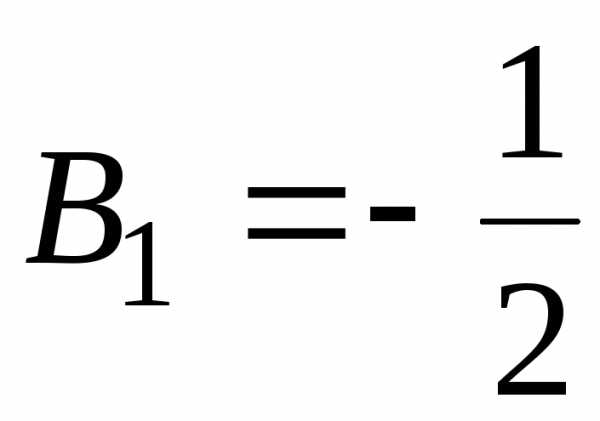 .
. Замечание. Если коэффициенты  ,
, найдены верно, то слева и справа в (7.7)
стоят одинаковые многочлены. Следовательно,
их коэффициенты при одинаковых степенях
должны быть равны. Установим это:
найдены верно, то слева и справа в (7.7)
стоят одинаковые многочлены. Следовательно,
их коэффициенты при одинаковых степенях
должны быть равны. Установим это:
Таким образом, коэффициенты найдены верно. Итак, мы получили тождество
.
Тогда
.
Пример 7.5. .
Представим дробь, стоящую под знаком интеграла, в виде суммы простейших дробей. Так как оба множителя, стоящих в знаменателе, имеют степень 1, представление будет иметь вид
. (7.9)
Заметим, что если в знаменателе стоит квадратный трёхчлен , то в числителе обязательно должен стоять многочлен первой степени .
Приводим правую часть (7.9) к общему знаменателю. Тогда
,
откуда следует
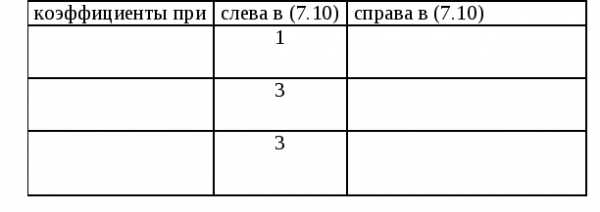
. (7.10)
Нужно определить
три коэффициента
.
Используем удобные значения: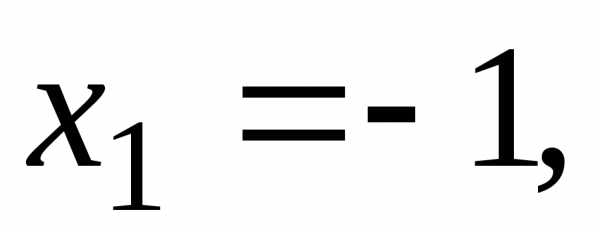

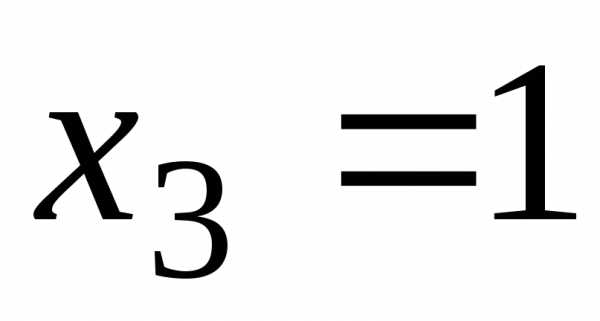 .
Подставим их последовательно в (7.10).
Получим
.
Подставим их последовательно в (7.10).
Получим
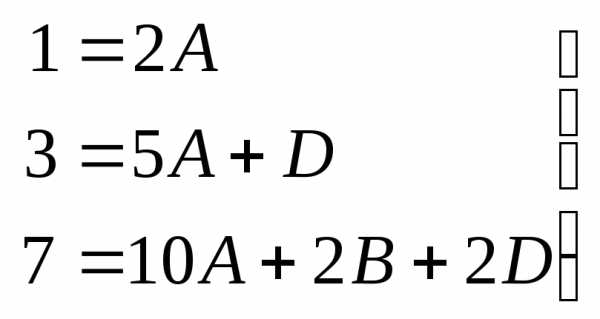 .
(7.11)
.
(7.11)
Система (7.11) имеет решение:
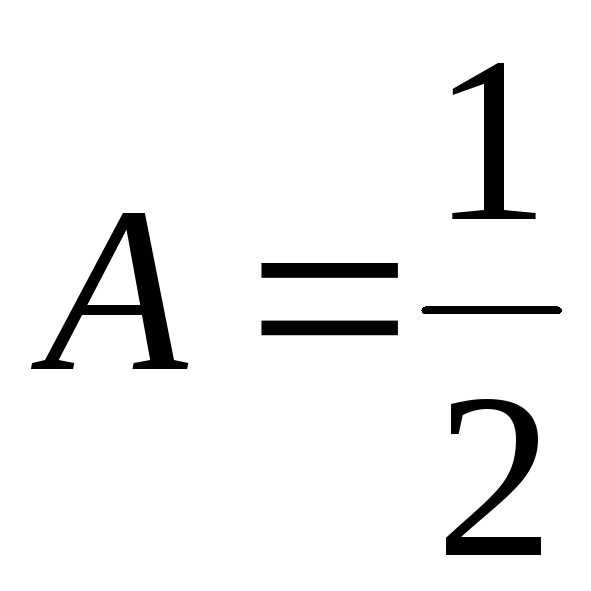 ;
; 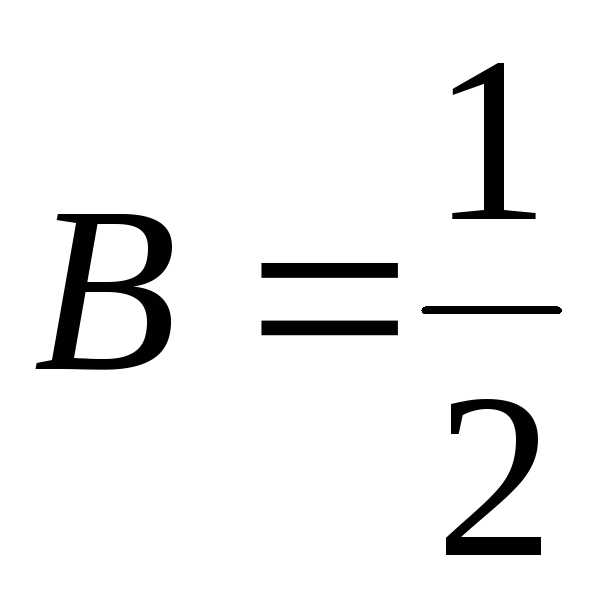 ;
; .
.
Проверим полученный результат.
Получено тождество
.
Следовательно,
.
Отдельно вычислим 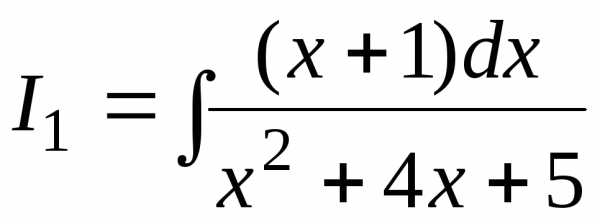 ,
используя формулы
,
используя формулы
.
.
Итак,
.
Пример 7.6. .
Разлагаем знаменатель на множители:
.
Выписываем общий вид представления дроби в виде суммы простейших дробей и сразу же приводим сумму дробей к общему знаменателю:
.
Составляем равенство числителей двух равных дробей с одинаковыми знаменателями:
. (7.12)
Выбираем удобные
значения  :
: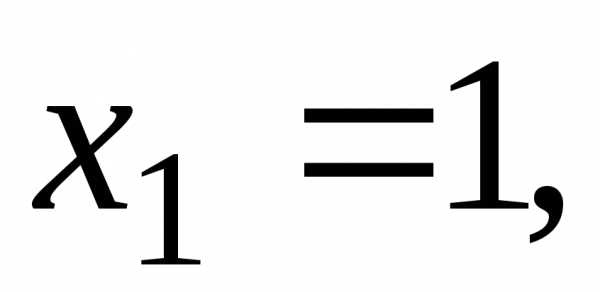
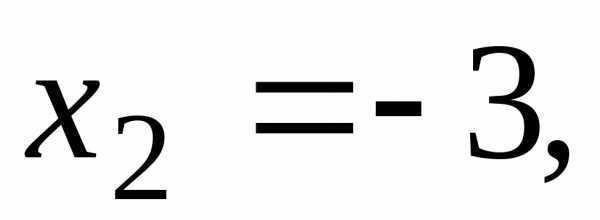
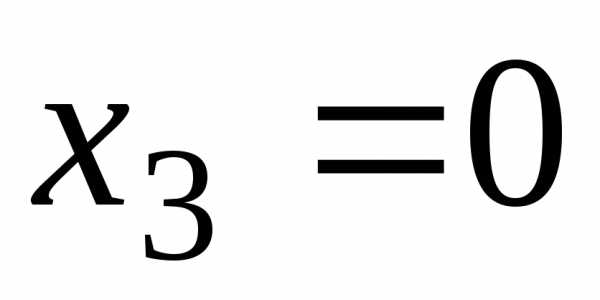 ,
,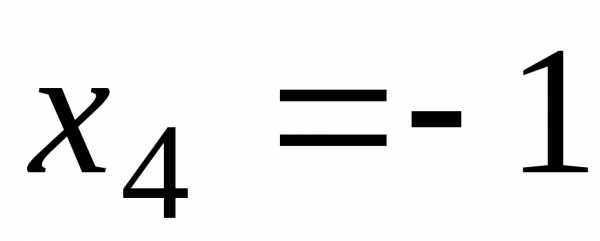 и составляем систему уравнений для
определения четырёх коэффициентов:.
и составляем систему уравнений для
определения четырёх коэффициентов:.
 .
(7.13)
.
(7.13)
Решаем систему
(7.13): 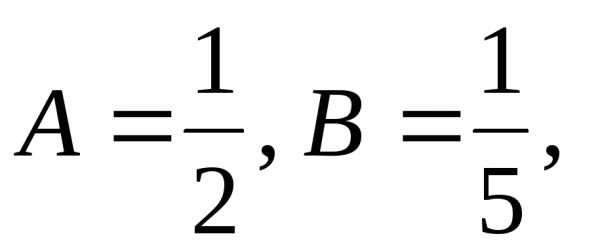
, .
Проверим полученные значения.
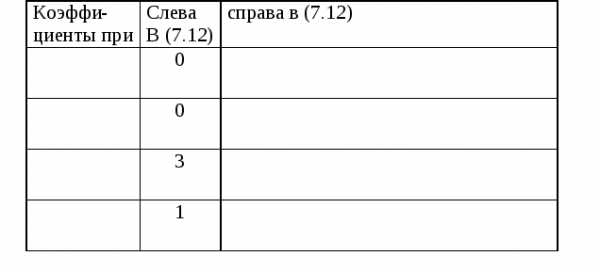
Таким образом,
.
Интегрирование неправильных дробей.
Чтобы проинтегрировать
неправильную дробь
,
где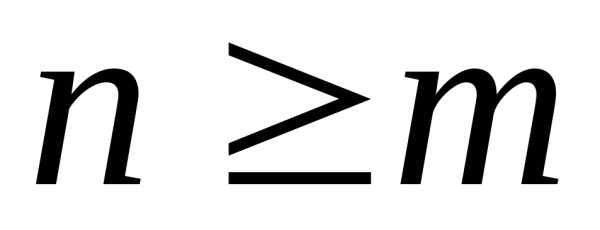 ,
её следует представить в виде суммы
многочлена и правильной дроби. Для этого
сначала следует представить
,
её следует представить в виде суммы
многочлена и правильной дроби. Для этого
сначала следует представить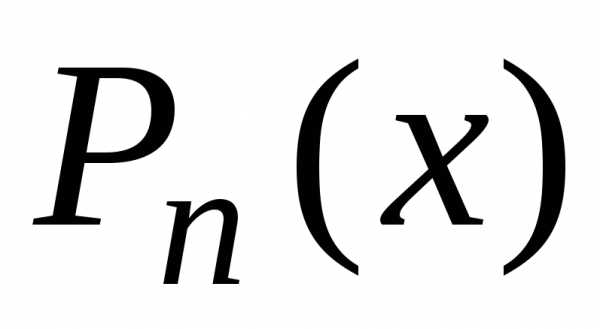 в виде
в виде
, (7.14)
где степень
многочлена 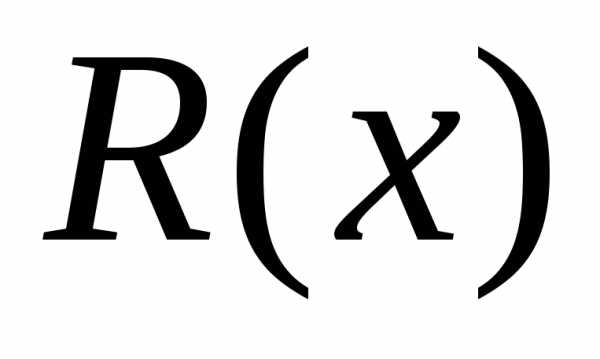 меньше, чем степень многочлена
меньше, чем степень многочлена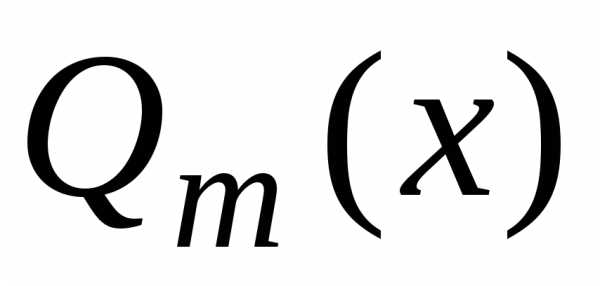 .
Представление (7.14) равносильно делению
многочлена
.
Представление (7.14) равносильно делению
многочлена на многочлен
на многочлен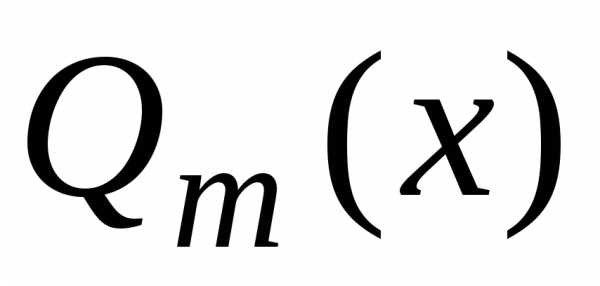 с остатком. В формуле (7.14) многочлен
с остатком. В формуле (7.14) многочлен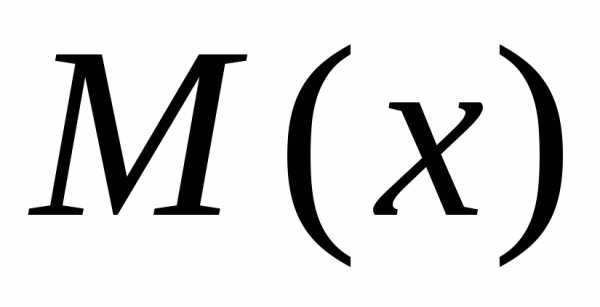 является частным, а многочлен
является частным, а многочлен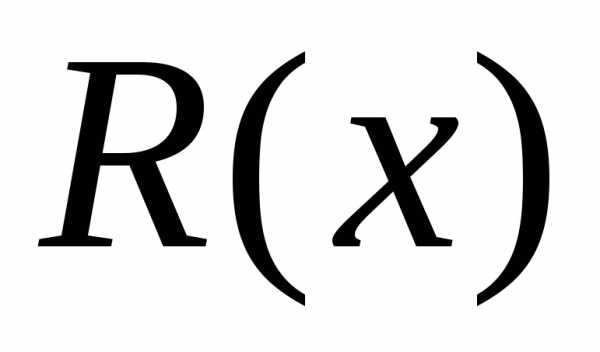 является остатком. Затем равенство
(7.14) следует почленно поделить на
является остатком. Затем равенство
(7.14) следует почленно поделить на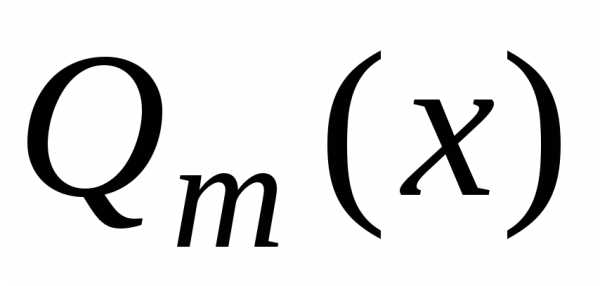 .
Мы получим
.
Мы получим
.
Здесь 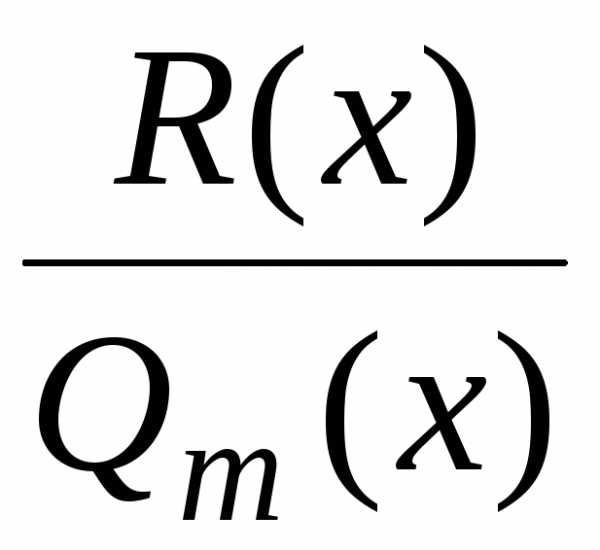 – правильная дробь.
– правильная дробь.
Представление
(7.14) иногда легко угадать (если 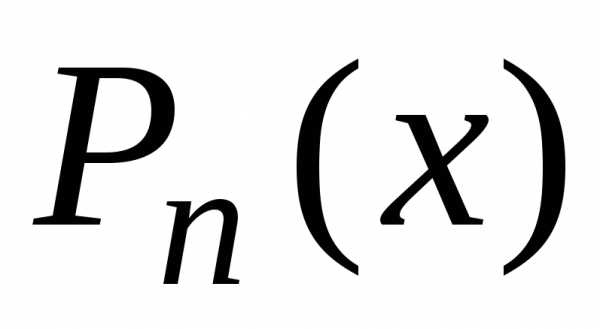 иимеют достаточно простой вид), но, как
правило, оно получается в результате
деления
иимеют достаточно простой вид), но, как
правило, оно получается в результате
деления на
на “уголком”.
“уголком”.
Приведём примеры.
Пример 7.7.
.
Пример 7.8.
.
Пример 7.9. Подынтегральная функция является неправильной рациональной дробью. Разделим числитель этой дроби на знаменатель с остатком.
.
Вычислим отдельно
.
Окончательно,
.
Пример
7.10. 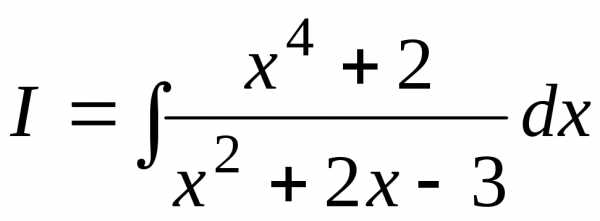 .
Поделим числитель на знаменатель с
остатком.
.
Поделим числитель на знаменатель с
остатком.
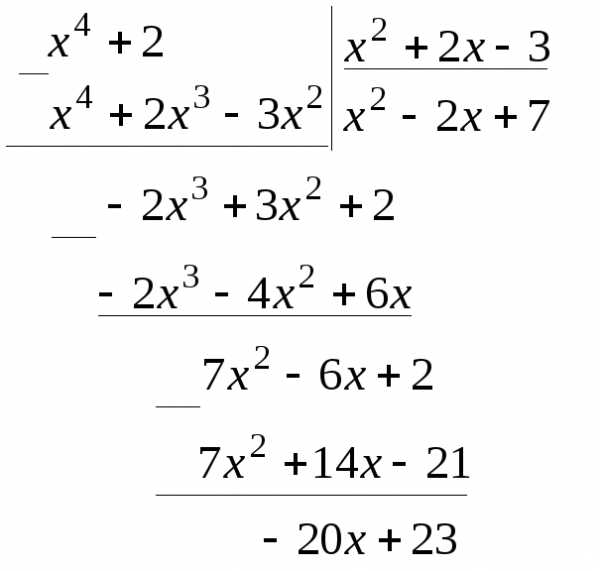
.
Вычислим отдельно . Разложим правильную дробь на простейшие дроби.
.
.
Подставим в полученное тождество последовательно значения переменной . Тогда
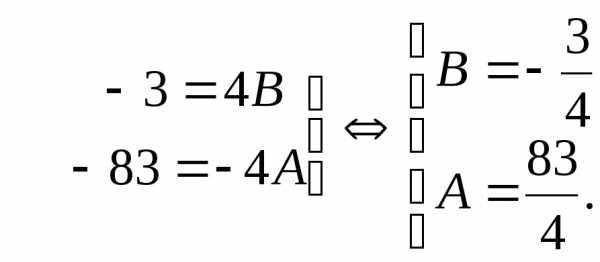
Получим .
Окончательно,
.
studfiles.net
§5. Интегрирование рациональных функций.
Рациональной функцией называется функция, являющаяся отношением двух многочленов (полиномов):
Если Q(x) ≡ 1, то f(x) = P(x) , т.е. многочлен является частным случаем рациональной функции – целая рациональная функция. Рациональную функцию (1) /Q(x)≢1/ называют дробно-рациональной функцией (или рациональной дробью).
Без ограничения общности можно считать, что многочлены P(x) и Q(x) не имеют одинаковых нулей (корней), т. к. в противном случае можно сократить дробь (1) на общие множители.
Рациональною дробь (1) называют правильной, если степень числителя ниже степени знаменателя, т. е. n < m. Если же n ≥ m, (1) называется неправильной.
Если рациональная дробь (1) неправильная, то её можно всегда представить в виде суммы целой рациональной функции (целой части) и правильной рациональной дроби. /например, деля числитель на знаменатель как два полинома/:
гдеR(x) – полином, P1(x)/Q1(x) – правильная дробь.
Интегрирование полинома не составляет труда, поэтому будем рассматривать
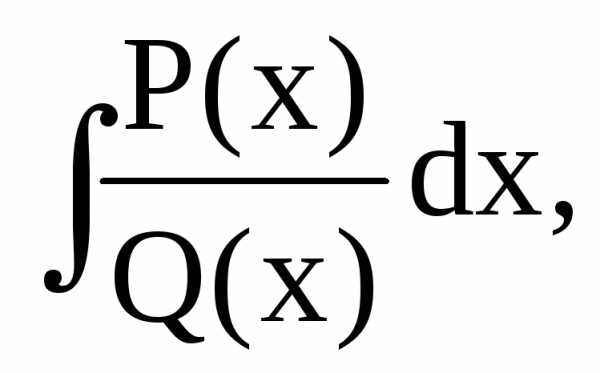
полагая P(x)/Q(x) правильной.
1. Изучим сначала интегрирование простейших (элементарных) рациональных дробей.
Определение. Правильные рациональные дроби вида
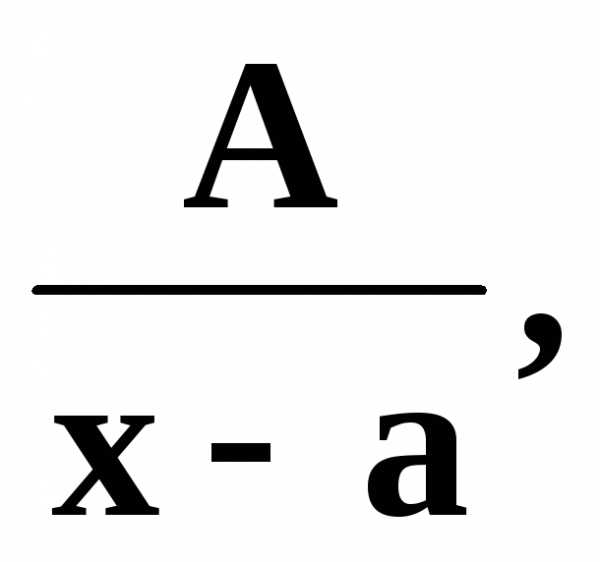
I.
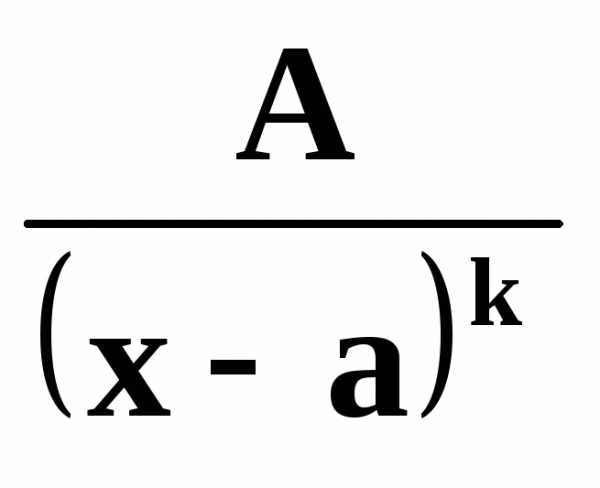
II. /k – натуральное число ≥ 2/,
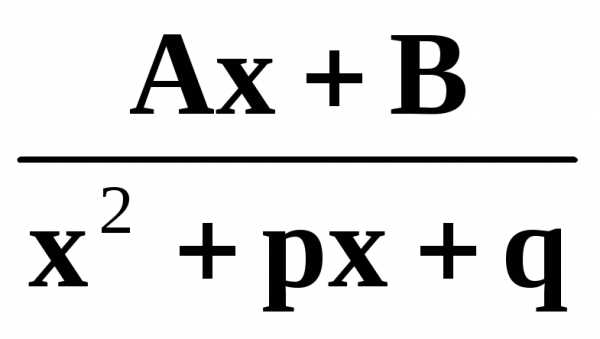
III. /знаменатель не имеет действительных корней, т. е.
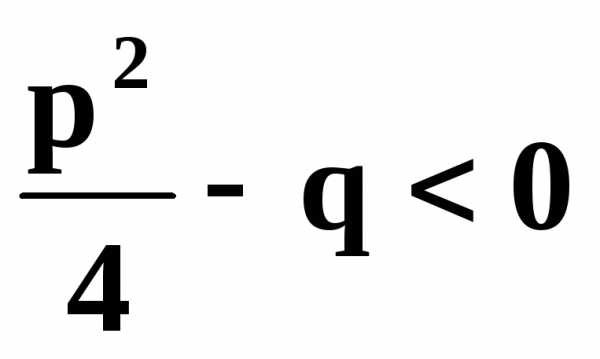
; A, B, a, p, q – действительные числа /,
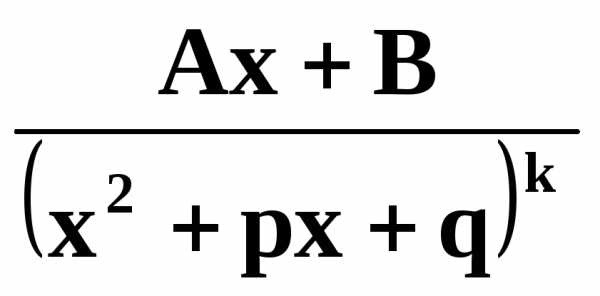
IV. /k – натуральное число ≥ 2; знаменатель не имеет действительных корней/,
называются соответсвенно простейшими рациональными дробями I, II, III и IV типов.
Интегрирование дробей первых трёх типов осуществляется просто.
/см. §3/.
Интегрирование простейших дробей IV типа осуществляется таким же методом, но выкладки значительно сложнее. Мы в этом же параграфе рассмотрим метод Остроградского, который позволит интегрировать любые рациональные дроби, применяя интегралы только от простейших дробей первых трёх типов.
2. Разложение рациональной дроби в сумму рациональных дробей. Справедлива (доказательство опускаем) следующая
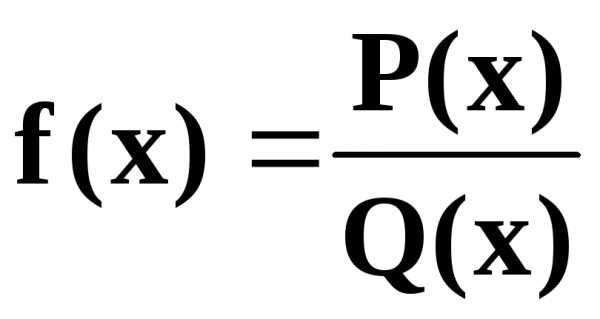
Теорема Всякая правильная несократимая рациональная дробь может
быть представлена как сумма конечного числа простейших рациональных дробей, а именно
если(2)
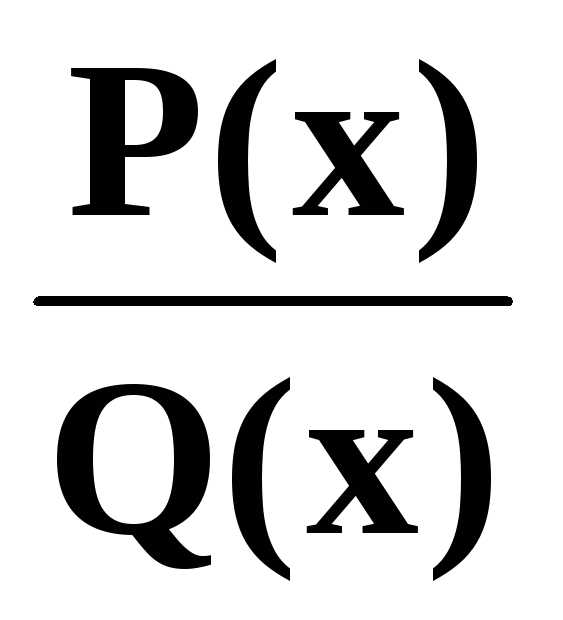
т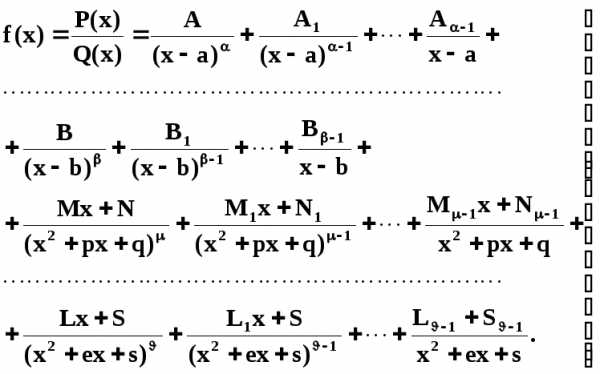 о
дробь может быть представлена
в виде:
о
дробь может быть представлена
в виде:
(3)
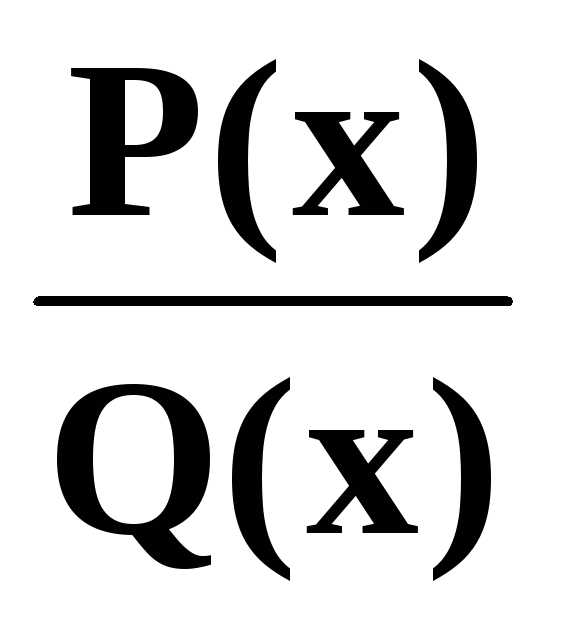 На
практике эту теорему применяют следующим
образом. Каким – либо образом знаменатель
дробиQ(x) представляют в виде (2),
причём квадратные трёхчлены имеют
дискриминанты отрицательные и потому
уже не могут разлагатся в произведение
линейных множителей с действительными
коэффициентами. Затем пишут для дроби
На
практике эту теорему применяют следующим
образом. Каким – либо образом знаменатель
дробиQ(x) представляют в виде (2),
причём квадратные трёхчлены имеют
дискриминанты отрицательные и потому
уже не могут разлагатся в произведение
линейных множителей с действительными
коэффициентами. Затем пишут для дроби
соответствующее разложение (3) с буквенными коэффициентами A,A1, … L-1,
S-1. Эти коэффициенты определяют по методу неопределённых коэффициентов. Равенство (3) есть тождество, поэтому, приведя дроби справа к наименьшему общему знаменателю (он, очевидно будет равен Q(x)), получают тождественное равенство числителей, двух многочленов – P(x) и того, который получится справа. Приравнивая коэффициенты при одинаковых степенях x, получают систему линейных уравнений относительно A, A1, A2, … L-1, S-1, из которой их и определяют.
Замечание 1. Уравнение для определения коэффициентов можно получать и другим способом. Т. к. полученное равенство числителей есть тождество, то давая x конкретные (удобные!) значения, имеют необходимые уравнения для определения этих коэффициентов (более простые, чем в описанной выше системе).
Замечание 2. Из выше изложенного следует такой вывод: неопределённый интеграл от рациональной функции всегда может быть выражен через конечное число элементарных функций.
Примеры 1)Вычислить интеграл
Подинтегральная функция f(x) является правильной рациональной дробью. Знаменатель уже разложен в произведение простых (неприводимых) множителей, т. к. x2 + 2 не имеет действительных корней /x1,2 = i 2/.
Разложим подинтегральную дробь в сумму простейших дробей:
Приведём дроби справа к наименьшему общему знаменателю и приравняем числители:
x3 + 4x2 + 6 A(x2 + 2) + B(x +1)(x2 + 2) + (Cx + D)(x +1)2. (4)
или x3 + 4x2 + 6 = (B + C)x3 + (A + B + 2C +D)x2 + (2B + 2D + C)x + (2A + 2B + D).
Приравнивая коэффициенты при x3, x2, x1, x0, получим систему четырёх линейных уравнений с четырмя неизвестными A, B, C, D:
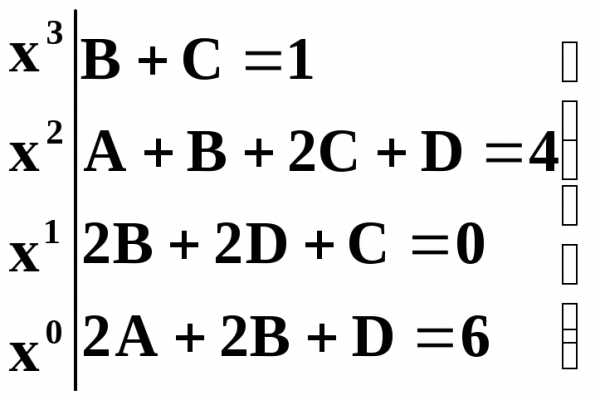
(5)
Ещё из тождества (4) при удобном значении x = – 1 получаем дополнительное простое уравнение: 3A = 9, откуда A = 3
Последующее решение системы (5) даст: B = 1/3, C =2/3, D = –2/3
Итак,
2) Вычислить самостоятельно
Ответ:
studfiles.net
1.6 Интегрирование рациональных функций
Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют элементарные функции.
Определение. Функция
,
где – заданные числа (коэффициенты), называетсямногочленом или полиномом или целой рациональной функцией степени n.
Отношение двух многочленов
называется рациональной
функцией или рациональной дробью.
Рациональная дробь будет правильной,
если степень многочлена в числителе
меньше степени многочлена в знаменателе 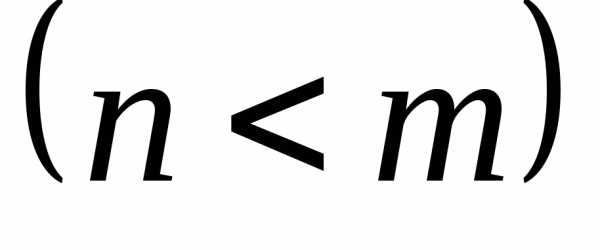 ,
инеправильной в противном случае
,
инеправильной в противном случае  .
.
Рассмотрим,
как вычисляются интегралы  от рациональных дробей.
от рациональных дробей.
Если дробь
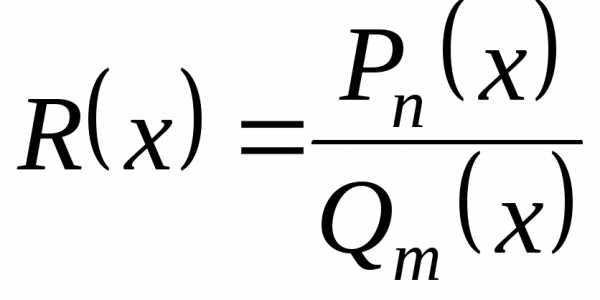
неправильная, то
следует разделить (как обычно, столбиком)
числитель на знаменатель. Частное 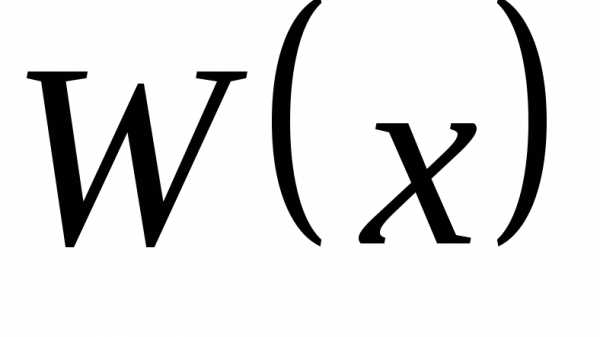 и остаток
и остаток будут многочленами, причем степень
остатка
будут многочленами, причем степень
остатка меньше степени делителя
меньше степени делителя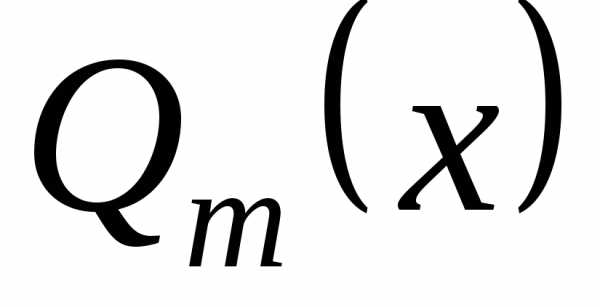 :
:
.
Пример
;  .
.

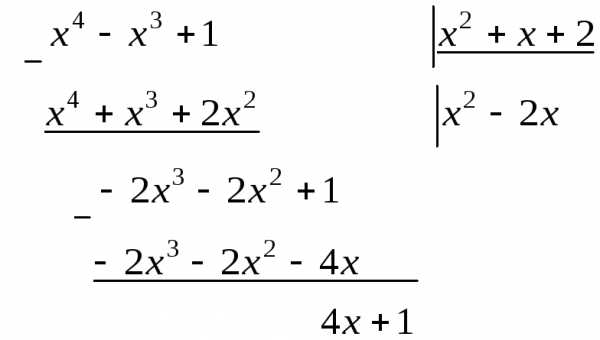

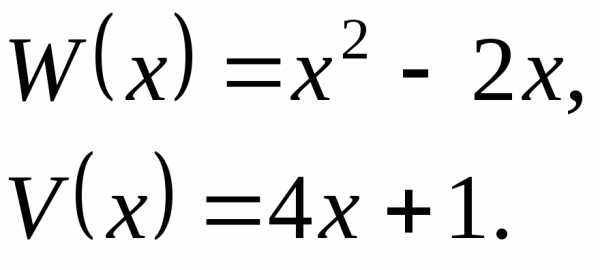
Дробь  – правильная, а интеграл
– правильная, а интеграл от многочлена
от многочлена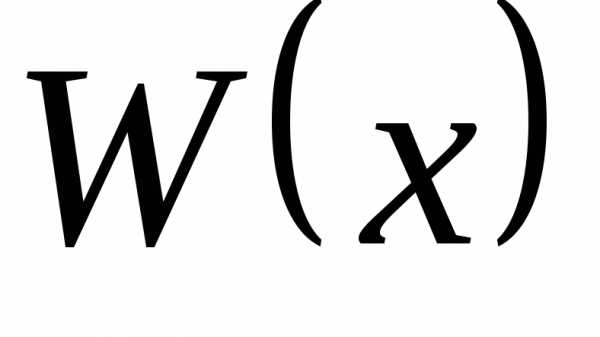 легко берется методом непосредственного
интегрирования.
легко берется методом непосредственного
интегрирования.
Таким образом,
интегрирование неправильной дроби 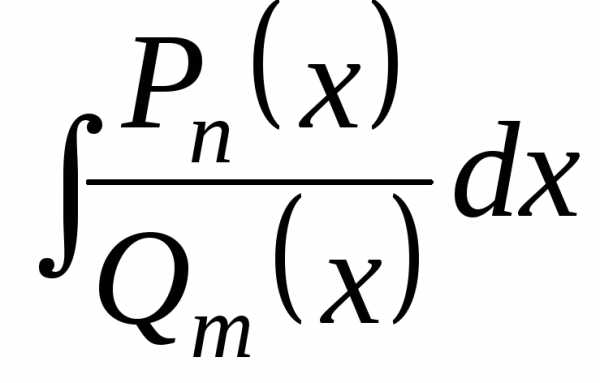 свелось по сути к интегрированию
правильной дроби
свелось по сути к интегрированию
правильной дроби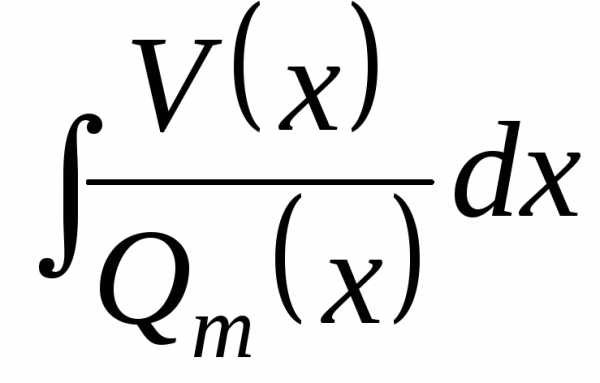 :
:
.
Поэтому достаточно научиться интегрировать правильные дроби.
Известно (см.,
например, ч.1, раздел 5.3), что многочлен 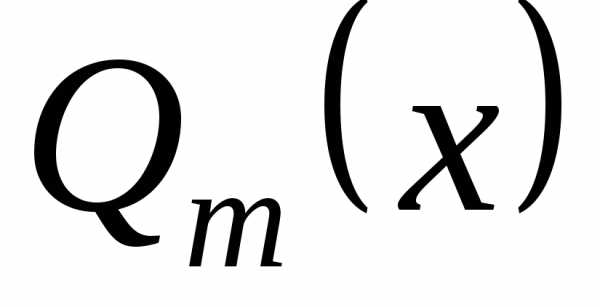 с действительными коэффициентами может
быть разложен на линейные и квадратичные
действительные множители:
с действительными коэффициентами может
быть разложен на линейные и квадратичные
действительные множители:
где 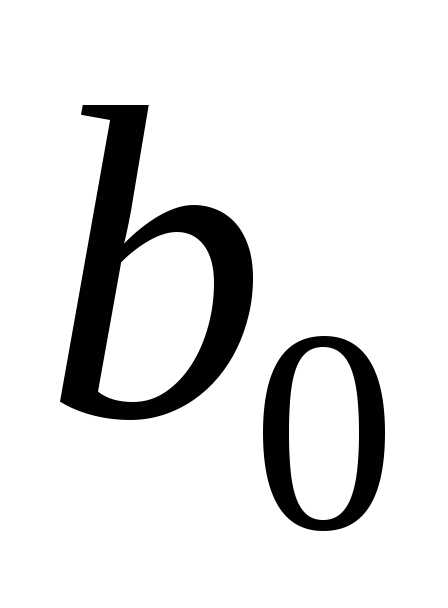 – старший коэффициент многочлена. Каждый
линейный множитель
– старший коэффициент многочлена. Каждый
линейный множитель 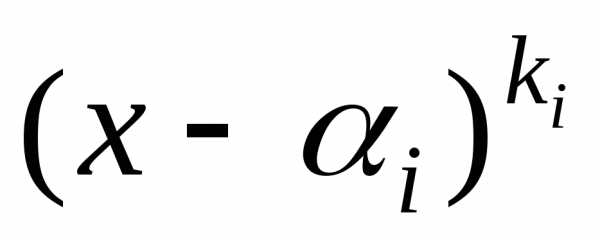 соответствует действительному корню
соответствует действительному корню кратности
кратности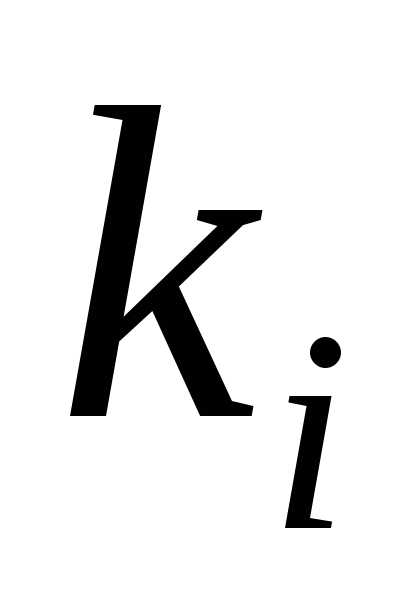 ,
а каждый квадратичный множительсоответствует паре комплексно-сопряженных
корней
,
а каждый квадратичный множительсоответствует паре комплексно-сопряженных
корней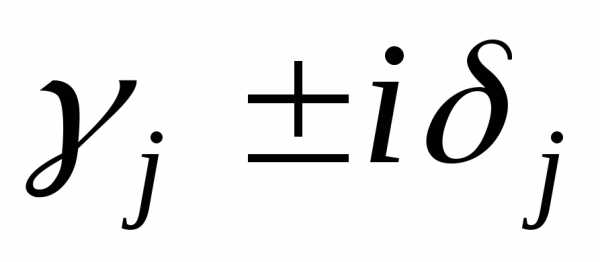 кратности
кратности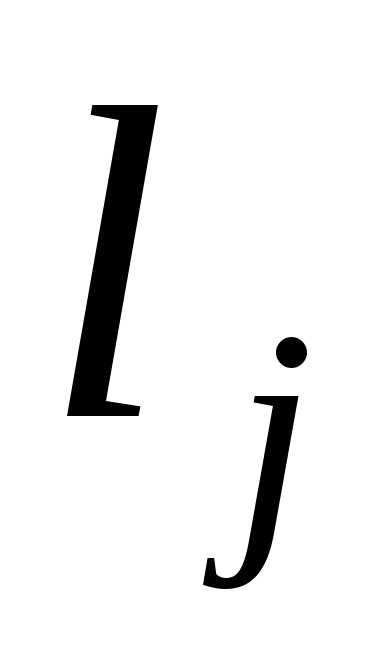 ,
причем.
,
причем.
В высшей алгебре доказывается, что всякая правильная дробь может быть единственным образом разложена на сумму так называемых простейших дробей:
,
где – некоторые действительные числа –
коэффициенты разложения. Для их
определения умножим обе части разложения
на 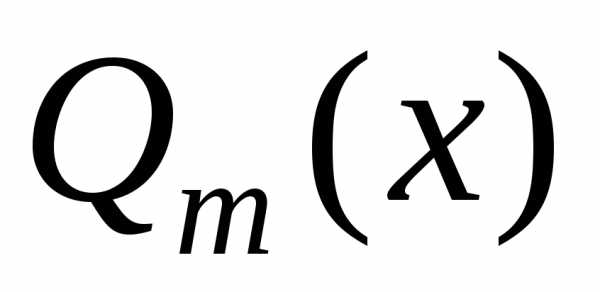 и приравняем коэффициенты, стоящие при
равных степенях
и приравняем коэффициенты, стоящие при
равных степенях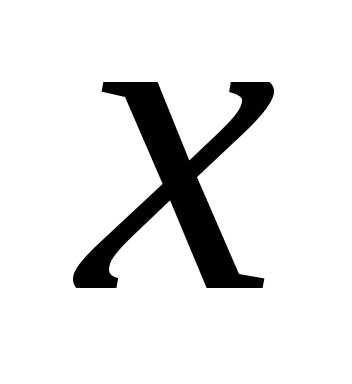 ,
у многочлена, который получится в правой
части разложения и многочлена
,
у многочлена, который получится в правой
части разложения и многочлена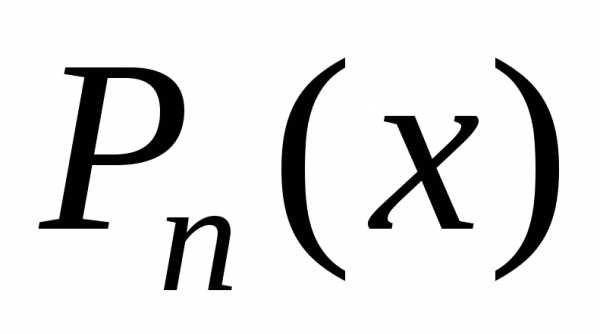 .
В результате получим систему линейных
алгебраических уравнений, из которой
и найдем неизвестные коэффициенты
разложения. Такой метод отыскания
коэффициентов разложения правильной
рациональной дроби на простейшие дроби
называетсяметодом
неопределенных коэффициентов.
.
В результате получим систему линейных
алгебраических уравнений, из которой
и найдем неизвестные коэффициенты
разложения. Такой метод отыскания
коэффициентов разложения правильной
рациональной дроби на простейшие дроби
называетсяметодом
неопределенных коэффициентов.
Пример.
Разложить
правильную рациональную дробь 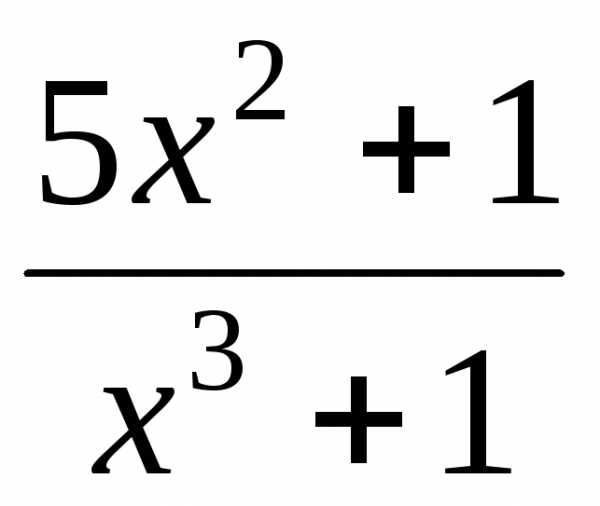 на простейшие дроби.
на простейшие дроби.
Так как , то разложение имеет вид
.
Умножая обе части
равенства на 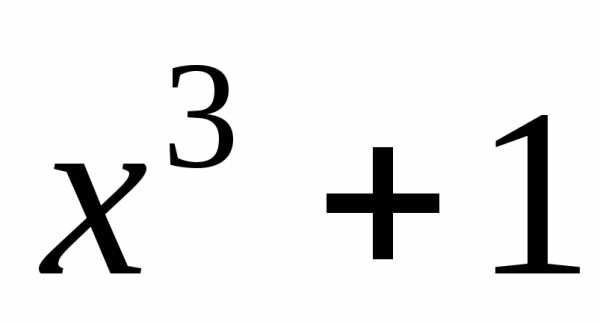 ,
получаем
,
получаем
или
.
Приравнивая
коэффициенты при одинаковых степенях 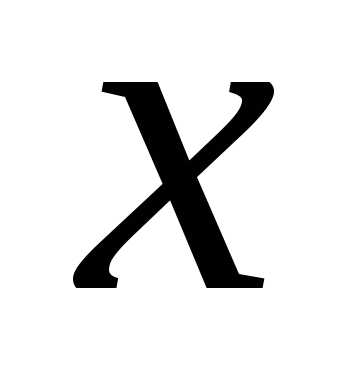 ,
получаем систему линейных алгебраических
уравнений относительно неизвестных
коэффициентов разложения
,
получаем систему линейных алгебраических
уравнений относительно неизвестных
коэффициентов разложения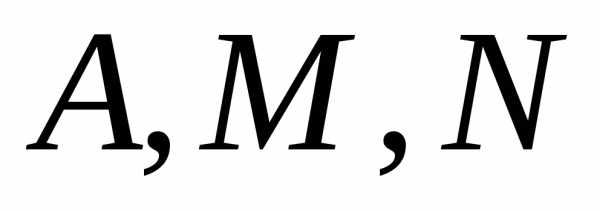 :
:
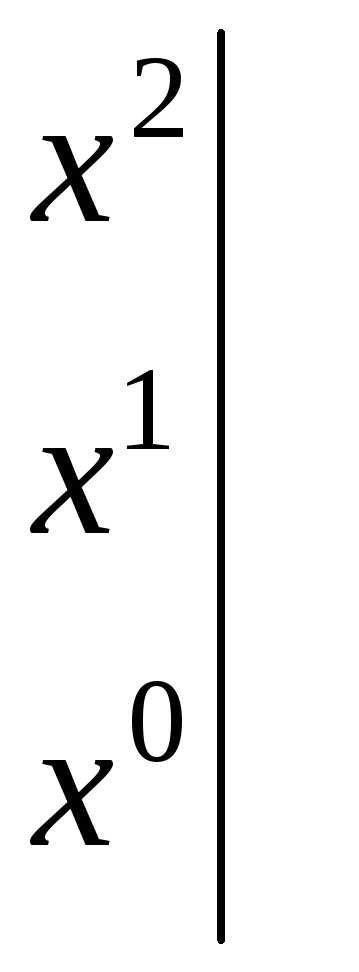
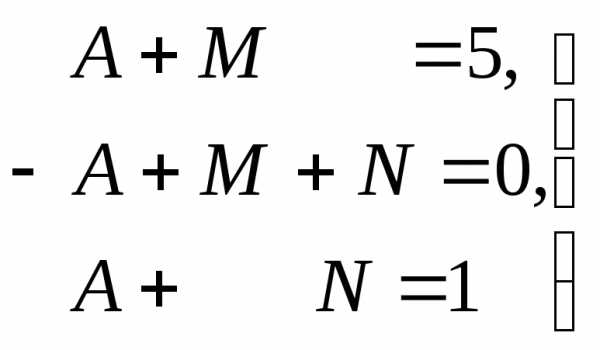 .
.
Решение системы , поэтому искомое разложение имеет вид:
.
Замечание. Систему линейных уравнений для определения
неизвестных коэффициентов разложения
можно также получить, придавая 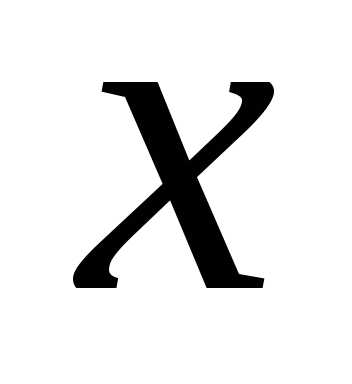 последовательно столько различных
произвольных значений, сколько имеется
неизвестных коэффициентов (в данном
примере – три):
последовательно столько различных
произвольных значений, сколько имеется
неизвестных коэффициентов (в данном
примере – три):
,
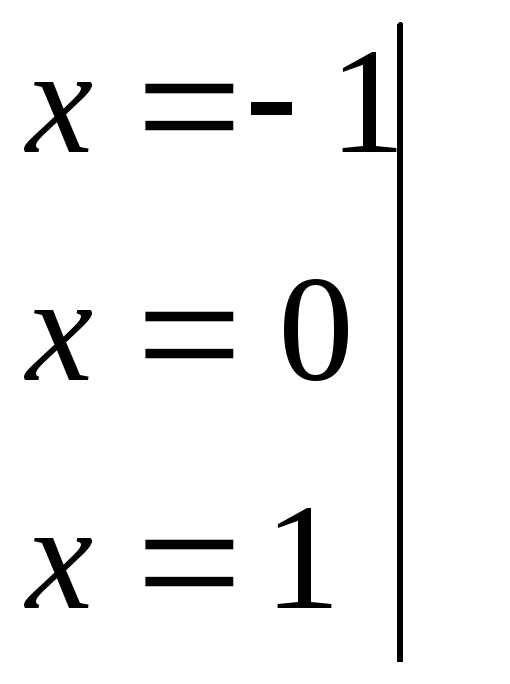
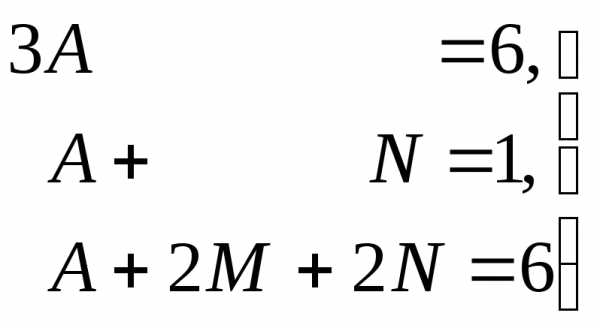

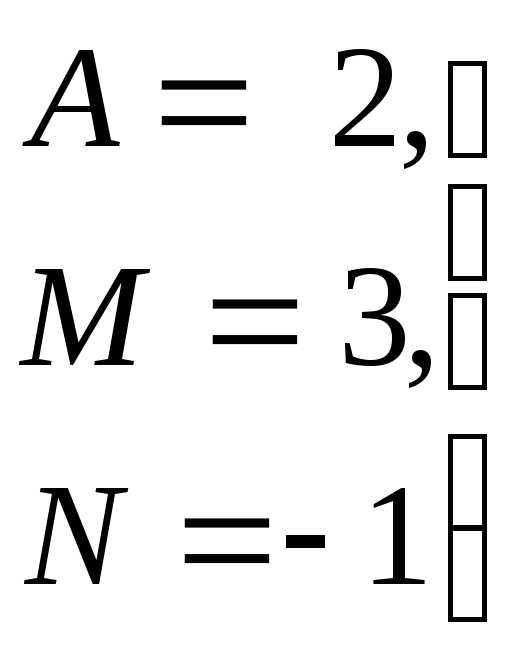 .
.
Из изложенного следует, что задача интегрирования правильной рациональной дроби сводится, в свою очередь, к нахождению интегралов от простейших дробей следующих четырех типов:
I)  ;II)
;II) 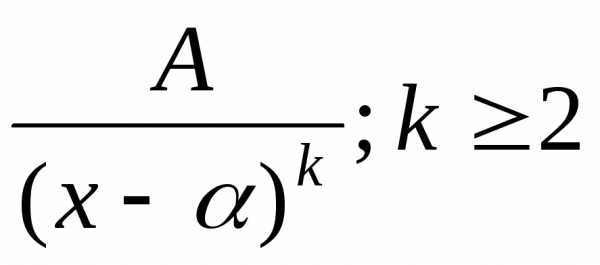 ;
;
III) ; IV) .
Дроби I и II типов элементарно интегрируются при помощи подстановки :
I) .
II) .
Для вычисления интеграла от дроби III типа представим квадратный трехчлен в виде
.
Учитывая, что , введем в рассмотрение действительную постоянную. Сделав подстановку, будем иметь:
=
= 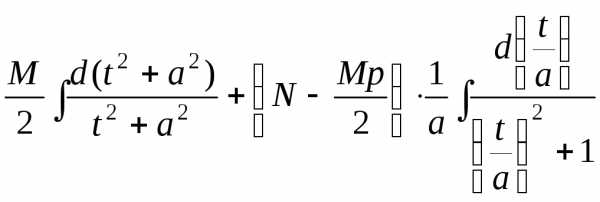 =
=
==
= .
Пример
Остается вычислить интеграл от дроби IV типа.
Используя введенные выше обозначения , будем иметь:
Введем обозначения:
Интересующий нас интеграл будет найден, если будут найдены интегралы I и Jk :
.
Интеграл I берется элементарно:
Для вычисления интеграла Jk установим для него рекуррентную (возвратную) формулу, сводящую вопрос о вычислении Jk к вычислению Jk-1 .
Можно записать
(при  ):
):
Для вычисления последнего интеграла применим формулу интегрирования по частям:
Находим
.
Из последнего равенства получаем рекуррентную формулу
 ,
,
по которой интеграл 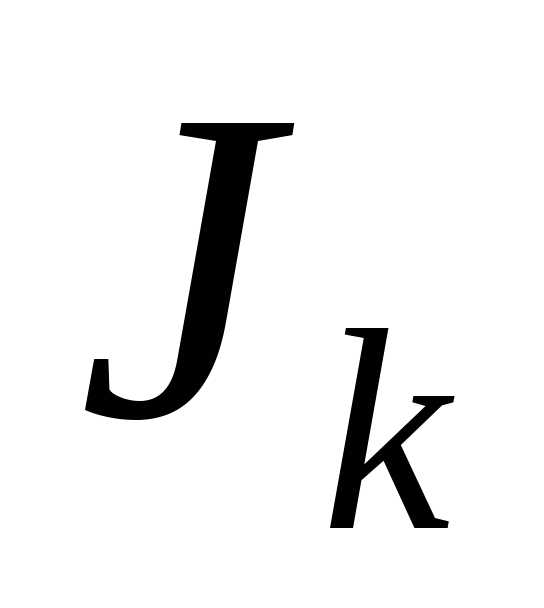 можно выразить через интеграл
можно выразить через интеграл ,
затем
,
затем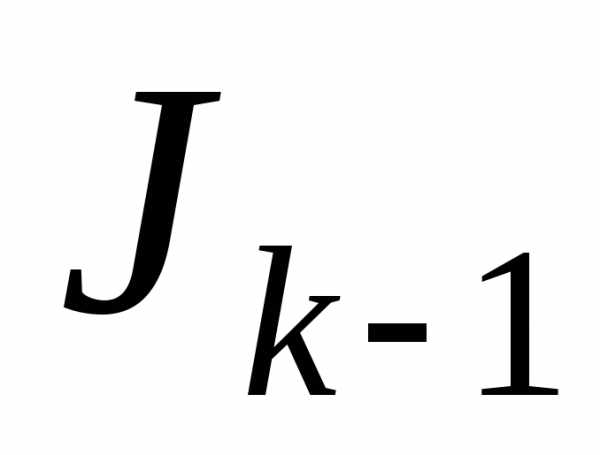 ,
в свою очередь, выразить через
,
в свою очередь, выразить через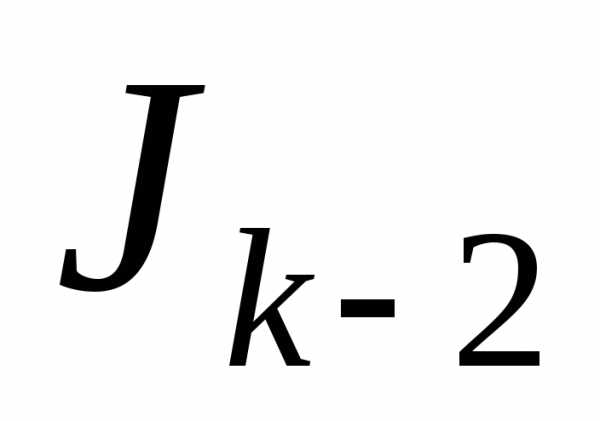 и т.д. Процесс вычисления
и т.д. Процесс вычисления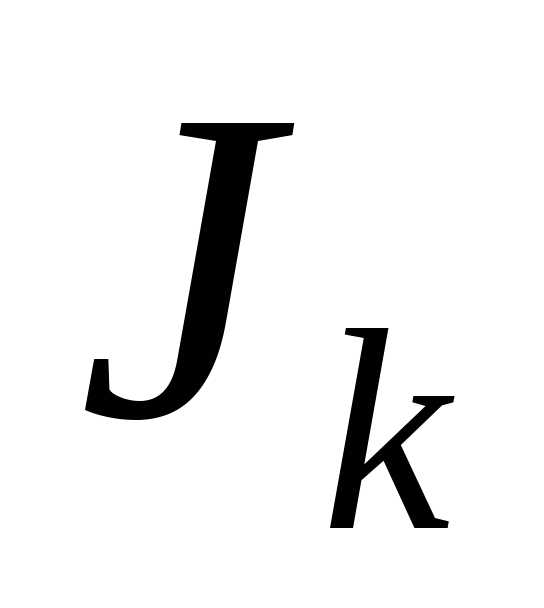 продолжаем до тех пор, пока не дойдем
до
продолжаем до тех пор, пока не дойдем
до
Итак, нами вычислены интегралы от всех четырех простейших дробей. Установлено, что интегрирование любой рациональной функции сводится к интегрированию многочлена и конечного числа простейших дробей, интегралы от которых выражаются через рациональные функции, логарифмы и арктангенсы. Иными словами, любая рациональная функция интегрируется в элементарных функциях.
studfiles.net
Интегрирование рациональных функций (5-6).
Интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.
Интегрирование правильной рациональной дроби сводится к интегрированию простейших дробей вида I—IV.
Интегрирование правильной рациональной дроби:
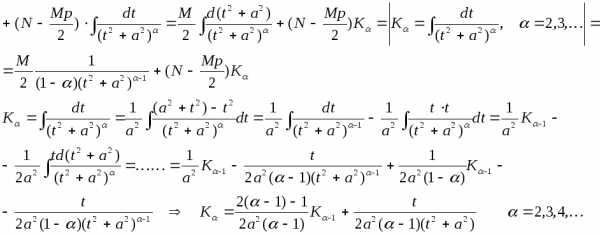 Зная
вычисляемК2,
зная К2 вычисляем К3 и т. д. При
разложении правильной рациональной
дроби на сумму простейших дробей вида I—IV с неопределенными коэффициентами
необходимо определить эти коэффициенты
для этого используем метод неопределенных
коэффициентов.
Зная
вычисляемК2,
зная К2 вычисляем К3 и т. д. При
разложении правильной рациональной
дроби на сумму простейших дробей вида I—IV с неопределенными коэффициентами
необходимо определить эти коэффициенты
для этого используем метод неопределенных
коэффициентов.
Для того чтобы найти коэффициенты А1, А2, … , Мαs, Nαs и т.д. приведем правую часть к наименьшему общему знаменателю т. е. к Q(x), после этого приравняем коэффициенты стоящие при одинаковых степенях в левой и правой частях этих дробей в результате получаем систему линейных уравнений относительно этих коэффициентов решая которые находят эти коэффициенты. Замечание: Часть коэффициентов в разложении правильной рациональной дроби на простые могут быть найдены более простым методом, методом вычеркивания, а именно коэффициенты при старших степенях x(x—ai) т. е. Аα1,.., Вα2
Интегрирование некоторых тригонометрических
функций (подстановки 😉 (7).
Рассмотрим
интегралы от выражения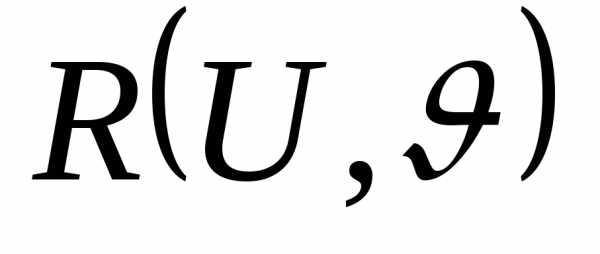 -рациональная
дробь от двух переменных
-рациональная
дробь от двух переменных  ,
т.е. отношение двух многочленовдвух переменных, например;
,
т.е. отношение двух многочленовдвух переменных, например;
используют другие подстановки, которые также рационализируют исходный интеграл. Рассмотрим некоторые из этих подстановок. Для этого нам потребуются следующие свойства рациональных функций:
1)
2)
2.Если то рационализируется подстановкой
Действительно,
т.е. рационализируется.
3.Если , торационализируется подстановкой
4.Если , то рационализируется подстановкой
т.е. рационализируется.
5.Интегралы вида
Интегрируется применением тригонометрических функций
Интегрирование некоторых тригонометрических
функций
(подстановка 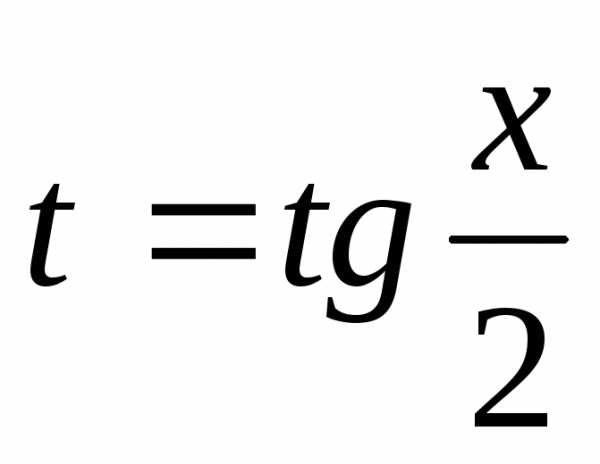 ) (8).
) (8).
Рассмотрим
интегралы от выражения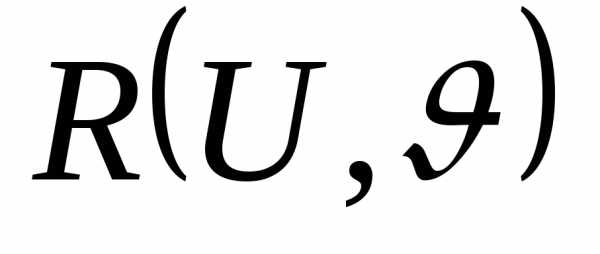 -рациональная
дробь от двух переменных
-рациональная
дробь от двух переменных 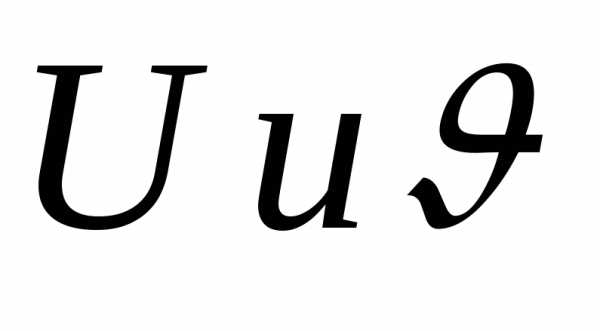 ,
т.е. отношение двух многочленовдвух переменных, например;
,
т.е. отношение двух многочленовдвух переменных, например;
1.рационализируется,
т.е. сводятся к интегралу от рациональной
дроби относительно новой переменной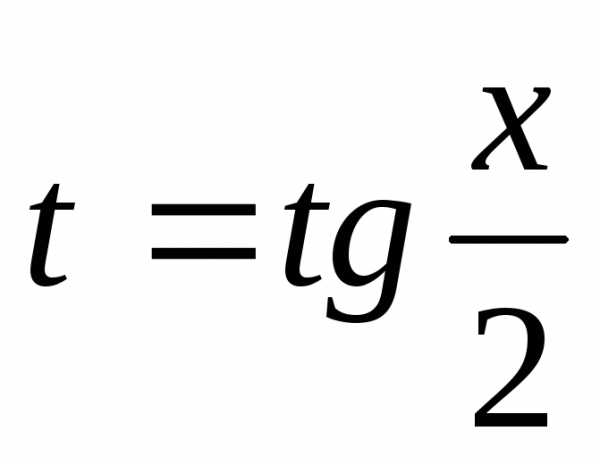 и
называется универсальной тригонометрической
подстановкой. Эта подстановка довольно
громоздкая.
и
называется универсальной тригонометрической
подстановкой. Эта подстановка довольно
громоздкая.
Действительно,
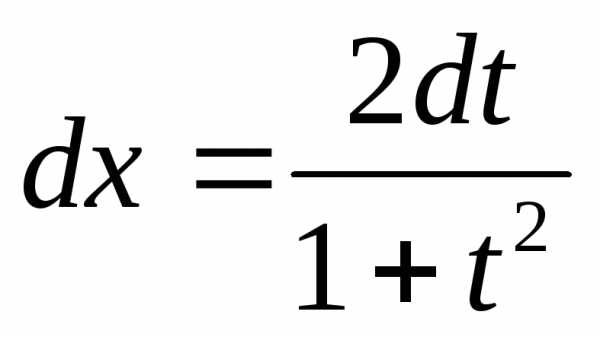
Воспользуемся формулами:
Тогда
т.к.
рациональная дробь от рациональной
дроби есть рациональная дробь, то-рационализируется.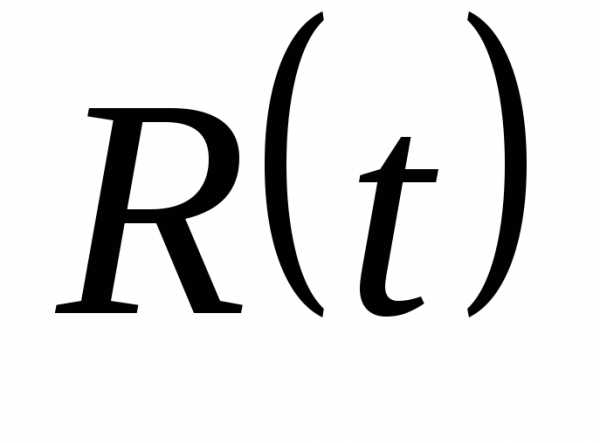 -рациональная
дробь.
-рациональная
дробь.
Интегрирование некоторых иррациональных функций интегралы от линейных иррациональностей, интегралы от дробно линейных иррациональностей (9).
1. Интегралы от линейных иррациональностей.
Рассмотрим интегралы вида:
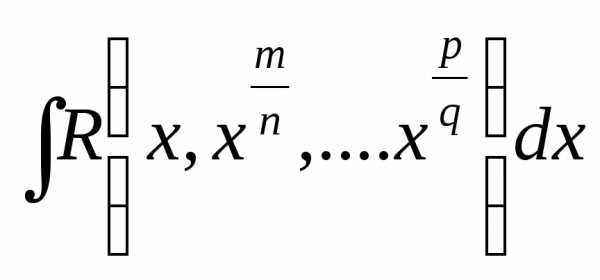 называются
интегралы от линейных иррациональностей,
где R-рациональные
дроби от своих аргументов,
называются
интегралы от линейных иррациональностей,
где R-рациональные
дроби от своих аргументов, 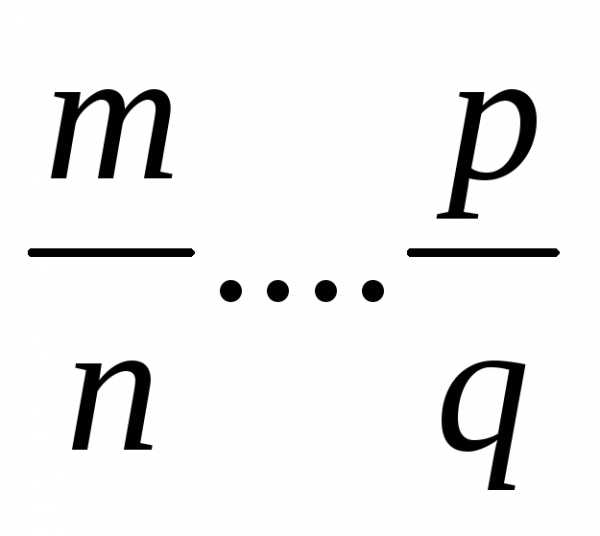 -несократимые
арифметические дроби.
-несократимые
арифметические дроби.
Такие
интегралы рационализируются подстановкой 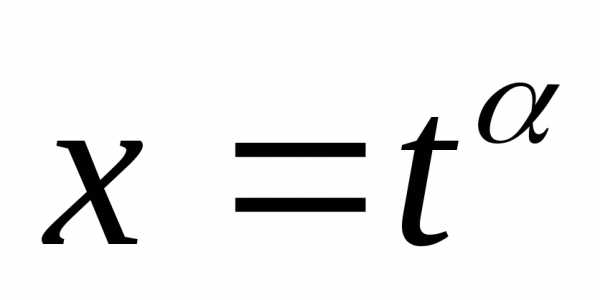 ,
где
,
где
,
где 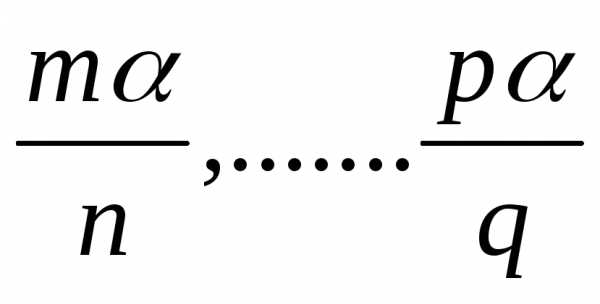 —
целые числа
—
целые числа
, т.е. рационализируется.
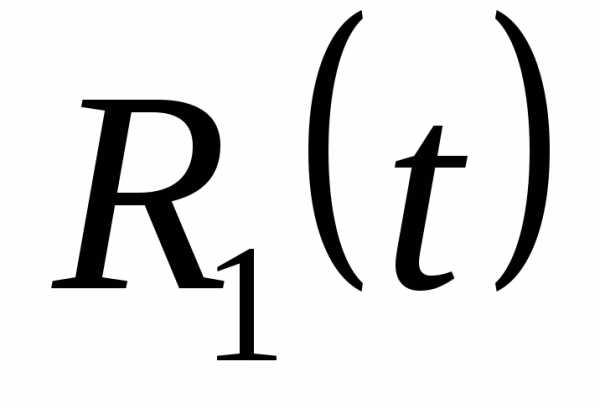 —
рациональная дробь.
—
рациональная дробь.
 Интегралы
от дробно линейных иррациональностей:
Интегралы
от дробно линейных иррациональностей:
Интегралы
вида:
называются интегралами от дробно
линейных иррациональностей, они
рационализируются подстановкой.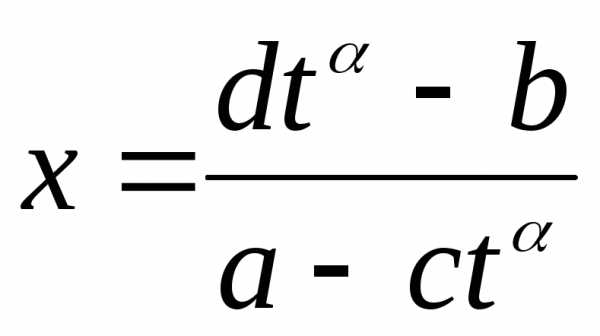
целые
числа, 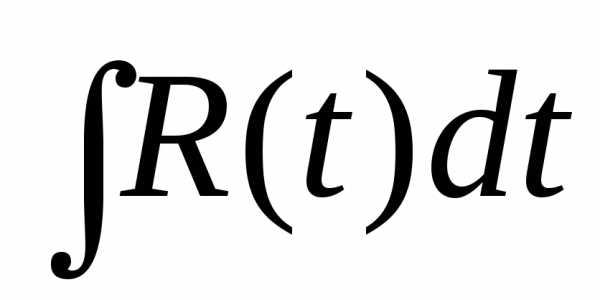 R—
рациональная дробь по t.
R—
рациональная дробь по t.
studfiles.net
Интегрирование рациональных дробей
ТЕМА: Интегрирование рациональных дробей.
Внимание! При изучении одного из основных приемов интегрирования: интегрирования рациональных дробей – требуется для проведения строгих доказательств рассматривать многочлены в комплексной области. Поэтому необходимо изучить предварительнонекоторые свойства комплексных чисел и операций над ними.
Интегрирование простейших рациональных дробей.
Если P(z) и Q(z) – многочлены в комплексной области, то — рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q.
Любую неправильную дробь можно представить в виде: ,
где
P(z) = Q(z) S(z) + R(z),
a R(z) – многочлен, степень которого меньше степени Q(z).
Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как является правильной дробью.
Определение 5. Простейшими (или элементарными) дробями называются дроби следующих видов:
1) , 2) , 3) , 4) .
Выясним, каким образом они интегрируются.
1)
2)
3) (изучен ранее).
Теорема 5. Всякую правильную дробь можно представить в виде суммы простейших дробей (без доказательства).
Следствие 1. Если — правильная рациональная дробь, и если среди корней многочлена будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа:
Пример 1.
Следствие 2. Если — правильная рациональная дробь, и если среди корней многочлена будут только кратные действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го и 2-го типов:
Пример 2.
Следствие 3. Если — правильная рациональная дробь, и если среди корней многочлена будут только простые комплексно — сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го типа:
Пример 3.
Следствие 4. Если — правильная рациональная дробь, и если среди корней многочлена будут только кратные комплексно — сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:
Пример 4.
Для определения неизвестных коэффициентов в приведенных разложениях поступают следующим образом. Левую и правую часть разложения , содержащего неизвестные коэффициенты, умножают на Получается равенство двух многочленов. Из него получают уравнения на искомые коэффициенты, используя, что:
1. равенство справедливо при любых значениях Х (метод частных значений). В этом случае получается сколько угодно уравнений, любые m из которых позволяют найти неизвестные коэффициенты.
2. совпадают коэффициенты при одинаковых степенях Х (метод неопределенных коэффициентов). В этом случае получается система m – уравнений с m – неизвестными, из которых находят неизвестные коэффициенты.
3. комбинированный метод.
Пример 5. Разложить дробь на простейшие.
Решение:
Найдем коэффициенты А и В.
1 способ — метод частных значений:
2 способ – метод неопределенных коэффициентов:
Ответ:
Интегрирование рациональных дробей.
Теорема 6. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.
Доказательство.
Представим рациональную дробь в виде: . При этом последнее слагаемое является правильной дробью, и по теореме 5 ее можно представить в виде линейной комбинации простейших дробей. Таким образом, интегрирование рациональной дроби сводится к интегрированию многочлена S(x) и простейших дробей, первообразные которых, как было показано, имеют вид, указанный в теореме.
Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.
Пример 1. Найти интеграл
Подынтегральная функция является правильной рациональной дробью. Разложение на неприводимые сомножители знаменателя имеет вид Это означает, что разложение подынтегральной функции в сумму простейших дробей имеет следующий вид:
Найдем коэффициенты разложения комбинированным методом:
Таким образом,
Пример 2. Найти интеграл
Подынтегральная функция – неправильная дробь, поэтому выделяем целую часть:
Первый из интегралов – табличный, а второй вычислим разложением правильной дроби на простейшие:
Имеем по методу неопределенных коэффициентов:
Таким образом,
studfiles.net
13.4. Интегрирование рациональных функций.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема: Если — правильная рациональная дробь, знаменательP(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x — a)…(x — b)(x2 + px + q)…(x2 + rx + s)), то эта дробь может быть разложена на элементарные по следующей схеме:
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
Т.к. (, то
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
Итого:
Пример.
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль.
Таким образом:
3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1).
Тогда:
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
Окончательно получаем:
=
Пример.
Найдем неопределенные коэффициенты:
Тогда значение заданного интеграла:
Лекция 14. Основные методы интегрирования (продолжение).
14.1. Интегрирование некоторых тригонометрических функций.
Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.
Интеграл вида .
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
,
Тогда
Таким образом:
Описанное выше преобразование называется универсальной тригонометрической подстановкой.
Пример.
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
Интеграл вида если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
Функция может содержатьcosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
Пример.
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл вида если
функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда
Пример.
Интеграл вида
функция R четная относительно sinx и cosx.
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Тогда
Пример.
Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
Пример.
Пример.
Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.
Пример.
Пример.
Иногда применяются некоторые нестандартные приемы.
Пример.
Итого
studfiles.net

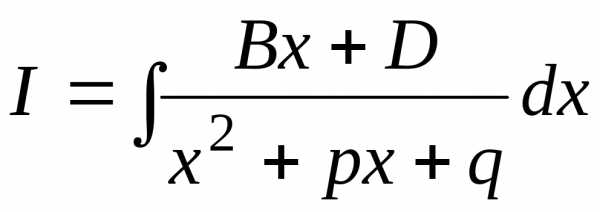 ,
где
,
где .
.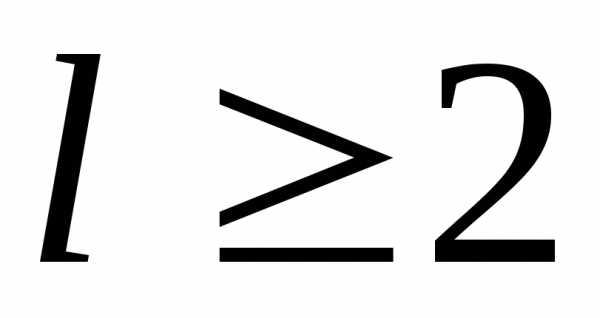 ,
,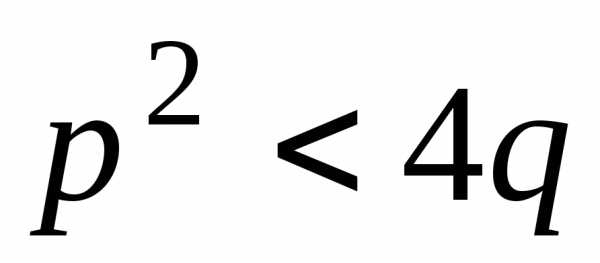 ,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.
,
непосредственное интегрирование
является столь громоздким, что следует
пользоваться справочником.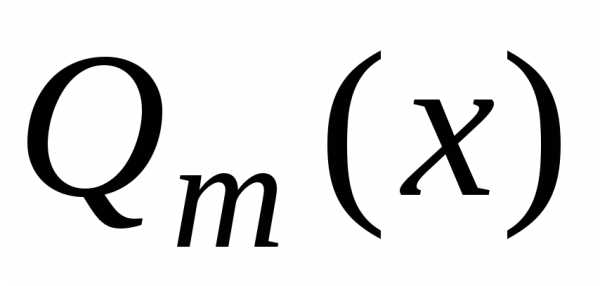 следует разложить на множители вида
следует разложить на множители вида